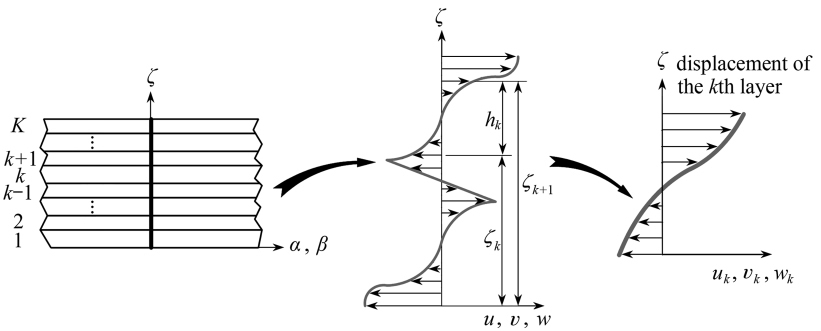
图1 层合结构位移场沿厚度方向的分布形式
Fig. 1 Distribution of the displacement field along the transverse direction of a laminated structure
ⓒ 应用数学和力学编委会,ISSN 1000-0887
常见的复合材料结构有弥散增强结构、单向增强结构、层合结构、三维整体复合结构、混杂结构等几大类.其中,层合结构由于其结构多样性较好、参数可设计性强、性价比优等特点应用最为广泛.如,燃气轮机叶片、客机蒙皮、船舶螺旋桨、水下潜航器耐压壳等[1-2].
在层合结构制造和使用过程中,涉及到复合材料工艺和设计,同时涉及到大量的振动计算分析问题.由于组成材料的各向异性及呈层性等特点,层合结构受载后的应力状态和振动行为往往十分复杂,在理论建模中通常对其进行单层等效.层合结构建模理论主要有:基于Kirchhoff-Love假设的经典等效单层理论、考虑了横向剪切变形和转动惯量的剪切变形理论、考虑层间锯齿效应的锯齿理论以及三维层合理论[3-13].经典等效单层理论和剪切变形理论都是传统的单一材料结构理论对层合结构的直接推广应用.这两种理论都是先在厚度方向上把层合结构等效成各向异性的单一薄层结构,然后用结构中面的位移或者应力分量描述结构整体的力学和振动行为.层合结构各铺层通常情况下具有各自独立的材料性质,这就导致了相邻两层间的密度、Poisson(泊松)比和弹性模量等材料参数不尽相同.由于结构变形时的位移和横向应力需要满足层间连续条件,使得这类结构振动时的位移沿厚度方向呈较明显的锯齿形变化(见图1).因此,当结构厚度比较大或者各层材料差异较为明显时,位移连续但是层间应力不连续的等效单层理论建模误差急剧增加.锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论.这类理论往往通过在面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件.但该理论一般不满足上下表面自由边界条件,也无法得到准确的层间应力.直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和前面提到的等效单层理论及锯齿理论最大的区别在于结构的每一子层都是用独立的函数来描述的三维实体.只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对于其他较为复杂的边界条件、铺层以及结构类型,只能借助数值方法或者其他近似解法来求解[14].

图1 层合结构位移场沿厚度方向的分布形式
Fig. 1 Distribution of the displacement field along the transverse direction of a laminated structure
现有的有限元商业软件也可以用于层合结构的二维或者三维振动问题求解.这类方法具有较强的适用性,应用范围也较为广泛,然而它们也存在着一定的局限性.例如,当结构层数非常多且各铺层材料性质差异较大时,为了能够精确描述结构的位移或者应力分布,需要在厚度方向划分足够多的单元.为了避免单元形状发生畸变,在结构面内方向必然需要大量的单元,从而导致计算速度降低以及需要大量存贮空间等问题[14].此外,结构的每一层都要单独划分网格,占用了大量的时间和精力,计算效率低,而且在参数分析中,结构各铺层的厚度和铺层方式一旦改变,整个结构都必须重新划分网格,计算结果继承性不强.
在复杂层合结构系统中,各结构单元的厚度、刚度、铺层方式等往往不尽相同,横向伸缩和剪切变形以及层间连续条件的影响也不尽相同.因此,若所有结构都采用三维理论进行建模势必会造成计算量过大,求解困难;而如果都采用二维简化理论进行求解,则精度过低,可能失去计算意义.因此,研究和建立具有较高建模精度和计算效率的理论和方法就具有重要的应用价值.基于上述考虑,本文提出了一种可以根据实际需求实现不同建模精度的层合结构高阶分层建模理论——基于改进Chebyshev级数的高阶分层(modified Chebyshev polynomial based high-order layerwise, MCPBHLW)理论.该理论位移场由线性位移场和高阶位移场两部分组成,线性位移场决定了实际位移的总体分布趋势,而高阶位移场对线性位移场进行局部修正.高阶位移场由具有统一表达式的改进Chebyshev级数表示,因而在实际编程应用中具有较好的灵活性,针对不同的建模精度需求,仅需通过改变高阶截断阶数来实现高阶位移场的配置而不需要逐一重新编程处理.下文详细推导了层合结构基于MCPBHLW理论和广义谱方法的自由振动特征方程,通过算例对MCPBHLW理论的计算精度进行了验证,研究了不同几何参数、边界条件、层合方式下层合梁、板、壳的自由振动特性.
考虑如图2所示的双曲层合壳体.假设该壳体由K层具有不同材料性质的铺层复合而成.以壳体底面为参考面,建立正交曲线坐标系O′αβζ.其中,α和β沿底面的主曲率线方向,ζ沿厚度方向;Rα和Rβ代表α和β方向的主曲率半径.以第k铺层为研究对象,假设其上下表面横向坐标分别为ζk+1和ζk;uk,vk和wk为壳体第k铺层上任意一点沿α,β和ζ方向的位移分量,hk=ζk+1-ζk为该层厚度.
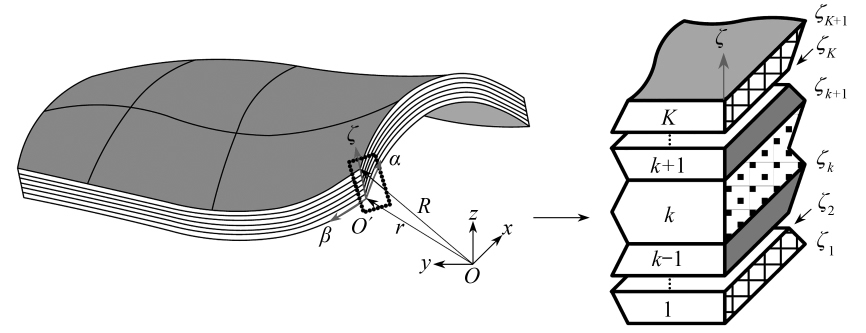
图2 双曲层合壳体几何模型及坐标系统
Fig. 2 Geometry and the curvilinear coordinate system for doubly curved laminated shells
基于MCPBHLW理论思想,层合结构任意第k铺层的初始位移场定义为如下形式:
(1)
其中,ubk,vbk,wbk,utk,vtk,wtk为线性位移场的面内分量;ujk,vjk,wjk为高阶位移场的面内分量;ψbk,ψtk为线性位移场的横向分量;ψjk为高阶位移场的横向分量;Jk为截断阶数.ψbk,ψtk,ψjk形式如下:
(2)
(3)
式中,Tj-1为第j-1阶Chebyshev级数,具体表达式为
(4)
由式(2)可知,改进的Chebyshev级数具有统一的表达式,这为MCPBHLW理论在实际工程中的编程和应用提供了极大便利,从而可以实现任意阶的建模精度.
将铺层上下表面横向坐标代入式(2),有
(5)
联合式(1)和(5)得
(6)
可以看出,线性位移场面内分量ubk,vbk,wbk实际上是铺层k下表面的位移场而utk,vtk,wtk为铺层上表面的位移场.这样假设的目的在于: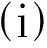 保证结构位移场沿厚度方向呈锯齿分布,为横向应力沿层间连续分布提供可能;
保证结构位移场沿厚度方向呈锯齿分布,为横向应力沿层间连续分布提供可能; 方便整体方程列式的组装.线性位移场面内分量ubk,vbk,wbk既是第k铺层下表面位移场,又是第k-1铺层上表面的位移场,从而在后续系统矩阵方程组装中仅需要将同一层间界面位移场对应的刚度和质量矩阵对应相加即可,保证了铺层之间的紧密连续.
方便整体方程列式的组装.线性位移场面内分量ubk,vbk,wbk既是第k铺层下表面位移场,又是第k-1铺层上表面的位移场,从而在后续系统矩阵方程组装中仅需要将同一层间界面位移场对应的刚度和质量矩阵对应相加即可,保证了铺层之间的紧密连续.
当层合壳体因振动产生微小位移时,壳体第k铺层上任意点的6个应变分量为
(7)
其中,εkα,εkβ,εkζ分别表示主应变,γkαβ,γkαζ,γkβζ为面内及横向剪切应变,Aα,Aβ和Aξ为Lamé常数[15].将式(1)代入式(7)得
(8)
其中,I为6×6单位矩阵,线性位移场和高阶位移场的应变分量分别为
(9)
因此,该子层上任意一点的应力状态可由Hooke(胡克)定律直接得到
(10)
其中,Ck为与材料本身属性有关的刚度系数矩阵,Tk为与铺层角有关的转换矩阵 [16].根据式(10),铺层k的应变能和动能方程可写为
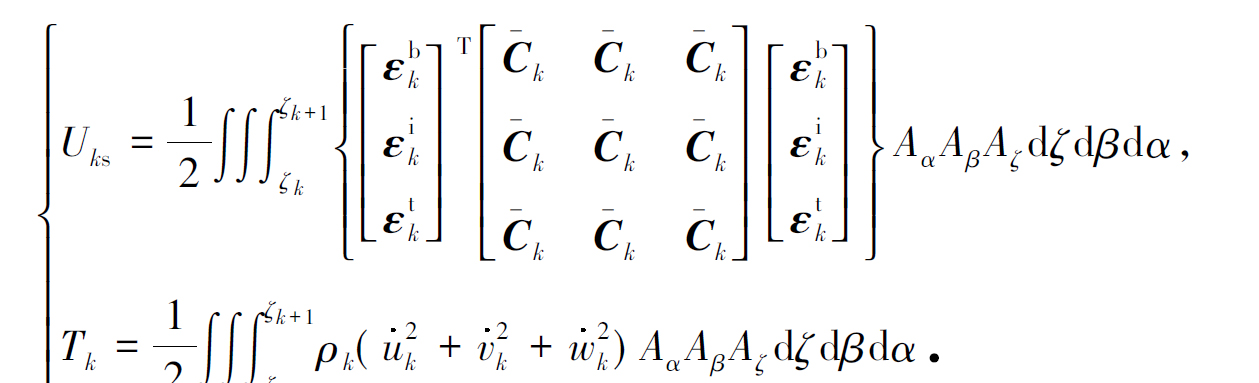
(11)
借助Hamilton(哈密尔顿)变分原理,式(11)可推导得到结构的振动控制微分方程,具体见文献[17].
假设该子层的边界条件为
(12)
其中l=0,1.
针对层合结构振动问题,由于结构几何形状、边界条件以及铺层方式的限制,绝大部分问题都无法得到精确解析解.基于MCPBHLW理论,本文结合传统谱方法和罚函数方法建立了适用于一般边界条件和铺层形式的层合壳体振动特性求解方法,具体推导过程见文献[18-20].与传统谱方法相比,该方法扩大基函数选取范围的同时在处理边界条件具有很好的灵活性.针对给定的边界条件,仅需要通过改变边界条件参数来完成边界条件的施加而不需要逐一重新编程处理.下面简要给出求解过程.
根据谱方法思想,位移场面内分量ξλk(ξ=u,v,w;λ=b,i,t)可表示为
(13)
其中,ξλmnk(ξ=u,v,w;λ=b,i,t)为谱展开系数,Tn,Tm分别为第n和m阶Chebyshev多项式. 引入Lagrange(拉格朗日)乘子法和罚函数法,一般边界约束下层合结构子层的边界约束方程可以写成如下泛函:
(14)
式中ηαlku,ηαlkv,ηαlkw,ηβlku,ηβlkv,ηβlkw为边界条件系数;kαlku,kαlkv,kαlkw,kβlku,kβlkv,kβlkw为罚函数.以一般多层复合壳体结构为例,不同边界条件取值如表1所示.Πklm由Lagrange乘子法引入,用于放松边界约束条件;Πkp由罚函数法引入,一方面用于保证计算的收敛性和稳定性,另一方面用于处理弹性边界条件[21-22].
表1 不同边界条件下边界系数取值情况(α=αl边为例)
Table 1 Boundary coefficients for various classical boundaries (at the end ofα=αl)
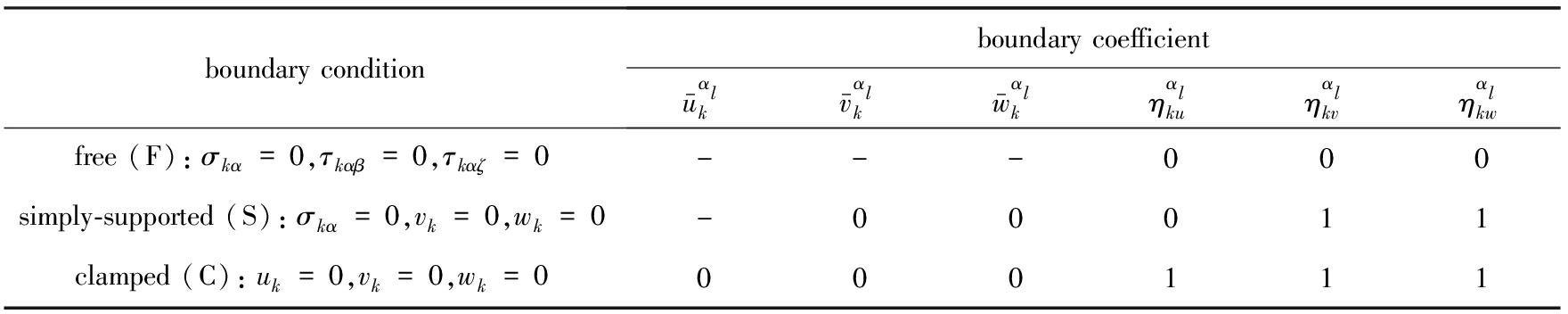
boundary conditionboundary coefficientu-αlkv-αlkw-αlkηαlkuηαlkvηαlkwfree (F):σkα=0,τkαβ=0,τkαζ=0---000simply-supported (S):σkα=0,vk=0,wk=0-00011clamped (C):uk=0,vk=0,wk=0000111
因此,子层k的自由振动能量泛函可以写为
(15)
令泛函Πktotal对位移面内分量谱的展开系数的变分为0,即
(16)
从而得到铺层的系统方程为
(17)
其中
(18)
因此,根据界面连续条件,仅需要将同一层间界面位移场对应的刚度和质量矩阵对应相加即可得到结构的系统方程矩阵:
(19)
其中

 ⋮⋮⋮⋮⋮⋱,
⋮⋮⋮⋮⋮⋱,(20)

 ⋮⋮⋮⋮⋮⋱.
⋮⋮⋮⋮⋮⋱.(21)
在求解自由振动问题中,方程(17)实质上描述了一个标准的特征方程,通过求解该特征方程,便能获得结构固有频率和特征向量.将特征向量代入位移场面内分量延展式,再代入初始位移场即可得到结构模态振型.对于位移和应力分布等静力学计算,只需先将外力功加到式(15),然后将式(19)方程右端替换为求得的外力功向量,即可求得任意载荷下层合结构空间上任意位置的位移及应力分布情况.
下文通过层合梁(长L,厚h)、板(长a,宽b,厚h)和圆柱壳(长L,内径R,厚h)自由振动特性计算算例来检验MCPBHLW理论的计算精度及前文理论推导的正确性.为了描述方便,采用字母F、S、C来分别代表自由、简支及固支等经典边界条件.同时,以逆时针顺序对结构的边界条件进行标记.以层合板为例,C-F-S-S表示板的x=x0,y=y0,x=x1和y=y1边的边界条件分别为固支、自由、简支、简支.层合梁和圆柱壳结构依此类推.
首先,以层合梁的二维弹性精确解析解 [23]为基准,验证MCPBHLW理论的计算精度.表2给出了两端简支[0°/90°]层合梁基于MCPBHLW理论得到的前5阶频率参数Ω=ωL2×ρ/(E3h2)与精确解的对比情况.层合梁各子层厚度均等,组成材料参数相同,为:E3=10 GPa,E1=25E3,ν13=0.25,G13=5 GPa,ρ=1 389 kg/m3.计算中分别考虑了中厚度比h/L=0.1和大厚度比h/L=0.2两种情况.可以看出,MCPBHLW理论具有良好的收敛特性和计算精度,高阶位移场截断阶数取Jk=4时的计算结果与精确解完全吻合.此外,在大厚度比情况下,即使仅考虑线性位移场(Jk=0),MCPBHLW理论的建模偏差也不超过8%.
表2 两端简支[0°/90°]层合梁前5阶无量纲频率参数Ω=ωL2ρ/(E3h2)
Table 2 The 1st 5 frequency parametersΩ for S-S supported, [0°/90°] laminated beams
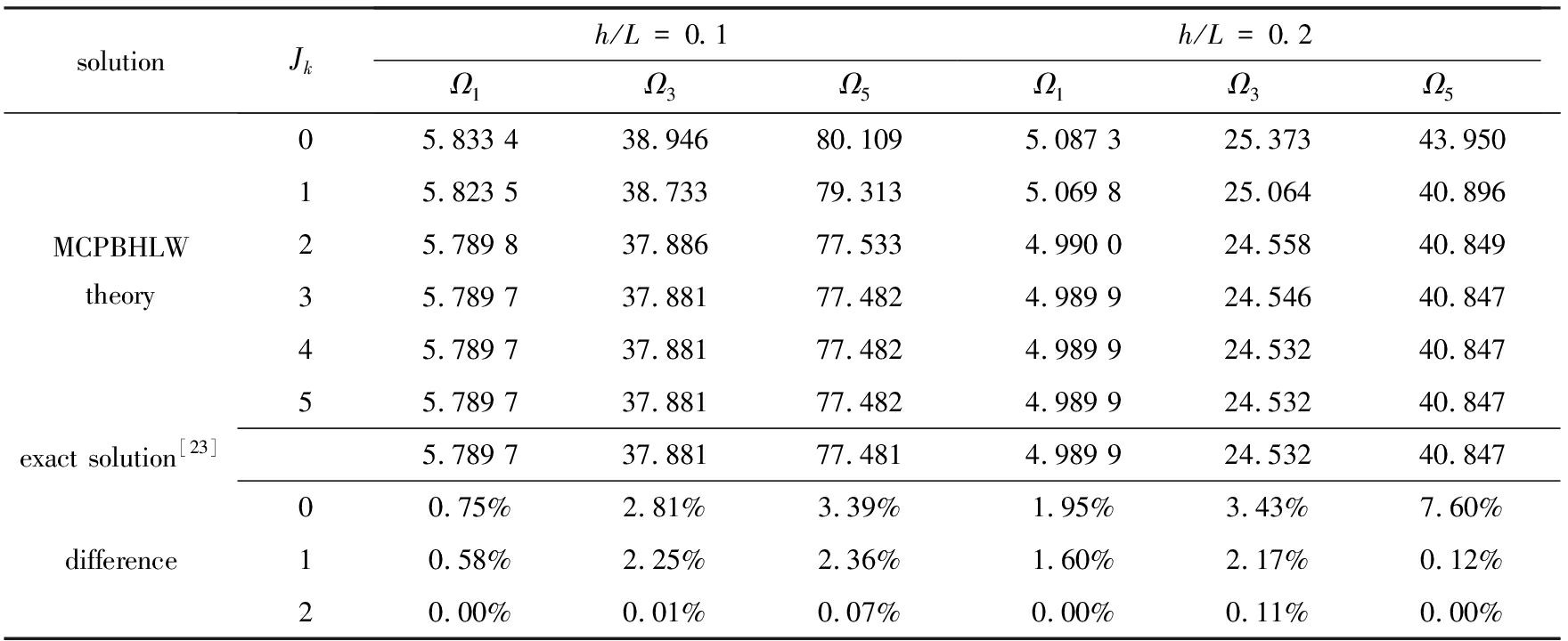
solutionJkh/L=0.1Ω1Ω3Ω5h/L=0.2Ω1Ω3Ω5MCPBHLWtheory05.833 438.94680.1095.087 325.37343.95015.823 538.73379.3135.069 825.06440.89625.789 837.88677.5334.990 024.55840.84935.789 737.88177.4824.989 924.54640.84745.789 737.88177.4824.989 924.53240.84755.789 737.88177.4824.989 924.53240.847exact solution[23]5.789 737.88177.4814.989 924.53240.847difference00.75%2.81%3.39%1.95%3.43%7.60%10.58%2.25%2.36%1.60%2.17%0.12%20.00%0.01%0.07%0.00%0.11%0.00%
图3给出了不同厚长比和边界条件下,[0°/90°]层合梁基于MCPBHLW理论计算得到的前3阶频率参数Ω=ωL2ρ/(E3h2)与经典等效梁理论(CBT)解、一阶剪切变形层合梁理论(FSDT)解的对比情况(CBT和FSDT解采用文献[24]所述方法求得).层合梁各子层厚度均等,组成材料参数与表2算例所用一致.图中考虑了Jk =0,1,2,3,4共5种高阶位移场模式的计算结果.可以看出,对于各层材料参数差异不大的一般层合梁,FSDT可以给出较好的低阶振动频率,而忽略了横向剪切变形的CBT建模精度较低.
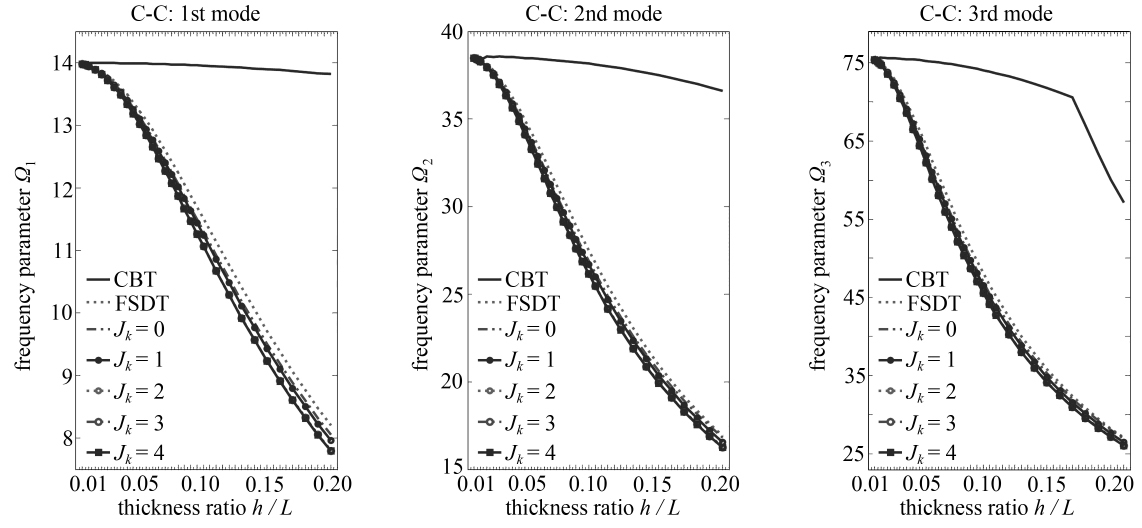
图3 不同边界条件下[0°/90°]层合梁基于不同理论的计算结果随厚长比的变化情况
Fig. 3 Frequency parameters for [0°/90°] laminated beams of various
thickness-to-length ratios and boundary conditions
图4给出了不同厚长比条件下,两端简支软芯夹层梁基于CBT、FSDT和MCPBHLW理论计算得到的前3阶无量纲频率参数Ω=ωL2ρface/(Eface3h2)与二维弹性精确解析解[23]的对比情况.夹层梁的表层为金属铝(E=70.23 GPa,ν=0.33,ρ=2 820 kg/m3),芯体为橡胶材料(E=2.684 416 MPa,ν=0.498,ρ=999 kg/m3),表层和芯体的厚度比取为hf/hc=1/8.图中考虑了Jf-Jc-Jf=0-0-0,0-1-0,0-2-0,0-3-0,0-4-0,1-4-1共6种高阶位移场模式.可以看出,基于MCPBHLW理论的计算结果与精确解十分吻合.而基于CBT及FSDT的计算结果相对于精确解的偏差较大,即使是厚长比仅为0.01,这两种等效单层理论的计算偏差也达到了100%以上.这说明MCPBHLW理论具有良好的计算精度,也一定程度上证明了等效单层理论确实不适合用于像软芯夹层梁这类各层材料性质差异较为明显的层合结构的建模计算.
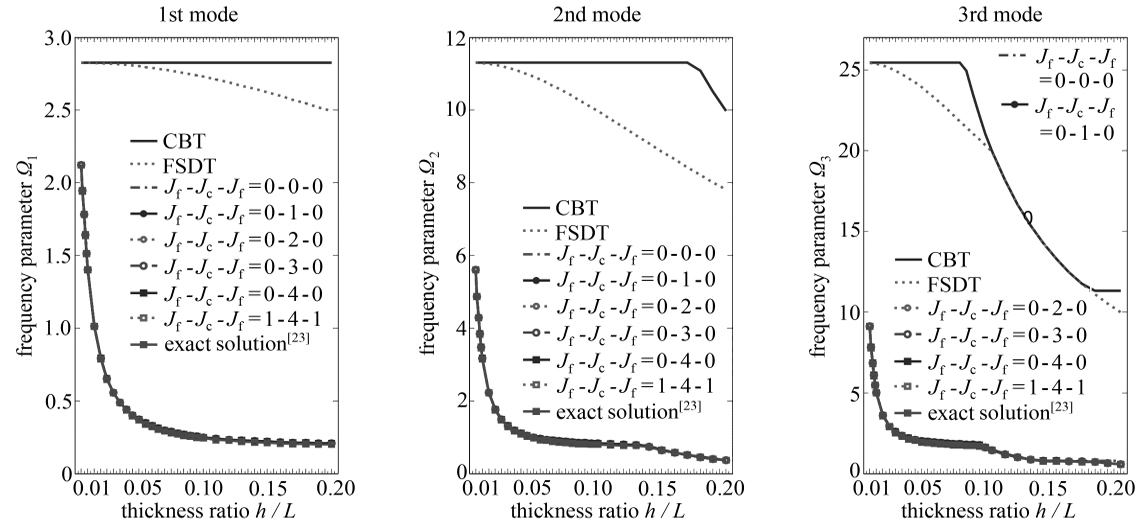
图4 两端简支[Al/橡胶/Al]软芯夹层梁基于不同理论的计算结果随厚长比的变化情况
Fig. 4 Frequency parameters for S-S supported, [Al/rubber/Al] laminated beams
of various thickness-to-length ratios
下面以层合板为例,进一步考察MCPBHLW理论的建模精度和效率.
表3给出了在横向面载荷作用下四边简支[0°/90°/0°]层合板基于MCPBHLW理论得到的位移和应力计算结果与Pagano报告的三维精确解 [25]的对比情况.层合板的材料参数和几何参数分别为:ET= 106 Pa,EL/ET=25,GLT=0.5ET,GTT=0.2ET,νLT=νTT=0.25;b/a=3,h/a=0.5.横向面载荷形式如下:p(α,β,ζ=h)=p0sin(πα/a)sin(πβ/b).为了便于对比验证,表3中考虑了下列位移和应力参数:
(22)
(23a)
(23b)
从表3中可知,基于MCPBHLW理论计算的位移和应力分布在Jk=5时达到收敛状态,与精确解非常接近,高阶位移场取Jk=2与Jk=5的最大计算偏差小于3.7%,这说明该理论具有良好的收敛性质和建模精度.
为了进一步验证MCPBHLW理论在预测层间应力方面的准确性,图5、6分别给出了α=a/4,β=b/4和α=3a/4,β=3b/4处的位移和应力沿厚度的分布情况.可以看出,高阶位移场取Jk=2和Jk=6时计算得到的位移和应力分布曲线基本重合,且在层间界面处连续.表3和图5、6的结果说明了MCPBHLW理论能够给出较精确的层间应力.
表3 四边简支[0°/90°/0°]层合板在横向面载荷作用下的位移和应力分布情况
Table 3 Displacement and stress distributions of a [0°/90°/0°] laminated plate
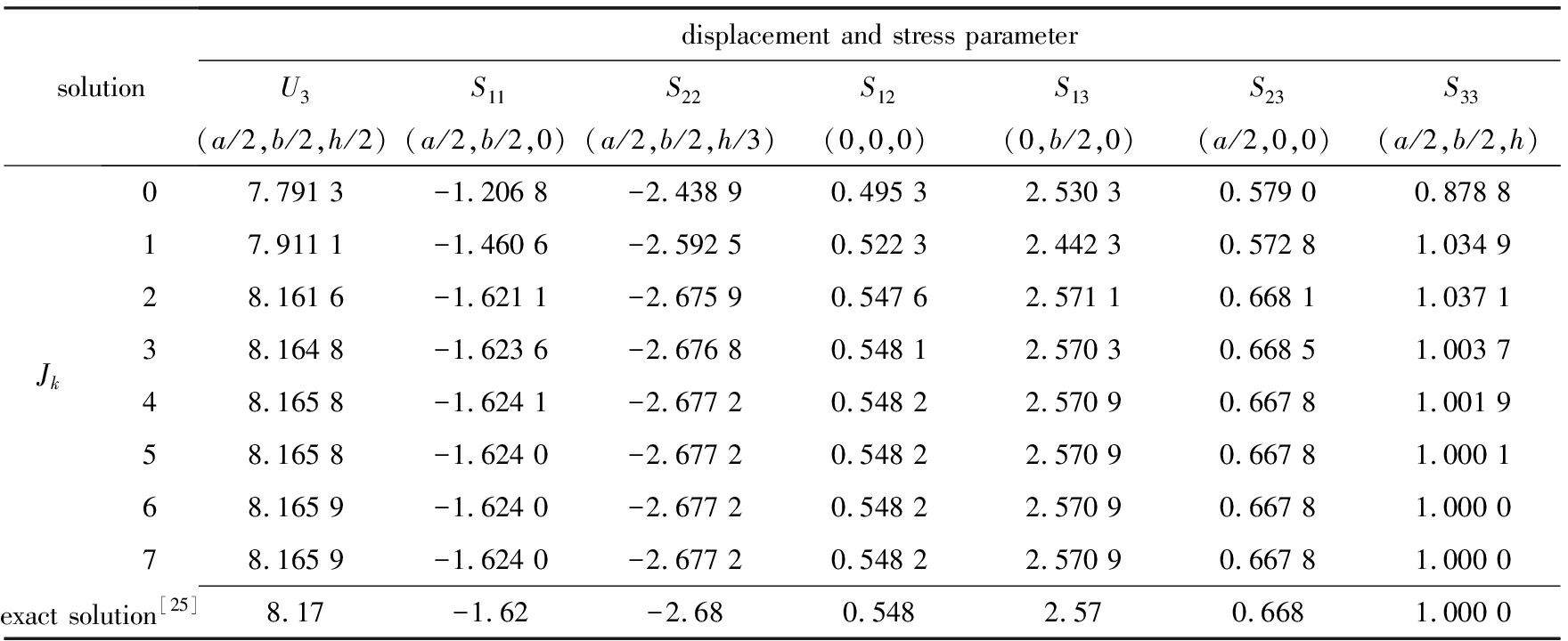
solutiondisplacement and stress parameterU3(a/2,b/2,h/2)S11(a/2,b/2,0)S22(a/2,b/2,h/3)S12(0,0,0)S13(0,b/2,0)S23(a/2,0,0)S33(a/2,b/2,h)Jk07.791 3-1.206 8-2.438 90.495 32.530 30.579 00.878 817.911 1-1.460 6-2.592 50.522 32.442 30.572 81.034 928.161 6-1.621 1-2.675 90.547 62.571 10.668 11.037 138.164 8-1.623 6-2.676 80.548 12.570 30.668 51.003 748.165 8-1.624 1-2.677 20.548 22.570 90.667 81.001 958.165 8-1.624 0-2.677 20.548 22.570 90.667 81.000 168.165 9-1.624 0-2.677 20.548 22.570 90.667 81.000 078.165 9-1.624 0-2.677 20.548 22.570 90.667 81.000 0exact solution[25]8.17-1.62-2.680.5482.570.6681.000 0
表4给出了不同边界条件下,基于MCPBHLW理论计算的[0°/90°]2和[0°/90°]4层合板的无量纲基频Ω=ωhρ/E2与文献[26-27]计算结果的对比情况.文献[26]采用的是基于三维弹性理论的区域分解法,文献[27]采用的是基于三维弹性理论的状态空间-微分求积混合法.层合板的材料参数和几何参数分别为:E1/E2=10或40,E2=E3=2 GPa,G12=G13=0.6E2,G23=0.5E2,ν12=ν13=0.25,ν23=0.49,ρ=1 450 kg/m3;a=b=1,h/a=0.1.可以看出,基于MCPBHLW理论的计算结果与文献[26]给出的数据对比良好,而文献[27]计算结果往往比本文及文献[26]略高.这是由于文献[27]采用了近似边界处理手段,不同方法之间计算精度有所差异.
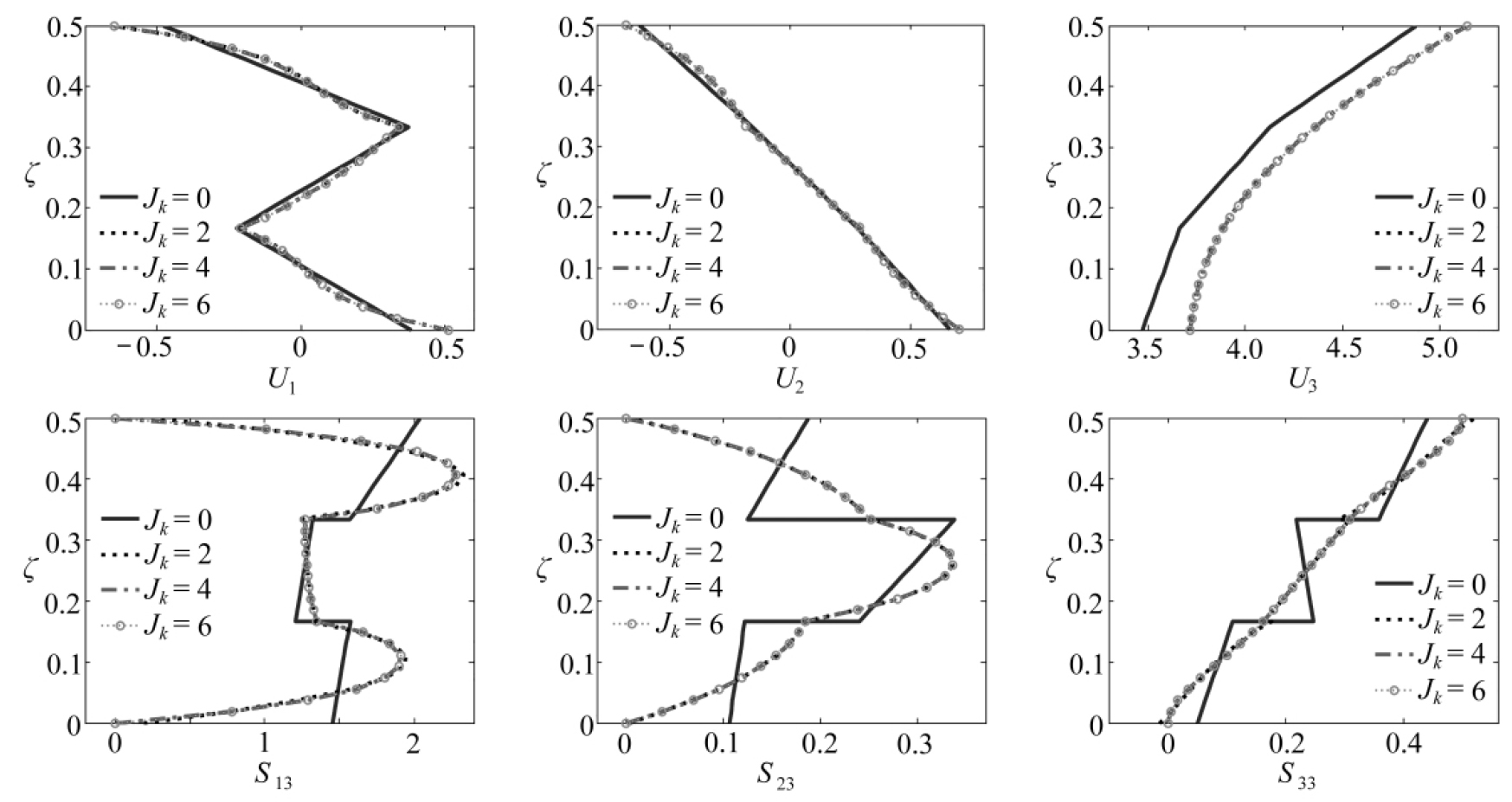
图5 横向面载荷下,四边简支[0°/90°/0°]层合板在α=a/4,β=b/4处的位移和应力分布情况
Fig. 5 Displacement and stress distributions of a [0°/90°/0°] laminated plate forα=a/4,β=b/4
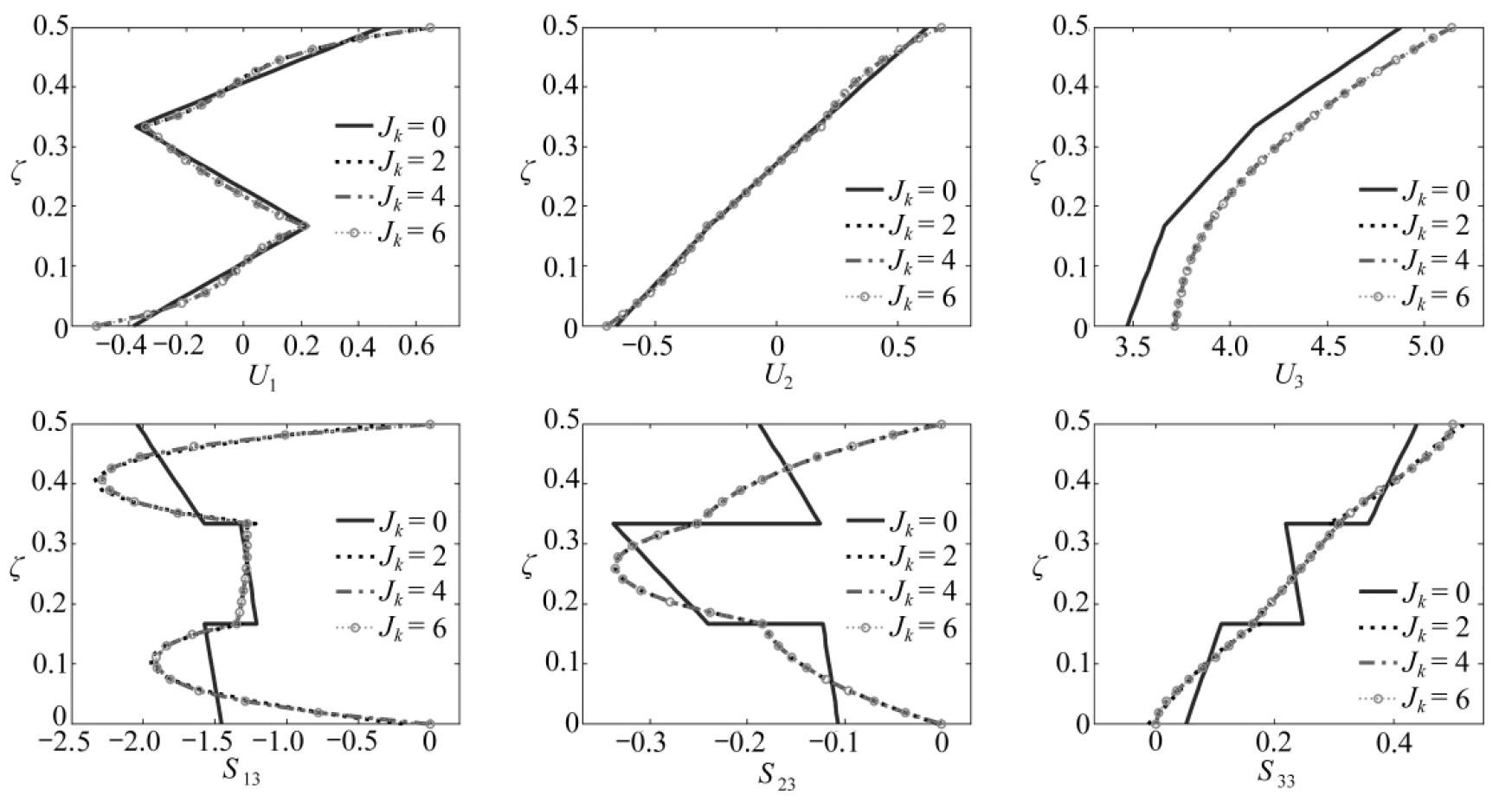
图6 横向面载荷下,四边简支[0°/90°/0°]层合板在α=3a/4,β=3b/4处的位移和应力分布情况
Fig. 6 Displacement and stress distributions of a [0°/90°/0°] laminated plate forα=3a/4,β=3b/4
表5给出了四边简支边界条件下,基于MCPBHLW理论计算的[0°/90°]层合板的无量纲基频Ω=ωhρ/E2与经典等效单层板理论(CPT)解[28]、FSDT解[28]、三维弹性理论解[26]及Reddy分层理论解(LWPT)[29]的对比情况.层合板的各层材料参数与表3算例所用一致(E1/E2= 40),几何参数为a=b=1.可以看出,不同理论之间计算精度有所差异.其中,MCPBHLW理论解与三维弹性理论解[26]及Reddy分层理论解[29]对比良好.此外,对于各层材料参数差异不大的一般层合板,FSDT可以给出较好的低阶振动频率.
表4 不同边界条件下[0°/90°]2和[0°/90°]4层合板无量纲基频Ω=ωhρ/E2
Table 4 Fundamental frequency parametersΩ of [0°/90°]2 and [0°/90°]4 laminated plates
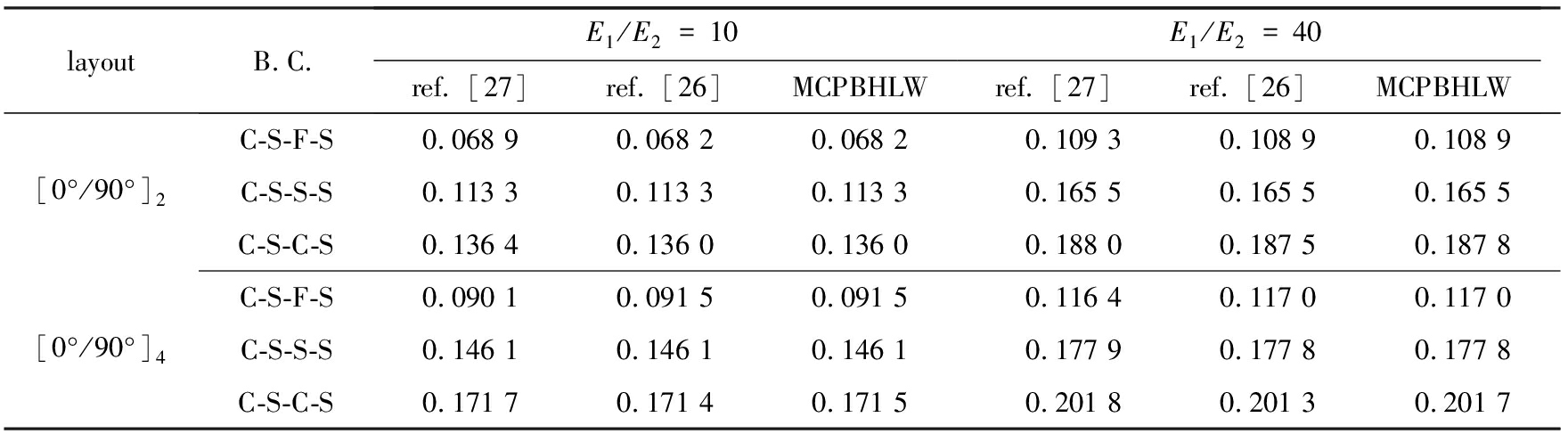
layoutB.C.E1/E2=10ref. [27]ref. [26]MCPBHLWE1/E2=40ref. [27]ref. [26]MCPBHLW[0°/90°]2C-S-F-S0.068 90.068 20.068 20.109 30.108 90.108 9C-S-S-S0.113 30.113 30.113 30.165 50.165 50.165 5C-S-C-S0.136 40.136 00.136 00.188 00.187 50.187 8[0°/90°]4C-S-F-S0.090 10.091 50.091 50.116 40.117 00.117 0C-S-S-S0.146 10.146 10.146 10.177 90.177 80.177 8C-S-C-S0.171 70.171 40.171 50.201 80.201 30.201 7
表5 四边简支[0°/90°]层合板无量纲基频Ω=ωhρ/E2
Table 5 Fundamental frequency parametersΩ of simply-supported [0°/90°] laminated plates
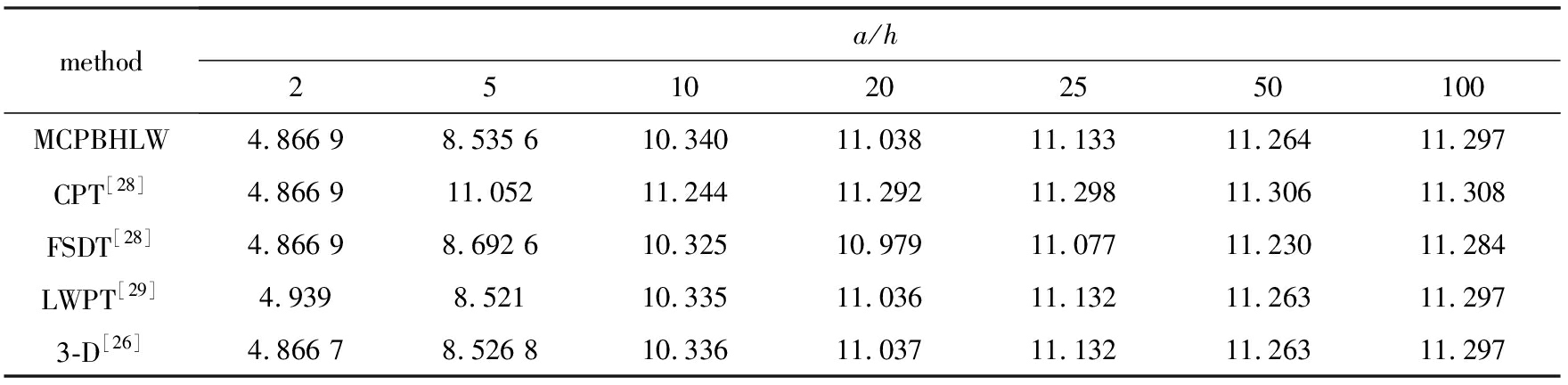
methoda/h2510202550100MCPBHLW4.866 98.535 610.34011.03811.13311.26411.297CPT[28]4.866 911.05211.24411.29211.29811.30611.308FSDT[28]4.866 98.692 610.32510.97911.07711.23011.284LWPT[29]4.9398.52110.33511.03611.13211.26311.2973-D[26]4.866 78.526 810.33611.03711.13211.26311.297
图7给出了不同厚长比下,四边自由[0°/90°]层合方板基于CPT、FSDT和MCPBHLW理论得到的第1、3、5阶固有频率的对比情况(CPT和FSDT解依据文献[28]方法求得).层合方板材料参数与表5算例所用一致.可以看出,对于各层材料参数差异不大的一般层合板,FSDT可以给出较好的低阶振动频率,而CPT建模精度较低.
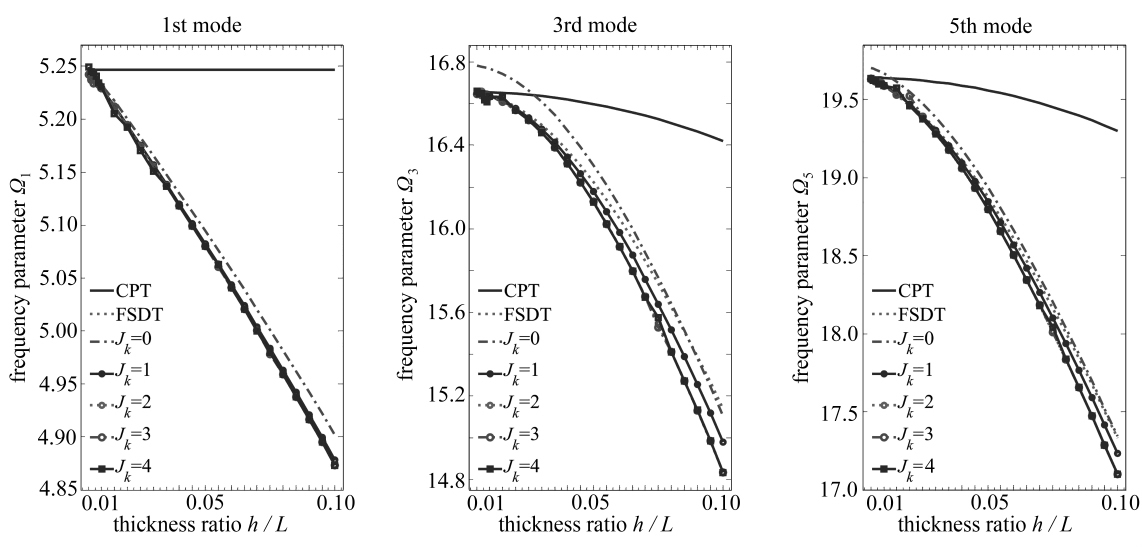
图7 四边自由[0°/90°]层合方板基于不同理论的计算结果随厚长比的变化情况
Fig. 7Fundamental, 3rd and 5th frequency parametersΩ for the [0°/90°] laminated plate of various thickness-to-length ratios and F-F-F-F boundary conditions
表6给出了高阶位移场配置变化时,四边固支[Al/橡胶/Al]软芯夹层板的前24阶固有频率(Hz)的收敛情况.夹层板表层和芯层的材料参数与图4算例所用一致,几何参数为:hf/hc=1/8,a=b=1 m,h/a=0.05.可以看出,MCPBHLW理论具有良好的建模精度和效率.其中,仅考虑线性位移场(Jf-Jc-Jf=0-0-0)的计算结果相对于截断阶数为“Jf-Jc-Jf=3-5-3”的计算结果之间的最大偏差约为10%.此外还可以看出,CPT和FSDT相对于MCPBHLW理论计算结果的偏差较大.
表6 四边固支[Al/橡胶/Al]软芯夹层板的前24阶固有频率(单位: Hz)
Table 6 The 1st 24 natural frequencies for [Al/rubber/Al] sandwich plates of C-C-C-C boundary conditions(unit: Hz)

Jf-Jc-Jfnatural frequencyf1f2f3f4f21f22f23f240-0-037.29371.16571.165102.07351.56351.56391.22391.220-1-037.18370.94270.942101.75350.98350.98375.89377.730-2-037.17970.93170.931101.74350.68350.68373.40373.400-3-037.17870.93170.931101.73350.35350.35371.18371.180-4-037.17870.92870.928101.73350.34350.34371.12371.120-5-037.17870.92870.928101.73350.34350.34371.12371.121-5-134.79165.72765.72793.836319.98319.98354.90354.902-5-234.78965.72165.72193.825319.90319.90354.81354.813-5-334.78365.70765.70793.803319.83319.83354.77354.77CPT440.79899.02899.021 325.63 629.93 629.93 644.53 783.8FSDT413.92808.56808.561 151.22 847.23 077.33 077.33 183.1
图8给出了不同厚长比条件下,四边自由[Al/橡胶/Al]软芯夹层方板基于CPT、FSDT和MCPBHLW理论得到的第1、5、10阶固有频率的对比情况.夹层板各层材料参数与表6算例所用一致.对比图4和图8可知,基于连续位移假设的等效单层理论的建模精度较低.
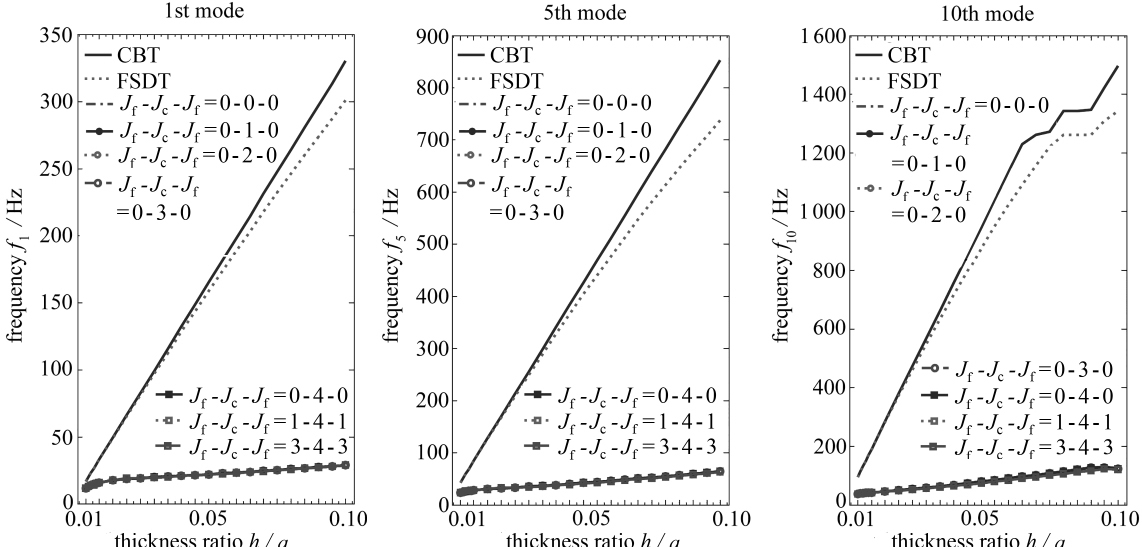
图8 四边自由[Al/橡胶/Al]软芯夹层板基于不同理论的计算结果随厚长比的变化情况
Fig. 8 Fundamental, 5th and 10th frequencies for [Al/rubber/Al] sandwich plates of
various thickness-to-length ratios and F-F-F-F boundary conditions
表7给出了不同厚长比和边界条件下,[0°/90°/0°]层合方板前5阶频率参数Ω=ωa2×ρ/(E2h2).层合板各铺层厚度均等且材料参数相同,为:E2=E3=10 GPa,E1=15E2,G12=G13=0.6E2,G23=0.5E2,ν12=ν13=ν23=0.25,ρ=1 450 kg/m3.可以看出,层合板的频率随着厚长比的增加而增加.这是因为层合板厚度增加时,其刚度与质量之比相应增加.但当厚度接近面内最小尺寸时,结构的各阶模态将发生变化,这一规律不再适用.此外,随着边界约束增强,层合板频率参数也相应增大.
表7 不同厚长比下[0°/90°/0°]层合方板前5阶频率参数Ω=ωa2ρ/(E2h2)
Table 7 Frequency parametersΩ for [0°/90°/0°] layered plates of various thickness ratios
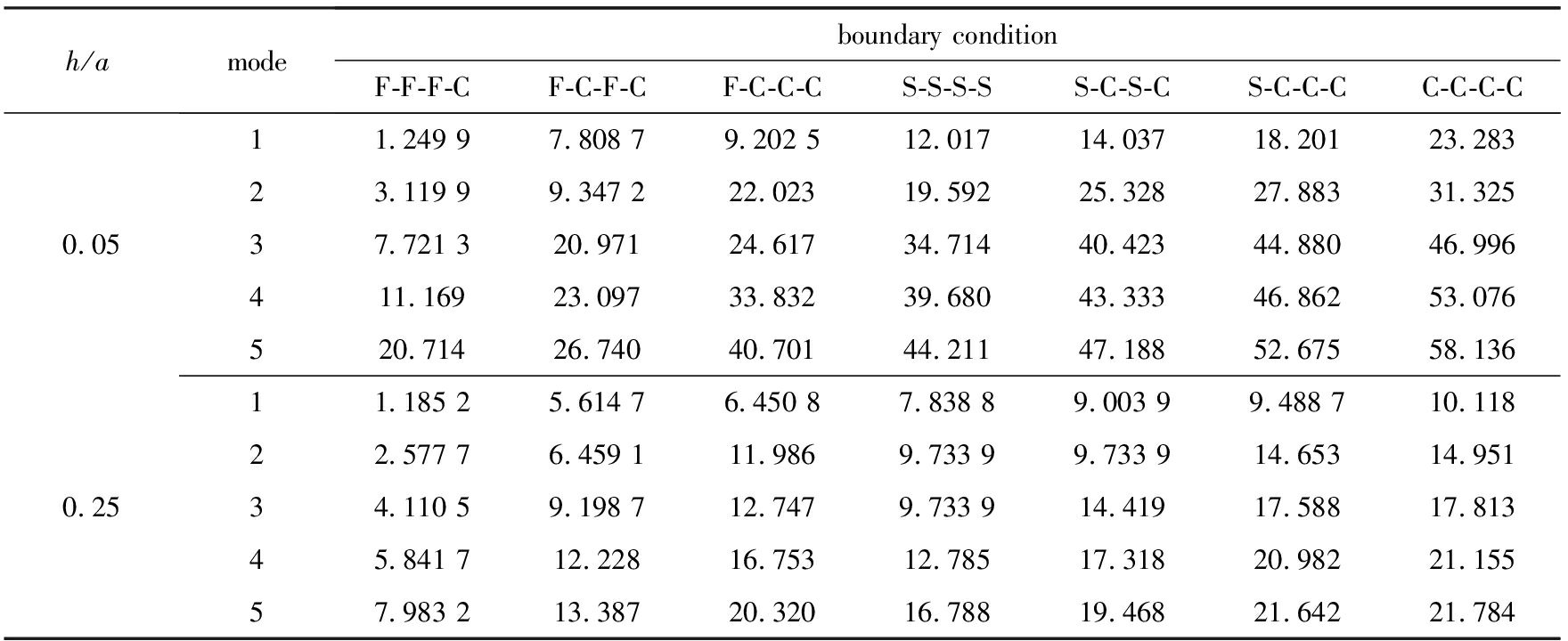
h/amodeboundary conditionF-F-F-CF-C-F-CF-C-C-CS-S-S-SS-C-S-CS-C-C-CC-C-C-C0.0511.249 97.808 79.202 512.01714.03718.20123.28323.119 99.347 222.02319.59225.32827.88331.32537.721 320.97124.61734.71440.42344.88046.996411.16923.09733.83239.68043.33346.86253.076520.71426.74040.70144.21147.18852.67558.1360.2511.185 25.614 76.450 87.838 89.003 99.488 710.11822.577 76.459 111.9869.733 99.733 914.65314.95134.110 59.198 712.7479.733 914.41917.58817.81345.841 712.22816.75312.78517.31820.98221.15557.983 213.38720.32016.78819.46821.64221.784

图9 [0°/90°/0°]层合板C-F-C-F边界条件下的振动频率和模态振型
Fig. 9 Frequency parameters and mode shapes for [0°/90°/0°] layered plates
with C-F-C-F restraints and various dimensions
图9给出了[0°/90°/0°]层合板C-F-C-F边界条件下的频率参数和模态振型.层合板材料参数与表7所用相同,厚长比为h/a=0.1.对比b/a=1,0.5时层合板的第一阶模态振型和频率可以发现,结构y方向尺寸改变引起的结构刚度的改变对某些阶数模态刚度的影响很小,频率参数不变.
最后以层合圆柱壳为例,验证MCPBHLW理论的计算精度.
表8给出了不同边界条件和周向波数下,本文计算得到的软芯夹层圆柱壳结构的第一阶固有频率与文献[30]的对比情况.该圆柱壳表层为金属铝, 夹层为蜂窝材料, 各层的材料参数[E1,E2,E3,ν12,ν13,ν23,G12,G13,G23,ρ]为: face-[70.23 GPa, 70.23 GPa, 70.23 GPa, 0.33, 0.33, 0.33, 26.4 GPa, 26.4 GPa, 26.4 GPa, 2 820 kg/m3], core-[6.89 MPa, 6.89 MPa, 6.89 MPa, 0, 0, 0, 3.45 MPa, 3.45 MPa, 3.45 MPa, 97 kg/m3].各层的厚度比为hface∶hcore=1∶8.圆柱壳的几何参数取:R=0.9 m,L=1 m,h=0.1 m.文献[30]采用的是基于三维弹性理论的区域分解法.可以看出,本文方法具有良好的计算精度,两组解之间的最大误差不超过0.66%.
表8 不同边界条件和周向波数下软芯夹层圆柱壳第一阶固有频率(单位: Hz)
Table 8 The 1st frequencies of sandwich cylindrical shells of various thickness ratios and circumferential wave numbers(unit: Hz)
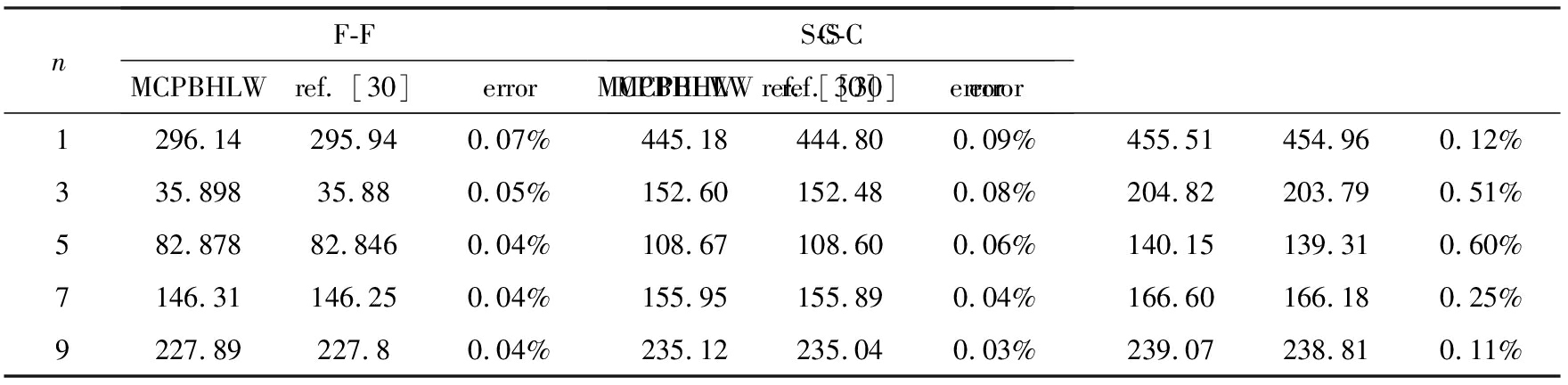
nF-FMCPBHLWref. [30]errorS-SMCPBHLWref. [30]errorC-CMCPBHLWref. [30]error1296.14295.940.07%445.18444.800.09%455.51454.960.12%335.89835.880.05%152.60152.480.08%204.82203.790.51%582.87882.8460.04%108.67108.600.06%140.15139.310.60%7146.31146.250.04%155.95155.890.04%166.60166.180.25%9227.89227.80.04%235.12235.040.03%239.07238.810.11%
表9给出了不同铺层角、周向波数及边界条件下[0°/ϑ/0°]层合圆柱壳的第一阶频率参数Ω=ωL2ρ/(E2h2).各子层厚度均等,材料参数相同,取:E2=E3=10 GPa,E1=15E2,G12=G13=0.6E2,G23=0.5E2,ν12=ν13=ν23=0.25,ρ=1 450 kg/m3.壳体几何尺寸如下:R=1,L/R=2,h/L=0.1.可以看出,周向波数为n=1时,F-F边界条件下的频率参数比F-S、F-C、S-S、S-C高.这是由于在F-F边界条件下,壳体前两阶模态为刚体运动模态,频率为0,表中忽略了刚体模态频率.一般来说,边界约束越强,结构刚度越大,对应阶数的频率越高.
表9 不同周向波数及边界条件下[0°/ϑ/0°]层合圆柱壳的第一阶频率参数Ω=ωL2ρ/(E2h2)
Table 9 Frequency parametersΩ for [0°/ϑ/0°] layered cylindrical shells of various boundary conditions and circumferential wave numbers
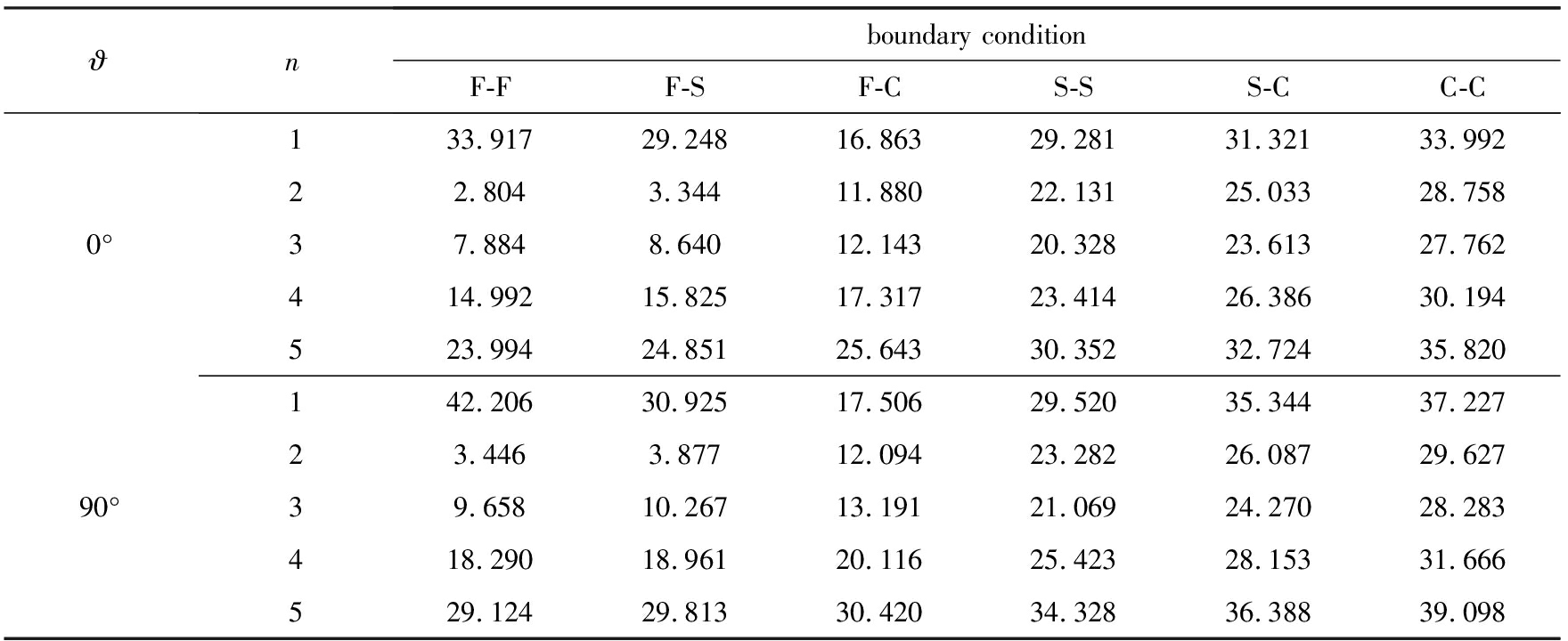
ϑnboundary conditionF-FF-SF-CS-SS-CC-C0°133.91729.24816.86329.28131.32133.99222.8043.34411.88022.13125.03328.75837.8848.64012.14320.32823.61327.762414.99215.82517.31723.41426.38630.194523.99424.85125.64330.35232.72435.82090°142.20630.92517.50629.52035.34437.22723.4463.87712.09423.28226.08729.62739.65810.26713.19121.06924.27028.283418.29018.96120.11625.42328.15331.666529.12429.81330.42034.32836.38839.098
本文提出了一种考虑了横向伸缩及剪切变形、位移场满足层间锯齿状连续的层合结构振动高阶分层建模理论——基于改进Chebyshev级数的高阶分层理论.该理论位移场由线性位移场和高阶位移场两部分组成,线性位移场决定了实际位移的总体分布趋势,而高阶位移场对线性位移场进行局部修正,使其趋近于实际位移分布形状.高阶位移场由具有统一表达式的改进Chebyshev级数表示,因而在实际编程应用中具有较好的灵活性,针对不同的建模精度需求,仅需通过改变高阶截断阶数来实现高阶位移场的配置而不需要逐一重新编程处理.通过对不同边界条件和铺层方式下层合梁、板、圆柱壳自由振动进行分析,发现MCPBHLW理论具有较高的建模精度和计算效率.与等效单层理论相比,MCPBHLW理论从独立铺层入手进行独立建模,同时考虑了横向剪切变形、横向伸缩变形、横向应力等因素的影响且位移场满足层间锯齿状连续.与传统锯齿理论相比,MCPBHLW理论考虑了横向伸缩变形,不论是面内位移还是横向位移在厚度方向皆满足锯齿分布,位移场形式统一,不受铺层方式和结构形式的限制,具有较好的灵活性和普适性.与三维层合理论相比,MCPBHLW理论可以根据实际需求实现不同建模精度,提高计算效率.
[1] 刘人怀, 薛江红. 复合材料层合板壳非线性力学的研究进展[J]. 力学学报, 2017,49(3): 487-506.(LIU Renhuai, XUE Jianghong. Development of nonlinear mechanics for laminated composite plates and shells[J].Chinese Journal of Theoretical and Applied Mechanics, 2017,49(3): 487-506.(in Chinese))
[2] 缪旭弘, 郭凤水, 贾地. 国外潜艇吸隔声材料研究现状及关键技术分析[C]//船舶水下噪声学术讨论会. 西安, 2007.(MIU Xuhong, GUO Fengshui, JIA Di. Research on development and key technical of submarine sound insulation materials in foreign countries[C]//Academic Seminar on Underwater Noise of Ships. Xi’an, 2017.(in Chinese))
[3] QATU M S.Vibration of Laminated Shells and Plates[M]. San Diego: Elsevier, 2004.
[4] REDDY J N.Mechanics of Laminated Composite Plates and Shells:Theory and Analysis[M]. Florida: CRC Press, 2003.
[5] WU Z, MA R, CHEN W. A refined three-node triangular element based on the HW variational theorem for multilayered composite plates[J].Composite Structures, 2017,161: 132-144.
[6] WU Z, CHEN W. A global higher-orderzig-zag model in terms of the HW variational theorem for multilayered composite beams[J].Composite Structures, 2016,158: 128-136.
[7] LIU B, XING Y F, QATU M S, et al. Exact characteristic equations for free vibrations of thin orthotropic circular cylindrical shells[J].Composite Structures, 2012,94(2): 484-493.
[8] XING Y, LIU B, XU T. Exact solutions for free vibration of circular cylindrical shells with classical boundary conditions[J].International Journal of Mechanical Sciences, 2013,75(4): 178-188.
[9] JIN G, YE T, CHEN Y, et al. An exact solution for the free vibration analysis of laminated composite cylindrical shells with general elastic boundary conditions[J].Composite Structures, 2013,106: 114-127.
[10] JIN G, YE T, MA X, et al. A unified approach for the vibration analysis of moderately thick composite laminated cylindrical shells with arbitrary boundary conditions[J].International Journal of Mechanical Sciences, 2013,75(10): 357-376.
[11] YE T, JIN G, SHI S, et al. Three-dimensional free vibration analysis of thick cylindrical shells with general end conditions and resting on elastic foundations[J].International Journal of Mechanical Sciences, 2014,84: 120-137.
[12] 徐坤, 陈美霞, 谢坤. 正交各向异性功能梯度材料平板振动分析[J]. 噪声与振动控制, 2016,36(4): 14-20.(XU Kun, CHEN Meixia, XIE Kun. Vibration analysis of orthotropic functionally graded plates[J].Noise and Vibration Control, 2016,36(4): 14-20.(in Chinese))
[13] 丁皓江, 陈伟球, 徐荣桥. 横观各向同性层合矩形板弯曲、振动和稳定的三维精确分析[J]. 应用数学和力学, 2001,22(1): 16-22.(DING Haojiang, CHEN Weiqiu, XU Rongqiao. On the bending, vibration and stability of laminated rectangular plates with transversely isotropic layers[J].Applied Mathematics and Mechanics, 2001,22(1): 16-22.(in Chinese))
[14] 吕朝锋. 基于状态空间架构的微分求积法及其应用[D]. 博士学位论文. 杭州: 浙江大学, 2006.(LÜ Chaofeng. State-space-based differential quadrature method and its applications[D]. PhD Thesis. Hangzhou: Zhejiang University, 2006.(in Chinese))
[15] SAADA A S.Elasticity:Theory and Applications[M]. 2nd ed. Florida: Ross Publishing Inc, 2009.
[16] YE T, JIN G, SU Z. Three-dimensional vibration analysis of sandwich and multilayered plates with general ply stacking sequences by a spectral-sampling surface method[J].Composite Structures, 2017,176: 1124-1142.
[17] REDDY J N.Energy Principles and Variational Methods in Applied Mechanic[M]. New York: John Wiley & Sons, 1984.
[18] YE T, JIN G, SU Z. A spectral-sampling surface method for the vibration of 2-D laminated curved beams with variable curvatures and general restraints[J].International Journal of Mechanical Sciences, 2016,110: 170-189.
[19] JIN G, YE T, SU Z. Elasticity solution for vibration of 2-D curved beams with variable curvatures using a spectral-sampling surface method[J].International Journal for Numerical Methods in Engineering, 2017,111(11): 1075-1100.
[20] YE T, JIN G, ZHANG Y. Vibrations of composite laminated doubly-curved shells of revolution with elastic restraints including shear deformation, rotary inertia and initial curvature[J].Composite Structures, 2015,133: 202-225.
[21] 瞿叶高, 华宏星, 谌勇, 等. 复合材料旋转壳自由振动分析的新方法[J]. 力学学报, 2013,45(1): 139-143.(QU Yegao, HUA Hongxing, CHEN Yong, et al. A new method for free vibration analysis of composite laminated shelles of revolution[J].Chinese Journal of Theoretical and Applied Mechanics, 2013,45(1): 139-143.(in Chinese))
[22] 瞿叶高, 孟光, 华宏星, 等. 基于区域分解的薄壁回转壳自由振动分析[J]. 应用力学学报, 2013,30(1): 1-6.(QU Yegao, MENG Guang, HUA Hongxing, et al. Free vibration analysis of thin shells of revolution based on domain decomposition method [J].Chinese Journal of Applied Mechanics, 2013,30(1): 1-6.(in Chinese))
[23] YE T, JIN G. Elasticity solution for vibration of generally laminated beams by a modified Fourier expansion-based sampling surface method[J].Computers &Structures, 2016,167: 115-130.
[24] YE T, JIN G, YE X, et al. A series solution for the vibrations of composite laminated deep curved beams with general boundaries[J].Composite Structures, 2015,127: 450-465.
[25] PAGANO N J. Exact solutions for rectangular bidirectional composites and sandwich plates[J].Journal of Composite Materials, 1970,4(1): 20-34.
[26] QU Y, WU S, LI H, et al. Three-dimensional free and transient vibration analysis of composite laminated and sandwich rectangular parallelepipeds: beams, plates and solids[J].Composites Part B:Engineering, 2015,73: 96-110.
[27] CHEN W Q, LÜ C F. 3D free vibration analysis of cross-ply laminated plates with one pair of opposite edges simply supported[J].Composite Structures, 2005,69(1): 77-87.
[28] YE T, JIN G, SU Z, et al. A modified Fourier solution for vibration analysis of moderately thick laminated plates with general boundary restraints and internal line supports[J].International Journal of Mechanical Sciences, 2014,80: 29-46.
[29] NOSIER A, KAPANIA R, REDDY J. Free vibration analysis of laminated plates using a layer-wise theory[J].AIAA Journal, 2013,31(12): 2335-2346.
[30] QU Y, MENG G. Dynamic analysis of composite laminated and sandwich hollow bodies of revolution based on three-dimensional elasticity theory[J].Composite Structures, 2014,112: 378-396.