ⓒ 应用数学和力学编委会,ISSN 1000-0887
在解决实际工程问题的过程中,Schwarz-Christoffel变换(以下简称SC变换)模型有着重要的作用,SC变换能够把一个二维空间上复杂边界几何体映射到另一个二维空间上形状简单的几何体,从而可以简化工程中复杂边界问题的处理.SC变换在油气地下渗流力学、岩土力学、流体力学和电磁学等研究领域有着广泛的应用.目前有关SC变换数值计算方法有一些新的研究成果,王刚等[1-2]对多边形区域到上半平面映射和槽型区域映射方法进行研究,采用Newton-Raphson(牛顿-拉夫森)迭代法进行求解.祝江鸿等[3-4]采用SC变换Laurent级数模型导出地下开挖隧洞断面到单位圆映射的计算方法,但对于复杂开挖洞面,级数构成项较多,求解复杂.皇甫鹏鹏等[5]、朱大勇等[6]和王润富[7]都以SC变换级数模型建立了多边形区域到单位圆映射模型,但级数模型构成复杂,计算量大,精度难以控制.徐趁肖等[8]研究了复杂边界单连通区域共形映射模型,采用复变三角插值理论,利用法线迭代收敛方法,将任意复杂边界单连通区域问题映射到单位圆区域进行求解,但三角差值中涉及到复杂的级数计算.王志良等[9]和王振武等[10]在研究浅埋隧道围岩应力场计算与地下矩形洞室应力分布复变函数解的过程中,采用共形映射公式为Laurent级数表示形式,其系数的求解方法复杂.李明等[11]和袁林等[12]在矩形巷道围岩应力与变形黏弹性研究的过程中,建立了矩形巷道到单位圆的共形映射变换,但只考虑了矩形4个顶点与单位圆周的映射关系.施高萍等[13]和陈凯等[14]在进行矩形巷道孔边应力的弹性分析时,建立了单位圆外域共形映射到洞室外域的映射函数,并以Laurent级数有限项对该问题进行了求解.何峰等[15]和赵凯等[16]在矩形巷道围岩应力分布特征研究时,将圆形区域共形映射到矩形区域上,但只考虑了矩形3个顶点与圆形边界的对应关系.文献[17]研究了多边形区域到条带状区域变换的理论模型,并建立带状区域到矩形映射数学模型.
通过上述研究成果可知,多边形区域到圆形、矩形区域的映射在求解不规则边界问题中有着重要的作用,尽管采用级数法可以将复杂区域边界映射到简单规则区域,但计算复杂,级数项及其系数确定较困难.本文借鉴前人研究成果,对多边形区域到矩形区域映射的数学模型[17]进行数值计算方法研究.采用一次参数变换,变换映射模型积分形式,建立其与Gauss-Jacobi型积分的关系,提出了在积分路径中搜寻奇异点,进而寻求合理的积分子路径,在子路径采用修正Gauss-Jacobi积分进行求解.通过上述方法解决了计算过程中出现的奇异积分问题,同时也提高了积分精度,结合Levenberg-Marquardt最优化算法求解非线性积分方程组,完成了从多边形区域到带状区域的映射的计算,然后结合第一类Jacobi椭圆函数,建立了带状区域与矩形区域的映射关系,通过求解复参数第一类Jacobi椭圆函数,完成带状区域到矩形区域映射的数值计算.
在复平面w上有N(N≥4)边形,它的顶点与内角分别为wk和παk(k=1,2,…,N).将带状区域边界上的点映射到w平面多边形区域顶点的SC变换[17]公式为
(1)
其中,A为伸缩系数,C为变换中心,παk为w平面多边形内角,z为带状区域边界点,fj(ξ)为分段函数,具体表达式如下:
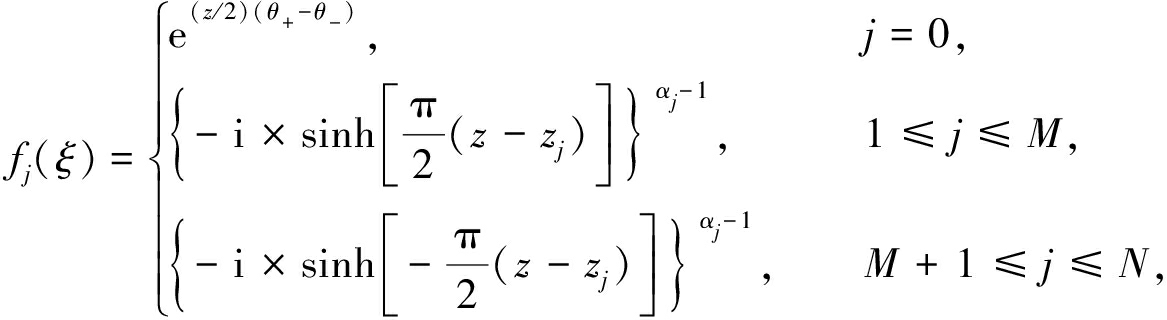
(2)
其中,i为虚数单位,M为带状区域下边界点的个数,N为多边形区域顶点的总个数,θ+为带状区域左边的无限远点的角度,θ-为带状区域右边的无限远点的角度,则θ+=θ-=π.
上半平面变换为矩形区域可由第一类椭圆积分函数表示,若已知矩形基本参数,则矩形映射到上半平面可由其反函数表示,即第一类椭圆函数.借助第一类椭圆函数,将图1中的带状区域映射到矩形区域,映射变换[17-18]可由式(3)表示:
(3)
其中,u为矩形区域,l为椭圆函数的模,由选择变换的矩形顶点决定.映射点的对应关系如图1所示.
但在实际工程问题研究中,一般多边形区域是已知的,需求解与多边形顶点对应的矩形顶点及边界上的映射点.根据Riemann原理,要确定式(1),则参数zk(k=1,2,…,N)中有3个点必须选定.这样不妨假定z1=0,即选定映射为矩形长边的第一个顶点.第二点取映射为矩形长边的第二个顶点,如图1中的z2点,该点的取值为映射模量,由选定矩形的长边与短边比值决定.第三点取映射为矩形顶点的第四点,该点落在虚轴上,取值等于i,如图1中的z5=i.但也可根据实际工程问题的需要,选择其他点.在上述假定的条件下,式(1)中zk(k=1,2,…,N)满足下述条件:
(4)
即z必须位于带状区域边界上,点位次序为逆时针顺序.
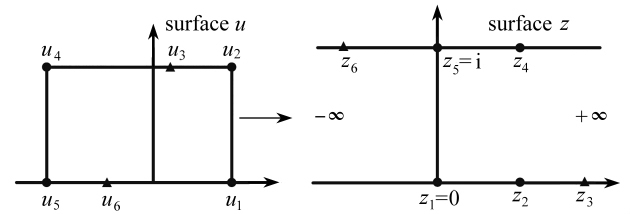
图1 矩形区域到带状区域变换示意图
Fig. 1 The rectangular domain to the strip domain transformation diagram
若选定矩形长边第一个顶点位于坐标原点时,则式(1)中的C等于0,这样有利于问题的简化,因此可得多边形顶点wk(k=1,2,…,N)为
(5)
根据式(3),采用相邻两点之间的边长比值可消去伸缩系数,这样可以减少未知量的求解,因此可得
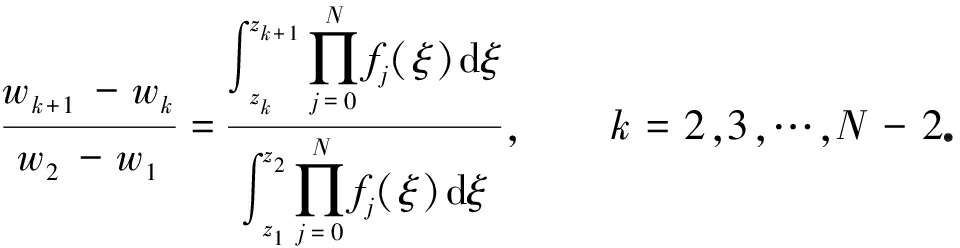
(6)
令
则式(6)可表示为
(7)
根据式(7),可得N-3个关系式,其中未知量为zk(k=1,2,…,N-3).通过求解式(7)非线性积分方程组,可求得未知参数zk.
根据式(5)可求得伸缩系数A:
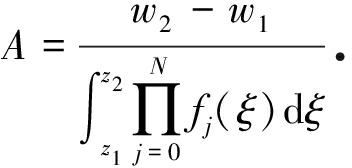
(8)
根据以上分析,为了求解带状区域到多边形区域映射参数问题式(7),必须计算式(6)的积分.根据实际问题分析可知,式(6)积分路径在带状区域边界上,在带状区域的上下边界上含有无穷远点,无穷远点的处理方法可参考文献[18].积分起点zk和终点zk+1为奇点,为了求解式(6)的奇异积分,对Ik做一次参数变换:
令
代入式(7)可得
(9)
其中
为了将式(9)处理为Gauss-Jacobi型积分,对fk(ξ)表达式中的第k个因子采用Taylor(泰勒)级数展开,取其线性部分.保证求解变量z满足式(4)情况下,式(9)积分起点和终点都存在奇异点,起点奇异点为(1+ξ)αk-1项,终点奇异点为fk(ξ)表达式中的第k个因子.因此,对于上式直接采用Gauss-Jacobi型积分显然不合理,若对带状区域上边界或下边界对应点进行积分时,可将积分区间以区间的中点为界划分为两个子区间,进行两段积分,每段积分保证只含有一个奇异点,即(1+ξ)αk-1项.通过上述修改,每个子区间能够满足Gauss-Jacobi型积分式(9)条件.
根据文献[19],式(9)可表示为
(10)
其中,xq为权函数(1-t)0(1+t)αi-1在区间[-1,1]正交多项式的零点,Qq为权值,n为正交多项式的次数,根据文献[20],其值由积分Ik的精度决定,有关xq和Qq的求解参见文献[21].
在采用迭代法求解式(7)时,积分Ik计算才是关键,文献[20]中研究结果表明可以通过增加正交多项式的次数提高积分精度.本文通过试验研究表明积分路径长度对积分的精度也有一定程度的影响,因此为了保证积分精度,必须确定合理的积分路径长度.
在迭代过程中,当αk-1<0时,积分路径(zk,zk+1)区间端点存在奇异点,可将区间划分为两个子区间.具体方法如下.
第1步 以路径(zk,zk+1)中点将积分式(7)分为两个子区间,其积分可表示为
式中,zmid为路径(zk,zk+1)的中点.
第2步 确定积分路径长度,合理积分路径长度由下式确定:
式中,L为合理积分路径长度,m;α为积分路径长度加权因子,一般取α∈0.5,1,2,α取值较大时,则积分路径长度较长,但积分精度有所下降,反之,积分路径长度较短,精度有所增加,但计算时间也相应增加,本文取α=1.
第3步 若L<1,积分路径太长,将积分区间变换为[zk,zk+L×(zmid-zk)],在此区间上采用校正后的零点和权值进行积分.
第4步 移动积分路径,下一步积分区间为[zk+L×(zmid-zk),zmid],进行第2步,计算L,若L<1,进行第3步.
第5步 若L≥1,采用校正后的零点和权值进行积分.
根据式(9)的推导过程,结合权函数正交多项式的性质,可将权函数W(t)=(1-t)α(1+t)β正交多项式的零点和权值进行校正[19].
校正后的零点为
(11)
考虑Gauss-Jacobi型积分式(10),校正后的权值为
(12)
对非线性系统式(7)求解过程中,还得考虑约束条件式(4).本次求解的参数为复变量,参考文献[22-23],对复变量参数约束条件进行变换,一是消除约束条件限制,二是建立复参数与实参数之间的关系,简化求解问题.
在多边形区域中选定4个点,与带状区域上所对应的点如图2所示的z1,zb,zc和zd,下标b,c和d表示点位的次序,其位置分别表示为z1=0,zb=m,zc=m+i和zd=i.其中m为映射模量,其值由带状区域对应多边形区域选定的4个点来决定.m等于选取第1点到第2点之间的多边形边长之和与第3点到第4点之间的多边形边长之和的比值.
第1个点到第b个点的初值可由下式确定:
第b+1个点到第c-1个点的初值可由下式确定:
第c个点到第d个点的初值可由下式确定:
第d+1个点到第N个点的初值可由下式确定:
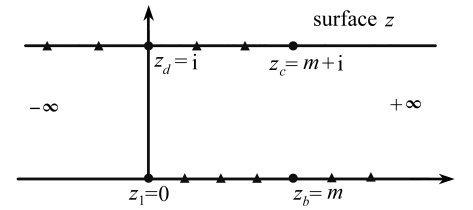
图2 带状区域边界点初始化示意图
Fig. 2 Diagram of the boundary point initialization in the strip domain
根据文献[23-24]对实参数的变换方法,结合文献[17]中的变换思想,建立复参数与实参数的变换关系.求解的未知参数只有N-3个,因此只需建立N-3个实参数,其步骤如下.
第1步 计算z平面相邻两点的距离:
第2步 第1个点到第b-2个点变换:
其中,r0,j为第j个经过变换的实参数.
第3步 第c+1个点到d-1个点的变换:
第4步 第b-1个点的变换,k=b-1,
第5步 第b+1个点到c-1个点的变换.
首先对这些点进行指数运算,指数运算的结果看作一个向量,在向量的第一个元素前面插入1,在向量最后一个元素后面插入-1,然后对该向量进行差分运算,将计算的结果看作一个新的向量,最后对新向量中的元素再进行变换,即对相邻两个元素做相除运算.具体计算公式如下:
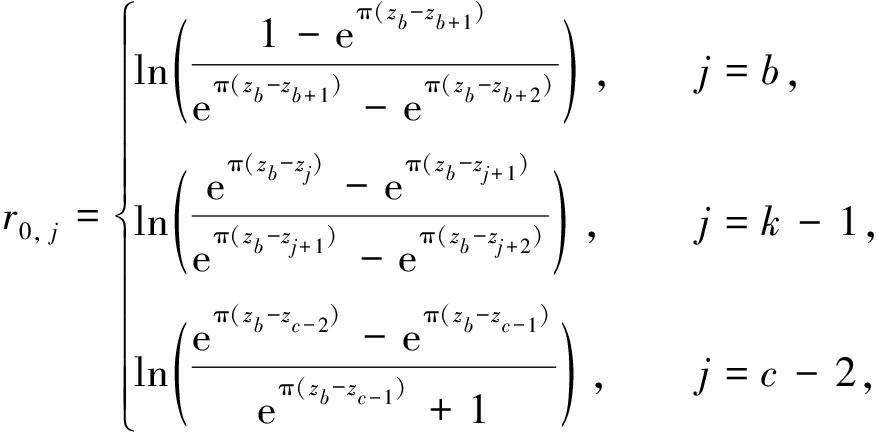
其中
第6步 第d-2个点到N-3个点的变换.
变换的思路与第5步相似,在指数运算过程中,需要对这些变换点的实部做指数运算.具体计算公式如下:
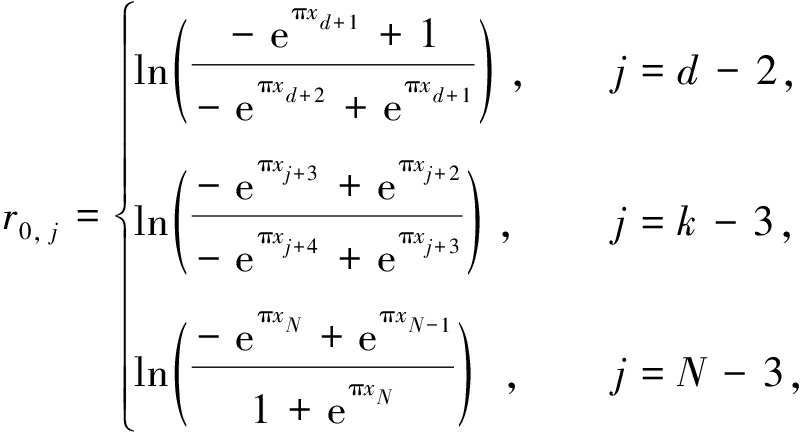
其中,k=d-2,d-1,…,N-3;x表示变换点的实部.通过上述6步的变换,建立N个复参数与N-3个实参数的关系.
进行实参数变换主要是因为采用Newton法、拟Newton法、共轭梯度法和Levenberg-Marquardt等算法求解非线性方程组式(7)时,其Ik运算结果均为实数,而未知数为复参数.若直接采用Ik的计算结果与其导数直接校正下一步的结果,无法保证满足式(4)的约束条件,因此必须建立实参数与复参数之间的对应关系,并且还能够将实参数的结果通过逆变换还原到复参数[17],同时未知数zk也满足式(4)的条件,其具体步骤如下.
第1步 令![]() 此时已经包含z1=0,下面步骤对
此时已经包含z1=0,下面步骤对![]() 中的元素进行更新.
中的元素进行更新.
第2步 第2个点到第b-1个点变换:
其中,![]() 为第k个经过逆变换的复参数.
为第k个经过逆变换的复参数.
第3步 第c+1个点到第d-1个点变换:
其中,k=c+1,c+2,…,d-1.这里特别需要注意,j是从d-3倒序至k-2.
第4步b,c和d点的变换.
对于b点的变换,由无约束条件变换的第4步和初始化可得
(13)
其中,xc与xc+1分别为c点与c+1点的实部.因为r0,b-1在无约束条件变换的第4步已经算出, 根据初始化规则, 结合图2, 可得zb=xc,因此从式(13)可解出zb,即可得b点逆变换的计算公式:
其中,![]() 在第3与第4步已求出.c点变换,
在第3与第4步已求出.c点变换,![]() 点变换,
点变换,![]()
第5步 第b+1个点到第c-1个点变换.
在无约束变换过程中对初值做了对数变换,为了将其还原,首先令
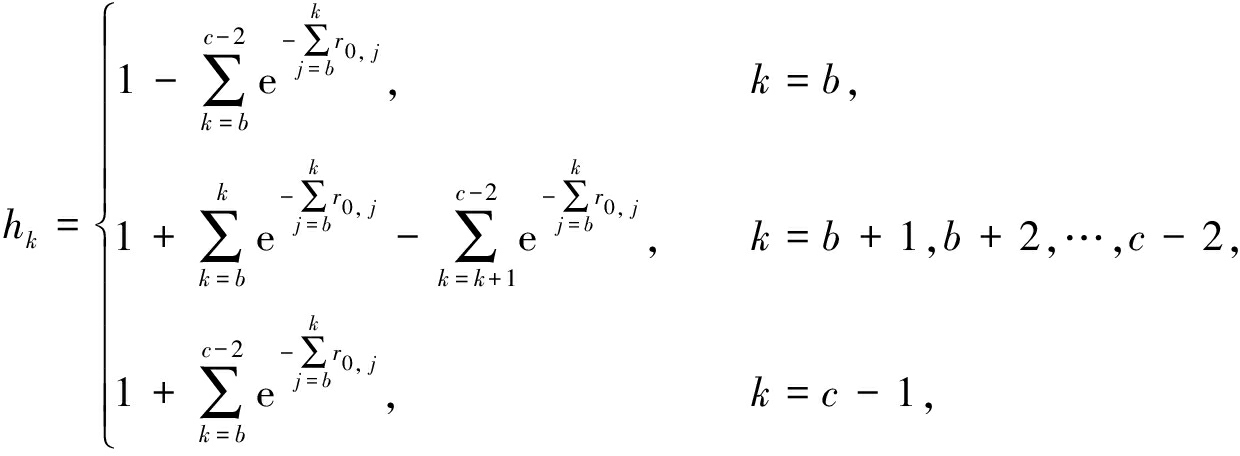
则![]() 可表示为
可表示为
第d+1个点到第N个点变换与上述方法类似,只需将求和部分的起点b改为d-2,终点c-2改为N-3即可.可以证明,通过上述变换,![]()
由于非线性方程组的求解算法很多,鉴于篇幅有限,本文只采用了Levenberg-Marquardt算法[25]求解式(7)非线性方程组.Levenberg-Marquardt算法中涉及到两个参数ρ与σ,根据图3,ρ与σ取值与迭代次数N、绝对误差e的关系曲线可以看出,ρ与σ取值对收敛速度有影响,通过反复的数值试验得出:ρ对收敛速度的影响很小,取ρ∈[0.1,0.9],而σ对收敛的速度的影响较大,取σ∈[0.1,0.5].在参数ρ与σ满足上述取值时,对如图4所示规则的多边形区域进行计算,迭代45次就可以达到10-9次方的计算精度.这里推荐ρ=0.5,σ=0.2.
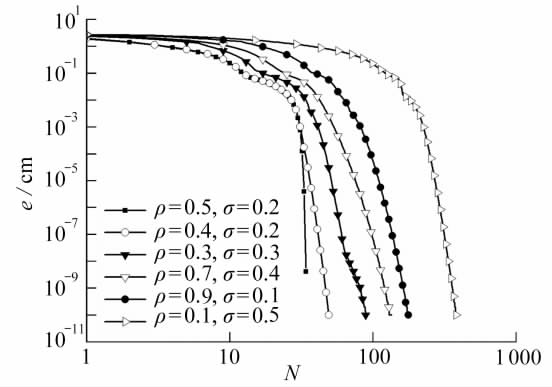
图3 Levenberg-Marquardt算法中参数、迭代次数与绝对误差关系曲线
Fig. 3 The relationship curves of the number of iterations, the absolute error and
the parameter in the Levenberg-Marquardt algorithm
通过上述求解,基本完成了带状区域到多边形区域映射的计算,得到了带状区域边界与多边形区域边界的对应关系.然而,要得到矩形边界的对应点,必须根据椭圆函数的模[17]进行第一类椭圆积分计算.因为带状区域的宽度为1,而z1,zb,zc和zd决定了矩形左半部分,则右半部分可以通过解析延拓得到[18],因此椭圆函数的模取e-2πRe(zb-z1),得到矩形长宽参数,也就确定了矩形的4个顶点,椭圆积分计算方法可参见文献[26].本文计算矩形长宽参数也是为了控制复参数椭圆函数计算,因为椭圆函数为一个双周期纯亚函数,其周期与矩形的长宽有关[18],若矩形的4个顶点确定之后,则椭圆函数周期也就确定了.后续进行复参数第一类椭圆函数计算时, 必须保证除矩形4个顶点之外, 其他点受这4个顶点约束, 按照逆时针顺序落在矩形边界上.
 >
>
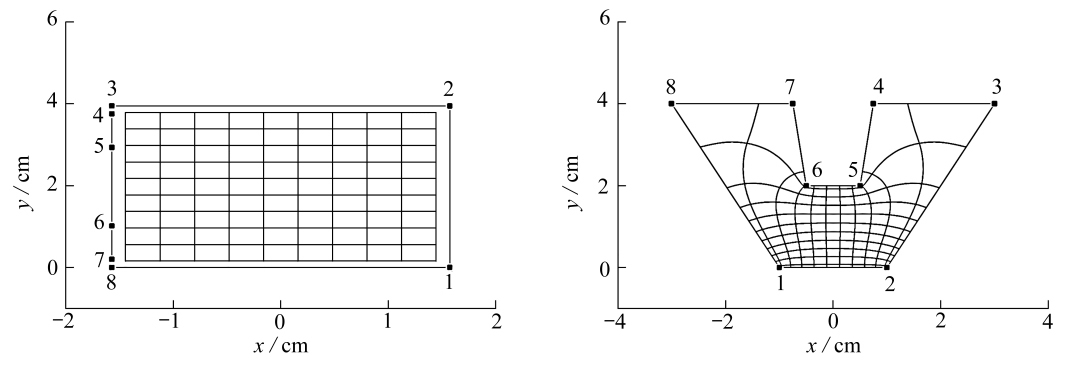
(a) 矩形区域(b) 对称多边形区域
(a) The rectangular domain(b) The polygonal domain
图4 多边形区域到矩形映射变换
Fig. 4 Mapping transformation of the polygonal domain to the rectangular domain
通过计算式(3),可得到带状区域到矩形区域的映射关系,但通过式(7)的求解,得到参数z为带状区域的复参数.在文献[26]中,采用级数法、椭圆函数加法定理与精细积分相结合的方法对实参数的椭圆函数数值计算方法做了研究,现有部分计算类软件仅支持实参数椭圆函数的计算.本文涉及到复参数椭圆函数的计算,借助Landen变换[27],可将第一类复参数椭圆函数数值算法描述如下.
第1步 输入矩形区域边界u,输入由椭圆积分得到的矩形4个顶点.若z中含有矩形上半平面的点,用矩形的宽度减去该点,将其变换到矩形的下半平面.
第2步 若l<4ε,ε为椭圆函数计算误差限,一般取10-16,则
第3步 若l>10-3,令
进行第1步递归调用,计算sn(u|l),dn(u|l),cn(u|l),否则进行第3步.
第4步 令
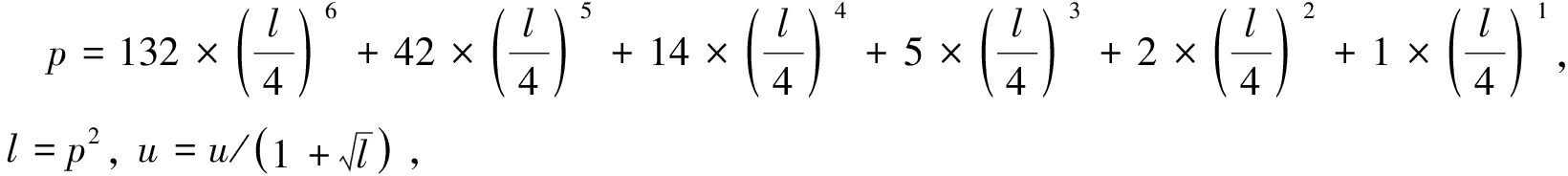
进行第1步递归调用,计算sn(u|l),dn(u|l),cn(u|l),否则进行第5步.
第5步 计算椭圆函数
通过上述数值计算方法可以看出, 在已知矩形区域边界时, 可以将矩形区域映射到带状区域.但文中的带状区域边界已经求出, 因此, 必须事先给出矩形边界初始化值u,通过函数sn(u|l)得到z值,根据所求z值与多边形区域到带状区域的z值相比较,若对应点位误差满足终止条件,则停止计算,否则采用Newton法矫正初始化值u,然后再次迭代计算z值,直到满足所需精度为止.
通过上述分析,在求得变换参数u之后,将其代入式(3),求出带状区域边界z值,然后将z值代入式(6),可得w平面上|wk+1-wk|的计算值,最后利用已知的多边形区域顶点信息,可求解|wk+1-wk|的真值,根据真值与计算值,采用边长绝对误差进行精度评定:
(14)
其中k=1,2,…,N-1.
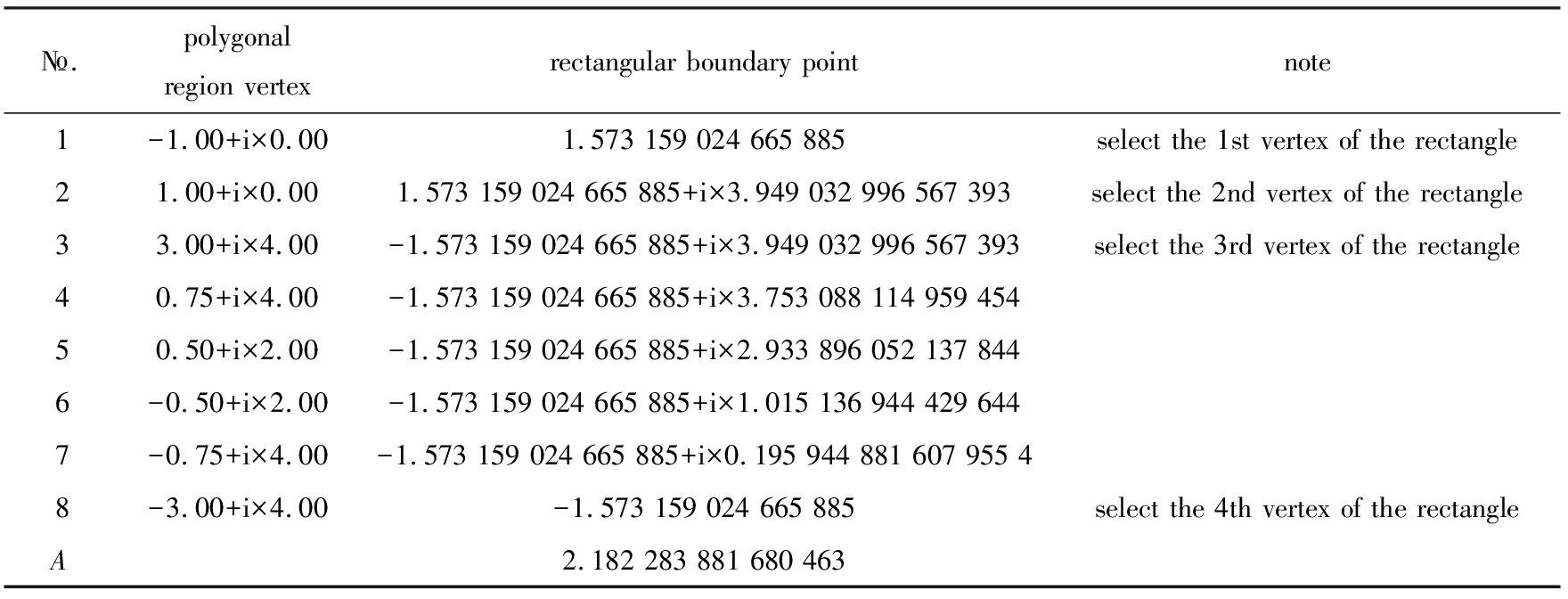
平面封闭多边形区域如图4所示,为8个顶点的封闭多边形.在变换时,选择多边形区域的第1,2,3,8共4个顶点,如图4(b)所示,这4个点分别对应矩形的4个顶点.经过映射变换,将对称的多边形区域变换到矩形区域,顶点的对应关系如图4(a)实心方形点所示.具体参数设置如下,在计算非线性方程组时,正交多项式次数为8,积分路径长度的加权因子α=1,非线性方程组的绝对误差为10-14,Levenberg-Marquardt算法中的ρ=0.5,σ=0.2,在得到带状区域的映射点后,由矩形到带状区域的椭圆函数计算时设置的限差为10-14.最后通过精度评定式(14)得到图4映射变换的精度为9.60×10-13,具体的计算结果见表1.
表1 多边形区域到矩形区域映射计算结果
Table 1 Calculation results of the polygonal regions to rectangular regions mapping
№.polygonal region vertexrectangular boundary pointnote1-1.00+i×0.001.573 159 024 665 885select the 1st vertex of the rectangle21.00+i×0.001.573 159 024 665 885+i×3.949 032 996 567 393select the 2nd vertex of the rectangle33.00+i×4.00-1.573 159 024 665 885+i×3.949 032 996 567 393select the 3rd vertex of the rectangle40.75+i×4.00-1.573 159 024 665 885+i×3.753 088 114 959 45450.50+i×2.00-1.573 159 024 665 885+i×2.933 896 052 137 8446-0.50+i×2.00-1.573 159 024 665 885+i×1.015 136 944 429 6447-0.75+i×4.00-1.573 159 024 665 885+i×0.195 944 881 607 955 48-3.00+i×4.00-1.573 159 024 665 885select the 4th vertex of the rectangleA2.182 283 881 680 463
对于非对称区域,本文选取不规则条带状区域,将其边界离散,形成如图5所示的多边形区域.在条带区域向矩形区域映射过程中,首先在带状区域中选取两点,这两点对应矩形的长边两个端点,然后按照逆时针方向选取其他两点,对应矩形的短边两个端点.在图5不规则条带状区域中,选取第1点与第13点作为矩形的长边两个端点,其他两个点为第14点与第27点,作为矩形的短边两个端点.在映射过程中,尽可能保证带状区域的长边方向与矩形区域的长边一致,这样能够避免在计算积分式(7)中产生群聚现象,因为映射变换过程要严格保证点位的次序,如果矩形短边上对应的点过多,可能导致某些映射点分布过于集中,从而导致式(7)积分值太小或趋近于0而发生群聚现象.
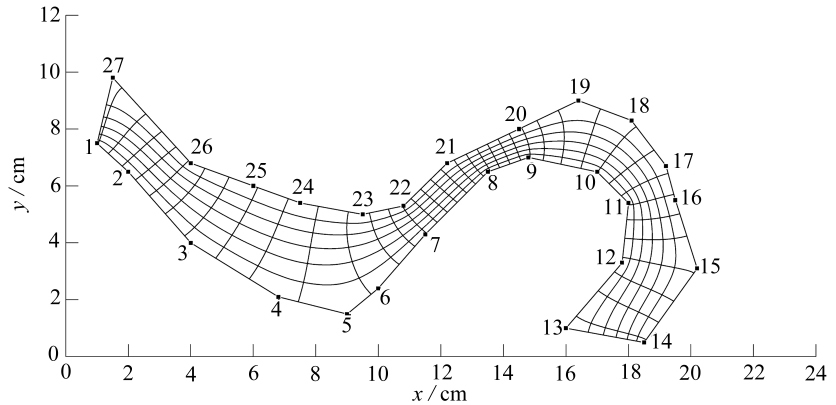
图5 带状区域映射变换
Fig. 5 Mapping transformation of the strip domain
通过上述两个示例可以看出,带状区域到矩形区域的映射,映射函数在映射区域上满足Cauchy-Riemann条件,因此矩形区域的正交网格映射到多边形区域上,网格仍然满足正交性,如图4、图5所示.
1) 矩形区域到多边形区域共形映射变换模型求解难点在于奇异积分计算、初值处理与复参数椭圆函数的计算.从常规Gauss-Jacobi型积分出发,对带状区域到多边形区域映射的模型进行一次参数变换,变换积分方程形式,以积分路径中的奇异点为界,寻求合理积分子路径,在子路径采用修正Gauss-Jacobi积分方法有效地克服奇异积分计算的困难.
2) 对于初值条件的处理,通过建立复参数与实参数函数关系,对其进行互逆运算,消除了约束条件,从而将常规非线性方程组求解Levenberg-Marquardt算法应用到复参数奇异积分方程组的求解中.
3) 在矩形区域到带状区域的映射变换过程中涉及的Jacobi椭圆函数,采用Landen变换,完成了复参数Jacobi椭圆函数的计算.
4) Levenberg-Marquardt算法在求解多边形区域到带状区域映射的非线性系统是可行的,当参数ρ与σ选择适当,Levenberg-Marquardt算法收敛较快.
5) 通过8个顶点对称多边形到矩形映射,27个顶点的条带状区域到矩形映射的计算表明,本文给出的从矩形区域到多边形区域共形映射的数值算法具有可操作性.
[1] 王刚, 许汉珍, 顾王明, 等. 数值许瓦尔兹-克力斯托夫变换与数值高斯-雅可比型积分[J]. 海军工程大学学报, 1994,1(2): 25-34.(WANG Gang, XU Hanzhen, GU Wangming, et al. Numerical Schwarz-Christoffel transformation and numerical Gauss-Jacobi quadrature[J].Journal of Naval Academy of Engineering, 1994,1(2): 25-34.(in Chinese))
[2] 王刚, 陆小刚, 顾王明. 槽形内域中的数值许瓦尔兹-克力斯托夫保角变换[J]. 海军工程大学学报, 1995,1(4): 16-23.(WANG Gang, LU Xiaogang, GU Wangming. Numerical Schwarz-Christoffel conformal mapping in channel region[J].Journal of Naval Academy of Engineering, 1995,1(4): 16-23.(in Chinese))
[3] 祝江鸿. 隧洞围岩应力复变函数分析法中的解析函数求解[J]. 应用数学和力学, 2013,34(4): 345-354.(ZHU Jianghong. Analytic functions in stress analysis of the surrounding rock for caverns with the complex variable theory[J].Applied Mathematics and Mechanics, 2013,34(4): 345-354.(in Chinese))
[4] 祝江鸿, 杨建辉, 施高萍, 等. 单位圆外域到任意开挖断面隧洞外域共形映射的计算方法[J]. 岩土力学, 2014,35(1): 175-183.(ZHU Jianghong, YANG Jianhui, SHI Gaoping, et al. Calculating method for conformal mapping from exterior of unit circle to exterior of cavern with arbitrary excavation cross-section[J].Rock and Soil Mechanics, 2014,35(1): 175-183.(in Chinese))
[5] 皇甫鹏鹏, 伍法权, 郭松峰. 基于边界点搜索的洞室外域映射函数求解法[J]. 岩石力学, 2011,32(5): 1418-1424.(HUNAGFU Pengpeng, WU Faquan, GUO Songfeng. A new method for calculating mapping function of external area of cavern with arbitrary shape based on searching points on boundary[J].Rock and Soil Mechanics, 2011,32(5): 1418-1424.(in Chinese))
[6] 朱大勇, 钱七虎, 周早生. 复杂形状洞室映射函数的新解法[J]. 岩石力学与工程学报, 1999,18(3): 279-282.(ZHU Dayong, QIAN Qihu, ZHOU Zaosheng. New method for calculating mapping function of opening with complex shape[J].Chinese Journal of Rock Mechanics and Engineering, 1999,18(3): 279-282.(in Chinese))
[7] 王润富. 一种保角映射法及其微机实现[J]. 河海大学学报, 1991,19(1): 86-90.(WANG Runfu. A method of conformal mapping and its computer implementation[J].Journal of Hohai University, 1991,19(1): 86-90.(in Chinese))
[8] 徐趁肖, 朱衡君, 齐红元. 复杂边界单连通域共形映射解析建模研究[J]. 工程数学学报, 2002,19(4): 135-138.(XU Chenxiao, ZHU Hengjun, QI Hongyuan. Analytically modeling of complicated boundary simply connected region conformal mapping[J].Journal of Engineering Mathematics, 2002,19(4): 135-138.(in Chinese))
[9] 王志良, 申林方, 姚激. 浅埋隧道围岩应力场的计算复变函数求解法[J]. 岩土力学, 2010,31(1): 86-90.(WANG Zhiliang, SHEN Linfang, YAO Ji. Calculation of stress field in surrounding rocks of shallow tunnel using computational function of complex variable method[J].Rock and Soil Mechanics, 2010,31(1): 86-90.(in Chinese))
[10] 王振武, 牛铮铮, 冯秀苓. 地下矩形洞室应力分布的复变函数解[J]. 北华航天工业学院学报, 2010,20(4): 86-90.(WANG Zhenwu, NIU Zhengzheng, FENG Xiuling. A semi-analytical elastic stress solution for perimeter stresses of rocks around a rectangular[J].Journal of North China Institute of Aerospace Engineering, 2010,20(4): 86-90.(in Chinese))
[11] 李明, 茅献彪. 基于复变函数的矩形巷道围岩应力与变形粘弹性分析[J]. 力学季刊, 2011,32(2): 195-202.(LI Ming, MAO Xianbiao. Based on the complex variable functions of rectangular roadway surrounding rock stress and deformation viscoelastic analysis[J].Chinese Quarterly of Mechanics, 2011,32(2): 195-202.(in Chinese))
[12] 袁林, 高召宁, 孟祥瑞. 基于复变函数法的矩形巷道应力集中系数黏弹性分析[J]. 煤矿安全, 2013,44(2): 196-200.(YUAN Lin, GAO Zhaoning, MENG Xiangrui. Viscoelastic analysis of stress concentration coefficient in rectangular roadway based on complex variable function[J].Safety in Coal Mines, 2013,44(2): 196-200.(in Chinese))
[13] 施高萍, 祝江鸿, 李保海, 等. 矩形巷道孔边应力的弹性分析[J]. 岩土力学, 2014,35(9): 2587-2601.(SHI Gaoping, ZHU Jianghong, LI Baohai, et al. Elastic analysis of hole-edge stress of rectangular roadway[J].Rock and Soil Mechanics, 2014,35(9): 2587-2601.(in Chinese))
[14] 陈凯, 唐治, 崔乃鑫, 等. 矩形巷道围岩应力解析解[J]. 安全与环境学报, 2015,15(3): 124-128.(CHEN Kai, TANG Zhi, CUI Naixin, at el. Analytical solution of rectangular roadway surrounding rock stress[J].Journal of Safety and Environment, 2015,15(3): 124-128.(in Chinese))
[15] 何峰, 唐治, 朱小景, 等. 矩形巷道围岩应力分布特征[J]. 数学的实践与认识, 2015,45(20): 128-134.(HE Feng, TANG Zhi, ZHU Xiaojing, et al. Stress distribution characteristics of rectangular roadway surrounding rocks[J].Mathematics in Practice and Theory, 2015,45(20): 128-134.(in Chinese))
[16] 赵凯, 刘长武, 张国良. 用弹性力学的复变函数法求解矩形硐室周边应力[J]. 采矿与安全工程学报, 2007,24(3): 361-365.(ZHAO Kai, LIU Changwu, ZHANG Guoliang. Solution for perimeter stresses of rocks around a rectangular chamber using the complex function of elastic mechanics[J].Journal of Mining and Safety Engineering, 2007,24(3): 361-365.(in Chinese))
[17] HOWELL L H, TREFETHEN L N. A modified Schwarz-Christoffel transformation for elongated regions[J].Society for Industrial and Applied Mathematics, 1990,11(5): 928-949.
[18] 拉夫连季耶夫 М А, 沙巴特 Б В. 复变函数论方法[M]. 6版. 施祥林, 夏定中, 吕乃刚, 译. 北京: 高等教育出版社, 2006.(ЛАВРЕНТЬЕВ М А, ШАБАТ Б В.Methods of the Theory of Complex Function[M]. 6th ed. SHI Xiangling, XIA Dingzhong, LÜ Naigang, transl. Beijing: Higher Education Press, 2006.(Chinese version))
[19] COSTAMAGNA E. A new approach to standard Schwarz-Christoffel formula calculations[J].Microwave and Optical Technology Letters, 2002,32(3): 196-199.
[20] DRISCOLL T A. Algorithm 843: improvements to the Schwarz-Christoffel toolbox for MATLAB[J].ACM Transactions on Mathematical Software, 2005,31(2): 239-251.
[21] 崔建斌, 姬安召, 鲁洪江, 等. Schwarz Christoffel变换数值解法[J]. 山东大学学报(理学版), 2016,51(4): 104-111.(CUI Jianbin, JI Anzhao, LU Hongjiang, et al. Numerical solution of Schwarz Christoffel transform[J].Journal of Shandong University(Natural Science), 2015,51(4): 104-111.(in Chinese))
[22] 崔建斌, 姬安召, 王玉风, 等. 单位圆到任意多边形区域的Schwarz Christoffel变换数值解法[J]. 浙江大学学报(理学版), 2017,44(2): 161-167.(CUI Jianbin, JI Anzhao, WANG Yufeng, et al. Numerical solution method for Schwarz-Christoffel transform from unit circle to arbitrary polygon area[J].Journal of Zhejiang University(Science Edition), 2017,44(2): 161-167.(in Chinese))
[23] NATARAJAN S, BORDAS S, MAHAPATRA D R. Numerical integration over arbitrary polygonal domains based on Schwarz-Christoffel conformal mapping[J].International Journal for Numerical Methods in Engineering, 2009,80(1): 103-134.
[24] CROWDY D. The Schwarz-Christoffel mapping to bounded multiply connected polygonal domains[J].Proceedings Mathematical Physical &Engineering Science, 2005,146(2061): 2653-2678.
[25] 刘浩. 大规模非线性方程组和无约束优化方法研究[D]. 博士学位论文. 南京: 南京航空航天大学, 2008.(LIU Hao. Research on methods for large-scale nonlinear equations and unconstrained optimization[D]. PhD Thesis. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008.(in Chinese))
[26] 姚征. 椭圆函数的精细积分改进算法[J]. 数值计算与计算机应用, 2008,29(4): 251-260.(YAO Zheng. The improved precise integration method for elliptic functions[J].Journal on Numerical Methods and Computer Applications, 2008,29(4): 251-260.(in Chinese))
[27] ABRAMOWITZ M, STEGUN I A.Handbook of Mathematical Functions With Formulas,Graphs,and Mathematical Tables[M]. Washington DC: Dover Publications, 1996.