ⓒ 应用数学和力学编委会,ISSN 1000-0887
孤子波是非线性方程的一个很重要的研究内容.许多学者在激波、量子力学、光波散射、神经网络、大气物理等方面都做了一些孤子波理论的研究[1-8].求解孤子波已有了很多新的方法, 例如齐次平衡法、双曲函数法、辅助方程法、椭圆函数法等[9-13].非线性孤子波的定性理论也不断地被研究.孤子波渐近方法就是孤子波理论的一种新的研究方法.它是用扰动理论的渐近展开式将非线性方程转化为能够求解的方程来处理.这种方法完全摆脱了对逆散射变换的直接方法.变分迭代方法就是属于这种新方法.该方法的优点在于计算简便,思路简明,可得到较高近似度的解.本文就是利用变分迭代方法来求解一类问题的孤子行波近似解析解.
近来,许多学者讨论了非线性问题的近似理论,近似方法也不断地优化.笔者及其合作者利用一些渐近方法来研究一类数学物理问题[14-23].本文首先构造一个变分迭代式,然后进行迭代计算,得到了相应强非线性波动方程的孤立波的任意次精度近似解.
考虑如下强非线性波动方程:
(1)
其中系数a,c1,c2和d均为正常数,n是正整数,f为关于其变量为充分光滑的有界函数.
首先做行波变换:
(2)
设u(s)=w(t,x),则方程(1)为
(3)
其中G(s,u)=f(t,x,w).
引入一个泛函F[u]:
(4)
式中![]() 为u的限制变量,λ为Lagrange乘子[24-25].将泛函式(4)进行变分运算δF:
为u的限制变量,λ为Lagrange乘子[24-25].将泛函式(4)进行变分运算δF:
令泛函F的变分为零(δF=0).于是λ(ξ,s)应满足
(5)
(6)
由式(5)、(6)可解得
(7)
于是由式(4)、(7), 可构造方程(3)解的变分迭代关系式:
(8)
为了求方程(3)的孤子波解, 今取如下非线性微分方程的孤子波解为变分迭代式(8)的初始迭代u0(s):
(9)
现采用双曲函数待定系数法来求解非线性方程(9)的孤子波解.
设
(10)
这里A,B和l为待定常数.故
(11)
(12)
将式(10)~(12)代入方程(9):
合并上式同类项, 并令其系数为零,有
于是有
将上述结果代入式(10), 便得到初始迭代方程(9)的孤立子解u0(s):
(13)
由式(8)、(13), 可得方程(3)的一次变分迭代解u1(s):

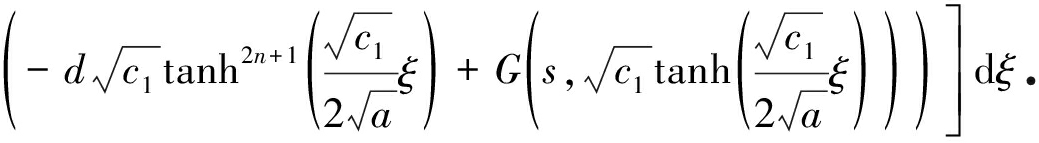
(14)
进而可得方程(3)的二次变分迭代解u2(s):
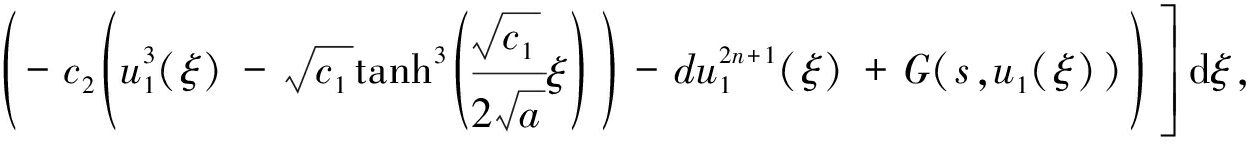
(15)
其中u1由式(14)表示.
继续用相同的方法,还能得到方程(3)孤子波解的更高次近似解.
由此,便得到方程(3)的变分迭代近似解序列un(s).由泛函分析变分的极值理论[26-27]知,函数序列un(s)在区域[0,M]上是一致收敛的,其中M为足够大的常数,而且极限函数u(s)是方程(3)的解.于是un(s)就是波动方程(2)的第n次变分迭代孤子波近似解.
再由行波变换(2),un(x-at)就是超非线性波动方程(1)的第n次变分迭代孤子行波近似解wn(t,x):
wn(t,x)=wn-1(t,x)-
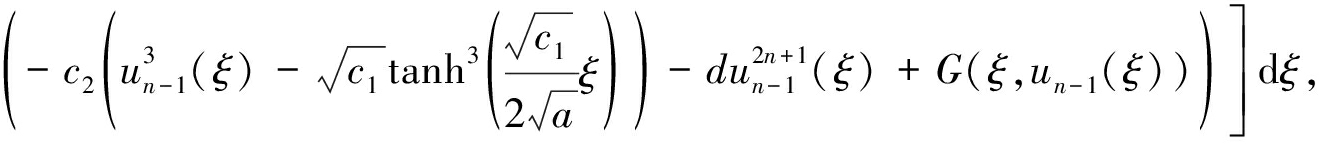
其中w0由式(13)决定,wj(j=1,2,…,n-1)可依次地确定.
例 考虑如下一个简单的非线性波动方程:
(16)
做行波变换s=x-t,方程(16)的解w(t,x)=u(s)满足
(17)
由式(7), 对应的Lagrange乘子为
(18)
于是由式(8)、(18), 可构造方程(16)解的变分迭代关系式:
(19)
由式(13), 取方程
的孤立子解
(20)
为迭代式(19)的初始迭代.再由式(20)和(14), 不妨取小参数ε=5×10-3,波动方程(17)解的一次迭代u1(s)为
(21)
非线性波动方程(17)的初始迭代u0(s)和一次近似变分迭代u1(s)的曲线图形分别见图1和图2.
由式(15)和(21), 波动方程(17)解的二次迭代u2(s)为
其中u1由式(21)表示.
继续用相同的方法,还能得到非线性方程(17)孤子波解的更高次近似解.
利用行波变换s=x-t,便得到非线性波动方程(16)对应的变分迭代初始行波解w0(t,x)和变分迭代一次近似行波解w1(t,x):
其曲面图如图3和图4所示.

图1 方程(17)的孤子波u0(s)的曲线图2 方程(17)的孤子波u1(s)的曲线
Fig. 1 The curve of solitary waveu0(s)Fig. 2 The curve of solitary waveu1(s)
to eq. (17) to eq. (17)
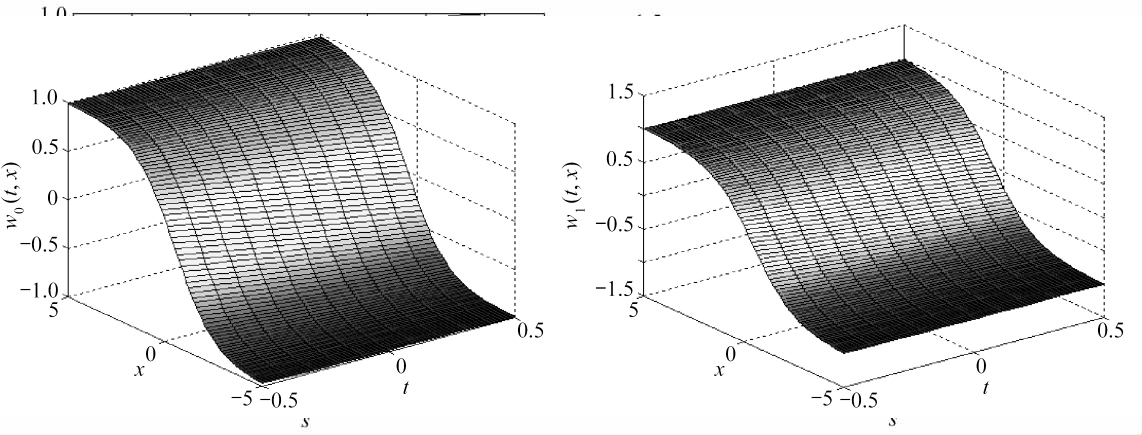
图3 方程(16)的孤子波w0(t,x)的曲面图4 方程(16)的孤子波w1(t,x)的曲面
Fig. 3 The surface of solitary wavew0(t,x)Fig. 4 The surface of solitary wavew1(t,x)
to eq. (16) to eq. (16)
波动方程(16)解的二次迭代w2(t,x)为
其中u1由式(21)表示.
继续用相同的方法,还能得到非线性方程(16)的更高次孤子波行波近似解.
变分迭代方法是一种泛函的解析求解方法,并且方法简单.它不同于通常的数值模拟方法.用变分迭代方法得到的近似解析式还能进行解析运算.事实上,波动方程(1)的孤子波解,提供了一个构造任意次精度的孤子波近似解.它还可以通过解析运算从定量的角度来研究有关孤子波的其他有关的定性性态.
致谢 本文作者衷心感谢亳州学院教学研究项目(重点项目)(2017zdjy02)和亳州学院自然科学研究项目(重点项目)(BY2017B02)对本文的资助.
[1] MCPHADEN M J, ZHANG D. Slowdown of the meridional overturning circulation in the upper Pacific Ocean[J].Nature, 2002,415(6872): 603-608.
[2] LOUTSENKO I. The variable coefficient Hele-Shaw problem, integrability and quadrature identities[J].Communications in Mathematical Physics, 2006,268(2): 465-479.
[3] GEDALIN M. Low-frequency nonlinear stationary waves and fast shocks: hydrodynamical description[J].Physics of Plasmas, 1998,5(1): 127-132.
[4] PARKES E J. Some periodic and solitary travelling-wave solutions of the short-pulse equation[J].Chaos Solitons &Fractals, 2008,38(1): 154-159.
[5] GU Daifang, PHILANDER S G H. Interdecadal climate fluctuations that depend on exchanges between the tropics and extratropics[J].Science, 1997,275(5301): 805-807.
[6] 马松华, 强继业, 方建平. (2+1)维Boiti-Leon-Pempinelli系统的混沌行为及孤子间的相互作用[J]. 物理学报, 2007,56(2): 620-626.(MA Songhua, QIANG Jiye, FANG Jianping. The interaction between solitons and chaotic behaviours of (2+1)-dimensional Boiti-Leon-Pempinelli system[J].Acta Physica Sinica, 2007,56(2): 620-626.(in Chinese))
[7] 潘留仙, 左伟明, 颜家壬. Landau-Ginzburg-Higgs方程的微扰理论[J]. 物理学报, 2005,54(1): 1-5.(PAN Liuxian, ZUO Weiming, YAN Jiaren. The theory of the perturbation for Landau-Ginzburg-Higgs equation[J].Acta Physica Sinica, 2005,54(1): 1-5.(in Chinese))
[8] 吴国将, 韩家骅, 史良马, 等. 一般变换下双Jacobi椭圆函数展开法及应用[J]. 物理学报, 2006,55(8): 3858-3863.(WU Guojiang, HAN Jiahua, SHI Liangma, et al. Double Jacobian elliptic function expansion method under a general function transform and its applications[J].Acta Physica Sinica, 2006,55(8): 3858-3863.(in Chinese))
[9] 马松华, 吴小红, 方建平, 等. (3+1)维Burgers系统的新精确解及其特殊孤立子结构[J]. 物理学报, 2008,57(1): 11-17.(MA Songhua, WU Xiaohong, FANG Jianping, et al. New exact solutions and special soliton structures for the (3+1)-dimensional Burgers system[J].Acta Physica Sinica, 2008,57(1): 11-17.(in Chinese))
[10] 李帮庆, 马玉兰. (G′/G)展开法和(2+1)维非对称Nizhnik-Novikov-Veselov系统的新精确解[J]. 物理学报,2009,58(7): 4373-4378.(LI Bangqing, MA Yulan. (G′/G)-expansion method and new exact solutions for (2+1)-dimensional asymmetrical Nizhnik-Novikov-Veselov system[J].Acta Physica Sinica, 2009,58(7): 4373-4378.(in Chinese))
[11] 周振春, 马松华, 方建平, 等. (2+1)维孤子系统的多孤子解和分形结构[J]. 物理学报, 2010,59(11): 7540-7545.(ZHOU Zhenchun, MA Songhua, FANG Jianping, et al. Multi-soliton solutions and fractal structures in a (2+1)-dimensional soliton system[J].Acta Physica Sinica, 2010,59(11): 7540-7545.(in Chinese))
[12] 高亮, 徐伟, 唐亚宁, 等. 一类广义Boussinesq方程和Boussinesq-Burgers方程新的显式精确解[J]. 物理学报, 2007,56(4): 1860-1869.(GAO Liang, XU Wei, TANG Yaning, et al. New explicit exact solutions of one type of generalized Boussinesq equations and the Boussinesq-Burgers equation[J].Acta Physica Sinica, 2007,56(4): 1860-1869.(in Chinese))
[13] 李向正, 李修勇, 赵丽英, 等. Gerdjikov-Ivanov方程的精确解[J]. 物理学报, 2008,57(4): 2031-2034.(LING Xiangzheng, LI Xiuyong, ZHANG Liying, et al. Exact solutions of Gerdjikov-Ivanov equation[J].Acta Physica Sinica, 2008,57(4): 2031-2034.(in Chinese))
[14] 石兰芳, 聂子文. 应用全新G′/(G+G′)展开方法求解广义非线性Schrödinger方程和耦合非线性Schrödinger方程组[J]. 应用数学和力学, 2017,38(5): 539-552.(SHI Lanfang, NIE Ziwen. Solutions to the nonlinear Schrödinger equation and coupled nonlinear Schrödinger equations with a newG′/(G+G′)-expansion method[J].Applied Mathematics and Mechanics, 2017,38(5): 539-552. (in Chinese))
[15] 石兰芳, 莫嘉琪. 一类强非线性方程Robin问题奇摄动解[J]. 应用数学, 2017,30(2): 247-251.(SHI Lanfang, MO Jiaqi. A class of singular perturbation solutions to strong nonlinear equation Robin problems[J].Mathematica Applicata, 2017,30(2): 247-251.(in Chinese))
[16] FENG Yihu, MO Jiaqi. Asymptotic solution for singularly perturbed fractional order differential equation[J].Journal of Mathematics, 2016,36(2): 239-245.
[17] FENG Yihu, CHEN Xianfeng, MO Jiaqi. The shock wave solution of a class of singularly perturbed problem for generalized nonlinear reaction diffusion equation[J].Mathematica Applicata, 2017,30(1): 1-7.
[18] 冯依虎, 莫嘉琪. 一类非线性非局部扰动LGH方程的孤子行波解[J]. 应用数学和力学, 2016,37(4): 426-433.(FENG Yihu, MO Jiaqi. Soliton travelling wave solutions to a class of nonlinear nonlocal disturbed LGH equations[J].Applied Mathematics and Mechanics, 2016,37(4): 426-433.(in Chinese))
[19] 冯依虎, 石兰芳, 莫嘉琪. 关于将飞秒脉冲激光用于纳米金属薄膜传导系统的研究[J]. 工程数学学报, 2017,34(1): 13-20.(FENG Yihu, SHI Lanfang, MO Jiaqi. Study of transfers system for femtosecond pulse laser to nano metal film[J].Chinese Journal of Engineering Mathematics, 2017,34(1): 13-20.(in Chinese))
[20] 冯依虎, 陈怀军, 莫嘉琪. 一类非线性奇异摄动自治微分系统的渐近解[J]. 应用数学和力学, 2017,38(5): 355-363.(FENG Yihu, CHEN Huaijun, MO Jiaqi. Asymptotic solution to a class of nonlinear singular perturbation autonomic differential system[J].Applied Mathematics and Mechanics, 2017,38(5): 355-363.(in Chinese))
[21] 冯依虎, 林万涛, 莫嘉琪. 大气中尘埃扩散方程行波解[J]. 吉林大学学报(理学版), 2016,54(2): 234-240.(FENG Yihu, LIN Wantao, MO Jiaqi. Travelling wave solution for dust diffusion equation in atmosphere[J].Journal of Jilin University(Science Edition), 2016,54(2): 234-240.(in Chinese))
[22] 冯依虎, 林万涛, 莫嘉琪. 一类大气量子等离子流体动力学孤立子波渐近解[J]. 吉林大学学报(理学版), 2017,55(3): 474-480.(FENG Yihu, LIN Wantao, MO Jiaqi. Asymptotic solution for a class of quantum plasma fluid dynamics solitary wave in atmosphere[J].Journal of Jilin University(Science Edition), 2017,55(3): 474-480.(in Chinese))
[23] 冯依虎, 莫嘉琪. 一类广义奇摄动非线性双曲型积分-微分方程模型[J]. 吉林大学学报(理学版), 2017,55(5): 1055-1060.(FENG Yihu, MO Jiaqi. A class of generalized nonlinear hyperbolic integral-differential equation with singular perturbation model[J].Journal of Jilin University(Science Edition), 2017,55(5): 1055-1060.(in Chinese))
[24] LEBEDEV L P, CLOUD M J.The Calculus of Variations and Functional Analysis With Optimal Control and Applications in Mechanics[M]. New York: World Scientific, 2003.
[25] 何吉欢. 工程和科学计算中的近似非线性分析方法[M]. 郑州: 河南科学技术出版社, 2002.(HE Jihuan.Approximate Nonlinear Analytical Methods in Engineering and Sciences[M]. Zhengzhou: Henan Science and Technology Press, 2002.(in Chinese))
[26] DE JAGER M, JIANG F R.The Theory of Singular Perturbations[M]. Amsterdam: North-Holland Publishing Co, 1996.
[27] BARBU L, MOROSANU G.Singularly Perturbed Boundary-Value Problems[M]. Basel: Birk-häuser, 2007.