引 言
在自然界和工程技术中,高速运转的传送带、磁带、锯片、缆绳等,都可以看成是一段连续体在轴向运动,即为轴向运动的一维结构.轴向运动体系的研究可以追溯到19世纪人们对轴向运动的弦线的研究.轴向运动的弦线不能承受弯矩、轴向压力和剪力,必须承受一定的拉力来保持其直线形态,而梁有抗弯刚度,可以承受压力和剪力,具有更多力学特性,因此人们开始更多地研究轴向运动梁的问题.19世纪以来,关于轴向运动梁问题的研究主要集中于模态分析、参数激振及其稳定性、能量和实验分析等.对于轴向运动梁非线性振动发展出的研究方法可分为三大类:谐波平衡法、摄动法和等效线性法.
目前国内外的学者对轴向运动梁的横向振动问题进行了大量的研究.Gosselin等[1]研究了具有不同轴向运动速度的悬臂梁在液体里伸缩时的动力学和稳定性特性.Al-Bedoor和Khulief [2]在Euler梁理论的假设下,使用Newton第二定律得到轴向运动梁模型的一般运动偏微分方程,并对方程求解.Park等[3]运用Hamilton原理推导运动方程并用Galerkin离散得到Euler描述和Lagrange描述下轴向运动梁的动力学响应,不过未考虑自重对振动响应的影响.Pellicano和Vestroni[4]在轴向运动梁理论的基础上, 研究了在简谐激励下轴向运动简支梁在大速度范围下的响应.Cepon和Boltezar[5]研究了在两支撑点间以一轴向速度运动结构的弹性振动.齐亚峰等[6]研究了轴向运动简支梁的振动响应分析.马国亮、陈立群[7]研究了轴向运动梁的横向随机响应.陈荣泉、余小刚[8]对轴向运动体系的横向振动进行了分析.李成澄、赵凤群[9]对轴向运动变截面黏弹性梁的振动和稳定性进行了分析.李山虎等[10]研究了轴向运动悬臂梁的独立模态振动.戎艳天、胡宇达[11]研究了磁场环境中移动载荷作用下轴向运动梁的磁弹性参强联合共振问题.但是,对轴向运动梁问题的研究文献中也存在一些问题乃至错误.例如,高等教育出版社出版的《振动力学》(刘延柱(第二版))[12],在进行轴向运动梁动力学方程的推导时,有些论述不易理解;还有研究具有裂纹的轴向运动梁振动问题时,一些文献采用Euler描述来建立具有裂纹的轴向运动梁的动力学方程,求解时假设在某一固定的Euler坐标处存在裂纹,这样的问题在物理上是不可能实现的.针对轴向运动梁振动问题研究中存在的问题,本文对什么是轴向运动梁横向振动问题以及研究轴向运动梁横向振动问题的方法进行了论述,指出了轴向运动梁振动问题研究中存在的一些错误并进行了更正.针对一端可看作固定边界条件的轴向运动悬臂梁,基于连续体的模态叠加法推导了轴向运动梁动力响应的计算公式,进行了实例计算,并对计算结果进行了详细的讨论.
1 轴向运动梁横向振动问题及其动力学方程推导
轴向运动梁的简易模型如图1所示,两固定于地面的支座相距为l,梁穿过两支座套筒以一定的速度沿水平方向(即x轴向)运动.轴向运动梁的讨论对象是介于支座之间不断流动的物体.因此,需从Euler的运动场概念出发,将梁截面的速度、加速度等所有物理量均视为场坐标x和时间t的函数.

图1 轴向运动梁
Fig. 1 The axially moving beam
文献[12]中推导并得到了考虑轴向力作用效应的轴向运动梁横向振动的动力学方程.当不考虑轴向力对轴向运动梁横向振动的影响时,可将其推导过程简述如下.
设两支座间的距离为l,梁的物理参数:材料密度为ρ,截面面积为s,抗弯刚度为EI,以速度v(t)沿x轴运动.由于轴向运动存在,挠度w(x,t)随时间的变化率,即横向速度和加速度的计算必须按照速度场概念进行.由于轴向运动,场坐标x随时间的变化率为
(1)
计算w(x,t)对时间的导数时必须考虑上述x坐标的变化率,导出
(2)
对时间再次求导,得到加速度
(3)
当仅讨论自由振动时,将式(3)代入梁弯曲振动方程,略去激励项,可得
(4)
若梁作轴向匀速运动,令v=v0代入上式简化为常系数微分方程:
(5)
在传统的结构动力学中,无轴向运动的受轴向压力作用梁的弯曲自由振动方程为
(6)
式(5)采用的是Euler坐标,式(6)采用的是Lagrange坐标.将式(5)和式(6)对比发现,从数学形式上,式(5)中的![]() 和式(6)中的
和式(6)中的![]() 相对应,表明轴向运动会产生类似于轴向力的效果.对受轴力作用的梁来说,当承受压力时,梁会发生横向失稳,因此,对轴向运动梁来说,特定速度下梁也会发生横向失稳,这也是轴向运动梁横向振动问题引起众多学者关注的原因.
相对应,表明轴向运动会产生类似于轴向力的效果.对受轴力作用的梁来说,当承受压力时,梁会发生横向失稳,因此,对轴向运动梁来说,特定速度下梁也会发生横向失稳,这也是轴向运动梁横向振动问题引起众多学者关注的原因.
关于Euler坐标和Lagrange坐标,Park等[3]详细介绍了Euler坐标和Lagrange坐标用来描述轴向运动梁振动问题的概念和区别,分别在Euler坐标和Lagrange坐标下推导出轴向运动梁的动力学方程并进行了结果对比.对比显示采用Euler坐标和Lagrange坐标来描述,虽然运动方程形式不同,但是轴向运动梁的振动实质是一样的.
Euler坐标和Lagrange坐标各有优缺点.Euler坐标相对地面是固定坐标系,Lagrange坐标是将坐标原点固定在运动梁上一点,是随梁一起运动的动坐标系.对图1所示的轴向运动梁,只关心两支座间的梁段横向振动时,采用Euler坐标,边界条件是固定的;若采用Lagrange坐标描述,轴向运动梁的振动方程和传统梁的振动方程是一样的,只是边界条件是不断变化的,系统为时变系统.
2 轴向运动梁研究文献中的问题
2.1 场坐标随时间的变化率的问题
文献[12]中,关于场坐标的描述为:由于轴向运动,场坐标x随时间的变化率为dx/dt=v(t),即式(1).
由图1可知,Euler坐标x为描述空间位置的坐标,与时间t是两个相互独立的物理量.式(1)从数学形式上表示场坐标x为时间的函数,并称其为场坐标x随时间的变化率.因此,从物理概念上是难以理解的.正确地理解和表述采用下面的方式更合理.
对于梁横截面的位置可采用Lagrange坐标X来描述,式(2)和(3)的物理意义为Lagrange坐标X对应横截面在横向的速度和加速度,因此,式(1)只是一种数学表达形式,不应解释为场坐标x为时间的函数,其物理意义为,梁作轴向运动时,Lagrange坐标X所对应的空间位置随时间的变化率.
同样的问题也存在于Fung等[13]所著文献中,文中采用Euler坐标,描述梁上任意一点的位置为(x(t),y),x是描述空间位置的物理量,与时间t是相互独立的,所以x(t)的表述在物理意义上也是不恰当的.
2.2 具有裂纹的轴向运动梁振动问题
在Yang等[14-15]所著文献中,研究了轴向运动裂纹梁横向振动问题.研究如图2所示轴向运动裂纹梁: 两支座间距为L,裂纹梁以一定速度穿过两支座进行运动.
梁截面宽b,高h,裂纹深度a,裂纹位置c,材料弹性模量及密度分别为E和ρ ,为引入裂纹场效应,采用裂纹梁连续等效刚度模型EIc(x).

图2 含开口裂纹梁
Fig. 2 A beam with a single opening crack
由于裂纹梁连续等效刚度的引入,可将含开口裂纹梁视为弯曲刚度为EIc在长度方向上变化的无裂纹梁,采用Euler描述导出了轴向运动梁的振动方程.
文献[14-15]后续算例讨论了裂纹相对位置c/L对轴向运动梁振动频率的影响.
由上可知,由于采用的是Euler描述,文献[14-15]求解的问题其物理实质为轴向运动梁在空间固定位置c处一直存在裂纹,显然,轴向运动梁在空间固定位置处一直存在裂纹在物理意义上是不可能实现的,所以,关于具有裂纹的轴向运动梁采用Euler描述来研究是存在问题的.
3 轴向运动悬臂梁动力响应计算方法
轴向运动悬臂梁模型如图3所示.长为L的梁以一定的速度沿水平方向(即x轴向)运动.悬臂梁左端扰度和转角为零,右端自由,因此,可称为轴向运动悬臂梁.对于轴向运动悬臂梁,Park等[3]运用Hamilton原理,分别采用Euler描述和Lagrange描述推导了其动力学方程,并用Galerkin离散求解了动力响应.但是,文献[3]中未说明建立动力学方程时位移零点的位置,从其计算结果来看,未考虑自重对振动响应的影响.
在振动力学中,一般以静平衡位置作为位移的零点(即坐标原点).由于梁在不断外伸的过程中,受自重作用,静平衡位置是不断变化的.因此,建立轴向运动梁的动力学方程时需指定统一的坐标原点.对于一端可看作固定边界条件的轴向运动悬臂梁,以水平位置即图中的x轴为坐标原点,把梁的自重等效为分布在梁上的均布载荷,利用悬臂梁的模态函数推导出含自重效应的轴向运动悬臂梁的动力响应计算公式.
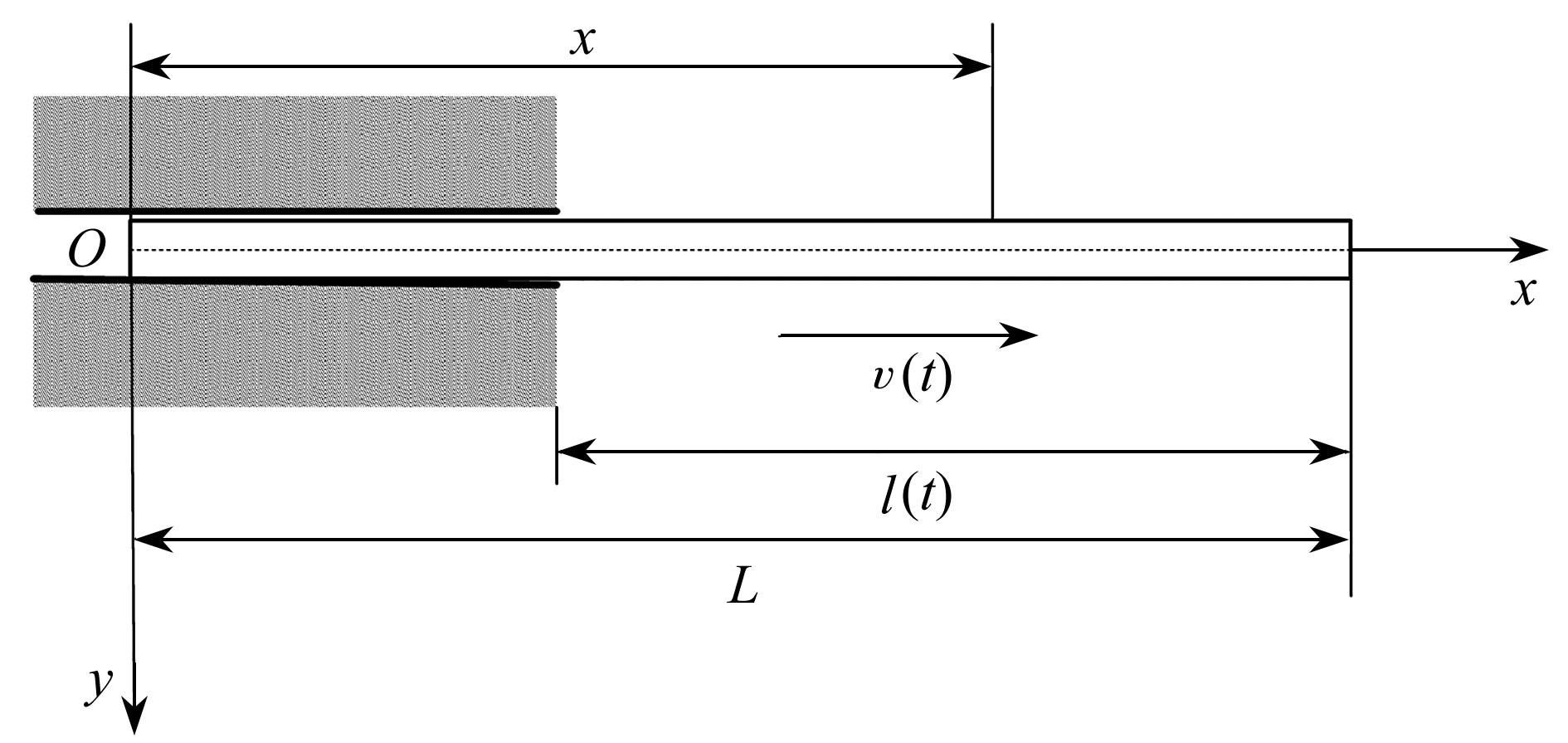
图3 轴向运动悬臂梁的模型
Fig. 3 The model for the axially moving cantilever beam
由于在梁运动的过程中,固定端的位置一直是在改变的.所以定义x为梁上一点到梁的最左端的距离,采用的是Lagrange坐标描述轴向运动梁.设梁的初始外伸长度为l0,速度为v(t),梁截面积为A,梁的实际外伸长度则是关于时间t的函数,即l=l0+v(t)t.
第一步,已知悬臂梁的模态函数为
φi(x)=c[cos(βix)-cosh(βix)+ξi(sin(βix)-sinh(βix))],
(7)
其中![]()
根据模态正则化原理![]() 求出系数c的值,然后可以得到正则模态函数
求出系数c的值,然后可以得到正则模态函数![]()
第二步,将响应写成模态函数的线性组合:
(8)
将上式代入等截面梁的动力学方程
得到
(9)
其中![]()
在只考虑自重的情况下,
因此,就可以求出Qi(t).在计算式(9)时,由于外伸长度是随时间变化的,所以动力学方程是时变的,对式(9)可采用Newmark-β法进行数值积分,并用MATLAB编程计算得到qi(t).
第三步,求初始条件.
首先,求模态坐标的初始条件qi(0):
初始时刻,梁的外伸长度为l0,处于静止状态.采用材料力学中的静挠度曲线,于是有
然后就可以得到qi(0).
初始时刻梁静止,因此模态坐标的初始速度为零.
第四步,得到振动响应函数w(x,t).取x=L,画出自由端挠度w随时间t变化的曲线.
4 计算实例及结果
在只考虑自重的情况下,给定轴向运动梁的基本参数如下.轴向运动梁全长L=3 m,初始外伸长度l0=1.8 m.材料的密度ρ=2.738 6×103 kg/m3,横截面的面积A=1.466 1×10-3 m2.横截面的惯性矩I=1.107 3×10-8 m4,弹性模量E=6.833 5×1010 Pa.计算不同轴向运动速度下轴向运动梁的横向振动响应.将梁的推出长度控制在1 m左右,计算时,式(8)中的n=4,即采用4阶截断模态.
4.1 匀速运动下梁的振动
设梁以匀速从左向右运动.图4和图5分别为v=0.1 m/s和v=0.2 m/s时自由端的挠度时间曲线,其中最大挠度分别为0.051 5 m和0.052 6 m.
两种不同速度条件下,轴向运动梁的挠度都是先减小后增大.速度越大,梁的振动幅度越大,最大挠度值也越大,而且挠度增大的速度也越快.
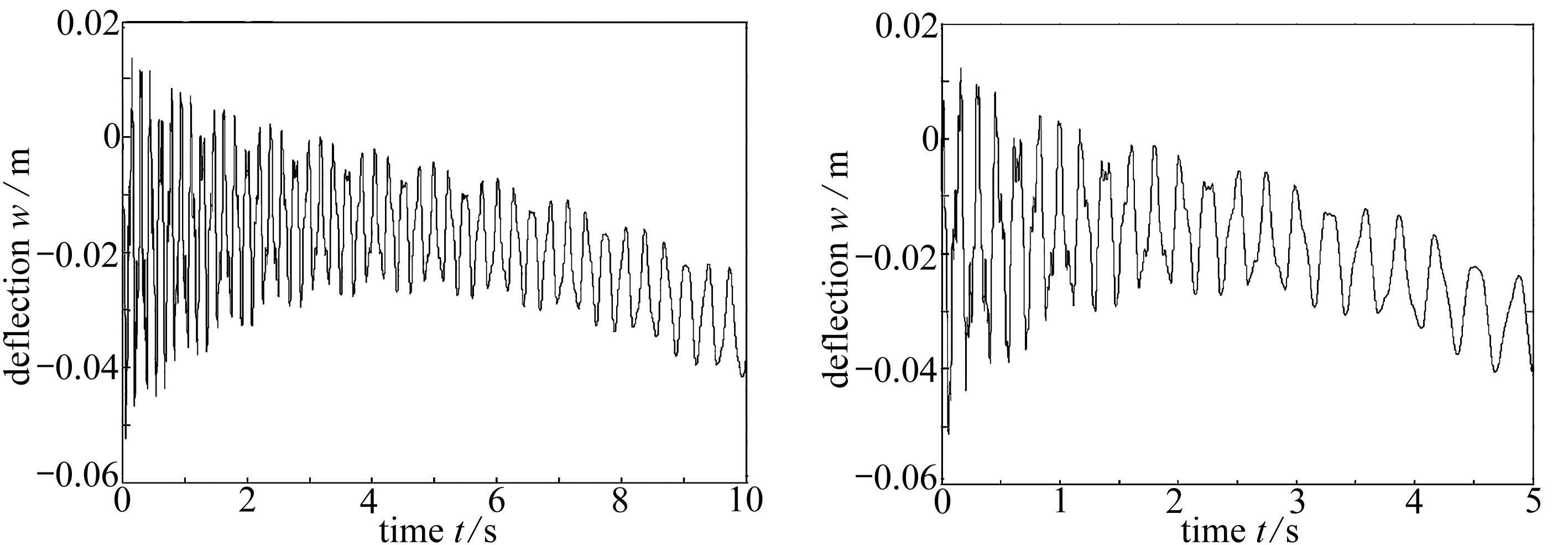
图4 速度为0.1 m/s图5 速度为0.2 m/s
Fig. 4 The speed is 0.1 m/sFig. 5 The speed is 0.2 m/s
4.2 变速运动下梁的振动
设梁从左向右运动的速度v=v0+at.
1) 给定初始速度v0为0.05 m/s,图6和图7分别为加速度a=0.01 m/s2和a=0.02 m/s2时自由端的挠度时间曲线,最大挠度分别为0.051 4 m和0.052 5 m.
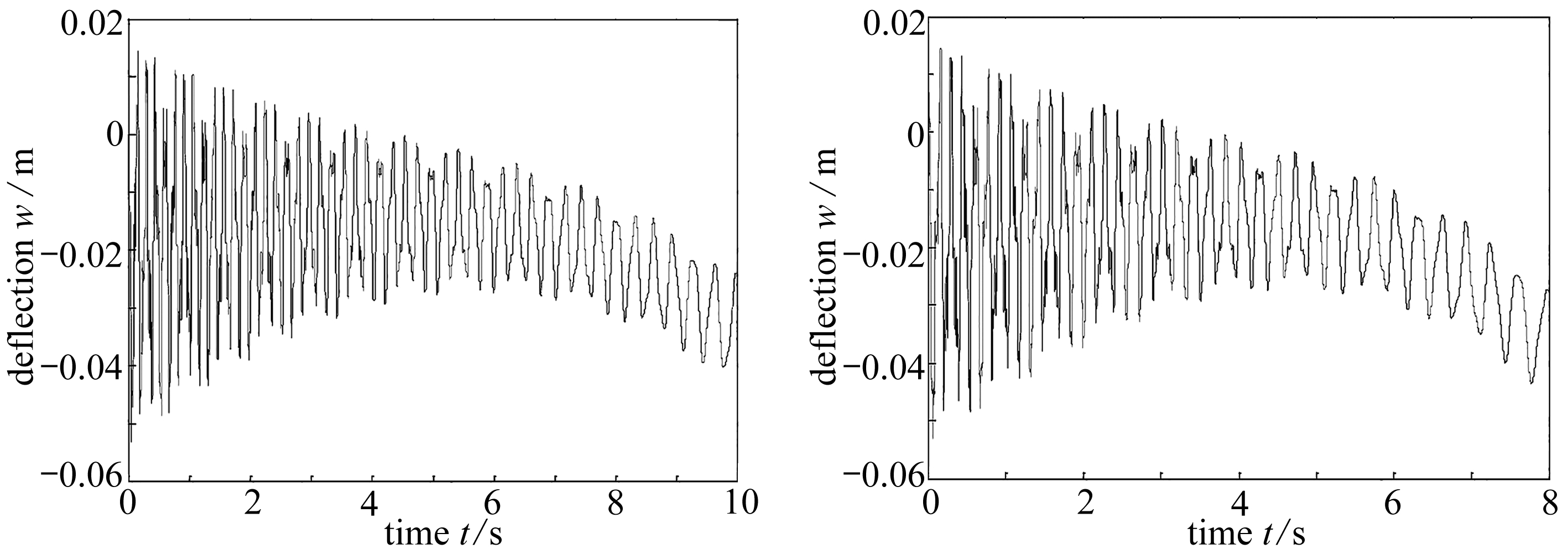
图6 加速度为0.01 m/s2图7 加速度为0.02 m/s2
Fig. 6 The acceleration is 0.01 m/s2 Fig. 7 The acceleration is 0.02 m/s2
从图6和图7可见,两者都是挠度先减小后增大,当加速度越大时,轴向运动梁的最大挠度值也越大,而且挠度增大的过程更加迅速.
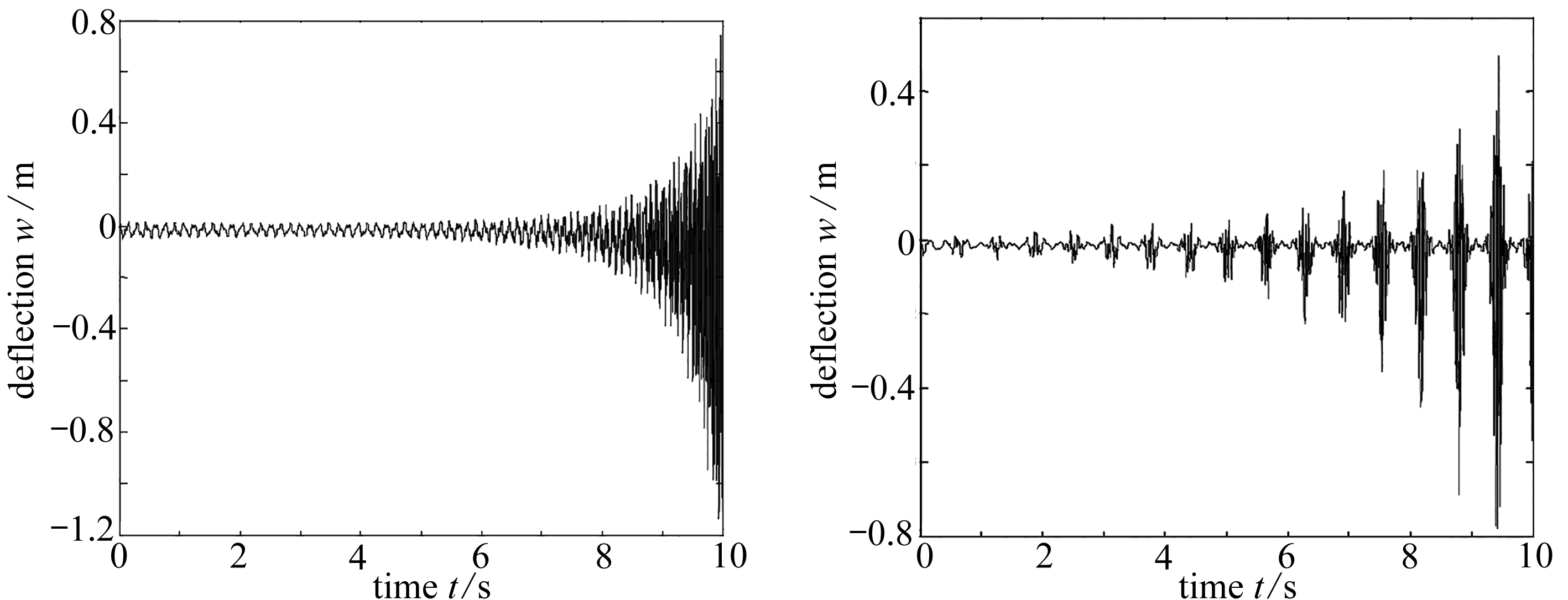
图8 加速度为-0.02 m/s2 图9 速度简谐变化
Fig. 8 The acceleration is -0.02 m/s2Fig. 9 The speed with a simple harmonic change
2) 给定初始速度v0为0.05 m/s,加速度a=-0.02 m/s2,此时梁做减速运动,其挠度与时间关系如图8所示.
从图8可以看到,轴向运动梁在8~10 s的时候出现了失稳现象,轴向运动梁有往回缩的情况.
4.3 速度简谐变化下梁的振动
设梁从左向右运动的速度v=v0+Hsin(ωt).给定初始速度v0为-0.05 m/s,H=3 m/s,ω=10 s-1时,其挠度和时间关系如图9所示.
从图9可以看到,轴向运动梁在8~10 s的时候出现了失稳现象.结合前面图8得出的图像,可以得到轴向运动梁的运动方向也会影响其振动响应这一结论.
5 结 论
本文对什么是轴向运动梁振动问题以及研究轴向运动梁振动问题的方法进行了论述,指出了对轴向运动梁振动问题研究中存在的一些错误并进行了更正.针对一端可看作固定边界条件的轴向运动悬臂梁,基于连续体的模态叠加法,推导了轴向运动梁动力响应的计算公式,进行了实例计算.通过大量的实例计算,并将得到的图像进行对比分析,得出了以下结论:不同速度下梁的挠度变化规律基本一致,都是先减小后增大;速度越大,轴向运动梁的振动幅度越大,其最大挠度值也越大;同时轴向运动梁往回缩的情况下,会在某一时刻出现失稳现象.所以,影响轴向运动梁振动响应的因素主要有速度和运动方向.
[1] GOSSELIN F, PAIDOUSSIS M P, MISRA A K. Stability of a deploying/extruding beam in dense fluid[J]. Journal of Sound and Vibration, 2007, 299(1/2): 123-142.
[2] AL-BEDOOR B O, KHULIEF Y A. An approximate analytical solution of beam vibrations during axial motion[J]. Journal of Sound and Vibration, 1996, 192(1): 159-171.
[3] PARK S, YOO H H, CHUNG J T. Eulerian and Lagrangian descriptions for the virbration analysis of a deploying beam[J]. Journal of Mechanical Science and Technology, 2013, 27(9): 2637-2643.
[4] PELLICANO F, VESTRONI F. Complex dynamics of high-speed axially moving systems[J]. Journal of Sound and Vibration, 2002, 258(1): 31-44.
[5] CEPON G, BOLTEZAR M. Computing the dynamic response of an axially moving continuum[J]. Journal of Sound and Vibration, 2007, 300: 316-329.
[6] 齐亚峰, 刘宁, 杨国来. 轴向运动简支梁振动响应分析[J]. 机械制造与检测技术, 2016, 37(12): 126-129.(QI Yafeng, LIU Ning, YANG Guolai. Vibration response analysis of simply supported beams with axial motion[J]. Mechanical Manufacturing and Inspection Technology, 2016, 37(12): 126-129.(in Chinese))
[7] 马国亮, 陈立群. 轴向运动梁的横向随机响应[J]. 振动与冲击, 2014, 33(9): 78-82.(MA Guoliang, CHEN Liqun. Random vibration response of axially moving beams[J]. Vibration and Shock, 2014, 33(9): 78-82.(in Chinese))
[8] 陈荣泉, 余小刚. 轴向运动体系横向振动控制的研究进展[J]. 机电技术, 2017(4): 117-120.(CHEN Rongquan, YU Xiaogang. Research on lateral vibration control of axial motion system[J]. Electromechanical Technology, 2017(4): 117-120.(in Chinese))
[9] 李成澄, 赵凤群. 轴向运动变截面粘弹性梁的振动与稳定性分析[J]. 振动与冲击, 2016, 35(14): 107-111.(LI Chengcheng, ZHAO Fengqun. Vibration and stability analysis of viscoelastic beams with variable axial motion[J]. Vibration and Shock, 2016, 35(14): 107-111.(in Chinese))
[10] 李山虎, 杨靖波, 黄清华, 等. 轴向运动悬臂梁的独立模态振动控制,Ⅰ: 近似理论分析[J]. 应用力学学报, 2002, 19(1): 35-38.(LI Shanhu, YANG Jingbo, HUANG Qinghua, et al. Independent model-space vibration control of an axially moving cantilever beam, part Ⅰ: theoretical analysis of approximation[J]. Journal of Applied Mechanics, 2002, 19(1): 35-38.(in Chinese))
[11] 戎艳天, 胡宇达. 移动载荷作用下轴向运动载流梁的参强联合共振[J]. 应用数学和力学, 2018, 39(3): 266-277.(RONG Yangtian, HU Yuda. Parametric joint resonance of axially moving current-carrying beam under moving load[J]. Applied Mathematics and Mechanics, 2018, 39(3): 266-277.(in Chinese))
[12] 刘延柱. 振动力学[M]. 2版. 北京: 高等教育出版社, 2011.(LIU Yanzhu. Vibration Mechanics[M]. 2nd ed. Beijing: Higher Education Press, 2011.(in Chinese))
[13] FUNG R F, LU P Y, TSENG C C. Non-linearly dynamic modeling of an axially moving beam with a tip mass[J]. Journal of Sound and Vibration, 1998, 218(4): 559-571.
[14] YANG E C, ZHAO X, LI Y H. Free vibration analysis for cracked FGM beams by means of a continuous beam model[J]. Shock and Vibration, 2015, 2015(4). DOI: 10.1155/2015/197049.
[15] 杨鄂川, 秦营, 赵翔, 等. 含轴向运动效应的裂纹梁横向振动频率研究[J]. 力学季刊, 2016, 37(1): 74-80.(YANG Echuan, QIN Ying, ZHAO Xiang, et al. Investigations on transversal vibration characteristics of cracked axially moving beams[J]. Quarterly Journal of Mechanics, 2016, 37(1): 74-80.(in Chinese))