引 言
我国黄土高原地貌沟壑纵横、支离破碎,加之黄土本身孔隙大、 结构疏松、 湿陷性明显,导致该地区极易发生山体滑坡、 泥石流、 地面塌陷等自然灾害,直接威胁隧道工程的施工安全[1-2].在黄土地貌下进行隧道开挖必然会引起周围围岩应力的重新分布,但如何选择合适的位置布置隧道使得引起围岩应力变化幅度较小就尤为重要.因此,采用不同的数学方法系统研究复杂形状隧道围岩体应力的计算,对隧道支护具有重要的工程指导意义.
目前,国内外对隧道围岩应力的计算做了大量的工作.Fahimifar等提出了静水应力场下Burger’s黏弹性体中圆形开挖断面隧洞的解析解[3];Gao等开展了高寒区圆形隧道的弹塑性应力解析解研究[4];Zhang等提出了横观各向同性岩石中深埋椭圆形隧道的位移解析解[5].相比较而言,对非圆形断面形状的地下洞室围岩力学解析解,在数学和力学上要复杂得多,原则上可采用弹性力学的复变函数方法获得其平面弹性问题的解析解[6].祝江鸿求解了围岩应力复变函数分析法中的两个解析函数[7].基于复变函数法的地下隧洞围岩力学分析,需将开挖边界线内域(外域)看成由单位圆内域(外域)共形映射而得[6-8],将以复杂开挖断面为边界的隧洞力学分析问题转化成以单位圆周线为边界的力学问题.朱大勇等同样以Laurent级数建立起单位圆外域-洞室外域的映射函数,利用三角函数系的正交性获取了函数中各项系数的表达式,阐明了计算点调整方法和系数求解的迭代过程,其不足之处是对于复杂的开挖洞形,映射函数构成项数多达200多项,计算量大且精度低[9].郑志强也采用Schwarz-Christoffel积分建立了单位圆与多边形的映射函数,研究了被积函数中未知参数的数值计算方法,解决了参数求解和参数精度问题[10],但获取参数只是解决问题的第一步,即明确了被积函数的表达式,被积函数的积分过程依然复杂.
综上所述,受地下隧道开挖断面形状的制约,地下隧道工程力学分析中的解析解成果主要集中在规则边界应力条件下的圆形、矩形及椭圆形洞室方面,但单位圆域到任意多边形之间的共形映射函数只是构建在数学理论上较完整,有Schwarz-Christoffel积分公式[11-12]、有理分式[13-14]、Taylor级数[15-16]等模型.已有的在隧道处在不规则围岩体下围岩应力的计算中往往都简化为规则围岩体处理,但在黄土高原上,由于实际地形地貌往往是不规则,在一定程度下并不能够简化处理,且简化处理与实际相差较大.
本文在前人研究的基础上,拟采用单位圆到任意多边形的Schwarz-Christoffel(SC)变换映射算法对隧道所处不规则围岩体进行映射建模,进而确定SC变换映射函数,依据平面应变问题,得出不规则围岩体隧道的复变应力函数值.通过算例,解出隧道所在四边形围岩体的复变函数应力值,并通过已有的有限元软件进行数值模拟,分析隧道所处4种不同形状下围岩体的应力场分布规律.
1 Schwarz-Christoffel变换
考虑到实际工程问题中往往会将复杂的问题简化为简单问题,但简化会带来许多不确定的因素,则将简单问题还原成实际工程问题就尤为重要.SC变换可将规则区域映射到复杂区域,方便解决实际问题.目前,SC变换在岩土力学、 电磁学、 材料力学等研究领域均有广泛的应用.
SC变换是将在z平面的单位圆映射到w平面上的N(N≥3)边形,其一般形式为
(1)
其中ξ和πaj分别为N边形的顶点和内角,K为形状系数,C为位置系数,zj为单位圆上的点.式(1)中的系数K和C为[17]
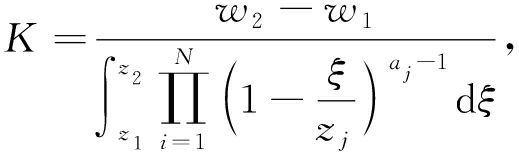
通过Gauss-Jacobi型积分得其解w(ξ),以积分路径的奇异点确定对系数进行修正,最后采用Levenberg-Marquardt算法进行参数优化,当参数选择恰当时,收敛速度相当快.
2 不规则围岩体隧道映射建模
在复杂地质构造下不规则的岩体中开挖隧道,开挖后隧道周围岩体应力重新分布,因此可将隧道围岩视为平面应力问题.映射建模思想是以单位圆为平台,隧道围岩体所在的单位圆上有N个节点,由于隧道的开挖引起各节点之间所受的围岩应力不同,在映射函数SC变换作用下,最终得到隧道在受力平衡时的多边形围岩体采动应力状态(映射建模思路如图1所示).相反,平衡时隧道围岩体形状在函数w-1(ξ)的映射下,保角映射到单位圆上,从而得出隧道围岩体原岩应力状态.
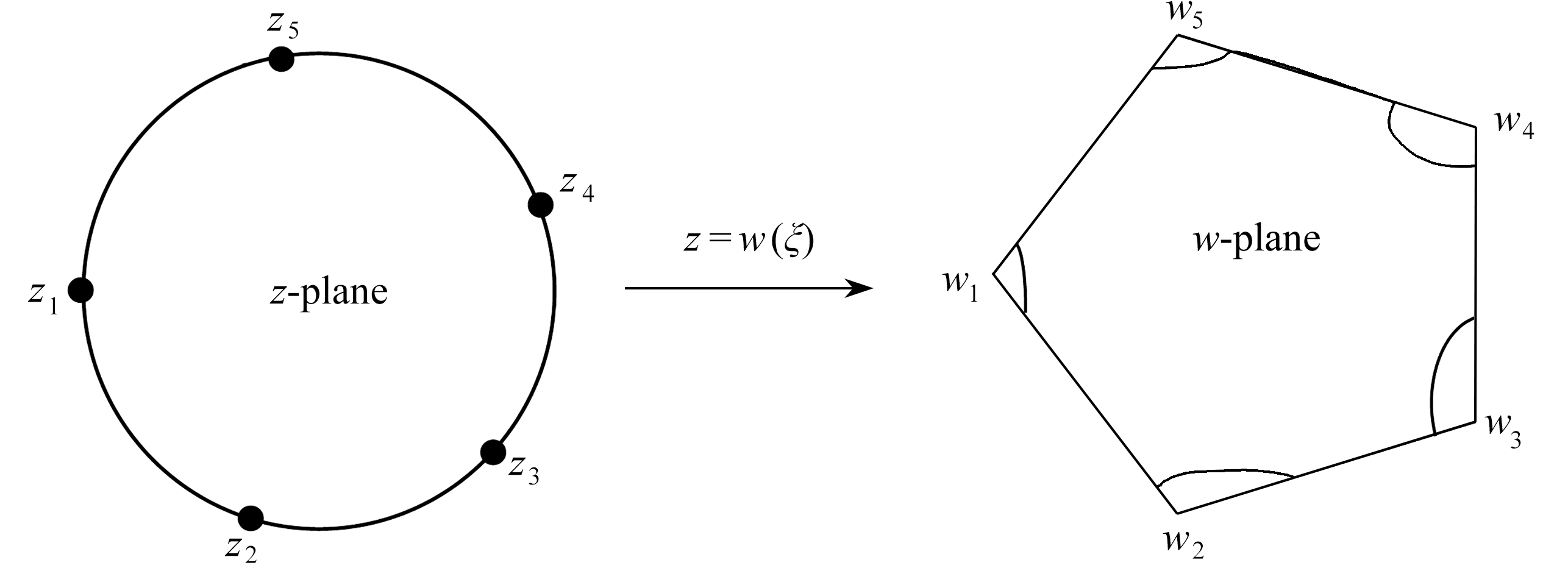
图1 单位圆到多边形映射思路图
Fig. 1 The mapping from a unit circle to a polygon
2.1 映射函数的确定
开挖后的隧道所在的围岩体形状与单位圆的映射函数分两步求得:
第一步 按照SC变换数值解法,在单位圆上任选一组对应点,固定w1,经过多次迭代,求得平衡时隧道所在围岩体形状上的顶点在单位圆上的映射点,同时求得K和C;
第二步 将求得的映射点w1,w2,w3,…,wn代入式(1)中,采用Levenberg-Marquardt算法进行计算,该算法既能保证精度,又能减少计算量,得到平衡时隧道所在围岩体形状与单位圆的映射函数w(ξ).
2.2 复变应力函数φ(ξ)和φ(ξ)求解
将隧道围岩体视为平面应力问题,根据复变函数理论,对于多边形围岩体隧道问题,运用保角变换将已经简化的单位圆隧道映射到多边形隧道进行计算.因此,运用映射函数w(ξ)将已知的单位圆映射到多边形上进行围岩应力计算.由弹性力学理论,进行多边形隧道围岩体应力计算,首先确定φ(ξ)和φ(ξ)两个解析函数,计算公式如下:
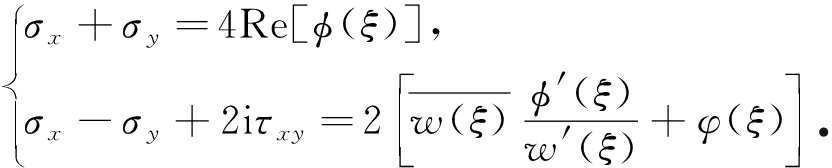
(2)
采用SC变换将z平面的单位圆映射到w平面上的多边形,因此,将式(1)代入式(2)分析整理可得
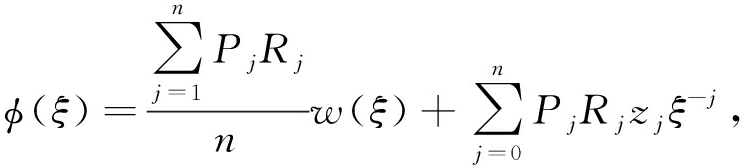
(3)
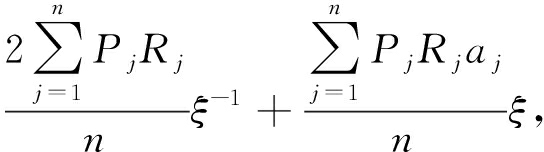
(4)
式中Pj为节点之间边所受到的力,Rj为该边到多边形中心点的距离.
围岩内任意一点的应力分量的转化可以利用弹性力学教程中的转轴公式求得[8]
σρ+σθ=4Re[φ(ξ)],
(5)
(6)
将式(3)、(4)代入式(5)、(6)中即可求出不规则围岩体隧道内任一点应力分量σρ和σθ.
3 算 例

图2 地形图
Fig. 2 The topographic map
以某隧道工程为研究对象,该隧道位于沟壑交错的黄土塬梁峁中,构造复杂、断层发育,加之上部厚重的黄土层、泥岩和泥质砂岩构成的复合盖层,隧道断面为圆形,原地形图如图2所示.需在地下906 m开挖一个圆形隧道,将该地质构造下的岩体简化为平面问题,如圆形、四边形、五边形、六边形岩体(见图3),假设岩体均质,且不再考虑简化后岩体中的结构面、裂隙和软弱夹层对强度的影响.
根据实际工程,建立岩体尺寸为长×宽=20 m×20 m的二维力学模型,其中圆形岩体中隧道尺寸D=1.5 m.岩体中隧道所处的岩体材料参数为:弹性模量E=17 GPa,Poisson比μ=0.3,密度ρ=2 600 kg/m3,内聚力c=0.8 MPa,内摩擦角β=60°.4种形状岩体应力分布分别为:
(a) 圆形.隧道顶板围岩体应力p1=20 MPa,左壁围岩体应力p2=16 MPa,右壁围岩体应力p3=12 MPa,底板围岩体应力为0 MPa;
(b) 六边形.隧道顶板围岩体应力p1=20 MPa,左上壁围岩体应力p2=16 MPa,右上壁围岩体应力p3=12 MPa,底板围岩体应力p4=8 MPa,左下、右下壁围岩体应力为0 MPa;
(c) 五边形.隧道顶板围岩体应力p1=20 MPa,左上壁围岩体应力p2=16 MPa,右上壁围岩体应力p3=12 MPa,左下、右下壁围岩体应力为0 MPa;
(d) 四边形.隧道顶板围岩体应力p1=20 MPa,左壁围岩体应力p2=16 MPa,右上壁围岩体应力p3=12 MPa,底板围岩体应力为0 MPa.
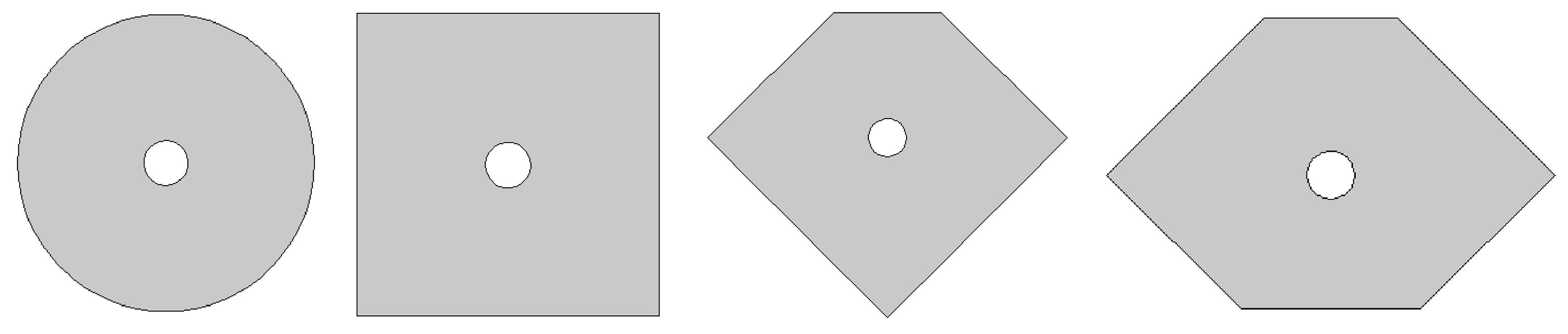
图3 地形简化计算图
Fig. 3 The simplified topographic calculation chart
3.1 隧道围岩应力解析解
在地应力测算准确的基础上,利用SC变换求得隧道围岩应力任一点的准确值,能够更好地布置隧道走向,同时为隧道支护提供精确的参数.
由于篇幅限制, 仅以方案(d)为例, 根据SC变换可知, 式(1)中N=4,C=0,则式(1)可变为
(7)
根据映射关系,可以得到
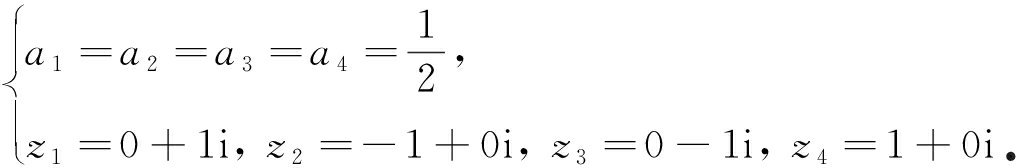
(8)
将式(8)代入式(7)中,得
(9)
其中
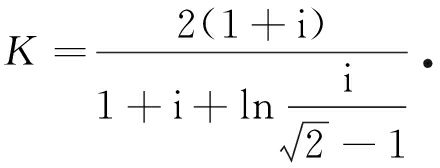
(10)
将式(9)代入式(10),可得SC变换映射函数:
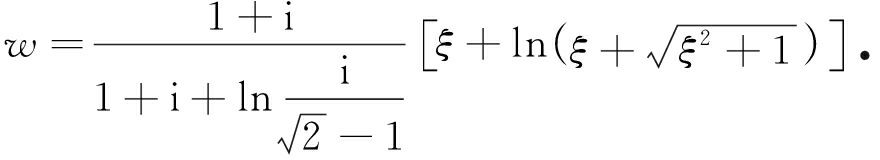
(11)
将式(11)代入复变应力函数式(3)、(4)中,可得
将求得的φ(ξ),φ(ξ)与式(5)、(6)联立,即可求出四边形围岩体内任一点的围岩应力分量σρ和σθ.
3.2 模拟验证
为了验证该算法的准确性和研究不规则围岩体中隧道的应力分布规律,可采用有限元软件COMSOL Multiphysics模拟圆形隧道处应力分布情况.
COMSOL Multiphysics是一款具有编程、算法和多学科交叉,兼具功能性、灵活性和实用性于一体,并且可以通过附加专业的求解模块进行多场耦合计算的高级数值仿真软件.
该模拟利用COMSOL Multiphysics求解步骤如下:
1) 建立图3所示的几何模型;
2) 模型控制方程选择固体力学模块方程,采用Mohr-Coulomb强度准则进行判断;
3) 根据上文所述进行材料自定义;
4) 进行自由三角形网格剖分;
5) 选择COMSOL中稳态求解器求解;
6) 得到隧道围岩的应力位移解.
仍以方案(d)为例,对隧道周应力和地表处位移进行比对,见图4.数值解和模拟解的数值计算结果中的周应力吻合较好,在θ=30°和θ=210°左右处有一定的偏差.这是由于解析方法是建立在有限域上,而尽管有限元模型取了较大的区域,但模型中地应力值的大小不等所引起的误差仍然存在,同时隧道壁若有损伤也会导致误差产生,总体来看,理论值较好地拟合了数值解.
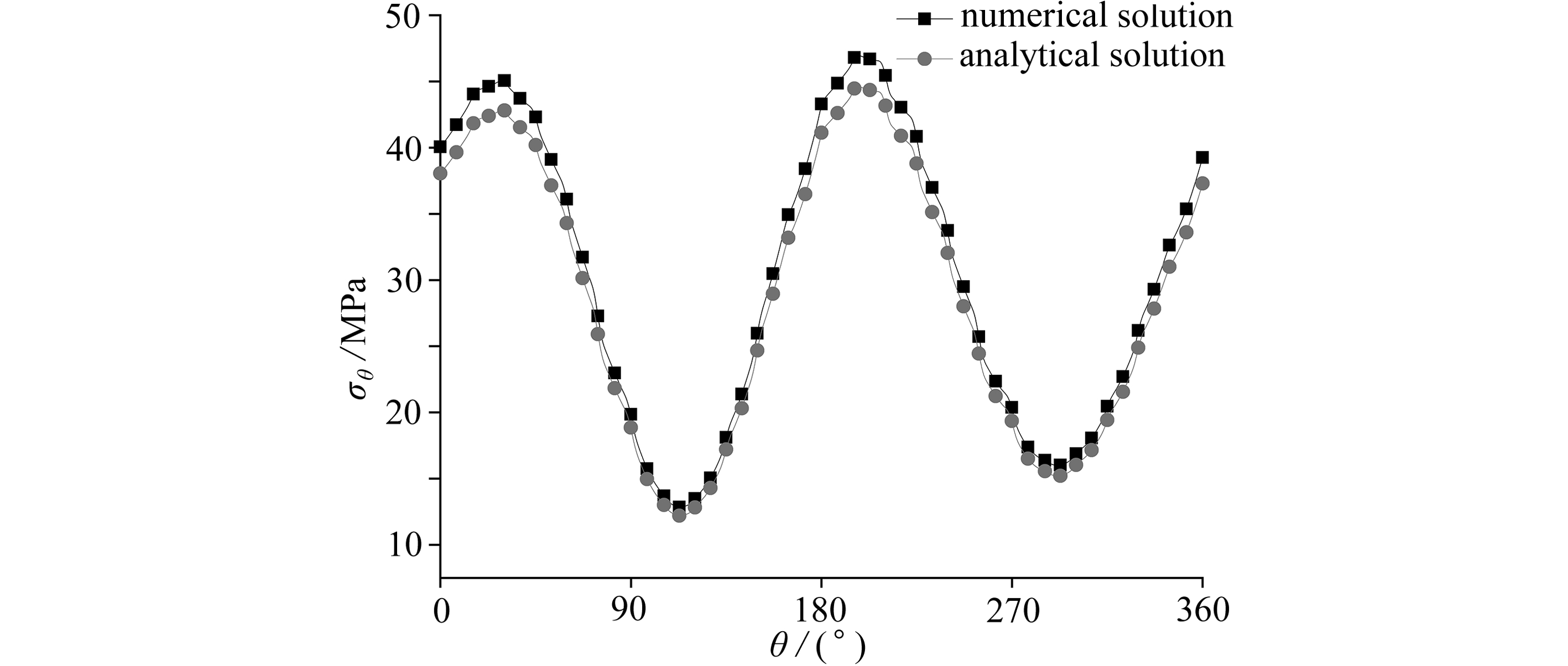
图4 隧道壁周向应力和位移解析解与数值解比较
Fig. 4 Comparison between the analytical solution and the numerical solution
of circumferential stresses in the tunnel wall
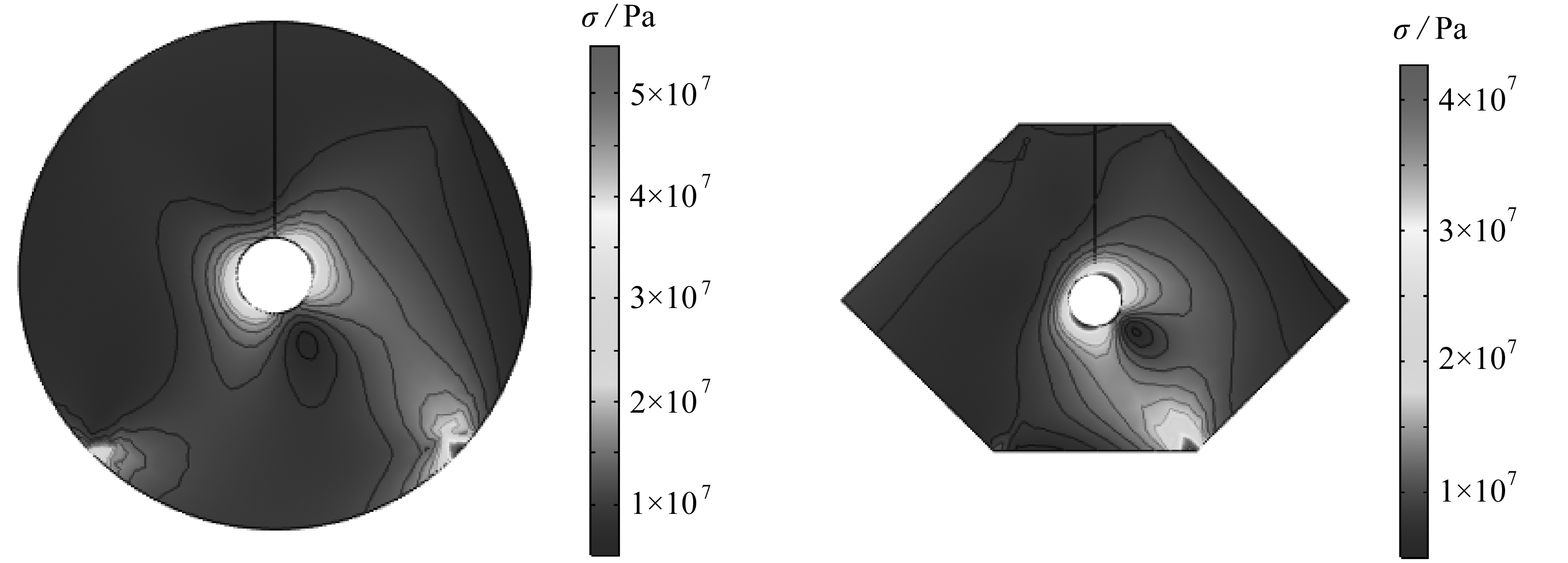
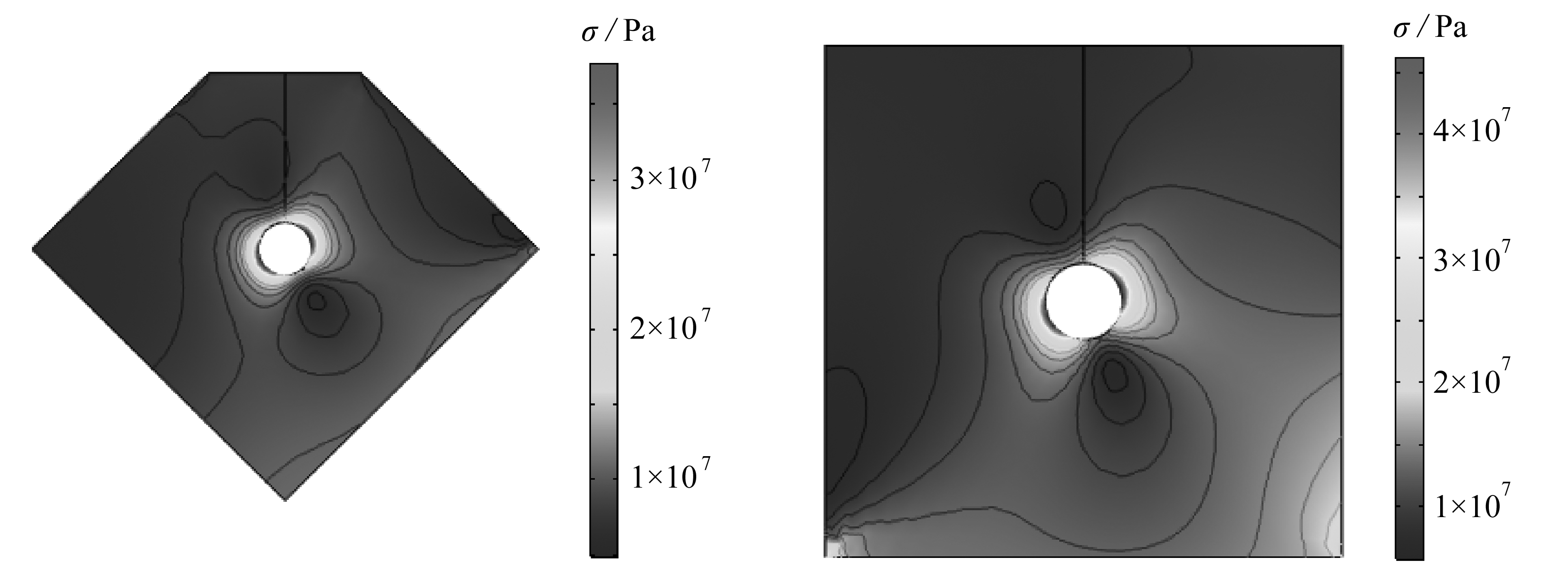
图5 隧道围岩体应力云图
Fig. 5 Stress nephograms of the surrounding rock mass of the tunnel
注 为了解释图中的颜色,读者可以参考本文的电子网页版本.
3.3 隧道围岩应力模拟解
隧道所处的岩体为不规则体,各个方向所受围岩应力不同,隧道开挖引起围岩应力的重新分布,应力从隧道表面向围岩体深部转移,直至形成新的平衡状态,且分布极不均匀.由“等效开挖”理论可知,断面形状不同,隧道矿压规律也不完全一致,隧道所处岩体的各个面围岩应力分布也不相同.
由于理论值计算量较大,下文将用模拟值来分析不规则岩体中隧道围岩应力分布.4种形状岩体下开挖隧道后围岩应力场分布如图5所示,隧道所在围岩体形状不同,隧道的应力集中程度不同.圆形、六边形、五边形和四边形围岩体内开挖的圆形隧道围岩体应力集中区均呈“耳状”.固定边指围岩应力为零,受力边指围岩应力不为零,结合不规则围岩受力可以看出,在固定边和受力边的铰点易出现应力集中现象,对圆形和六边形尤为明显.由此可见,从隧道围岩应力集中的程度来看,由于隧道围岩各个方向所受的力不同,隧道的轴线方向与最大应力方向不一致,且应力集中程度最高处总是与帮部应力最大值基本保持一致.这表明隧道两帮应力集中程度较高,易发生变形破坏.
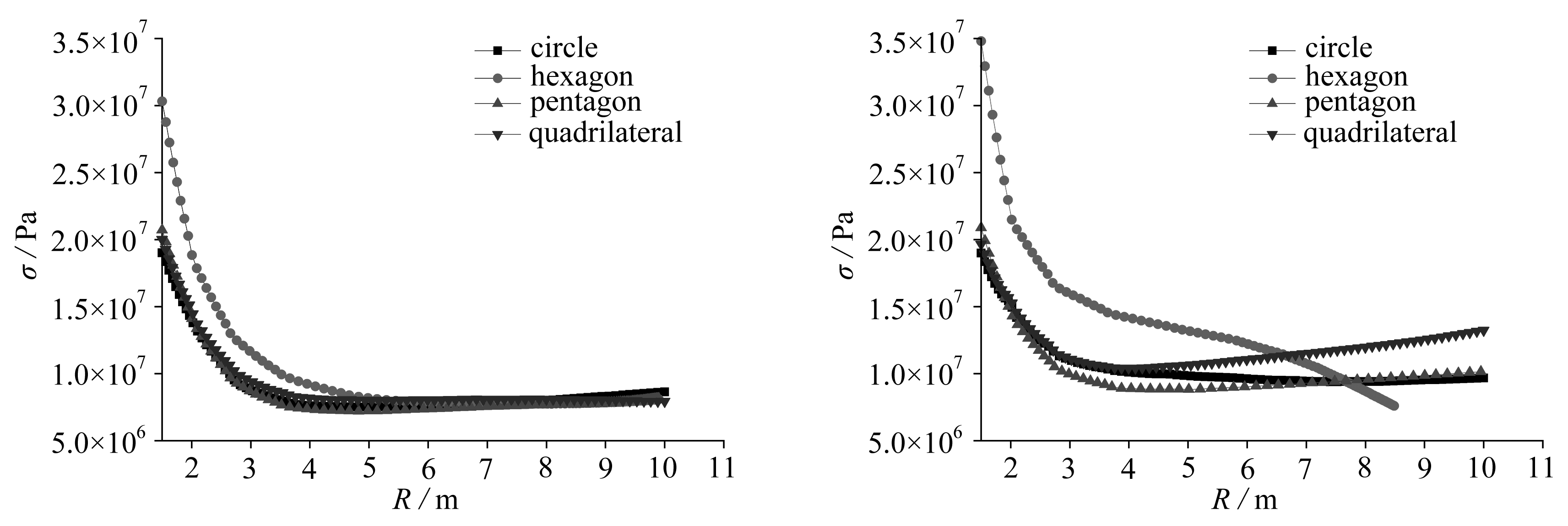
(a) 巷道顶板岩体应力图 (b) 巷道底板岩体应力图
(a) Stress diagram of the roof rock mass of the tunnel(b) Stress diagram of the floor rock mass of the tunnel
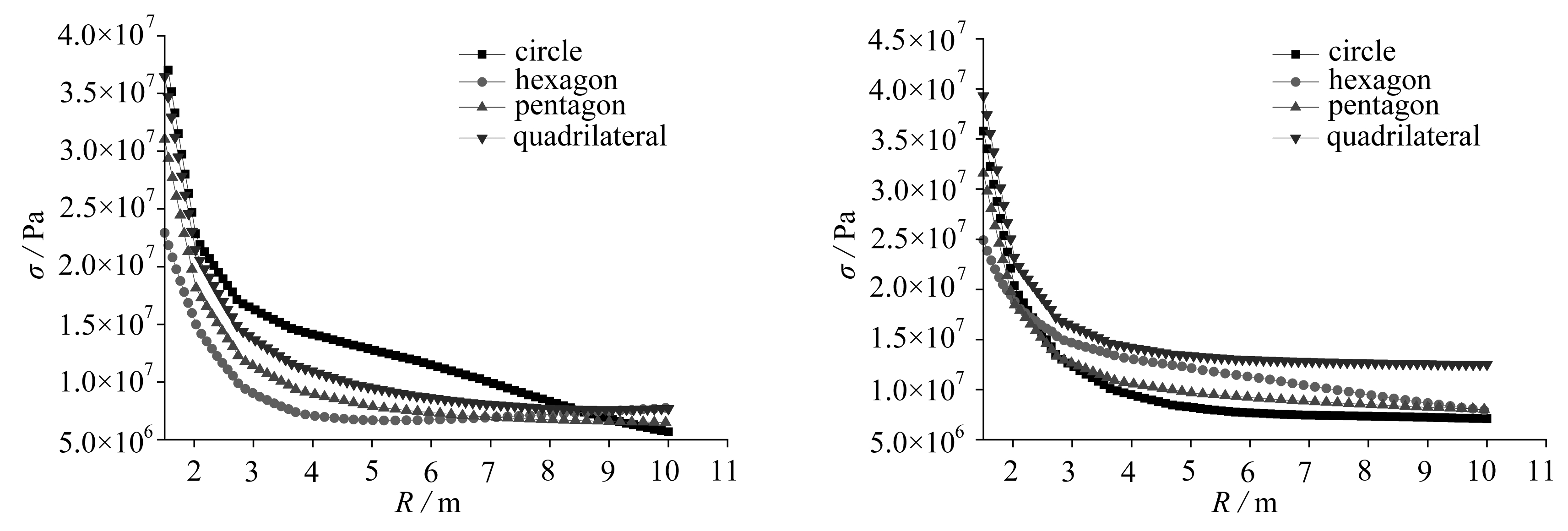
(c) 巷道左侧岩体应力图 (d) 巷道右侧岩体应力图
(c) Stress diagram of the left rock mass of the tunnel(d) Stress diagram of the right rock mass of the tunnel
图6 隧道四周的围岩体应力图
Fig. 6 Stress diagram of surrounding rock mass of tunnel
圆形、六边形岩体中的圆形隧道围岩应力集中程度最高,且在力的拐角点易出现应力集中现象;而五边形、四边形岩体中的隧道围岩应力集中程度偏低,在力的铰点也没有出现明显的应力集中现象.因此,在圆形、六边形岩体中开挖隧道更应该加强帮部和底部的支护.总之,选择合适的位置布置隧道可避免或减弱围岩应力集中现象,同时不能任意地简化隧道所处的围岩体形状,应准确勘探隧道所处的地形地貌,保证原始数据的真实性和计算结果的准确性.
对隧道围岩应力分析可知(图6),在4种不同形状岩体中同一圆形隧道的帮部和顶底板的最大主应力呈相同的变化趋势:圆形隧道在不同形状围岩体边界应力作用下,六边形岩体中的隧道在顶底板边界围岩应力最大,在距离1.5 m处,顶板边界围岩应力为30.3 MPa,底板边界围岩应力为35.1 MPa,其他3种形状近似相同,顶底板边界围岩应力约为20 MPa;随着离顶底板边界越远,围岩应力大约在巷道半径的2~3倍的距离减小到10 MPa左右时趋于稳定;左帮边界围岩应力从圆形、四边形、五边形、六边形依次减小;右帮边界围岩应力从四边形、圆形、五边形、六边形依次减小.
由此可知,隧道所在不同形状岩体对其稳定性有着较大的影响,圆形、四边形岩体中圆形隧道帮部围岩体稳定性较差,六边形岩体中隧道顶底板围岩体稳定性较差.加强隧道周围地应力的测量,提高隧道周围岩体的支护与加强,可以增强隧道的稳定性.
4 结 论
本文在复变函数理论基础上,结合弹性力学,建立了从单位圆映射到多边形的力学模型,对圆形隧道所处不同形状岩体下隧道围岩应力进行了研究,得出以下基本结论:
1) 基于SC变换求解映射函数的方法,对圆形隧道所处不规则断面形状岩体进行映射建模,确定了SC变换映射函数.依据平面应变问题,推导了不规则形状岩体的圆形隧道的复变应力函数φ(ξ)和φ(ξ)的表达式,并得出围岩体任一点应力分量σρ和σθ的解析通式.
2) 通过将处于沟壑交错黄土塬梁峁中的某隧道采用不同方案分析,利用解析解得出了圆形隧道所在的四边形岩体任意一点围岩应力分量σρ和σθ.为验证其正确性,在同等条件下对圆形隧道所处的四边形、五边形、六边形、圆形4种方案的岩体各个方向的应力进行数值模拟分析,得出了不规则形状岩体中的隧道围岩应力场分布的直观图像.
3) 圆形隧道所处岩体断面形状不同,隧道周围岩体所受的应力场分布基本一致,但隧道所在的圆形和六边形围岩体的应力集中程度最高,隧道底板岩体破坏较严重.
4) 在相同地应力条件下,圆形隧道周围岩体的形状对隧道的稳定性有着较大的影响.隧道的支护设计应从隧道周围岩体的地应力测量开始,在模型简化处理前,应准确进行地形地貌勘探,进而选择合适的隧道围岩体形状.
[1] 田尤, 杨为民, 黄晓, 等. 天水市麦积区幅黄土滑坡发育分布特征及其孕灾因素分析[J]. 地质力学学报, 2016, 22(1): 25-38.(TIAN You, YANG Weimin, HUANG Xiao, et al. Distribution characteristics and inducing factors of loess landslide in Maiji mappable unit, Tianshui[J]. Journal of Geomechanics, 2016, 22(1): 25-38.(in Chinese))
[2] 石玲, 王涛, 辛鹏. 陕西省宝鸡市地质灾害发育特征[J]. 地质力学学报, 2013, 19(4): 351-363.(SHI Ling, WANG Tao, XIN Peng. Development characteristics of the geo-harzards in Baoji city, Shaanxi province[J]. Journal of Geomechanics, 2013, 19(4): 351-363.(in Chinese))
[3] FAHIMIFAR A, TEHRANI F M, HEDAYAT A, et al. Analytical solution for the excavation of circular tunnels in a visco-elastic Burger’s material under hydrostatic stress field[J]. Tunnelling and Underground Space Technology, 2010, 25(4): 297-304.
[4] GAO G Y, CHEN Q S, ZHANG Q S, et al. Analytical elasto-plastic solution for stress and plastic zone of surrounding rock in cold region tunnels[J]. Cold Regions Science and Technology, 2012, 72: 50-57.
[5] ZHANG J U, HOU D Q, CHEN X P. Displacement analytical solution of a deep elliptical tunnel in transversely isotropic rock mass[J]. Advanced Materials Research, 2012, 402: 593-597.
[6] 陈子荫. 围岩力学分析中的解析方法[M]. 北京: 煤炭工业出版社, 1994.(CHEN Ziyin. Analytical Method for Mechanics Analysis of Surrounding Rock[M]. Beijing: China Coal Industry Publishing House, 1994.(in Chinese))
[7] 祝江鸿. 隧洞围岩应力复变函数分析法中的解析函数求解[J]. 应用数学和力学, 2013, 34(4): 345-354.(ZHU Jianghong. Analytic functions in stress analysis of the surrounding rock for caverns with the complex variable theory[J]. Applied Mathematics and Mechanics, 2013, 34(4): 345-354.(in Chinese))
[8] 吕爱钟, 张路青. 地下隧道力学分析中的复变函数方法[M]. 北京: 科学出版社, 2007.(LÜ Aizhong, ZHANG Luqing. Method of Complex Variable Function in Mechanical Analysis of Underground Tunnel[M]. Beijing: Science Press, 2007.(in Chinese))
[9] 朱大勇, 钱七虎, 周早生, 等. 复杂形状洞室映射函数的新解法[J]. 岩石力学与工程学报, 1999, 18(3): 279-282.(ZHU Dayong, QIAN Qihu, ZHOU Zaosheng, et al. New method for mapping function of complex shaped cavern[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(3): 279-282.(in Chinese))
[10] 郑志强. 单位圆到任意曲线保角变换的近似计算方法[J]. 应用数学和力学, 1992, 13(5): 449-457.(ZHENG Zhiqiang. An approximate method on the conformal mapping from a unit circle to an arbitrary curve[J]. Applied Mathematics and Mechanics, 1992, 13(5): 449-457.(in Chinese))
[11] 胡龙飞, 刘全坤, 冯秋红. 基于共形映射的壁板型材挤压模具型腔建模[J]. 机械工程学报, 2008, 44(8): 180-184.(HU Longfei, LIU Quankun, FENG Qiuhong. Modeling for shape extrusion of aluminum alloy flat-plate based on conformal mapping[J]. Chinese Journal of Mechanical Engineering, 2008, 44(8): 180-184.(in Chinese))
[12] 李成, 郑艳萍, 李大磊. 积分方程法对含复杂孔形复合材料板孔边应力分布的研究[J]. 机械强度, 2006, 28(6): 931-936.(LI Cheng, ZHENG Yanping, LI Dalei. Research on hole-edge stress distribution of composite materials plate with complex holes by integral equations method[J]. Journal of Mechanical Strength, 2006, 28(6): 931-936.(in Chinese))
[13] MUSKHELISHVILI N I. Some Basic Problems of the Mathematical Theory of Elasticity[M]. Groningen: P Noordhoff Ltd, 1953.
[14] 闻国椿. 共形映射和边值问题[M]. 北京: 高等教育出版社, 1985.(WEN Guochun. Conformal Mapping and Boundary Value Problems[M]. Beijing: Higher Education Press, 1985.(in Chinese))
[15] 徐趁肖, 齐红元, 朱衡君. 任意边界域映射建模理论及模具设计应用[J]. 机械工程学报, 2002, 38(9): 83-86.(XU Chenxiao, QI Hongyuan, ZHU Hengjun. Modeling theory of complicated contact region conformal mapping and application on diedesign[J]. Chinese Journal of Mechanical Engineering, 2002, 38(9): 83-86.(in Chinese))
[16] 徐趁肖, 朱衡君, 齐红元. 复杂边界单连通域共形映射解析建模研究[J]. 工程数学学报, 2002, 19(4): 135-138.(XU Chenxiao, ZHU Hengjun, QI Hongyuan. Analytically modeling of complicated boundary simply-connected region conformal mapping[J]. Chinese Journal of Engineering Mathematics, 2002, 19(4): 135-138.(in Chinese))
[17] 崔建斌, 姬安召, 王玉风, 等. 单位圆到任意多边形区域的Schwarz Christoffel变换数值解法[J]. 浙江大学学报(理学版), 2017, 44(2): 161-167.(CUI Jianbin, JI Anzhao, WANG Yufeng, et al. Numerical solution method for Schwarz Christoffel transformation from unit circle to arbitrary polygon area[J]. Journal of Zhejiang University(Science Edition), 2017, 44(2): 161-167.(in Chinese))
[18] 万世文. 深部大跨度隧道失稳机理与围岩控制技术研究[D]. 博士学位论文. 南京: 中国矿业大学, 2011.(WAN Shiwen. Research on collapse mechanism and surrounding rock control of long-span roadway in deep[D]. PhD Thesis. Nanjing: China University of Mining and Technology, 2011.(in Chinese))