引 言
到目前为止,工程上仍沿用Terzaghi[1]的经典一维固结理论来预测饱和土的沉降速率和超孔隙水压消散率的走势.众所周知,由于Terzaghi理论的局限性,对于饱和土体固结的预测与实际情形相差较大.不少学者已做了大量改进研究,使预测结果更接近于实际工程.对于饱和软黏土的研究,一直是一维固结理论研究的热点.Taylor和Merchant[2]首先将黏弹性Kelvin模型应用在饱和土的固结理论研究当中,并通过与经典弹性模型对比,发现黏弹性模型能更好地描述饱和土的固结机理.孙海忠等[3]将分数阶黏壶引入经典Kelvin模型中,描述了软黏土的蠕变过程,与试验结果比较,取得了较好的拟合效果.刘忠玉等[4]首次将弹壶模型应用于Kelvin黏弹性模型中,并研究了考虑单面排水边界条件和恒定均布荷载作用的流变固结问题,得出了与实验结果相一致的结论.汪磊等[5]用分数阶Kelvin模型,推导出了饱和土体一维固结的半解析解,并以此来描述土体固结过程中的沉降.
饱和土体的固结问题,除了考虑较为合理的黏弹性模型外,荷载对其作用的方式也是讨论的焦点之一.考虑变荷载作用,谢康和等[6]完成了饱和土体固结模型的推导,给出了任意层地基一维固结问题的解析解,并指出荷载的固结速率会随时间的增加而变小.蔡袁强等[7]在任意荷载的基础上,给出了成层黏弹性地基的一维固结解析解,并基于工程实例进行了有效验证.谢康和等[8]在考虑饱和软黏土大应变固结的基础上,得出加载速率越快,固结完成也相应越快.李传勋等[9]在变荷载的基础上,对基于指数形式渗流定律的一维固结问题进行计算分析,并得出渗流指数的变化与固结的关系.Zhu等[10]基于同时考虑时间和土层深度对附加应力的影响,给出了单层地基一维固结的解析解.卢萌盟等[11-12]基于逐级加荷载,得出了复合地基固结解析解,并在之后的研究中同时考虑了附加应力沿深度变化的情况,得出了相应的理论解.秦爱芳等[13]基于Fredlund非饱和土一维固结理论,得到了线弹性和黏弹性两种地基在线性加载情况下,非饱和土的固结理论解,并分析了不同工况下超孔隙水压力、超孔隙气压力和固结度的变化规律.Conte等[14-15]在Fourier级数的基础上,分别给出了单层土壤线性和非线性固结的两个解析解,其中通过选择合适的Fourier级数周期,可以适用于模拟各种加载方案.Xie等[16]针对双层饱和土,使用简化的k-σ′以及mv-σ′模型,研究了双层饱和土的固结行为,并提出了巩固其固结效果的方案.
围绕饱和土体固结问题,尽管目前已有较多的改进工作开展,但由于土体固结的复杂性,进一步完善地再现其固结行为仍然是迫切需要的.在已有的工作中,尚缺少同时考虑软黏土的黏弹性行为和载荷引起的总应力沿土层变化的研究,其预期能更好地反映工程实际情况.本文利用能够更好地描述土体黏弹性行为的基于弹壶修正的分数阶Kelvin模型,同时综合考虑载荷引起的总应力沿深度线性分布的变化特征,通过Laplace变化,获得了可以分析饱和软黏土一维固结的半解析解,这将为工程实际问题提供一定的理论基础.
1 改进的分数阶Kelvin模型
经综合比较,Riemann-Liouville(R-L)型分数阶微积分算子对描述黏弹性更具优势,其积分形式如下:
(1)
式中α为积分的阶数,t为时间,Γ(i)为Gamma函数,Γ(i)=![]() ti-1e-tdt(Re(i)>0).
ti-1e-tdt(Re(i)>0).
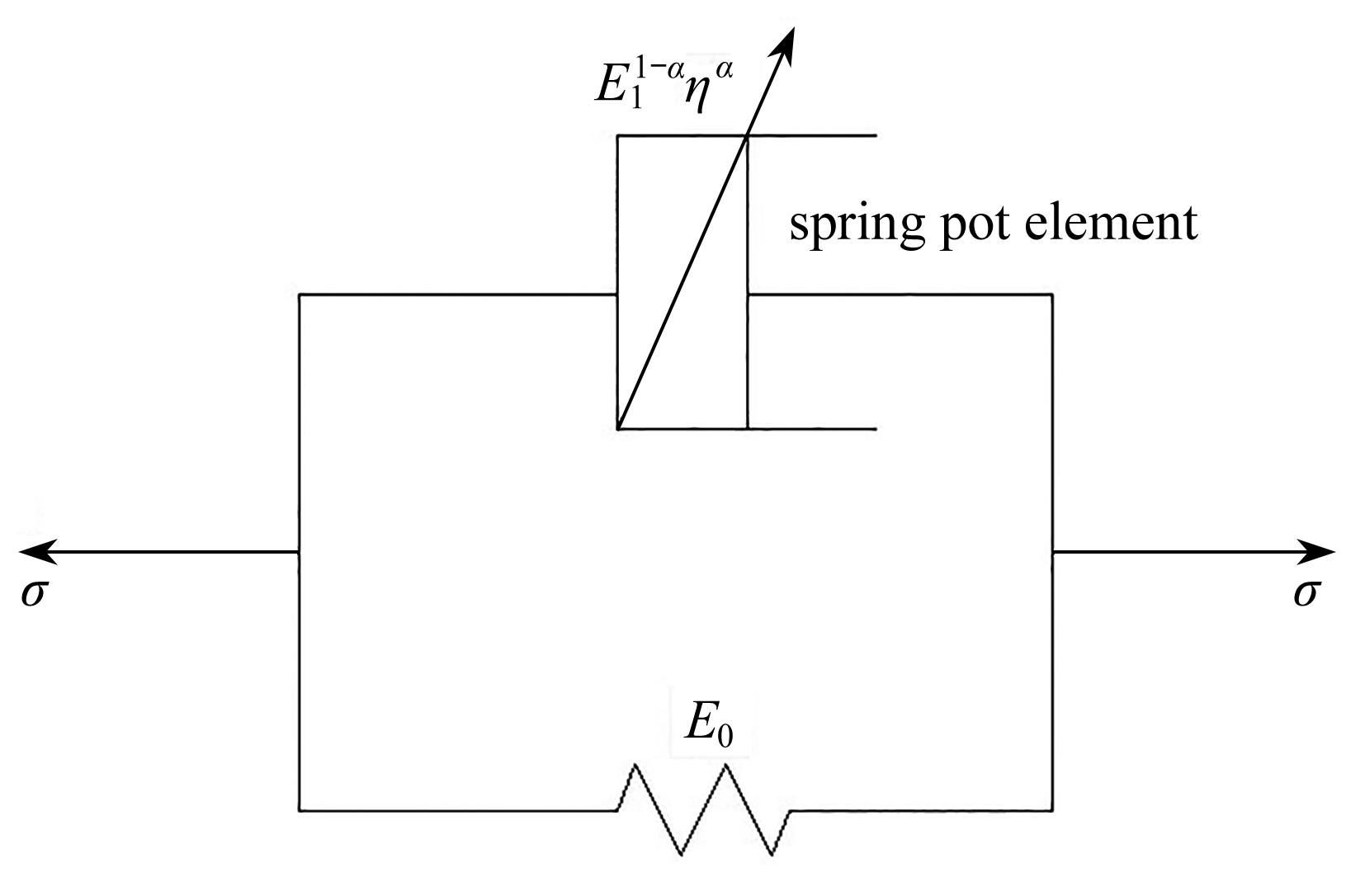
图1 改进的分数阶Kelvin模型
Fig. 1 The improved fractional Kelvin model
如图1所示,本文用Koeller[17]所提出的分数阶导数定义的弹壶元件替代Kelvin模型中的黏壶元件,即改进的分数阶Kelvin模型为
(2)
上式为本文所选取的黏弹性模型的表达式,其中σ′(t)为正应力,ε(t)为应变,E1为该弹壶的弹性模量,η为该弹壶的黏滞系数,α为分数阶阶数.当α=1时,其退化为经典的Kelvin模型;当η=0时,其退化为一个弹簧原件,即为Terzaghi固结理论中的弹性模型.
2 荷 载 形 式
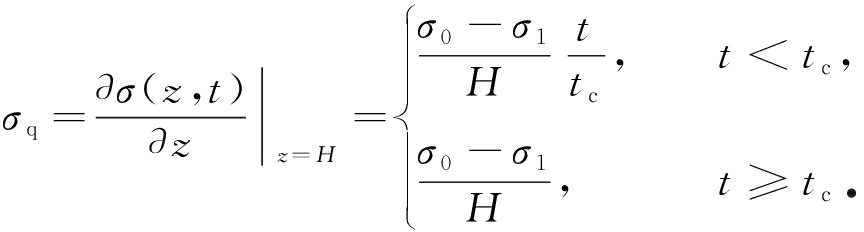
由于文献[18]中已经对土样的初始孔隙水压力沿土层深度的分布进行了详细说明,本文将采用文献[18]中所讨论的沿深度线性变化的形式作为研究条件.具体荷载形式如下:
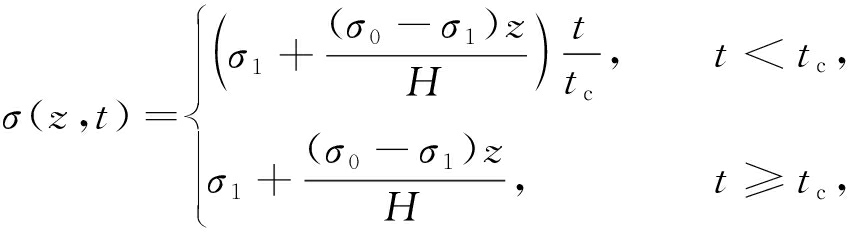
(3)
上式中σ(z,t)为总应力,H为土层厚度,σ0为z=0处的应力,σ1为z=H处的应力,tc为临界时间.
图2、3分别描述了总应力沿土层深度分布的规律以及总应力随时间的变化规律,即所用荷载和沿深度呈线性变化形式,这也符合实际工程中的地基处理常用的预压固结方式.
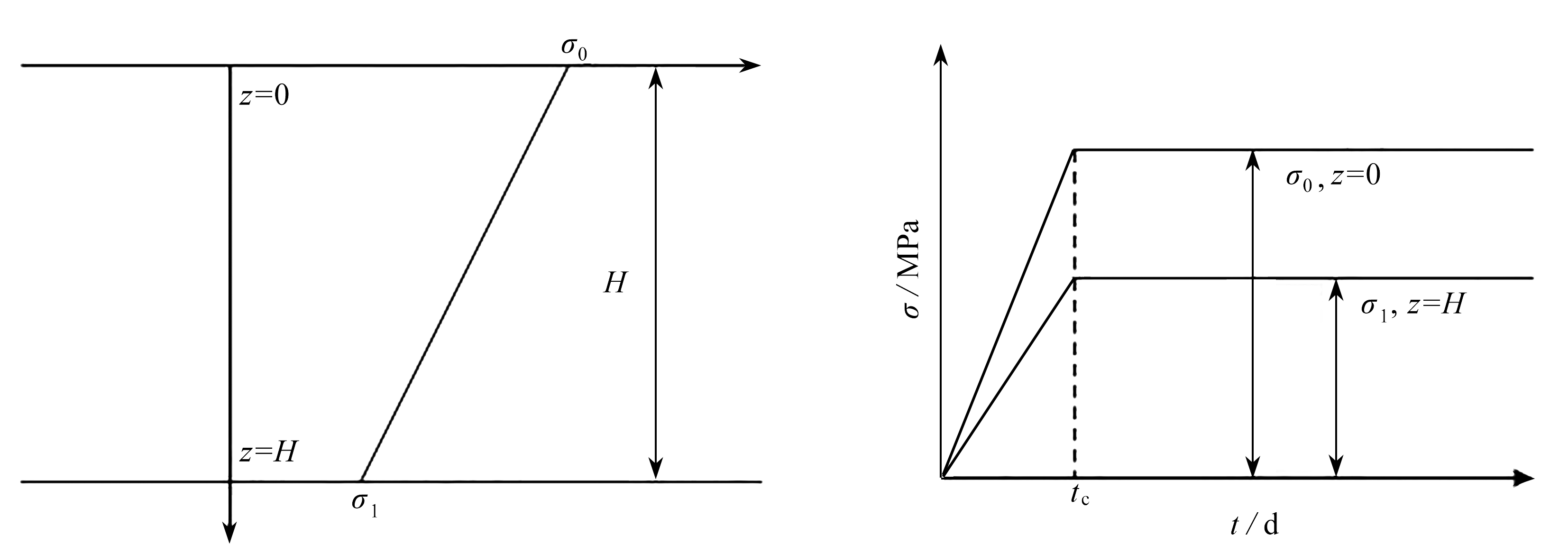
图2 顶部应力与底部应力沿深度变化图3 顶部应力与底部应力随时间变化
Fig. 2 The top stress and bottom stress Fig. 3 The top stress and bottom stress
changing along the depth changing with time
3 固结方程求解
由图4可知,H为土层厚度,u(z,t)为孔隙水压,σ′(z,t)为有效应力.由于土层微元体的流出和流入的流量差,近似等于它的体积变化,其他假定沿用Terzaghi经典一维固结定理[1],可得
(4)
其中kv为土层的渗透系数,γw=ρwg, ρw为水的密度,ε为土层的应变.
总应力与有效应力和孔隙水压力的关系为
σ(z,t)-σ′(z,t)=u(z,t).
(5)
将式(5)代入式(4),可得
(6)
分别对式(6)与式(2)进行Laplace变化,可得
(7)
(8)
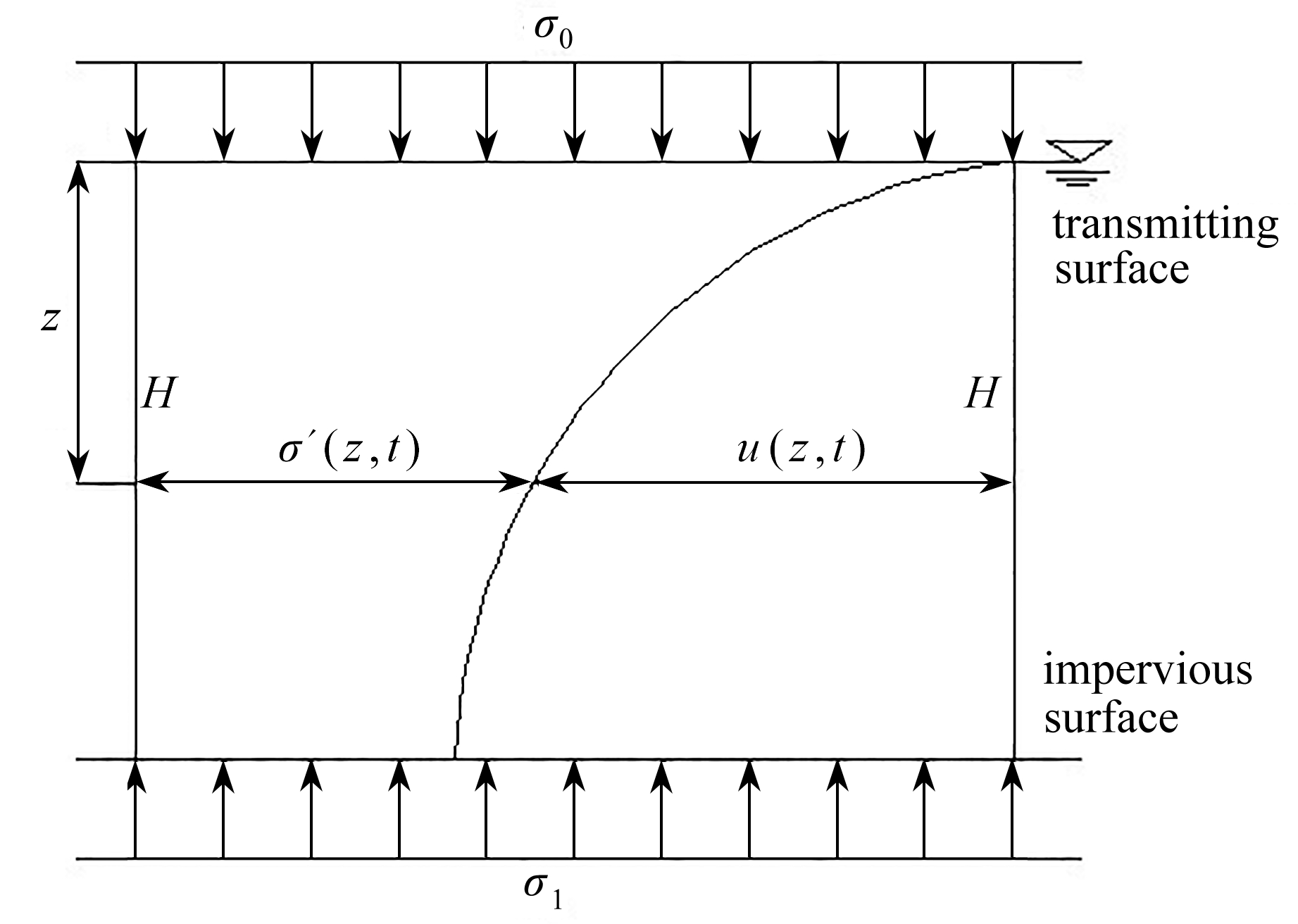
图4 饱和软黏土一维流变固结
Fig. 4 The 1D rheological consolidation of the saturated soft clay
将式(7)与式(8)结合,可得
(9)
考虑单面排水边界条件:
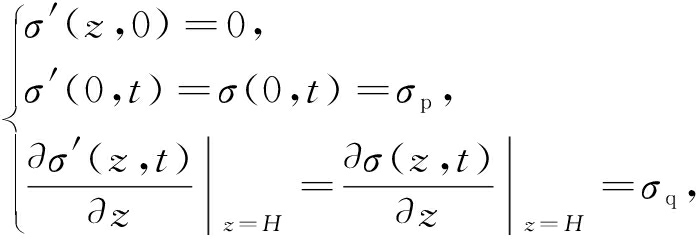
(10)
其中

对式(10)进行Laplace变化可得
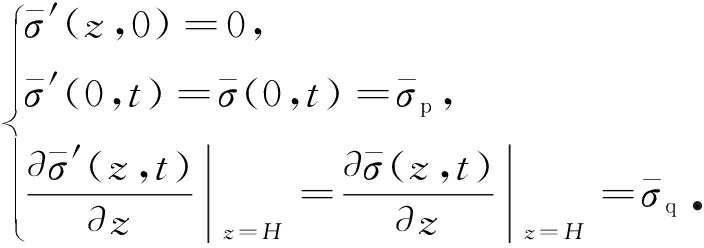
(11)
结合式(11)的边界条件,最终求解方程式(9)可得
(12)
其中![]()
本文所采用的一维流变固结模型的沉降量为
W(t)=![]() ε(z,t)dz.
ε(z,t)dz.
(13)
对式(13)进行Laplace变换:
(14)
将式(2)代入式(14),可得
(15)
将式(12)代入式(15),可得
(16)
引入Crump数值反演方法[19],式(16)可变换为
(17)
式中a=α-ln E′/(2T),其中本文选取α=0,E′=0.001,T根据每组参数不同而定(T>tmax).
4 算例验证与参数分析
为了说明该模型的可靠性,本文将所得的半解析解结果与李西斌[20]的试验结果及汪磊等[5]的理论结果分别进行了对比;进一步地,基于本文的半解析解,本文将分析相关参数对饱和软黏土体固结的影响.
4.1 算例验证
首先,基于李西斌[20]所做一维流变固结试验中的结果,本文开展了改进的分数阶Kelvin模型及普通分数阶Kelvin模型与其对比的分析.其中,对比的试验参数如表1所示.
表1 对比试验参数[20]
Table 1 Comparison test parameters[20]

q0/MPakv/(m·s-1)E/MPaη/(MPa·s)0.84×10-111651 125
基于李西斌[20]试验中所给的土样参数,图5给出了将本文改进的分数阶Kelvin模型半解析解与李西斌[20]的试验结果以及普通分数阶Kelvin模型结果进行对比的情况.对比后发现:在本文模型中取α=0.35,在普通分数阶Kelvin模型中取α=0.9时,可以获得与试验结果较为一致的曲线关系.从图5的对比曲线中可以看出,与普通分数阶Kelvin模型的结果对比,本文改进的分数阶Kelvin模型结果与试验结果具有更好的吻合度,即基本与试验曲线保持相当的一致性,说明了本文利用弹壶元件改进的分数阶Kelvin模型具有更好的可靠性.从以上的对比试验中也可以看到:对于分数阶阶数这种材料内禀参数的选取,不同的黏弹性模型所需的分数阶阶数不同,一定程度上与材料的参数相关.其中,有关于分数阶参数与材料参数的相关性,目前仍然是一个开放的问题,有待于进一步深入研究.
进一步地,基于文献[5]中的关于饱和软黏土体的参数值,具体为kv=1×10-7 m/s,γw=10 kN/m3,E(0,1)=12 MPa,H=19 m,η=230 MP·d.
图6所示为本文结果与文献[5]理论结果的对比,其中α均选取为0.6,tc均取为100 d.由图可知,本文结果与文献[5]结果趋势相同,固结前期快速上升,固结后期趋于平稳.然而,我们也可以发现,最终沉降量以及达到最终沉降的时间略有所不同,这主要归因于本文采用的是基于弹壶改进的分数阶Kelvin黏弹性模型,而文献[5]所采用的是普通分数阶Kelvin模型.
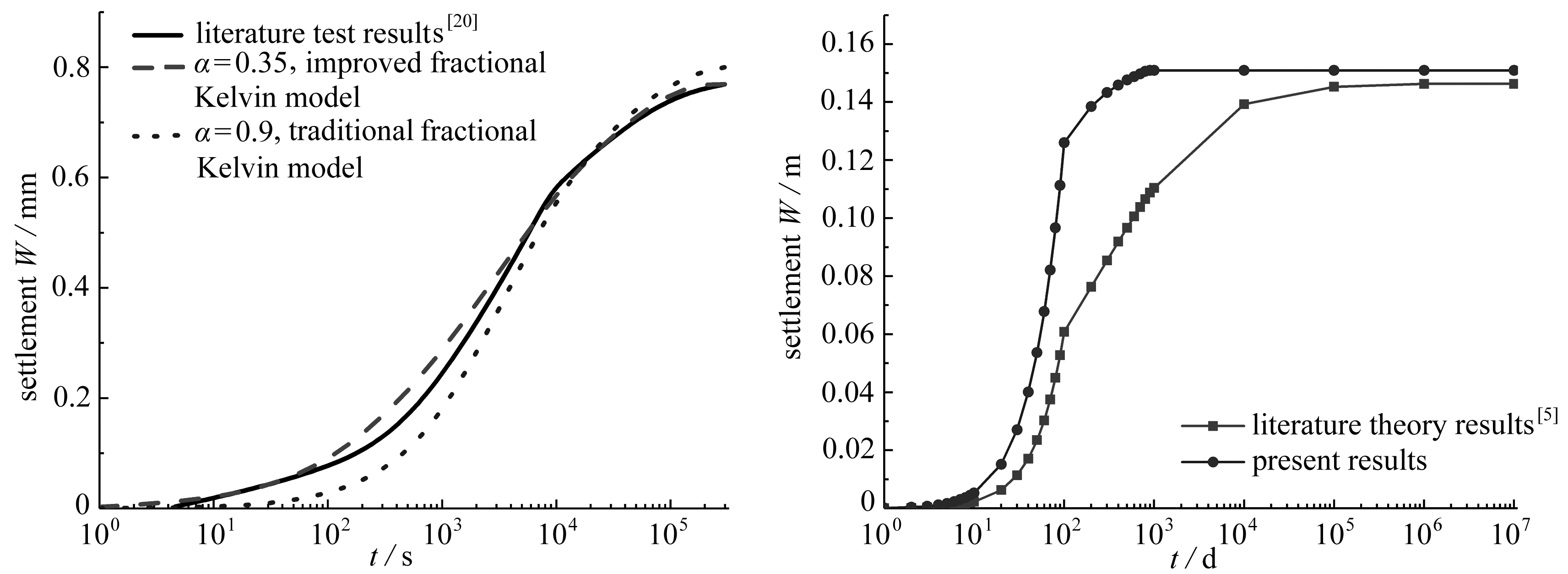
图5 本文结果与文献试验结果及普通分数阶Kelvin模型对比 图6 本文结果与文献结果对比
Fig. 5 Comparisons of the present results with those from the Fig. 6 Comparisons of the present results
literature test and the traditional fractional Kelvin model with the literature results
4.2 参数分析
基于改进的Kelvin黏弹性分数阶模型以及所获得的半解析解,本文将进一步考虑不同分数阶阶数α与不同应力比σ0/σ1对饱和软黏土体固结的影响,土样基本参数的选取与上文相同.

图7 分数阶阶数对饱和软黏土沉降的影响图8 分数阶阶数对饱和软黏土孔隙水压力的影响
Fig. 7 Influences of the fractional order on the Fig. 8 Effects of the fractional order on the pore
settlement of the saturated soft clay water pressure of the saturated soft clay
4.2.1 分数阶阶数α的影响
图7、8分别表示在α分别取0.3,0.6,0.9及tc取0 d(恒定荷载)情况下,饱和软黏土的固结沉降变化以及固结过程中的孔压变化.由图7可知,分数阶阶数越小,固结前期沉降速率越快,固结后期沉降速率反而越慢,且最终沉降量越小,达到最终沉降所需时间越长.由图8可知,在固结前期,分数阶阶数越小,孔压消散越慢,而到了固结中后期,分数阶阶数越小,孔压消散越快.综合比较图7、8可得沉降变化明显滞后于孔压变化,这很好地反映了饱和软黏土的蠕变特性,且分数阶阶数越小,效果越明显.正是因为本文模型中采用了分数阶弹壶,通过改变分数阶阶数可以同时改变土体的黏滞系数与弹性模量,即可以有效地描述土体的蠕变行为.
4.2.2 不同应力比σ0/σ1的影响
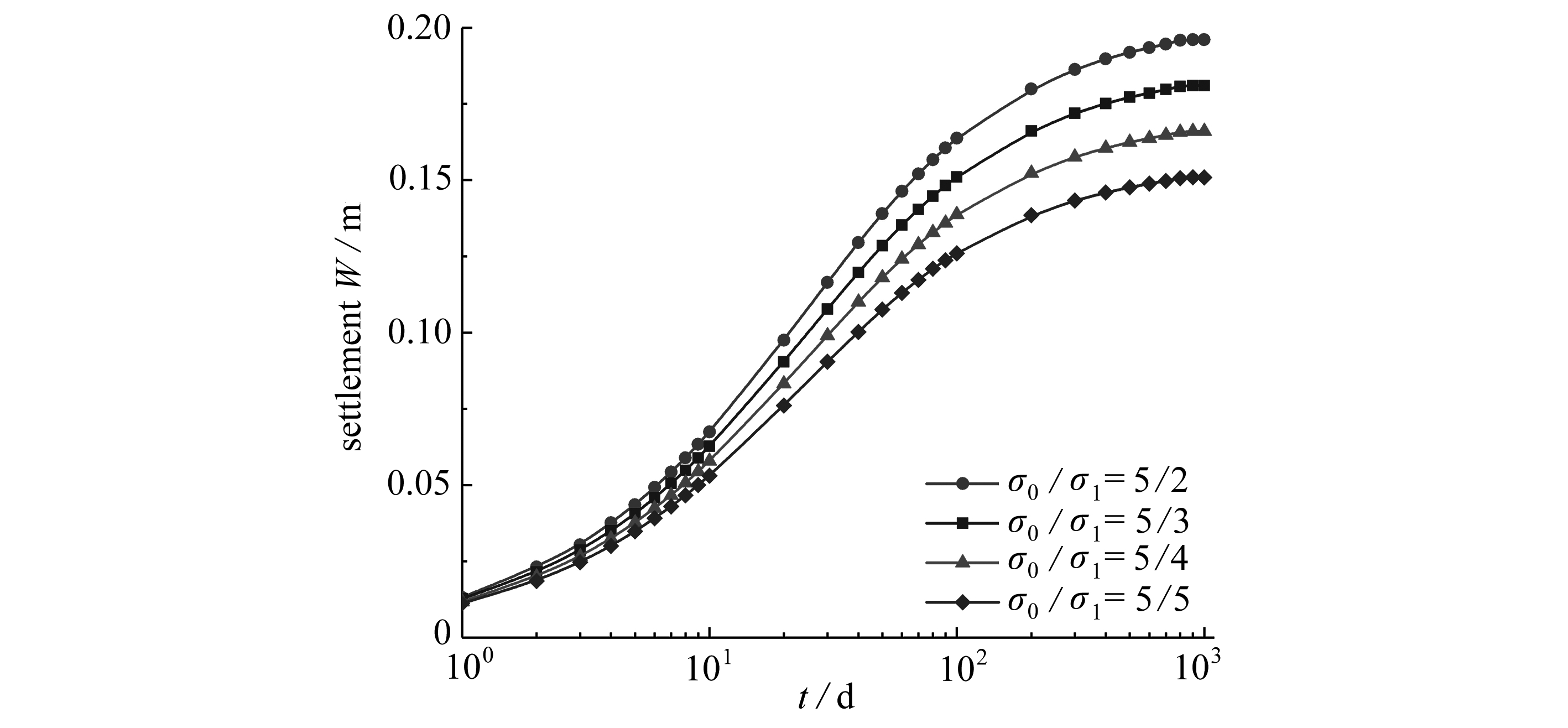
图9 应力比对饱和软黏土沉降的影响
Fig. 9 Effects of the stress ratio on the settlement of the saturated soft clay
图9表示不同总应力比σ0/σ1对饱和软黏土的固结沉降影响,从图中可以看出,随着总应力比的增大,软黏土体固结的最终沉降值越大,固结效果越好.由于排水边界在土体的顶部表面,所以在靠近排水表面设置大应力有利于土体的固结.
5 线性加载下的固结影响
在本节中,主要考虑一级线性加载以及两级线性加载方式对土体的固结影响.
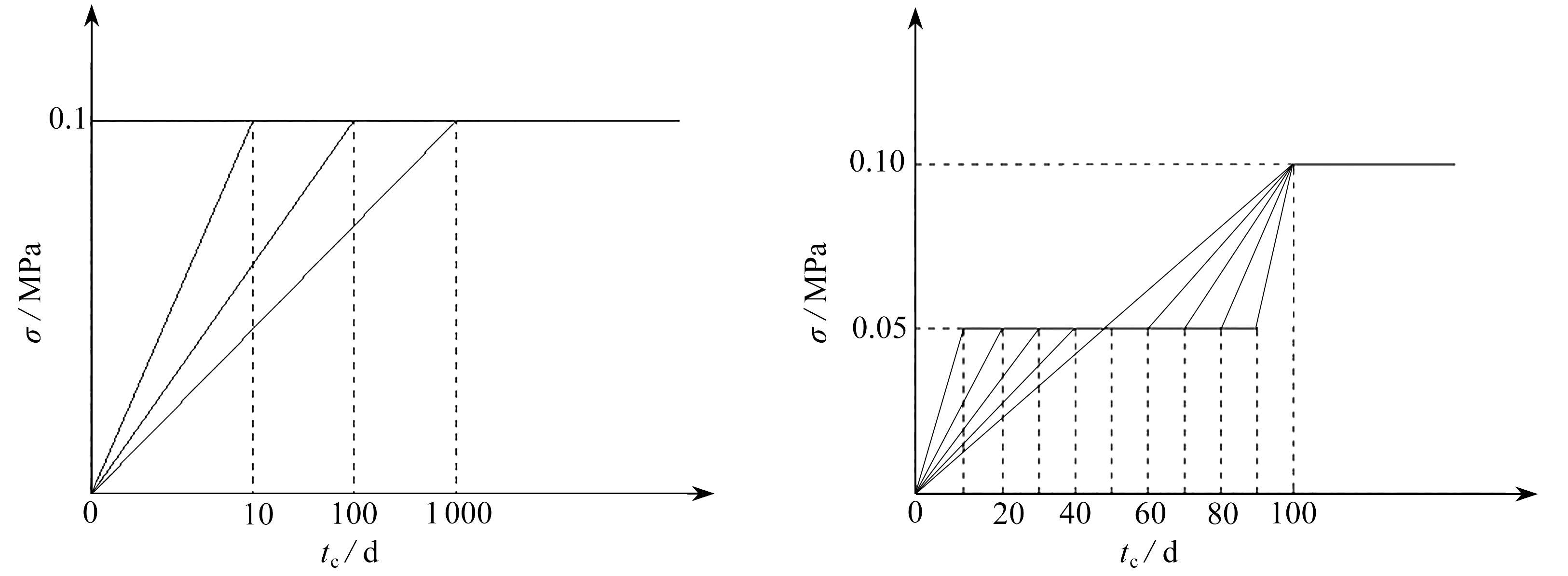
图10 一级线性加载形式 图11 两级线性加载形式
Fig. 10 The one-step linear loading scheme Fig. 11 The two-step linear loading scheme
5.1 线性加载的荷载形式
本文采用两种线性加载方式,一级线性加载(如图10所示),时间分别为tc=0, 10, 100, 1 000 d;两级线性加载(如图11所示)时间分别为tc1=10 d,tc2=10 d;tc1=20 d,tc2=20 d;tc1=30 d,tc2=30 d;tc1=40 d,tc2=40 d;tc1=50 d,tc2=50 d(第一加载阶段时间为tc1,第二加载阶段时间为tc2).对于不同的加载方式,主要体现为加载时间越短,加载的速率越快.具体的两种加载方式可参见图10、11.
5.2 不同线性荷载的影响
图12为一级线性加载下饱和软黏土体的沉降曲线,曲线显示不同的tc值对固结沉降的影响.图13表现的是两级线性加载下的沉降曲线.通过图12、13可以发现,随着tc值的增大,在荷载加载结束前,沉降的增长速率越慢; 在加载结束后, 对于不同的tc值, 最终固结沉降量均相同.这主要是由于tc值所代表的就是荷载的加载速率,tc越小加载速率越快,反之则越慢.其中,荷载的加载速率(tc值大小)体现的是加载期内荷载发展的速度,会影响沉降速率的变化,对最终荷载加载结束后的固结沉降无影响.
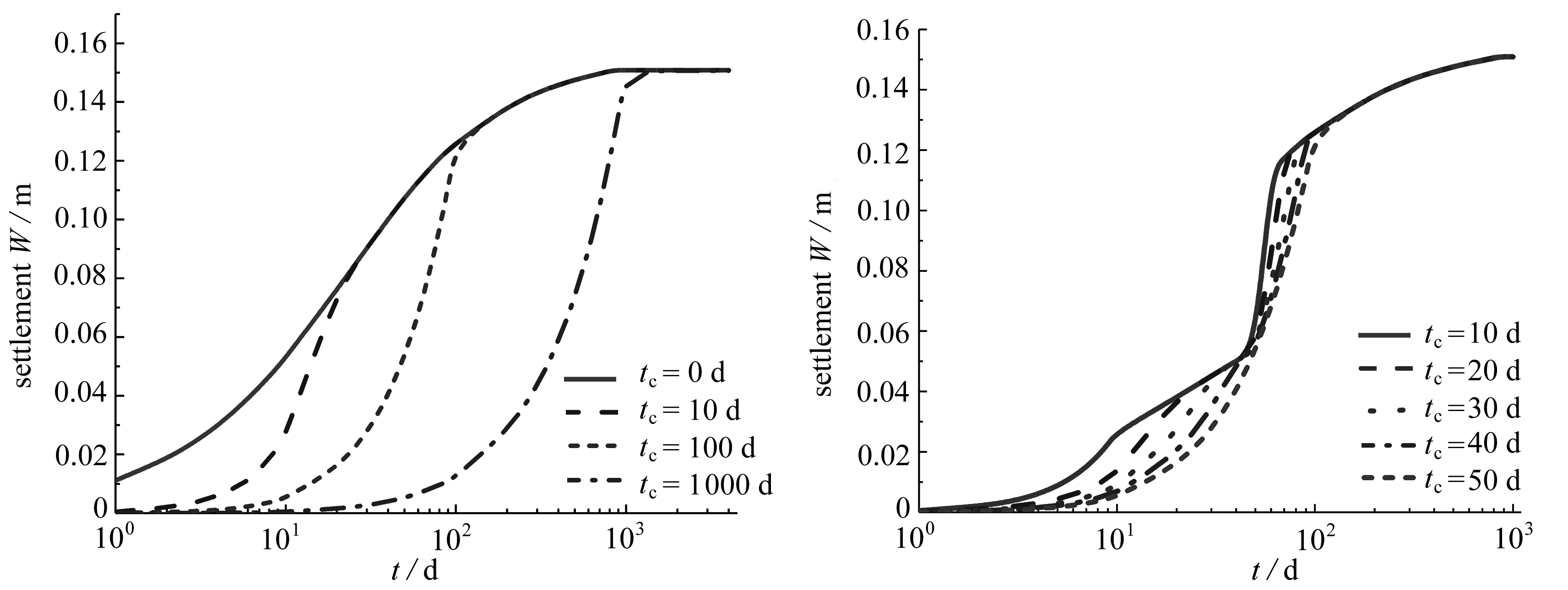
图12 一级线性加载下饱和软黏土体的沉降 图13 两级线性加载下饱和软黏土体的沉降
Fig. 12 Settlement of the saturated soft clay Fig. 13 Settlement of the saturated soft clay
under one-step linear loading under two-step linear loading
6 结 论
基于改进的分数阶Kelvin模型,本文通过Laplace变换以及Crump反演方法,获得了考虑总应力沿深度变化的线性荷载作用下饱和软黏土的半解析解.通过与文献试验结果及文献理论结果对比,说明了本模型的有效性.进一步地,本文分析了有关参数对饱和软黏土的影响,所得结论如下:
1) 通过与文献试验结果的对比,可以看出改进的分数阶Kelvin模型比普通的分数阶Kelvin模型有更好的吻合度.
2) 分数阶阶数越小,固结前期沉降速率越快,固结后期沉降速率反而越慢,且最终沉降量越小,达到最终沉降所需时间越长,孔压消散越快.
3) 饱和软黏土的沉降变化明显滞后于孔压变化,且随着分数阶阶数的减小,滞后效果越明显.
4) 通过分析一级和两级线性荷载作用下饱和软黏土的固结沉降可得,随着tc值的增大,在荷载加载结束前,沉降的增长速率越慢;在加载结束后,固结沉降量最终相同.
[1] TERZAGHI K. Theoretical Soil Mechanics[M]. New York: John Wiley and Sons Inc, 1943.
[2] TAYLOR D W, MERCHANT W. A theory of clay consolidation accounting for secondary compression[J]. Journal of Mathematics and Physics, 1940, 19(3): 167-185.
[3] 孙海忠, 张卫. 一种分析软土黏弹性的分数导数开尔文模型[J]. 岩土力学, 2007, 28(9): 1983-1986.(SUN Haizhong, ZHANG Wei. Analysis of soft soil with viscoelastic fractional derivative Kelvin model[J]. Rock and Soil Mechanics, 2007, 28(9): 1983-1986.(in Chinese))
[4] 刘忠玉, 杨强. 基于分数Kelvin模型的饱和黏土一维流变固结分析[J]. 岩土力学, 2017, 38(12): 1001-1009.(LIU Zhongyu, YANG Qiang. One-dimensional rheological consolidation analysis of saturated clay using fractional order Kelvin’s model[J]. Rock and Soil Mechanics, 2017, 38(12): 1001-1009.(in Chinese))
[5] 汪磊, 孙德安, 解益, 等. 任意荷载下分数阶导数饱和软黏土体一维固结[J]. 岩土工程学报, 2017, 39(10): 1823-1831.(WANG Lei, SUN Dean, XIE Yi, et al. One-dimensional consolidation of fractional derivative viscoelastic saturated soil under arbitrary load[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(10): 1823-1831.(in Chinese))
[6] 谢康和, 潘秋元. 变荷载下任意层地基一维固结理论[J]. 岩土工程学报, 1995, 17(5): 80-85.(XIE Kanghe, PAN Qiuyuan. One-dimensional consolidation theory of foundation in arbitrary layer under variable load[J]. Chinese Journal of Geotechnical Engineering, 1995, 17(5): 80-85.(in Chinese))
[7] 蔡袁强, 徐长节, 袁海明. 任意荷载下成层粘弹性地基的一维固结[J]. 应用数学和力学, 2001, 22(3): 307-313.(CAI Yuanqiang, XU Changjie, YUAN Haiming. One dimensional consolidation of layered and visco-elastic solids under arbitrary loading[J]. Applied Mathematics and Mechanics, 2001, 22(3): 307-313.(in Chinese))
[8] 谢康和, 郑辉, LEO C J. 变荷载下饱和软黏土一维大应变固结解析理论[J]. 水利学报, 2003, 34(10): 6-13.(XIE Kanghe, ZHENG Hui, LEO C J. Analytical solution for 1-D large strain consolidation of saturated soft clay under time-depending loading[J]. Journal of Hydraulic Engineering, 2003, 34(10): 6-13.(in Chinese))
[9] 李传勋, 谢康和, 卢萌盟, 等. 变荷载下基于指数渗流双层地基一维固结分析[J]. 岩土力学, 2012, 33(5): 1565-1571.(LI Chuanxun, XIE Kanghe, LU Mengmeng, et al. Analysis of one-dimensional consolidation of double-layered soil with exponential flow considering time-dependent loading[J]. Rock and Soil Mechanics, 2012, 33(5): 1565-1571.(in Chinese))
[10] ZHU G F, YIN J H. Consolidation of soil under depth-dependent ramp load[J]. Canadian Geotechnical Journal, 1998, 35(2): 344-350.
[11] 卢萌盟, 谢康和, 李瑛, 等. 逐级加荷下考虑施工扰动的复合地基固结解[J]. 工业建筑, 2009, 39(7): 56-60, 73.(LU Mengmeng, XIE Kanghe, LI Ying, et al. Analytical solution for the consolidation of a composite foundation considering the construction disturbance under progressive loading[J]. Industrial Construction, 2009, 39(7): 56-60, 73.(in Chinese))
[12] LU Mengmeng, XIE Kanghe, WANG Sanyong. 1-D consolidation of a single soil layer with depth-dependent stress by multi-stage loading[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(2): 330-336.
[13] 秦爱芳, 葛航. 线性加荷情况下非饱和土层一维固结特性分析[J]. 上海大学学报(自然科学版), 2016, 22(5): 624-636.(QIN Aifang, GE Hang. Analysis of one-dimensional consolidation characteristics in unsaturated soil under line loads[J]. Journal of Shanghai University (Natural Science), 2016, 22(5): 624-636.(in Chinese))
[14] CONTE E, TRONCONE A. One-dimensional consolidation under general time-dependent loading[J]. Canadian Geotechnical Journal, 2006, 43(11): 1107-1116.
[15] CONTE E, TRONCONE A. Nonlinear consolidation of thin layers subjected to time-dependent loading[J]. Canadian Geotechnical Journal, 2007, 44(6): 717-725.
[16] XIE K H, WANG K, WANG Y L, et al. Analytical solution for one-dimensional consolidation of clayey soils with a threshold gradient[J]. Computers and Geotechnics, 2010, 37(4): 487-493.
[17] KOELLER R C. Applications of fractional calculus to the theory of viscoelasticity[J]. Journal of Applied Mechanics, 1984, 51(2): 299-307.
[18] 张玉国. 散体材料桩复合地基固结理论研究[D]. 博士学位论文. 杭州: 浙江大学, 2005.(ZHANG Yuguo. Study on consolidation theory of composite foundation of granular material piles[D]. PhD Thesis. Hangzhou: Zhejiang University, 2005.(in Chinese))
[19] 何光渝, 王卫红. 精确的拉普拉斯数值反演方法及其应用[J]. 石油学报, 1995, 16(1): 96-104.(HE Guangyu, WANG Weihong. An application of an accurate and efficient numerical inversion of the Laplace transform in modern well-testing analysis [J]. Acta Petrolei Sinica, 1995, 16(1): 96-104.(in Chinese))
[20] 李西斌. 软土流变固结理论与试验研究[D]. 博士学位论文. 杭州: 浙江大学, 2005.(LI Xibin. Theory and experimental study on rheological consolidation of soft soil[D]. PhD Thesis. Hangzhou: Zhejiang University, 2005.(in Chinese))