引 言
随着科学技术的进步，相较于传统的混凝土桥梁结构，波形钢腹板作为一种新型桥梁结构，具有性价比高、施工简易的特点．随着土木工程事业的发展，对波形钢腹板特性的研究和探索也在不断深入，并且在整个土木行业内得到了迅速的发展和使用．以小跨径的混凝土箱梁为研究对象，可以得到由箱梁截面的刚性扭转和畸变产生的纵向翘曲正应力是恒载和活载共同作用时产生的纵向弯曲正应力的24%～26%[1-3]．新型桥梁结构波形钢腹板箱梁，是用波形钢腹板取代传统的混凝土腹板同时箱梁底板的厚度较混凝土箱梁有所减小，所以波形钢腹板组合箱梁的抗扭刚度、抗剪刚度、纵向及横向刚度与普通混凝土箱梁相比均有所下降，由于波形钢腹板本身的手风琴效应，相比于顶底板混凝土的纵向刚度和弯曲刚度，波形钢腹板的纵向刚度和弯曲刚度很小，对波形钢腹板箱梁中由畸变变形产生的翘曲正应力引起的弯矩抵抗作用很小，基本没有[4-6]．
王文[7]分别运用Umansky第二理论和弹性地基梁法对扭转翘曲应力和畸变应力进行了公式推导和求解，同时也分析了不同参数下扭转翘曲应力和畸变翘曲应力的变化情况．李时等[8]在考虑了非线性和几何初始缺陷的条件下，对波形钢腹板组合箱梁在剪力作用下的破坏机理做了研究，研究结果表明波形尺寸对剪切屈曲的强度影响很大．李宏江[9]对波形钢腹板组合箱梁的受弯特性及畸变扭转特性进行了分析，并提出对应的计算方法．Elgaaly等[10-11]通过借助21根实验梁的研究结果表明，波形钢腹板承担了整个波形钢腹板箱梁的剪力作用，并且得出屈曲变形是造成波形钢腹板破坏的主要原因．刘保东等[12]利用实测和有限元对波形钢腹板箱梁和混凝土箱梁进行了分析，其结果表明波形钢腹板组合箱梁扭转刚度较低，并提出了通过增设横隔板来改善扭转动力特性的方案．徐君兰等[13]从波形钢腹板箱梁结构和受力特性上进行了介绍并运用内力计算对其进行了研究．
本文在传统混凝土箱梁理论和已有文献的基础上，考虑了波形钢腹板的手风琴效应，用以势能驻值原理为基础的能量法分析求出了以畸变角为未知量的波形钢腹板箱梁畸变控制微分方程，采用初参数法解得箱梁的畸变角和畸变双力矩，最终得到纵向畸变翘曲正应力．
1 波形钢腹板箱梁的畸变荷载分解
单室波形钢腹板箱梁的横断面如图1所示，在竖向偏心荷载作用下，波形钢腹板箱梁会产生畸变效应，通常该偏心荷载又可分解为对称荷载和反对称荷载，而箱形梁截面在反对称荷载作用下会产生刚周边扭转变形和截面畸变变形．当箱形梁受到扭转荷载作用时可施加一虚拟的对角支撑来阻止截面变形，使截面只发生刚性扭转变形，而当解除这一虚拟对角支撑时，相当于施加一斜撑的反向力，截面将发生畸变变形，则该反向力就是箱形梁产生畸变变形的畸变荷载，具体分解如图2所示．
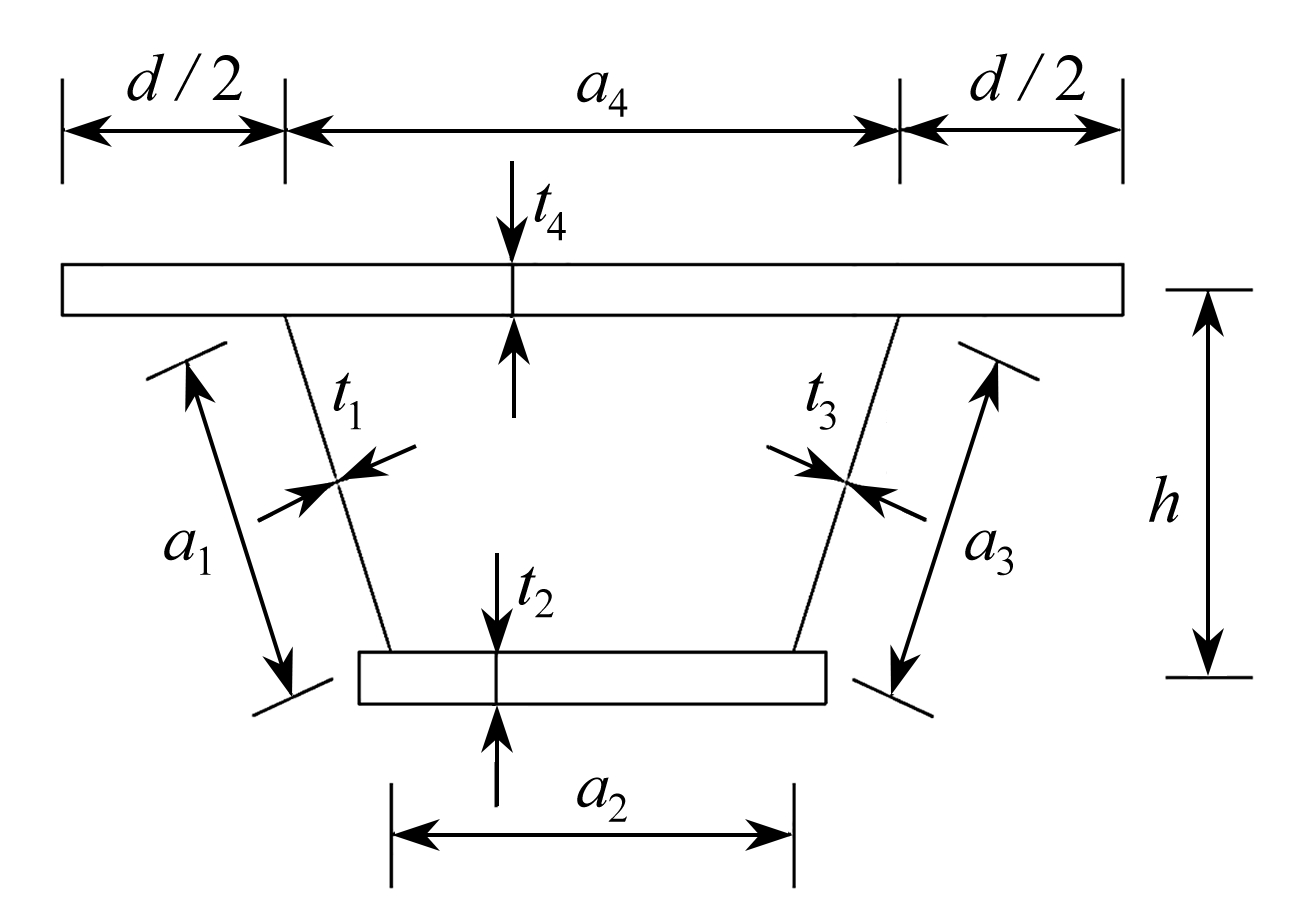
图1 箱梁横断面图
Fig. 1 The box girder cross section diagram
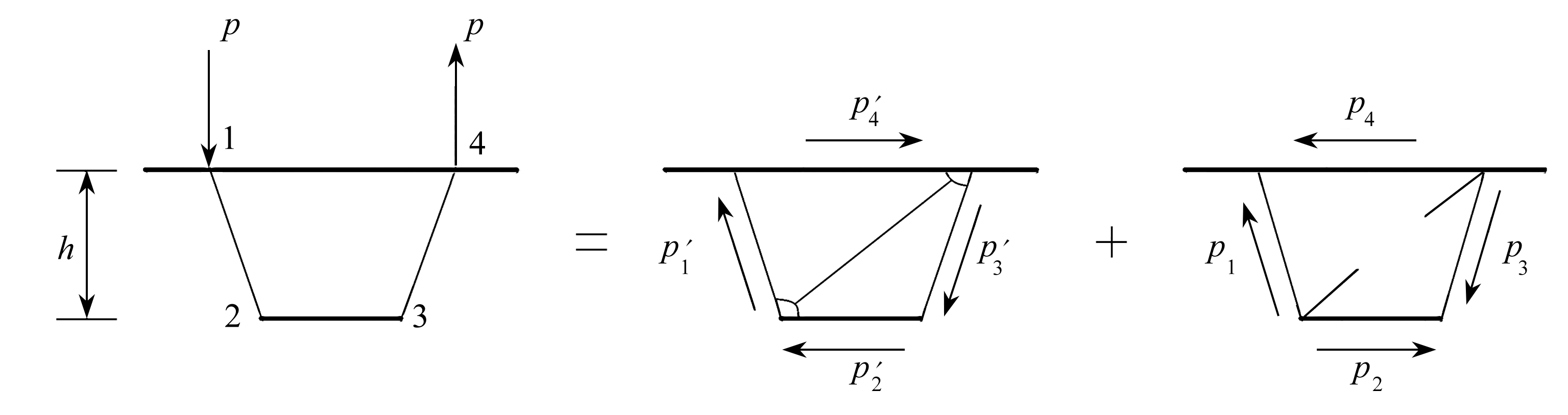
(a) 反对称荷载(b) 刚性扭转荷载 (c) 畸变荷载
(a) Antisymmetric loads(b) Rigid torsional loads (c) Distortion loads
图2 反对称荷载分解
Fig. 2 Decomposition of antisymmetric loads
在分析时忽略底板的悬臂部分，则根据力的平衡原理得畸变荷载的计算结果为
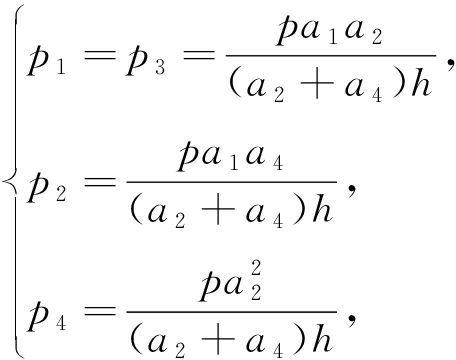
(1)
式中p1，p2，p3，p4为畸变荷载，a1，a2，a3，a4为波形刚腹板箱梁左斜腹板、底板、右斜腹板、顶板的宽度，h为梁高．
2 波形钢腹板箱梁的畸变位移
基于对传统混凝土箱梁畸变变形的分析方法，结合波形钢腹板组合箱梁结构的受力特点，首先截取单位长度的波形钢腹板箱梁单元体，将其看作框架结构并忽略底板悬臂部分，考虑组合箱梁结构断面的畸变位移，箱梁在畸变荷载作用下，框架的的畸变变形如图3所示．图3中h为梁高，a4/2，a2/2分别为顶底板宽度的一半，D为箱梁的畸变中心，即箱梁发生畸变时各板件切向位移共同对应的转动中心；O为形心，x轴和y轴为形心轴；θ为钢腹板的倾斜角度；过畸变中心D与x轴正半轴的波形钢腹板相交于A点，与y轴正半轴的底板相交于B点．由于波形钢腹板在纵向具有褶皱效应，所以在其发生畸变时，顶底板不产生畸变位移，仅底板B点移至B1点．本文将波形钢腹板箱梁畸变变形产生的位移定义为畸变角γ2．
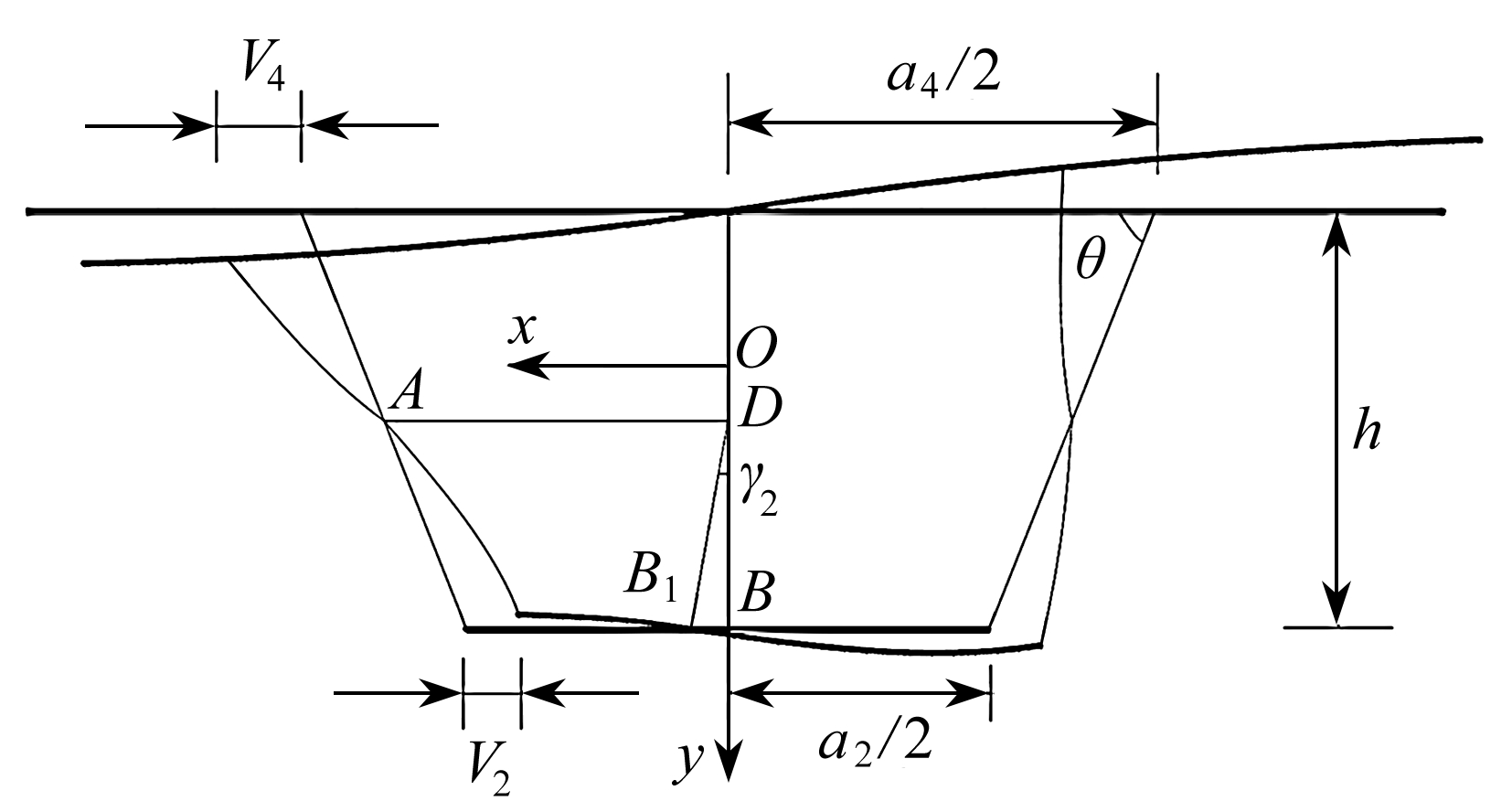
图3 箱形梁的畸变位移
Fig. 3 Distortion displacements of the box girder
根据图3可得箱梁畸变角的表达式为
(2)
式中V4，V2分别为顶板角点和底板角点的水平位移分量．
3 波形钢腹板箱梁的畸变总势能
3.1 基本假定
波形钢腹板箱梁的分析采用以下基本假定：
1) 箱梁的各个板元在自身平面内的变形满足平截面假定；
2) 组成箱形截面的各板件各周边长度不变；
3) 沿壁厚方向的应力变化不考虑，翘曲应力在壁厚方向均匀分布；
4) 波形钢腹板的纵向抗弯刚度很小，但不为零且不考虑它的抗弯性能；
5) 忽略波形钢腹板的剪切变形应变能．
3.2 波形钢腹板沿纵向单宽横向抗弯惯性矩I1
沿纵向取一个波形钢腹板节段，见图4，根据材料力学中移轴、转轴公式，可求得断面关于虚线轴的横向抗弯惯性矩为
(3)
式中I′1为图4断面关于虚线轴的惯性矩，Lc，Lb，α为波形刚腹板的形状参数，e为波形刚腹板的高度，t为波形刚腹板的厚度．
若q为波形钢腹板波纹的水平投影长度，则沿纵向单宽的横向抗弯惯性矩为
(4)
3.3 横向框架畸变应变能U1
取单位长度的梁段形成框架条如图5所示，受到的荷载分别为p1，p2，p3，p4．
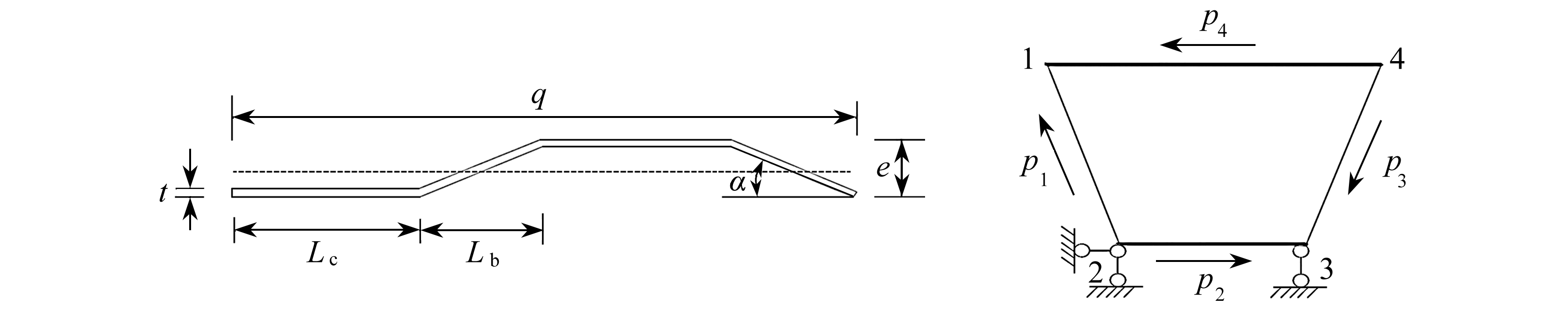
图4 钢腹板波纹形状图5 畸变荷载作用下的框架
Fig. 4 The steel web corrugated shapeFig. 5 The frame under distortion load
从图5可以看出，畸变角γ2(z)所产生的应变能与箱形梁顶板发生水平位移γ2a1sin θ所具有的应变能是等同的．现将图5所示的箱梁框架的顶板从a4/2处截开并代之相应的多余未知力，即得框架的基本体系如图6(a)所示，并分别绘出单位力M1图以及Mp图如图6(b)和6(c)所示．
(a) 基本体系(b) 单位力M1图(c) 外荷载Mp图
(a) The basic system (b) Unit force M1(c) External load Mp
图6 箱梁框架结构图
Fig. 6 The box girder frame structure
根据对称性δ2p=δ3p=δ12=δ13=0，故由力法方程
(5)
可解出X2=X3=0，X1=-δ1p/δ11，根据图乘法可得
(6)
(7)
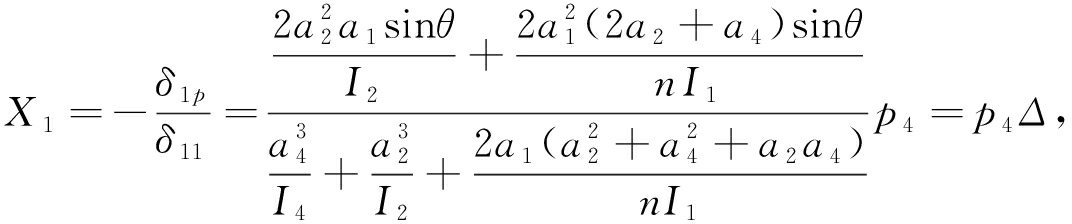
(8)
式中n为波形钢腹板本身的弹性模量E0与混凝土的弹性模量E的比值，nEI1为波形钢腹板等效为混凝土腹板后的抗弯刚度，
为沿轴向单位长度的底板横向抗弯惯性矩，
为沿轴向单位长度的顶板横向抗弯惯性矩，Δ为p4等于1时的剪力．
则各点的横向弯矩
如图7所示．
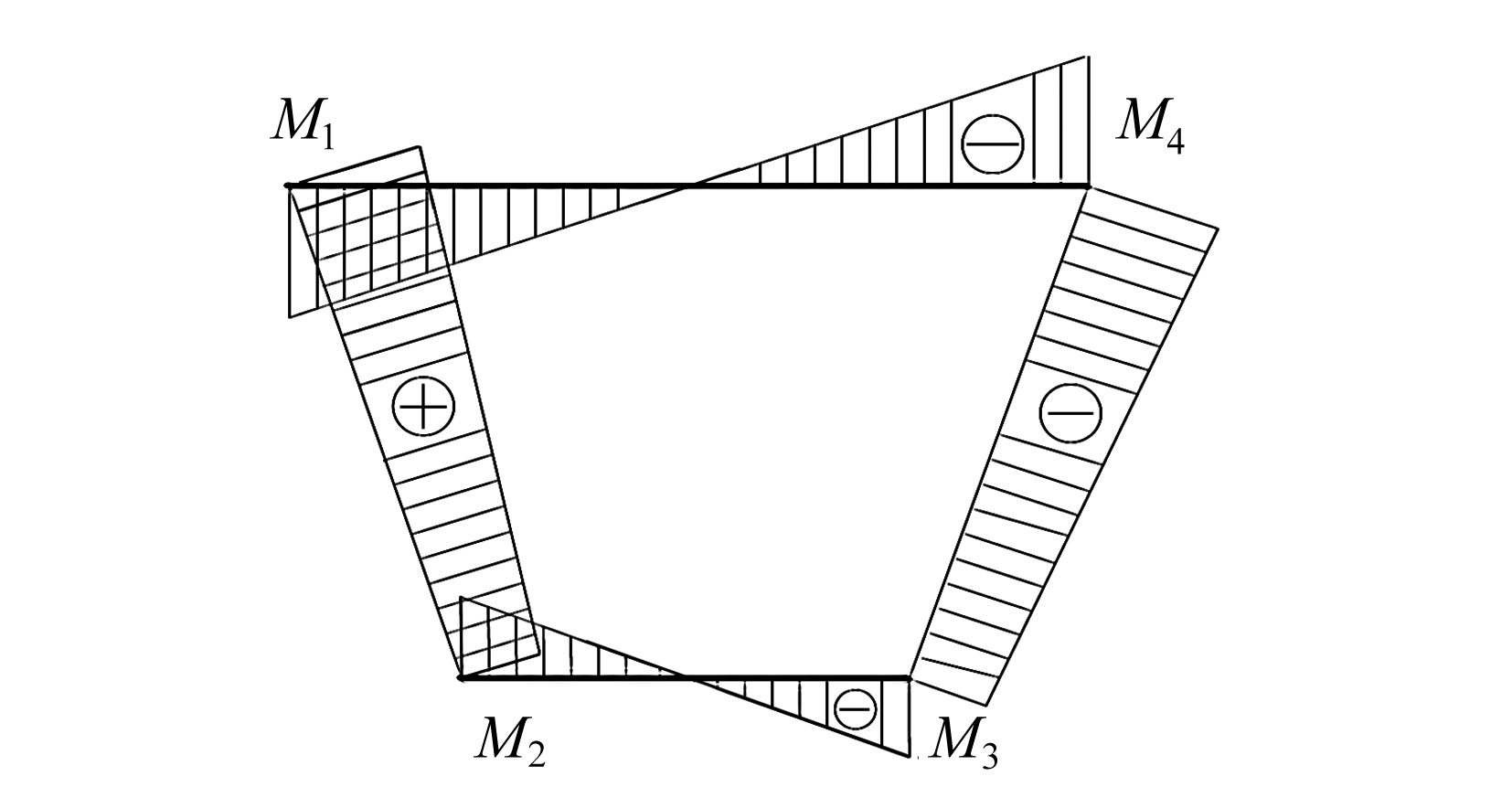
图7 框架横向弯矩图
Fig. 7 The frame transverse moment diagram
引入参数δv，即框架顶板上作用单位水平力时的水平位移．根据结构力学的位移计算式可得到作用于顶板上的力p4=1时框架顶板上的水平位移为
(9)
式中
为畸变荷载p4=1时的框架横向弯矩，M为畸变荷载p4作用时的框架横向弯矩．
当箱梁角点2产生畸变角γ2时，顶板的水平位移是γ2a1sin θ，所以，作用在顶板的水平力p4δv=γ2a1sin θ，则p4=γ2a1sin θ/δv代入图7所示框架相应角点的横向弯矩中可求出
(10)
(11)
式中K1，K2是与波形刚腹板箱梁尺寸及θ有关的常数．
因此波形钢腹板框架横向弯曲应变能为
(12)
则横向框架的畸变应变能为
(13)
式中
3.4 畸变翘曲应变能U2
由于畸变荷载自相平衡，则由此引起的翘曲应力σd也是自相平衡的．则有
波形钢腹板箱梁截面的翘曲应力的分布如图8所示．
图8 畸变引起的翘曲正应力分布图 图9 角点的畸变变位图
Fig. 8 The warpage normal stress distribution Fig. 9 Distortion displacements at corner points
diagram caused by distortion
引入参数β=σ1/σ2,即翘曲应力比，根据图8可得
(14)
(15)
式中M4，M2分别为顶底板翘曲正应力引起的面内弯矩， σ1为顶板与腹板交点处的应力， σ2为底板与腹板交点处的应力， d为两边悬臂板长度之和， t2为箱梁底板的厚度， t4为箱梁顶板的厚度．
根据∑M=0，即对竖轴y的弯矩等于零，可知
从以上式子中可以看出，箱梁截面尺寸是角点1和角点2处正应力之比的唯一影响因素，依据材料力学中的初等梁理论和两者间的比例关系可得到组成箱梁各板元的翘曲弯矩都可用底板与腹板角点处的应力σ2来表示，所以
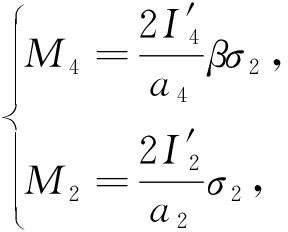
(16)
式中
为底板在自身平面内弯曲惯性矩，
为顶板在自身平面内的弯曲惯性矩．设波形钢腹板箱梁翘曲时沿轴向的变位为Vi(i=1，2，3，4)，即各板沿纵向翘曲时在自身平面内的挠度．I′1，I′2，I′3，I′4为各板在自身平面内的惯性矩，根据基本假定4)，有M1=M3=0，但EI′1=EI′3≠0．因为波形钢腹板具有褶皱效应，实际产生在钢腹板本身的纵向应变很小，故可认为波形钢腹板组合箱梁的顶底板不产生畸变位移即畸变角，箱梁的畸变角仅有钢腹板产生，变位图如图9所示．
根据初等梁理论[14]V″i=-Mi/EIi，因此
V″2=-M2/EI2， V″4=-M4/EI4．
畸变角为
对上式两边分别对z求二阶导数得
将V″2，V″4代入上式可得
(17)
因此
(18)
令
(19)
则
σ2=-EK4γ″2，
(20)
式中K4是受箱梁截面尺寸以及刚腹板的倾斜角度θ影响的常数．
因此波形钢腹板组合箱梁各板件的翘曲应变能为[15]
(21)
式中σi为箱梁各角点的翘曲应力，ti为箱梁各个板件的厚度．利用σ图自乘即得：
顶板
(22)
底板
(23)
故单位长度梁段的波形钢腹板箱梁的翘曲应变能为
(24)
则整个箱梁的翘曲应变能为
(25)
其中
3.5 畸变荷载势能V
(26)
3.6 畸变总势能Π
根据基本假定5)，忽略波形钢腹板的剪切变形应变能，即总势能仅由横向框架应变能U1、畸变翘曲应变能U2及外荷载势能V三部分组成，即得箱梁的畸变总势能Π为
Π=U1+U2+V=
(27)
4 畸变微分方程及其初参数解
对总势能表达式(27)进行一阶变分运算，可得
(28)
根据势能驻值原理，δΠ=0，则由式(28)可得控制微分方程如下：
(29)
其中
(30)
(31)
令
(32)
即
EJDγ″″2+EJRγ2-Vda2=0，
(33)
(34)
式中
通过求得的总势能一阶变分的表达式(28)可以求出畸变角及畸变翘曲对应的畸变矩和畸变双力矩如下式：
MD=-EJDγ‴2，
(35)
BD=-EJDγ″2，
(36)
式中JD为箱型梁畸变翘曲惯性矩，JR为箱型梁畸变框架惯性矩．
畸变微分方程(34)求解时的边界条件如下：
1) 固定端：γ2=0，γ′2=0；
2) 设置刚性横隔板的简支端：γ2=0，γ″2=0；
3) 设置刚性横隔板的自由端：γ2=0，γ‴2=0．
畸变微分方程(34)为四阶常系数非齐次线性微分方程，其对应齐次方程的通解为
γ2=C1sin(λz)sh(λz)+C2cos(λz)sh(λz)+
C3sin(λz)ch(λz)+C4cos(λz)ch(λz)，
(37)
式中γ0，γ′0，B0和M0分别为箱梁起始端的4个初参数解，即畸变角、畸变翘曲位移、畸变双力矩和畸变矩．则借助式(35)～(37)，可导出波形刚腹板箱梁的畸变角、畸变翘曲位移、畸变双力矩及畸变矩的初参数解为
(38)
γ0λ[cos(λz)sh(λz)-sin(λz)ch(λz)]，
(39)
BD=2λ2EJDγ0sin(λz)sh(λz)+B0cos(λz)ch(λz)+
λEJDγ′0[sin(λz)ch(λz)-cos(λz)sh(λz)]，
(40)
MD=2λ2EJDγ′0sin(λz)sh(λz)+M0cos(λz)ch(λz)+
λB0[sin(λz)ch(λz)+cos(λz)sh(λz)]-
2λ3EJDγ0[sin(λz)ch(λz)-cos(λz)sh(λz)]．
(41)
在以上初参数解的式子中，可以运用箱梁两端相应的边界条件求出4个初参数．如果箱梁跨内没有任何外荷载作用时，可利用初参数解，否则应补充相应的影响项．
5 算 例 分 析
1) 算例一
已知2种箱形截面如图10所示，计算跨径均为40 m，沿梁长等截面．混凝土的弹性模量为34.0 GPa，μ=0.166 7．荷载为跨中作用一偏心荷载p′=451.0 kN，偏心距e=2.35 m，波形钢腹板的顶底板为混凝土材料，顶板厚度t0=0.22 m，底板厚度tu=0.34 m；钢腹板采用1200型(Lc=0.33 m，Lb=0.27 m，h1=0.2 m)，腹板高度h为2.12 m，混凝土箱梁的腹板厚度为0.30 m，它的顶板厚度与波形刚腹板箱梁截面相同，波形钢板的弹性模量为210 GPa，μ=0.3．
(a) 波形钢腹板组合箱梁 (b) 混凝土箱梁
(a) The corrugated steel web composite box girder(b) The concrete box girder
图10 两种箱梁截面图(单位： m)
Fig. 10 Cross sections of 2 box girders(unit: m)
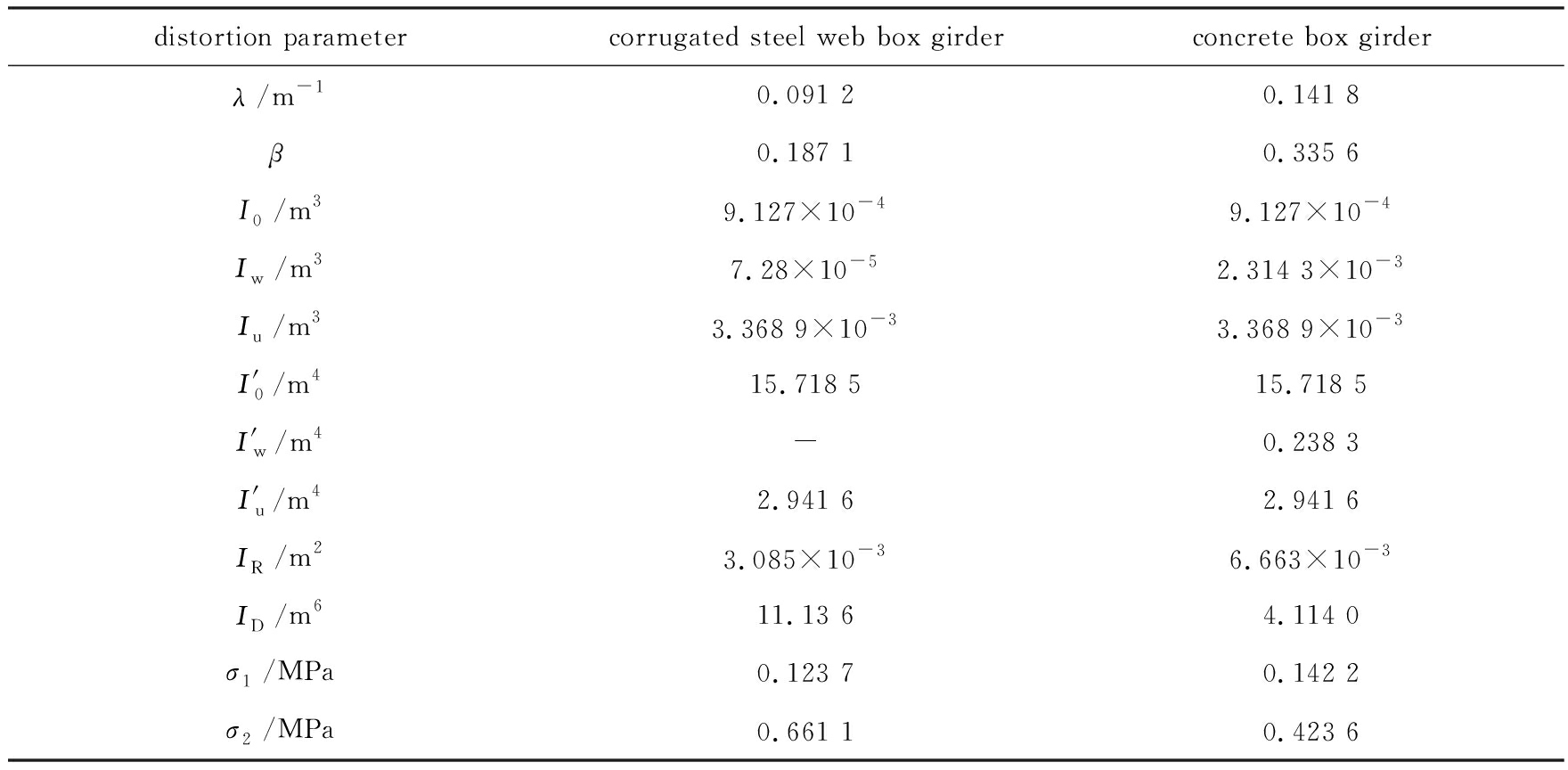
表1 波形钢腹板箱梁与混凝土箱梁截面跨中畸变正应力计算对比
Table 1 Comparison of the midspan distortion normal stresses between the corrugated steel
web box girder and the concrete box girder
distortion parametercorrugated steel web box girderconcrete box girder λ/m-10.091 20.141 8β0.187 10.335 6I0/m39.127×10-49.127×10-4Ιw/m37.28×10-52.314 3×10-3Ιu/m33.368 9×10-33.368 9×10-3Ι'0/m415.718 515.718 5Ι'w/m4-0.238 3Ι'u/m42.941 62.941 6ΙR/m23.085×10-36.663×10-3ΙD/m611.13 64.114 0σ1/MPa0.123 70.142 2σ2/MPa0.661 10.423 6
从表1两种箱梁的的数据对比分析得到，因为波形钢腹板的手风琴特性，相比混凝土顶底板的弯曲刚度，它的弯曲刚度很小，所以对箱梁的纵向弯曲和翘曲都起不到抵抗作用，导致波形钢腹板箱梁相比混凝土箱梁而言横向框架刚度很小以及由顶底板承担的纵向翘曲应力较大，算例一中，波形钢腹板组合箱梁由畸变产生的最大翘曲应力是传统混凝土箱梁的1.56倍．
2) 算例二
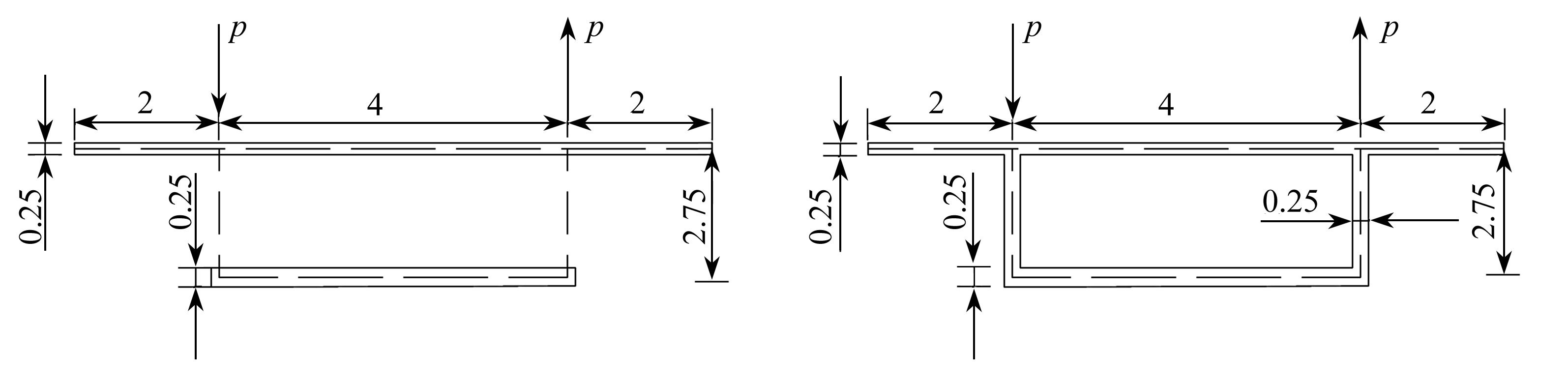
以文献[6]中的波形钢腹板组合箱梁和混凝土箱梁为例，已知2种箱形截面如图11所示，计算跨径均为40 m，沿梁长等截面．混凝土的弹性模量为34.5 GPa，μ=0.166 7．箱梁跨中施加反对称荷载p=50 kN，波形钢腹板的顶底板为混凝土材料，顶板厚度t0=0.25 m，底板厚度tu=0.25 m；钢腹板采用1200型(Lc=0.33 m，Lb=0.27 m，h1=0.2 m)，腹板高度h为2.75 m，波形钢板的弹性模量为210 GPa，μ=0.3．混凝土箱梁的截面尺寸和波形刚腹板箱梁一致．
(a) 波形钢腹板组合箱梁 (b) 混凝土箱梁
(a) The corrugated steel web box composite girder(b) The concrete box girder
图11 两种箱梁截面图(单位： m)
Fig. 11 Cross sections of 2 box girders(unit: m)
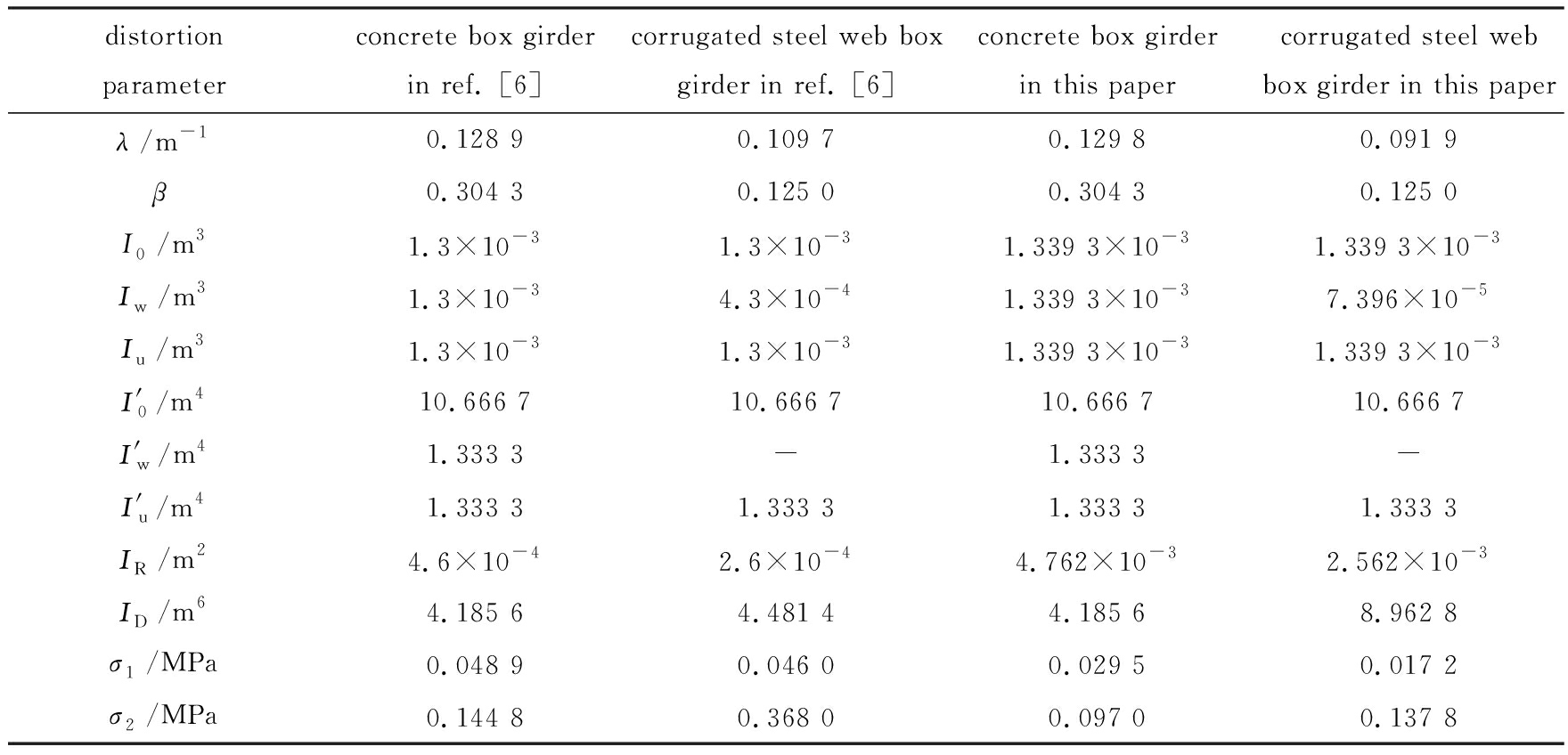
表2 截面畸变特性值
Table 2 Section distortion characteristic values
distortion parameterconcrete box girder in ref. [6]corrugated steel web box girder in ref. [6]concrete box girder in this papercorrugated steel web box girder in this paperλ/m-10.128 90.109 70.129 80.091 9β0.304 30.125 00.304 30.125 0I0/m31.3×10-31.3×10-31.339 3×10-31.339 3×10-3Ιw/m31.3×10-34.3×10-41.339 3×10-37.396×10-5Ιu/m31.3×10-31.3×10-31.339 3×10-31.339 3×10-3Ι'0/m410.666 710.666 710.666 710.666 7Ι'w/m41.333 3-1.333 3-Ι'u/m41.333 31.333 31.333 31.333 3ΙR/m24.6×10-42.6×10-44.762×10-32.562×10-3ΙD/m64.185 64.481 44.185 68.962 8σ1/MPa0.048 90.046 00.029 50.017 2σ2/MPa0.144 80.368 00.097 00.137 8
根据表2， 文献[6]中把波形钢板等效为正交异形板后， 利用平衡力系法推导了以畸变角为未知量的控制微分方程， 计算了箱梁各个板件的横向抗弯惯性矩和畸变翘曲惯性矩， 其中波形钢腹板箱梁和混凝土箱梁的横向抗弯惯性矩与本文计算结果不同．因为与传统混凝土箱梁相比， 波形钢腹板组合箱梁的横向抗弯刚度会有所减小， 所以本文的计算结果合理．按照本文的计算方法求得波形钢腹板组合箱梁由畸变产生的最大翘曲应力约是传统混凝土箱梁的1.42倍．
6 结 语
1) 本文首先从定义波形钢腹板箱梁的畸变位移即畸变角出发，以传统混凝土箱梁的畸变翘曲应力的推演过程为基础，得到了波形钢腹板箱梁畸变应力分析的方法，最后利用两个算例通过对比分析波形钢腹板箱梁和混凝土箱梁的畸变翘曲正应力，验证了本文分析方法和公式推导的合理性．
2) 本文通过结合波形钢腹板组合箱梁的受力特性，选取畸变中心的畸变角为畸变位移．按照初参数法求得的畸变翘曲应力与弹性地基梁比拟法的计算结果相差不大．采用本文的计算方法，在同等受力情况下，波形钢腹板箱梁的横向抗弯惯性矩较混凝土箱梁有所减小，而且波形钢腹板箱梁底板与腹板交点处的畸变翘曲正应力是混凝土箱梁对应位置处的1.5倍左右，小于相关文献的计算结果．
3) 通过能量变分法对波形钢腹板组合箱梁进行分析，利用初参数法求得箱梁截面畸变角、畸变翘曲位移、畸变双力矩及畸变力的一般公式．并且由于波形钢腹板的褶皱效应，在桥纵向可以自由伸缩，所以本文不考虑由顶底板翘曲引起的畸变位移，该方法很好地考虑了波形钢腹板组合箱梁的特征．
[1] 徐强, 万水. 波形钢腹板PC组合箱梁桥设计与应用[M]. 北京: 人民交通出版社, 2009.(XU Qiang, WAN Shui. Design and Application of PC Composite Box Girder Bridge With Corrugated Steel Webs[M]. Beijing: China Communications Press, 2009.(in Chinese))
[2] SAYED-AHMED E Y. Behaviour of steel and (or) composite girders with corrugated steel webs[J]. Canadian Journal of Civil Engineering, 2001, 28(4): 656-672.
[3] 郭金琼, 房贞政, 郑振. 箱形梁设计理论[M]. 北京: 人民交通出版社, 2008.(GUO Jinqiong, FANG Zhenzheng, ZHENG Zhen. Design Theory of Box Girder[M]. Beijing: China Communications Press, 2008.(in Chinese))
[4] 李宏江. 波形钢腹板箱梁扭转与畸变的实验研究及分析[D]. 博士学位论文. 南京: 东南大学, 2003.(LI Hongjiang. Experimental study and analysis of torsion and distortion of corrugated steel web box girder[D]. PhD Thesis. Nanjing: Southeast University, 2003.(in Chinese))
[5] 项海帆. 高等桥梁结构理论[M]. 北京: 人民交通出版社, 2001.(XIANG Haifan. Theory of Advanced Bridge Structure[M]. Beijing: China Communications Press, 2001.(in Chinese))
[6] 杨丙文, 黎雅乐, 万水, 等. 波形钢腹板箱梁畸变应力分析[J]. 东南大学学报(自然科学版), 2011, 41(5): 1065-1069.(YANG Bingwen, LI Yale, WAN Shui, et al. Stress analysis of box girders with corrugate steel webs under distorsion[J]. Journal of Southeast University(Natural Science), 2011, 41(5): 1065-1069.(in Chinese))
[7] 王文. 波形钢腹板箱梁扭转效应和畸变效应的分析与模型试验研究[D]. 硕士学位论文. 长沙: 湖南大学, 2008.(WANG Wen. Analysis and model test study on torsional effect and distortion effect of corrugated steel web box girder[D]. Master Thesis. Changsha: Hunan University, 2008.(in Chinese))
[8] 李时, 郭彦林. 波折腹板梁抗剪性能研究[J]. 建筑结构学报, 2001, 22(6): 49-54.(LI Shi, GUO Yanlin. Study on shearing resistance of beams with trapezoidally corrugated webs[J]. Journal of Building Structures, 2001, 22(6): 49-54.(in Chinese))
[9] 李宏江. 波形钢腹板预应力混凝土组合箱梁扭转与畸变研究进展[J]. 建筑结构学报, 2017, 38(7): 59-67.(LI Hongjiang. Research progress on torsion and distortion of prestressed concrete composite box girder with corrugated steel webs[J]. Journal of Building Structures, 2017, 38(7): 59-67.(in Chinese))
[10] ELGAALY M, SESHADRI A, HAMILTON R W. Bending strength of steel beams with corrugated webs[J]. Journal of structural engineering, 1997, 123(6): 772-782.
[11] ELGAALY M, SESHADRI A. Girder with corrugated webs under partial compressive edge loading[J]. Journal of structural engineering, 1997, 123(6): 783-791.
[12] 刘保东, 陈海波, 任红伟. 波纹钢腹板混凝土箱梁动力特性改善研究[J]. 中国铁道科学, 2008, 29(3): 29-33.(LIU Baodong, CHEN Haibo, REN Hongwei. Improvement study of the dynamic characteristics for concrete box-girder with corrugated steel webs[J]. China Railway Science, 2008, 29(3): 29-33.(in Chinese))
[13] 徐君兰, 顾安邦. 波形钢腹板组合箱梁桥的结构与受力分析[J]. 重庆交通学院学报, 2005, 24(2): 1-4, 34.(XU Junlan, GU Anbang. Analysis on structure and force principle of composite box-grider bridge with corrugated steel webs[J]. Journal of Chongqing Jiaotong University, 2005, 24(2): 1-4, 34.(in Chinese))
[14] 孙训方, 方孝淑, 关来泰. 材料力学[M]. 北京: 高等教育出版社, 2009.(SUN Xunfang, FANG Xiaoshu, GUAN Laitai. Mechanics of Materials[M]. Beijing: Higher Education Press, 2009.(in Chinese))
[15] 徐芝纶. 弹性力学[M]. 北京: 高等教育出版社, 2006.(XU Zhilun. Elasticity[M]. Beijing: Higher Education Press, 2006.(in Chinese))