引 言
非Newton流体广泛存在于自然界的各个领域，例如人体及大多数生物体内的血液、淋巴液等体液都属于非Newton流体，高分子聚合物的浓溶液及悬浮液一般为非Newton流体，食品工业中的番茄汁、蛋清、果酱等也都是非Newton流体．
对于非Newton流体，液体动力黏度μ不再是常数，而是与剪切速率有关，即非Newton流体的切应力与剪切速率不再满足线性关系．非Newton流体又分为时变性和非时变性两种．对非时变性非Newton流体，其动力黏度仅与剪切速率有关，与时间无关，一般称为广义Newton流体；而对于时变性非Newton流体，其动力黏度不仅与剪切速率有关，还受剪切持续时间的影响．非Newton流体具有很多Newton流体所不具备的特性，因此准确地模拟和预测非Newton流体的流动行为具有重要的工程意义．
随着计算机技术的高速发展，数值模拟方法在非Newton流体的研究中起到了越来越重要的作用[1]．模拟非Newton流体的数值方法主要分为两类：一类为有网格类方法，如有限元法[2]、有限差分法[3]、有限体积法[4]等；另一类为无网格类方法．光滑粒子动力学方法(smoothed particle hydrodynamics, SPH)[5-7]作为一种公认发展较早的无网格粒子型方法在非Newton流体的模拟方面已取得了一系列的研究成果．Zhou和Ge等[8]采用光滑粒子动力学法对非Newton流体Couette流的剪切稀化进行了模拟研究，结果表明了SPH模拟非Newton流体的有效性；Fan等[9]和Shamsoddini等[10]分别利用隐式SPH法和不可压SPH法对非Newton幂律流体进行了研究，表明了SPH法模拟幂律流体的有效性；Chaussonnet等[11]利用弱可压SPH法对黏弹性非Newton流体在高压空气作用下的力学响应进行了模拟，并与试验相对比，表明了SPH法模拟复杂非Newton流体问题的能力．
物质点法(material point method, MPM)[12-13]是一种相对新兴的粒子型方法，其具有Lagrange粒子和Euler背景网格双重描述，既包含了Lagrange粒子型无网格算法的优势，又可避免网格畸变和求解非线性对流项，可方便地追踪自由表面和粒子信息的时间历程；同时利用Euler型背景网格求解动量方程和梯度，可方便地施加各种边界条件，且避免了粒子搜索算法带来的巨大计算成本．
自提出之日起，物质点法已在涉及材料特大变形和破坏等一系列复杂工程问题中得到了广泛应用[14-16]．张雄等[17]和笔者及合作者[18]就物质点法与SPH法在求解高速冲击和流体流动问题中的求解精度和效率分别进行了对比研究， 结果表明： 在保证求解精度的同时， 物质点法相较SPH法具有较高的求解效率．但目前尚未见物质点法在非Newton流体中的相关研究报道．
非Newton流体种类繁多，在各种非Newton流体中，cross流和幂律流体同属于广义Newton流体，即其动力黏度仅与剪切速率有关而与时间无关，两者的本构模型简单易解，且可较好地用于分析工程实际问题，如水泥、黄黏土以及羰甲基纤维素等固体的悬浮液问题[19-20]．本文在传统物质点法的基础上，通过引入人工状态方程，对两类广义Newton流体(cross流和幂律流体)在平板Poiseuille和Couette流动下的特性进行分析研究，旨在表明物质点法在求解非Newton流体中的有效性．
1 理 论 方 法
1.1 物质点法
与各种数值方法一样，物质点法需满足连续介质力学的3个基本方程:
连续方程
·V=0;
(1)
运动方程
ρa=·σ+ρb;
(2)
能量方程
·(kT)+σ∶(⊗V),
(3)
式中ρ为质量密度，a为加速度矢量，b为单位体积力矢量，σ为Cauchy应力张量，T为温度，e为单位质量内能，k为热传导率，t为时间，V为速度矢量．
在物质点法中，求解域由若干Lagrange型物质点粒子离散，物质点粒子携带整个求解域的物理信息，包括应力、应变、质量、密度等．物质点粒子在整个计算过程中随求解域的变形而运动， 其各自质量保持不变， 因此连续性方程(1)自动满足； 本文未考虑热能交换， 因此可忽略能量方程(3)； 取虚位移δui作为权函数， 得到动量方程(2)在整个求解域Ω上的等效弱积分形式[12-13]：
(4)
式(4)中左端第一项可写作
(5)
在本质边界Γu处，位移已知，即δui|Γu=0；在自然边界Γt处，应力边界条件为
代入式(5)，得
(6)
将式(6)代入式(4)，得
(7)
将比应力
比面力
引入式(7)中, 同时引入边界层厚度h， 则dA=dV/h，可得
(8)
由于物质点法将连续体离散为一系列物质点，连续体的密度可写为
(9)
将式(9)代入式(8)，得
(10)
在物质点法中，物质点粒子和背景网格节点的各个物理量可通过插值函数进行相互映射．本文采用有限元单元传统4节点平面单元的形函数作为插值函数N， 即物质点粒子p处的位移uip及其导数uip, j、 位移增量δuip可由节点I处的位移uiI和位移增量δuiI映射得到(本文中若无特别说明， 则分别由p代表物质点粒子， i和j代表张量形式中的哑指标， I代表背景网格节点)：
uip=NIpuiI，
(11)
uip, j=NIp, juiI，
(12)
δuip=NIpδuiI．
(13)
相应的背景网格节点I处的质量mI可由物质点粒子p的质量mp映射得到
mI=NIpmp．
(14)
将式(11)～(14)代入式(10)，得在背景网格节点I处的运动方程：
(15)
考虑δuiI的任意性，得背景网格节点I处的运动方程：
(16)
代入比应力
比面力
式(16)可写为
(17)
利用当前时间步下各物质点携带的质量、应力和密度信息，结合应力边界和体力条件，通过求解式(17)可得当前子步下各个背景网格节点的速度和加速度信息，进而可得到各物质点粒子的加速度、速度和位置信息：
(18)
(19)
(20)
物质点上的应力信息可由材料模型得到．
1.2 材料模型
1.2.1 本构模型
对流体材料其本构模型可写为[21]
(21)
式中Pp为物质点粒子p处的压力，μ为流体动力黏度系数，
为应变率张量：
(22)
1.2.2 人工状态方程
对不可压缩流体的计算，一般通过引入人工状态方程将不可压缩流体看作弱可压缩来求解流体压力P[22]以提高计算效率，本文采用在求解Newton流体[23-24]和非Newton流体[9，25]中均广泛使用的人工状态：
(23)
式中
为人工体积模量，ρ0为参考密度，γ=7.0．
1.2.3 非Newton流体模型
对Newton流体，其动力黏度系数μ为常数；而对非Newton流体，其动力黏度系数μ与剪切速率
有关．本文主要考虑两种非Newton流体：cross流和幂律流体，两者的动力黏度μ与剪切速率的关系式分别为
(24)
(25)
式中μ0和μ∞分别为零剪切率和高剪切率下的动力黏度；K，M和n为液体常数．对cross流，定义常数a=μ∞ /μ0，则a=1,a<1，a>1分别对应Newton流体、剪切稀化和剪切稠化cross流；对于幂律流体，n=1,n<1，n>1分别对应Newton流体、剪切稀化和剪切稠化幂律流体．
2 计算模型及结果分析
分别研究两种非Newton流体(cross流和幂律流体)在平板Poisuille流和Couette流中的流动表现．对cross流，液体常数取K=M=1.0，分别考虑5种不同材料参数，分别为：Newton流体(a=1)、剪切稀化cross流体(a=0.25,0.5)、剪切稠化cross流体(a=2.0,4.0)．对幂律流体同样计算5种不同材料参数，即Newton流体(n=1)、剪切稀化幂律流体(n=0.6,0.8)、剪切稠化幂律流体(n=1.2,1.4)．本文计算中取人工体积模量K=143 Pa，参考密度ρ0=1 000 kg/m3，计算时间步长为5 μs，μ0=1×10-6 Pa·s．
2.1 Poiseuille流
Poiseuille流模型如图1所示， 静止于两固定平板中间的流体在恒定体力F作用下， 开始运动直至稳定．计算模型的几何尺寸为H=1 mm和L=0.5 mm， 体积驱动力为F=8 mm/s2； 对Newton流体，其稳态最大速度为
即对Newton流体稳态最大速度为1 mm/s．取背景网格为边长为1/20 mm的正方形，每个背景网格内布置有2×2个物质点粒子．
图1 Poiseuille流计算模型
Fig. 1 The model for the Poiseuille flow
Morris等[23]给出了Newton流体Poiseuille流速度随高度和时间变化的理论解：
(26)
图2给出了Newton流体Poiseuille流的物质点法求解结果[18]，其中图2(a)给出了Newton流体Poiseuille流最大水平速度随时间的变化规律，图2(b)给出了不同时刻下物质点法和SPH法所得的速度在高度方向的分布曲线，可以看出物质点法所得结果与精确解吻合较好，且较SPH法具有较高的稳定性和求解精度．
图3～5分别给出了非Newton流体Poiseuille流的物质点法模拟结果．其中图3(a)和图3(b)分别给出了不同cross流和幂律流体模型下Poiseuille流在y=H/2截面处的平均速度随时间的变化规律；图4和图5分别给出了t=0.05 s时刻，不同cross流和不同幂律流模型下平均剪切速率和平均无量纲动力黏度随高度方向的变化规律．
由图3(a)和图3(b)可以看出：对于剪切稠化液体，Poiseuille流更快地达到稳定，且得到的稳态最大速度要小于Newton流体的值，对于剪切稀化流体则恰好相反．由图4和图5可以看出：在Poiseuille流中，中心截面处的剪切速率最小，越靠近上下边界，剪切速率越大，剪切速率和动力黏度沿高度中心呈对称分布．结果表明物质点法可以很好地反映非Newton流体的剪切稀化和剪切稠化现象，即对剪切稀化流体，随着剪切速率的增大，动力黏度逐渐减小；对剪切稠化流体，随着剪切速率的增大，动力黏度逐渐增大．
(a) 最大水平速度随时间的变化规律(b) 不同时刻下物质点法和SPH法所得的
(a) The time history of the maximum velocity 速度在高度方向的分布曲线
along the x-axis (b) Comparisons of the velocity profiles between the MPM
and SPH simulations and the theoretical solutions
for the Poiseuille flow problem
图2 Newton流体Poiseuille流物质点法求解结果
Fig. 2 The MPM results of the Newtonian Poiseuille flow
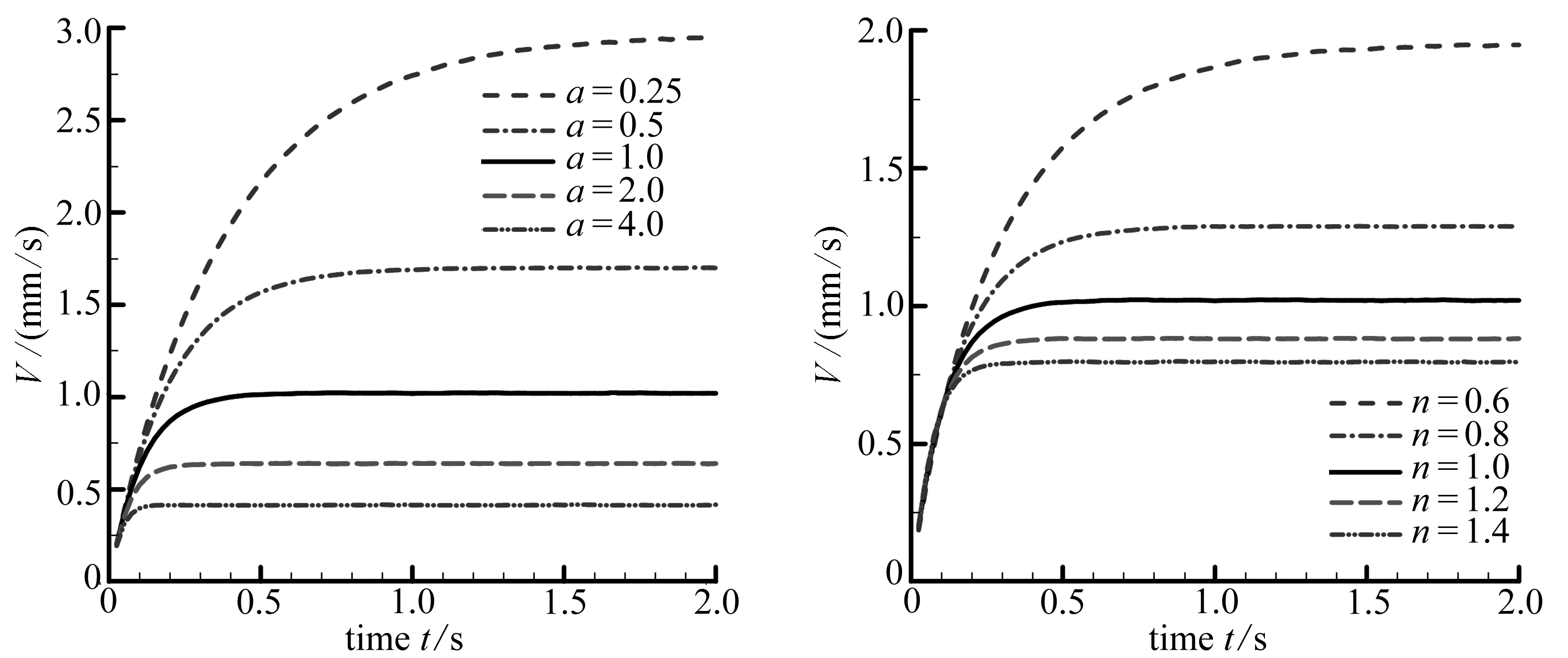
(a) Cross流(b) 幂律流
(a) The cross flow (b) The power-law flow
图3 非Newton流体的物质点法求解结果
Fig. 3 The MPM results of the non-Newtonian fluid flow
由图4(a)和图4(b)可以看出：剪切稀化cross流体的动力黏度(a=0.25，0.5)均要小于初始黏度(a=1.0)；而剪切稠化cross流体(a=2.0，4.0)的动力黏度总是大于初始黏度．图5(a)和图5(b)表明：对幂律流体，当应变速率大于1时，剪切稀化(n=0.6，0.8)和剪切稠化(n=1.2，1.4)幂律流体的动力黏度分别小于和大于液体的初始黏度(n=1.0)；而当应变速率小于1时，剪切稀化幂律流体(n=0.6，0.8)的动力黏度将大于液体的初始黏度(n=1.0)，相对应的剪切稠化幂律流体(n=1.2，1.4)的动力黏度要小于初始黏度(n=1.0)．
由图3和图5可以看出，对剪切稀化幂律流体(如n=0.6，0.8时)，在高度中心位置附近处的液体黏度也大于初始液体黏度，而在靠近上下边界处的液体黏度要小于初始液体黏度，考虑其最终稳态速度和到达稳态时间均大于Newton流体时的情形，因此可以得出结论：平板Poiseuille流的最终稳态速度和到达稳态时间是由靠近上下边界处的液体黏度和液体所受体力所决定．
(a) 平均剪切速率 (b) 平均无量纲动力黏度
(a) The average shear rates(b) The average dynamic viscosities
图4 t=0.05 s时刻不同cross流模型下Poiseuille流随高度方向的变化规律
Fig. 4 The Poiseuille flow along the y-axis for the cross flow model at t=0.05 s
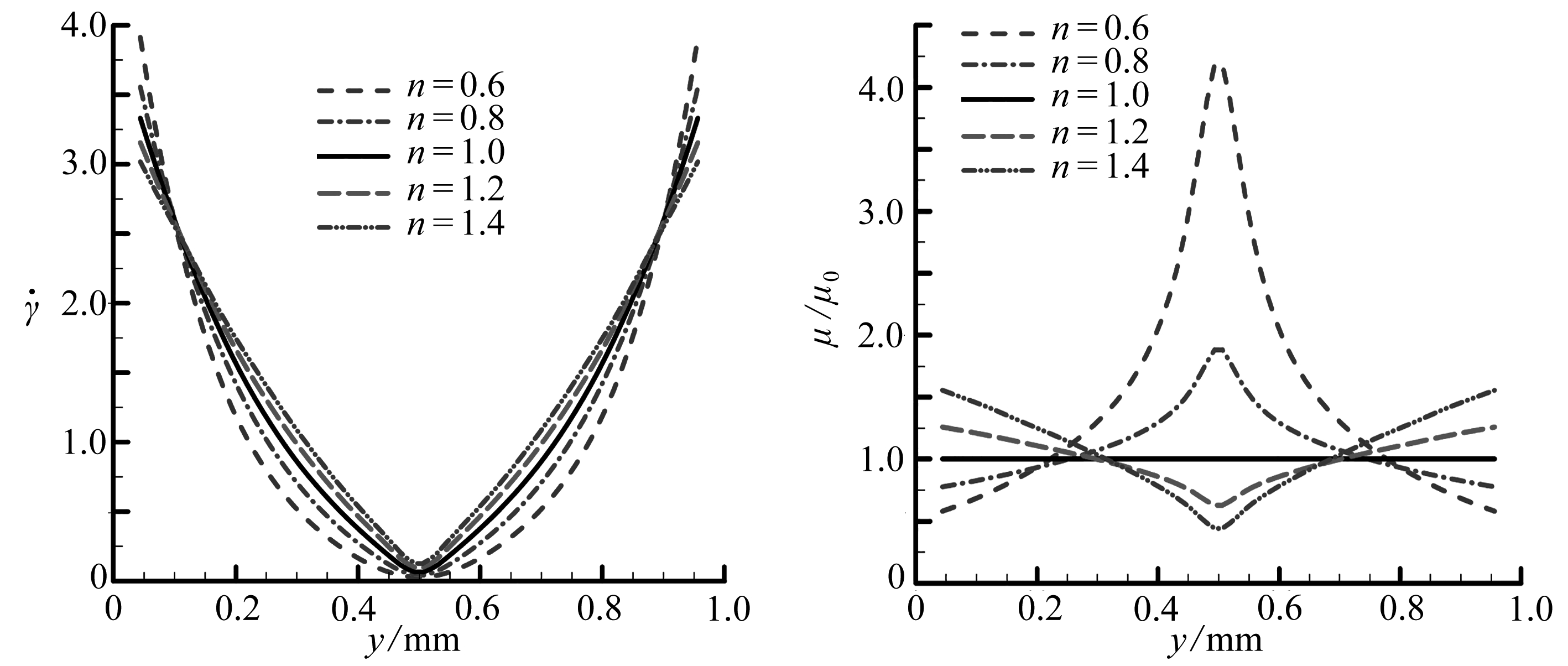
(a) 平均剪切速率 (b) 平均无量纲动力黏度
(a) The average shear rates(b) The average dynamic viscosities
图5 t=0.05 s时刻不同幂律流模型下Poiseuille流随高度方向的变化规律
Fig. 5 The Poiseuille flow along y-axis for the power-law flow model at t=0.05 s
2.2 Couette流
Couette流模型如图6所示，下平板固定不动，上平板以恒定速度V0运动， 同时驱动初始静止于上下平板间的流体运动， 直至达到平衡．计算模型的几何尺寸同样取为H=1 mm和L=0.5 mm，上平板恒定速度V0=0.1 mm/s；对Newton流体，其中间位置处的稳态速度为V(H/2,∞)=0.05 mm/s．同样地，计算背景网格取边长为1/20 mm的正方形，每个背景网格内布置有2×2个物质点粒子．
Morris等[23]给出了Newton流体Couette流速度随时间和高度分布的理论解：
(27)
图6 Couette流计算模型
Fig. 6 The model for the Couette flow
图7 Newton流体Couette流的物质点求解结果
Fig. 7 The MPM results of the Newtonian Couette flow
(a) cross流 (b) 幂律流
(a) The cross flow (b) The power-law flow
图8 Couette流在y=H/2截面处平均速度随时间的变化规律
Fig. 8 The time-histories of average velocities of the Couette flow at section y=H/2
图7给出了Newton流体Couette流的物质点法求解结果[18]，其中图7(a)给出了Newton流体Couette流在y=H/2处的最大水平速度随时间的变化规律；图7(b)给出了不同时刻下物质点法和SPH法所得的速度在高度方向的分布曲线，可以看出物质点法所得结果与精确解吻合较好．
图8～10分别给出了非Newton流体Couette流的物质点法模拟结果．图8给出了不同cross流和幂律流模型下Couette流在y=H/2截面处的平均速度随时间的变化规律；图9和图10分别给出了t=0.05 s时刻，不同cross流和不同幂律流模型下Couette流平均剪切速率和平均无量纲动力黏度随高度方向的变化规律．
由图8可以看出：当a=1.0和n=1.0时，即Newton流体时，计算所得稳定速度与理论解一致；对于不同的剪切稀化和剪切稠化液体，Couette流最终达到稳定的时间虽然不同，但最终的稳定速度一致．
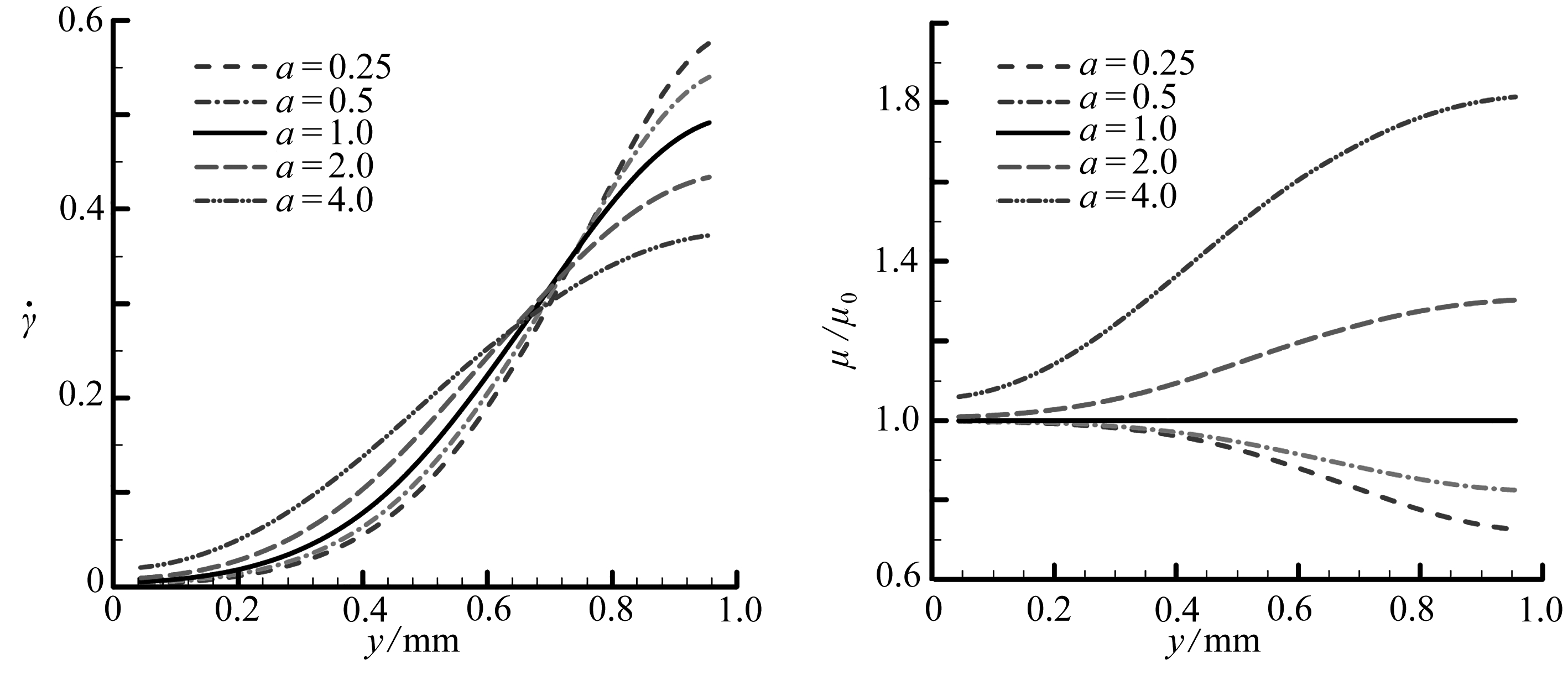
(a) 平均剪切速率 (b) 平均无量纲动力黏度
(a) The average shear rates(b) The average dynamic viscosities
图9 t=0.05 s时刻不同cross流模型下Couette流随高度方向的变化规律
Fig. 9 The Couette flow along the y-axis for different cross flow models at t=0.05 s
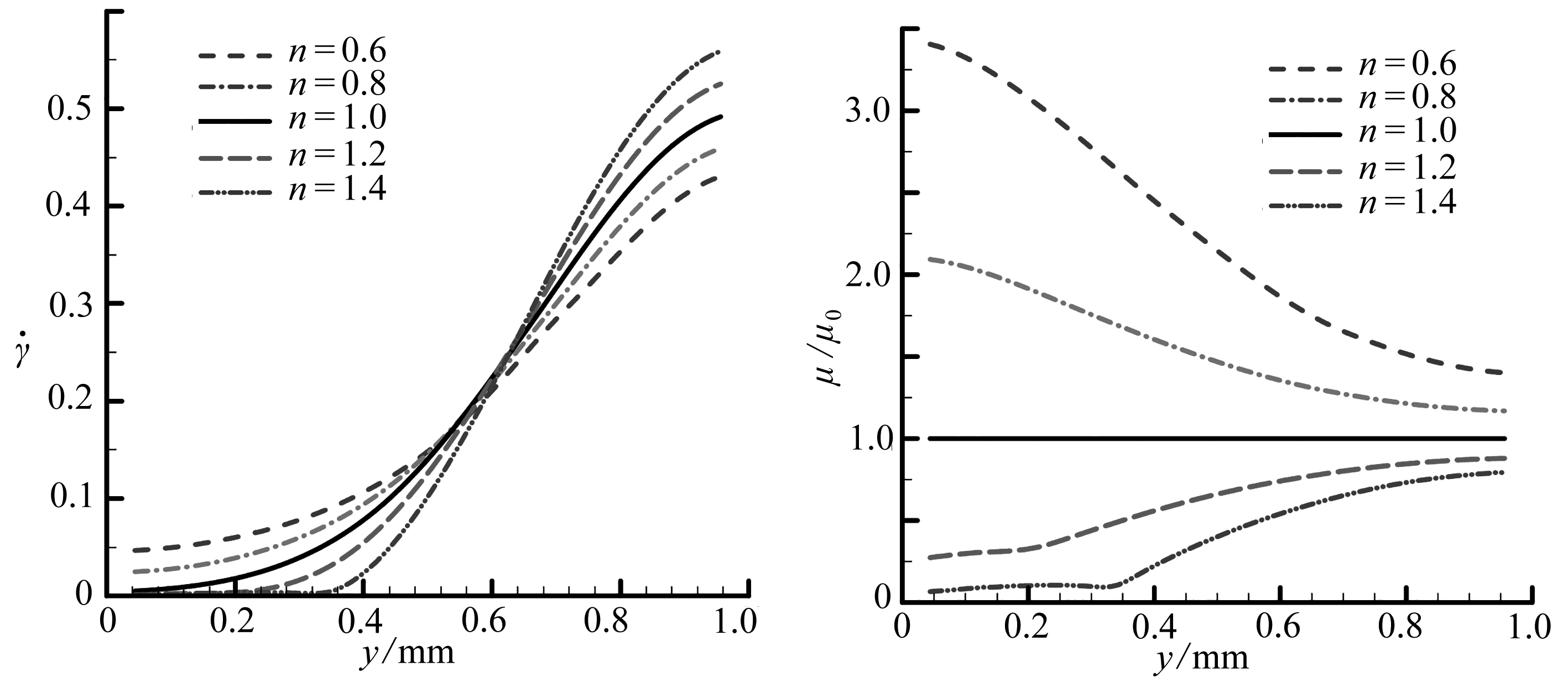
(a) 平均剪切速率 (b) 平均无量纲动力黏度
(a) The average shear rates(b) The average dynamic viscosities
图10 t=0.05 s时刻不同幂律流模型下Couette流随高度方向的变化规律
Fig. 10 The Couette flow along the y-axis for different power-law flow models at t=0.05 s
由图9和图10可以看出：在Couette流中，距离移动上平板越近处，剪切速率越大，越靠近上下边界，剪切速率越小．对剪切稀化流体，随着应变速率的减小，动力黏度逐渐增大；对剪切稠化流体，随着应变速率的减小，动力黏度逐渐降低．
由图10可以看出，对幂律流体，当剪切速率小于1时，剪切稀化幂律流体(n=0.6，0.8)的动力黏度要大于液体的初始黏度(n=1.0)，因此其将更快地达到稳定状态，如图8所示，即Couette流到达稳态所需时间与液体黏度有关，但其稳态速度大小只与平板的移动速度有关．
3 结 论
本文基于传统的物质点法，通过引入人工状态方程，研究了两种非Newton流体(cross流和幂律流体)，在剪切稠化和剪切稀化情况下，Poiseuille流和Couette流的流动特性，从模拟结果可以看出：
1) 物质点法所得Newton流体下的Poiseuille流和Couette流模拟结果与理论解吻合较好；
2) 物质点法可很好地模拟非Newton流体的流动特性，即对剪切稀化流体，随着应变速率的减小，动力黏度逐渐增大；对剪切稠化流体，随着应变速率的减小，动力黏度逐渐降低，表明了物质点法模拟非Newton流体的可行性；
3) 平板Poiseuille流的稳态速度和到达稳态时间与液体所受体力呈正比，与上下边界处的液体黏度呈反比；平板Couette流的稳态速度只与平板的移动速度有关与液体黏度无关，但其到达稳态时间与液体黏度有关．
致谢 本文作者衷心感谢江西理工大学博士启动基金(JXXJBS18042)对本文的资助．
[1] CROCHET M J, DAVIES A R, WALTERS K. Numerical Simulation of Non-Newtonian Flow[M]. Amsterdam: Elsevier, 2012.
[2] BAAIJENS F P T, HULSEN M A, ANDERSON P D. The use of mixed finite element methods for viscoelastic fluid flow analysis[M]//Encyclopedia of Computational Mechanics. John Wiley & Sons, 2018: 481-498.
[3] 张茂林, 吴清松, 李传亮, 等. 非牛顿流体的差分方法研究[J]. 西南石油学院学报, 2000, 22(1): 5-8.(ZHANG Maolin, WU Qingsong, LI Chuanliang, et al. Research on the formulation of finite difference methods for non Newtonian fluids in porous media[J]. Journal of Southwest Petroleum Institute, 2000, 22(1): 5-8.(in Chinese))
[4] 袁世伟, 赖焕新. 幂律非牛顿流体流动的有限体积算法[J]. 华东理工大学学报(自然科学版), 2013, 39(3): 364-369. (YUAN Shiwei, LAI Huanxin. A finite volume method for calculating flows of power-law non-Newton fluids[J]. Journal of East China University of Science and Technology(Natural Science Edition), 2013, 39(3): 364-369.(in Chinese))
[5] GINGOLD R A, MONAGHAN J J. Smoothed particle hydrodynamics: theory and application to non-spherical stars[J]. Monthly Notices of the Royal Astronomical Society, 1977, 181(3): 375-389.
[6] LIU G, LIU M B. Smoothed Particle Hydrodynamics: a Meshfree Particle Method[M]. World Scientific Publishing Company, 2003.
[7] 徐丞君, 徐胜利, 刘庆源. 修正压力梯度粒子近似SPH方法计算大密度比界面流动[J]. 应用数学和力学, 2019, 40(1): 20-35.(XU Chengjun, XU Shengli, LIU Qingyuan. Modified particle approximation to pressure gradients in the SPH algorithm for interfacial flows with high density ratios[J]. Applied Mathematics and Mechanics, 2019, 40(1): 20-35.(in Chinese))
[8] ZHOU G, GE W, LI J. Smoothed particles as a non-Newtonian fluid: a case study in Couette flow[J]. Chemical Engineering Science, 2010, 65(6): 2258-2262.
[9] FAN X, TANNER R I, ZHENG R. Smoothed particle hydrodynamics simulation of non-Newtonian moulding flow[J]. Journal of Non-Newtonian Fluid Mechanics, 2010, 165(5/6): 219-226.
[10] SHAMSODDINI R, SEFID M, FATEHI R. Incompressible SPH modeling and analysis of non-Newtonian power-law fluids, mixing in a microchannel with an oscillating stirrer[J]. Journal of Mechanical Science and Technology, 2016, 30(1): 307-316.
[11] CHAUSSONNET G, KOCH R, BAUER H, et al. Smoothed particle hydrodynamics simulation of an air-assisted atomizer operating at high pressure: influence of non-Newtonian effects[J]. Journal of Fluids Engineering, 2018, 140(6): 61301. DOI: 10.1115/1.4038753.
[12] SULSKY D, CHEN Z, SCHREYER H. A particle method for history-dependent materials[J]. Computer Methods in Applied Mechanics and Engineering, 1994, 118(1): 179-196.
[13] SULSKY D, ZHOU S, SCHREYER H. Application of a particle-in-cell method to solid mechanics[J]. Computer Physics Communications, 1995, 87(1): 236-252.
[14] 廉艳平, 张帆, 刘岩, 等. 物质点法的理论和应用[J]. 力学进展, 2013, 43(2): 237-264.(LIAN Yanping, ZHANG Fan, LIU Yan, et al. Material point method and its applications[J]. Advances in Mechanics, 2013, 43(2): 237-264. (in Chinese))
[15] 王宇新, 李晓杰, 王小红, 等. 炸药爆轰物质点法三维数值模拟[J]. 应用数学和力学, 2015, 36(2): 198-206.(WANG Yuxin, LI Xiaojie, WANG Xiaohong, et al. 3D simulation of explosive detonation with the material point method[J]. Applied Mathematics and Mechanics, 2015, 36(2): 198-206. (in Chinese))
[16] MA S, ZHANG X, QIU X M. Comparison study of MPM and SPH in modeling hypervelocity impact problems[J]. International Journal of Impact Engineering, 2009, 36(2): 272-282.
[17] 张雄, 刘岩, 张帆, 等. 极端变形问题的物质点法研究进展[J]. 计算力学学报, 2017, 34(1): 1-16.(ZHANG Xiong, LIU Yan, ZHANG Fan, et al. Recent progress of material point method for extreme deformation problems[J]. Chinese Journal of Computational Mechanics, 2017, 34(1): 1-16.(in Chinese))
[18] SUN Z, LI H, GAN Y, et al. Material point method and smoothed particle hydrodynamics simulations of fluid flow problems: a comparative study[J]. Progress in Computational Fluid Dynamics, 2018, 18(1): 1-18.
[19] 陈文芳, 蔡扶时. 非牛顿流体的一些本构方程[J]. 力学学报, 1983, 19(1): 16-26.(CHEN Wenfang, CAI Fushi. Some constitutive equations for non-Newtonian fluids[J]. Chinese Journal of Theoretical and Applied Mechanics, 1983, 19(1): 16-26.(in Chinese))
[20] 陈文芳. 非牛顿流体力学[M]. 北京: 科学出版社, 1984.(CHEN Wenfang. The Mechanics of Non-Newtonian Fluids[M]. Beijing: Science Press, 1984.(in Chinese))
[21] 周光坰, 严宗毅, 许世雄, 等. 流体力学(上)[M]. 北京: 高等教育出版社, 2001.(ZHOU Guangjiong, YAN Zongyi, XU Shixiong, et al. The Fluid Mechanics
[M]. Beijing: Higher Education Press, 2001.(in Chinese))
[22] LI J G, HAMAMOTO Y, LIU Y, et al. Sloshing impact simulation with material point method and its experimental validations[J]. Computers & Fluids, 2014, 103: 86-99.
[23] MORRIS J P, FOX P J, ZHU Y. Modeling low Reynolds number incompressible flows using SPH[J]. Journal of Computational Physics, 1997, 136(1): 214-226.
[24] MONAGHAN J J. Simulating free surface flows with SPH[J]. Journal of Computational Physics, 1994, 110(2): 399-406.
[25] XIANG H, CHEN B. Simulating non-Newtonian flows with the moving particle semi-implicit method with an SPH kernel[J]. Fluid Dynamics Research, 2015, 47(1): 15511. DOI: 10.1088/0169-5983/47/1/015511.