符 号 注 释
C井筒储集系数，m3/MPaS 表皮系数，无因次Ctj介质压缩系数(j=m, f, v)，MPa-1x，y，z平面任意位置坐标，mqsc生产总流量，m3/hxw，yw，zw中心坐标，m
瞬时流量，m3/hh储层厚度，mkj储层渗透率(j=m, f, v)，mDhw储层打开厚度，mpw考虑井储和表皮井底压力，MPaφj介质孔隙度(j=m, f, v)pwv不考虑井储和表皮井底压力，MPaLf裂缝半长，mpj介质储层压力(j=m, f, v)，MPaλ启动压力梯度, MPa/mvj水平和垂向流体运动速度(j=h, z)，m/sγ应力敏感系数pe原始储层压力，MPake原始储层渗透率，mDr任意位置径向距离，mδ无限小垂直距离，mK0(x)零阶第二类修正Bessel函数ε无限小径向距离，mI0(x) 零阶第一类修正Bessel函数μ流体黏度，mPa·sωj弹性储容比(j=m, f, v)sLaplace变量λj窜流系数(j=mf, vf, mv)(·)e原始状态(·)D无因次变量
Laplace空间变量(·)h,z分别代表水平和垂直方向
Fourier变换1 D=0.986 9 μm2
引 言
缝洞型碳酸盐岩储层在我国油气资源开发中占有重要的地位，主要以新疆塔河油田下奥陶系碳酸盐岩为主，该区域的储集空间主要以构造裂缝以及沿裂缝形成的岩溶缝洞为主，裂缝和溶洞特征明显[1-2]，但实际开采过程油井往往需要经过压裂改造才能获得更大的产量，这表明该储层存在明显的低渗特征．基于Laplace空间点源函数基本理论[3-4]，我国学者关于缝洞型碳酸盐岩油藏的直井、水平井、压裂井和多分支水平井等试井模型都有了一定的研究[5-8]，绘制了相应的特征曲线并分析了其影响因素．对于低渗透碳酸盐岩油藏而言，在石油开采过程中存在应力敏感效应的影响，同时，低渗透储层还存在低速非Darcy渗流现象．对于低速非Darcy渗流，一般考虑用启动压力梯度来描述其渗流方程[9]．罗二辉等[10-11]考虑启动压力梯度和动边界的共同影响，建立并求解考虑井储和表皮影响的低速非Darcy非稳态渗流试井数学模型；曹丽娜等[12]基于Laplace变换和正交变换求得考虑启动压力梯度水平井试井模型，根据定产与定压关系得到井底压力变化曲线；孟凡坤等[13]基于点源函数基本理论建立了考虑应力敏感影响碳酸盐岩斜井试井解释模型并分析其生产动态关系．关于低渗油藏压裂井试井模型的研究，付春权等[14]基于椭圆流动模型建立了考虑启动压力梯度影响有限导流压裂井试井模型；刘文超等[15]考虑三重介质油藏介质变形与垂直裂缝井闭合的影响，建立了考虑应力敏感影响试井解释数学模型，采用有限差分求得井底压力解；刘启国等[16]、李顺初等[17]分别就夹角断层多段压裂水平井和考虑应力敏感储层影响时井底压力动态特征和解的结构进行分析．
基于前人的研究，笔者应用点源函数和渗流力学基本原理，建立考虑应力敏感和启动压力梯度影响的三孔单渗并行嵌套直井压裂井试井解释数学模型．利用Laplace变换、有限余弦Fourier变换和逆变换得到井底压力解，最后利用Stehfest数值反演得到实空间井底压力解，绘制了压力和压力导数特征曲线并进行影响因素分析．从理论上阐述其变化规律并为低渗缝洞型油藏实际试井资料的解释提供了理论指导．
1 试井模型的建立与求解
1.1 物理模型描述
缝洞型低渗碳酸盐岩油藏由裂缝、溶洞和基质组成，其中裂缝起导流作用，基质和溶洞主要起储集作用．基质和溶洞中的流体通过裂缝流入井筒，只考虑裂缝向井筒供液，其物理模型示意图如图1所示．
图1 三孔单渗并行嵌套压裂井物理模型
Fig. 1 The physical model for a fractured well of single permeability parallel with nesting 3 apertures
为了更好地建立试井解释数学模型，其基本假设条件如下： 1) 顶底封闭、侧向无限大边界油井以定产量qsc生产； 2) 渗流规律满足低速非Darcy定律，储层厚度均匀，流体不可压缩且各向异性； 3) 渗透率和黏度不随压力变化； 4) 忽略重力和毛管力的影响； 5) 压裂裂缝关于井筒对称，裂缝可以完全压开，也可以部分压开．根据连续性方程、状态方程和运动方程建立三重介质渗流微分方程．
1.2 数学模型建立与求解
考虑储层应力敏感时，储层渗透率与压力呈指数变化规律[18]，具体关系表达式如下：
k=kee-γ(pe-p)．
(1)
根据Pascal[9]给出的启动压力梯度渗流表达式，结合式(1)得到同时考虑应力敏感和启动压力梯度时，裂缝系统的渗流速度为
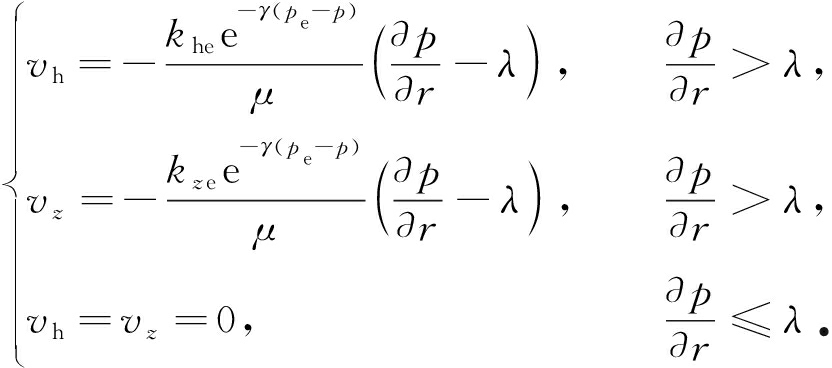
(2)
为了计算方便，定义以下无因次变量：
将上式代入渗流微分方程，得到考虑应力敏感和启动压力梯度的无因次渗流微分方程和边界条件如下：
1) 裂缝渗流微分方程
(3)
2) 溶洞渗流微分方程
(4)
3) 基质渗流微分方程
(5)
4) 初始条件
pfD(rD,zD,tD=0)=pmD(rD,zD,tD=0)=pvD(rD,zD,tD=0)=0；
(6)
5) 顶底封闭边界和侧向无限大外边界
(7)
pfD(rD→∞,zD,tD)=0；
(8)
6) 内边界条件
(9)
对式(3)～(9)进行Laplace变化并整理得到Laplace空间渗流微分方程如下：
(10)
式中
f(s)=ωf+
式(10)是非线性很强的渗流微分方程和内边界条件，直接求解比较困难，通过Pedrosa[19]提出的摄动变换将非线性方程转化为线性方程，摄动变换具体方法如下：
(11)
式(10)经过摄动变换并取其零阶解之后变为
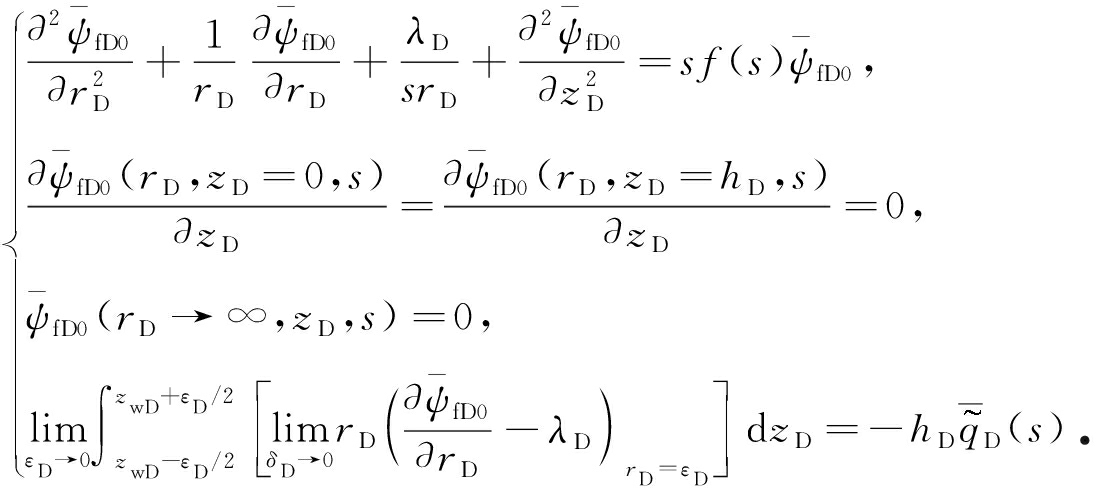
(12)
通过对式(11)关于zD进行有限余弦Fourier变换，变换之后的方程为
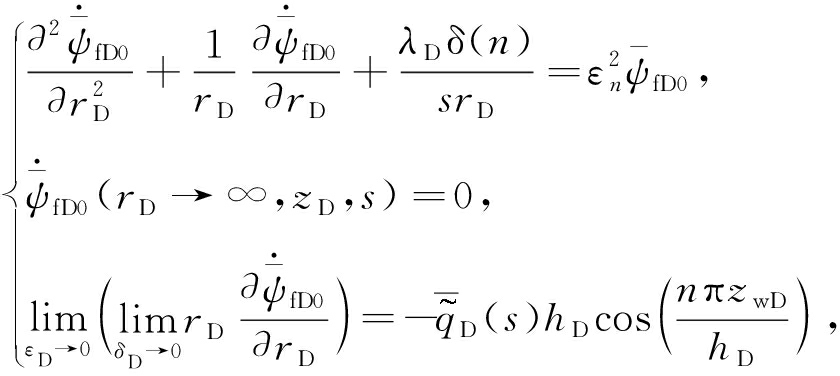
(13)
式中
方程组(13)中裂缝渗流微分方程的通解分两种情况：
1) 当n=0时，
(14a)
2) 当n≠0时,
(14b)
结合内外边界条件求得系数A和B并对其解进行Fourier余弦逆变换可以得到顶底封闭、侧向外边界无限大点源解如下：
(15)
式中
为了求得压裂井井底压力解，需要对式(15)所给出的点源解进行积分，分别对xw从-Lf到Lf积分得到水平线源解，在沿z方向从zw-hw/2到zw+hw/2积分得到面源解，最终得到考虑应力敏感和启动压力梯度三孔单渗嵌套压裂井井底压力如下：
(16)
式(16)就是经过摄动变换之后压裂井的压力解，其中第二项关于启动压力梯度项的计算采用复合Simpson数值积分得到，将上式代入式(11)得到同时考虑应力敏感和启动压力梯度低渗碳酸盐压裂井的压力解，取xD=0.732得到无限导流压裂井井底压力解:
(17)
根据Duhamel原理，得到考虑井储和表皮影响时井底压力解：
(18)
2 模 型 验 证
利用Stehfest[20]数值反演计算式(18)得到实空间无因次井底压力解，为了验证本文模型的正确性，将本文计算结果与文献[14]给出的计算低渗油藏考虑启动压力梯度实空间解析解进行对比．为了模型的可比性，取文献[14]中的无因次裂缝导流能力为1 000 000；取本文模型中f(s)=1，γD=10-10．从图2可以看出，本文简化模型与文献[14]所给的计算结果很吻合，因此，可以采用本文方法准确地计算缝洞型低渗碳酸盐岩井底压力解．
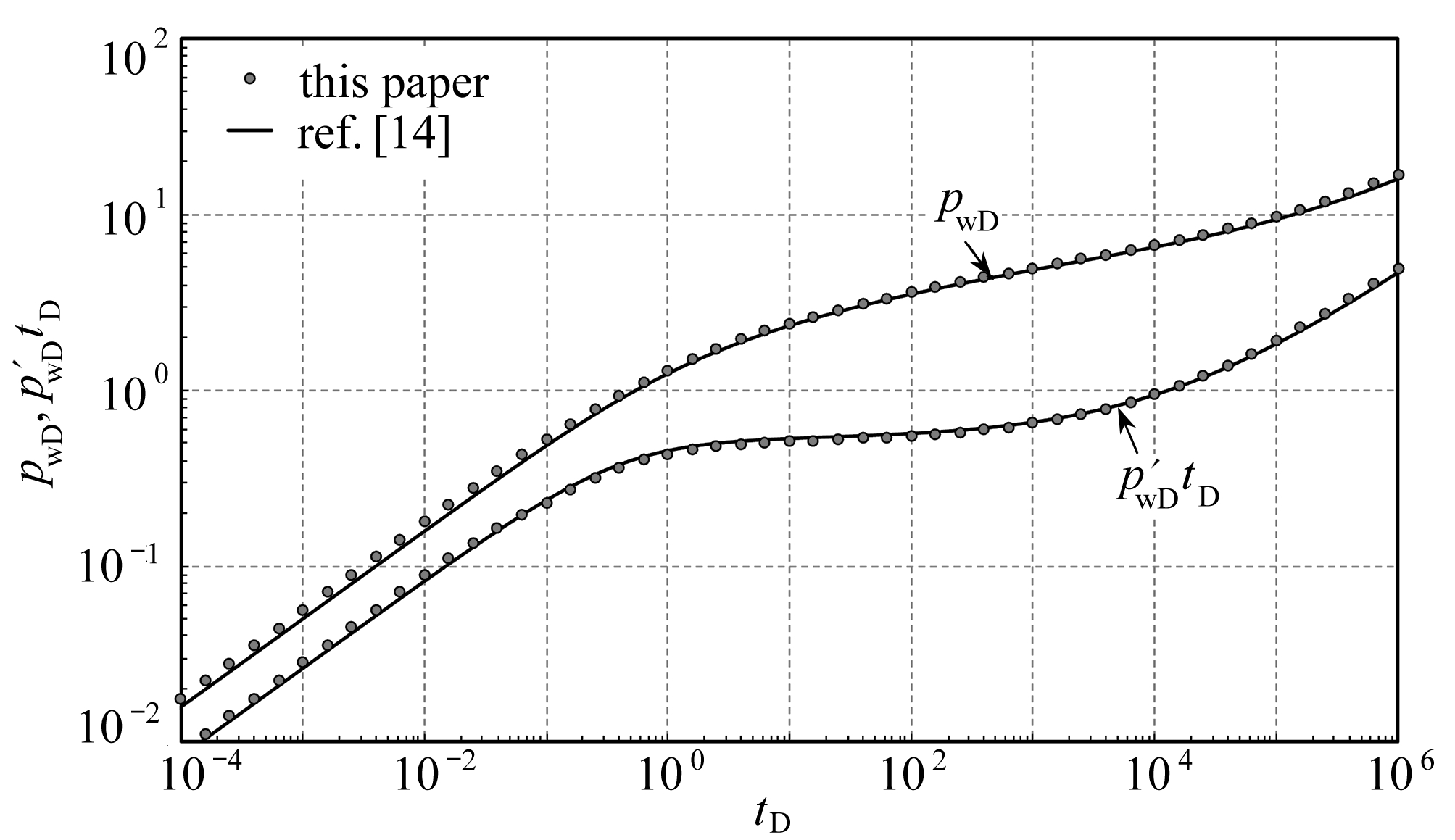
图2 模型验证对比
Fig. 2 Model verification comparison
3 特征曲线与影响因素分析
3.1 特征曲线阶段分析
根据压力导数曲线特征，缝洞型低渗碳酸盐岩油藏井底压力曲线可分为7个流动阶段，如图3所示．
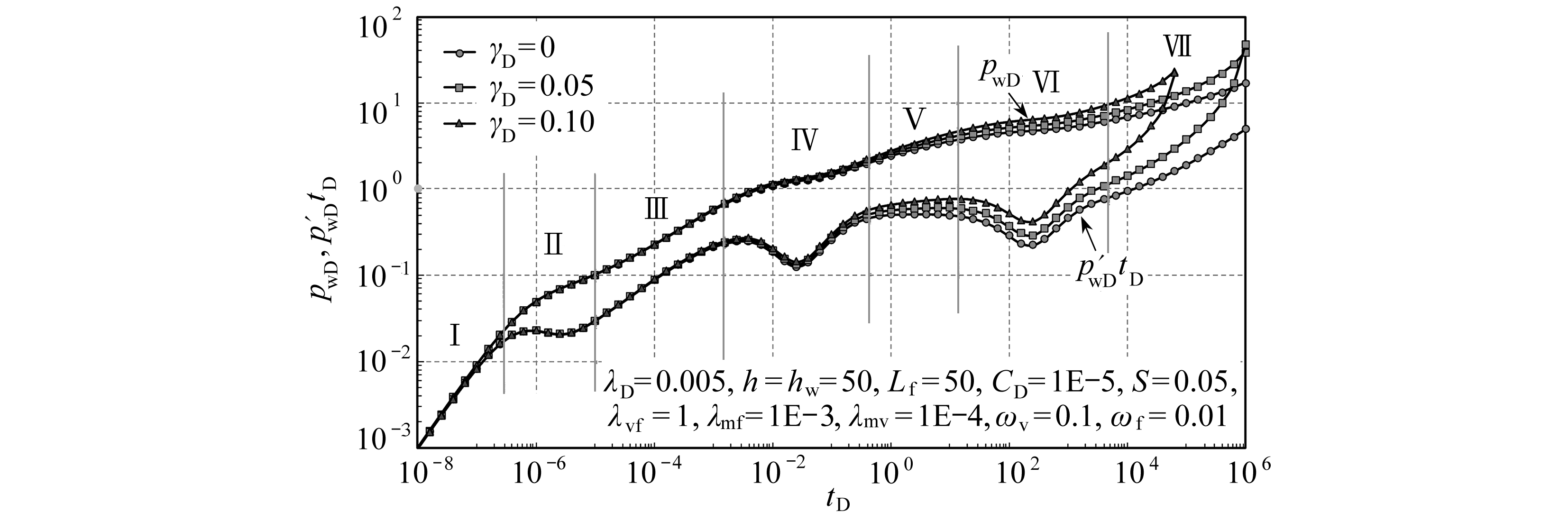
图3 缝洞型低渗碳酸盐岩油藏压裂井试井理论曲线
Fig. 3 Well test curves of fracture-cavity low-permeability carbonate reservoir for hydraulic fractured wells
每个阶段的压力及其导数曲线特征如下：
第Ⅰ阶段为纯井储阶段，该阶段压力和压力导数重合且呈斜率为1的直线；第Ⅱ阶段为井储和表皮反应阶段，压力导数曲线呈“驼峰”；第Ⅲ阶段为储层向压裂裂缝的线性流阶段，该阶段压力导数曲线呈斜率为0.5的直线；第Ⅳ阶段为溶洞流体向裂缝窜流阶段，压力导数曲线呈“凹子”，“凹子”的深浅与基质和溶洞的弹性储容比有关；第Ⅴ阶段为溶洞-裂缝系统径向流阶段，该阶段压力导数由于受到地层应力敏感效应的影响，压力和压力导数曲线上翘，无因次应力系数越大，曲线上翘越明显，不考虑应力敏感时压力导数曲线呈值为0.5的水平线；第Ⅵ阶段为基质流体向裂缝和溶洞窜流阶段，压力导数曲线呈“凹子”，“凹子”的深浅与溶洞的弹性储容比有关；第Ⅶ阶段为系统径向流动阶段，该阶段压力导数由于受到地层应力敏感效应和启动压力的影响，压力和压力导数曲线上翘，并且上翘开始的时间主要受启动压力梯度的影响．
3.2 影响因素分析
图4为无因次启动压力梯度和打开程度对曲线的影响．从图中可以看出，启动压力梯度主要影响径向流阶段压力导数曲线变化，启动压力梯度越大，说明储层物性越差，流体流动所消耗的压降就越大，因此，压力和压力导数曲线上翘，并且启动压力梯度越大，压力导数曲线上翘开始的时间越早(图4(a))．压裂井打开程度主要影响早期阶段压力导数曲线变化形态，打开程度越大，储层流体流入井筒消耗的压降损失越小，压力和压力导数曲线越低； 打开程度越小， 线性流阶段越不明显， 球形流特征越明显， 球形流在压力导数曲线上的主要特征为斜率为-1/2的直线．
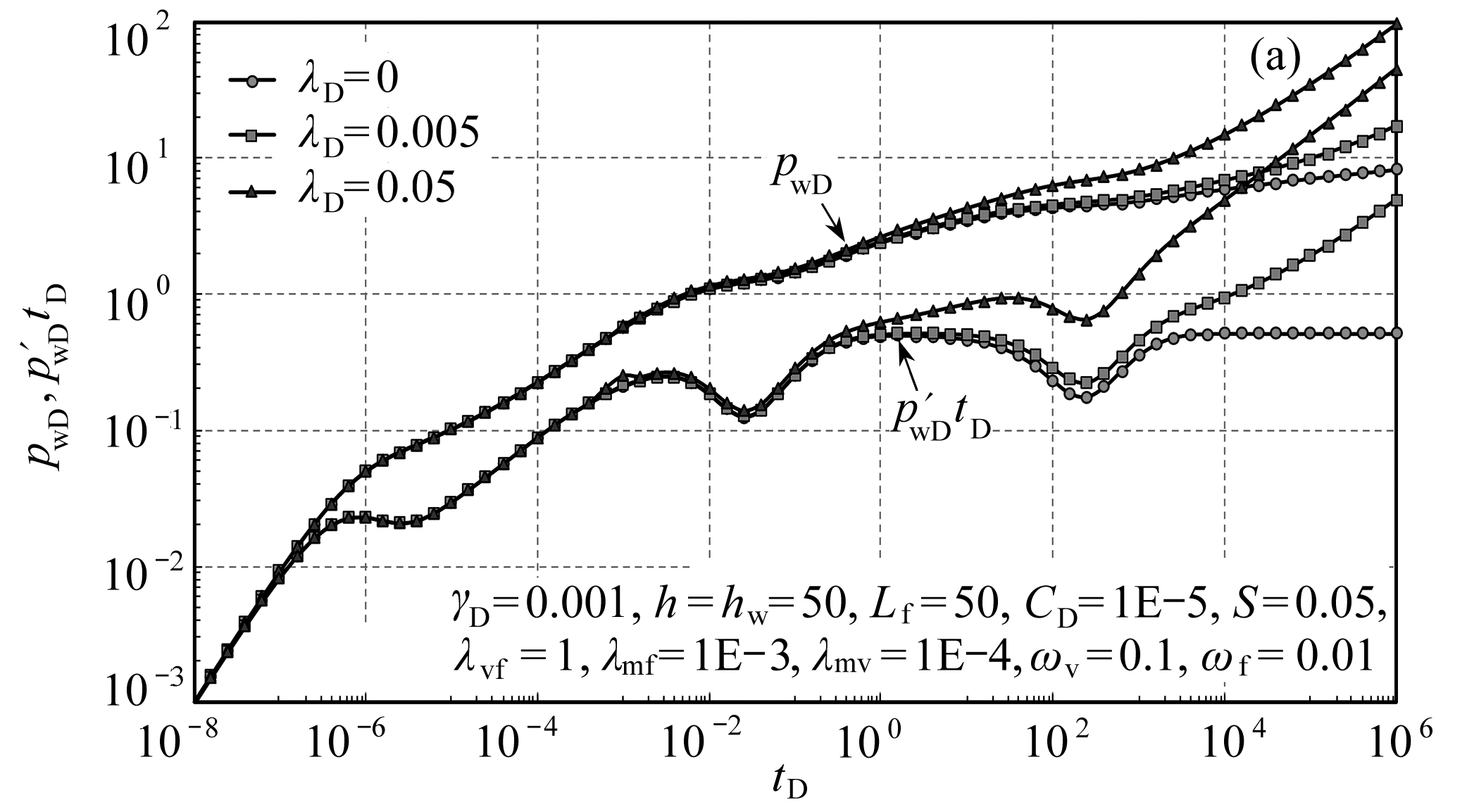
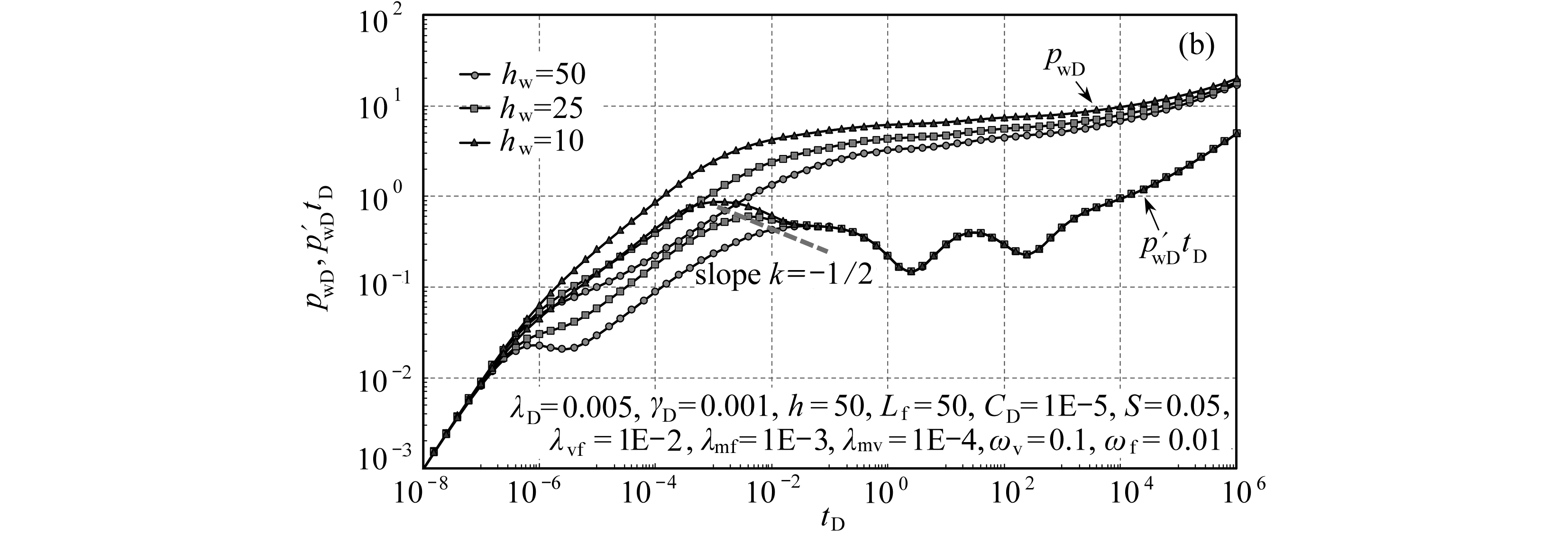
图4 无因次启动压力梯度和打开程度对曲线的影响
Fig. 4 The curves influenced by dimensionless threshold pressure gradients and opening heights
图5为窜流系数对曲线的影响．对于碳酸盐岩三孔单渗并行嵌套窜流油藏而言，存在三重窜流，基质向裂缝窜流、基质向溶洞窜流和溶洞向裂缝窜流．该模型中和裂缝直接相连接的有基质和溶洞系统，溶洞向裂缝的窜流系数越大，流体从溶洞向裂缝窜流的时间就越早，在压力导数曲线上的特征主要表现为第一个“凹子”出现的时间(图5(a))；基质向裂缝窜流的窜流系数越大，流体从基质向裂缝窜流的时间就越早，在压力导数曲线上的特征主要表现为第二个“凹子”出现的时间(图5(b))；基质中还有一部分流体首先窜流到溶洞，随后窜流到裂缝，通过和图5(a)、5(b)对比之后可以发现，基质向裂缝和溶洞窜流都只影响第二个“凹子”的开始时间，由于基质中有一部分流体需要经过溶洞窜流到裂缝，因此，在相同数量级差别的情况下，基质向溶洞的窜流系数变化比基质向裂缝的窜流系数变化对压力导数曲线第二个“凹子”影响小，其变化规律与图5(a)和图5(b)相同(图5(c))．
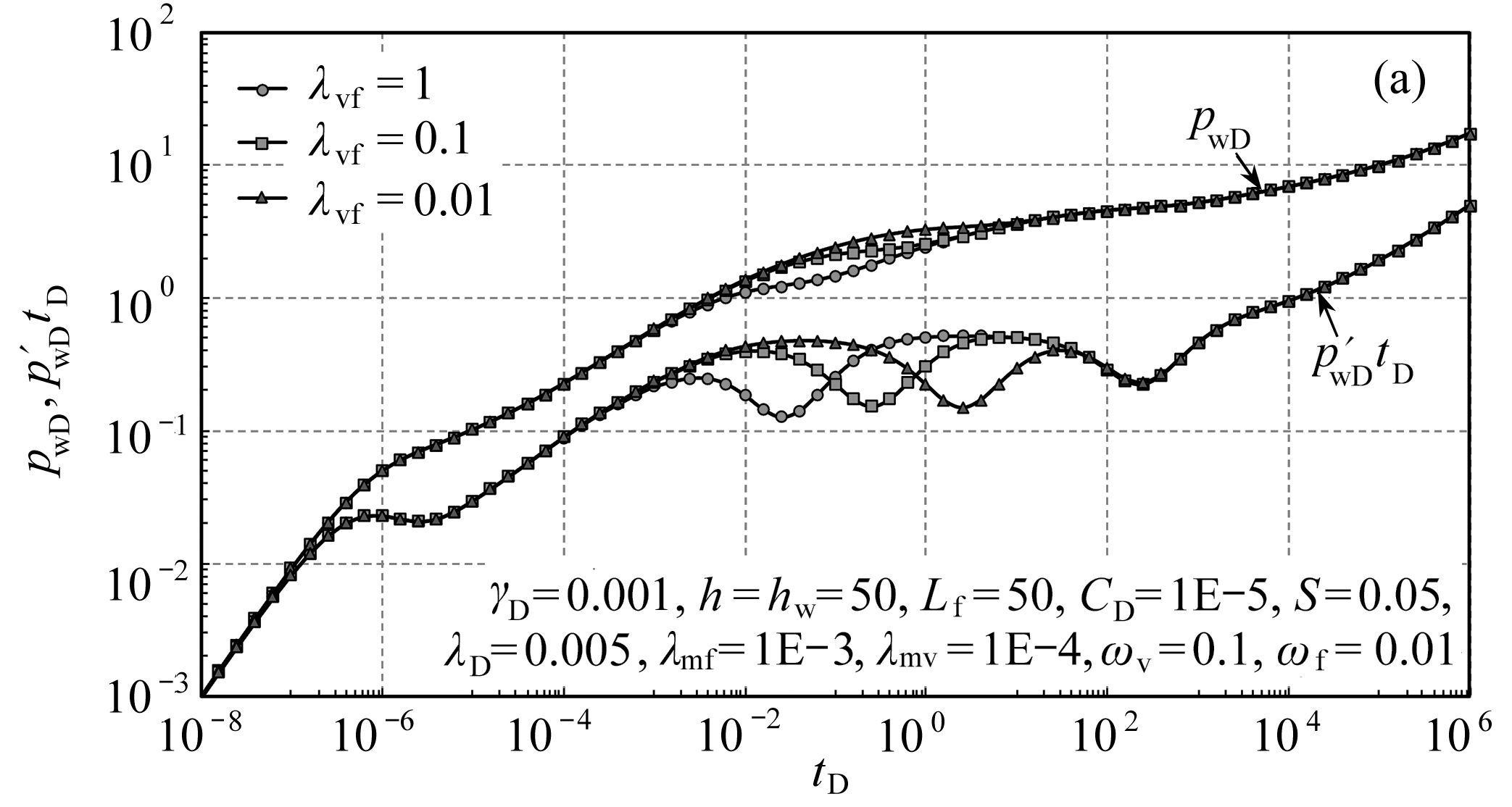
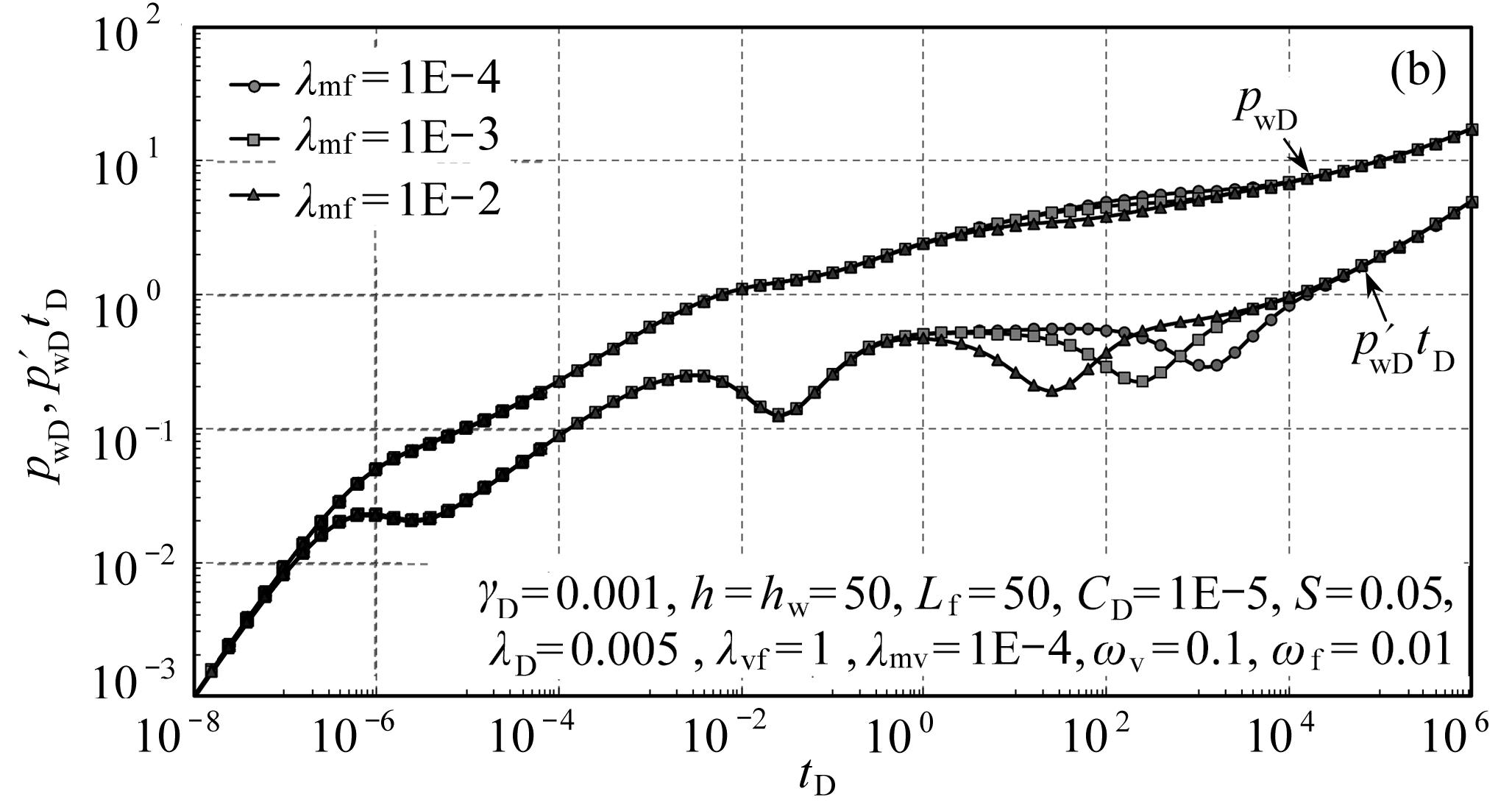
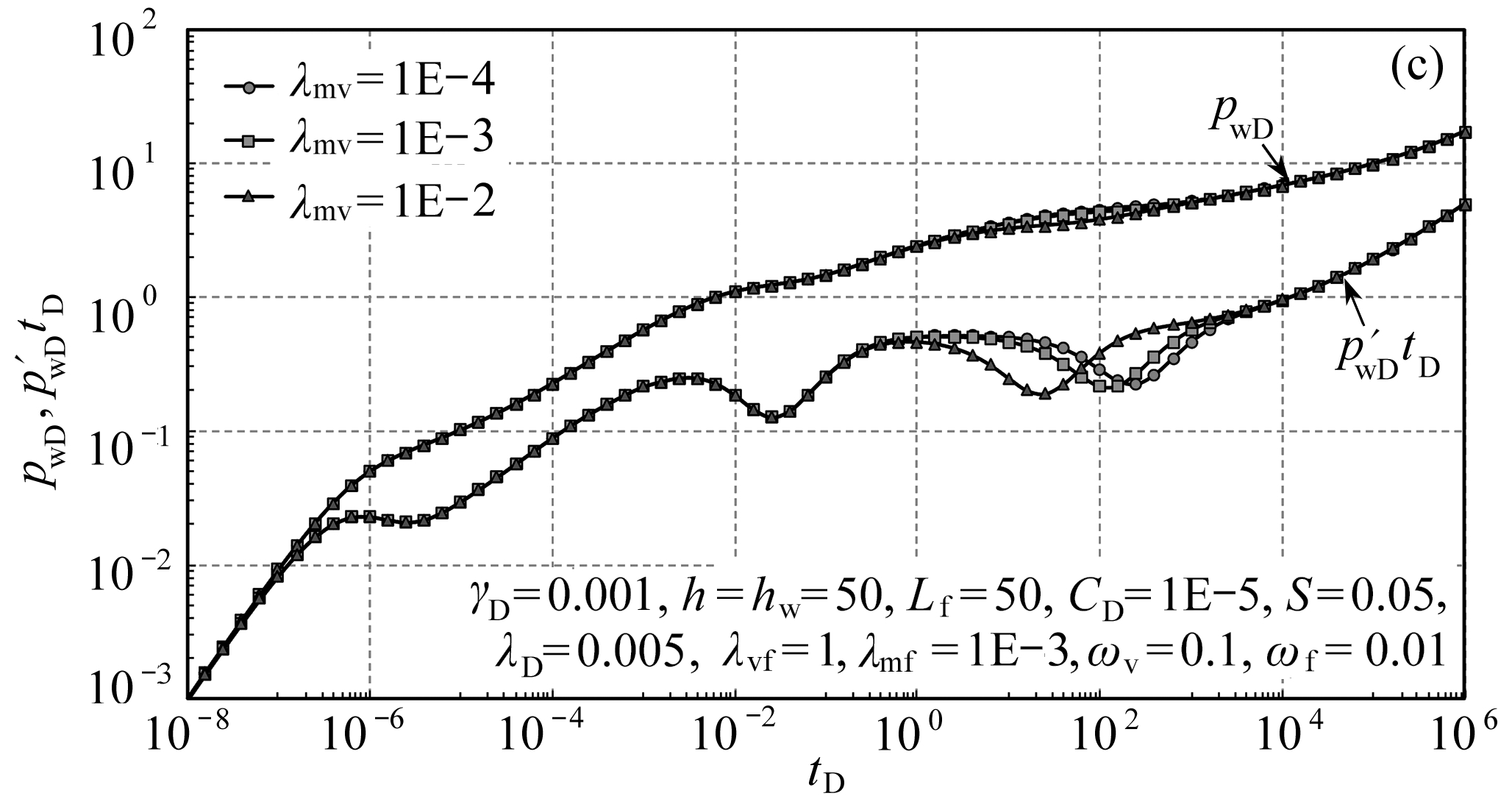
图5 窜流系数对曲线的影响
Fig. 5 The curves influenced by interporosity flow coefficients
图6为弹性储容比对曲线的影响．弹性储容比代表某一基质储存流体能力的大小，其值越大，该介质储存流体的能力越强，在压力导数曲线上的特征主要为弹性储容比越大，“凹子”就越宽越深．对于碳酸盐岩三孔单渗并行嵌套油藏而言，基质弹性储容比主要影响第一个“凹子”的宽度与深度，其值越大，第一个“凹子”就越宽越深(图6(a))；对于溶洞而言，其弹性储容比越大，溶洞流体向裂缝窜流消耗的压差越小，第一个“凹子”越深，基质中的流体向溶洞窜流消耗的压降越大，第二个“凹子”越浅越窄(图6(b))．
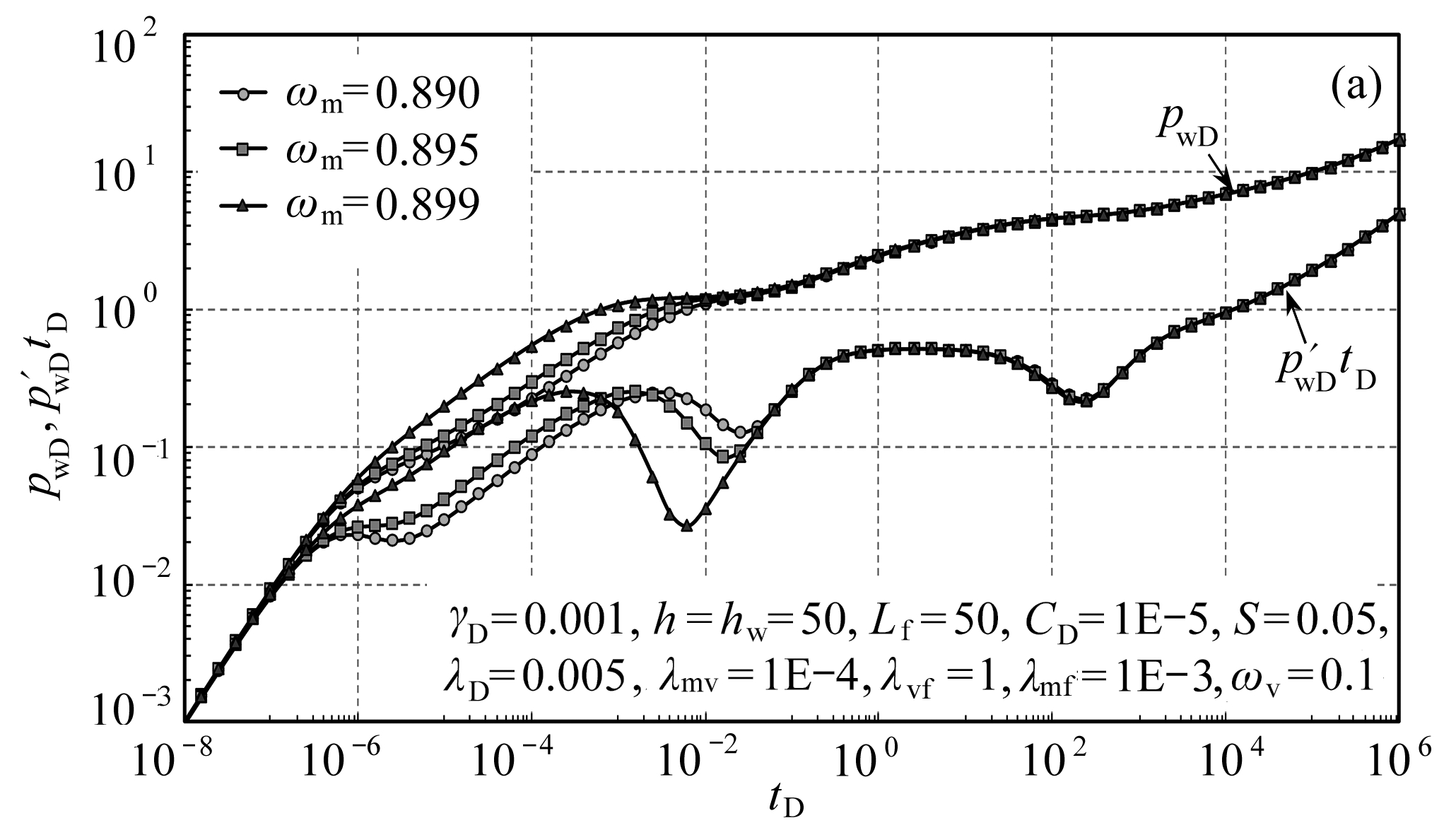
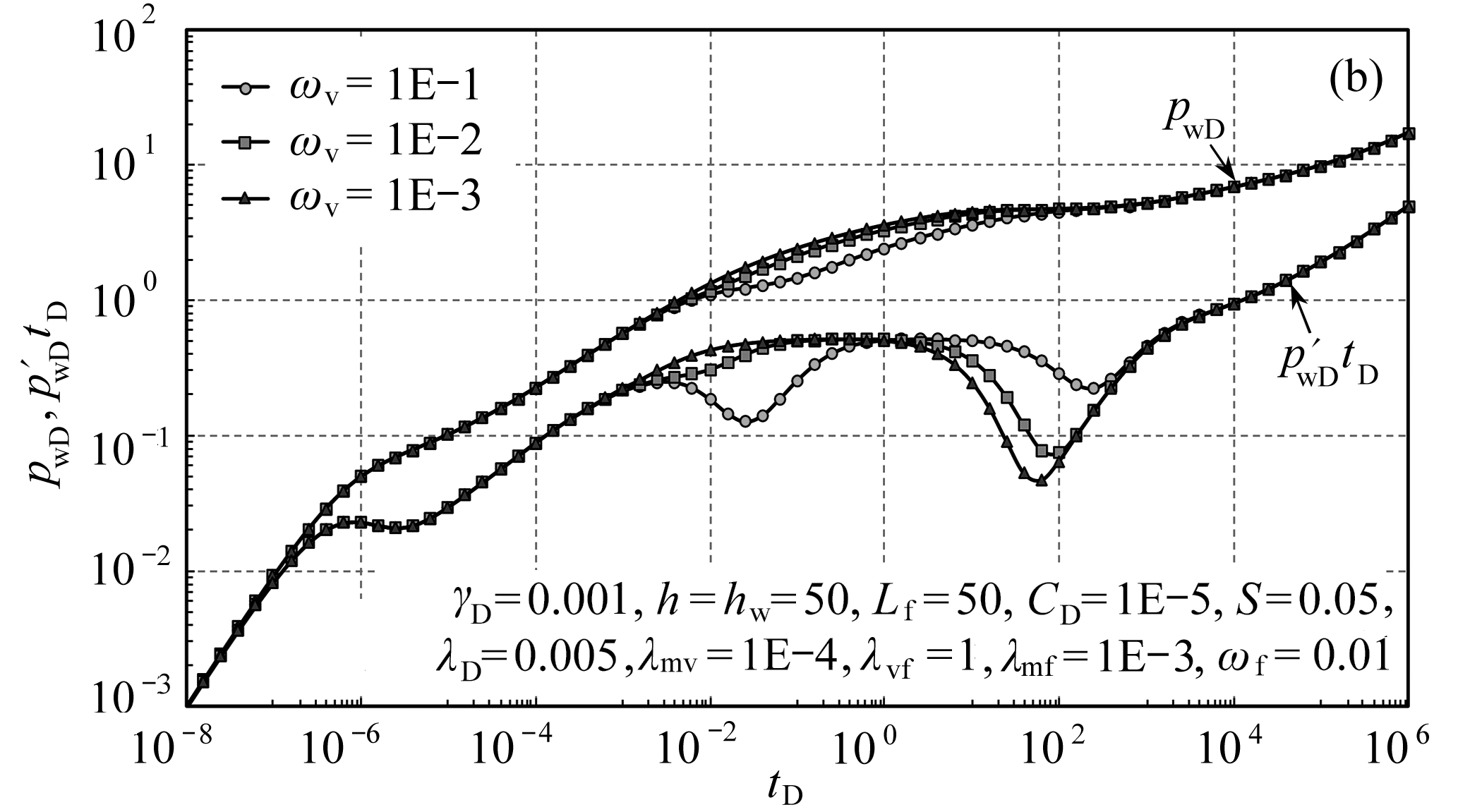
图6 弹性储容比对曲线的影响
Fig. 6 The curves affected by elastic storativity ratios
4 结 论
本文建立同时考虑应力敏感和启动压力梯度影响的缝洞型低渗碳酸盐岩油藏压裂井试井解释数学模型，根据本文研究得到以下几点结论：
1) 该特征曲线总体上分为四个主要的流动特征阶段：斜率为1的纯井储阶段、斜率为0.5的线性流阶段、压力导数呈 “凹子”的窜流阶段和值为0.5的径向流阶段．
2) 应力敏感系数越大，压力导数上翘越明显；启动压力梯度越大，压力导数上翘时间越早；压裂井打开程度越小，斜率为-1/2的直线特征越明显．
3) 溶洞向裂缝窜流系数主要影响第一个“凹子”出现的时间，基质向裂缝和溶洞窜流主要影响第二个“凹子”出现的时间，窜流系数越大，“凹子”出现时间越早； 基质弹性储容比越大， 第一个“凹子”越宽越深， 溶洞弹性储容比越大， 第一个“凹子”越宽越深， 第二个“凹子”相反．
[1] 李阳, 侯加根, 李永强. 碳酸盐岩缝洞型储集体特征及分类分级地质建模[J]. 石油勘探与开发, 2016, 43(4): 600-606.(LI Yang, HOU Jiagen, LI Yongqiang. Features and hierarchical modeling of carbonate fracture-cavity reservoirs[J]. Petroleum Exploration and Development, 2016, 43(4): 600-606.(in Chinese))
[2] 张希明. 新疆塔河油田下奥陶统碳酸盐岩缝洞型油气藏特征[J]. 石油勘探与开发, 2001, 28(5): 17-22.(ZHANG Ximing. The characteristics of lower ordovician fissure-vug carbonate oil and gas pools in Tahe oil field, Xinjiang[J]. Petroleum Exploration and Development, 2001, 28(5): 17-22. (in Chinese))
[3] OZKAN E, RAGHAVAN R. New solutions for well-test-analysis problems, part 1: analytical considerations (includes associated papers 28666 and 29213)[J]. Society of Petroleum Engineers, 1991, 6(3): 359-368.
[4] OZKAN E, RAGHAVAN R. New solutions for well-test-analysis problems, part 2: computional considerations (includes associated papers 18615)[J]. Society of Petroleum Engineers, 1991, 6(3):369-378.
[5] 王海涛, 张烈辉. 基于源函数法的油层部分射开顶底封闭各向异性的三重介质油藏不稳定渗流[J]. 大庆石油学院学报, 2008, 32(3): 29-33.(WANG Haitao, ZHANG Liehui. Solution to the unsteady flow problem in anisotropic triple-porosity reservoir with impermeable top and bottom boundaries and a partially penetrating vertical well based on the source function approach[J]. Journal of Daqing Petroleum Institute, 2008, 32(3): 29-33.(in Chinese))
[6] 王海涛, 李成全, 张烈辉, 等. 三重介质油藏负表皮系数水平井瞬态压力的有效算法[J]. 中国石油大学学报(自然科学版), 2012, 36(4): 112-117.(WANG Haitao, LI Chengquan, ZHANG Liehui, et al. An efficient calculation method of transient pressure responses of horizontal wells with negative skin factors in triple-porosity reservoirs[J]. Journal of China University of Petroleum(Edition of Natural Science), 2012, 36(4): 112-117.(in Chinese))
[7] 程时清, 张利军, 李相方. 三重介质分支水平井试井分析[J]. 水动力学研究与进展, 2009, 24(2): 127-132.(CHENG Shiqing, ZHANG Lijun, LI Xiangfang. Well-test analysis of multi-branched horizontal wells in a triple medium reservoir[J]. Chinese Journal of Hydrodynamics, 2009, 24(2): 127-132.(in Chinese))
[8] 任俊杰, 郭平, 汪周华. 三重介质油藏斜井压力动态特征分析[J]. 水动力学研究与进展, 2012, 27(1): 7-15.(REN Junjie, GUO Ping, WANG Zhouhua. Dynamical characteristic analysis of inclined well in triple medium reservoir[J]. Chinese Journal of Hydrodynamics, 2012, 27(1): 7-15.(in Chinese))
[9] PASCAL H. Nonsteady flow through porous media in the presence of a threshold gradient[J]. Acta Mechanica, 1981, 39(3/4): 207-224.
[10] 罗二辉, 胡永乐. 三重介质低渗油藏非达西非稳态渗流研究[J]. 中国矿业大学学报, 2013, 42(1): 100-104.(LUO Erhui, HU Yongle. A study of non-Darcy transient flow in triple porosity media with low permeability reservoir[J]. Journal of China University of Mining & Technology, 2013, 42(1): 100-104.(in Chinese))
[11] 罗二辉, 胡永乐, 王磊, 等. 缝洞型低渗透碳酸盐岩油藏产量递减曲线分析[J]. 大庆石油学院学报, 2012, 36(2): 86-90.(LUO Erhui, HU Yongle, WANG Lei, et al. Analysis of production decline curves in naturally vuggy and fractured carbonate reservoir with low permeability reservoir[J]. Journal of Daqing Petroleum Institute, 2012, 36(2): 86-90.(in Chinese))
[12] 曹丽娜, 李晓平, 罗诚, 等. 裂缝性低渗气藏水平井不稳定产量递减探讨[J]. 西南石油大学学报(自然科学版), 2017, 39(3): 103-110.(CAO Lina, LI Xiaoping, LUO Cheng, et al. Investigation of unstable production decline in fractured low-permeability gas reservoir horizontal wells[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2017, 39(3): 103-110.(in Chinese))
[13] 孟凡坤, 雷群, 何东博, 等. 应力敏感性碳酸盐岩气藏斜井生产动态规律分析[J]. 东北石油大学学报, 2018, 42(2): 95-102.(MENG Fankun, LEI Qun, HE Dongbo, et al. Production performance analysis for slanted wells in stress-sensitive carbonate gas reservoirs[J]. Journal of Northeast Petroleum University, 2018, 42(2): 95-102.(in Chinese))
[14] 付春权, 尹洪军, 刘宇, 等. 低速非达西渗流垂直裂缝井试井分析[J]. 大庆石油地质与开发, 2007, 26(5): 53-56.(FU Chunqun, YIN Hongjun, LIU Yu, et al. Well testing analysis for vertical fracture well with low-velocity non-Darcy flow[J]. Petroleum Geology & Oilfield Development in Daqing, 2007, 26(5): 53-56.(in Chinese))
[15] 刘文超, 姚军. 三重介质油藏有限导流垂直裂缝井的流-固耦合模型[J]. 工程力学, 2013, 30(3): 402-409.(LIU Wenchao, YAO Jun. The fluid-solid coupling model of finite conductivity vertically fractured well in the reservoir with triple porosity medium[J]. Engineering Mechanics, 2013, 30(3): 402-409.(in Chinese))
[16] 刘启国, 徐有杰, 刘义成, 等. 夹角断层多段压裂水平井试井求解新方法[J]. 应用数学和力学, 2018, 39(5): 558-567.(LIU Qiguo, XU Youjie, LIU Yicheng, et al. A new well test analysis method for multi-stage fractured horizontal wells with angle faults[J]. Applied Mathematics and Mechanics, 2017, 2018, 39(5): 558-567.(in Chinese))
[17] 李顺初, 任丽, 郑鹏社, 等. 基于应力敏感的天然裂缝性页岩气藏双孔模型解的结构[J]. 应用数学和力学, 2017, 38(2): 233-242.(LI Shunchu, REN Li, ZHENG Pengshe, et al. Similar structure of the solution to the dual-porosity model for naturally fractured shale gas reservoirs based on stress sensitivity[J]. Applied Mathematics and Mechanics, 2017, 38(2): 233-242.(in Chinese))
[18] RAGHAVAN R, CHIN L Y. Productivity changes in reservoirs with stress-dependent permeability[J]. SPE Reservoir Evaluation & Engineering, 2002, 7(4). DOI: 10.2118/77535-MS.
[19] PEDROSA O A. Pressure transient response in stress-sensitive formations[C]//SPE California Regional Meeting. Oakland, California, 1986.
[20] STEHFEST H. Numercial inversion of Laplace transforms[J]. Communication of the ACM, 1970, 13(1): 47-49.