引 言
直升机旋翼常会发生桨叶与桨尖涡靠近相遇的情况,形成特有的桨涡干扰现象,此时桨叶表面的气动载荷分布可能出现较大脉动,导致旋翼出现较高的振动和噪声水平.因此,降低桨涡干扰效应对提高直升机寿命以及降低噪声水平非常关键[1].
为降低桨涡干扰效应,国内外学者采用了独立桨距控制(IBC)[2-3]、高阶谐波控制(HHC)[4-5]以及主动后缘襟翼控制(ACF)[6]等方法,一定程度上降低了桨涡干扰效应,但上述方法均属于主动控制方法,需要复杂的控制系统,技术实现较为困难.相比于主动控制方法,被动控制方法具有结构简单、无需外部能量输入而易于实施等特点[7].Brooks[8]、 Tangler等[9]、史勇杰等[10]和孙传伟等[11]研究了不同桨尖形状的桨叶对桨涡干扰效应的抑制作用,研究表明,采用不同桨尖形状的桨叶可以减弱或者分散桨尖涡, 从而达到降低桨涡干扰效应的效果, 但降低桨涡干扰效应的水平有限.因此, 需要进一步研究更加简单且能有效降低桨涡干扰效应的方法.
开孔方法作为一种简单且成熟的被动控制方法,已被应用于气动力及噪声等的控制研究,例如:Dahdi等[12]和Eljack等[13]先后对翼型表面进行开孔处理,研究了多孔表面翼型对大气湍流在翼型上产生的非定常载荷的影响,研究表明,合理布置表面开孔位置可以降低大气湍流对翼型载荷的影响;李博等[14]和张宗茂等[15]采用叶片开通孔的方法研究了开孔叶片对风机涡流噪声的影响,研究表明,合理选择孔的参数不仅可以降低涡流噪声,而且可使这种方法对气流产生的影响较小.
国外,Lee[16]提出采用多孔桨叶前缘来降低桨涡干扰效应,研究表明这种方法可以减小前缘的压力脉动,降低桨涡干扰噪声.但需要说明的是,上述研究采用了速度穿透模型模拟表面孔的作用,忽略了孔内部的流动细节.国内采用开孔方法降低桨涡干扰效应的研究尚属空白.因此,本文对非升力NACA 0012翼型的前缘进行开孔处理,在不同参数(来流速度、涡的强度、干扰距离)下,分析了翼型前缘开孔方式(孔的宽度、倾斜角)对桨涡干扰效应的影响,找到了有效降低桨涡干扰效应的途径.
1 理论分析和几何模型
1.1 理论分析
降低桨涡干扰效应的方法主要分为主动控制和被动控制.主动控制技术主要通过改变干扰距离实现降低桨涡干扰效应的目的,而现有被动控制方法是以改变涡的特性降低桨涡干扰效应为目标.已有研究表明,桨涡干扰噪声主要来源于桨叶前缘的压力脉动[17],即:不管是改变干扰距离还是改变涡的特性,最终目的是降低桨叶前缘的压力脉动.基于这种考虑,Lee[16]提出采用多孔前缘桨叶的方法,并取得了一定的成果,但研究没有真正在翼型表面进行开孔,而是采用了速度穿透模型模拟表面孔的作用.因此,可以设想在翼型前缘进行开孔处理研究其对桨涡干扰效应的影响.
桨涡干扰效应主要表现为振动和噪声,而噪声的数值计算比较困难.文献[18]指出BVI导致的升力系数波动幅值Δcl与来流速度U∞、干扰距离yv和涡的强度Γ有关,关系式如下:
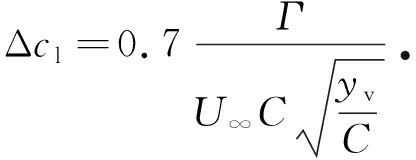
(1)
文献[19]研究表明桨涡干扰噪声远场声压p′与桨尖速度和涡的强度Γ有关,因为本文研究对象为二维翼型,所以桨尖速度可看成来流速度U∞,关系式如下:
(2)
由式(1)、(2)可得
p′∝Δcl.
(3)
基于上述分析,本文在翼型前缘进行开孔处理,并以Δcl衡量整个干扰过程中旋涡对翼型产生干扰作用的强弱.
1.2 几何模型
本文采用已有实验结果的NACA 0012翼型作为验证数值模拟方法有效性的基准翼型.在基准翼型的基础上分别采用4种不同的前缘开孔方式,如图1所示,model 1和model 2采用直孔,model 3和model 4采用斜孔,孔的中心均位于翼型0.25C位置.图中θ为倾斜角,d为孔的宽度.
(a) Model 1 (θ=0°, d=0.05C)(b) Model 2 (θ=0°, d=0.025C)

(c) Model 3 (θ=30°, d=0.05C)(d) Model 4 (θ=30°, d=0.025C)
图1 几何模型示意图
Fig. 1 Schematic view of geometric models
2 计 算 方 法
本文采用多松弛时间(multiple relaxation time,MRT)格子Boltzmann方法(lattice Boltzmann method,LBM)[20]对流场进行求解.
MRT LBM通过转换矩阵M将粒子分布函数由速度空间转化到矩空间.在矩空间,粒子分布函数f的演化方程如下:
(4)
式中δt为时间步长, eα为离散速度, S为对角碰撞矩阵, |m〉=M·|f〉, 符号|·〉表示列向量.
本文的研究对象为二维翼型,采用了D2Q9格子离散速度模型,离散速度为
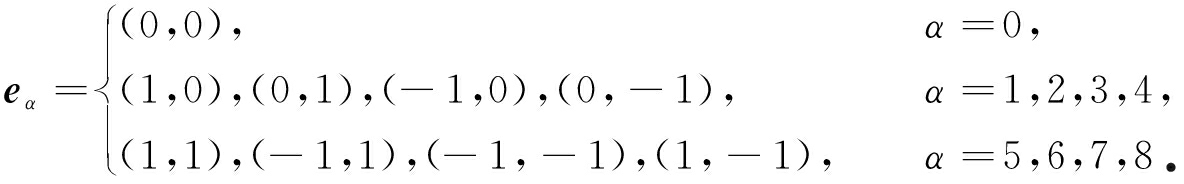
(5)
相应的平衡态分布函数![]() 为
为
(6)
式中ρ为流体密度,u为流体速度,ωα为权重系数,![]() 为格子声速.
为格子声速.
式(6)中对应的权重系数ωα为
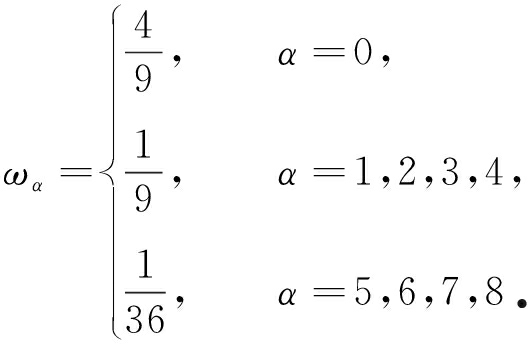
(7)
流场各点宏观变量包括密度ρ和速度u,可以由微观粒子分布函数计算:
(8)
同时,宏观压强可以表示为
(9)
桨涡干扰的非定常特性以及数值方案的耗散问题是进行桨涡干扰研究的主要难点,本文采用了适用于非定常、复杂湍流流动的LES[21]对湍流进行解析,亚格子模型采用动态亚格子模型.
由于干扰主要作用在翼型附近,所以计算网格采用了多尺度模式,并在涡的运动轨迹区进行了区域加密.为了降低LES方法的计算需求,对近壁区流动采用壁面函数近似,壁面区域格子尺寸为3×10-3C,其中C为翼型弦长,最大的y+为40.计算区域大小为30C×20C,定义左右x=±15C分别为速度进口和压力出口边界条件,上下边界y=±10C为周期边界条件,翼型曲边界采用反弹(bounce-back)[20]边界条件处理.因为壁面位置并不一定恰好位于流体区域内部邻近固体壁面格子节点和固体内部邻近固体壁面格子节点的正中间,为解决这一限制,采用了文献[22-23]中的改进方法.图2(a)和2(b)分别给出了全局和翼型壁面附近局部的网格图.
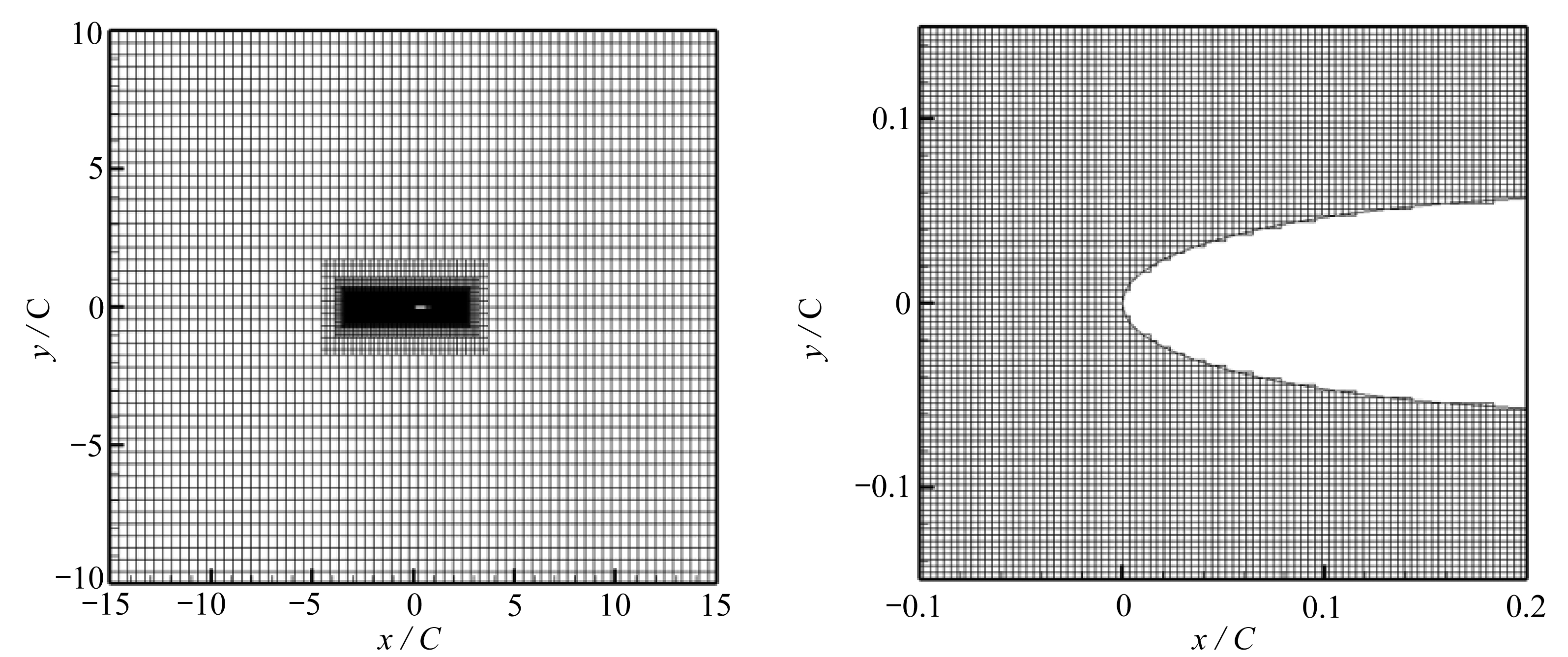
(a) 全局网格(b) 局部网格
(a) The overall mesh(b) The local mesh
图2 翼型格子分布网格图
Fig. 2 The mesh for the airfoil
3 计算结果和分析
3.1 数值方法验证
为验证本文数值方法,采用了与文献[24]相同的计算条件, 首先对NACA 0012翼型在没有涡干扰条件下的流场进行了计算.该计算采用的网格与用于翼涡干扰流场计算所采用的网格相同.图3为本文计算结果和文献[24]实验结果的翼型压力系数分布曲线.可以看出, 本文翼型压力系数计算结果与实验结果吻合良好, 说明本文采用带壁函数的LBM-LES方法是可靠的.
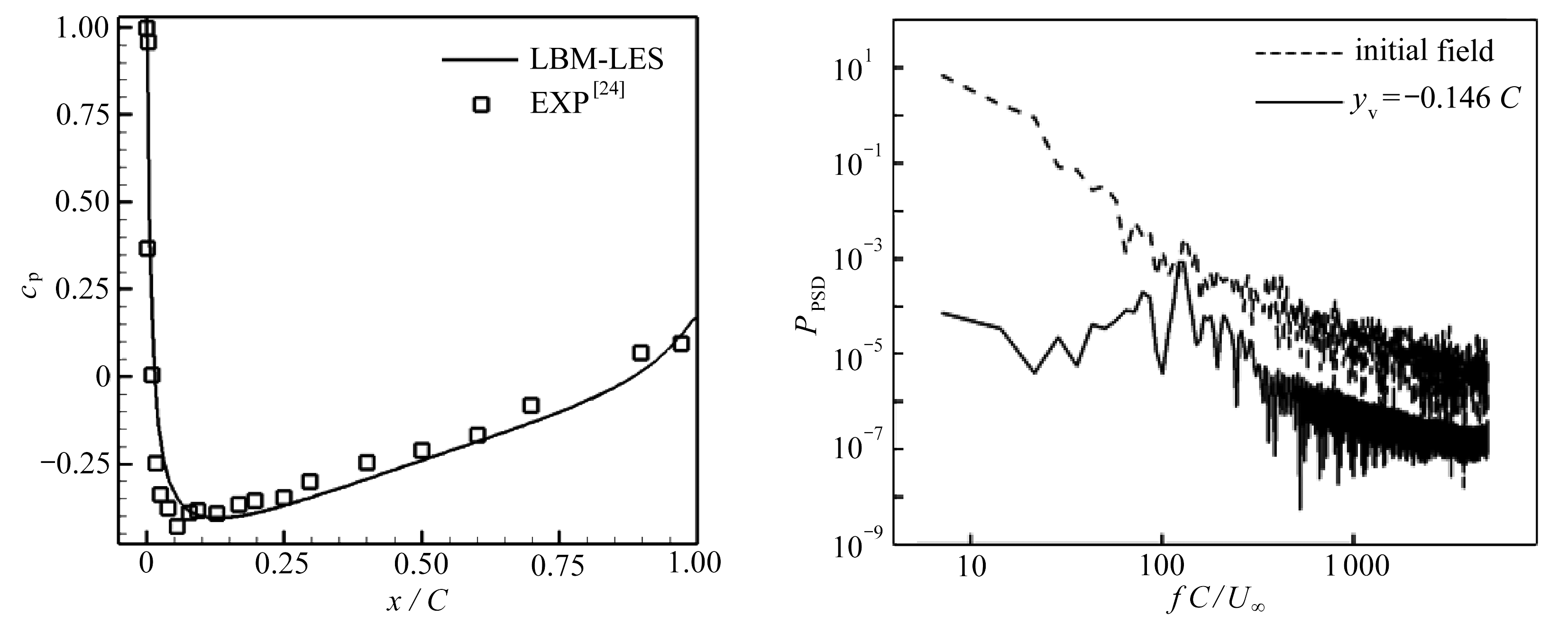
图3 NACA 0012翼型压力系数曲线 图4 探测点(0.01C,0.054C)处静压的功率谱密度
Fig. 3 The pressure coefficient distribution Fig. 4 The power spectral density of the static
of airfoil NACA 0012 pressure at (0.01C,0.054C)
本文以上述NACA 0012翼型在没有涡干扰时的流场作为翼涡干扰流场的初始场,并选用Lamb-Oseen涡模型对翼涡干扰流场进行了计算,Lamb-Oseen涡模型的环量Γ=-0.15U∞C,负号表示涡的旋转方向,规定顺时针旋转的涡为负,涡核半径rc=0.05C,涡的初始位置(xv,yv)=(-3C,-0.46C),其中xv为涡相对于翼型前缘的位置,yv为涡与翼型之间的垂直距离.
图4为翼型前缘上翼面靠近壁面(0.01C,0.054C)处初始场与翼涡干扰流场静压的功率谱密度(power spectral density,PSD).可以看出,本文LES方法能够得到在较高波数范围内初始场和干扰场静压的脉动;涡对翼型流场在大尺度上的影响非常大,相比较而言,在小尺度内较小,所以干扰引起的影响主要是在较大尺度的含能区,即大涡区,而对惯性子区和耗散区影响较小,这进一步说明对于桨涡干扰问题LES方法是比较合适的,且桨涡干扰流场的网格尺度可以和没有涡干扰初始流场相同.
涡向翼型靠近过程中,且在涡与翼型干扰之前,需要保持涡的特性不会发生变化.图5为涡与翼型干扰之前4个不同时刻涡在y方向的速度型,横坐标x/C表示涡核中心距翼型前缘的距离.可以看出,在涡的运动过程中涡在y方向的速度型基本上没有改变,说明本文LES方法具有足够低的耗散性保持涡的特性.
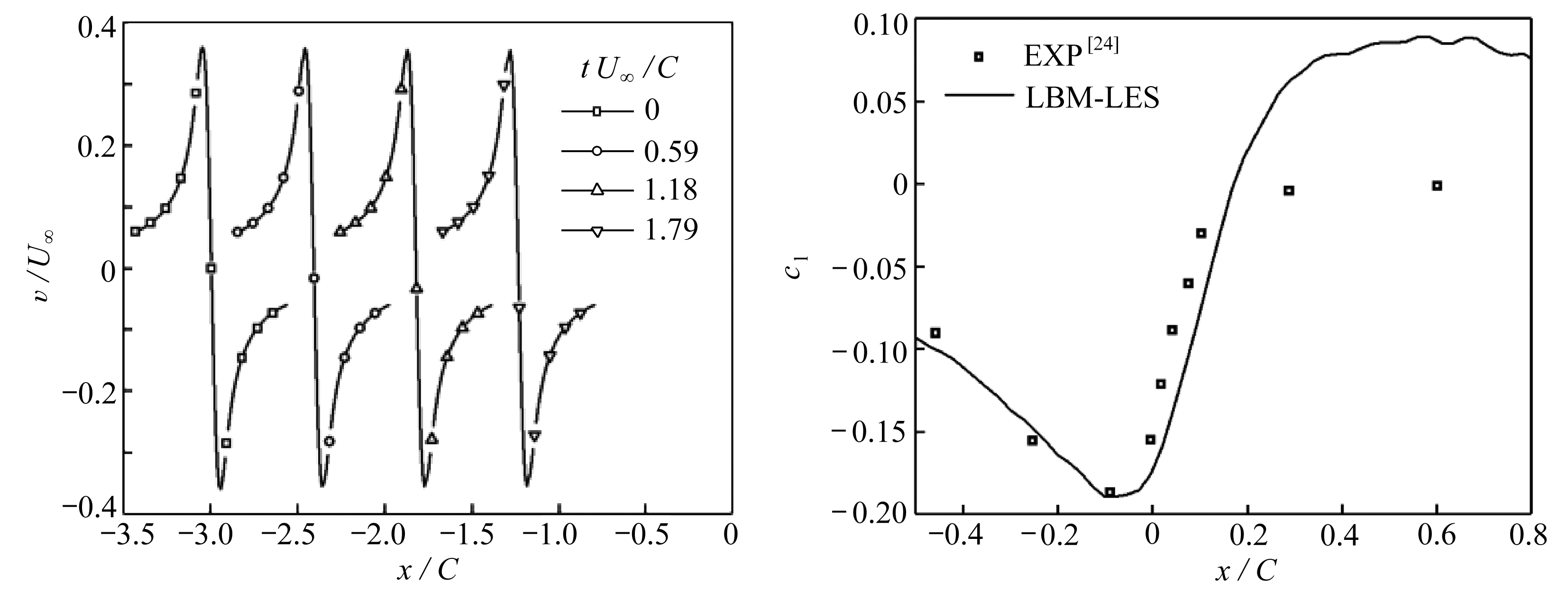
图5 不同时刻涡在y方向的速度型图6 升力系数图
Fig. 5 Vortex velocity profiles in the y direction Fig. 6 The lift coefficient
at different moments
图6为本文计算和实验[24]的升力系数图.可以看出,涡到达翼型前缘附近时,升力系数最小,干扰效应最强,然后升力系数逐渐增加,约30%弦长处,升力系数最大,出现第二次强干扰,然后升力系数逐渐变小,干扰变弱.和实验结果相比,数值结果在第二次强干扰附近有较大偏差,在此之前的升力系数基本吻合,出现较大偏差的原因可能是在第一次强干扰后,三维涡会破裂而不能简化为二维简单情况;这也说明桨涡干扰在第一次强干扰时具有二维特征,而第二次强干扰时具有明显的三维特征,但三维效应对翼涡干扰的影响研究不在本文讨论范围内.
3.2 开孔对翼涡干扰效应的影响
3.2.1 弱干扰时开孔对翼涡干扰效应的影响
表1为本文的计算工况.case 1中涡核中心与翼型弦线之间有一定的垂直距离, 干扰较弱, 而case 2中涡核中心正对着翼型弦线, 干扰较强, 在本文分别称case 1和case 2为弱干扰和强干扰.表中3种不同来流速度对应的基于翼型弦长的Reynolds数分别为3×105,1.2×106和2×106.
表1 工况
Table 1 Cases

parametercase 1case 2(xv,yv)(-3,-0.146)(-3,0)U∞/(m/s)12.2,48.8,85.07512.2,48.8,85.075Γ/(U∞C)-0.16-0.16rc/C0.050.05α/(°)00
图7为case 1工况下,来流速度U∞=12.2 m/s时,model 1、model 3以及没有开孔的基准翼型的升力系数图.可以看出,升力系数的变化可分为3个阶段:第1阶段,涡与翼型基本上不发生干扰(x/C<-1.5),升力系数均在0附近,开孔对升力系数影响较小;第2阶段,从涡与翼型开始干扰(x/C=-1.5)到涡到达翼型前缘(x/C=0)附近,升力系数呈下降趋势,随着干扰变强,直孔和斜孔的影响也在变强;第3阶段,从涡经过翼型前缘(x/C=0)到x/C=0.33附近,升力系数呈上升趋势,同样直孔和斜孔的影响也在变强.与基准翼型相比,开孔均有效降低了翼涡干扰的Δcl,这说明开孔能够有效降低桨涡干扰效应.
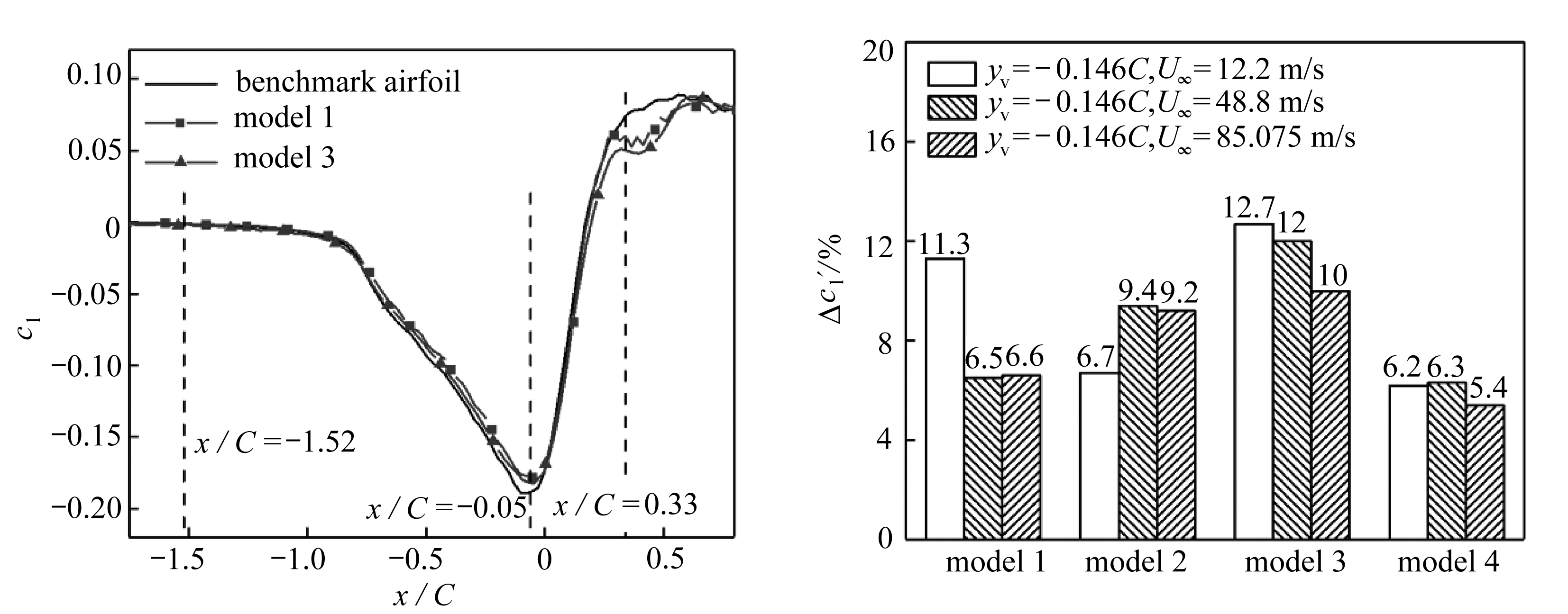
图7 弱干扰下模型升力系数图图8 弱干扰时Δcl的相对减小量
Fig. 7 The lift coefficient under weak interaction Fig. 8 The relative percent reduction of Δcl
图8为弱干扰时4种模型与基准翼型相比Δcl的相对减小量Δc′l(%).可以看出,不同的模型在多种流动条件下均能有效降低干扰效应,且model 3的效果在低速和高速时都最好,这说明斜孔比直孔更能有效地降低干扰效应.孔的宽度对干扰效应的影响因来流速度不同而具有不同的规律:低速时,孔尺寸变小会使得降低效果变弱;而较高速度时,斜孔的孔尺寸变小会使得降低效果变弱,直孔的孔尺寸变小反而会使得降低效果变强.
3.2.2 强干扰时开孔对翼涡干扰效应的影响
图9为强干扰时4种模型与基准翼型相比Δcl的相对减小量Δc′l(%).由图可以看出,强干扰时,开孔翼型在不同来流速度下也均能降低翼涡干扰效应,和弱干扰时情况相同,model 3的效果在低速和高速时都最好,但是孔尺寸对效果的影响规律不一样.对于直孔,孔尺寸变小,降低效果变强,斜孔却反之.
为分析不同开孔方式对翼型升力系数的影响,本文对基准翼型以及4种模型分别在U∞=12.2 m/s的均匀来流中计算了攻角α=2°,4°,6°时的升力系数.图10为4种模型与基准翼型相比升力系数的相对减小量c′l(%).可以看出,开口方式对升力系数的影响很小,而孔的宽度是影响升力系数损失大小的主要因素,孔的宽度越大翼型的升力系数损失越严重.如果考虑减小开孔对升力系数的影响,综合对比分析图8~10,可以得出,model 2既能有效降低干扰效应,同时对翼型升力系数的影响也较小.
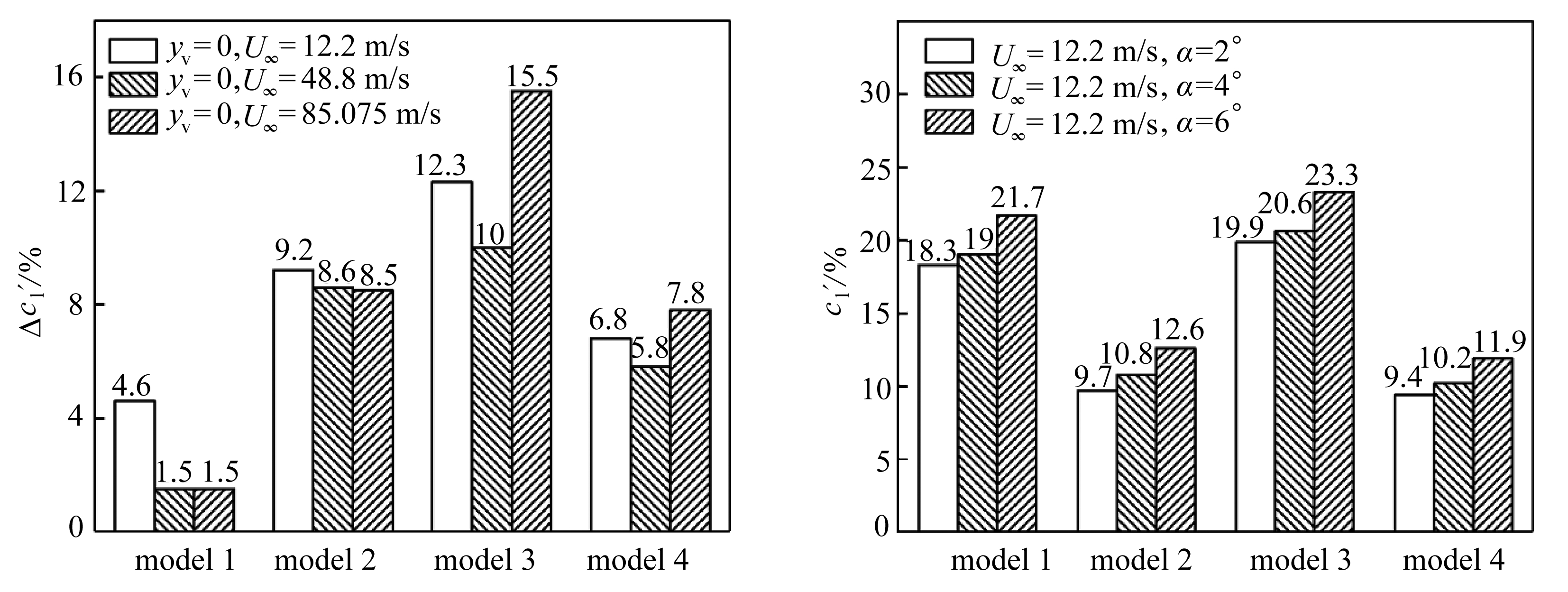
图9 强干扰时Δcl的相对减小量图10 升力系数的相对减小量
Fig. 9 The relative percent reduction of ΔclFig. 10 The relative percent reduction of the lift coefficient
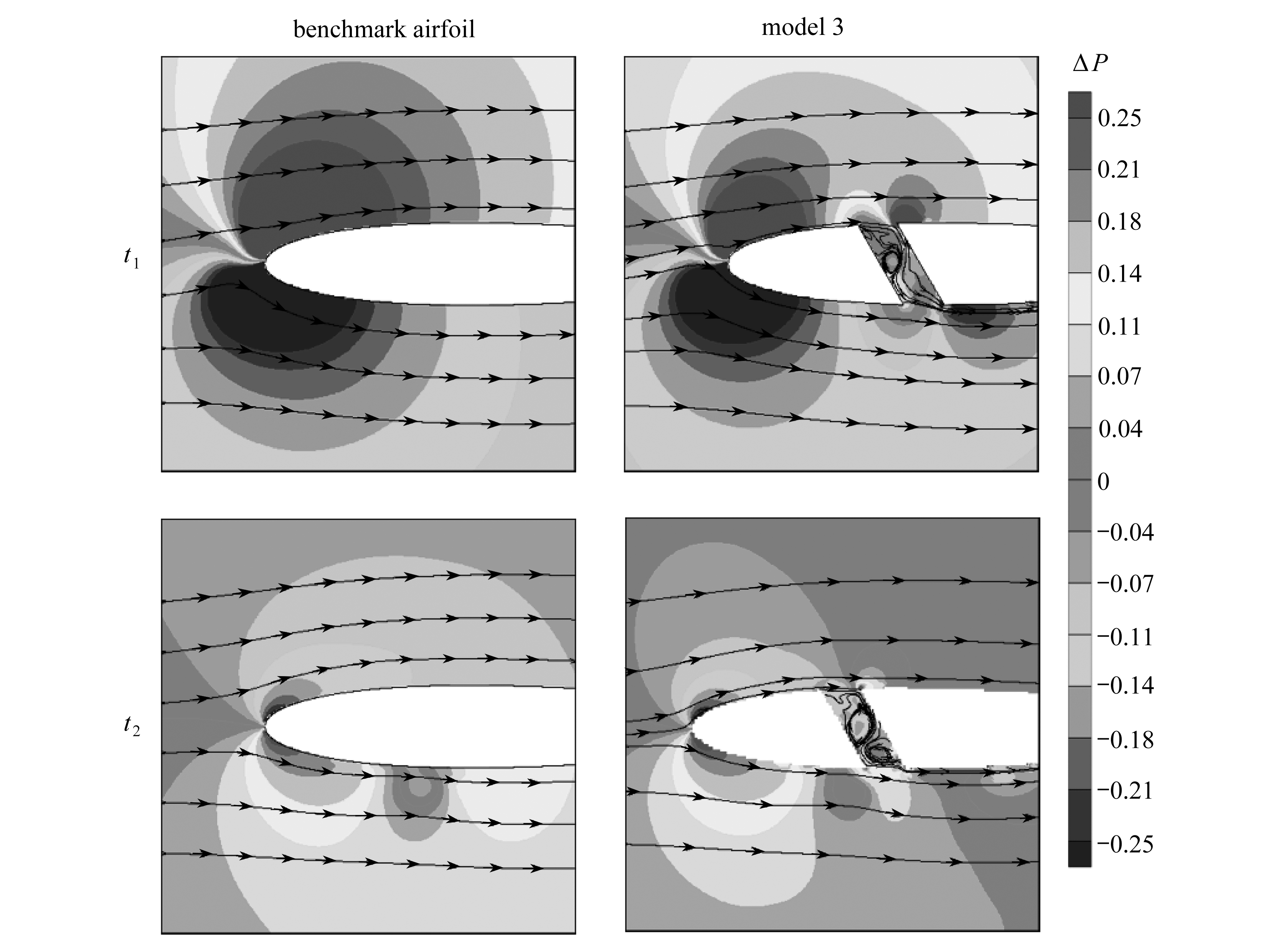
图11 桨涡干扰时的流场与未发生干扰时流场的压强差图及桨涡干扰时的流线图
Fig. 11 The pressure difference contour between the flow field under blade-vortex interaction and the flow field
without blade-vortex interaction, and streamlines of the flow field under blade-vortex interaction
鉴于此,为考虑三维效应的影响,选用了model 2的开孔方式,在强干扰、来流速度U∞=12.2 m/s的条件下,对展长为0.2C的开孔三维翼型和未开孔三维翼型进行了翼涡干扰的计算.结果表明,与未开孔三维翼型相比,开孔三维翼型的升力系数波动幅值降低了8.6%,与未考虑三维效应影响时相比,该开孔方式降低干扰效应的效果仅下降了0.6%,因此,可以得出,对于三维翼型与涡的干扰,本文的开孔方法也能有效地降低干扰效应.
为分析翼型前缘开孔降低桨涡干扰效应的机理,本文对基准翼型和model 3在来流速度U∞=12.2 m/s时的强干扰流场进行了分析.图11为桨涡干扰时的流场与未发生干扰时流场的压强差即涡干扰引起的扰动压强图,以及桨涡干扰时的流线图,图中t1和t2分别表示升力系数达到最小值和最大值对应的时刻.可以看出,对应t1和t2时刻的两次干扰对流场的影响均主要集中在翼型前缘附近,但影响规律相反,且t1时刻的干扰对流场的影响明显比t2时刻强.在干扰发生的相同时刻,与基准翼型相比,model 3上、下翼面的扰动压强差明显降低,t1时刻,气流从扰动压强大的上翼面通过孔流向下翼面,降低了上翼面的扰动压强,并减慢了下翼面气流速度,增大了下翼面的扰动压强;t2时刻,气流从扰动压强小的上翼面通过孔流向下翼面,增加了上翼面的扰动压强,并加快下翼面的气流速度,降低了下翼面的扰动压强.综合来看,开孔主要是通过调节上、下翼面的压强达到有效降低干扰效应的目的.
4 结 论
本文采用不同前缘开孔方式的模型和无孔的基准翼型进行了翼涡干扰的数值模拟,在不同来流速度、涡的强度和干扰距离条件下,分析了前缘开孔方式对翼涡干扰效应的影响,得到以下结论:
1) 在弱干扰条件下,低速时,孔尺寸变小会使得降低效果变弱;较高速度时,斜孔的孔尺寸变小会使得降低效果变弱,直孔的孔尺寸变小反而会使得降低效果变强.
2) 在强干扰条件下,不管来流是低速还是高速,对于直孔,孔尺寸变小,降低效果变强,斜孔却与之相反.
3) 翼型前缘的孔隙,可以有效降低翼涡的干扰效应;在不同Reynolds数和干扰距离下,宽度为0.05C的斜孔的降低效果优于文中其他开孔方式;如果考虑对翼型气动性能的影响,宜采用0.025C宽度的直孔,能有效降低干扰效应的同时,使不同迎角下翼型的升力系数损失较小.
以上研究是本文针对NACA 0012对称翼型不可压缩桨涡干扰流场展开的,翼型和压缩性对控制效果的影响,将会在下一步的研究工作中进行.
[1] 史勇杰, 招启军, 徐国华. 旋翼桨-涡干扰气动特性计算及参数影响研究[J]. 航空学报, 2010, 31(6): 1106-1114.(SHI Yongjie, ZHAO Qijun, XU Guohua. Numerical calculation and parametric study of aerodynamics of rotor blade-vortex interaction[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(6): 1106-1114.(in Chinese))
[2] 倪同兵, 招启军, 马砾. 基于IBC方法的旋翼BVI噪声主动控制机理[J]. 航空学报, 2017, 38(7): 120-132.(NI Tongbing, ZHAO Qijun, MA Li. Active control mechanism of rotor BVI noise based on IBC method[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(7): 120-132.(in Chinese))
[3] NI Tongbing, ZHAO Qijun, MA Li. Parameter influence analyses of IBC active control on rotor BVI noise based upon an integrated CFD/CSD/FW-Hpds method[J]. Acta Aerodynamica Sinica, 2018, 36(3): 417-431.
[4] BROOKS T F, BOOTH E R, JOLLY J R, et al. Technical notes: reduction of blade-vortex interaction noise through higher harmonic pitch control[J]. Journal of the American Helicopter Society, 1990, 35(1): 86-91.
[5] 王亮权, 徐国华, 史勇杰, 等. 高阶谐波控制对旋翼桨-涡干扰载荷和噪声的影响[J]. 航空学报, 2017, 38(7): 65-74.(WANG Liangquan, XU Guohua, SHI Yongjie, et al. Influence of higher harmonic control on airload and acoustics of rotor blade-vortex interaction[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(7): 65-74.(in Chinese))
[6] DIETERICH O, ENENKL B, ROTH D. Trailing edge flaps for active rotor control-aeroelastic characteristics of the ADASYS rotor system[C]//Annual Forum Proceeding-American Helicopter Society, 2006.
[7] ZHANG M M, XU J Z. Active control of fluctuating pressure induced by blade-vortex interaction[J]. Science China Technological Sciences, 2011, 54(4): 862-868.
[8] BROOKS T F. Studies of blade-vortex interaction noise reduction by rotor blade modification[C]//Proceedings of the 1993 National Conference on Noise Control, 1993: 57-66.
[9] TANGLER J L, WOHLFELD R M, MILEY S J. An experimental investigation of vortex stability, tip shapes, compressibility and noise for hovering model rotors[R]. Washington: NASA, 1973.
[10] 史勇杰, 苏大成, 徐国华. 桨叶气动外形对直升机桨-涡干扰噪声影响研究[J]. 南京航空航天大学学报, 2015, 47(2): 235-242.(SHI Yongjie, SU Dacheng, XU Guohua. Research on influence of shape parameters on blade-vortex interaction noise of helicopter rotor[J]. Nanjing University of Aeronautics and Astronautics, 2015, 47(2): 235-242.(in Chinese))
[11] 孙传伟, 陆洋, 高正. 锯齿状桨尖旋翼悬停气动特性试验研究[J]. 空气动力学学报, 2001, 19(4): 446-451.(SUN Chuanwei, LU Yang, GAO Zheng. An experiment of hover performance with new shape blade tip[J]. Acta Aerodynamica Sinica, 2001, 19(4): 446-451.(in Chinese))
[12] DAHDI B, MAMOU M, KHALID M, et al. Investigation of skin porosity damping effects on free stream disturbance induced unsteady wing loads[J]. Aeronautical Journal, 2012, 116(1184): 1041-1060.
[13] ELJACK E, ALQADI I, KHALID M. Numerical simulation of surface porosity in presence of wing-vortex interaction[J]. Aircraft Engineering and Aerospace Technology: an International Journal, 2015, 87(5): 443-453.
[14] 李博, 钱红玉, 张立, 等. 叶片穿孔小型轴流风扇气动性能的研究[J]. 浙江理工大学学报, 2013, 30(1): 76-80.(LI Bo, QIAN Hongyu, ZHANG Li, et al. Aerodynamic performance study on small axial fan with perforation blades[J]. Journal of Zhejiang Institute of Science and Technology, 2013, 30(1): 76-80.(in Chinese))
[15] 张宗茂, 顾熙棠. 降低轴流风机噪声的两种方法[J]. 宁波大学学报, 1989, 2(1): 79-87.(ZHANG Zongmao, GU Xitang. Two methods on the noise reduction in axial flow fans[J]. Journal of Ningbo University, 1989, 2(1): 79-87.(in Chinese))
[16] LEE S. Reduction of blade-vortex interaction noise through porous leading edge[J]. AIAA Journal, 1994, 32(3): 480-488.
[17] LEE S, BERSHADER D. Head-on parallel blade-vortex interaction[J]. AIAA Journal, 2015, 32(1): 16-22.
[18] RENZONI P. Discrete vortex modeling of a blade-vortex interaction[D]. PhD Thesis. Troy: Rensselaer Polytechnic Institute, 1987.
[19] LEVERTON J W, TAYLOR F W. Helicopter blade slap[J]. Journal of Sound & Vibration, 1966, 4(3): 8345-8357.
[20] LI C G, MAA J P Y. Multi-relaxation-time lattice Boltzmann simulations of lid driven flows using graphics processing unit[J]. Applied Mathematics & Mechanics(English Edtion), 2017, 38(5): 1-16.
[21] 崔桂香, 许春晓, 张兆顺. 湍流大涡数值模拟进展[J]. 空气动力学学报, 2004, 22(2): 121-129.(CUI Guixiang, XU Chunxiao, ZHANG Zhaoshun. Progress in large eddy simulation of turbulent flows[J]. Acta Aerodynamica Sinica, 2004, 22(2): 121-129.(in Chinese))
[22] CHEN L, YU Y, HOU G. Sharp-interface immersed boundary lattice Boltzmann method with reduced spurious-pressure oscillations for moving boundaries[J]. Physical Review E, 2013, 87(5): 053306.
[23] NIU X D, SHU C, CHEW Y T, et al. A momentum exchange-based immersed boundary-lattice Boltzmann method for simulating incompressible viscous flows[J]. Physics Letters A, 2006, 354(3): 173-182.
[24] STRAUS J, RENZONI P, MAYLE R E. Airfoil pressure measurements during a blade vortex interaction and a comparison with theory[J]. AIAA Journal, 1990, 28(2): 222-228.