引 言
矩阵指数函数的精细积分方法由钟万勰先生提出[1-4],将矩阵指数计算的精度提高到计算机精度,随后基于计算结构力学与最优控制之间的模拟理论,该方法被扩展到两端边值问题的计算,并成功地解决微分Riccati方程的求解.迄今,对弹性力学、结构力学、波导控制、滤波问题等精细积分算法都有了广泛的应用.精细积分算法是解析法在数值方法上的映射,它适宜处理一阶常微分方程组,这里常微分方程的理论是以一阶方程为标准型的,如状态空间法和Hamilton体系下的理论往往将微分方程组化归为一阶形式.
矩阵指数函数的计算是精细积分方法的核心.它有两个要点:一个是将加法转化为乘法的运算,即指数加法定理或2N类的算法;另一个是计算时的增量存储,以防止计算机的舍入操作,甚至失去精度.对于非齐次方程,外力引起的响应可由Duhamel积分求出.精细积分算法的精度分析如下:执行矩阵乘法通常有一些算术舍入误差,另外就是幂级数展开式的截断误差.
为了充分发挥精细积分方法高精度的功效,人们正致力于研究避免矩阵求逆的精细积分方法,其发展基本沿着两个方向进行:一是研究增维方法.顾元宪等[5-6]提出了增维精细积分法.向宇等[7]及文献[8-9]对其进一步做了改进,提高了时间效率.二是研究Duhamel项的积分方法.张森文等[10]和汪梦甫等[11]分别利用Simpson积分公式、Gauss积分公式求解了Duhamel积分.其次是在继承精细积分方法思想的基础上研究Duhamel项的精细积分方法.谭述君等[12]以及富明慧等[13]对于非齐次项为一些特定类型函数的情况,分别给出了精确的计算方法,得到了数值上逼近计算机精度的结果.
文献[14-17]建立了精细-Runge-Kutta法、样条精细积分法、精细积分-FFT方法等改进方法.文献[18-19]分别研究了两端边值问题和结构弹性撞击的精细积分法.结合精细积分技术,文献[20-22]在求解非线性问题时分别基于插值积分法、迭代法、同伦摄动法求解.关于精细积分法的更多应用请参考文献[23-25].
对于整数阶微分方程,精细积分方法在理论和实际工程上都获得了广泛而深入的研究[3-4].近年来,研究者们意识到分数阶微积分具有广阔的应用前景,但是分数阶微积分的解析求解存在较大困难[26],所以发展分数阶微积分的数值算法是一个迫切需要解决的问题.这些算法包括有限差分法、有限元法、Lagrange乘子法、积分方程法等.但这些方法还不够理想.当前精细积分在分数阶常微分方程求解的应用上处于起步阶段,如文献[27-28]把分数阶微分动力方程近似转化为整数阶微分方程后研究.与文献[27]使用的方法不同,本文直接基于分数阶常微分方程的解析解给出一种有效的算法:分数阶微分方程的精细积分法.数值算例的结果说明了所提方法的有效性和精度.
1 分数阶常微分方程及其解析解
分数阶线性定常微分方程的一般形式如下[1-2]:
其中,x(t)= [x1(t),x2(t),…,xn(t)]T,x(t)∈ Rn,A ∈ Rn×n,初值条件为 x(0)= [x1(0),x2(0),…,xn(0)]T.本文时间分数阶导数的定义中时间域的下限等于初始时刻.
当α=1时,式(1)即为整数阶微分方程x(t)=Ax(t).利用分数阶导数的Laplace变换及其逆变换得其解x(t)如下:
式中Eα,β(z)为双变量Mittag-Leffler函数(下面简称为ML函数),其公式如下:
下面类比整数阶微分方程的精细积分法[3-10],对式(2)中的函数Eα,β(z)进行精细计算,并给出分数阶微分方程的精细积分法.
2 分数阶精细积分法
2.1 ML函数矩阵的精细计算
以下通过迭代法讨论ML函数Eα,1(z)的精细计算.

其中
指数函数的精细积分法中,指数函数满足加法原理,即exp(Aη)=[exp(Aη/m)]m.而ML函数不满足这个性质.记f(X)=I+Q1,其中![]() 系时,在经典指数函数的关系基础上增加修正项R(X).即
系时,在经典指数函数的关系基础上增加修正项R(X).即
欲使f(2X)=I+Q2,应有
由式(6)得如下迭代:
其中函数R的近似表达式为
系数bk可用ak(k=2,3,…,∞)表示,具体关系见2.2小节.
实际数值计算时,函数R的表达式近似地取为有限项.当Q1和Q2的多项式定义式分别截取m1,m2项,所得函数R的多项式次数为max(m2,2m1).为提高精度,一般取m2≥m1.
欲求t=η时的响应,需求f(Aηα)的值.类似整数阶精细积分法,对Aηα分割N次,逐步![]()
记m=2N,当N=20时,m=1 048 576.由于η本来是不大的时间区段,则τ=ηα/m是较小的时间区段.对于τ区段,有
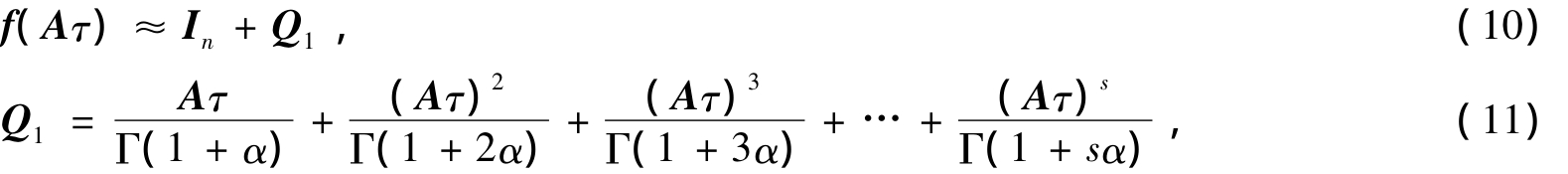
其中s为整数,类比整数阶精细积分,取s=[4/α],[·]表示Gauss函数,Q1是一个小量矩阵. 因此,式(8)相当于执行以下赋初值和循环语句:
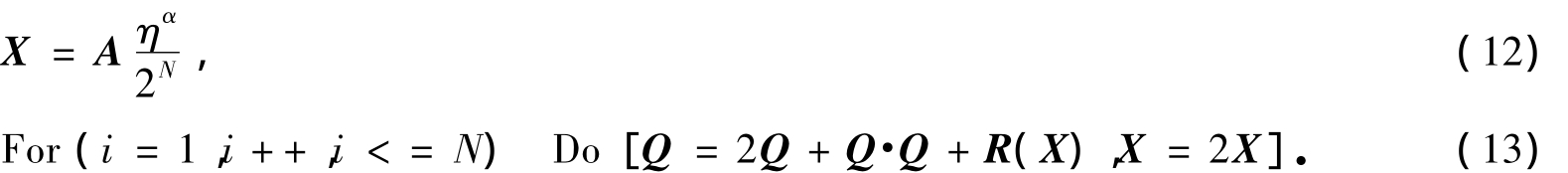
当循环结束时有
与整数阶精细积分类似,以上计算中注意了加法的舍入误差问题.
对比常规的整数阶精细积分,称基于式(12)~(14)的计算为ML函数矩阵的精细计算.
由式(2)和(12)知,所用时间点(时刻)为 t0,21/αt0,22/αt0,23/αt0,…,η,其中 t0= η/2N/α .对比0<α<1,α=1和α>1的情况发现:α>1时,这些时刻的分布比常规精细积分所用的时刻更紧凑;而0<α<1时,这些时刻的分布比常规精细积分所用的时刻更稀疏.
2.2 修正项的表达式
如多项式![]()
和式(7)的截取项数分别为m1=m2=4,得多项式R(X)系数bk(k=2,3,…,8)的结果见表1 .
表1 m1=m2=4时R(X)表达式中的多项式系数bk(k=2,3,…,8)
Table 1 Coefficients bkof R(X)form1=m2=4(k=2,3,…,8)
7 8 bk 2a2-a2 k 23456 1 6a3-2a1a2 -a22-2a1a3+14a4 -2a2a3-2a1a4 -a23-2a2a4 -2a3a4 -a2 4
表1中,f(2X)和f(X)的多项式近似式截取项相同.若f(2X)和f(X)的多项式近似式截取项不同,如分别取成2m,m次多项式,在特定的情况下,能够提高精度.如m1=4,m2=8,得多项式系数bk(k=2,3,…,8)的结果见表2.为了比较,再取m1=4,m2=16时,得多项式系数 bk(k=2,3,…,16)的结果见表3.
表2 m1=4,m2=8时R(X)表达式中的多项式系数bk(k=2,3,…,8)
Table 2 Coefficients bkof R(X)form1=4,m2=8(k=2,3,…,8)

k 2345 bk 2a2-a2 1-a1a2+6a3 -a2 2-2a1a3+14a4 -2a2a3-2a1a4+32a5 k 678 bk -a2 3-2a2a4+64a6 -2a3a4+128a7 256a8-a2 4
表3 m1=4,m2=16时R(X)表达式中的多项式系数bk(k=2,3,…,16)
Table 3 Coefficients bkof R(X)form1=4,m2=16(k=2,3,…,16)

k 2345 bk 2a2-a21-a1a2+6a3 -a22-2a1a3+14a4 -2a2a3-2a1a4+30a5 k 678≥9 bk-a2 3-2a2a4-2a1a5+62a6-2a3a4-2a2a5-2a1a6+128a7 256a8-2a2a6-a24-2a3a5…
对比表1~3可以发现,各项系数bk部分相同,部分有所区别(k=2,3,…,8),且与分数阶次α有关.实际编程运算时,m1,m2的取值需根据参数α的值、矩阵A及待求解时刻t决定.当 α≥1时,ML函数的级数展开式收敛很快,因此通常m1≥10;而当0<α<1时,m1,m2的取值比α≥1时的结果大.
2.3 计算量
由于矩阵加法的计算量较乘法小很多,故所提方法的计算量主要集中于矩阵的乘法.在计算R(X)时,表达式宜采用如下形式:
设R(X)的多项式次数为p,则每计算一次R(X)需做p-1次矩阵乘法运算和p次矩阵加法运算.由式(13),还需加上一次Q·Q对应的乘法运算.式(13)中的迭代循环次数为N,而每次迭代含p次矩阵乘法运算,其中n维矩阵相乘的运算量为n3,故总运算量近似为Npn3.因此,所提的分数阶精细积分方法计算量是整数阶精细积分法的p倍.
2.4 误差
与常规精细积分类似,误差包含两部分,即ML函数的近似表达式对应的误差和计算中数值计算的舍入误差.前者实际上由迭代表达式(13)决定,与参数m1,m2和α有关,其误差体现在R的近似表达式![]() 与准确表达式的截断误差上.所提计算ML函数矩阵的方法对应误差的公式如下:
与准确表达式的截断误差上.所提计算ML函数矩阵的方法对应误差的公式如下:
其中矩阵R(m1,m2)按照式(9)计算,· 代表矩阵范数.
所提方法的精度主要取决于修正项R(X)的精度.而修正项多项式Rp(X)(下标p为多项式的次数,由2.1小节知p=max(m2,2m1))可化为t的多项式,其关于t的次数为pα.因此,只要合理选取m1,m2即可达到控制输出的精度.
3 非齐次方程解的精细计算
回顾分数阶非齐次方程D(α)x(t)=Ax(t)+u(t),这里考虑了外部激励u(t)作用,外部激励引起的解可由如下积分得到:
如果u(t)的解析表达式已知,可对式(17)中的ML函数按定义展开,再做积分运算,所得结果是一个多项式函数.然后可对多项式函数采用相应的精细积分格式计算.
当u(t)的解析表达式未知时,可设tk~tk+1之间用线性插值如下:
其中p0,p1可由u0,u1表示.
式(17)中,右端第一项为齐次解,可按第2节方法计算.右端第二项是含有矩阵ML函数的积分,在处理时应充分利用矩阵ML函数定义的级数展开式:

其中
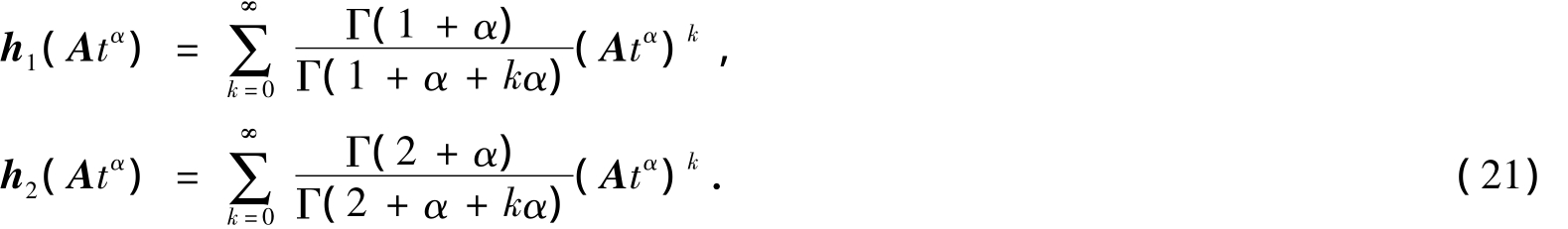
采用增量形式存储如下:
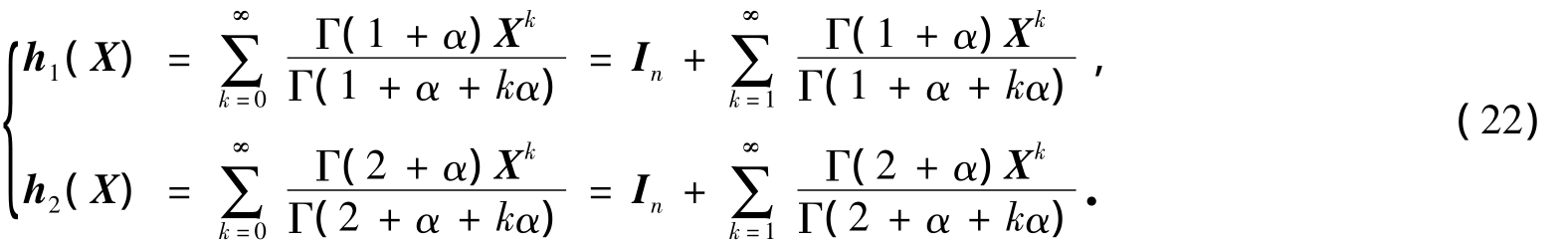
求t=η时的响应,需求h1(Aηα)和h2(Aηα)的值.类似整数阶精细积分法,对Aηα分割![]() .由于η本来是不大的时间区段,则τ=ηα/m是较小的时间区段.对于τ区段,有
.由于η本来是不大的时间区段,则τ=ηα/m是较小的时间区段.对于τ区段,有
其中Qi(i=1,2)为小量,可根据定义式(22)截取前若干项.
类似第2节中ML函数的求法,可分别建立hi(2X)(i=1,2)与hi(X)的迭代关系式,并求出对应的修正项R(X).具体表达式略去.
4 算 例
4.1 算例1
这里考虑特殊情况α=1,其解析解为x1(t)=Eα,1(tα),x2(t)=0.计算中时间分割为N=15段.m1和m2选取了7组值(具体见表4),所得结果与精确解进行对照.其中划线的结果表示所得值与精确值的偏差比其他的相对较大.
表4 x1(t)的精确解与精细积分解对照
Table 4 The solutions of the precise integration method compared with the exact results

m1,m2 t 13 17 10,12 2.718 28 148.418 8 107.83 442 896 2.418 7 ×10 1 4 9 7 14,14 2.718 28 148.413 8 103.08 442 413 2.415 5 ×107 15,15 2.718 28 148.413 8 103.08 442 413 2.415 5 ×107 10,20 2.718 28 148.431 8 108.02489 510 2.995 76 ×107 455 662 2.415 5 ×107 15,30 2.718 28 148.413 8 103.41 443 432 2.478 46 ×107 15,19 2.718 28 148.413 8 103.18 442 497 2.416 76 ×107 analytical 2.718 28 148.413 8 103.08 442 413 2.415 5 ×10 12,24 2.718 28 148.414 8 115.08 7
从表4可以看出,m1=10,m2=20和m1=12,m2=24时的部分结果有一定误差(分别为2.99%,10.6%和24.02%),但其他组解的误差均较小(在1%以内).这说明合理选取m1和m2的值将使得误差大大缩小,并趋向精确解.从而验证所提分数阶精细积分方法的有效性.
4.2 算例2
分数阶齐次微分动力学方程如下[29]:
其中 Dp为 Caputo分数导数算子,a3=0.5,a2=0,a1=0,a0=1,x(0)=0,x'(0)=1 .
方程可以转化为状态方程形式:
其中
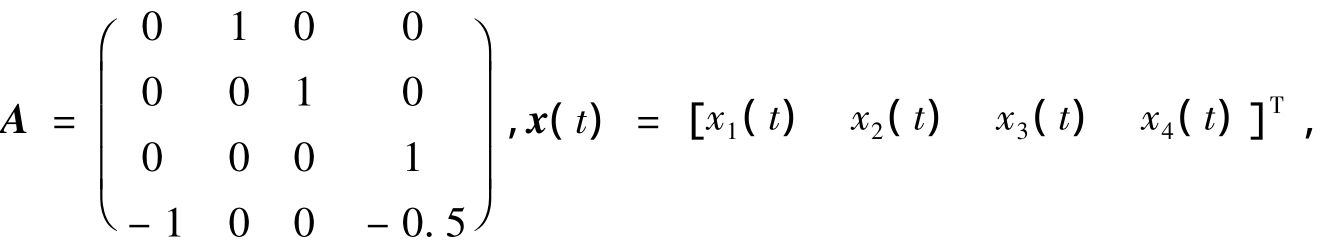
初值为x(0)= [0 0 1 0]T.
按解析解式(2)计算,截取项数n分别取55和131,所得响应曲线见图1.注意α较小且待求解对应的时刻较大时,ML函数展开式收敛较慢,故取132项.
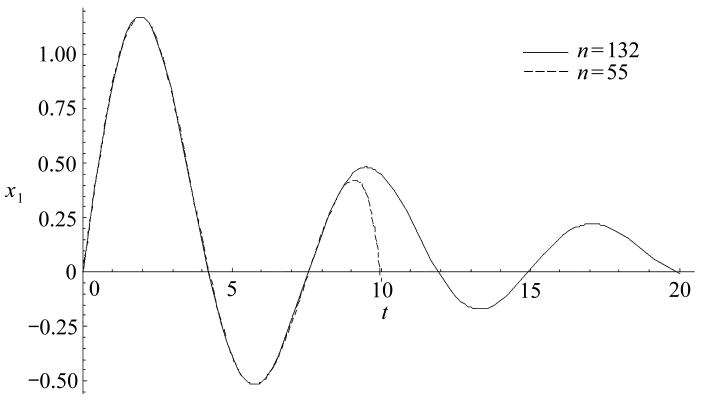
图1 取不同项数时解析解的曲线
Fig.1 Curves of the analytical solution fordifferent numbers of items
运用分数阶精细积分法时,选取时间步长η=0.5,迭代次数N=15,m1和m2分别选取如下 3 组值:1)m1=20,m2=60;2)m1=30,m2=90;3)m1=40,m2=130,所得计算结果与解析解曲线的对比见图2和图3.
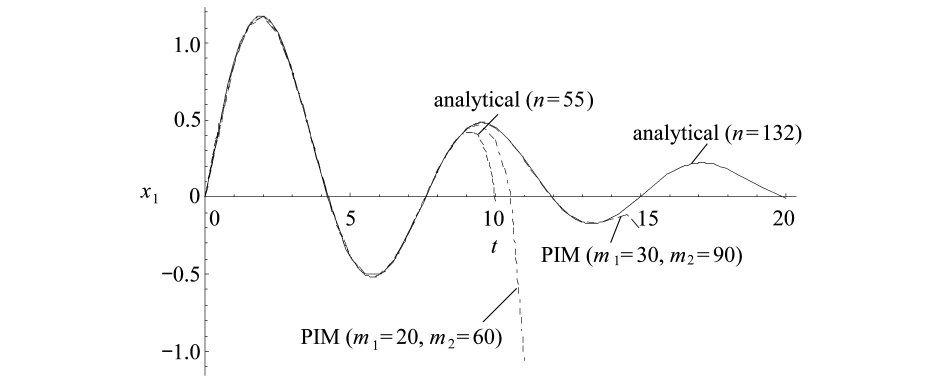
图2 精细积分法解与解析解的对比
Fig.2 Comparison of the curves of the PIM with those of the analytical solution
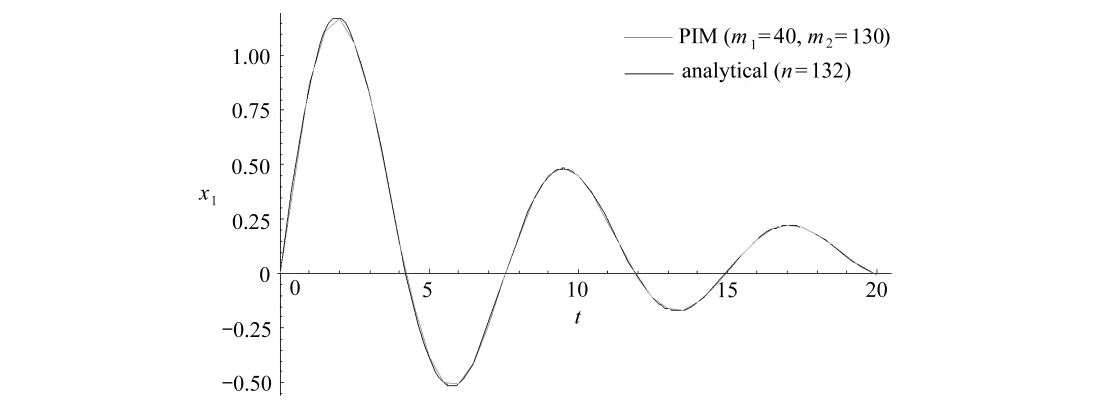
图3 精细积分法解(m1=40,m2=130时)与解析解重合
Fig.3 The curve of the PIM(m1=40,m2=130)coinciding with that of the analytical solution
由图2和图3可知,精细积分法求得的解和准确解在一定时间段内完全吻合,但随着时间t的增长,欲使计算结果的误差变小,需增大m1和m2的值.图3中精细积分法计算时取时间步长η=0.5,故所得曲线为折线.
4.3 算例3
Bagley-Trovik 动力学方程如下[30-31]:
其中,Dp为Caputo分数导数算子,
方程可以转化为状态方程形式:D1/2y(t)=Ay(t)+u(t),其中
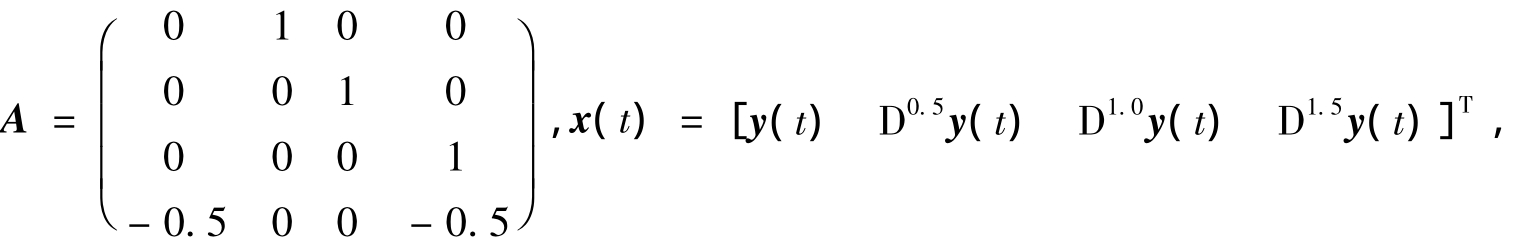
初值为 x(0)=[0 0 0 0]T.非齐次项u(t)为常数项,即p0=[0 0 0 8]T,0≤t≤1,而t>1后,方程转化为齐次方程.
对于0≤t≤1,精细积分法计算时,使用式(20)和(22)计算非齐次方程的解;再利用式(2)和(13)计算齐次方程(t>1时)的解.注意在两个时间区段计算中,t=1时的状态变量应保持连续.另外,选取时间步长η =0.5,迭代次数N=15,参数m1,m2分别取40和130.
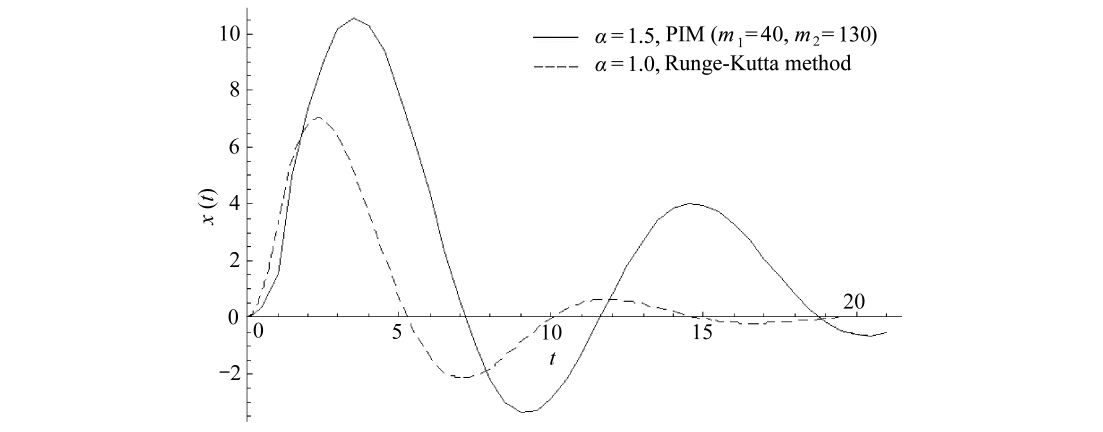
图4 非齐次分数阶微分方程位移解与整数阶阻尼时的解对应曲线
Fig.4 The displacement curve of the fractional differential equation and that of the equation with integral-orderdamping
图4 和图5给出了α=1.5时的位移曲线和速度曲线.为与整数阶阻尼(即α=1)的情形对比,图4和图5中也给出相应的位移曲线和速度曲线(使用了Runge-Kutta方法).对比发现,分数阶阻尼时的位移、速度曲线振动幅度均较整数阶阻尼时剧烈,即此时位移和速度的记忆性较强[26].
图4中的位移曲线(α=1.5时)与文献[30]中的曲线变化趋势类似,但本文的峰值相对大一些,这是由采用的分数阶导数定义不同所致.文献[30]中使用了便于数值计算的RL定义,而本文采用的Caputo分数导数便于工程应用.
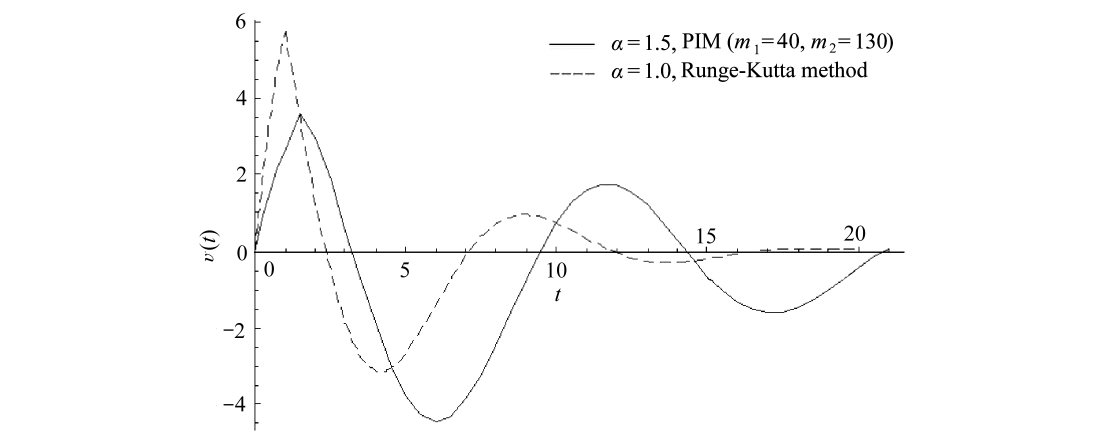
图5 非齐次分数阶微分方程速度解与整数阶阻尼时的解对应曲线
Fig.5 The velocity curve of the fractional differential equation and that of the equation with integral-orderdamping
5 结 论
本文提出分数阶常微分方程的精细积分法,得到如下结论:
1)针对分数阶常微分方程解析解中的ML函数不满足加法原理(而常规的指数函数满足)这一特点,在迭代关系中加入修正项.
2)对于解函数中含有小数指数的幂函数问题,引入X=Atα变量把多项式解函数转化为整数多项式函数,从而便于应用含修正项的精细积分.
3)与常规整数阶精细积分法对比,应用分数阶精细积分计算不同时刻的响应时,需根据初始时刻的响应(即初值)推算待求时刻的响应.
4)由于分数阶常微分问题解析解中的ML函数不满足加法原理,迭代计算式中存在修正项而使计算量大增.分数阶微分问题的精细积分方法的计算量是普通整数阶精细积分法的p倍,其中p是多项式R(X)的次数.
5)对于分数阶常微分方程,算例包含齐次和非齐次(其中非齐次项为分段常数项)两种情况.算例结果显示,合理选择f(X)和f(2X)对应的函数截断项数,能够取得较好的计算结果.本文方法在理论上能达到解析解的精度,还有无条件稳定、对时间步长不敏感等优势.
[1] 钟万勰.暂态历程的精细计算方法[J].计算结构力学及其应用,1995,12(1):1-6.(ZHONG Wanxie.Precise integration fortransient analysis[J].Computational Structure Mechanics and Applications,1995,12(1):1-6.(in Chinese))
[2] ZHONG W X.On precise integration method[J].Journal of Computationaland Applied Mathematics,2004,163(1):59-78.
[3] 钟万勰,高强.辛破茧:辛拓展新层次[M].大连:大连理工大学出版社,2011.(ZHONG Wanxie,GAO Qiang.Broken Cocoon:New Steps forSymplectic Extension[M].Dalian:Dalian University of Technology Press,2011.(in Chinese))
[4] 钟万勰.应用力学的辛数学方法[M].北京:高等教育出版社,2005.(ZHONG Wanxie.Symplectic Solution Methodology in Applied Mechanics[M].Beijing:HigherEducation Press,2005.(in Chinese))
[5] 顾元宪,陈飚松,张洪武.结构动力方程的增维精细积分法[J].力学学报,2000,32(4):447-456.(GU Yuanxian,CHEN Biaosong,ZHANG Hongwu.Precise time-integration with dimension expanding method[J].Acta Mechanica Sinica,2000,32(4):447-456.(in Chinese))
[6] CHEN B S,TONG L Y,GU Y X.Precise time integration forlineartwo-point boundary value problems[J].Applied Mathematics Computation,2006,175(1):182-211.
[7] 向宇,袁丽芸,邹时智,等.求解非线性动力方程的一种齐次扩容精细积分法[J].华中科技大学学报(自然科学版),2007,35(8):109-111.(XIANG Yu,YUAN Liyun,ZOU Shizhi,et al.An extended homogeneous capacity integration method with high precision to solve nonlineardynamic equation[J].Journal of Huazhong University of Science and Technology(Nature Science),2007,35(8):109-111.(in Chinese))
[8] 张素英,邓子辰.非线性动力方程的增维精细积分法[J].计算力学学报,2003,20(4):423-426.(ZHANG Suying,DENG Zichen.Increment-dimensional precise integration method fornonlineardynamic equation[J].Chinese Journal of Computational Mechanics,2003,20(4):423-426.(in Chinese))
[9] 张继锋,邓子辰.结构动力方程的增维分块精细积分法[J].振动与冲击,2008,27(12):88-90.(ZHANG Jifeng,DENG Zichen.Dimensional increment and partitioning precise integration method forstructural dynamic equation[J].Journal of Vibration and Shock,2008,27(12):88-90.(in Chinese))
[10] 张森文,曹开彬.计算结构动力响应的状态方程直接积分法[J].计算力学学报,2000,17(1):94-97.(ZHANG Senwen,CAO Kaibin.Direct integration of state equation method fordynamic response of structure[J].Chinese Journal of Computational Mechanics,2000,17(1):94-97.(in Chinese))
[11] 汪梦甫,周锡元.结构动力方程的更新精细积分方法[J].力学学报,2004,36(2):191-195.(WANG Mengfu,ZHOU Xiyuan.Gauss precise time integration of structural dynamic analysis[J].Engineering Mechanics,2004,36(2):191-195.(in Chinese))
[12] 谭述君,钟万勰.非齐次动力方程Duhamel项的精细积分[J].力学学报,2007,39(3):374-381.(TAN Shujun,ZHONG Wanxie.Precise integration method forDuhamel terms arising from non-homogenous dynamic systems[J].Chinese Journal of Theoreticaland Applied Mechanics,2007,39(3):374-381.(in Chinese))
[13] 富明慧,刘祚秋,林敬华.一种广义精细积分法[J].力学学报,2007,39(5):672-677.(FU Minghui,LIU Zuoqiu,LIN Jinghua.A generalized precise time step integration method[J].Chinese Journal of Theoreticaland Applied Mechanics,2007,39(5):672-677.(in Chinese))
[14] 高小科,邓子辰,黄永安.基于三次样条插值的精细积分法[J].振动与冲击,2007,26(9):75-77,82.(GAO Xiaoke,DENG Zichen,HUANG Yongan.A high precise direct integration based on cubic spline interpolation[J].Journal of Vibration and Shock,2007,26(9):75-77,82.(in Chinese))
[15] 富明慧,梁华力.一种改进的精细-龙格库塔法[J].中山大学学报(自然科学版),2009,48(5):1-5.(FU Minghui,LIANG Huali.An improved precise Runge-Kutta integration[J].Acta Scientiarum Naturalium Universitatis Sunyatseni,2009,48(5):1-5.(in Chinese))
[16] 张文志,富明慧,刘祚秋.结构动力方程的精细积分-FFT方法[J].中山大学学报(自然科学版),2008,47(6):12-15.(ZHANG Wenzhi,FU Minghui,LIU Zuoqiu.Precise integration-FFT method forstructural dynamics[J].Acta Scientiarum Naturalium Universitatis Sunyatseni,2008,47(6):12-15.(in Chinese))
[17] 富明慧,廖子菊,刘祚秋.结构动力方程的样条精细积分法[J].计算力学学报,2009,26(3):379-384.(FU Minghui,LIAO Ziju,LIU Zuoqiu.Spline precise time-integration of structural dynamic analysis[J].Chinese Journal of Computational Mechanics,2009,26(3):379-384.(in Chinese))
[18] 张文志,富明慧,蓝林华.两端边值问题的通用精细积分法[J].中山大学学报(自然科学版),2010,49(6):15-19.(ZHANG Wenzhi,FU Minghui,LAN Linhua.General precise integration method fortwo-point boundary value problems[J].Acta Scientiarum Naturalium University Sunyatseni,2010,49(6):15-19.(in Chinese))
[19] 鲍四元,邓子辰.结构撞击响应的一种弹性模型及其精细求解[J].工程力学,2008,25(6):14-17.(BAO Siyuan,DENG Zichen.An elastic modeland its precise solution forstructural impact response[J].Enginerrng Mechanics,2008,25(6):14-17.(in Chinese))
[20] 吕和祥,于洪洁,裘春航.精细积分的非线性动力学积分方程及其解法[J].固体力学学报,2001,22(3):303-308.(L Hexiang,YU Hongjie.An integral equation of non-lineardynamics and its solution method[J].Acta Mechanica Solid Sinica,2001,22(3):303-308.(in Chinese))
[21] 张洵安,姜节胜.结构非线性动力方程的精细积分算法[J].应用力学学报,2000,17(4):164-168.(ZHANG Xun’an,JIANG Jiesheng.The precise integration algorithm fornonlineardynamic equations of structures[J].Chinese Journal of Applied Mechanics,2000,17(4):164-168.(in Chinese))
[22] 梅树立,张森文.基于精细积分技术的非线性动力学方程的同伦摄动法[J].计算力学学报,2005,22(6):666-670.(MEI Shuli,ZHANG Senwen.Homotopy perturbation method fornonlineardynamic equations based on precise integration technology[J].Chinese Journal of Computational Mechanics,2005,22(6):666-670.(in Chinese))
[23] 吴泽艳,王立峰,武哲.大规模动力系统高精度増维精细积分方法快速算法[J].振动与冲击,2014,33(2):188-192.(WU Zeyan,WANG Lifeng,WU Zhe.Fast algorithm forprecise integration with high accuracydimension expanding method with forlarge-scale dynamic systems[J].Journal of Vibration and Shock,2014,33(2):188-192.(in Chinese))
[24] 张洪武.参变量变分原理与材料和结构力学分析[M].北京:科学出版社,2010.(ZHANG Hongwu.The ParameterVariation Principle and Materials and Structural Mechanics Analysis[M].Beijing:Science Press,2010.(in Chinese))
[25] 钟万勰,姚征.椭圆函数的精细积分算法:应用力学进展[M].北京:科学出版社,2004.(ZHONG Wanxie,YAO Zheng.The Precise Integration Method forJacobi Elliptic Functions and Application:Computation Method[M].Beijing:Science Press,2010.(in Chinese))
[26] 陈文,孙洪广.分数阶微分方程的数值算法:现状和问题[J].计算机辅助工程,2010,19(2):1-2.(CHEN Wen,SUN Hongguang.Status and problems of numericalalgorithm on fractional differential equations[J].ComputerAided Engineering,2010,19(2):1-2.(in Chinese))
[27] 银花,陈宁,赵尘,等.分数导数型粘弹性结构动力学方程的数值计算[J].南京林业大学学报,2010,34(2):115-118.(YIN Hua,CHEN Ning,ZHAO Chen,et al.A numericalalgorithm of the dynamics equation of the fractional derivative viscoelasticity structure[J].Journal of Nanjing Forestry University(Natrual Science Edition),2010,34(2):115-118.(in Chinese))
[28] 薛齐文,魏伟.含分数阶导数微分方程的数值求解[J].大连交通大学学报,2009,30(5):88-92.(XUE Qiwen,WEI Wei.Numerical solution fordifferectial equations offractional order[J].Journal of Dalan Jiaotong University,2009,30(5):88-92.(in Chinese))
[29] 王振滨,曹广益.分数微积分的两种系统建模方法[J].系统仿真学报,2004,16(4):810-812.(WANG Zhenbin,CAO Guangyi.Two system modeling methods using fractional calculus[J].Journal of System Simulation,2004,16(4):810-812.(in Chinese))
[30] 沈淑君,刘发旺.解分数阶Bagley-Torvik方程的一种计算有效的数值方法[J].厦门大学学报(自然科学版),2004,43(3):306-311.(SHEN Shujun,LIU Fawang.A computat ionally effective numerical method forthe fractional orderBagley-Torvik equation[J].Journal of Xiamen University(Natural Science),2004,43(3):306-311.(in Chinese))
[31] BAGLEY R L,TORVIK P J.On the appearance of the fractional derivative in the behaviorof real materials[J].Journal of Applied Mechanics,1984,51(2):294-298.