引 言
作为大跨度桥梁中的典型,斜拉桥在交通运输工程中起着十分关键的作用,其抗震性能备受关注.在斜拉桥的纵桥向,采用飘浮体系是一种对抗震有利的结构体系.它可以通过延长结构周期来减小地震内力,但由于刚度小和阻尼低的特点,其极易在梁端产生过大的地震位移.因此,往往需要在主梁与桥塔连接处设置黏滞阻尼器来控制主梁地震位移[1-2].
纵飘斜拉桥的抗震性能与黏滞阻尼器参数选取密切相关,许多学者对阻尼器参数设计方法开展了大量研究,但大多数研究都是根据全桥有限元模型,采用非线性时程方法进行计算,然后根据参数分析结果总结规律现象,如 Zhu等[3]、王志强等[4]、杨德健等[5]的研究.这种“试算法”工作量大、耗时长且效率低下,最终得到的结果普适性存疑,往往代表性不足.Hwang等[6]针对高速公路常规梁桥,基于等效阻尼比的概念,推导了黏滞阻尼器的参数设计公式,但该公式仅适用于规则梁桥.叶爱君[7]提出利用径向基函数神经网络建立阻尼器参数与结构地震响应之间的映射关系,进而选取所需的阻尼器参数.孙传智等[8]根据响应面法拟合结构响应关于阻尼器参数的函数表达式,将阻尼器参数优化问题转化成非线性规划的问题.上述两种方法是结合结构地震响应的数学寻优设计,虽然能够避免单纯依靠经验选取阻尼器参数所带来的不确定性,但是方法还不够简化,直接应用于实际工程存在困难.鉴于此,本文提出了基于双质点模型的纵飘斜拉桥黏滞阻尼器参数简化分析方法.在正弦波作用下,将双质点模型的解析解、数值解以及全桥模型计算结果进行对比分析,从理论解析角度验证了简化模型的可靠性.本文的简化分析模型可为纵飘斜拉桥的阻尼器参数设计提供一种简便实用的方法.
1 简化分析模型
1.1 纵飘斜拉桥双质点简化模型
在地震作用下,飘浮体系斜拉桥主梁的水平纵向惯性力全部通过拉索传至索塔,而辅助墩和过渡墩的质量相对索塔和主梁而言可忽略.由此,可采用如图1所示的双质点简化模型模拟其在地震作用下的一阶响应行为[9-10].
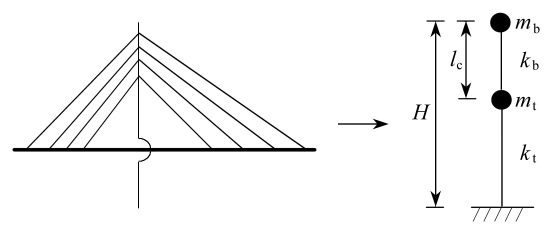
图1 双质点简化模型
Fig.1 A double-mass simplified model
图1 中,主梁质量mb堆聚在塔顶;索塔质量换算成等效质量mt,沿高度较均匀的索塔可用塔身总质量乘以0.24估算得到[9];H为塔高,lc为斜拉索的等效摆长,可近似取上塔柱的高度;kt为索塔抗推刚度;根据单摆原理可以得到主梁的等效摆动刚度为
式中,g为重力加速度,ρ为主梁的体密度,h为主梁梁高,Iy为主梁抗弯惯性矩,其余符号意义同前.
根据多自由度体系的自由振动方程,可知简化模型的特征方程式为

求解方程式(2),解得自振频率为

将式(3)代入到式(2)中,通过归一化可得出振型向量:
1.2 黏滞阻尼器等效线性模型
为了简化分析,有必要将非线性黏滞阻尼器进行等效线性化处理.本文采用能量耗散等效原理,即在简谐荷载u=u0sin(ωt)的激励下,非线性黏滞阻尼器与线性阻尼在一个振动周期内所耗散的能量相等.
在一个振动周期内非线性黏滞阻尼器所耗散的能量Ed为
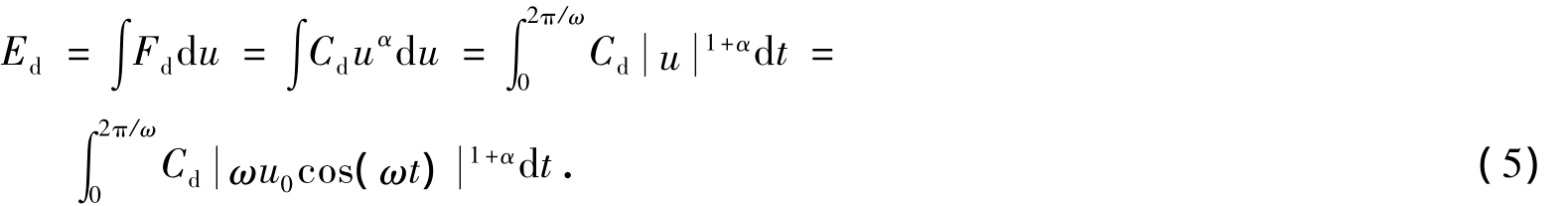
在相同周期内等效线性阻尼所耗散的能量Eequi为
式中,Fd,Cd,α分别为非线性黏滞阻尼器的阻尼力、阻尼系数和速度指数;u和u分别为阻尼器两端的相对速度和相对位移;ω为简谐荷载频率;Fequi,Cequi分别为等效线性阻尼力和阻尼系数.
根据耗能相等原则Ed=Eequi,有
式中,λ =22+α(Γ2(1+ α/2)/Γ(2+ α)),其取值可在报告 FEMA 273[11]中查找;u0为黏滞阻尼器的最大行程,可近似取主梁的最大位移;Γ(·)为Gamma函数.
1.3 简化模型运动方程求解
在图1所示的双质点简化模型基础上,加入黏滞阻尼器等效线性阻尼Cequi,可以得到考虑黏滞阻尼器的等效线性分析模型,如图2所示,其中Cb,Ct分别为主梁和索塔的阻尼系数,可按结构阻尼比3%换算得到.
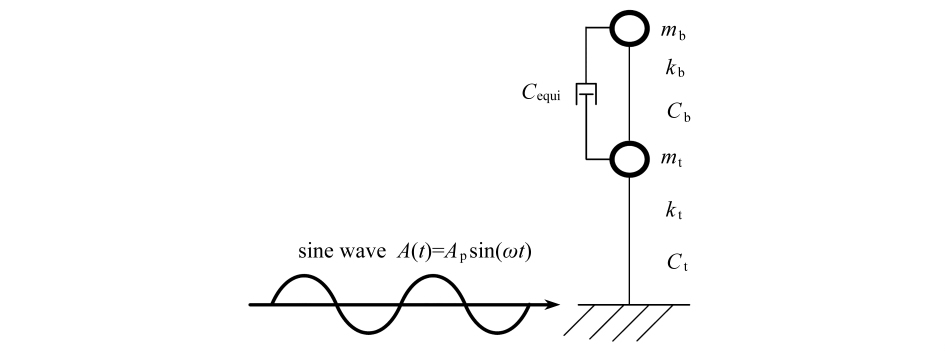
图2 考虑黏滞阻尼器的双质点简化模型
Fig.2 A double-mass simplified model including the viscous damper
根据图2的双质点模型,基于d’Alembert原理建立其运动方程如下:
式中
分别为双质点体系的质量矩阵、阻尼矩阵和刚度矩阵![]()
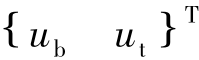 分别表示双质点体系的位移、速度和加速度时程向量;I表示单位列向量;ug表示地面加速度时程,当输入为正弦波荷载时,ug=Apsin(ωt).
分别表示双质点体系的位移、速度和加速度时程向量;I表示单位列向量;ug表示地面加速度时程,当输入为正弦波荷载时,ug=Apsin(ωt).
将主梁质点编号为1,主塔质点编号为2,由振型叠加法可知,第n阶振型分量的位移可由振型向量n乘以振型坐标Yn(t)得到:
式(8)左乘振型向量 ,当m≠n时,根据振型正交性可得
,当m≠n时,根据振型正交性可得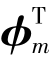 Mn=0,
Mn=0, Kn=0,假定阻尼矩阵C也满足正交条件TmCn=0,则有
Kn=0,假定阻尼矩阵C也满足正交条件TmCn=0,则有
其中,Mn= TnMn,Cn= TnCn,Kn= TnKn,Pn(t)= Tnp(t)分别称为第n阶振型的广义质量、广义阻尼、广义刚度和广义动荷载.方程(10)两边同除Mn,则运动方程可表示为
式中,ζn=Cn/(2ωnMn)称为第n阶模态阻尼比.
初始条件为
求解方程(11),得稳态反应解:
其中
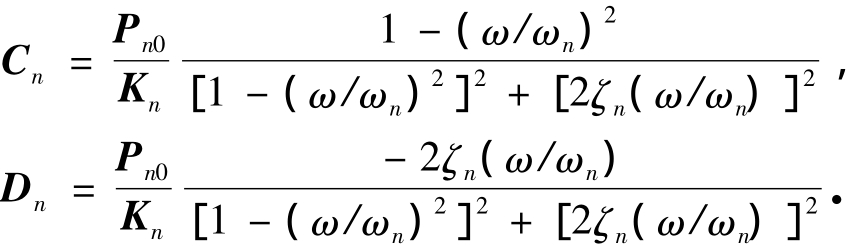
方程(11)的瞬态反应解为
其中
式(13)、(14)中,ω为荷载频率,ωn为体系自振频率![]()
因此,双质点简化模型的各质点位移响应表达式如下所示:
总位移
主梁位移
2 简化模型验证
2.1 桥例概况与全桥分析模型
某飘浮体系斜拉桥的跨径布置为50 m+158 m+392 m+158 m+50 m=808 m,索塔采用纵向双柱构成的帆形混合塔,索塔总高138 m,桥面以上高100 m.主梁为单箱三室钢箱梁,高3.5 m,宽29.5 m,采用单索面布置,每个塔柱共布置16对斜拉索,在塔、梁间共设置4个黏滞阻尼器,速度指数 α取0.3,阻尼系数Cd取5 000 kN·(m·s-1)-0.3.采用有限元软件 SAP2000建立了全桥分析模型,如图3所示.主梁、索塔、边墩以及辅助墩均采用线弹性梁单元模拟,其中主梁、索塔和桥墩均考虑了受压构件的二阶效应.斜拉索采用空间桁架单元模拟,按Ernst公式修正其垂度效应,并考虑恒载初始内力引起的几何刚度影响.球钢支座采用弹塑性双折线模型模拟,以考虑支座摩擦的影响.黏滞阻尼器采用Maxwell模型模拟,体系阻尼采用Rayleigh模型,桩-土-结构相互作用采用简化的6×6土弹簧模拟.

图3 全桥分析模型
Fig.3 The analytical model forthe whole bridge
2.2 简化模型与分析工况
根据桥例设计参数,按照图1、2所示的简化模型,采用第1节的计算公式可得mb=9 146 t,mt=7 268 t,kb=37 403 kN·m -1,kt=55 555 kN·m -1,Cb=1 132 kN/(m·s-1),Ct=1 848 kN/(m·s-1),由式(3)可得桥例的第一阶自振周期为4.315 s,全桥模型计算得到的第一阶自振周期为4.184 s,两者相差3.13%,精度较高.
为了验证第1节的简化分析方法,本文主要进行3种模型和分析方法的对比:
①按照第1节的过程和公式对双质点简化模型进行解析求解;
②仍按照第1节的过程计算简化模型的相关参数,但采用SAP2000建立双质点简化模型进行数值分析,与方法①的差别主要在于本方法采用迭代求解,且可进行包括实际地震波在内的各种复杂动力荷载的求解,是对本文简化分析方法的拓展;
③按照图3所示的方法,采用SAP2000建立全桥精细化有限元分析模型,并考虑了各种可能的非线性因素.
考虑到3种分析方法中,解析求解过程对实际地震动较困难;而且,由于任意地震波均可通过Fourier变换为正弦波的级数展开式.因此,为了方便双质点简化模型的解析求解,本小节采用正弦波荷载进行对比分析[12].为了在正弦波荷载中考虑地震动频谱特性的影响,本文根据文献[13]的研究,采用正弦波峰值加速度Ap与峰值速度Vp的比值Ap/Vp来衡量频谱的特征.一般来说,具有丰富低频成分的近场脉冲型地震动的Ap/Vp值较小,特征周期较长;而高频成分较高的常规远场地震动的Ap/Vp值较大,特征周期较短.
假设正弦波的加速度时程曲线为A(t)=Apsin(ωt),通过对A(t)积分可得速度时程:
正弦波在不同荷载频率ω下的峰值加速度Ap与峰值速度Vp的比值为
上式中,Tg为地震动的卓越周期.
2.3 对比验证分析结果
取正弦波的卓越周期 Tg=2 s,则其频率ω =3.14 rad·s-1,峰值加速度Ap调整为0.25g,在该正弦波输入下,根据式(7),当速度指数α取0.3,阻尼系数Cd取值为1 000,5 000,10 000 kN·(m·s-1)-0.3时,或当 Cd=5 000 kN·(m·s-1)-α,α 值分别取0.1,0.5 和0.9 时,可以得出相应的等效阻尼系数Cequi.通过解析分析和数值分析得到3种分析方法在不同阻尼器参数下的主梁位移时程曲线,如图4所示,其中,SM、WM分别表示简化模型和全桥模型(后同).
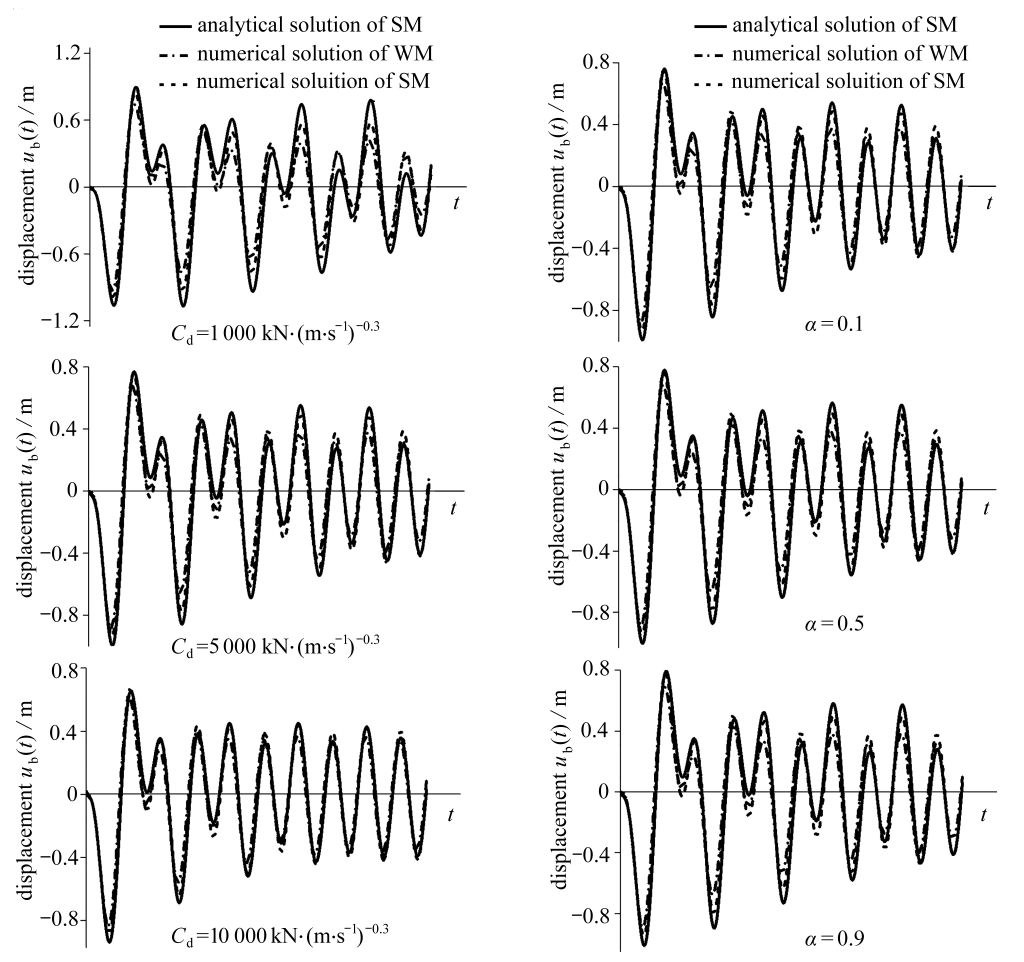
图4 不同阻尼器参数下主梁位移时程曲线对比
Fig.4 Comparison of displacementhistory curves of the girderunderdifferent damperparameters
图4 中三者对应的主梁位移时程曲线形态均保持良好的一致性.以全桥模型计算结果为准,在各阻尼器参数下,双质点数值解的主梁位移包络值最大计算误差为5.3%,平均误差仅为4.6%;而解析解与双质点数值解的主梁位移包络值最大计算误差为6.6%,平均误差为6.1%,表明本文的双质点简化模型在不同黏滞阻尼器参数下,无论采用解析方法还是采用数值方法,均具有很好的精度.
为了进一步研究在不同地震动特性下简化方法的适用性,设置以下两种工况:工况a,将正弦波的峰值加速度Ap分别调整为0.1g,0.3g和0.5g,卓越周期Tg取2 s;工况b,改变与地震动频谱特性相关 ω 的取值,分别取 6.28,4.19,2.093 rad·s-1,对应的卓越周期 Tg分别为 1,1.5,3 s,并将Ap取为0.25g,以此考察包括加速度峰值和频谱特性在内的地震动特性的影响.按式(7)计算阻尼器等效模型时,速度指数 α 取0.3,阻尼系数 Cd取5 000 kN·(m·s-1)-0.3.

图5 不同地震动特性下主梁位移时程曲线对比
Fig.5 Comparison of displacementhistory curves of the girderunderdifferent ground motion characteristics
如图5所示,三者的主梁位移时程曲线形态吻合良好.以全桥模型计算结果为准,在不同地震动强度作用下,双质点简化模型的解析解主梁位移包络值最大计算误差为11.2%,最小误差为11%;双质点简化模型的数值解最大和最小计算误差均为5%.在不同频谱特性地震作用下,双质点简化模型的解析解最大和最小误差分别为12.3%和2.5%;双质点简化模型的数值解最大和最小误差分别为3.4%和1.6%,误差均满足工程精度要求,说明简化方法在不同地震动特性下也具有良好的适用性.
飘浮体系斜拉桥属于典型的柔性体系,纵向刚度较小,结构的基本周期较长[14-16],为了使分析结果更加普遍化,分别将双质点模型的主梁质量mb改变为0.5倍、1.5倍和2.0倍,计算在不同飘浮体系周期下双质点简化模型的适用性情况.仅仅出于对比,因此全桥模型也采用相同的方法改变主梁质量,而忽略因主梁质量变化所导致的斜拉桥其他各参数的变化.
图6显示出在不同体系周期下三者的主梁位移时程曲线几乎保持一致.以全桥模型计算结果为准,双质点简化模型解析解的主梁位移包络值最大计算误差为10.4%,最小误差为9.7%;双质点简化模型数值解的最大误差为5.1%,最小误差仅为1.6%,平均误差为3.7%,表明本文提出的简化模型分析方法对于不同的飘浮体系斜拉桥均具有良好的适用性.
5 结 论

图6 不同体系周期下主梁位移时程曲线对比Fig.6 Time history curves of the girderdisplacement of the simplified model underdifferent system periods
根据飘浮体系斜拉桥的动力响应特征,结合结构动力学原理,提出了基于双质点模型的纵飘斜拉桥黏滞阻尼器参数简化分析方法,在正弦波作用下,对全桥模型、双质点数值解和解析解的计算结果进行对比分析,主要结论如下:
1)对于算例,采用双质点简化模型和全桥模型得到的基本周期分别为4.315 s和4.184 s,误差仅为3.13%,说明双质点简化模型可用于飘浮体系斜拉桥自振周期的简化计算.
2)在各阻尼器参数下,双质点简化分析方法均能得到与全桥模型非常接近的计算结果,如双质点模型数值求解结果的最大误差为5.3%,平均误差仅为4.6%,表明双质点简化分析方法具有很好的精确度.
3)在不同地震动强度下,全桥模型、双质点数值解和解析解三者计算结果的最大误差为11.2%,最小仅为5%;在不同频谱特性下,最大和最小计算误差分别为12.3%和1.6%;而对于不同的体系周期,最大和最小误差分别为10.4%和1.6%,误差总体较小.说明在不同地震动特性和体系周期下,该简化分析方法均具有良好的适用性.
本文提出的双质点模型简化分析方法精度较高,实用性强且适用性广,与全桥有限元模型相比,双质点模型建模简单、计算高效,能进行各种复杂地震荷载输入求解.因此在纵飘斜拉桥黏滞阻尼器选型时,可采用本文的双质点模型进行参数优化.
[1] 韩振峰,叶爱君.千米级斜拉桥的纵向减震体系研究[J].地震工程与工程振动,2015,35(6):64-70.(HAN Zhenfeng,YE Aijun.Research on the longitudinal earthquake-reduction system of cable-stayed bridges overkilometers[J].Earthquake Engineering and Engineering Vibration,2015,35(6):64-70.(in Chinese))
[2] 徐略勤,刘津成,刘营,等.独塔宽幅斜拉桥基于能力需求比的抗震性能评估[J].桥梁建设,2016,46(4):11-16.(XU Lueqin,LIU Jincheng,LIU Ying,et al.Seismic performance assessment of cable-stayed bridge with single pylon and wide deck based on capacity demand ratio method[J].Bridge Construction,2016,46(4):11-16.(in Chinese))
[3] ZHU J,ZHANG W,ZHENG K F,et al.Seismic design of a long-span cable-stayed bridge with fluid viscous dampers[J].Practice Periodical on Structural Design and Construction,2016,21(1):1-11.
[4] 王志强,胡世德,范立础.东海大桥粘滞阻尼器参数研究[J].中国公路学报,2005,18(3):37-42.(WANG Zhiqiang,HU Shide,FAN Lichu.Research on viscous damperparameters of Donghai bridge[J].China Journal of Highway and Transport,2005,18(3):37-42.(in Chinese))
[5] 杨德健,耿辰,宋佳楠.基于多点激励下黏滞阻尼器在斜拉桥中的减震效果分析[J].世界地震工程,2015,31(2):34-42.(YANG Dejian,GENG Chen,SONG Jianan.Multipoint excitationbased vibration effect analysis of viscous dampers in cable-stayed bridge[J].World Earthquake Engineering,2015,31(2):34-42.(in Chinese))
[6] HWANG J S,TSENG Y S.Design formulations forsupplemental viscous dampers to highway bridges[J].Earthquake Engineering & Structural Dynamics,2010,34(13):1627-1642.
[7] 叶爱君.径向基函数(RBF)神经网络在桥梁减震设计中的应用仿真[J].系统仿真技术,2006,2(1):31-37.(YE Aijun.The application of RBF neural network to seismic design of bridges[J].System Simulation Technology,2006,2(1):31-37.(in Chinese))
[8] 孙传智,李爱群,缪长青,等.减震结构粘滞阻尼器参数优化分析[J].土木建筑与环境工程,2013,35(1):80-85.(SUN Chuanzhi,LI Aiqun,MIAO Changqing,et al.Parameteroptimization analysis of viscous dampers fordissipation structure[J].Civil Engineering and Environmental Engineering,2013,35(1):80-85.(in Chinese))
[9] 袁万城,闫冬.斜拉桥纵飘频率简化计算方法[J].同济大学学报(自然科学版),2005,33(11):1423-1427.(YUAN Wancheng,YAN Dong.Simplified calculational method offloating frequency forcable-stayed bridges[J].Journal of Tongji University(Natural Science),2005,33(11):1423-1427.(in Chinese))
[10] 张文学,寇文琦,陈盈,等.基于双质点模型斜拉桥纵向一阶自振周期计算[J].桥梁建设,2016,46(3):98-102.(ZHANG Wenxue,KOU Wenqi,CHEN Ying,et al.Calculation offirstorderlongitudinal natural vibration periods of cable-stayed bridges based on double-masspoint models[J].Bridge Construction,2016,46(3):98-102.(in Chinese))
[11] FEMA.Guidelines and commentary forthe seismic rehabilitation of buildings:FEMA report 273[R].The Building Seismic Safety Council,1997.
[12] 罗骁,张新燕,张珺,等.基于谐波平衡法的尾流激励的叶片振动降阶模型方法[J].应用数学和力学,2018,39(8):892-899.(LUO Xiao,ZHANG Xinyan,ZHANG Jun,et al.A reducedordermodel method forblade vibration due to upstream wake based on the harmonic balance method[J].Applied Mathematics and Mechanics,2018,39(8):892-899.(in Chinese))
[13] KRAMER S L.Geotechnical Earthquake Engineering[M].New Jersey:Prentice Hall,1996.
[14] 叶爱君,胡世德,范立础.超大跨度斜拉桥的地震位移控制[J].土木工程学报,2004,37(12):38-43.(YE Aijun,HU Shide,FAN Lichu.Seismic displacement control forsuper-long-span cable-stayed bridges[J].China Civil Engineering Journal,2004,37(12):38-43.(in Chinese))
[15] 邓育林,雷凡,何雄君.地震作用下大跨斜拉桥主桥与多联引桥伸缩缝处连锁碰撞效应研究[J].土木工程学报,2015,48(2):87-95.(DENG Yulin,LEI Fan,HE Xiongjun.Study on effects of pounding at expansion joints on seismic responses of long-span cable-stayed bridges between main span and multiple approach spans underearthquakes[J].China Civil Engi-neering Journal,2015,48(2):87-95.(in Chinese))
[16] 邵旭东.桥梁工程[M].4版.北京:人民交通出版社,2016.(SHAO Xudong.Bridge Engineering[M].4th ed.Beijing:China Communications Press,2016.(in Chinese))