引 言
分数阶偏微分方程不仅在物理学、生物学、流体力学、化学、信号处理、控制理论等众多领域中有重要的应用,而且在动力系统、拟混沌动力系统、混沌动力行为、复杂物质的动力学和多孔介质的动力学等领域中也有应用.因此,寻找分数阶偏微分方程的精确解和数值解对理解非线性的物理现象是很有价值的.近年来,许多方法已用来构建分数阶偏微分方程的精确解,如首次积分法[1-2]、Adomian 分析法[3-7]、变分迭代法[8-9]、exp展开法[10-12]、(G′/G)-展开法[13-14].
本文主要考虑如下的(3+1)维时间分数阶 Kd V-Zakharov-Kuznetsov方程[15-18]:
其中,a和c是常数,α是分数阶导数.Kd V-ZK方程是研究冷热电子、离子流以及等离子体构成的流体的方程.Sahoo等[15]用改进的子方程方法来构建方程(1)的精确分析解.Mace等[16]用exp方法获得了方程(1)的三角函数解、有理函数解、椭圆函数解.Ozkan等[18]用Kudryashov方法、exp函数方法和函数变量方法来推导了方程(1)的三角解、双曲线功能解和周期解.
本文中的分数阶微分算子是Ju marie的修正 Riemann-Liouville导数[19-20]:
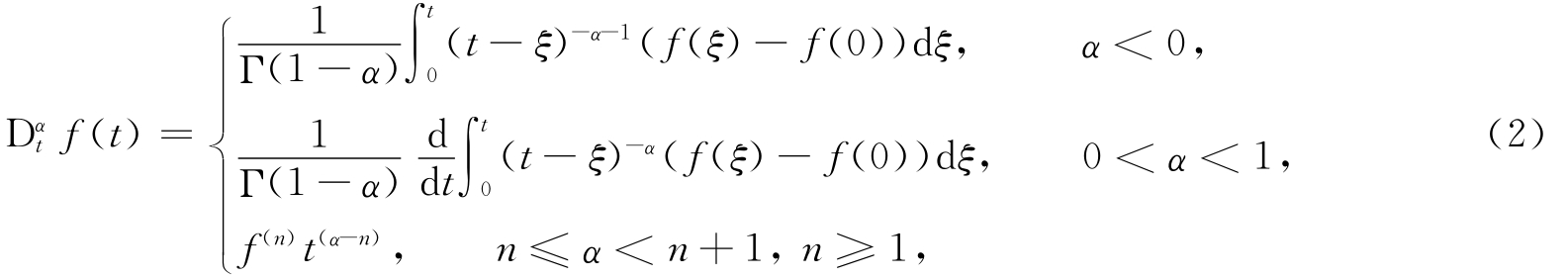
其中,Γ(·)为Ga mma函数.
为了研究方程(1)的性态和更多的解,本文将用拟设方法来获得奇异孤子解、亮孤子解以及拓扑孤子解.用动力系统分支方法[21-22]分析分支相图的轨道及构建其行波解.
1 应用拟设方法
1.1 奇异孤子解
拟设
其中τ=B(x+y+z-ktα/Γ(1+α)),A和B 是常参数,k是孤子的速度.将式(3)代入方程(1),并平衡色散项和非线性项,得p=2.令系数分别为0,则可得
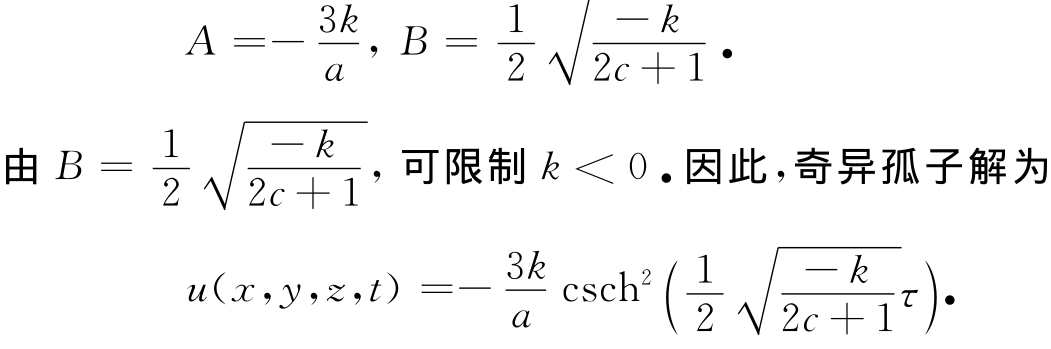
1.2 亮孤子解
拟设
将式(4)代入方程(1),并平衡色散项和非线性项,得p=2.令系数分别为0,则可得

1.3 拓扑孤子解
拟设
将式(5)代入方程(1),并平衡色散项和非线性项,得p=2.令系数分别为0,则可得
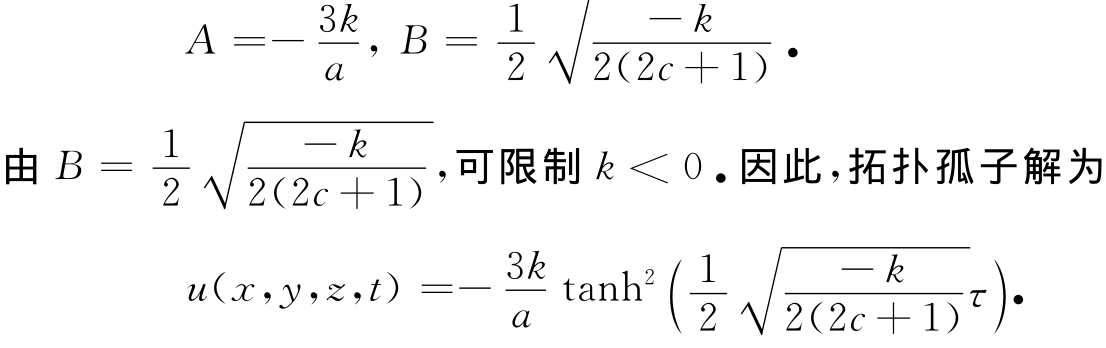
2 分支相图和定性分析
对方程(1)作行波变换
并对ξ积分两次,令积分常数为0,可得
令v′=y,得平面动力系统:

对系统(6)首次积分可得下面的Hamilton函数:
其中h是Hamilton量.设

显然,f(v)有两个零点:v 0和v 1,其中v 0=0,v 1=2k/a.假设(v i,0)(i=0,1)是系统(6)的一个奇点,则系统在奇点(v i,0)的特征值为
利用微分方程定性理论可得下面的结论:
(ⅰ)若f′(v i)>0,则奇点(v i,0)是鞍点.
(ⅱ) 若f′(v i)<0,则奇点(v i,0)是中心.
(ⅲ)若f′(v i)=0,则奇点(v i,0)是退化的鞍点.
由以上结论,借助数学软件MAPLE可得到系统(6)的分支相图(图1~8).
为了研究系统相图中的轨线与方程行波解之间的关系,设
其中h是Hamilton量.接下来考虑系统的轨道和Hamilton量h之间的关系,设
根据图1、2,可以得到下面的定理.
定理1 当a<0,2c+1>0,k>0,则有f′(v 0)>0,f′(v 1)<0,因此(v 0,0)是鞍点,(v 1,0)是中心(图1).
(ⅰ) 当h*<h<0,系统(6)有一个周期轨道L 2和一个特殊轨道L 3.
(ⅱ) 当h>0或者h<h*,系统(6)没有任何轨道.
(ⅲ)当h=0,系统(6)有一个同宿轨道L 1,两个特殊轨道L★1和L*1.
(ⅳ) 当h=h*,系统(6)有一个特殊轨道L 4.
定理2 当a<0,2c+1>0,k<0,则有f′(v 0)<0,f′(v 1)>0,因此(v 0,0)是中心,(v 1,0)是鞍点(图2).
(ⅰ) 当0<h<h*,系统(6)有一个周期轨道L 6和特殊轨道L 7.
(ⅱ) 当h=0,系统(6)有一个特殊轨道L 8.
(ⅲ)当h=h*,系统(6)有一个同宿轨道L 5,两个特殊轨道L★5和L*5.
根据动力系统定性理论[23-24]相关知识,偏微分方程的一个光滑孤立波解对应于一个行波方程的光滑同宿轨,偏微分方程的一个周期波解对应于一个行波方程的光滑周期轨.由以上结论,我们有下面的命题.
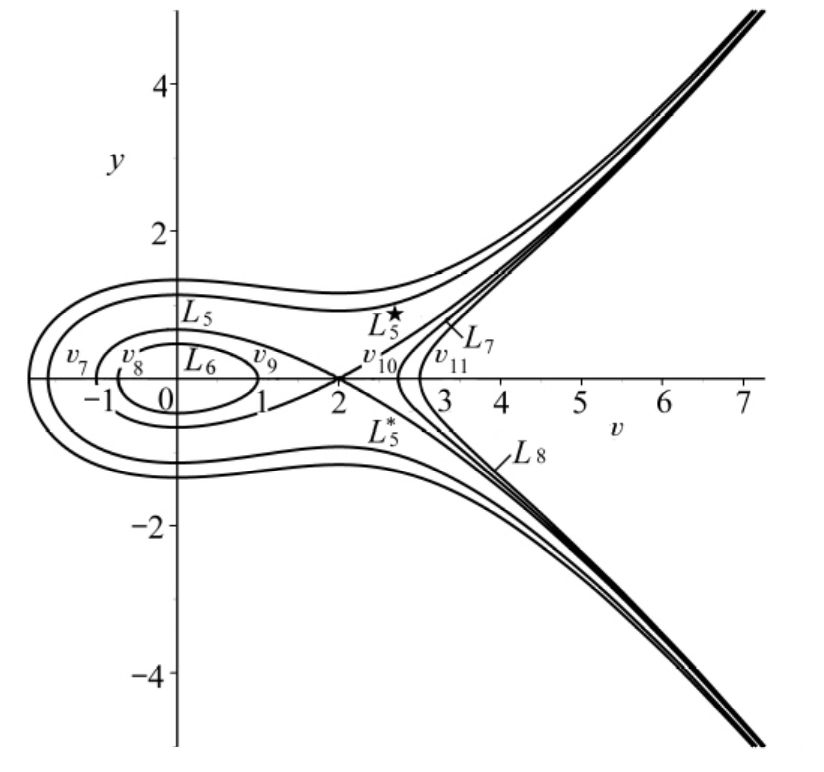
图2 当a<0,2c+1>0,k<0时,系统(6)的相位图
Fig.2 The phase portrait of system(6)f or
a<0,2c+1>0,k<0

图1 当a<0,2c+1>0,k>0时,系统(6)的相位图
Fig.1 The phase portrait of syste m(6)f or case case
a<0,2c+1>0,k>0
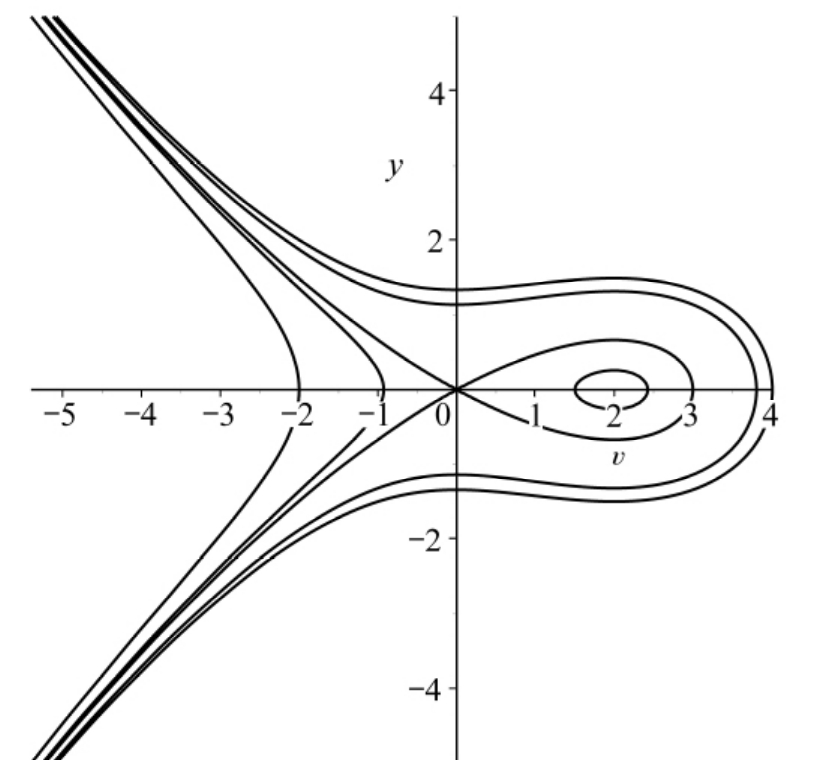
图3 当a>0,2c+1>0,k<0时,系统(6)的相位图
Fig.3 The phase portrait of syste m(6)f or case case
a>0,2c+1>0,k<0
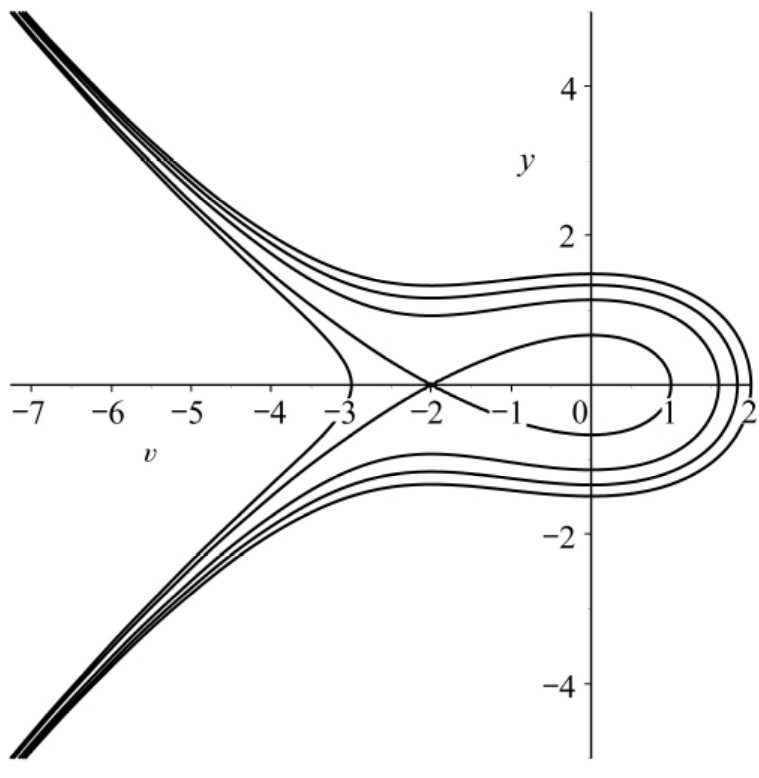
图4 当a>0,2c+1>0,k>0时,系统(6)的相位图
Fig.4 The phase portrait of system(6)f or
a>0,2c+1>0,k>0
定理3 若a<0,2c+1>0,k>0,有(图1):
(ⅰ) 当h=0,方程(1)有一个孤立波解和一个奇异孤立波解.
(ⅱ) 当h*<h<0,方程(1)有一个周期波解和一个奇异波解.
(ⅲ) 当h=h*,方程(1)有一个周期奇异波解.
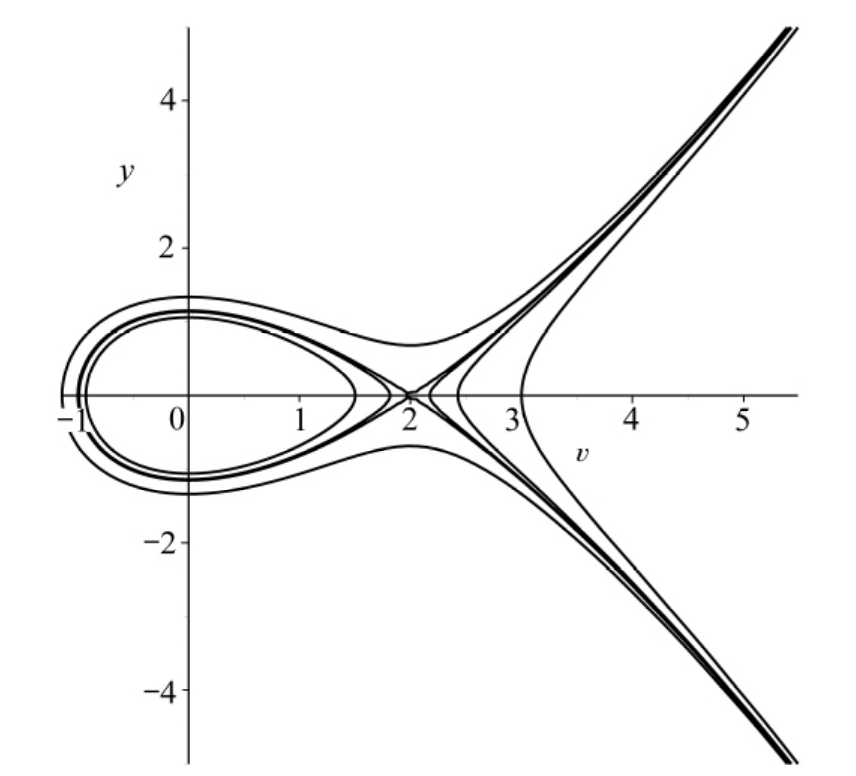
图5 当a>0,2c+1<0,k>0时,系统(6)的相位图
Fig.5 The phase portrait of syste m(6)f or case case
a>0,2c+1<0,k>0
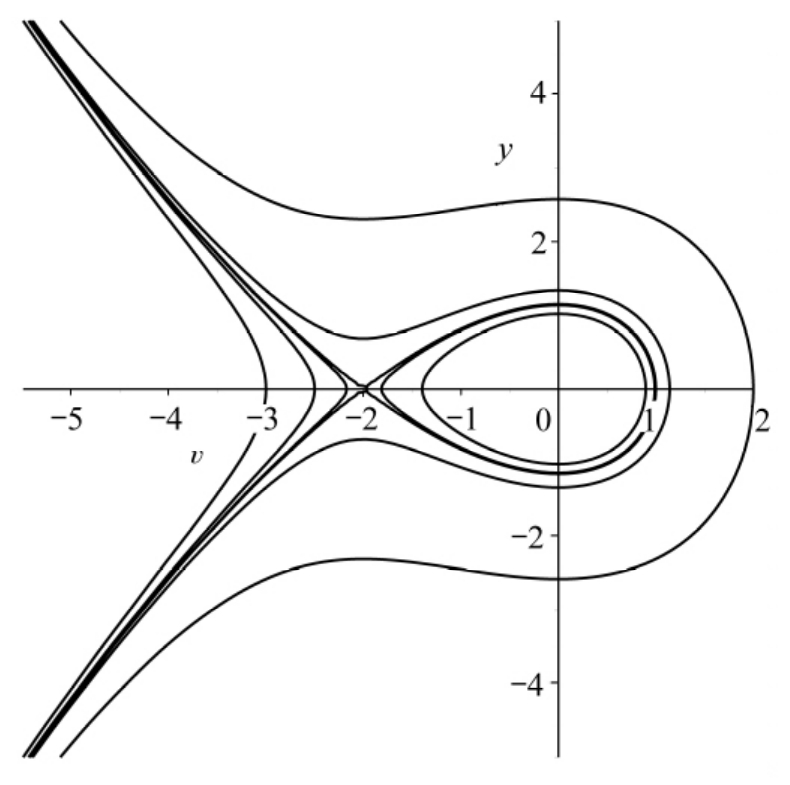
图6 当a<0,2c+1<0,k>0时,系统(6)的相位图
Fig.6 The phase portrait of system(6)f or
a<0,2c+1<0,k>0
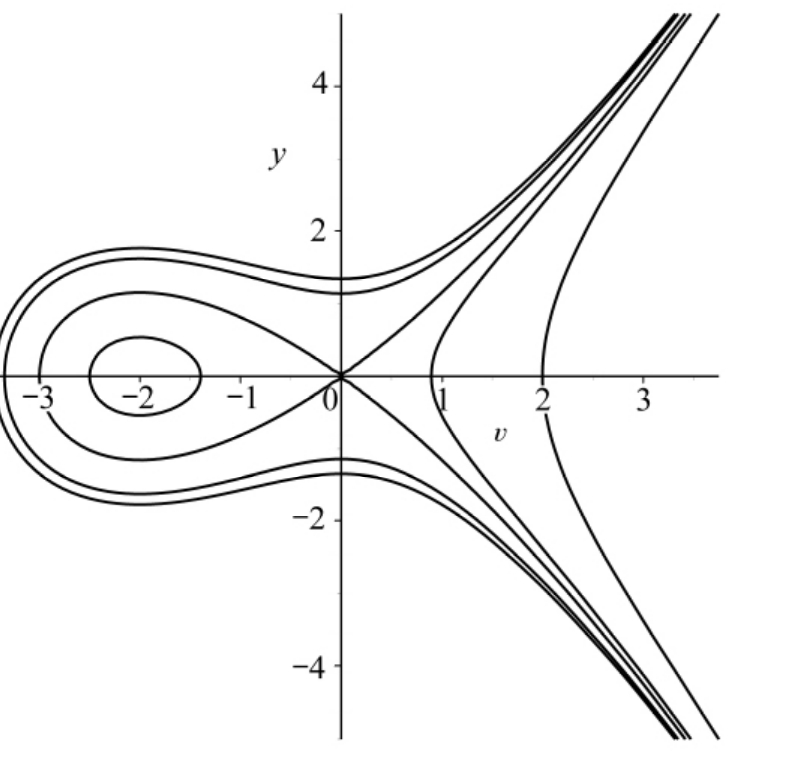
图7 当a>0,2c+1<0,k<0时,系统(6)的相位图
Fig.7 The phase portrait of syste m(6)f or case case
a>0,2c+1<0,k<0

图8 当a<0,2c+1<0,k<0时,系统(6)的相位图
Fig.8 The phase portrait of system(6)f or
a<0,2c+1<0,k<0
定理4 若a<0,2c+1>0,k<0,有(图2):
(ⅰ) 当h=h*,方程(1)有一个孤立波解和一个奇异孤立波解.
(ⅱ) 当0<h<h*,方程(1)有一个周期波解和一个奇异波解.
(ⅲ)当h=0,方程(1)有一个周期奇异波解.
2.1 精确行波解及其联系
首先,我们研究当a<0,2c+1>0,k>0时,方程(1)的显式行波解.
(ⅰ)从分支相图1,可注意到有一条过鞍点(0,0)的同宿轨道L 1,两条特殊轨道L★1和L*1,它们在(v,y)平面的表达式为
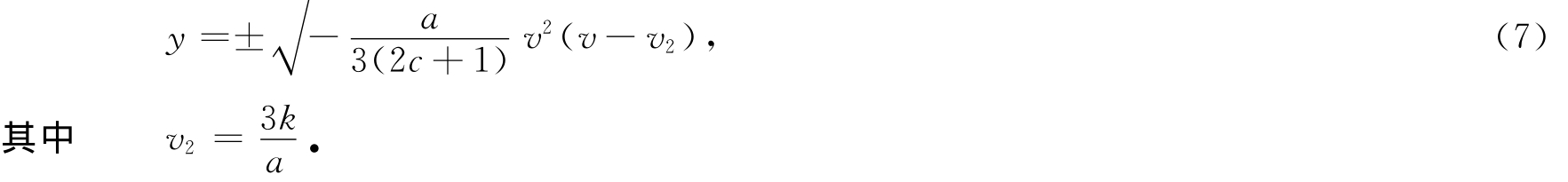
将式(7)代入系统(6)并且沿轨道L 1,L★1和L*1积分可得

完成上面的积分,可得到方程的一个孤立波解和爆破波解:
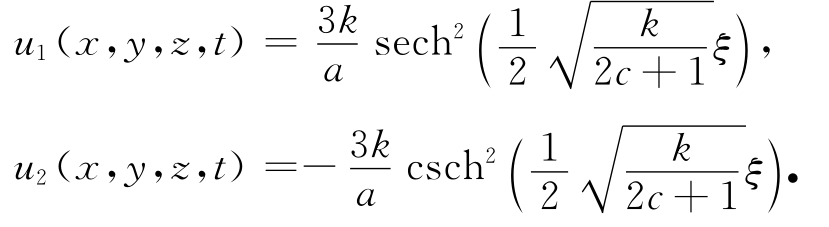
(ⅱ) 从分支相图1,可注意到有一条过点 (v 3,0),(v 4,0)的周期轨道L 2 和过点(v 5,0)的周期轨道L 3.它们在(v,y)平面的表达式为
其中 v 3<v 4<v 5.
将式(8)代入系统(6)并且沿轨道L 2和L 3积分可得
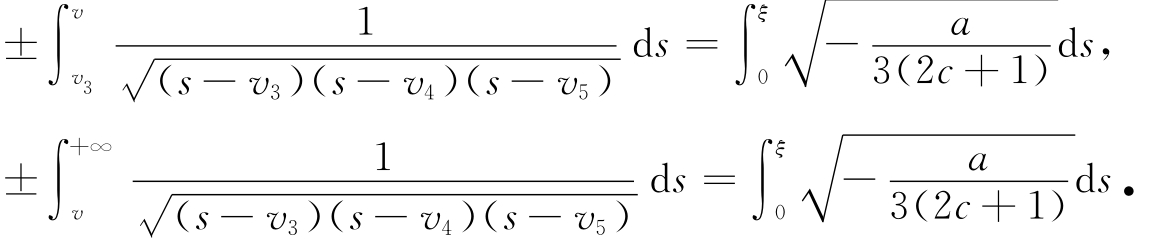
完成上面的积分,可得如下的周期波解和爆破波解:

(ⅲ)从分支相图1,可注意到有一条特殊轨道L 4,它与中心(v 1,0)有相同的Hamilton量.它在(v,y)平面的表达式为

将式(9)代入系统(6)并且沿轨道L 4积分,可得
完成上面的积分,可得如下的周期爆破波解:
其次,我们研究当a<0,2c+1>0,k<0时方程(1)的显式行波解.
(ⅰ)从分支相图2,可注意到有一条过鞍点(v 1,0)的同宿轨道L 5,两条特殊轨道L★5和L*5,它们在(v,y)平面的表达式为
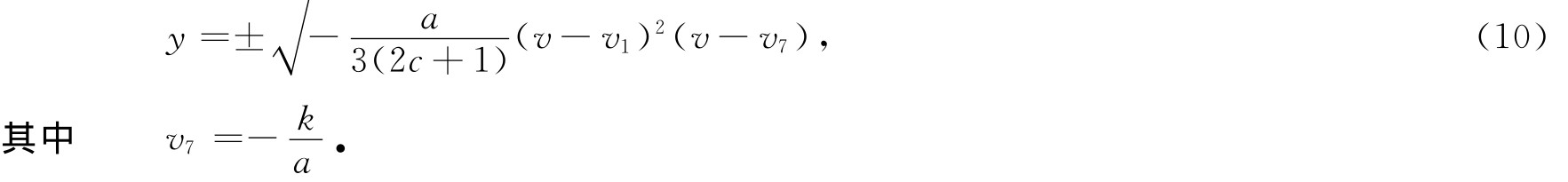
将式(10)代入系统(6)并且沿轨道L 5,L★5和L*5积分可得
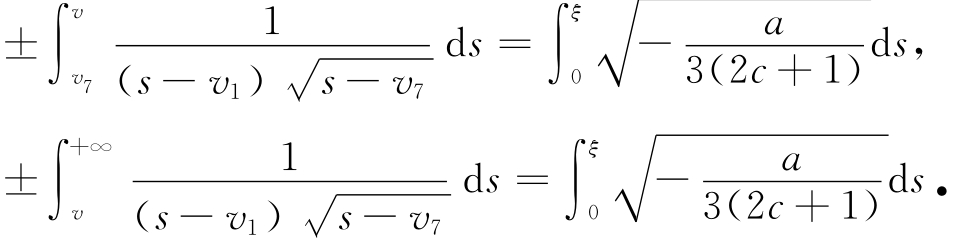
完成上面的积分,可得如下的孤立波解和爆破波解:

(ⅱ) 从分支相图2,可看到过点 (v 8,0),(v 9,0)的轨道L 6 和过点(v 10,0)的特殊轨道L 7 .它们在(v,y)平面的表达式为
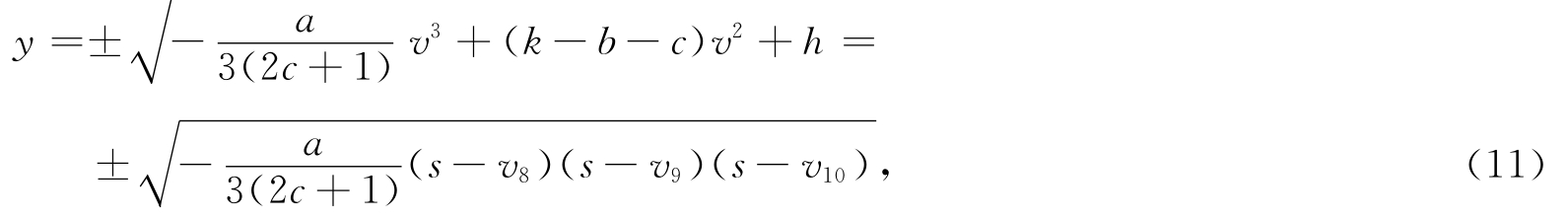
其中 v 8<v 9<v 10.
将式(11)代入系统(6)并且沿轨道L 6和L 7积分可得
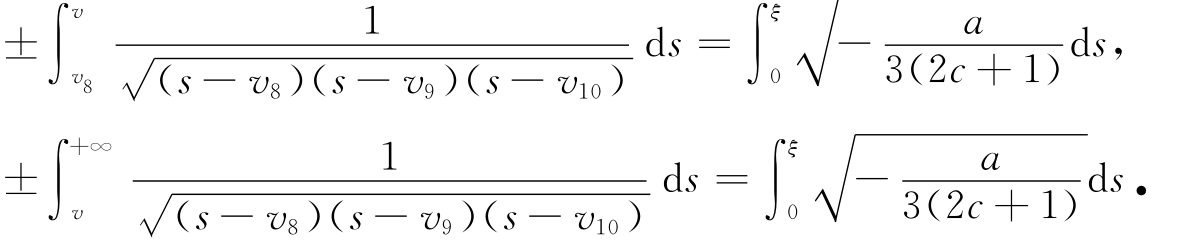
完成上面的积分,可得如下的周期波解和爆破波解:
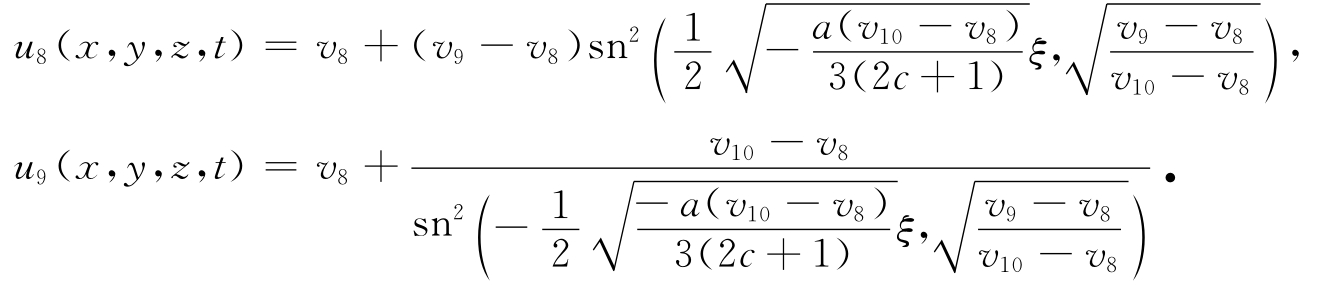
(ⅱ)从分支相图2,可注意到一条特殊轨道L 8,它与中心(0,0)有相同的Ha milton量.它在(v,y)平面的表达式为
将式(12)代入系统(6)并且沿轨道L 8积分可得
完成上面的积分,可得如下的周期爆破波解:
当a>0,2c+1>0,k<0;a>0,2c+1>0,k>0;a>0,2c+1<0,k>0;a<0,2c+1<0,k>0;a>0,2c+1<0,k<0;a<0,2c+1<0,k<0时,结果与上面类似,就不一一详细求解.
最后,研究方程行波解之间的联系.
(ⅰ) 令h→0-,从而有
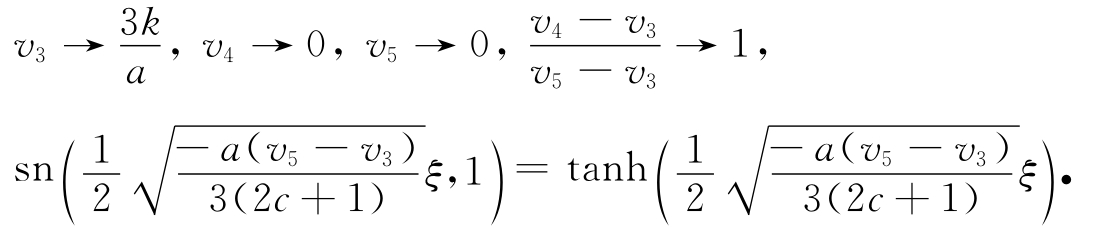
因此,可得v 3(x,t)→v 1(x,t),v 4(x,t)→v 2(x,t).
(ⅰ) 令h→ (h*)+,从而有
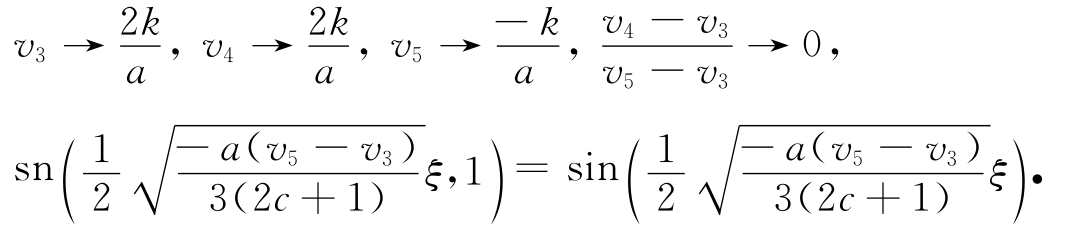
因此,可得v 4(x,t)→v 5(x,t).
(ⅱ) 令h→ (h*)-,从而有
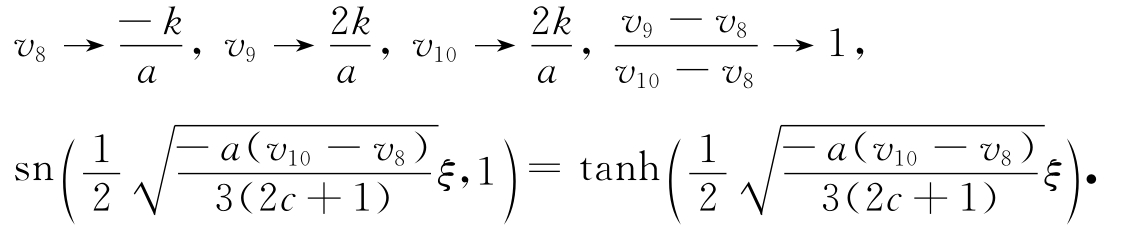
因此,可得v 8(x,t)→v 6(x,t),v 9(x,t)→v 7(x,t).
(ⅲ) 令h→0+,从而有
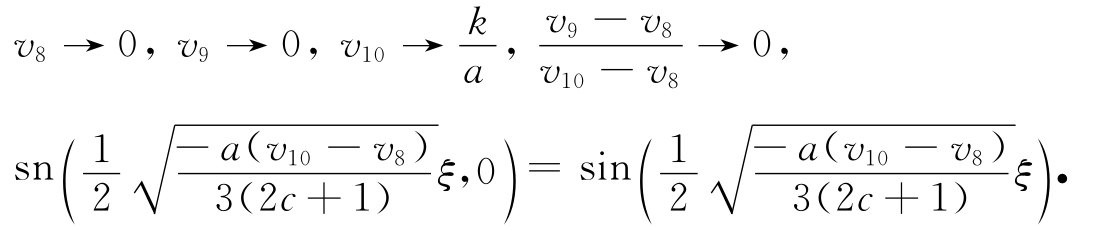
因此,有v 9(x,t)→v 10(x,t).
3 结 论
本文利用拟设方法、微分方程定性理论和动力系统分支方法,研究了(3+1)维时间分数阶Kd V-Zakharov-Kuznetsov方程的相图分支分析及其行波解.首先利用拟设方法得到了方程奇异孤子解、亮孤子解、拓扑孤子解.其次,引入行波变换,将方程转换为平面系统,进而研究了平
面系统的分支分析,得到了系统的相位图.根据分支分析和相位图得到了方程的行波解,获得的行波解有助于描述一些自然现象和发生自然现象的规律.例如,用旋转大气波的孤子解来解释木星的红斑和其他特征、用KdV-Burgers方程的单调激波解和振荡激波解来分析湍流形成的机理和湍流串级散裂过程、等离子体的离子声波、冷等离子体的磁流体波的运动等.
[1] BIN L.The first integral method for some time fractional differential equations[J].Journal of Mathematical Analysis and Applications,2012,395(2):684-693.
[2] BULENT K,MUSTAFA I.The first integral method for the time fractional Kaup-Boussinesq system with time dependent coefficient[J].Applied Mathematics and Computation,2015,254:70-74.
[3] MEHMET G S,FEVZI E.The homotopy analysis method for solving the time-fractional Fornberg-Whitham equation and comparison with Adomian’s decomposition method[J].Applied Mathematical Modelling,2013,37(20/21):8876-8885.
[4] HASSEINE A,BART H J.Adomian decomposition method solution of population balance equations foraggregation,nucleation,growth and breakup processes[J].Applied Mathematical Modelling,2015,39(7):1975-1984.
[5] LORIN E,YANG X,ANTOINE X.Frozen Gaussian approximation based domain decomposition methods for the linear Schrodinger equation beyond the semi-classical regime[J].Journal of Computational Physics,2016,315(2):221-237.
[6] JUN S D,TEMUER C L,RANDOLPH R,et al.The Adomian decomposition method with convergence acceleration techniques for nonlinear fractional differential equations[J].Computers and Mathematics With Applications,2013,66(5):728-736.
[7] TRUSHIT P,RAMAKANTA M.A study on temperature distribution,efficiency and effectiveness of longitudinal porous fins by using Adomian decomposition Sumudu transform method[J].Procedia Engineering,2015,127:751-758.
[8] EMRAH U,AHMET G.Solution of conformable fractional ordinary differential equations via differential transform method[J].Optik,2016,128:264-273.
[9] SEAKWENG V,PIN L.On numerical contour integral method for fractional diffusion equations with variable coefficients[J].Applied Mathematics Letters,2017,64:137-142.
[10] OZKAN G,HASAN A.Soliton solution of fractional-order nonlineardifferential equations based on the exp-function method[J].Optik,2016,127(20):10076-10083.
[11] OZKAN G,ESIN A,AHMET B,et al.Different methods for(3+1)-dimensional space-time fractional modified KdV-Zakharov-Kuznetsov equation[J].Computers and Mathematics With Applications,2016,71:1259-1269.
[12] EMAD A B,ABDEL S,GAMAL F H.Multi-wave solutions of the space-time fractional Burgers and Sharma-Tasso-Olver equations[J].Ain Shams Engineering Journal,2016,7(1):463-472.
[13] MEHMET E,MOHAMMAD M,ABDULLAH S,et al.Dark and singularoptical solitons with Kundu-Eckhaus equation by extended trial equation method and extended G′/G-expansion scheme[J].Optik,2016,127(22):10490-10497.
[14] SAHOO S,SAHA S R.Solitary wave solutions for time fractional third order modified KdV equation using two reliable techniques(G′/G)-expansion method and improved(G′/G)-expansion method[J].Physica A,2016,448:265-282.
[15] SAHOO S,SAHA S R.Improved fractional sub-equation method for(3 + 1)-dimensional generalized fractional KdV-Zakharov-Kuznetsov equations[J].Computers and Mathematics With Applications,2015,70(2):158-166.
[16] MACE R L,HELLBERG M A.The Korteweg-de Vries-Zakharov-Kuznetsov equation for electronacoustic waves[J].Physics of Plasmas,2001,8:2169-2656.
[17] MELIKE K,AHMET B.A novelanalytical method for time-fractional differential equations[J].Optik,2016,127(20):8209-8214.
[18] OZKAN G,ESIN A,AHMET B.Various methods for solving time fractional KdV-Zakharov-Kuznetsov equation[J].AIP Conference Proceedings,2016,1738(1):290013.
[19] JUMARIE G.Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results[J].Computers and Mathematics With Applications,2006,51(9/10):1367-1376.
[20] JUMARIE G.Table of some basic fractional calculus formulae derived from a modified Riemann-Liouvillie derivative for nondifferentiable functions[J].Applied Mathematics Letters,2009,22(3):378-385.
[21] SONG Ming,LIU Zhengrong,ZERRAD E,et al.Singular solitons and bifurcation analysis of quadratic nonlinear Klein-Gordon equation[J].Applied Mathematics &Information Sciences,2013,7(4):1333-1340.
[22] BISWAS A,SONG M,HOURIA T,et al.Solitons,shock waves,conservation laws and bifurcation analysis of Boussinesq equation with power law nonlinearity and dual dispersion[J].Applied Mathematics and Information Sciences,2013,8(3):949-957.
[23] CHOW S N,HALE J K.Method of Bifurcation Theory[M].New York:Springer-Verlag,1982.
[24] GUCKENHEIMER J,HOMES P.Nonlinear Oscillations,Dynamical Systems and Bifurcations of Vector Fields[M].New York:Springer-Verlag,1999.