引 言
奇异摄动问题的研究一直以来是一个热门问题，许多学者在很多领域做了大量的研究工作［1－6］.最近几十年来，学者们把奇摄动理论和方法运用到了分数阶微分方程上.莫嘉琪［7］研究了一类奇摄动非线性分数阶微分方程Cauchy问题，在适当的条件下，利用奇异摄动理论和方法得到解的形式渐近展开式；Shi和Mo［8］又研究了一类奇摄动分数阶微分方程初值问题；林学渊等［9］和莫嘉琪等［10－11］研究了不同分数阶奇异摄动问题，得出了一些结论.所有这些分数阶问题解决了许多常规的导数不能描述和解决的实际问题，例如许多复杂的渗流现象、热传导现象以及神经元和神经网络等，这些问题的研究丰富和发展了奇异摄动理论.同时，带有小参数的时滞奇摄动也是广大学者研究和探讨的问题.Wang等［12］利用一些奇摄动方法研究了具有边界摄动的非线性时滞反应扩散方程奇摄动问题；Mo等［13］讨论了一类具有两参数时滞奇摄动非线性问题的冲击波解，在适当的条件下，利用匹配法和微分不等式理论，构造了原问题的冲击波奇摄动解，并讨论了它的渐近性态；Mo［14］和欧阳成［15］分别研究了一些时滞微分问题及微分差分方程在一定条件下的一致有效渐近解.本文把这两类问题进行了综合，研究了一类分数阶时滞非线性问题，利用奇摄动理论和方法构造了一类分数阶时滞微分方程的渐近解，并用微分不等式理论证明了渐近解的一致有效性.
考虑以下的非线性分数阶奇异摄动时滞问题：
这里ε是个很小的正常数.函数y（x）的α分数阶导数Dαx定义为
其中Γ（·）为Gamma函数，α为小于1的正分数.
首先做如下假设：
（H1）函数f（x，y），A（ε）和B（ε）关于其变量在其变化区域内为足够光滑函数.
（H2）函数f（x，y（x－ε））≤0，且存在正的常数δ，使得f′y（x，y（x－ε））≤－δ＜0.
（H3）退化问题f（x，y）＝0仅有唯一单调解y 0（x）.
1 外部解
将函数y（x－ε）展开成ε的幂级数形式如下：
代入式（1），有
设时滞问题（1）的外部解形如
将式（6）代入式（5），并将右端函数按照ε的各阶次幂进行展开，比较等式两边ε的各阶次幂系数相等，得
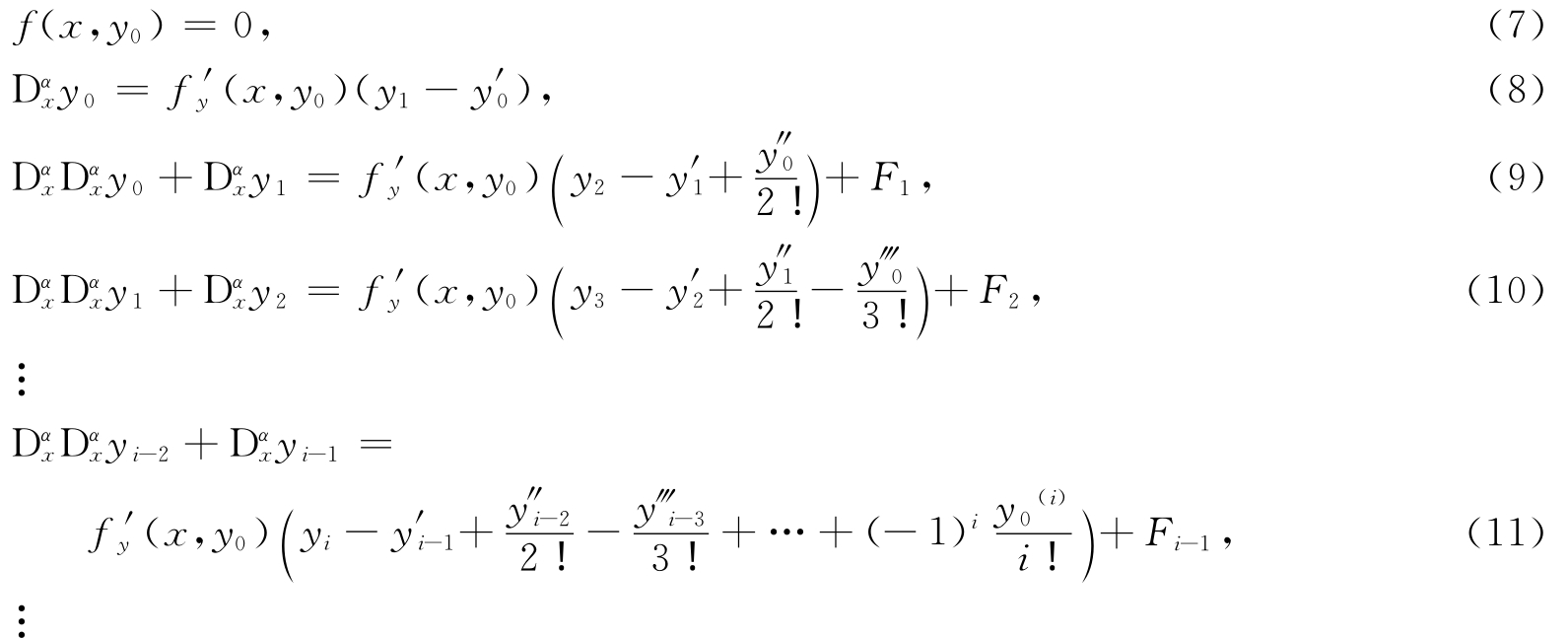
由假设（H3）及以上各式都是代数方程可依次得y i（x），其中
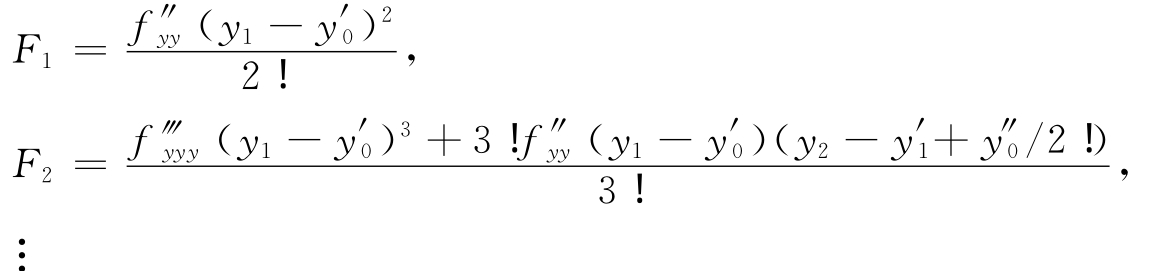
F i的表达式都可依次由前式确定，故其结构省略.将y i（x）代入式（6），便得到了原问题的外部解.显然，由此构造的外部解不一定满足条件（2）、（3），为此需要构造边界层校正项Z和W .
2 构造边界层校正项
首先构造在x＝0附近的边界层校正项Z，为此设分数阶时滞问题（1）～（3）的解为
其中τ＝x／ε为伸长变量，且
将式（13）、（12）和式（6）代入式（5）和式（2）、（3），按照ε的各阶次幂展开式（5）右端的函数及A（ε），B（ε），并比较等式两边ε的各阶次幂系数相等，可得
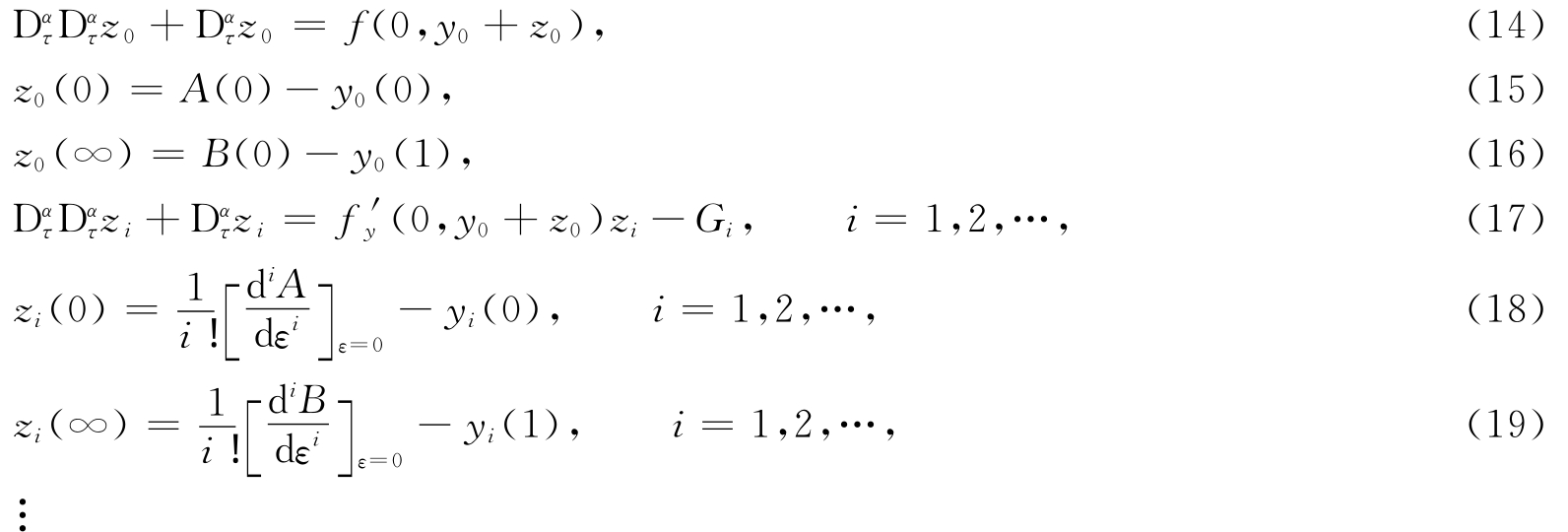
而Gi，i＝1，2，… 是由y 0，y 1，…，y i 和z 0，z 1，…，z i－1 逐次确定的已知函数，其结构从略.
由分数阶微分方程（14），我们能得到以下Volterra积分系统：
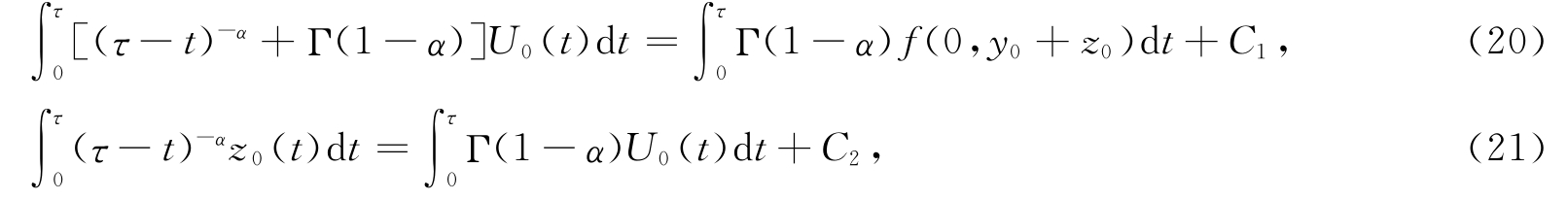
其中C 1，C 2为任意常数，解Volterra积分系统（20）、（21）并结合条件（15）、（16）能够得到z 0（τ）.类似地，可依次求出z 1（τ），z 2（τ），…，将其代入式（13），可得到在x＝0附近的边界层校正项Z（τ，ε）.又由假设（H2）知，函数z i（τ），i＝0，1，… 具有性质［16］：
其中k i＋1 ≤k i，i＝0，1，… 为正常数.
再构造在x＝1附近的边界层校正项W，为此设分数阶时滞问题（1）～（3）的解为
其中η＝ （x－1）／ε为伸长变量，且
将式（24）、（13）、（6）和式（23）代入式（5）和式（2）、（3），按照ε的各阶次幂展开式（5）右端的函数及A（ε），B（ε），并比较等式两边ε的各阶次幂系数相等，得
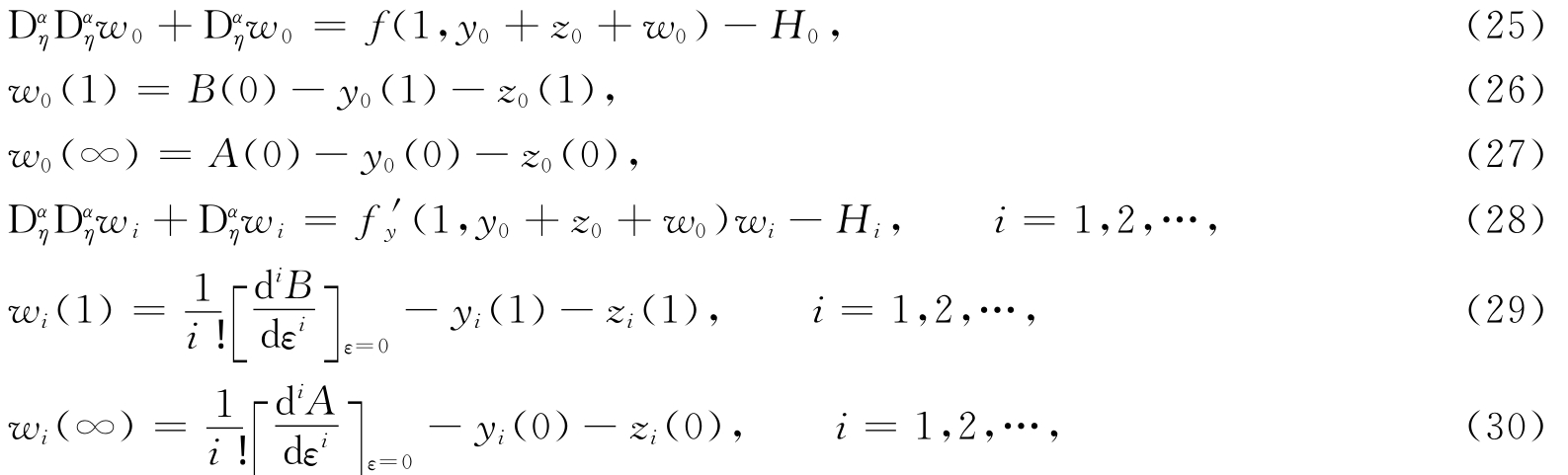
而 H i，i＝0，1，… 是由y 0，y 1，…，y i，z 0，z 1，…，z i 及w 0，w 1，…，wi－1 逐次确定的已知函数，其结构从略.
由分数阶微分方程（25），我们能得到以下Volterra积分系统：
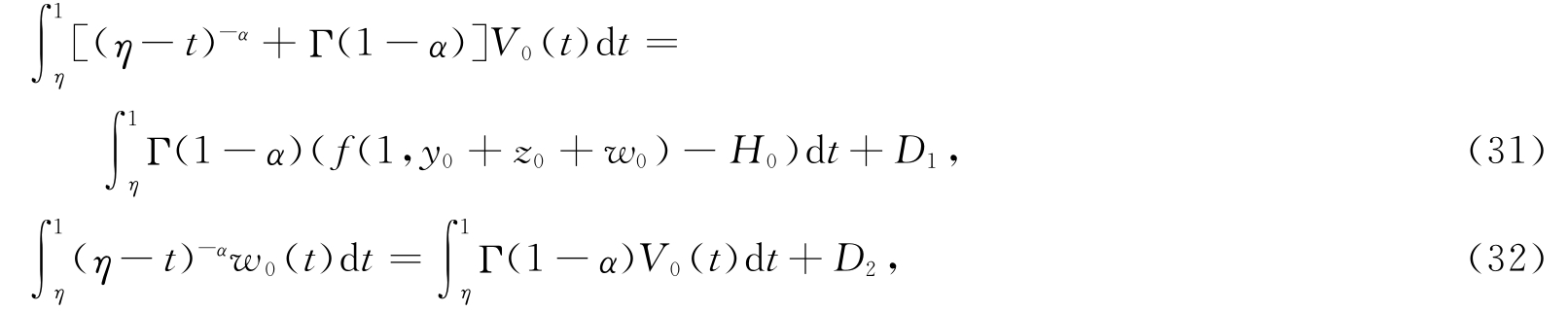
其中D 1，D 2为任意常数，解 Volterra积分系统（31）、（32）并结合条件（26）、（27）能够得到w 0（η）.类似地，可依次求出w 1（η），w 2（η），…，将其代入式（24），可得到在x＝1附近的边界层校正项W（η，ε）.又由假设（H2）知，函数w i（η），i＝0，1，… 具有性质［16］：
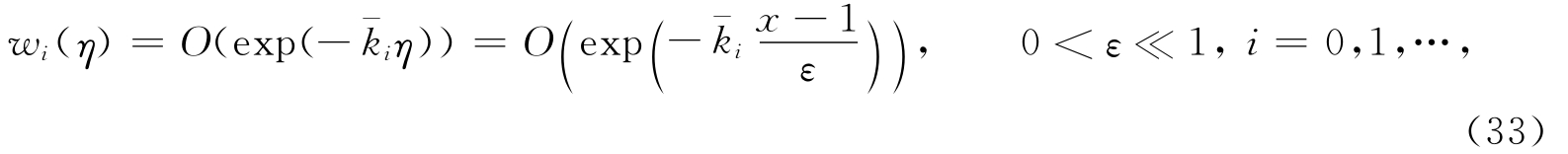
其中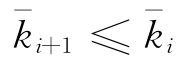
，i＝0，1，… 为正常数.
由式（6）、（13）、（24）和（23）及以上讨论所确定的y i（x），z i（τ）及w i（η），i＝0，1，…，我们得到分数阶非线性时滞奇摄动问题（1）～（3）的形式渐近展开式为
3 渐近展开式的一致有效性
下面证明以上的展开式为关于ε一致有效的展开式.首先给出如下定义.
定义1 设存在两个光滑函数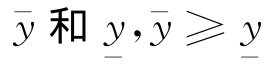
，且分别满足
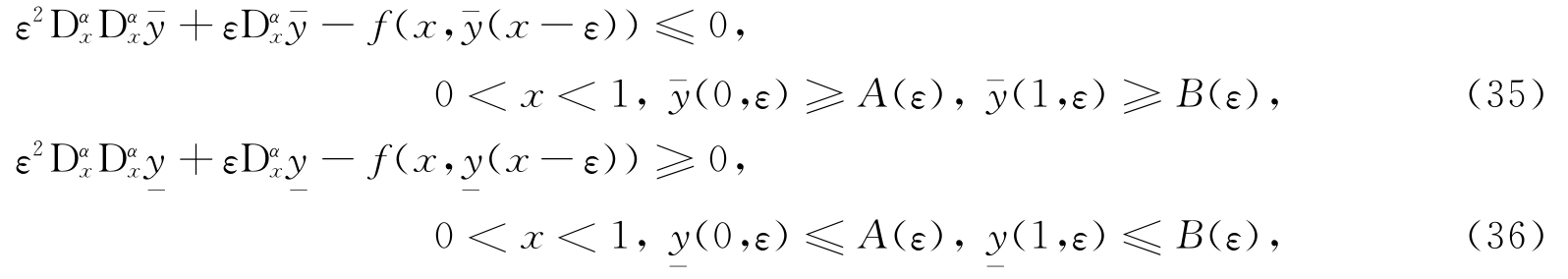
则分别称y－ 和y为问题（1）～（3）的上解和下解.
定理1 在假设（H1）～（H3）的条件下，y－（x，ε）和y（x，ε）分别为分数阶奇摄动边值问题
的上解和下解，则问题（1）～（3）存在一个解y（x，ε），且有关系式：
证明 利用数学归纳法证明定理，先按以下迭代关系式构造函数序列：
分别以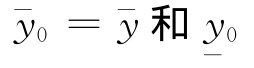
＝y为式（37）、（38）的初始迭代函数，可分别依次构造
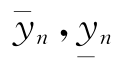，n＝0，1，…-.于是可得到两个函数列 
，现讨论它们的收敛性态.
设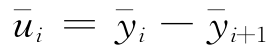
，i＝0，1，… .因此，当i＝0时，
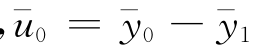，由假设（H2），则有
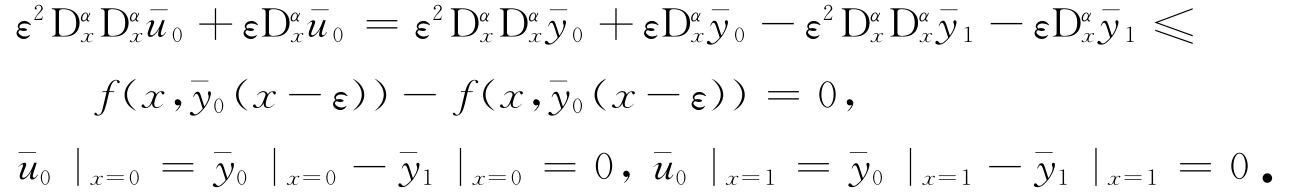
于是由极值原理［17］得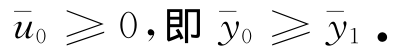
于是由极值原理得
.因此，由数学归纳法知
同样的方法，类似可得
以及
通过以上讨论结合Arzela-Ascoli定理，分数阶时滞奇摄动边值问题（1）～（3）有一个解y（x，ε），使得
定理1证毕.
定理2 在假设（H1）～（H3）下，分数阶时滞奇摄动边值问题（1）～（3）有一个解y（x，ε），且具有如下关于ε的一致有效的渐近展开式：
证明 首先构造两个辅助函数α（x，ε），β（x，ε），定义如下：
其中r为适当大的正常数，将在随后的证明中给出.显然
且对于足够小的ε，存在一个正常数δ1，使得
故选取r＞δ1，就可得到
同理，类似可得
下面证明
仅证明式（45），类似的方法证明式（46）.事实上，由假设和式（22）、（33），存在一个正常数δ2，使得
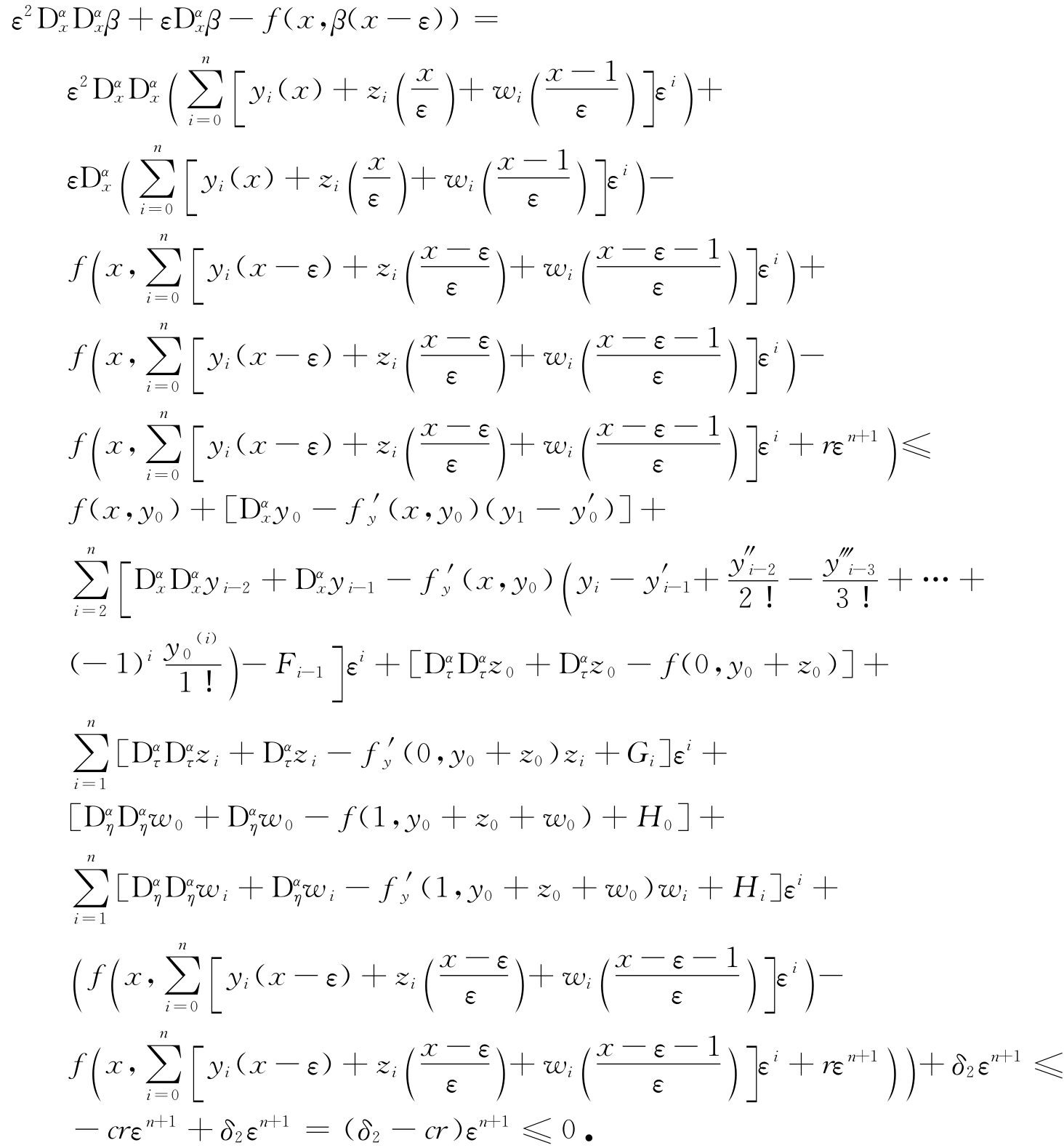
上式成立只需要选择足够的r＞δ2／c即可，所以式（45）成立，同理可证式（46）成立.故函数β（x，ε）和α（x，ε）分别为问题（1）～（3）的上解和下解.由定理1知，分数阶非线性时滞奇摄动边值问题（1）～（3）有一个解y（x，ε），且满足关系式：
α（x，ε）≤y（x，ε）≤β（x，ε）.
再由式（40）、（41）得式（39）成立，定理2证毕.
4 结 论
对分数阶时滞奇摄动边值问题（1）～（3），在假设（H1）～（H3）下，构造了问题的外部解和边界层解，得出了如下的一致有效的形式渐近解：
本文讨论的分数阶时滞奇摄动问题，其时滞变量和小参数都是同一个ε.笔者可以继续推广，研究时滞变量和小参数不同时的问题，也即双参数的分数阶时滞奇摄动问题，这将是笔者今后努力研究的方向.
［1］ NAYFEH A H.Introduction to Perturbation Techniques［M］.New York：John Wiley ＆Sons Inc，1981.
［2］ DE JAGER E M，FURU J F.The Theory of Singular Perturbation［M］.Amsterdam：North-Holland Publishing Co，1996.
［3］ BOHA.The shock solution fora class of sensitive boundary value problems［J］.Jour nal of Mathe matical Analysis and Applications，1999，235（1）：295-314.
［4］ 倪明康，林武忠.边界层函数法在微分不等式中的应用［J］.华东师范大学学报（自然科学版），2007（3）：1-10.（NI Mingkang，LIN Wuzhong.Application of boundary layer function method in differential inequality［J］.Jour nal of East China Nor mal University（Natural Science），2007（3）：1-10.（in Chinese））
［5］ 葛志新，陈咸奖，陈松林.一类含有分数阶导数的二自由度耦合系统［J］.应用数学和力学，2017，38（11）：1300-1308.（GE Zhixin，CHEN Xianjiang，CHEN Songlin.A class of 2-DOF coupled systems with fractional-orderderderivatives［J］.Applied Mathematics and Mechanics，2017，38（11）：1300-1308.（in Chinese））
［6］ 冯依虎，陈怀军，莫嘉琪.一类非线性奇异摄动自治微分系统的渐近解［J］.应用数学和力学，2018，39（3）：355-363.（FENG Yihu，CHEN Huaijun，MO Jiaqi.Asy mptotic solution to a class of nonlinear singular perturbation autonomous differ ential systems［J］.Applied Mathe matics and Mechanics，2018，39（3）：355-363.（in Chinese））
［7］ 莫嘉琪.非线性分数阶微分方程的奇摄动［J］.应用数学学报，2006，29（6）：1085-1089.（MO Jiaqi.Singularly perturbed problems for nonlinear fractional differential equation［J］.Act a Mathe maticae Applicat ae Sinica，2006，29（6）：1085-1089.（in Chinese））
［8］ SHI J R，MO J Q.Asy mptotic solution fora class of singularly perturbed initial value problem of fractional differential equation［J］.Act a Scientiar u m Naturaliu m Universit atis Nankaiensis，2015，48（5）：60-64.
［9］ 林学渊，谢峰.一类非线性分数阶微分方程的奇异摄动［J］.东华大学学报（自然科学版），2009，35（2）：238-240.（LIN Xueyuan，XIE Feng.Singular perturbation fora kind of nonlinear fractional differential equations［J］.Jour nal of Donghua Universit y（Natural Science），2009，35（2）：238-240.（in Chinese））
［10］ 莫嘉琪，温朝晖.一类非线性奇摄动分数阶微分方程的渐近解［J］.系统科学与数学，2010，30（12）：1689-1694.（MO Jiaqi，WEN Zhaohui.Asy mptotic solution fora class of nonlinear singularly perturbed for fractional differential equation［J］.Jour nal of Systems Science and Mathematical Sciences，2010，30（12）：1689-1694.（in Chinese））
［11］ FENG Y H，MO J Q.Asy mptopic solution for singularly perturbed fractional orderdifferential equation［J］.Jour nal of Mathe matic，2016，36（2）：239-245.
［12］ WANG W K，SHI L F，HAN X L，et al.Singular perturbation problem for reaction diff usion time delay equation with boundary perturbation［J］.Chinese Jour nal of Engineering Mathe matics，2015，32（2）：291-297.
［13］ MO J Q，WANG W G，CHEN X G，et al.The shock wave solutions for singularly perturbed time delay nonlinearboundary value problems with t wo parameters［J］.Mathe matica Applicat a，2014，27（3）：470-475.
［14］ MO J Q.The shock solutions fora class of singularly perturbed time delay boundary value problems［J］.Jour nal of Anhui Nor mal Univer sity（Natural Science），2013，36（4）：314-318.
［15］ 欧阳成.具有小延迟的微分－差分方程渐近解［J］.吉林大学学报（理学版），2008，46（4）：628-932.（OUYANG Cheng.Asy mptotic solution of initial value problems fordifferential-difference equation with small time delay［J］.Jour nal of Jilin University（Science Edition），2008，46（4）：628-632.（in Chinese））
［16］ DELBOSCO D，RODINO L.Existence and uniqueness for nonlinear fractional differential equation［J］.Jour nal of Mathe matical Analysis and Applications，1996，204：609-625.
［17］ 莫嘉琪.一类两参数半线性奇摄动问题解的渐近性态［J］.应用数学学报，2009，32（5）：903-908.（MO Jiaqi.The Asy mptotic behaviorof solution fora class of semilinear singular perturbed problem with t wo parameters［J］.Act a Mathe maticae Applicat ae Sinica，2009，32（5）：903-908.（in Chinese））