引 言
多目标优化问题就是向量极值问题,即在一定条件下极大化或极小化向量值函数.对于此类问题,如何定义最优解的概念是一个首要问题.在多目标优化问题中,向量空间没有全序关系,只有偏序关系,因此向量优化最优解与数值优化最优解有本质区别.1896年,Pareto首先提出多目标优化问题.1951年,Koop mans[1]在生产和分配的活动中也提出了多目标最优化问题,他第一次提出Pareto有效解的概念.由于有效解的范围较大,在某些向量优化问题中不利于研究其性质,所以在有效解的基础上产生了真有效解.1951年,Kuhn和Tucker[2]提出了Kuhn-Tucker真有效解的概念;1968年,Geoffrion[3]在Kuhn-Tucker真有效解的基础上给出了Geoffrion真有效解的概念;1977年,Bor wein[4]利用切锥定义了Bor wein真有效解;1979年,Benson[5]利用投影锥给出了Benson真有效解的概念;1982年,Henig[6]利用闭凸锥引进了Henig真有效解的概念.在这些解的概念的基础上,学者们开始研究它们的相关课题,如真有效解间的关系、解的等价性、最优性条件以及对偶理论.
最初研究的多目标优化问题基本是确定性的优化问题,但是,在实际问题中存在很多不确定的影响因素,这一现象引起了学者们的极大关注.鲁棒优化[7]是在内部结构和外部环境可能都不确定的情况下提出的一种新的优化方法,它的目的是求得一个解,对于可能出现的所有情况,约束条件均满足,并且使最坏情况下目标函数的函数值最优.鲁棒优化已成为解决不确定性问题的可行工具,许多学者在多目标优化问题鲁棒解的概念及性质的研究中取得了一些显著成果[8-11].2013年,Geor giev等[12]提出线性多目标优化问题的鲁棒有效解的概念,并得到了鲁棒有效解的充要条件;2015年,Za mani等[13]证明了在约束集为紧性条件下,目标函数为凸函数时鲁棒有效解的充要条件;2018年,Morteza等[14]研究了在一般锥序的情况下,加上紧性条件,每个范数鲁棒有效解都是Henig真有效解.
本文在一定条件下,研究多目标优化问题鲁棒有效解与真有效解的关系和鲁棒有效解的最优性条件,并给出具体例子加以说明.在第1节,给出了一些基本概念和结论.在第2节,首先研究了鲁棒有效解与真有效解的关系,然后研究了鲁棒有效解的最优性条件.在第3节,对本文内容进行了总结.
1 预备知识
设Rn是n维Euclid空间,Rn+是它的非负象限.对Rn中的非空子集Ω,intΩ,clΩ,coneΩ分别表示Ω的拓扑内部、拓扑闭包和锥包.
Ω的正极锥和严格正极锥分别为
对任意x-∈clΩ,Ω在x-的切锥和法锥分别定义为

特别地,当Ω是凸集时,法锥的等价定义为
N(Ω,x-){=x*∈Rn:〈x*,x-x-〉≤0,x∈}Ω.
对任意的x,y∈Rn,引进如下序关系:

考虑如下多目标优化问题:
其中,ΩRn为非空子集,f:Ω→Rp,且f的每一个分量f i,i∈P= {1,2,…,p}是局部Lipschitz函数.
定义1[15] 设x- ∈Ω:
(ⅰ) 若不存在x∈Ω,使得f(x)≤f(x-),则称x- 是(MOP)的有效解.
(ⅱ)若不存在x∈Ω,使得f(x)<f(x-),则称x- 是(MOP)的弱有效解.
(ⅲ)若T(f(Ω)+R p+,f(x-))∩(-R p+)= {0},则称x- 为(MOP)的Bor wein真有效解.
(ⅳ)若cl cone(f(Ω)-f(x-)+Rp+)∩(-Rp+)={0},则称x- 为(MOP)的Benson真有效解.
(ⅴ)若x-是(MOP)的有效解,且存在M>0,使得对任意的i∈P和x∈Ω满足f i(x)<f i(x-),总存在满足f j(x)>f j(x-)的j∈P 使得 (f i(x-)-f i(x))/(f j(x)-f j(x-))≤ M,则称x-为(MOP)的Geoffrion-真有效解,简称为G-真有效解.
2015年,Za mani等在文献[13]中给出了如下形式的鲁棒有效解:令ε>0,记集合C(ε)=![]() ∈N{=1,2,…,}n.
∈N{=1,2,…,}n.
定义2[13] 设x- ∈Ω 是(MOP)的有效解.若存在ε>0,对任意的C∈C(ε),x- 为如下问题的有效解:
则称x-为(MOP)的鲁棒有效解.
定义3[16] 设Ω为凸集,f:Ω→R.若对任意x 1,x 2∈Ω,λ∈ (0,1)有f(λx 1+(1-λ)x 2)<λf(x 1)+(1-λ)f(x 2),则称f为Ω 上的严格凸函数.
定义4[16] 设f:Rn→R在点x-∈Rn是局部Lipschitz函数,f在点x-处沿方向v∈Rn的广义方向导数定义为
f在点x-处的Clar ke次微分定义为
定义5[13] f在x-处的下降方向的集合定义为
文献[13]中,在一定条件下研究了鲁棒有效解和G-真有效解的关系,利用切锥和次微分给出了鲁棒有效解的必要条件.
引理1[13] 设Ω 是紧集.若x- 是(MOP)的鲁棒有效解,则x- 是(MOP)的G-真有效解.
引理2[13] 若x- 是(MOP)的鲁棒有效解,则T(Ω,x-)∩G(x-)= {0}.
定义6[17] 称f在Ω上是次类凸的,如果存在ρ∈-int R p+使得对任意的x,y∈Ω,λ∈(0,1)和ε>0,存在z∈Ω满足
或等价定义为f(Ω)+int Rp+ 是凸集.
注1 根据文献[15],Benson真有效解与G-真有效解等价.由文献[17]可知,当f为次类凸时,Bor wein真有效解与Benson真有效解等价.文献[18]中表明,次类凸不能减弱为次似凸或邻近次似凸,即cone(f(Ω))+int Rp+ 凸或cl cone(f(Ω)+Rp+)凸.
定义7[19] 设ψ:Ω→R,如果对任意x∈Ω,ξ∈ψ(x-),总存在w∈Ω使得
〈ξ,w〉≥0ψ(x)≥ψ(x-),
则称ψ在点x-处是伪凸函数.
2 鲁棒有效解的最优性条件研究
本节将研究鲁棒有效解和真有效解的关系,给出鲁棒有效解的必要条件和充分条件.
2.1 鲁棒有效解与真有效解的关系
首先,给出鲁棒弱有效解的定义,研究鲁棒弱有效解、鲁棒有效解与真有效解的关系.
定义8 如果存在ε>0,对任意C∈C(ε),x-为如下问题的弱有效解:
则称x-∈Ω是(MOP)的鲁棒弱有效解.
由定义可知,鲁棒有效解必定是鲁棒弱有效解,但反之需要一些条件才能成立.
定理1 设Ω为凸集,x-∈Ω,f(x)在Ω上是严格凸函数.若x-是(MOP)的鲁棒弱有效解,则x-是(MOP)的鲁棒有效解.
证明 假设x-不是(MOP)的鲁棒有效解,则对任意的ε>0,存在C∈C(ε),x∈Ω{\x}-使得
由于f(x)为Ω上的严格凸函数,故f(x)+Cx也为Ω上的严格凸函数,从而对任意的λ∈(0,1)有
结合式(1)有
f(λx+ (1-λ)x-)+C(λx+ (1-λ)x-)<f(x-)+Cx-,
这与x-是鲁棒弱有效解矛盾,故x-是鲁棒有效解.
注2 定理1中f(x)在Ω上是严格凸函数这一条件是否可减弱为一般凸函数还值得进一步研究.下面的例子可以说明即使不满足这个条件,定理1的结果也可能成立.
例1 在(MOP)中,令p=2,Ω=R,且f:Ω→R 2定义为
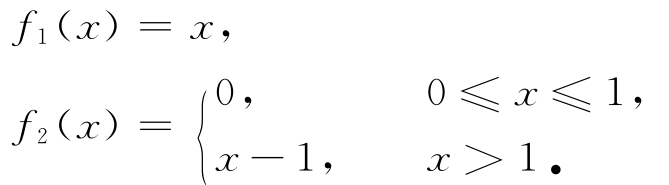
令x-=0,则存在ε=1/2使得x-既是鲁棒弱有效解,也是鲁棒有效解.
引理1在紧性的条件下给出鲁棒有效解与G-真有效解的关系,并举例说明紧性的条件必不可少.在没有任何条件时,鲁棒弱有效解蕴含着Bor wein真有效解.
定理2 若x-是(MOP)的鲁棒弱有效解,则x-为(MOP)的Bor wein真有效解.
证明 假设x- 不是(MOP)的Bor wein真有效解,则存在0≠d∈T(f(Ω)+R p+,f(x-))∩(-R p+).不妨设d 1 <0,d i ≤0,i=2,3,…,p.由切锥的定义知,存在t k↓0,d k →d使得
从而存在x k∈Ω{\x}-,p k∈R p+使得f(x-)+t k d k=f(x k)+p k,即
下证对任意的ε>0,存在矩阵C∈C(ε)和x k∈Ω{\x}-使得f(x k)+Cx k<f(x-)+Cx-,即x-不是鲁棒弱有效解.令C j(j∈P)为矩阵C的行向量.
当j=1,k充分大时,(d k)1 <0,f 1(x-)+(t k d k)1 =f 1(x k)+(p k)1,故
取C1 =0,则f 1(x-)-f 1(x k)>C 1(x k-x-),即
当j≠1时,(d k)j分两种情况.
考虑第一种情况:(d k)j <0,故 (p k)j- (t k d k)j >0.取C j =0,有f j(x-)-f j(x k)>C j(x k -x-),故
考虑第二种情况:(d k)j≥0,对任意ε>0,由t k↓0,d k→d知,当k充分大时,有-ε<-
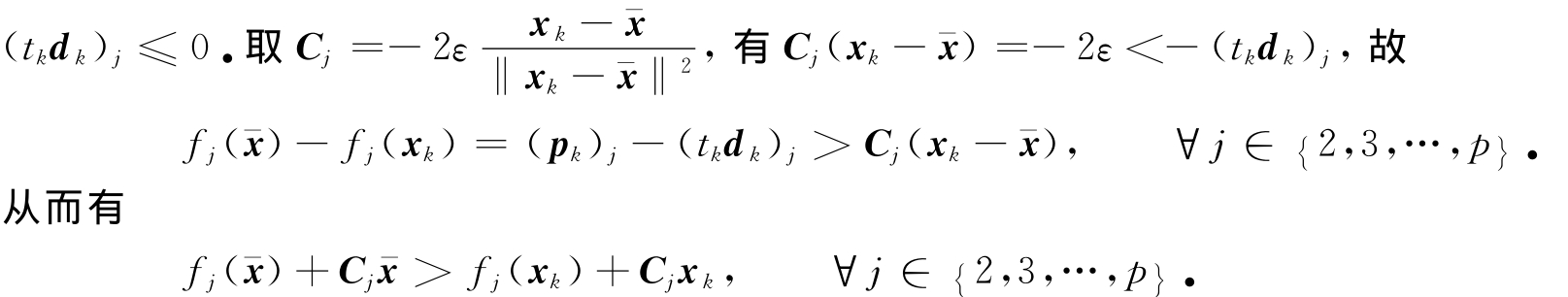
综上所述,有f(x-)+Cx- >f(x k)+Cx k .这与x- 是鲁棒弱有效解矛盾,所以x- 是(MOP)的Borwein真有效解.
下面通过例子来说明定理2的合理性.
例2 在(MOP)中,令p=2,Ω=R,且f:Ω→R 2定义为
容易验证x-=1是鲁棒有效解(考虑ε=1/10),且由图1可知,x-=1是Bor wein真有效
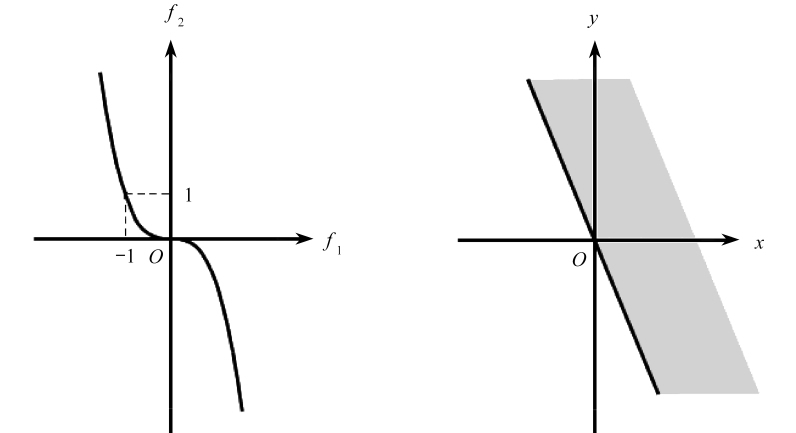
图1 f(Ω)与T(f(Ω)+R2+,f(1))
Fig.1 f(Ω)and T(f(Ω)+R 2+,f(1))
解. 定理2只是充分条件,而并非必要条件,见例3.
例3 在(MOP)中,令p=2,Ω=R,且f:Ω→R 2定义为

考虑x- =1,由图2可知,x- 是Bor wein真有效解.对任意的ε>0,令C= (c 1,c 2)T=(ε/4,ε/2)T,x- 不是如下问题的有效解:
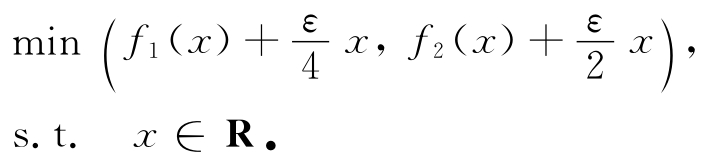
事实上,对任意的ε>0,取xε=-1/ε,有
即存在xε ∈R使得f(xε)+C xε<f(x-)+C x-,故x- =1不是鲁棒弱有效解.
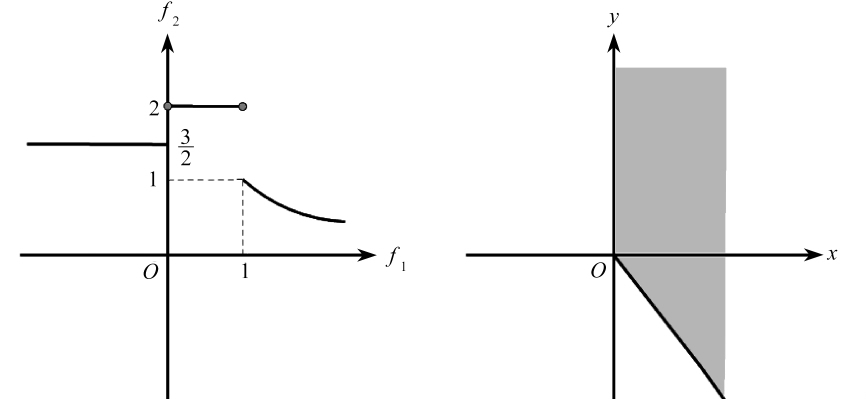
图2 f(Ω)与T(f(Ω)+R 2+,f(1))
Fig.2 f(Ω)and T(f(Ω)+R 2+,f(1))
由注1中Bor wein真有效解与Benson真有效解的等价性,还可以得到如下结果.
推论1 设f在Ω 上是次类凸函数.若x-是(MOP)的鲁棒弱有效解,则x-是(MOP)的Benson真有效解或G-真有效解.
文献[13]中例3.1表明,在非紧性的条件下鲁棒有效解不能推出G-真有效解.实际上是因为该例子中f不是次类凸的.当f是次类凸时,即使没有紧性,也可以得到G-真有效解,下面的例子可以说明这个问题.
例4 在(MOP)中,令p=2,Ω=R,且f:Ω→R 2定义为
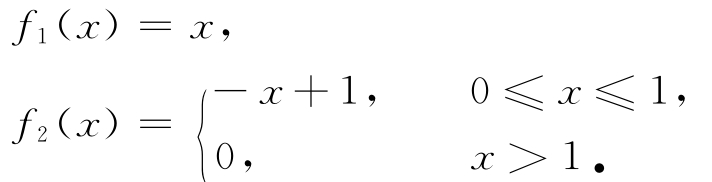
容易验证x-=0是(MOP)的有效解,而且x-还是鲁棒有效解(考虑ε=1/2),故由定理2知,x-是(MOP)的Bor wein真有效解.又由于f是次类凸的,所以由推论1知,x-是(MOP)的Benson真有效解,故x-是(MOP)的G-真有效解.
鲁棒有效解与真有效解的关系如下所示:
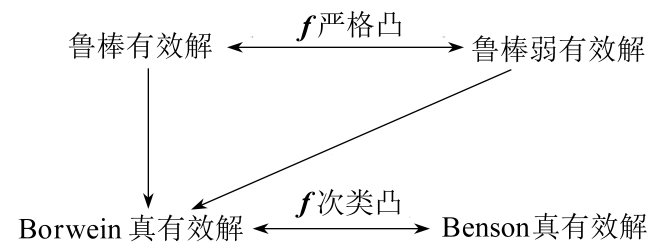
注3 2018年,Morteza等将自然锥序Rp+推广到一般锥序K,研究了当Ω为紧集时,锥序K下的鲁棒有效解能推出锥序K下的Henig真有效解(见文献[14]中定理4.2).可以类似证明,在去掉紧性的条件下,不一定能得到Henig真有效解,但是能得到局部Henig真有效解.
推论2 若x-是(MOP)的鲁棒有效解,则x-是(MOP)的局部Henig真有效解.
2.2 鲁棒有效解的最优性条件
最优性条件是最优化问题的最优解所必须满足的条件.本节研究了在次类凸性假设下鲁棒弱有效解的必要性条件,在伪凸性假设下鲁棒有效解的充要条件.
引理3[4] 设N,KRn是两个闭凸锥,且满足N∩K{=}0,则(-N+)∩(K s+)≠.
定理3 设Ω为凸集,x-∈Ω,f i(i∈P)是次类凸函数.若x-是鲁棒弱有效解,则存在λ=(λ1,λ2,…,λp)T >0使得0∈ ∑pi=1λif i(x-)+N(Ω,x-).
证明 因为x-是鲁棒弱有效解,由定理2和注1知,x-是Benson真有效解,即
由引理3知,
从而存在λ>0使得λT(f(Ω)-f(x-)+R p+)≥0,这表明x- 是min x∈ΩλT f(x)的最优解,故存在λ>0使得
定理4 令Ω 是凸集,x-∈Ω,f是伪凸函数,则x- 是鲁棒有效解当且仅当T(Ω,x-)∩G(x-)={0}.
证明 必要性由引理2知显然成立.
下面证明充分性.首先证明x-是有效解.假设x-不是有效解,则存在x 0∈Ω使得f(x 0)-f(x-)∈-Rp+\{0}.因为Ω是凸集,故x 0-x- ∈T(Ω,x-).由于f是伪凸函数,则对任意的μ*∈Rp+\{0},μ*f是伪凸函数,这表明
这说明x-x- ∈G(x-),故0≠x-x- ∈T(Ω,x-)∩G(x-),这与假设矛盾,故x- 是有效解.余下证明与文献[14]中定理5.1?的证明类似.
下面通过例子说明定理4的合理性.
例5 在(MOP)中,令p=2,Ω=R,且f:Ω→R 2定义为
考虑x-=-1,容易验证存在ε=1/10使得x-是鲁棒有效解,并且有
T(Ω,x-)∩G(x-)= {0}.
3 结 论
本文主要研究了多目标优化问题鲁棒有效解与真有效解之间的关系,并给出鲁棒有效解的最优性条件,推广了文献[13]中的定理3.1和文献[14]中的定理4.2、定理5.1,得出如下结论:
1)在f是严格凸函数的条件下,给出鲁棒有效解与鲁棒弱有效解的等价性.
2)在没有任何条件下,给出鲁棒弱有效解与Bor wein真有效解的关系.从而得出:当f为次类凸函数时,鲁棒弱有效解意味着Benson真有效解或G-真有效解.
3)在f是次类凸函数时,利用线性标量化方法给出鲁棒弱有效解的必要条件.同时,在f是伪凸函数时,给出了鲁棒有效解的充要条件.
[1] KOOPMANS T C.Analysis of production as an efficient combination of activities[J].Analysis of Production and Allocation,1951,158(1):33-97.
[2] KUHN H W,TUCKER A W.Nonlinear programming[C]//Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability.Berkeley,San Francisco,USA,1951.
[3] GEOFFRION A M.Proper efficiency and the theory of vector maximization[J].Journal of Mathematical Analysis and Applications,1968,22(3):618-630.
[4] BORWEIN J M.Proper efficient points for maximizations with respect to cones[J].SIAM Journal on Control and Optimization,1977,15(1):57-63.
[5] BENSON H P.An improved definition of proper efficiency for vector maximization with respect to cones[J].Journal of Mathematical Analysis and Applications,1979,71(1):232-241.
[6] HENIG I.Proper efficiency with respect to cones[J].Journal of Optimization Theory and Applications,1982,36(3):387-407.
[7] BENTAL A,NEMIROVSKI A.Robust truss topology design via semidefinite programming[J].SIAM Journal on Optimization,1997,7(4):991-1016.
[8] KUROIWA D,LEE G M.On robust multiobjective optimization[J].Journal of Nonlinear and Convex Analysis,2012,40(2/3):305-317.
[9] EHROGOTT M,IDE J,SCHOBEL A.Minimax robustness for multi-objective optimization problems[J].European Journal of Operational Research,2014,239(1):17-31.
[10] IDE J,SCHOBEL A.Robustness for uncertain multi-objective optimization:a survey and analysis of different concepts[J].OR Spectrum,2016,38(1):235-271.
[11] GOBERNA M A,JEYAKUMAR V,LI G,et al.Robust solutions of multi-objective linear semi-infinite programs under constraint date uncertain[J].SIAM Journal on Optimization,2014,24(3):1402-1419.
[12] GEORGIEV P J,LUC D T,PRDALOS P.Robust aspects of solutions in deterministic multiple objective linear programming[J].European Journal of Operational Research,2013,229(1):29-36.
[13] ZAMANI M,SOLEIMANI-DAMANEH M,KABGANI A.Robustness in nonsmooth nonlinear multiobjective programming[J].European Journal of Operational Research,2015,247(2):370-378.
[14] MORTEZA R,MAJID S D.Robustness in deterministic vectoroptimization[J].Journal of Optimization Theory and Applications,2018,179(1):137-162.
[15] SAWARAGI Y,NAKAYAMA H,TANINO T.Theory of Multiobjective Optimization[M].London:Academic Press,1985.
[16] MARKO M M,PEKKA N.Nonsmooth Optimization[M].London:World Scientific,1992.
[17] 杨新民.Benson真有效解与Borwein真有效解的等价性[J].应用数学,1994,7(2):246-247.(YANG Xinmin.Equivalence between Benson proper efficient solution and Borwein proper efficient solution[J].Applied Mathematics,1994,7(2):246-247.(in Chinese))
[18] 李小燕,高英.多目标优化问题Proximal真有效解的最优性条件[J].应用数学和力学,2015,36(6):668-676.(LI Xiaoyan,GAO Ying.The optimality conditions of Proximal proper efficient solution for multi-objective optimization[J].Applied Mathematics and Mechanics,2015,36(6):668-676.(in Chinese))
[19] FAKHAR M,MAHYARINIA M R,ZAFARANI J.On nonsmooth robust multiobjective optimization under generalized convexity with applications to portfolio optimization[J].European Journal of Operational Research,2018,265(1):39-48.