引 言
在声散射[1]、流体力学[2]、量子化学[3]、Helmholtz方程[4]、Maxwell方程[5-6]等诸多科学计算和工程应用领域都会遇到各类微分方程或积分方程,通过采用有限元、有限差分等离散化技术,这些问题最终都归结于以下两类复线性方程组的求解.
第一类复线性方程组为
Ax=b,
(1)
其中A∈Cn×n为非Hermite矩阵,x,b∈Cn.
第二类具有多个右端项的复线性方程组为
AX=B,
(2)
其中A∈Cn×n为非Hermite矩阵,X,B∈Cn×p,p≪n.
由于在实际工程问题的数值计算中,大规模的线性方程组求解所占比重较大,因此高效求解上述两类线性方程组一直是各领域追求的目标,并且具有重要的理论意义和使用价值,故而吸引了众多学者的关注.目前,对于非Hermite线性方程组和具有多个右端项的非Hermite线性方程组的求解主要集中于Krylov子空间方法的研究.
针对大规模的复非对称线性方程组法的求解,若不考虑存储量限制,则被广泛应用的一类Krylov子空间方法有广义最小残量(GMRES)法[7]以及相关GMRES的改进方法[8],该类方法具有非常好的鲁棒性.若考虑存储量的限制,目前主要常用的一类Krylov子空间方法有稳定化双共轭梯度(BiCGSTAB)法[9]、广义积型双共轭梯度(GPBiCG)法[10]、双共轭A-正交残量稳定化(BiCORSTAB)法[11]、广义积型双共轭A-正交残量(GPBiCOR)法[12]、GCORS2法[13]等.针对多右端项大规模线性方程组的求解,目前主要的迭代法有总体CGS(Gl-CGS)方法[14]、总体广义积型BiCG(Gl-GPBiCG)方法[15]、总体GPBiCG_plus(Gl-GPBiCG_plus)方法[15-16]等.
然而,由于实际工程计算中计算规模、存储量、计算效率等因素的限制,直接采用上述方法往往不能满足高效这一要求.故而预处理技术就成为了当前广泛应用的方法[13,15-17],并通过该预处理方法达到算法收敛速度快、稳定性和鲁棒性好的目的.但针对不同类型的方程组,设计相应的高效预处理方法依旧是目前众多研究者研究的方向.因此,本文主要针对求解非Hermite线性方程组(1)和具有多个右端项的复线性方程组(2)的若干迭代算法(GCORS2[13]、BiCORSTAB[11]、Gl-GPBiCG[15]和Gl-GPBiCG_plus[15]),提出了一种预处理方法,并通过对这些迭代算法进行预处理,进而加速其算法的收敛速度,改善了算法稳定性和鲁棒性.
文中内积定义为:若x,y∈Cn,则其内积为〈x,y〉=yHx,由此导出向量的2-范数为![]() 若X,Y∈Cn×p,则其内积为〈X,Y〉=tr(YHX),由此导出矩阵的Frobenius范数为
若X,Y∈Cn×p,则其内积为〈X,Y〉=tr(YHX),由此导出矩阵的Frobenius范数为![]()
1 预处理方法
为了加快非Hermite线性方程组(1)和具有多个右端项的复线性方程组(2)的求解速度,目前最常用的方法是采用预处理技术对相应算法进行预处理.因此,本文通过对若干迭代算法采用预处理技术求解线性方程组.
1.1 预处理思想
该预处理方法的思想为:采用与实线性方程组加速求解的类似方法,通过构造预处理条件子M-1,使其近似于系数矩阵A的逆矩阵,即M-1≈A-1,其中M-1=(M1M2)-1.而后对非Hermite线性方程组(1)预处理,得到相应的预处理方程
其中![]() 对于具有多个右端项的复线性方程组(2)的求解采用同样的预处理技术.本文仅考虑右预处理,故令M1=I,M2=M,拟通过这种预处理技术,使得系数矩阵的奇异值分布更加集中,从而加快了GCORS2[13]、BiCORSTAB[11]、Gl-GPBiCG[15]和Gl-GPBiCG_plus[15]的收敛速度.
对于具有多个右端项的复线性方程组(2)的求解采用同样的预处理技术.本文仅考虑右预处理,故令M1=I,M2=M,拟通过这种预处理技术,使得系数矩阵的奇异值分布更加集中,从而加快了GCORS2[13]、BiCORSTAB[11]、Gl-GPBiCG[15]和Gl-GPBiCG_plus[15]的收敛速度.
1.2 预处理条件子的选取
令A=(aij)n×n=D-N,其中
故
A-1=(D-N)-1=(I-D-1N)D-1,
其中I为单位矩阵.又由于
(I-D-1N)-1≈I+D-1N+…+(D-1N)q-1,
因此选取预处理条件子M-1为
M-1=(I+D-1N+…+(D-1N)q-1)D-1,
其中 q≥1.
注1 基于预处理条件子M-1的选取,可发现,随着内迭代次数q的增加,计算量也相应增加.因此,如何适当选取内迭代次数对于提升预处理算法的收敛速度至关重要.此外,本文仅考虑右预处理,若考虑左预处理,则令M1=M,M2=I,预处理条件子选取一样,唯一区别在于预处理算法中迭代步骤的处理,但左预处理与右预处理技术目的均是提高算法的收敛速度和改善算法的稳定性.因此,左预处理有着同样的效果,在此不再赘述.
2 若干预处理迭代算法
首先考虑非Hermite线性方程组(1),拟采用预处理技术对GCORS2[13]和BiCORSTAB[11]进行预处理.
2.1 预处理GCORS2算法
下面给出GCORS2算法[13]的预处理算法(记作PGCORS2算法):
第1步 给定初始向量x0,计算r0=b-Ax0;选择![]() 使得
使得![]() 其中p(t)是以t为变量的任意阶多项式.
其中p(t)是以t为变量的任意阶多项式.
第2步 置![]()
![]() 0.
0.
第3步 若‖rk‖2≤ε‖r0‖2,计算停止,其中ε∈R+;否则,计算
第4步 置k![]() k+1,转第2步.
k+1,转第2步.
从PGCORS2算法可以看出,该算法相较于GCORS2算法多求解了两个线性方程组![]() 与
与![]() 下面首先给出求解线性方程
下面首先给出求解线性方程![]() 的迭代格式.
的迭代格式.
根据预处理条件子M-1的形式,选取![]() 则相应的迭代格式如下:
则相应的迭代格式如下:
for l=0,1,…,q-1,
end
类似地,选取![]() 可得到求解线性方程
可得到求解线性方程![]() 的迭代格式如下:
的迭代格式如下:
for l=0,1,…,q-1,
end
对于PGCORS2算法,当q处于一定范围内时,系数矩阵特征值的密集程度会随着内迭代次数q的增大而更集中,进而加快了GCORS2算法的收敛速度.根据类似的预处理方式,可得到BiCORSTAB算法[11]的预处理算法.
2.2 预处理BiCORSTAB算法
下面给出BiCORSTAB算法[11]的预处理算法(记作PBiCORSTAB算法):
第1步 给定初始向量x0,计算r0=b-Ax0;选择![]() 使得
使得![]() 置k
置k![]() 0.
0.
第2步 若‖rk‖2≤ε‖r0‖2,计算停止,其中ε∈R+;否则,计算
若ρk=0,方法失效;否则,计算
βk=ρkαk/(ρk-1ωk), pk=M-1rk+βk(pk-1-ωk-1M-1qk-1),
(若k=0,则![]()
若‖xk‖2≤ε,xk+1=xk+αkpk;否则,计算
第3步 置k![]() k+1,转第2步.
k+1,转第2步.
从PBiCORSTAB算法可以看出,该算法相较于BiCORSTAB算法多求解了两个线性方程组![]() 与
与![]() 对于这两个线性方程组的预处理迭代格式与2.1小节的迭代格式类似,这里不再赘述.
对于这两个线性方程组的预处理迭代格式与2.1小节的迭代格式类似,这里不再赘述.
其次,考虑具有多个右端项的复线性方程组(2),拟采用预处理技术对Gl-GPBiCG算法[15]和Gl-GPBiCG_plus算法[15]进行预处理.
2.3 预处理Gl-GPBiCG算法
下面给出Gl-GPBiCG算法[15]的预处理算法(记作PGl-GPBiCG算法):
第1步 给定初始元素X0,计算R0=B-AX0,选择![]() 使得
使得![]()
第2步 置T-1=W-1=On×p, β-1=0, k![]() 0.
0.
第3步 若‖Rk‖F≤ε‖R0‖F,计算停止,其中ε∈R+;否则,计算
Yk=Tk-1-Rk-αkWk-1+αkAPk,
Tk=Rk-αkAPk, M-1Tk=M-1Rk-αkM-1APk,
(若k=0,则ζk=〈AM-1Tk,Tk〉F/〈AM-1Tk,AM-1Tk〉F,ηk=0),
Uk=ζkM-1APk+ηk(M-1Tk-1-M-1Rk+βk-1Uk-1),
Zk=ζkM-1Rk+ηkZk-1-αkUk,
Xk+1=Xk+αkPk+Zk, Rk+1=Tk-ηkYk-ζkAM-1Tk,
第4步 置k![]() k+1,转第2步.
k+1,转第2步.
从PGl-GPBiCG算法可以看出,该算法相较于Gl-GPBiCG算法多求解了两个具有右端项的线性方程组![]() 与
与![]() 对于这两个线性方程组的迭代格式与2.1小节的迭代格式类似.值得注意的是, 对于
对于这两个线性方程组的迭代格式与2.1小节的迭代格式类似.值得注意的是, 对于![]() 的求解, 需先求解APk,而后采用预处理迭代格式.
的求解, 需先求解APk,而后采用预处理迭代格式.
2.4 预处理Gl-GPBiCG_plus算法
下面给出Gl-GPBiCG_plus算法[15]的预处理算法(记作PGl-GPBiCG_plus算法):
第1步 给定初始元素X0,计算R0=B-AX0,选择![]() 使得
使得![]()
第2步 置P-1=U-1=Z-1=On×p,β-1=0,k![]() 0.
0.
第3步 若‖Rk‖F≤ε‖R0‖F,计算停止,其中ε∈R+;否则,计算
(若k=0,则ζk=〈AM-1Rk,Rk〉F/〈AM-1Rk,AM-1Rk〉F,ηk=0),
Uk=ζkAPk+ηk(AZk-1+βk-1Uk-1), Tk=Rk-αkAPk,
Zk=ζkM-1Rk+ηkZk-1-αkM-1Uk,
第4步 置k![]() k+1,转第2步.
k+1,转第2步.
从PGl-GPBiCG_plus算法可以看出,该算法相较于Gl-GPBiCG_plus算法多求解了两个具有右端项的线性方程组![]() 与
与![]() 对于这两个线性方程组的迭代格式与2.1小节的迭代格式类似.
对于这两个线性方程组的迭代格式与2.1小节的迭代格式类似.
注2 通过观察上述给出的4种预处理算法,可发现,随着内迭代次数q的增加,矩阵乘法运算和加法运算随之增多,这也就意味着内迭代计算量的增加.然而,由于内迭代次数在一定范围内的增加会减少整体算法的循环次数,进而导致外循环计算量的减少.因此从整体角度出发,为了确保算法精度的同时缩短计算时间,需寻求内迭代计算量增加与外循环计算量减少的平衡点.本文通过算例验证(未在本文列出),当内迭代次数q>4时,整体迭代次数减少,但计算时间增多,因此后续提供的算例仅考虑q=1,2,4的情况.
3 数值算例与结果分析
对于非Hermite线性方程组(1)和具有多个右端项的复线性方程组(2),分别采用GCORS2算法[13]、BiCORSTAB算法[11]、Gl-GPBiCG算法[15]、Gl-GPBiCG_plus算法[15]、PGCORS2算法、PBiCORSTAB算法、PGl-GPBiCG算法及PGl-GPBiCG_plus算法进行对比分析,以此验证预处理算法的有效性.此外通过观察预处理条件子,可知该类预处理仅对部分元素进行处理,适用于大型稀疏矩阵线性方程组的求解,如果对稠密矩阵进行预处理,将会大大增加计算量,导致算法效率的下降,故对于稠密矩阵线性方程组的求解并不适用.因此,本文算例主要针对稀疏矩阵线性方程.在算例中,初始向量x0=0∈Cn(X0=0∈Cn×p),rk=b-Axk(Rk=B-AXk),其中xk(Xk)表示第k步迭代向量,rk(Rk)表示第k步迭代误差,终止条件满足‖rk‖2/‖r0‖2≤10-8(即‖Rk‖F/‖R0‖F≤10-8),即算法中提及的ε=10-8,此外GCORS2算法[13]、BiCORSTAB算法[11]中选取![]() 算法[15]、Gl-GPBiCG_plus算法[15]中选取
算法[15]、Gl-GPBiCG_plus算法[15]中选取![]() 算例中k,t及lres分别表示计算近似解的迭代次数、迭代时间和相对残量范数,其中相对残量范数定义为lres=lg(‖rk‖2/‖r0‖2)(即lres=lg(‖Rk‖F/‖R0‖F)).
算例中k,t及lres分别表示计算近似解的迭代次数、迭代时间和相对残量范数,其中相对残量范数定义为lres=lg(‖rk‖2/‖r0‖2)(即lres=lg(‖Rk‖F/‖R0‖F)).
本文所有算例均使用双精度浮点运算并在MATLAB R2017b平台上运行,电脑配置:CPU为PC-Interl(R) Core(TM) i7-6700,3.40 GHz,内存为16 GB.
例1 为了验证PGCORS2算法和PBiCORSTAB算法求解非Hermite线性方程组(1)的有效性和鲁棒性,该算例主要针对源于声散射、二维对流扩散和有限差分Laplace(拉普拉斯)算子问题通过转换得到的YOUNG1C、CDDE1和GR_30_30矩阵进行测试,更多细节请详见文献[18],方程(1)中右端项选取b=(i,…,i)T.3个测试矩阵的计算结果对比详见表1,相应算法的收敛性行为详见图1~3.
表1 预处理方法求解YOUNG1C、CDDE1及GR_30_30的数值结果
Table 1 Numerical results of YOUNG1C, CDDE1 and GR_30_30 obtained with preconditioning methods

methodYOUNG1Ckt/slresCDDE1kt/slresGR_30_30kt/slresGCORS2[13]2190.023-8.0611030.019-8.859500.013-8.231PGCORS2(q=1)1910.025-8.6111030.023-8.872500.016-8.231PGCORS2(q=2)940.017-8.281510.014-8.047280.011-8.074PGCORS2(q=4)700.015-8.572360.009-8.207200.009-8.355BiCORSTAB[11]4470.034-8.0401980.020-8.321500.010-8.071PBiCORSTAB(q=1)5290.048-8.3571830.026-8.310500.013-8.071PBiCORSTAB(q=2)1840.020-8.024770.013-8.202310.009-8.139PBiCORSTAB(q=4)1190.018-8.008520.009-8.312180.006-8.137
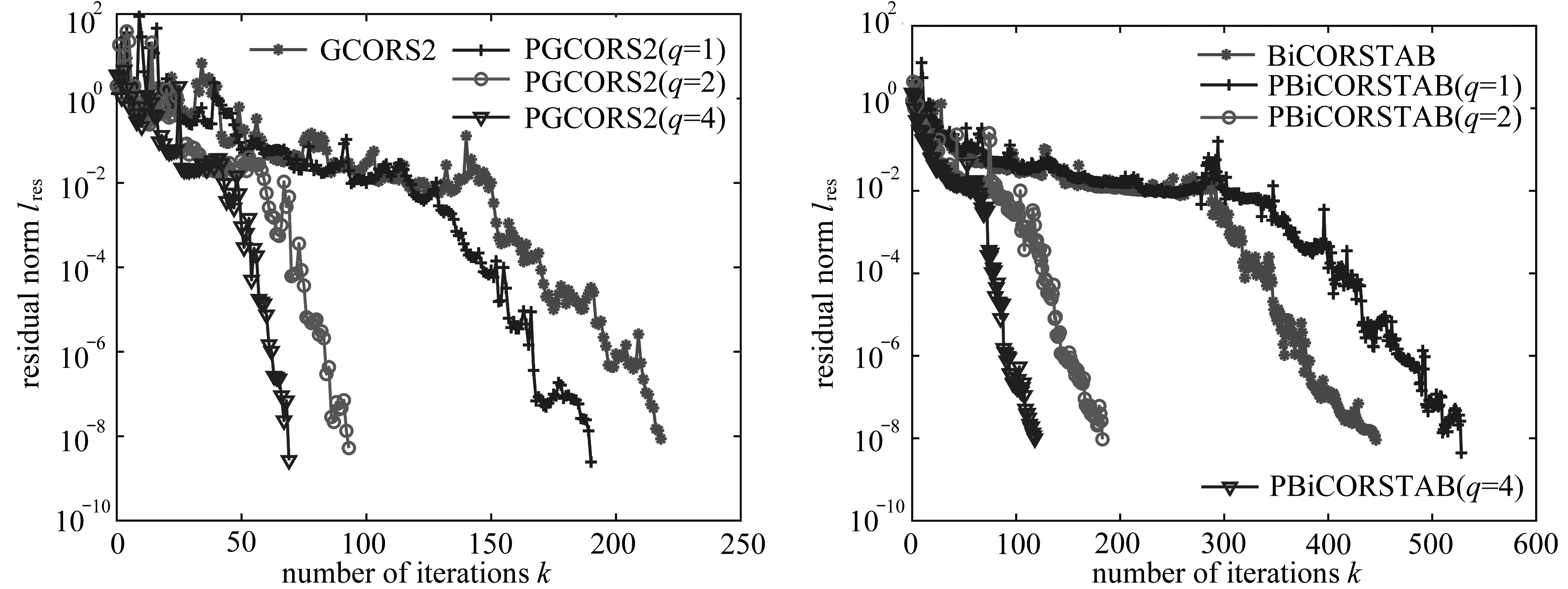
(a) PGCORS2 (b) PBiCORSTAB
图1 例1中YOUNG1C的收敛结果
Fig. 1 Convergence histories of YOUNG1C for example 1
基于表1和图1~3的数值结果,采用GCORS2、BiCORSTAB及相应的预处理算法求解线性方程组(1)可得到如下相关结论:
1) 对于测试矩阵YOUNG1C,GCORS2算法在迭代时间和迭代次数两方面所表现出的收敛性行为均优于BiCORSTAB算法,该结论与文献[13]保持一致.类似地,测试矩阵CDDE1和GR_30_30同样呈现出相关收敛性行为.另外从图表中的数据可知,PGCORS2算法的收敛性行为同样优于PBiCORSTAB算法,迭代时间较少,且稳定性较好.
2) 从图与表中的数据可知,当预处理算法的内迭代次数q=1时,预处理算法(PGCORS2、PBiCORSTAB)与原算法的迭代次数比较接近,特别是测试矩阵CDDE1和GR_30_30,这是由于此时的预处理条件子M-1=D-1 为对角阵,预处理算法相较于原算法影响很小.因此,当q=1时,预处理算法与原算法的迭代次数几乎相同.
3) 从图与表中的数据可知,对于同一测试算例,当内迭代次数q在一定范围时,PGCORS2和PBiCORSTAB算法的收敛速度随着内迭代次数的增加而相应的加快,所用迭代时间相应减少.特别地,当内迭代次数q=4时,预处理算法收敛速度最快,且迭代时间和迭代次数达到最小.
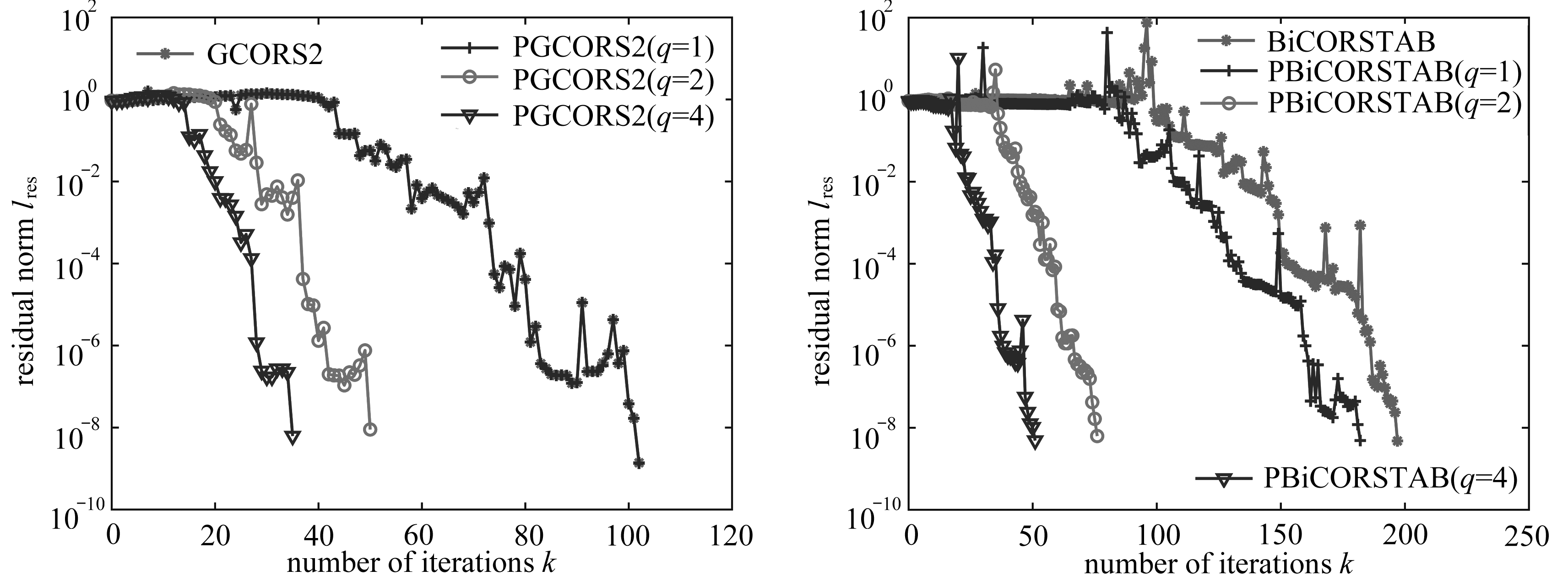
(a) PGCORS2 (b) PBiCORSTAB
图2 例1中CDDE1的收敛结果
Fig. 2 Convergence histories of CDDE1 for example 1
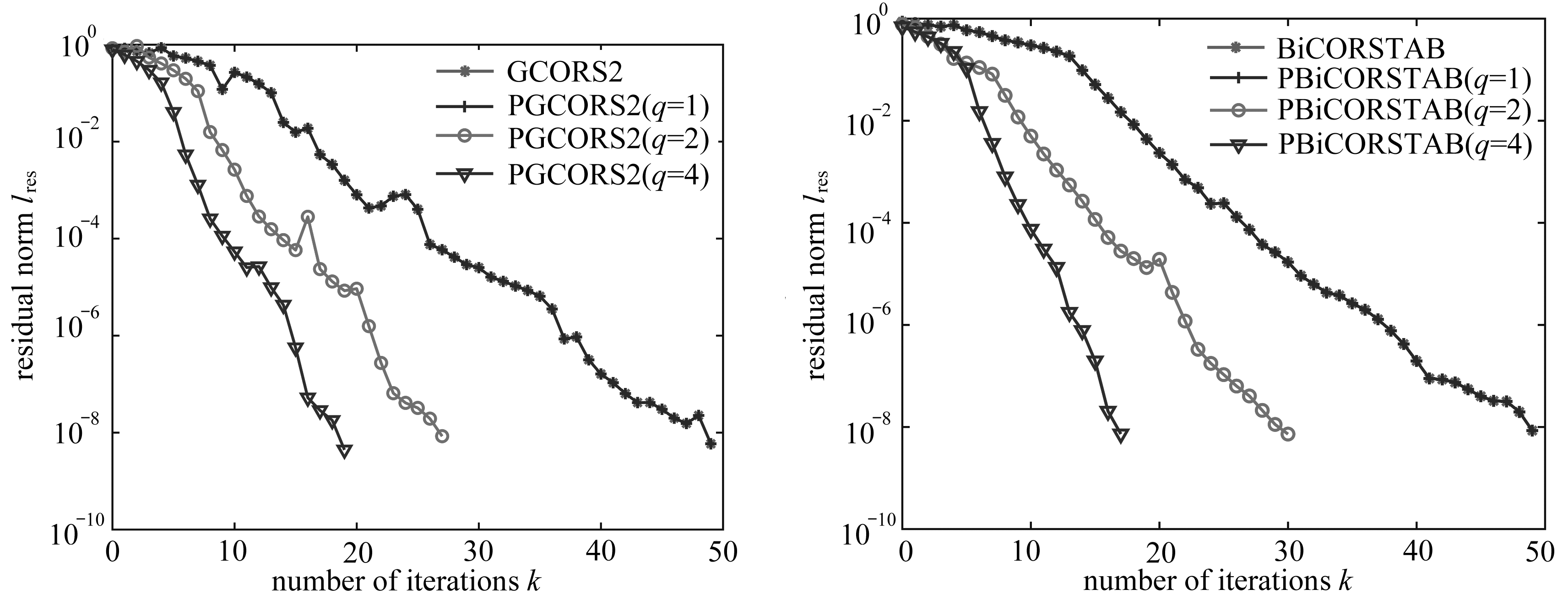
(a) PGCORS2 (b) PBiCORSTAB
图3 例1中GR_30_30的收敛结果
Fig. 3 Convergence histories of GR_30_30 for example 1
例2 对于带有多个右端项的非Hermite线性方程组(2),考虑阶数为4 000的复Toeplitz矩阵[13,15]:

其符号函数为f(z)=iγz-1+4+z2+0.7z3.通过改变参数γ,可得到与符号函数f(z)相关的谱和伪谱.因此,参数γ会影响到Gl-GPBiCG[15]、Gl-GPBiCG_plus[15]、GCORS2[13]及相关预处理方法的收敛性行为.方程(2)中右端项选取B=A×E,p=5≪n,其中E=(eij)n×p,且eij=1.算例的计算结果对比详见表2,相应算法的收敛性行为详见图4和图5.
表2 不同参数γ下预处理方法求解算例2的数值结果
Table 2 Numerical results for example 2 with different values of parameter γobtained with preconditioning methods
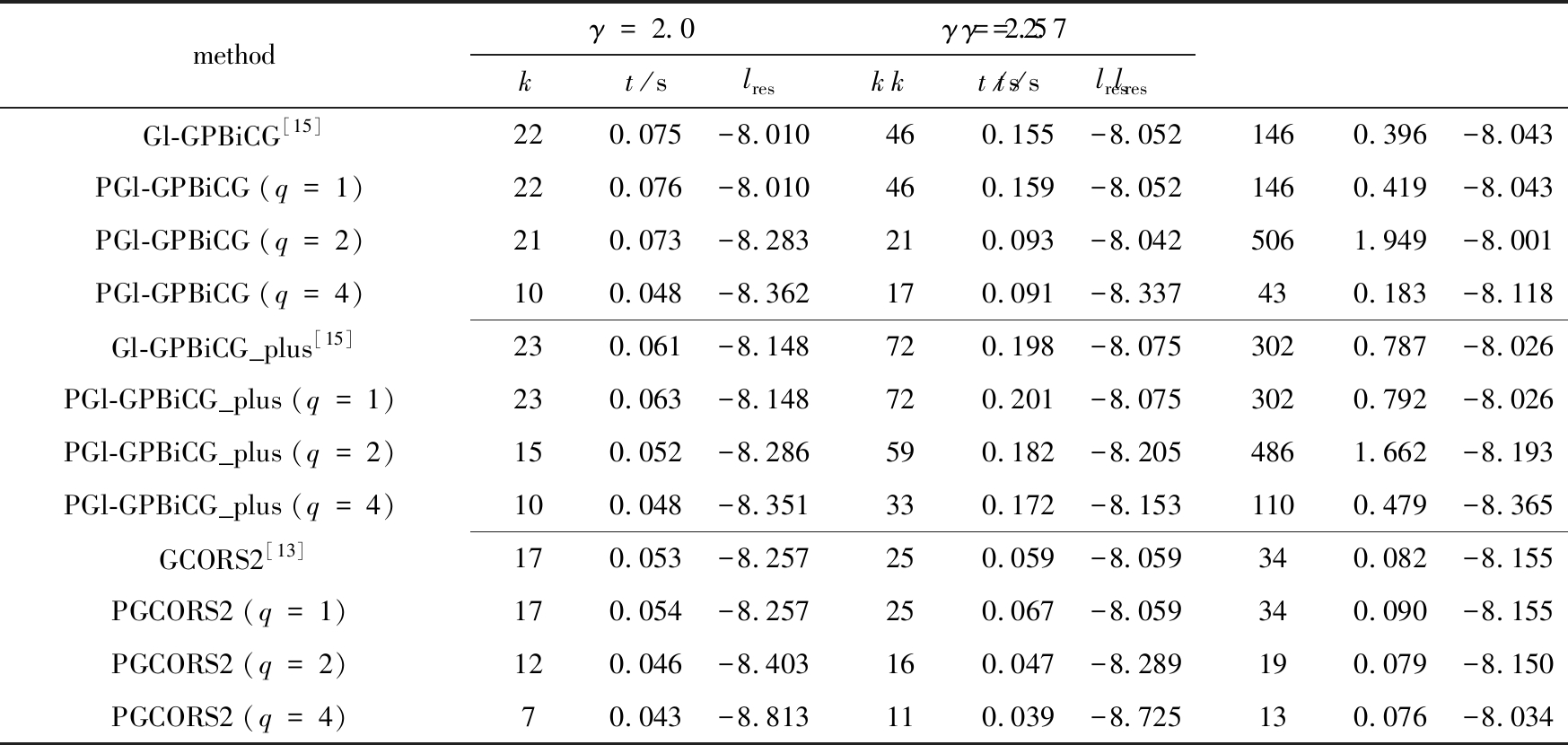
methodγ=2.0kt/slresγ=2.5kt/slresγ=2.7kt/slresGl-GPBiCG[15]220.075-8.010460.155-8.0521460.396-8.043PGl-GPBiCG(q=1)220.076-8.010460.159-8.0521460.419-8.043PGl-GPBiCG(q=2)210.073-8.283210.093-8.0425061.949-8.001PGl-GPBiCG(q=4)100.048-8.362170.091-8.337430.183-8.118Gl-GPBiCG_plus[15]230.061-8.148720.198-8.0753020.787-8.026PGl-GPBiCG_plus(q=1)230.063-8.148720.201-8.0753020.792-8.026PGl-GPBiCG_plus(q=2)150.052-8.286590.182-8.2054861.662-8.193PGl-GPBiCG_plus(q=4)100.048-8.351330.172-8.1531100.479-8.365GCORS2[13]170.053-8.257250.059-8.059340.082-8.155PGCORS2(q=1)170.054-8.257250.067-8.059340.090-8.155PGCORS2(q=2)120.046-8.403160.047-8.289190.079-8.150PGCORS2(q=4)70.043-8.813110.039-8.725130.076-8.034
基于表2、图4和图5的数值结果,采用Gl-GPBiCG、Gl-GPBiCG_plus、GCORS2及相应的预处理算法求解带有多个右端项的线性方程组(2)可得到如下相关结论:
1) 从表2中的数据可知,对于不同的参数γ,GCORS2算法所用的迭代时间和迭代次数均少于Gl-GPBiCG和Gl-GPBiCG_plus算法.且从图4、图5中看出,当预处理算法的内迭代次数q=1时,3种预处理算法(PGCORS2、PGl-GPBiCG和PGl-GPBiCG_plus)与原算法的迭代次数几乎接近,收敛曲线几近重合,这一现象与例1中结果保持一致.
2) 从表2数据可知,当γ=2.0,2.5时,3种算法的预处理算法的收敛速度均随着内迭代次数的增加而相应加快,所用迭代时间相应减少.特别地,当内迭代次数q=4时,预处理算法收敛速度最快,且迭代时间和迭代次数达到最小.而当γ=2.7时,可从图5(a)、(b)中可知,PGl-GPBiCG和PGl-GPBiCG_plus算法在内迭代次数为q=2时,收敛性行为呈现骤增骤降趋势,且高于q=1时的迭代次数,而PGCORS2算法却保持良好的收敛性行为.这说明参数γ会影响到PGl-GPBiCG和PGl-GPBiCG_plus算法的收敛行为,但对PGCORS2算法影响极小,因此PGCORS2算法呈现较好的收敛性行为.
基于算例2的结果,可知GCORS2算法的预处理算法表现出较好的收敛性行为.因此,以下算例进一步验证预处理算法求解带有多个右端项的线性方程组(2)的有效性和可行性.
例3 对于带有多个右端项的非Hermite线性方程组(2),考虑Helmholtz方程[4,13]:
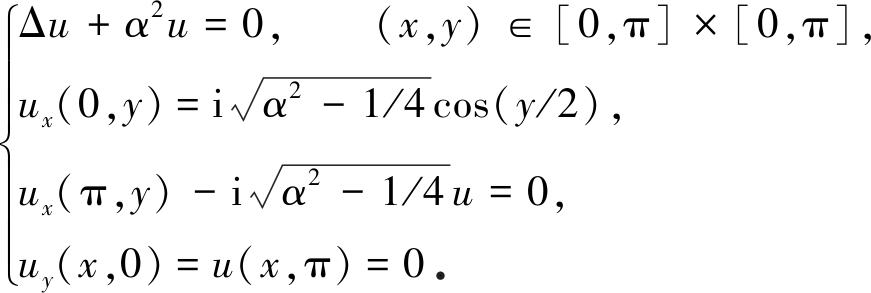
通过中心差分格式离散Helmholtz方程,离散后所得线性方程组系数矩阵阶数为(m+1)×m,其中步长选取h=1/m,右端项选取B=A×E,p=5≪n,其中E=(eij)n×p,且eij=1.该算例仅考虑α=2.77,4.16两种情况.算例的计算结果对比详见表3,相应算法的收敛性行为详见图6.
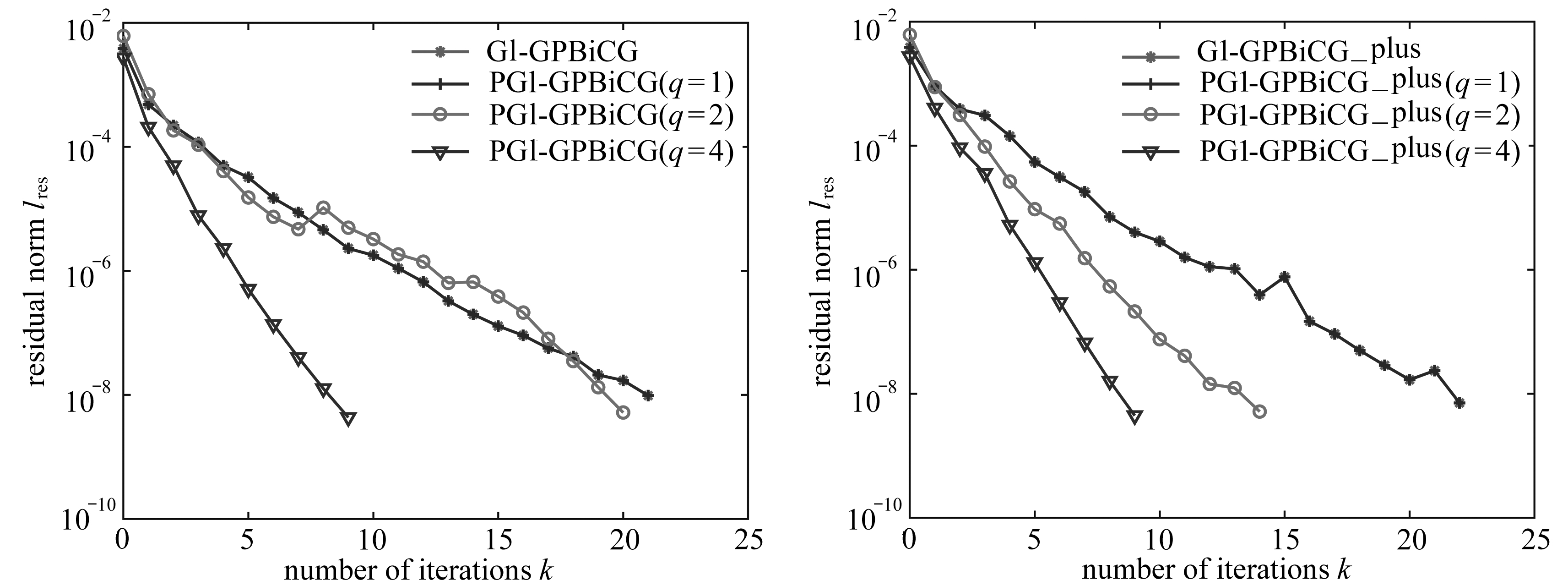
(a) PGl-GPBiCG (b) PGl-GPBiCG_plus

(c) PGCORS2
图4 例2中参数γ=2.0的收敛结果
Fig. 4 Convergence histories for example 2 withγ=2.0
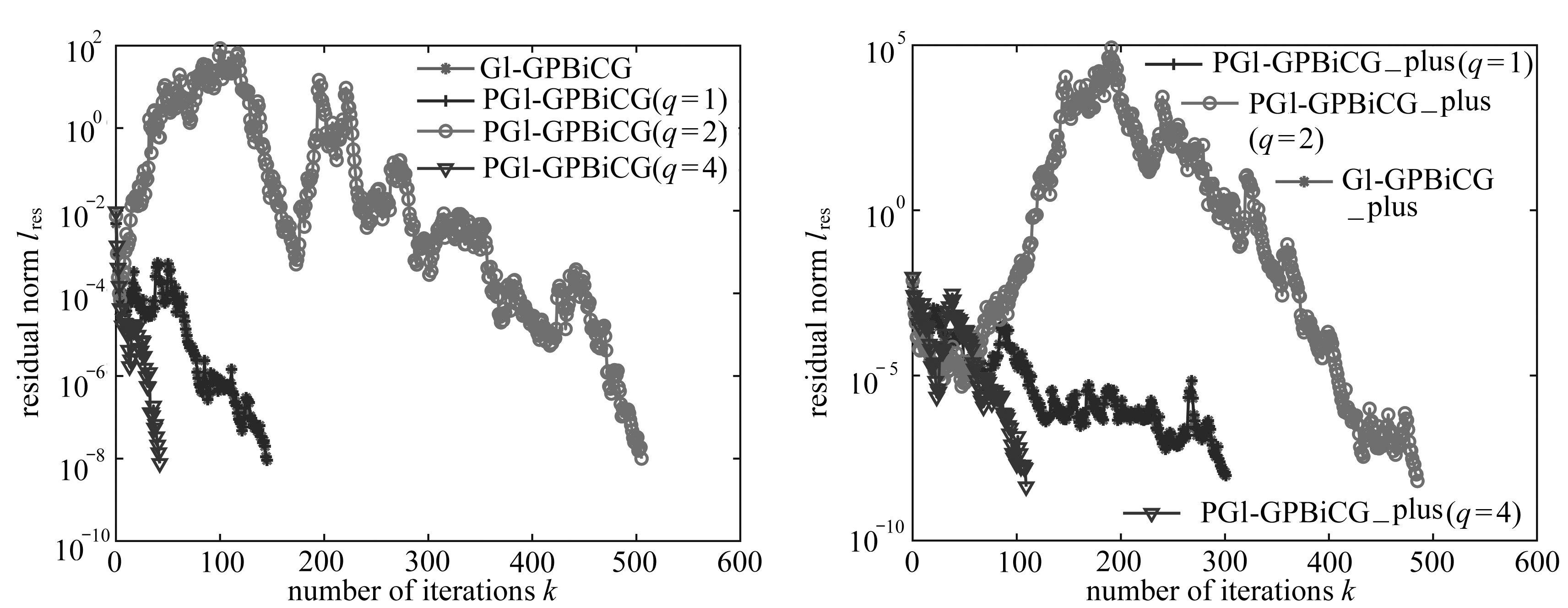
(a) PGl-GPBiCG (b) PGl-GPBiCG_plus
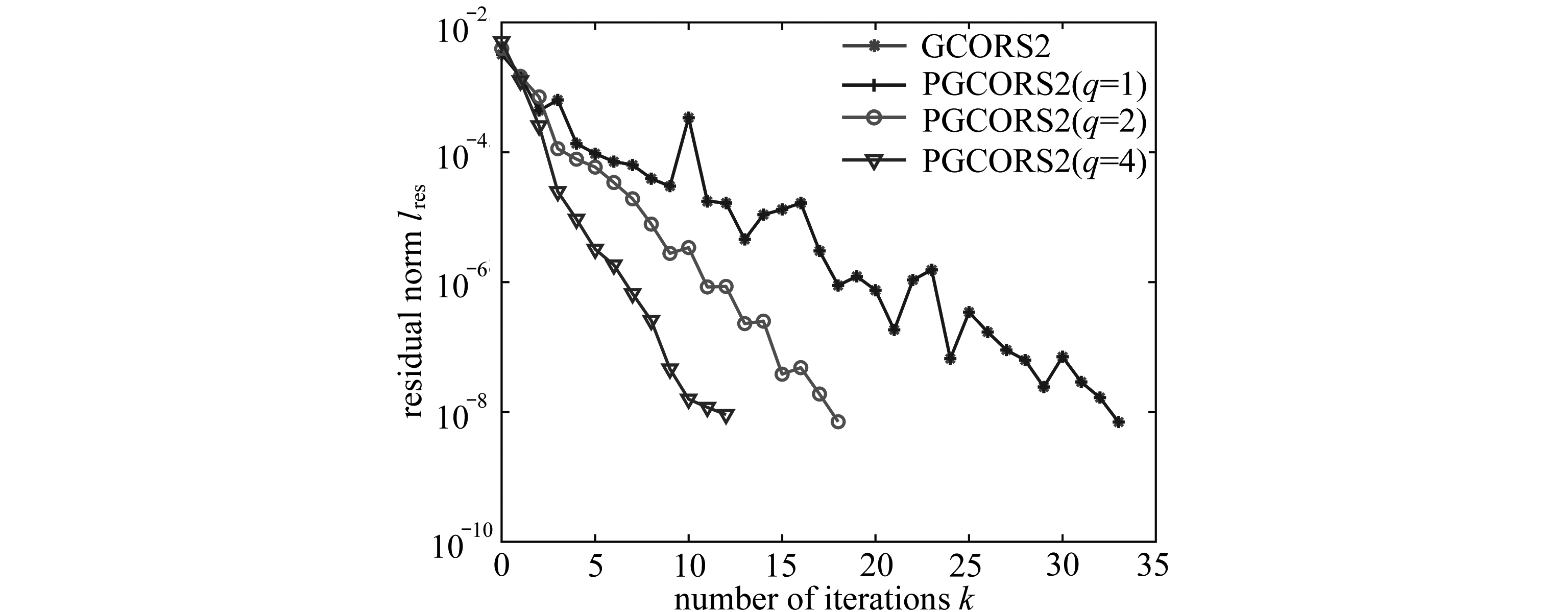
(c) PGCORS2
图5 例2中参数γ=2.7的收敛结果
Fig. 5 Convergence histories for example 2 withγ=2.7
表3 不同参数α下预处理方法求解算例3的数值结果
Table 3 Numerical results for example 3 with different values of parameter αobtained with preconditioning methods

mαGCORS2[13]kt/slresPGCORS2(q=1)kt/slresPGCORS2(q=2)kt/slresPGCORS2(q=4)kt/slres802.773171.77-8.043171.80-8.031881.23-8.261331.20-8.111002.773962.14-8.093962.16-8.152231.76-8.001581.67-8.221202.774757.65-8.034757.81-8.002665.75-8.001905.14-8.29804.164312.21-8.014232.32-8.023311.93-8.102321.78-8.011004.164902.33-8.044952.35-8.023742.05-8.162691.95-8.141204.166236.38-8.166236.55-8.153184.76-8.002264.26-8.03
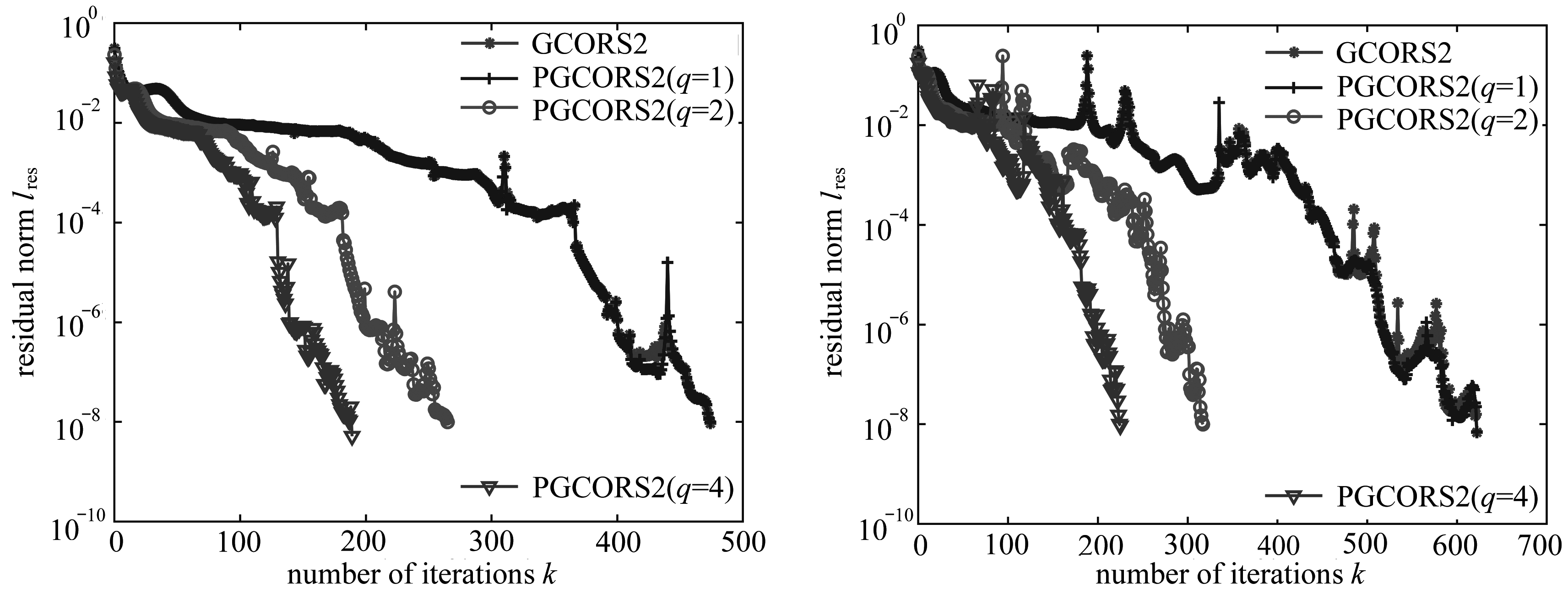
(a) α=2.77 (b) α=4.16
图6 例3中PGCORS2算法的收敛结果(m=120)
Fig. 6 Convergence histories for example 3 with m=120
基于表3和图6数值结果,采用GCORS2算法及相应的预处理算法求解带有多个右端项的线性方程组(2)可得到如下相关结论:
1) 从表3中的数据可知,对于不同的参数α,当计算规模从6 480(m=80)增加到14 520(m=120)时,PGCORS2依旧保持良好的收敛性行为.当q=1时,PGCORS2与GCORS2的迭代次数几乎接近,收敛曲线几近重合(可从图6中看出);当q=4时,PGCORS2算法收敛速度最快,且迭代时间和迭代次数达到最小.
2) 从图6中可知,对于同一规模的Helmholtz方程,随着参数α的增加,PGCORS2和GCORS2算法所用迭代次数增多.这说明参数α影响GCORS2和PGCORS2的收敛性行为,但PGCORS2算法相较于GCORS2算法依旧具有良好的收敛速度.
4 结 束 语
本文主要采用若干预处理迭代算法求解非Hermite线性方程组(1)和具有多个右端项的复线性方程组(2).通过预处理技术,有效地提高了求解线性方程组的效率,大大降低计算时间.以下针对相关预处理算法进行总结:
1) 考虑非Hermite线性方程组(1)的求解,PGCORS2收敛速度和迭代时间均优于PBiCORSTAB算法,具有良好的收敛性行为.考虑具有多个右端项的复线性方程组(2)的求解,PGCORS2算法的收敛速度和迭代时间均优于PGl-GPBiCG算法和PGl-GPBiCG_plus算法,具有良好的收敛性行为.这进一步说明预处理算法加快了原算法的收敛速度.
2) 针对于文中所提到的所有预处理算法,当内迭代次数q=1时,由于此时的预处理条件子M-1=D-1为对角阵,预处理算法相较于原算法影响很小.因此,预处理算法与原算法的迭代次数几乎接近,收敛曲线较为相似.当内迭代次数q=4时,预处理算法收敛速度均达到最快,迭代时间和迭代次数达到最小.
[1] BAZ N F S V, KLEEFELD A, LEEM K H, et al. Sampling method based projection approach for the reconstruction of 3D acoustically penetrable scatterers[J]. Linear Algebra and Its Applications, 2016, 495(15): 289-323.
N F S V, KLEEFELD A, LEEM K H, et al. Sampling method based projection approach for the reconstruction of 3D acoustically penetrable scatterers[J]. Linear Algebra and Its Applications, 2016, 495(15): 289-323.
[2] SADD Y. A flexible inner-outer preconditioned GMRES algorithm[J]. SIAM Journal on Scientific Computing, 1993, 14(2): 461-469.
[3] BAI A, DAY D, DONGARRA J, et al. A test matrix collection for non-Hermitian eigenvalue problems: CS-97-355[R]. Knoxville, TN: Department of Computer Science, University of Tennessee, 1997.
[4] BAYLISS A, GLODSTEIN C I, TURKEL E. An iteration method for the Helmholtz equation[J]. Journal of Computational Physics, 1983, 49(3): 443-457.
[5] HU Q Y, YUAN L. A plane-wave least-squares method for time-harmonic Maxwell’s equations in absorbing media[J]. SIAM Journal on Scientific Computing, 2014, 36(4): 1937-1959.
[6] HUTTUNEN T, MALINEN M, MONK P. Solving Maxwell’s equations using the ultra weak variational formulation[J]. Journal of Computational Physics, 2007, 223(2): 731-758.
[7] SAAD Y, SCHULTZ M H. A generalized minimum residual algorithm for solving nonsymmetirc linear systems[J]. SIAM Journal on Scientific and Statistical Computing, 1986, 7(3): 856-869.
[8] DU K. GMRES with adaptively deflated restarting and its performance on an electromagnetic cavity problem[J]. Applied Numerical Mathematics, 2011, 61(9): 977-988.
[9] VAN DERVORST H A. Bi-CGSTAB: a fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems[J]. SIAM Journal on Scientific and Statistical Computing, 1992, 13(2): 631-644.
[10] DEHGHAN M, MOHAMMADI-ARANI R. Generalized product-type methods based on bi-conjugate gradient (GPBiCG) for solving shifted linear systems[J]. Computational and Applied Mathematics, 2017, 36(4): 1591-1606.
[11] ZHAO L, HUANG T Z, JING Y F, et al. A generalized product-type BiCOR method and its application in signal deconvolution[J]. Computers and Mathematics With Applications, 2013, 66(8): 1372-1388.
[12] GU X M, HUANG T Z, CARPENTIERI B, et al. A hybridized iterative algorithm of the BiCORSTAB and GPBiCOR methods for solving non-Hermitian linear systems[J]. Computers and Mathematics With Applications, 2015, 70(12): 3019-3031.
[13] ZHANG J H, DAI H. Generalized conjugate A-orthogonal residual squared method for complex non-Hermitian linear systems[J]. Journal of Computational Mathematics, 2014, 32(3): 248-265.
[14] 张建华, 戴华. 求解具有多个右端项线性方程组的总体CGS算法[J]. 高等学校计算数学学报, 2008, 30(4): 390-399.(ZHANG Jianhua, DAI Hua. Global CGS algorithm for linear systems with multiple right-hand sides[J]. Numerical Mathematics a Journal of Chinese Universities, 2008, 30(4): 390-399.(in Chinese))
[15] ZHANG J H, DAI H. Global GPBiCG method for complex non-Hermitian linear systems with multiple right-hand sides[J]. Computational and Applied Mathematics, 2016, 35(1): 171-185.
[16] 张建华. 非Hermitian线性方程组的若干迭代方法及其预处理[D]. 博士学位论文. 南京: 南京航空航天大学, 2016.(ZHANG Jianhua. Some iterative methods and their preconditioned variants for non-Hermitian linear systems[D]. PhD Thesis. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016.(in Chinese))
[17] 富明慧, 李勇息. 求解病态线性方程组的预处理精细积分法[J]. 应用数学和力学, 2018, 39(4): 462-469.(FU Minghui, LI Yongxi. A preconditioned precise integration method for solving ill-conditioned linear equations[J]. Applied Mathematics and Mechanics, 2018, 39(4): 462-469.(in Chinese))
[18] DAVIS T A, HU Y F. The university of Florida sparse matrix collection[J]. ACM Transactions on Mathematical Software, 2011, 38(1): 1-25.