引 言
对机翼气动外形的优化一直是飞机设计研究的重要内容.近年来,基于计算流体动力学(computational fluid dynamics, CFD)的翼形优化成为了重要方法.然而,机翼优化需要反复的CFD计算,较为困难,尤其是在多学科优化[1]和可靠性设计[2]时,采用CFD和其他数值方法的计算时间往往非常巨大,导致相关研究难以开展.为此,近年来研究者积极进行基于实验设计和响应面的优化方法研究[1],但是即使借助实验设计的帮助,构造反映设计变量和目标之间关系的响应面还是需要大量的CFD数值模拟,计算代价也很大.为解决优化过程中CFD计算效率较低的问题,本文研究基于气动力降阶模型的优化方法.
气动力降阶模型(aerodynamic reduced order model,aerodynamic ROM)是一种描述翼型气动特性和扰动之间线性和非线性关系的数学模型[3].它通过已知的试验数据或者仿真结果,辨识扰动和气动特性之间的关系,并以简单的数学函数加以描述,而不是直接对原问题的模型进行求解.由于气动力降阶模型的数学形式简单、计算速度快,近年来发展迅速,并被广泛用于气动弹性振动的研究.Ghoreyshi等[3]综述了非定常气动力降阶模型在飞机控制和颤振分析中的最新进展和存在的问题.Silva[4]提出了基于Volterra级数的非线性气动力降阶模型,用于叶片颤振.Su等[5-6]基于Volterra级数降阶模型研究了叶栅的颤振性能.Xu等[7]利用高阶稀疏形式的Volterra级数降阶模型研究桥面的涡激振动,结果表明,该模型能够很好地再现涡激振动现象.Wong等[8]用Volterra级数降阶模型研究了上游涡对NACA0012翼型气动性能的影响.He[9]回顾了用于叶轮机械内流体分析的Fourier(傅里叶)方法.Yao等[10]提出了一种谐波平衡(harmonic balance,HB)法,研究了自由流中弹性固定圆柱体涡激振动的频率锁定效应,结果表明频率锁定现象被准确地预测.罗骁等[11]基于谐波平衡法建立了尾流激励的叶片振动降阶模型.Bourguet等[12]发展了本征正交分解(proper orthogonal decomposition,POD)的降阶模型,预测了小变形翼型的非定常跨音速可压缩绕流特征.Li等[13]建立了有外生变量动态自回归(auto regressive with exogenous input,ARX)的气动力降阶模型,用于扑翼模式优化,发现由于前缘涡的大尺度分离,大振幅时降阶模型的预测值与CFD模拟结果相差较大.Kou等[14]将ARX模型和径向基神经网络模型相结合,建立了一种降阶模型,用于预测机翼的大运动下非线性非定常气动力响应.
尽管上述研究取得了很大进展,但现有气动力降阶模型只能针对给定的结构.近年来,研究人员提出了研究可变结构的气动力降阶模型.王梓伊等[15]和Zhang等[16]分别研究后发现,目前的气动力降阶模型不能用于结构振型可变的问题,一旦参数改动引起振型变化, 就必须重新建立气动力降阶模型.在气动弹性优化和可靠性设计问题中,结构参数(如梁的尺寸和位置、蒙皮厚度等)需要不断地改变,也就必须不断地进行CFD求解, 计算量极大.针对结构可变的问题,王梓伊等[15]和Zhang等[16]分别提出以径向基函数振型和PCA振型而不是结构的固有振型为基模态,建立了一种适用于结构可变的非定常气动力降阶方法.Chen等[17]结合Kirsch法和POD建立了一种用于可变结构的气动力降阶模型.他们为形状可变结构的气动力降阶模型研究提供了新思路.就目前的研究状况来看, 形状可变结构的气动力降阶模型的研究还较少.
翼型优化是在一个初始翼型的基础上反复调整翼型参数和比较各参数翼型的气动力得到最优翼型的过程,其是一种形状可变的气动力优化问题.在优化过程中只要翼型调整幅度较小,则扰动后翼型的气动力可以采用气动力降阶模型求解.现有的气动力降阶模型都是关于动态位移和变形问题的,而翼型优化是一种静态扰动问题,但静态问题是动态问题的一种特例,因此气动力降阶模型适用于翼型优化问题.基于这两点,本文研究用于翼型优化的气动力降阶模型.
1 基于气动力降阶模型的翼型优化方法
1.1 翼型变化对气动力影响的降阶模型
将翼型周围的流场看作一个独立的气动力系统,系统的输入是翼型形状变量,系统的输出是流场的状态变量,包括流场压力、速度、温度等.这里选翼型表面的空气动力(压力和摩擦力)为输出量,则翼型变化对气动力影响的系统可表示为
p(x),τ(x) =Ψai, i=1,2,…,n,
(1)
式中,p(x)是翼型表面压力系数,τ(x)是翼型表面摩擦力因数,Ψ是系统,ai是第i个形状扰动,x=(x,y,z)为翼型表面的坐标点.
在小扰动条件下气动力系统是弱非线性系统,系统响应可以用非线性的原翼型气动力和扰动引起的响应线性叠加来表示.因此,翼型变化对气动力的影响可以表示为
(2)
式中,A0(x)是原翼型的压力系数,Ai(x)是第i个形状扰动ai引起压力系数变化的核函数,B0(x)是原翼型的表面摩擦力因数,Bi(x)是第i个形状扰动ai引起摩擦力因数变化的核函数.
当A0(x),Ai(x),B0(x)和Bi(x)已知时,在小扰动条件下形状改变后翼型的升力系数和阻力系数可以通过式(3)计算:
(3)
式中,θ是翼型表面法向与x轴的夹角,Cl是升力系数,Cd是阻力系数,![]() 是翼型表面弧长.
是翼型表面弧长.
1.2 基于径向基函数的翼型形状扰动参数化
由于翼型上下表面曲线有无限个坐标点,如果建立气动力降阶模型时逐点扰动翼型,那么输入参数将非常多.这里对翼型参数化,减少气动力降阶模型输入参数的数量.用于翼型优化的参数化方法很多.基于Ferguson曲线的翼型参数化方法,只需要前缘点切向量等6个变量就可以描述多种翼型[18].基于Hicks-Henne基函数的翼型在弦长上形成了6个封闭的单峰基函数,通过各基函数的叠加全局修正翼型[19].类别形状函数变换(class shape transformation, CST)的翼型参数化方法是一种基于形状函数与分类函数相乘的解析方法,该方法的优点是参数具有明确的几何含义、所需控制参数较少、形状拟合精度较高,但是适应能力有限[19].样条曲线翼型参数化方法的节点数量、函数阶数和控制点的横纵坐标均可变化,方法具有很强的灵活性,控制参数的选择对该方法的描述能力有很大影响[20].除这些方法外,常用的翼型参数化还有特征参数描述法、正交基函数法、Bézier曲线法、Bernstein曲线法、复合映射法等[21].
本文中翼型参数化采用基于径向基函数(radial basis function,RBF) [22]的参数化方法,具体的方法是用径向基函数拟合翼型形状扰动量,线性叠加原翼型和扰动量构成新翼型.采用该参数化方法的原因是径向基函数可以光滑地描述任意形状变化[16],另外,径向基函数参数对翼型的影响是局部的,以此减小各个参数对翼型和气动力的影响范围和影响强度.这种翼型描述形式与气动力降阶模型的形式完全一致,便于核函数和形状改变相互对应,非常适合在翼型的气动力降阶模型中采用.
基于径向基函数的参数化翼型如下:

(4)
fk(x)=e-(x-xk)2/0.01, k=1,2,…,6,
(5)
式中,yu0(x)和yd0(x)分别为原翼型的上、下表面点的纵坐标,x为原翼型的上、下表面点的横坐标,yu(x)和yd(x)分别为形状扰动后翼型的上、下表面纵坐标, fk(x)为径向基函数,ak为控制翼型形状的参数.xk为在翼型前缘和后缘之间选取的节点位置,0=x1<x2<…<xn-1<1,本文选x1=0.25,x2=0.35,x3=0.45,x4=0.55,x5=0.65,x6=0.75.
1.3 基于气动力降阶模型的翼型优化步骤
基于气动力降阶模型的优化方法分为以下7个步骤:
1) 采用径向基函数对翼型形状扰动进行参数化;
2) 建立原翼型的CFD模型,获得原翼型的气动力分布;
3) 对翼型形状的参数进行扰动,用CFD得到参数扰动后翼型的气动力分布;
4) 比较扰动前后翼型的气动力,得到形状参数变化对翼型气动力影响的核函数;
5) 用式(2)建立翼型表面压力系数和阻力系数的气动力降阶模型;
6) 给出一组形状参数,用气动力降阶模型和式(3)计算翼型升阻比;
7) 重复步骤6),得到不同参数下的升阻比,以升阻比最大为目标进行翼型优化.
2 基于气动力降阶模型的翼型优化方法的算例验证
2.1 NACA0012翼型气动力降阶模型的建立
以对称的NACA0012翼型为研究对象,验证基于气动力降阶模型的翼型优化方法.翼型的流场特性和气动力降阶模型的核函数用CFD模拟得到.CFD模拟采用Spalart-Allmaras湍流模型,理想空气体,0.63Ma,翼型攻角为0°.上下翼面采用相同的参数化方法.因为NACA0012翼型是对称翼型,上下翼面参数对翼型气动力的影响也是对称的,因此下文只给出上翼面各参数调整后的翼型气动力和核函数.
图1 各个参数扰动后的翼型
Fig. 1 Airfoils with parameter perturbations
(a) 压力系数p(b) 表面摩擦因数τ
(a) Pressure coefficients p(b) Skin friction coefficients τ
图2 上翼面参数扰动的气动力系数
Fig. 2 Upper surface aerodynamic forces due to parameter perturbations
上翼面各个参数扰动后的翼型见图1,图中各参数的扰动量都为0.01.原翼型和上翼面各参数扰动后翼型的压力系数和表面摩擦因数见图2.比较原翼型和上翼面各参数扰动后翼型的气动力并做归一化处理,得到上翼面各参数对压力系数和表面摩擦因数影响的核函数,见图3.将图3的核函数值代入式(2),得到上翼面各个参数对翼型压力系数和表面摩擦因数影响的气动力降阶模型.该气动力降阶模型可以用来预测翼型参数对压力系数和表面摩擦因数的影响,进一步可以用来预测翼型参数修改后翼型的升阻比.
(a) 压力系数核函数Ai(x) (b) 表面摩擦因数核函数 Bi(x)
(a) Pressure coefficient kernels Ai(x) (b) Skin friction coefficient kernels Bi(x)
图3 上翼面参数扰动对气动力影响的核函数
Fig. 3 Kernels of upper surface aerodynamic forces due to parameter perturbations
2.2 基于气动力降阶模型的NACA0012翼型优化
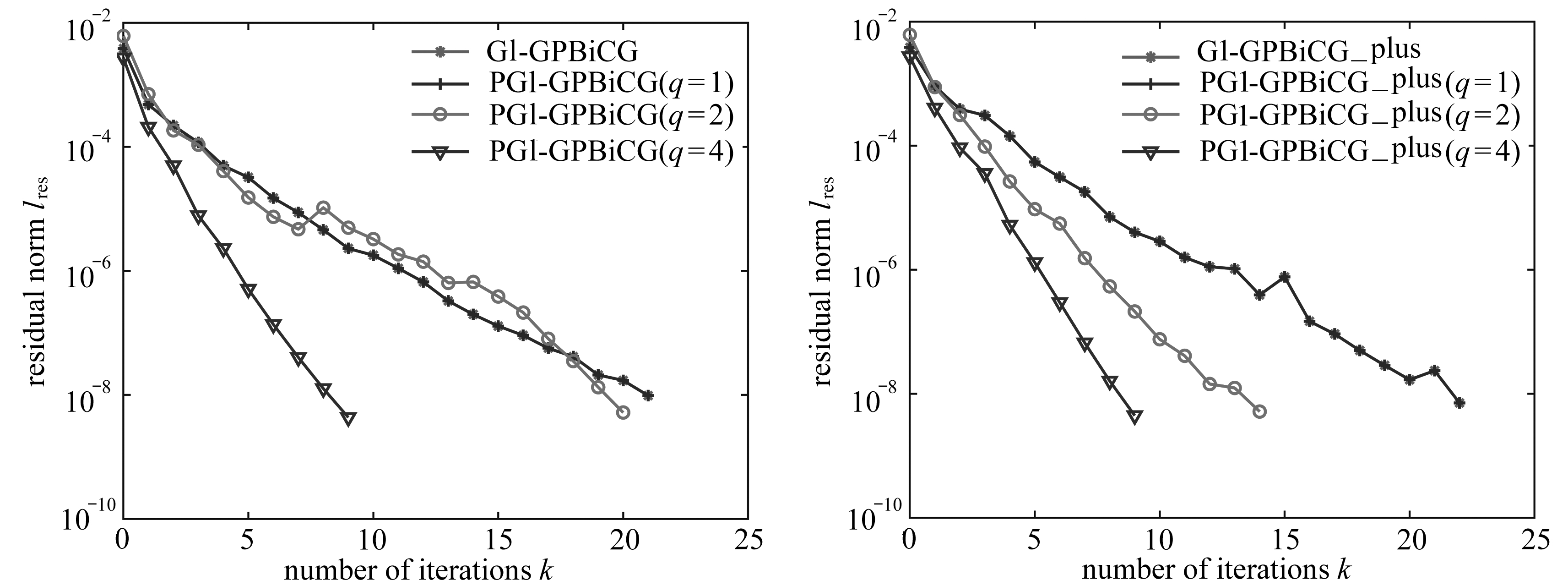
建立NACA0012翼型的气动力降阶模型,用式(3)计算翼型升阻比,采用遗传算法进行优化,以最大升阻比为优化目标,以上下翼面参数为设计变量,设计变量的上下限见表1.优化过程见图4,优化总迭代次数为326次,各变量的优化结果见表1.
表1 翼型的优化结果
Table 1 Optimized results of the airfoil
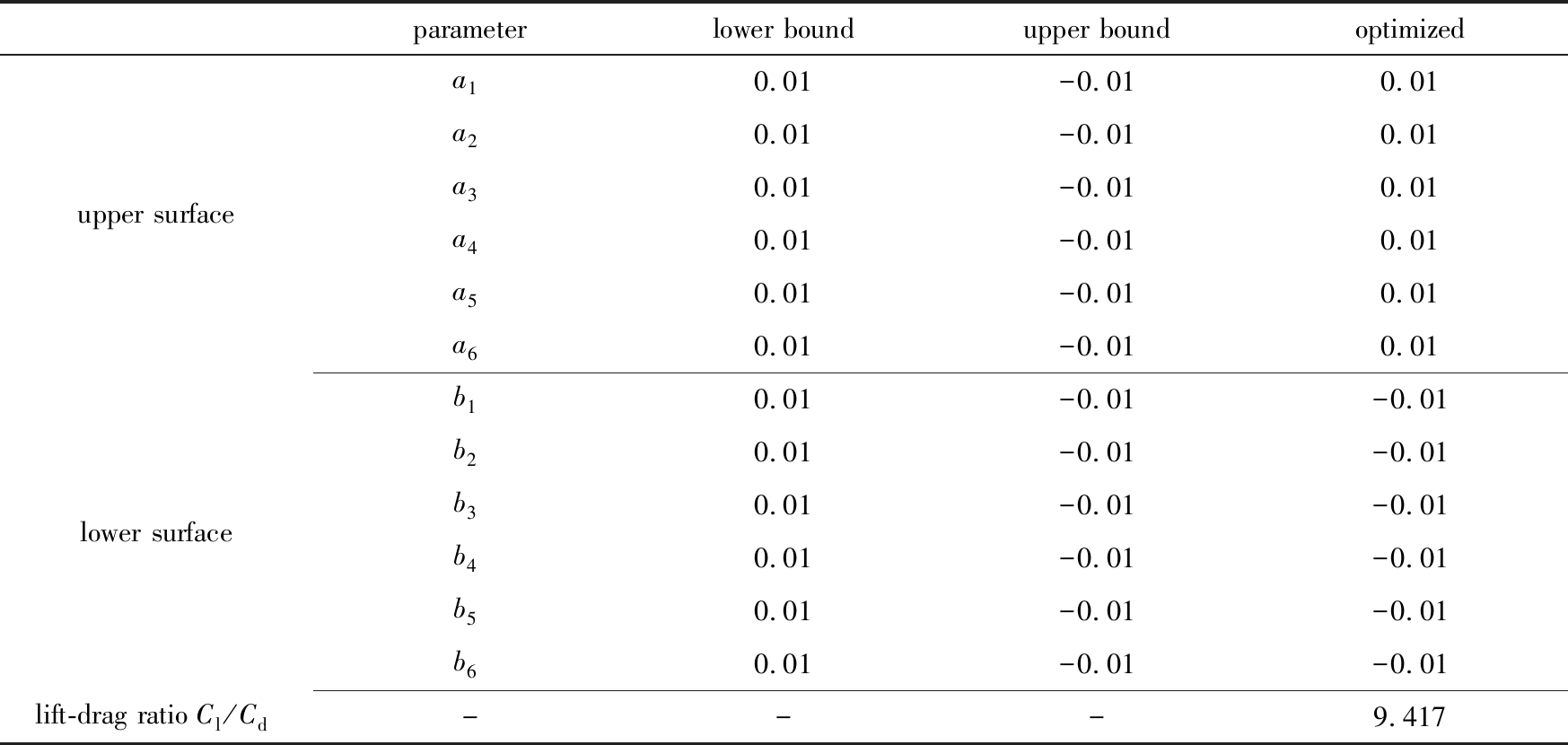
parameterlower boundupper boundoptimizedupper surfacea10.01-0.010.01a20.01-0.010.01a30.01-0.010.01a40.01-0.010.01a50.01-0.010.01a60.01-0.010.01lower surfaceb10.01-0.01-0.01b20.01-0.01-0.01b30.01-0.01-0.01b40.01-0.01-0.01b50.01-0.01-0.01b60.01-0.01-0.01lift-drag ratio Cl/Cd---9.417
(a) 迭代过程
(a) The iteration procedure

(b) 设计变量的优化结果
(b) The optimal results of the variables
图4 优化过程
Fig. 4 The optimization procedure
优化得到的翼型见图5,优化后翼型的压力系数和摩擦力因数见图6.为了验证气动力降阶模型的优化结果,图6也给出了CFD计算得到的优化后翼型的压力系数和摩擦力因数.从图中可以看出气动力降阶模型和CFD的结果一致.这说明基于气动力降阶模型的优化方法是可行的.根据图6所示压力系数和摩擦力因数,用式(3)计算翼型升力、阻力系数和最优升阻比,结果见表2.表2给出了用气动力降阶模型和CFD计算得到的升力系数、阻力系数和最优升阻比,从结果来看降阶模型和CFD的结果基本一致.
需要指出的是,本文所建立的气动力降阶模型是基于小扰动和弱非线性假设的[4].翼型气动性能和外形之间的关系是非线性的,在某些情况下翼型的变化可能导致表面气动力特性明显的改变,如气流分离转捩等[13,18].因此,当翼型变化较大时必须研究强非线性的气动力降阶模型,如:采用神经网络法、插值法和基函数更新法的气动力降阶模型[8,10,14,23].
图5 优化后的翼型
Fig. 5 The optimized airfoil
表2 升阻比Cl/Cd的优化结果
Table 2 Optimized lift-drag ratios Cl/Cd

methodlift coefficient Cldrag coefficient Cdoptimized lift-drag ratio Cl/CdCFD0.151 00.015 239.915ROM0.119 60.012 709.417
采用基于气动力降阶模型的优化方法优化NACA0012翼型,总耗时为4 h,其中包括:原NACA0012翼型的CFD计算耗时0.5 h;6个核函数辨识的CFD计算, 每个耗时0.5 h; 326次优化迭代耗时12 min.如果全部用CFD模型进行优化, 每次CFD计算需要0.5 h, 则总计耗时163 h.由此可知,采用基于气动力降阶模型可以极大地提高优化效率.
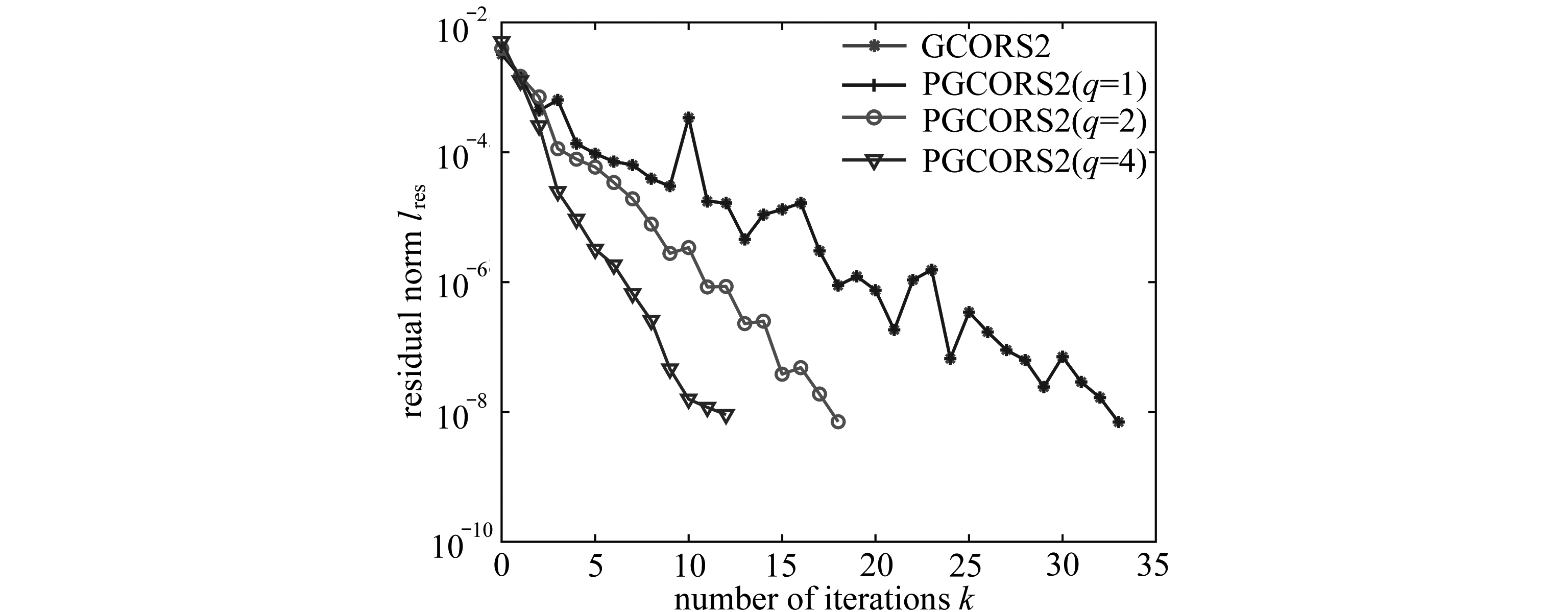
(a) 压力系数p(b) 表面摩擦因数τ
(a) Pressure coefficients p(b) Skin friction coefficients τ
图6 优化后的气动力
Fig. 6 Optimized aerodynamic forces
3 结 论
本文提出基于气动力降阶模型的翼型优化方法.其主要思想是采用径向基函数参数化翼型;用CFD得到参数变化对翼型气动力影响的核函数;基于叠加法建立翼型参数对气动力影响的降阶模型;最后用该气动力降阶模型代替CFD进行翼型优化.NACA0012翼型优化算例表明:气动力降阶模型和CFD得到的翼型压力系数和摩擦力因数基本一致,基于气动力降阶模型的优化方法是可行的,可以极大地提高翼型优化的速度.另外,需要指出的是,气动力降阶模型是基于小扰动和弱非线性假设的,当翼型变化较大时必须研究强非线性的气动力降阶模型,如:采用神经网络法、插值法和基函数更新法的气动力降阶模型.
致谢 本文作者衷心感谢飞行器结构完整性技术工业和信息化部重点实验室基金对本文的资助.
[1] ZHANG M C, GOU W X, LI L, et al. Multidisciplinary design and multi-objective optimization on guide fins of twin-web disk using Kriging surrogate model[J]. Structural & Multidisciplinary Optimization, 2017, 55(1): 361-373.
[2] WEI P F, WANG Y Y, TANG C H. Time-variant global reliability sensitivity analysis of structures with both input random variables and stochastic processes[J]. Structural and Multidisciplinary Optimization, 2017, 55(5): 1883-1898.
[3] GHOREYSHI M, JIRASEK A, CUMMINGS M R. Reduced order unsteady aerodynamic modeling for stability and control analysis using computational fluid dynamics[J]. Progress in Aerospace Sciences, 2014, 71: 167-217.
[4] SILVA W A. Reduced-order models based on linear and nonlinear aerodynamic impulse responses[J]. AIAA Journal, 1999, 233: 1-11.
[5] SU D, ZHANG W W, MA M S, et al. An efficient coupled method of cascade flutter investigation based on reduced order model[C]//49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference. San Jose City, USA, 2013.
[6] SU D, ZHANG W W, YE Z Y. A reduced order model for uncoupled and coupled cascade flutter analysis[J]. Journal of Fluids and Structures, 2016, 61: 410-430.
[7] XU K, ZHAO L, GE Y J. Reduced-order modeling and calculation of vortex-induced vibration for large-span bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2017, 167: 228-241.
[8] WONG A, NITZSCHE F, KHALID M. Formulation of reduced-order models for blade-vortex interaction using modifiedvolterra kernels[C]//The 30th European Rotorcraft Forum(ERF). Marseilles, France, 2004.
[9] HE L. Fourier methods forturbomachinery applications[J]. Progress in Aerospace Sciences, 2010, 46: 329-341.
[10] YAO W G, JAIMAN R K. A harmonic balance technique for the reduced-order computation of vortex-induced vibration[J]. Journal of Fluids and Structures, 2016, 65: 313-332.
[11] 罗骁, 张新燕, 张珺, 等. 基于谐波平衡法的尾流激励的叶片振动降阶模型方法[J]. 应用数学和力学, 2018, 39(8): 892-899.(LUO Xiao, ZHANG Xinyan, ZHANG Jun, et al. A reduced-order model method for blade vibration due to upstream wake based on the harmonic balance method[J]. Applied Mathematics and Mechanics, 2018, 39(8): 892-899.(in Chinese))
[12] BOURGUET R, BRAZA M, DERVIEUX A. Reduced-order modeling of transonic flows around an airfoil submitted to small deformations[J]. Journal of Computational Physics, 2011, 230(1): 159-184.
[13] LI X T, LIU Y L, KOU J Q, et al. Reduced-order thrust modeling for an efficiently flapping airfoil using system identification method[J]. Journal of Fluids and Structures, 2017, 69: 137-153.
[14] KOU J Q, ZHANG W W. Multi-kernel neural networks for nonlinear unsteady aerodynamic reduced-order modeling[J]. Aerospace Science and Technology, 2017, 67: 309-326.
[15] 王梓伊, 张伟伟. 适用于参数可调结构的非定常气动力降阶建模方法[J]. 航空学报, 2017, 38(6): 220829. DOI: 10.7527/S1000-6893.2017.120829.(WANG Ziyi, ZHANG Weiwei. Unsteady aerodynamic reduced-order modeling method for parameter changeable structure[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(6): 220829. DOI: 10.7527/S1000-6893.2017.120829.(in Chinese))
[16] ZHANG W W, CHEN K J, YE Z Y. Unsteady aerodynamic reduced-order modeling of an aeroelastic wing using arbitrary mode shapes[J]. Journal of Fluids and Structures, 2015, 58: 254-270.
[17] CHEN G, LI D F, ZHOU Q, et al. Efficient aeroelastic reduced order model with global structural modifications[J]. Aerospace Science and Technology, 2018, 76: 1-13.
[18] 梅小宁, 杨树兴, 陈军. 低雷诺数小型折叠无人机翼型优化设计[J]. 航空计算技术, 2010, 40(2): 14-17.(MEI Xiaoning, YANG Shuxing, CHEN Jun. Optimization design for low Reynolds number foldable Uav airfoil[J]. Aeronautical Computer Technique, 2010, 40(2): 14-17.(in Chinese))
[19] 黎旭, 龚春林, 谷良贤, 等. 基于CAD的半解析参数化几何建模方法[J]. 计算机与现代化, 2014(4): 1-7.(LI Xu, GONG Chunlin, GU Liangxian, et al. CAD-based semi-analytical parametric geometry modeling method[J]. Computer and Modernization, 2014(4): 1-7.(in Chinese))
[20] 张德虎, 席胜, 田鼎. 典型翼型参数化方法的翼型外形控制能力评估[J]. 航空工程进展, 2014, 5(3): 281-288.(ZHANG Dehu, XI Sheng, TIAN Ding. Geometry control ability evaluation of classical airfoil parametric methods[J]. Advances in Aeronautical Science and Engineering, 2014, 5(3): 281-288.(in Chinese))
[21] 廖炎平, 刘莉, 龙腾. 几种翼型参数化方法研究[J]. 弹箭与制导学报, 2011, 31(3): 160-164.(LIAO Yanping, LIU Li, LONG Teng. The research on some parameterized methods for airfoil[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(3): 160-164.(in Chinese))
[22] 吴宗敏. 径向基函数、散乱数据拟合与无网格偏微分方程数值解[J]. 工程数学学报, 2002, 19(2): 1-12.(WU Zongmin. Radial basis function scattered data interpolation and the meshless method of numerical solution of PDEs[J]. Journal of Engineering Mathematics, 2002, 19(2): 1-12.(in Chinese))
[23] 林谢昭, 胡振明. 流固耦合模型的适应性POD降阶方法研究现状[J]. 机械制造与自动化, 2017, 46(4): 78-84.(LIN Xiezhao, HU Zhenming. Present situation of adaptive POD method for fluid-solid coupling model[J]. Machine Building & Automation, 2017, 46(4): 78-84.(in Chinese))