李煜冬1， 王发
热传导问题广泛存在于数学物理、应用科学、工程等诸多领域[1-6]．研究热传导问题的有效数值模拟方法对实际工程问题有着非常重要的指导意义．
奇异边界法(singular boundary method, SBM)[7]是求解偏微分方程数值解的一种新型无网格边界配点法．该方法的优势在于： 1) 与边界元方法[8-10]相似，该方法仅需边界离散；与边界元方法的不同之处在于无需积分计算．2) 该方法无需网格生成，仅需配置边界源点，适合于复杂几何域和高维问题．3) 该方法避免了传统基本解方法中的虚假边界选取难题，同时保留了后者真正无网格、数学简单且易于编程的优点．奇异边界法的这些优点使得它在偏微分方程初边值问题求解中表现出极大的优势．目前该方法已经被成功应用于声学[11]、弹性力学[12]等领域．
基于动力学问题的时间依赖基本解，奇异边界法近年来已被用于扩散和对流扩散等流体力学问题[13-14]的数值模拟．本文将奇异边界法用于瞬态热传导问题的求解，发展了瞬态热传导问题的奇异边界法．MATLAB是面向科学计算的高级编程语言，是集科学计算、可视化、编程于一体的工程软件开发平台．为了进一步推广奇异边界法的应用，为各种实际工程提供有力的数值计算结果，以及为工程操作提供一些指导信息，本文将进行瞬态热传导问题的奇异边界法MATLAB实现和工具箱制作．
假定Ω是一个有界区域，Γ=∂Ω是区域Ω的边界，x为空间坐标．本文仅考虑二维和三维瞬态热传导问题，x∈ (x1,x2)和x∈ (x1,x2,x3)分别为二维和三维空间坐标．
瞬态热传导问题的控制方程为
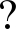2T(x,t), x∈Ω,
(1)
式中k表示热传导率，J/(m · s · K)；ρ为材料密度，kg/m3；c为材料的定压比热容，J/(kg · K)；T(x,t)表示该坐标x在t时刻的温度值，℃．
初始条件和Dirichlet边界条件可以表示为
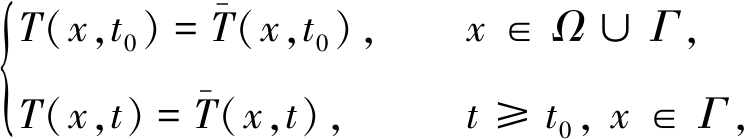
(2)
式中t0表示初始时刻，
表示初始条件和Dirichlet边界条件下的已知温度场．
上述瞬态热传导问题的时空基本解为
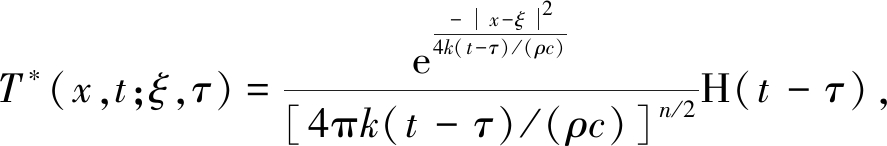
(3)
式中n为空间维度；(x,t)表示物理场点；(ξ,τ)表示物理源点；x-ξ表示点x与点ξ之间的Euclid距离；H(t)为Heaviside(赫维赛德)跃阶函数．
奇异边界法是一种边界型无网格配点法，以基本解作为插值基函数逼近问题的解．该方法将场点和源点重合地布置在物理边界上，通过引入源点强度因子(origin intensity factor, OIF)的概念避免了基本解的源点奇异性．对于上述瞬态热传导问题的求解，奇异边界法的基本公式可表述为
(4)
式中N表示源点数目，αj为待求系数，Aii表示源点强度因子．
数值试验发现，源点强度因子存在且是一个有限值，其仅依赖边界离散点的分布和所涉及的边界条件类型．反插值技术是一种求解源点强度因子的有效方法，下面将给出基于反插值技术的奇异边界法的具体实施过程．
对于瞬态热传导问题，考虑将源点放置在t=t0,x∈Ω∪Γ和t=t0+Δt,x∈Γ的物理边界域上，能够得到t=t0+Δt,x∈Ω的数值解，从而以t=t0+Δt的数值解作为下一步计算的初始条件，重复该过程，直到得到所研究问题的数值解．具体过程如下．
第一步 引入一个满足控制方程(1)的样本解Ts(y,t)，求解下述线性方程组中的未知系数βj：
(5)
式中样本点所对应的时刻tk与源点对应时刻τj不重合，所以式(3)不存在奇异性．计算中，Nk一般应不少于源点数目N，考虑将样本点布置在物理域Ω上，其空间坐标与源点相同，样本点时刻tk与源点时刻t相差一定距离，即tk满足tk=t+bΔt,b∈(0,1)．
第二步 反插值求解源点强度因子，用边界配点xi代替样本点yk，可得到
(6)
第三步 根据问题的初边值条件，利用式(6)所求得的源点强度因子建立奇异边界法的基本方程组，计算问题域内的瞬态热传导问题，求解插值系数αj．
第四步 选取t=t0+Δt时刻物理域内部若干点作为计算点，利用奇异边界法的基本方程组求得当前时刻若干点处的温度值，再以t=t0+Δt的数值解作为下一步计算的初值条件，直到得到所研究问题的奇异边界法数值解．
文献[14]提出的瞬态扩散方程源点强度因子的经验公式，相比于反插值技术更加简单，仅需求解一次线性方程组，在一维和二维问题求解中具有一定优势．这里简单介绍二维瞬态热传导问题的经验公式．其表达式如下：
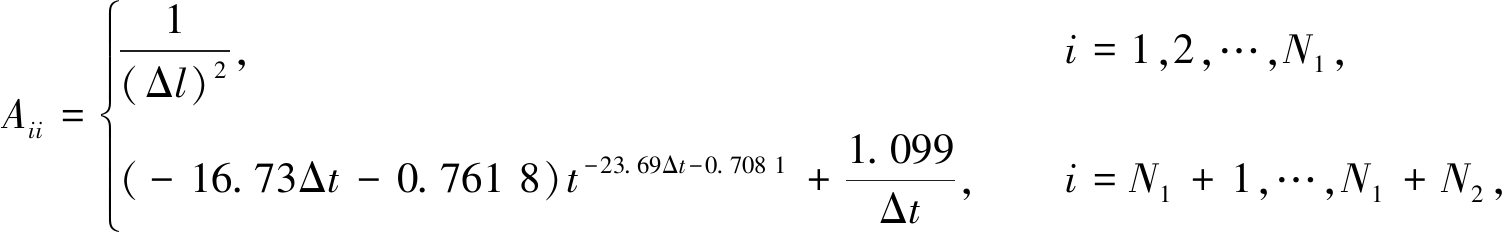
(7)
式中Δl表示空间步长；N1表示初始时刻的物理域内部源点数；N2表示非初始时刻的时间方向(t=t0+nΔt)下的边界源点数．
选取适当的边界节点和时间步长，根据初边值条件，可建立如下基本方程组：
Aα=b，
(8)
式中α为待求系数，b为初边值条件组成的向量．
(9)
针对瞬态热传导问题，以t=t0+Δt的数值解作为下一步插值的初始条件，反复迭代直到获得本文所研究问题的奇异边界法数值解．另外，发现如表1所示布置方式，源点在时间方向上的距离与n无关，则只需要1×N×N的循环次数．由式(8)构建一个通用矩阵，表1的源点布置方式使得迭代算法紧缩，仅需要对初边值条件进行矩阵变换，这样能够很大程度地优化算法，计算速度快，最终得到计算配点的奇异边界法数值解，即热传导的时空解．MATLAB程序见附录．
表1 源点布置方式
Table 1 The source point layout
time domainboundary source pointinternal source pointboundary source point0001dt11dt1dt2dt︙︙︙︙i-1(i-1)dt(i-1)dtidt
注 t=t0+ndt, n=0,1,2,…,i．
Note t=t0+ndt, n=0,1,2,…,i.
图形用户界面(graphics user interface, GUI)是由各种图形对象，如图形窗口、光标、按键、菜单、文字说明等对象构成的用户界面．在GUIDE平台下可实现对用户自定义界面的菜单、快捷键菜单以及各种控件的位置布置及属性编辑，从而设计出满足用户要求的图形界面．
首先通过工具箱生成人机交互界面，进行数据输入，键入回调，并解决数据的输出及显示问题．由此，便可创建求解瞬态热传导问题的图形用户界面，如图1所示．创建完成后便可将其用于实际工程仿真，为各种实际工程问题提供有力的数值计算结果，为工程操作提供一些指导信息．
图1 瞬态热传导求解界面
Fig. 1 The transient heat conduction solution interface
针对二维矩形区域[0.5 m,1.5 m]×[1 m,3 m]的瞬态热传导问题，其边界条件如下：
给定初始时刻、时间步长、最终时刻依次为t0=0，dt=0.01 s和t=1.0 s，分别采用基于反插值技术和经验公式的奇异边界法计算内部测试点在t=1.0 s时刻的温度分布．工具箱计算结果如图2所示．
(a) 基于反插值技术的计算结果
(a) Calculation results based on the inverse interpolation technique
(b) 基于经验公式的计算结果
(b) Calculation results based on the empirical formula
图2 MATLAB工具箱对于二维矩形区域的计算结果
Fig. 2 Calculation results with the MATLAB toolbox for a 2D rectangular zone
从图2中可以看出，无论是反插值技术的奇异边界法，还是经验公式的奇异边界法，均能准确模拟矩形区域上的瞬态热传导问题．也可看出，基于反插值技术的奇异边界法最大误差为0.017，基于经验公式的奇异边界法最大误差为0.007，表明基于经验公式的奇异边界法相比于反插值技术在二维矩形区域的瞬态热传导问题求解中更具优势，且计算简单．另外，MATLAB工具箱具有操作简单，运行速度快，界面交互友好迅捷的特点．
针对三维长方体区域[0.5 m,1.5 m]×[0.5 m,1.5 m]×[0.5 m,1.5 m]的瞬态热传导问题，其精确解如下：
T(x,y,z,t,α)=(sin(πx)+sin(πy)+sin(πz))e-αtπ2, α=0.4．
其边界条件为
Ts(x,y,z,t,α)=(sin(πx)+sin(πy)+sin(πz))e-αtπ2, x,y,z∈Γ， α=0.4．
给定初始时刻、时间步长、最终时刻依次为t0=0，dt=0.1 s和t=2.5 s，计算三维长方体区域的内部测试点在t=2.5 s时刻的奇异边界法数值解．工具箱的计算结果如图3所示．
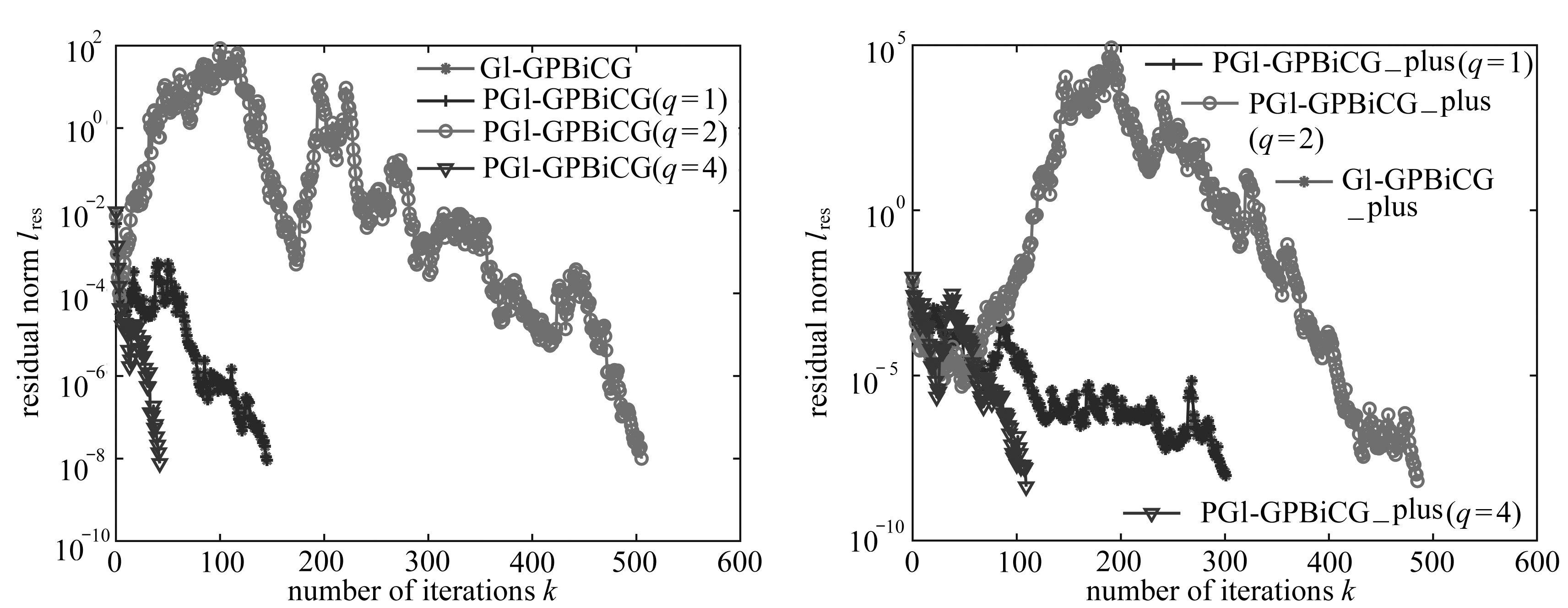
图3 MATLAB工具箱三维长方体区域的计算结果
Fig. 3 Calculation results with the MATLAB toolbox for a 3D rectangular region
从图3可以看出，对于三维长方体区域，同一时刻不同测试点温度的数值结果与相应的精确解高度吻合．此外，不同时刻同一点的温度变化模拟结果也相当精确，表明了本文方法的精确度和有效性．更重要的是，所建立的MATLAB工具箱操作简单，程序运行可靠，且运行速度快，界面交互友好迅捷．
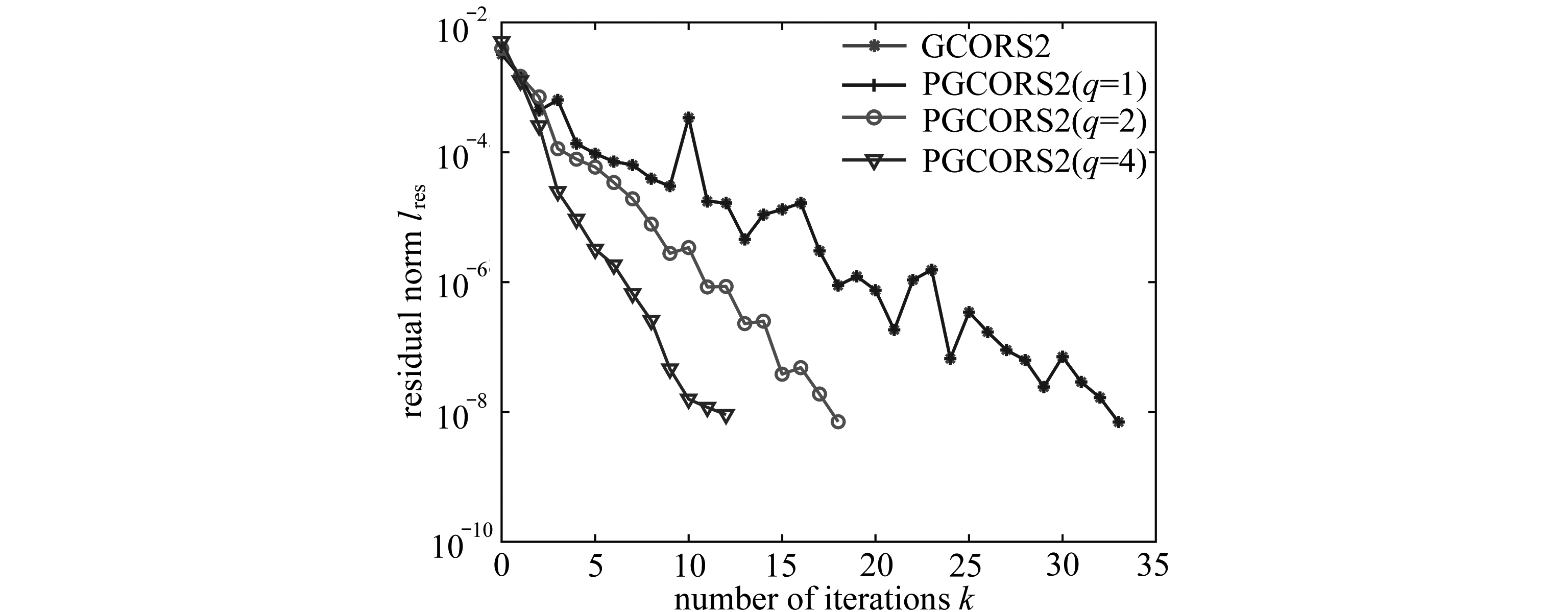
(a) 支撑圆坯 (b) 支撑圆坯边界配点
(a) A supporting round billet (b) Boundary matching points on the supporting round billet
图4 支撑圆坯及其物理条件
Fig. 4 A supporting round billet and the physical conditions
考虑一个由材料铝制作的支撑圆坯，其在低温环境下用于特殊物件的支撑，如图4(a)．这里将奇异边界法用于求解该圆坯瞬态温度场的实际工程问题．
材料铝的比热容c为0.88×103 J/(kg · ℃)，密度ρ为2.702×103 kg/m3，导热系数k或λ为237 J/(m · s · ℃)．对其施加特殊的低温状态，由如下边界温度函数给出：
Ts(x,y,z,t)=(sin(πx)-cos(πy)+sin(πz))e-ktπ2/(ρc)+
x2+y2+z2+6kt/(ρc)-10．
选取如图4(b)所示的125个边界源点上的边界温度值，计算t=3.0 s时刻的内部温度场． 在圆坯内部均匀测试240个计算点，能够得到该试件的温度场分布，计算结果如图5．
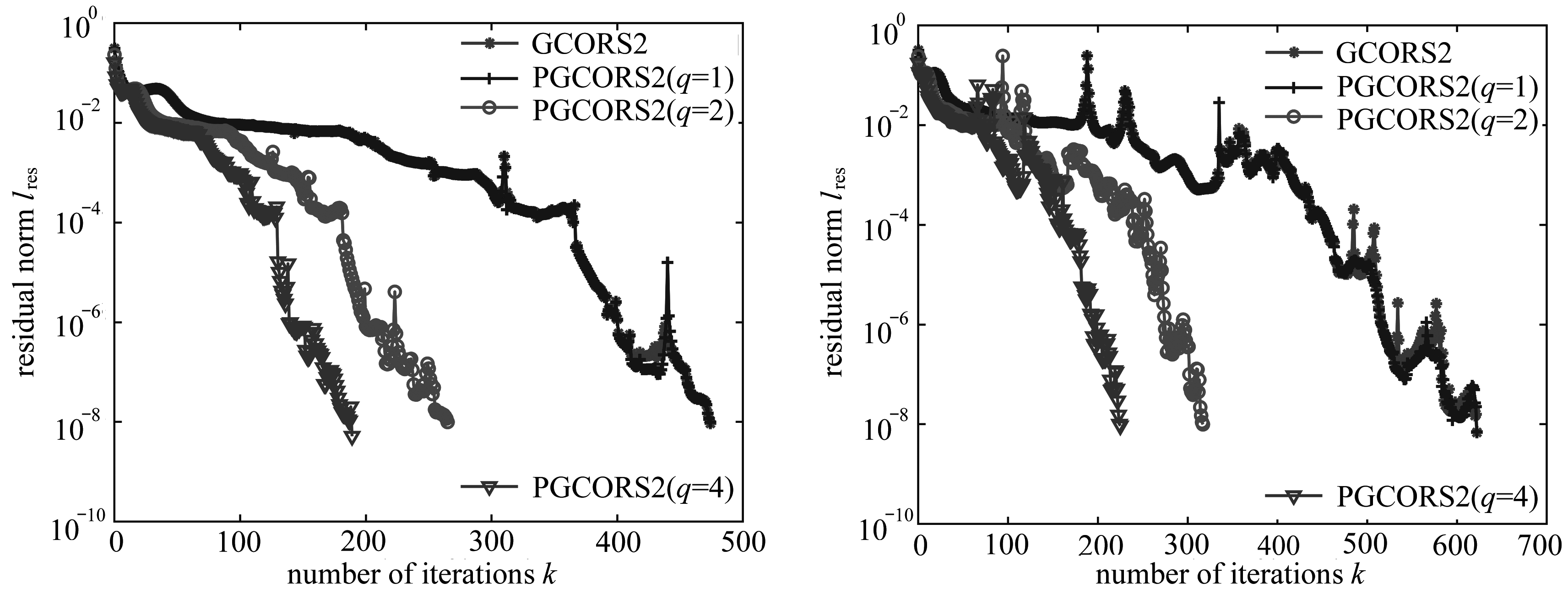
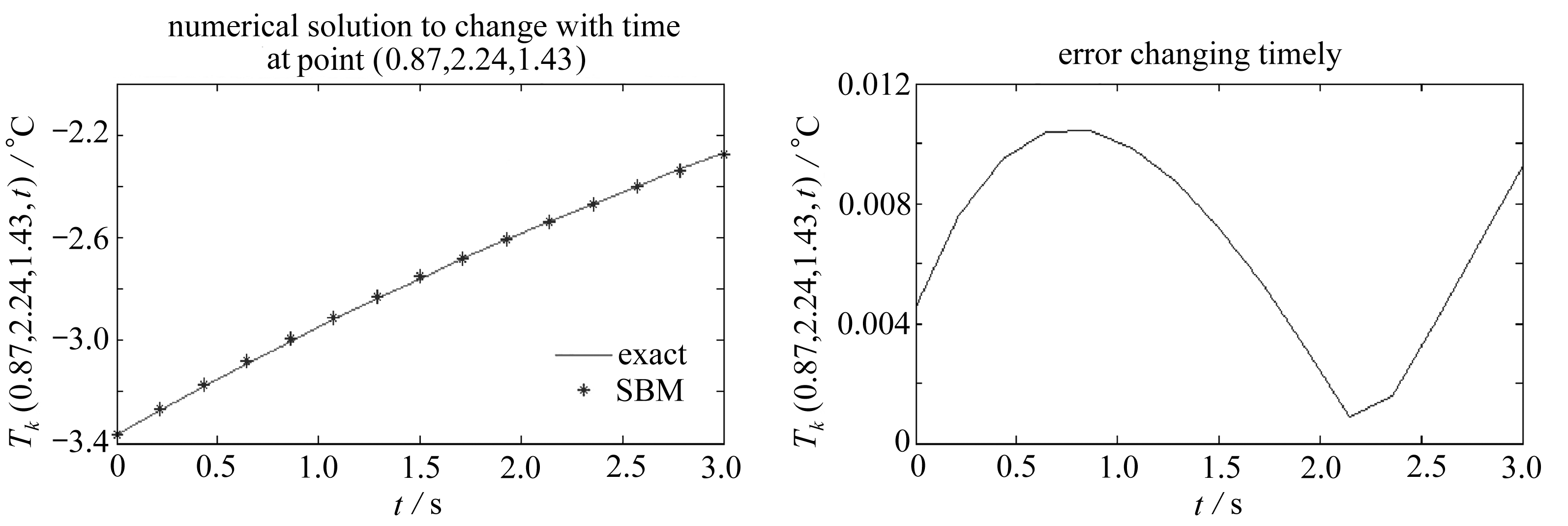
图5 支撑圆坯计算结果
Fig. 5 Calculation results for the supporting round billet
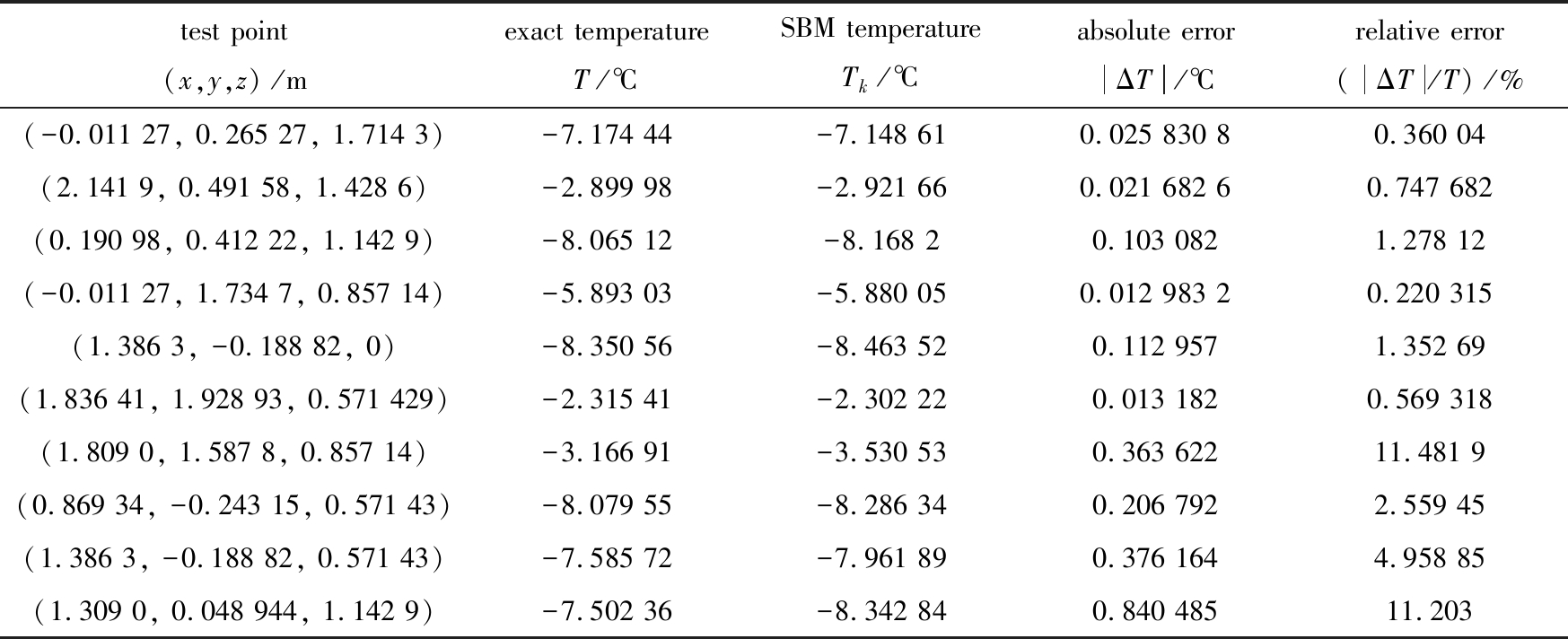
表2 t=3.0 s时刻部分测试点的温度
Table 2 The temperatures of at some test points, t=3.0 s
test point (x,y,z)/mexact temperatureT/℃SBM temperatureTk/℃absolute error ΔT/℃relative error (ΔT/T)/%(-0.011 27, 0.265 27, 1.714 3)-7.174 44-7.148 610.025 830 80.360 04(2.141 9, 0.491 58, 1.428 6)-2.899 98-2.921 660.021 682 60.747 682(0.190 98, 0.412 22, 1.142 9)-8.065 12-8.168 20.103 0821.278 12(-0.011 27, 1.734 7, 0.857 14)-5.893 03-5.880 050.012 983 20.220 315(1.386 3, -0.188 82, 0)-8.350 56-8.463 520.112 9571.352 69(1.836 41, 1.928 93, 0.571 429)-2.315 41-2.302 220.013 1820.569 318(1.809 0, 1.587 8, 0.857 14)-3.166 91-3.530 530.363 62211.481 9(0.869 34, -0.243 15, 0.571 43)-8.079 55-8.286 340.206 7922.559 45(1.386 3, -0.188 82, 0.571 43)-7.585 72-7.961 890.376 1644.958 85(1.309 0, 0.048 944, 1.142 9)-7.502 36-8.342 840.840 48511.203
表2列出了部分计算点的测试信息．可以看出，在不同的计算点上奇异边界法数值解与相应的精确解均十分接近，该界面能够有效地运用奇异边界法模拟支撑圆坯在低温环境下的瞬态温度场．
本文成功将基于反插值技术的奇异边界法用于求解瞬态热传导问题，发展了瞬态热传导的奇异边界法，并进行了MATLAB实现；所建工具箱能有效地解决二维和三维瞬态热传导问题，为瞬态热传导问题的数值分析和仿真提供一种简单高效的模拟工具．
3个算例分别采用工具箱模拟了二维、三维规则物理域和低温环境下支撑圆坯的瞬态热传导问题．其工具箱充分体现了该程序的运行可靠性，且运行速度快，界面交互友好迅捷．可为相关实际工程问题提供有力的数值计算结果，为工程操作提供一些指导信息，其有着非常重要的研究意义．同时也可看出， 本文所发展的奇异边界法数学简单， 编程容易， 计算速度快且精度高．
然而，反插值技术涉及到样本解和样本点，它们的选取具有一定的随意性，会影响算法精度．为此，还需对算法进行进一步的探究和优化．
附 录
MATLAB程序如下：
clear all
t0=0;t=2.5;dt=0.05;alph=0.1; %初始时刻,计算时刻,时间间隔,热传导系数
len=1;nodes=15;step_T=(t-t0)/dt; %边界长度,配点数,时间步长
[A ,Tti]=external_nodes(len,nodes); %空间边界区域布点
[sA]=internal_nodes(len,nodes); %空间内部区域布点
n=length(A);sn=length(sA);
cho=input(‘Enter the value of choosing solution:’); %输入1代表反插值求解；2代表经验公式求解
switch(cho)
case 1
AA=[A sA A]; %空间基础源点外内外布置方式如表1
[xAA,yAA,t,sst,bj,accurate]=timematrix_nodes(alph,AA,step_T,n,sn,dt);
%构建时空矩阵及边值存储矩阵,accurate精确解
[rr1,rr2]=Eucli(AA,n,sn); %Euclidean距离
[mA,mmA,oif]=IITSBM(alph,step_T,n,sn,dt,xAA,yAA,t,sst,rr1,rr2); %IITSBM(b=0.5)
[sbm]=IITSBM_iteration(n,sn,step_T,oif,mA,mmA,bj); %初边值矩阵变换
case 2
[AA2,in_coeff,sn2]=In_value_coeff(A,sA,Tti,alph,step_T,dt,n,sn); %构建非对角初始时空阵
[oif]=Empir_form(Tti,step_T,dt,n,sn2); %经验公式
[value_alph]=sol_alph(A,AA2,in_coeff,oif,alph,step_T,dt,n,sn2); %求解含oif的系数矩阵
[sol]=Coef_ma(A,sA,AA2,alph,step_T,dt,n,sn2); %待求内部区域系数阵
[sbm]=sol*value_alph; %SBM数值解
end.
[1] 赵金军, 彭海峰, 原志超. 三维变系数热传导问题边界元分析中几乎奇异积分计算[J]. 计算力学学报, 2015, 32(1): 7-13.(ZHAO Jinjun, PENG Haifeng, YUAN Zhichao. Evaluation of nearly singular integrals in boundary element analysis of 3D heat conduction problem with variable coefficients[J]. Chinese Journal of Computational Mechanics, 2015, 32(1): 7-13.(in Chinese))
[2] 高效伟, 曾文浩, 崔苗. 等参管单元及其在热传导问题边界元法中的应用[J]. 计算力学学报, 2016, 33(3): 328-334.(GAO Xiaowei, ZENG Wenhao, CUI Miao. Isoparametric tube elements and their application in heat conduction BEM analysis[J]. Chinese Journal of Computational Mechanics, 2016, 33(3): 328-334.(in Chinese))
[3] 李庆华, 陈莘莘. 基于无网格自然邻接点Petrov-Galerkin法求解带源参数瞬态热传导问题[J]. 动力学与控制学报, 2014, 12(2): 178-182.(LI Qinghua, CHEN Shenshen. Analysis of transient heat conduction problems with a source parameter based on meshless natural neighbour Petrov-Galerkin method[J]. Journal of Dynamics and Control, 2014, 12(2): 178-182.(in Chinese))
[4] 陈豪龙, 周焕林, 余波. 瞬态热传导问题的精细积分-双重互易边界元法[J]. 应用力学学报, 2017, 34(5): 835-841.(CHEN Haolong, ZHOU Huanlin, YU Bo. Precise integration DRBEM for solving transient heat conduction problems[J]. Chinese Journal of Applied Mechanics, 2017, 34(5): 835-841.(in Chinese))
[5] YANG K, GAO X W. Radial integration BEM for transient heat conduction problems[J]. Engineering Analysis With Boundary Elements, 2010, 34(6): 557-563.
[6] YU B, ZHOU H L, CHEN H L. Precise time-domain expanding dual reciprocity boundary element method for solving transient heat conduction problems[J]. International Journal of Heat and Mass Transfer, 2015, 91: 110-118.
[7] 陈文. 奇异边界法:一个新的、简单、无网格、边界配点数值方法[J]. 固体力学学报, 2009, 30(6): 592-599.(CHEN Wen. Singular boundary method: a novel, simple, meshfree, boundary collocation numerical method[J]. Chinese Journal of Solid Mechanics, 2009, 30(6): 592-599.(in Chinese))
[8] BREBBIA C A, TELLES J C F, WROBEL L C. Boundary Element Techniques: Theory and Applications in Engineering[M]. Springer Science & Business Media, 2012.
[9] 姚厚朴, 校金友, 文立华. 高阶边界元奇异积分的一种通用高效计算方法[J]. 计算力学学报, 2015, 32(1): 1-6, 13.(YAO H, XIAO Jinyou, WEN Lihua. An efficient method for numerically evaluating singular integrals in high order boundary element method[J]. Chinese Journal of Computational Mechanics, 2015, 32(1): 1-6, 13.(in Chinese))
[10] CUI M, XU B B, FENG W Z. A radial integration boundary element method for solving transient heat conduction problems with heat sources and variable thermal conductivity[J]. Numerical Heat Transfer Fundamentals, 2018, 73(1): 1-18.
[11] QU W, CHEN W, ZHENG C. Diagonal form fast multipole singular boundary method applied to the solution of high-frequency acoustic radiation and scattering[J]. International Journal for Numerical Methods in Engineering, 2017, 111(9): 803-815.
[12] GU Y, CHEN W, ZHANG C Z. Singular boundary method for solving plane strain elastostatic problems[J]. International Journal of Solids & Structure, 2011, 48(18): 2549-2556.
[13] WANG F J, CHEN W. Singular boundary method for transient convection-diffusion problems with time-dependent fundamental solution[J]. International Journal of Heat and Mass Transfer, 2017, 114: 1126-1134.
[14] WANG F J, CHEN W. Accurate empirical formulas for the evaluation of origin intensity factor in singular boundary method using time-dependent diffusion fundamental solution[J]. International Journal of Heat and Mass Transfer, 2016, 103: 360-369.
李煜冬(1997—)，男，硕士(E-mail: 863949642@qq.com);
王发杰(1986—)，男，副教授，博士(E-mail: wfj1218@126.com)；
男，教授，博士，博士生导师(通讯作者. E-mail: chenwen@hhu.edu.cn).