引 言
随着城市化进程的加速和交通运输业的蓬勃发展,交通量增长迅速,相当一部分已建成的高速公路已经不能满足交通量的迅速增长和社会发展的要求.相对于新建公路而言,改扩建可以节约占地,因此越来越多的高速公路需要改建或扩建来提高其通行能力.因此,对改扩建后道路两侧的边坡稳定性进行研究,并分析其滑移路径及过程具有十分重要的研究意义.目前,岩土工程领域常用的数值分析方法有基于连续介质力学的有限元法(FEM)、边界元法(BEM)、有限差分法(FDM)、光滑粒子流体动力学(SPH)法等,以及基于非连续介质力学的离散元法(DEM)、不连续变形分析方法(DDA)、数值流行元法(NMM)等.基于连续介质力学的FEM、FDM等方法由于后期网格畸变,对边坡失稳后的滑坡大变形分析存在一定的困难,仅适用于小变形问题,进行边坡失稳前的稳定性分析.SPH法是在连续介质力学理论下被开发出来的,它不受任何限制,该方法已经被广泛地应用于滑坡计算中[1-2],然而,该方法在边界条件上存在一些缺点.基于非连续介质力学的DEM已经被成功地用于模拟颗粒流动,并与实验室所得的数据相比较[3-5],但由于计算粒子连通性的高运算成本,DEM不能处理大的时间域或空间域,限制了其在岩土方向的发展.为克服以上数值计算方法在边坡稳定性分析中的不足,本文采用FEMLIP对边坡的稳定性进行分析,该方法可以模拟边坡滑坡大变形后的运动过程,十分适合处理大变形问题.
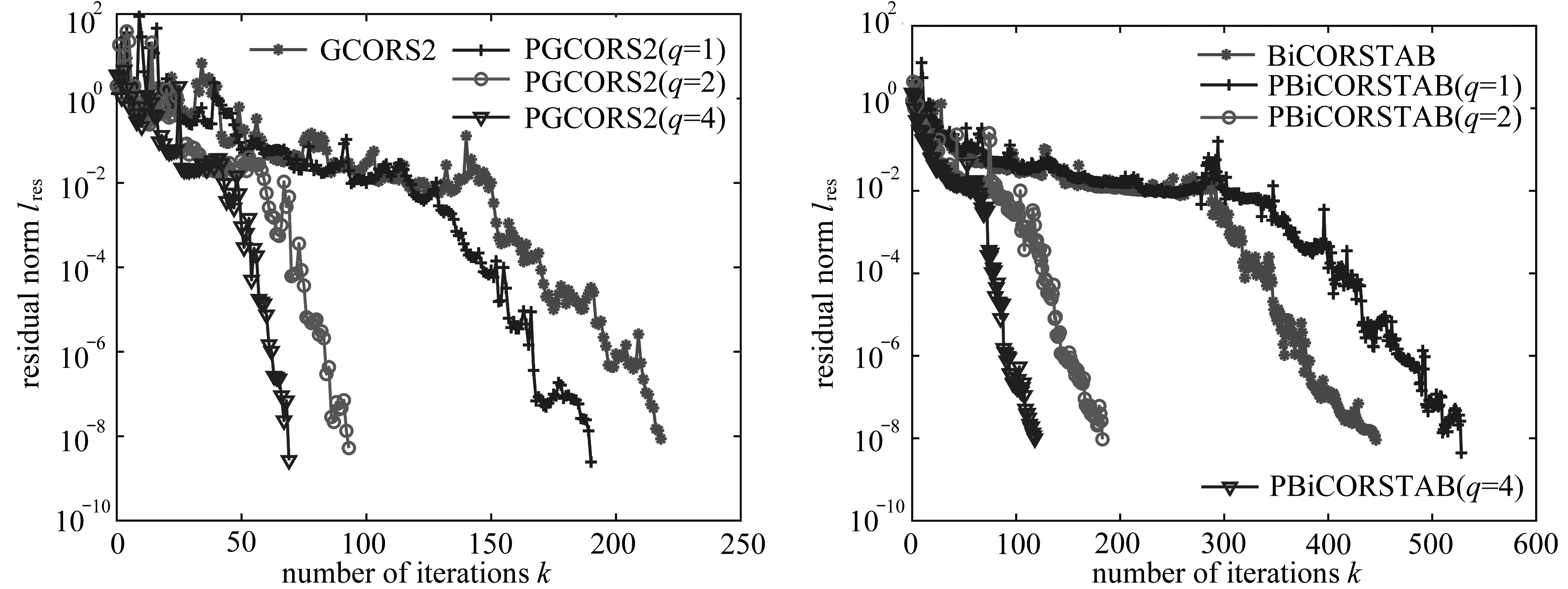
FEMLIP是在传统有限元法的基础上,结合等离子体研究中采用的粒子云网格法,发展起来的一种新的数值计算方法.传统FEM材料点和计算点一致,而FEMLIP数值计算方法是基于Lagrange材料点和Euler(欧拉)网格计算点的一种运动学上的离散,其材料点和计算点不一致,如图1所示.FEMLIP数值计算方法把Euler网格的鲁棒性和Lagrange粒子的灵敏性结合起来,并且可以考虑材料的历史行为,十分适合处理大变形问题.FEMLIP最早由Moresi和Dufour等[6]提出,用于解决地球物理方面的问题;Cuomo等[7]首次将黏弹塑性模型引入Lagrange积分点有限元程序中,并研究了排水条件下边坡垂直开挖的数值模拟;Prime等[8-9]将弹塑性关系与Bingham(宾汉姆)黏性定律相结合,建立了一种新的本构模型,并模拟了泥石流和支挡结构的相互作用;Li等[10-11]用流弹塑性模型模拟饱和土体,考虑饱和土体的渗透效应与整个泥浆流动的过程,并进行了降雨诱发泥石流的模拟.目前国内关于FEMLIP的研究较少,且研究的重点主要集中于地球物理领域.蒙伟娟、陈祖安等[12]基于非Newton(牛顿)流体的有效黏度模型,应用FEMLIP数值计算方法模拟地幔柱与岩石圈的相互作用过程;白帆、陈祖安等[13]基于岩石流变本构关系以及不同的熔融损耗关系,利用FEMLIP数值计算方法模拟地幔柱与岩石圈相互作用过程中的熔融损耗的变化.国内采用FEMLIP数值计算方法进行边坡的稳定性分析及边坡失稳后的滑坡大变形分析的研究还较少.
(a) FEM,材料点与计算点一致 (b) FEMLIP,材料点与计算点不一致
(a) FEM, material points and computational(b) FEMLIP, material points and computational points coincide points do not coincide
图1 传统FEM与FEMLIP对比
Fig.1 Comparison between the traditional FEM and the FEMLIP
本文在前人的研究基础上,主要进行了以下工作:首先采用C语言编写了基于黏弹塑性本构模型的边坡稳定性及失稳后滑坡大变形分析的程序;其次,通过一个典型的边坡稳定性分析例子,验证了本数值计算方法在模拟边坡稳定性时的正确性;最后,通过设计不同的边坡坡角及边坡强度研究其对边坡的稳定性及边坡滑坡的位移及速度的影响,并将结果与Katz等[14]采用DEM得到的结果进行对比分析,验证了FEMLIP数值计算方法模拟边坡稳定性的准确性.
1 理 论 基 础
FEMLIP数值计算方法的基本思想是Lagrange材料点和Euler网格计算节点在运动学上的离散性,将问题域用Euler网格和Lagrange材料点来描述,Lagrange材料点只代表在不同材料变形过程中携带的物理信息,且Euler网格在计算过程中不会同材料一起发生变形.对于给定的材料,把材料点作为单元上的积分点,利用Euler网格节点处的平衡方程计算速度场.在每个计算步结束时,速度从节点被内插到材料点,材料点相应地到达一个新状态.由于材料点存储了所有的材料属性,因此可以精确地跟踪它们.
1.1 平衡方程及变分方程
不考虑惯性力时,Euler网格节点处的平衡方程为
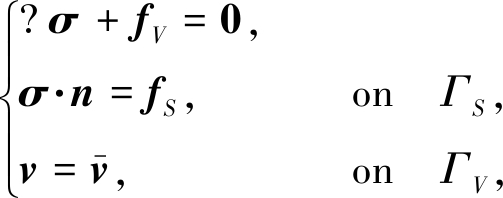
(1)
式中σ为Cauchy(柯西)应力,n为自由度方向,v为速度,![]() 为平均速度,fV为体力,fS为面力,ΓS为面力作用域的边界,ΓV为体力作用域的边界.
为平均速度,fV为体力,fS为面力,ΓS为面力作用域的边界,ΓV为体力作用域的边界.
虚拟速度场在运动学上必须满足下式:
v*=0,
(2)
式中v*为虚拟速度场.
该虚拟速度场对应于虚拟变形,即D(v*).更新的Lagrange法中的虚功原理反映了施加到系统上的外力在位移上所做的外虚功等于应力合力在变形上所做的内虚功,即
Pint=Pext ⟺ ∀![]()
(3)
式中Pint为内虚功,Pext为外虚功, v*T为虚拟速度场的转置矩阵.
对于不可压缩材料,式(3)需增加一项,该项必须是可积分的,但不一定是连续的,式(3)变为
∀![]()
(4)
式中q*为虚拟压力,D为应变率张量,tr(D)=Dii,q为压力,ξ为压缩模量.式(4)严格等同于相关的Euler方程,并将作为FEMLIP数值计算方法公式的基础.
1.2 控制方程
FEMLIP数值计算方法采用的动量方程[15]为
(5)
式中g为重力加速度,ρ为材料密度,α为热膨胀率,T为温度,η为黏度,Dij=(∂vi/∂xj+∂vj/∂xi)/2为变形速率张量,δij为Kronecker delta函数,
式(5)可以看作没有惯性项的Navier-Stokes方程,即Stokes方程.
为了简化结果,假设材料是不可压缩的,即
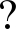 ·V=0.
·V=0.
(6)
1.3 本构关系
FEMLIP数值计算方法采用黏弹塑性本构模型,该模型中应变率张量由黏性应变率张量、弹性应变率张量和塑性应变率张量三部分组成[16]:
(7)
其中,![]() 为Jaumann条件,
为Jaumann条件,
(8)
结合上式,用差分形式表示τ,得
(9)
式中,![]() 为Jaumann应力速率,τ为Cauchy应力偏张量,G为剪切模量,λ为塑性乘子,D′为偏应变率张量,
为Jaumann应力速率,τ为Cauchy应力偏张量,G为剪切模量,λ为塑性乘子,D′为偏应变率张量,![]() 为黏性偏应变率张量,
为黏性偏应变率张量,![]() 为弹性偏应变率张量,
为弹性偏应变率张量,![]() 为塑性偏应变率张量,Δte为时间步长.
为塑性偏应变率张量,Δte为时间步长.
1.4 屈服准则
屈服时,令τ=τyield,式(9)可写为
(10)
其中
FEMLIP数值计算方法实际的破坏机理是通过有效黏度建立的[17]:
(11)
其中,J2为偏应变率张量第二不变量.屈服应力服从Mohr-Coulomb(摩尔-库伦)屈服准则,表达式如下:
τyield=C0+μσn,
(12)
式中C0为黏聚力,μ为摩擦因数,σn是破坏面上的法向应力.
1.5 应变软化
Tackley[18]已经证明,对岩体破坏后流动模拟中需要某种应变或应变率软化机制,以稳定破坏区域,通过修改上式得
(13)
(14)
式中,ε为应变,![]() 为应变率,ε0是应变软化项,
为应变率,ε0是应变软化项,![]() 是应变率软化项,
是应变率软化项,![]() 指数n1和n2分别描述函数f对应变及应变率的非线性关系[15].
指数n1和n2分别描述函数f对应变及应变率的非线性关系[15].
2 FEMLIP数值计算方法程序实现
根据上文所述的FEMLIP数值计算方法的基本方程及计算流程,本文基于C语言编制了用于分析边坡稳定性及边坡失稳后滑坡大变形的计算程序Ellipsis 3D,程序流程图见图2.
FEMLIP数值计算方法的基本流程如下:
1) 首先在前处理模块建立模型,模型由通用设置、对流-扩散参数、求解器设置、网格设置、输出文件、初始条件、边界条件及材料参数组成.其中通用设置、对流-扩散参数以及求解器可以按照用户需求进行修改,默认设置也可以满足基本的数值模拟需求;程序默认网格采用直角坐标系,默认z轴朝向正下方;该程序可以输出多个ASCII文件、PPM图像文件和二进制文件,其中ASCII文件包含网格节点信息(如速度、温度和压力等),二进制文件包含粒子信息,在此步骤中设置监测点、粒子的输出信息以及PPM图像的显示信息;在初始条件中,可以通过建立矩形、三角形和圆形来定义初始材料,并赋予其材料类型;在边界条件中,可以定义初始应力、速度和温度的边界条件;在材料参数中,可以单独定义每种材料的物理性质,例如密度、黏聚力等.
2) 执行程序,在每个时间步开始时,由Euler网格节点处的平衡方程计算节点处的速度场,时间步结束时,速度从节点被内插到Lagrange材料点.
3) 求解模型在此状态时内力及外力作用下的应力及应变率.
4) 利用二阶Runge-Kutta积分方法更新材料点的位置,材料点相应地遍历Euler网格达到新的状态,进入下一个时间步循环.
5) 将数据结果转换为可输出格式,输出所需的数据结果(如位移、速度及压力等).
6) 利用其他软件对数据进行后处理.
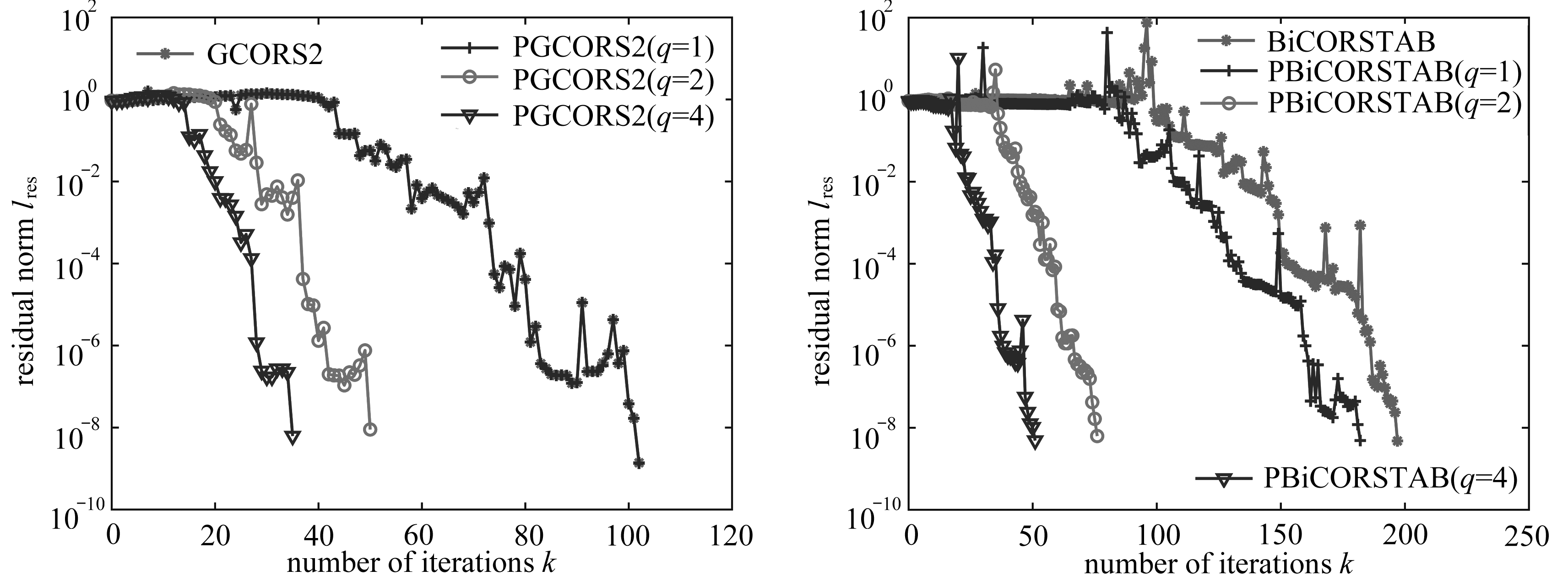
图2 Ellipsis 3D计算流程图
Fig. 2 The flow chart for the Ellipsis 3D calculation
3 FEMLIP数值计算方法的应用
3.1 边坡稳定性分析算例验证
由于FEMLIP数值计算方法的网格节点和材料点的离散性,FEMLIP具有支持大变形,同时追踪内部变量的能力,所以该方法既可以计算边坡的稳定性,同时可以对边坡失稳破坏后的滑坡大变形阶段进行分析.为验证本方法在分析边坡稳定性中的准确性,本文通过一个二维均质土坡分析算例进行验证,很多学者已采用多种方法对该算例进行验证分析(如极限平衡法、有限元法、SPH法等).算例边坡材料参数和FEMLIP模型如表1和图3所示.
表1 土体边坡材料参数
Table 1 Soil slope material parameters

cohesionc/Pafriction angleφ/(°)bulk density γ/(N·m-3)elastic modulus E/PaPoisson’s ratioν1.238×104202.0×1041.0×1080.35
图3 边坡算例模型图
Fig. 3 The slope model
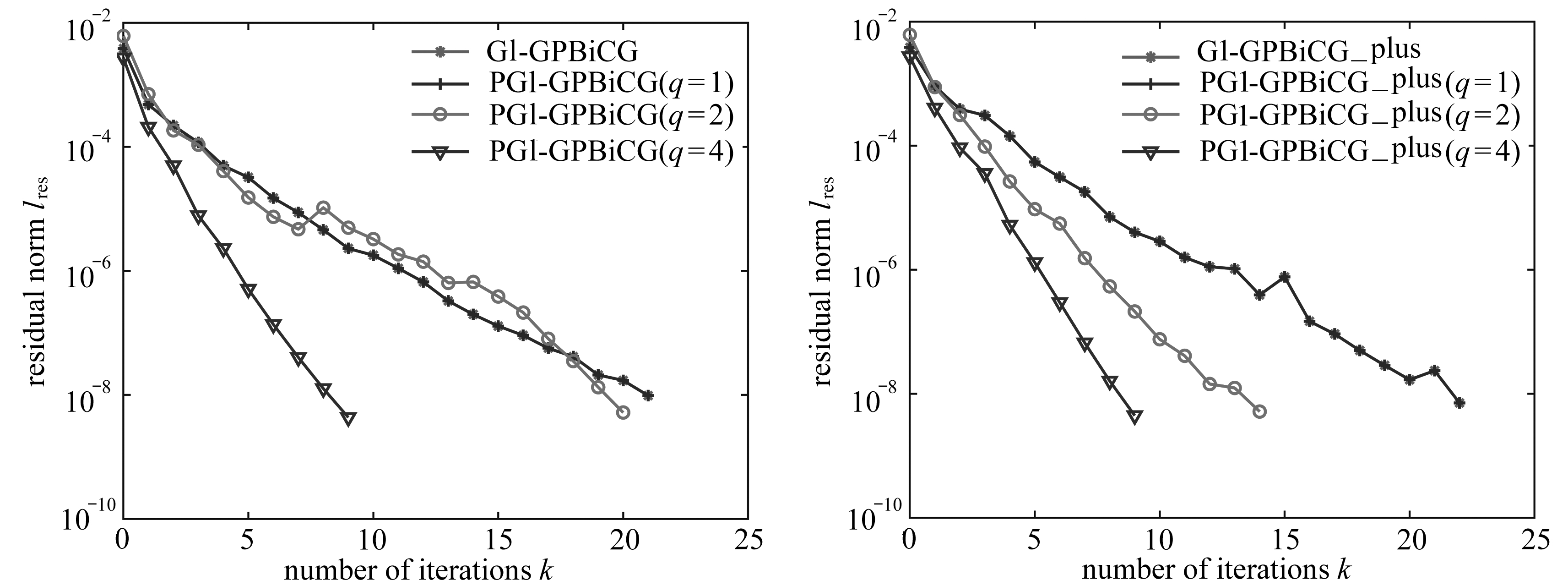
(a) Fs=1.01 (b) Fs=1.01 (c) Fs=1.03
图4 边坡塑性区分布图
Fig. 4 Distributions of the plastic zone of the slope
如图4所示,边坡塑性应变区从坡脚开始往坡顶贯通,滑移面近似呈圆弧形,滑移面与采用有限元法和极限平衡法得到的一致.按极限平衡法计算结果,该算例边坡的稳定性安全系数为1.0[19].由图4(c)可以看出,当安全系数达到1.03时,塑性区贯通,表示在FEMLIP程序中该边坡稳定性安全系数为1.03,这与极限平衡法得到的结果误差仅为3%,表明FEMLIP数值方法可以准确地对边坡的稳定性进行分析.
图5为边坡失稳破坏全过程图.从图5可以看出,边坡滑裂面近似呈圆弧形,符合边坡破坏的基本形式.在滑坡开始的阶段,滑坡体基本呈整体圆弧滑动,滑裂面附近的粒子发生较大的滑动.在滑坡发生的后期阶段,坡脚处粒子停止滑动,滑坡体在坡脚处堆积.

(a) Step 1 (b) Step 6 (c) Step 20
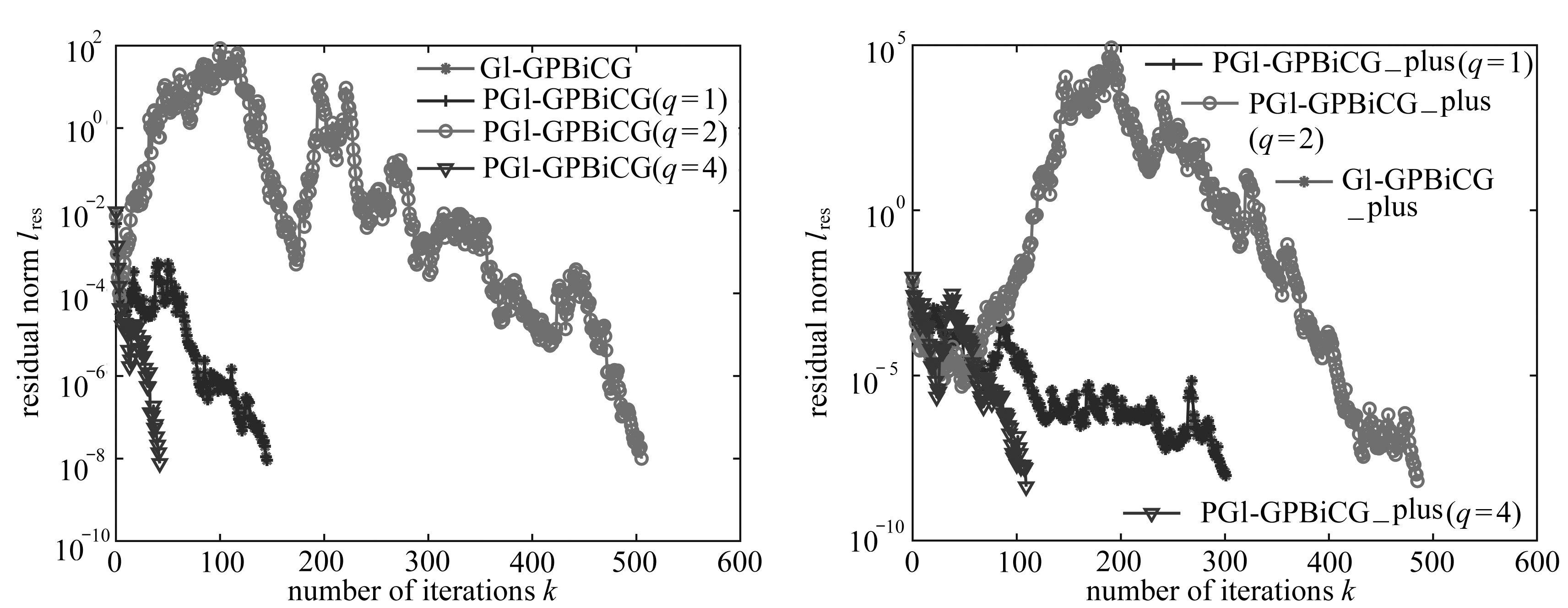
(d) Step 36 (e) Step 48 (f) Step 70
图5 边坡失稳破坏全过程图
Fig. 5 The slope instability process
3.2 边坡失稳破坏全过程的数值模拟
为了研究边坡坡角和强度对边坡稳定性的影响,建立边坡分析模型,如图6所示.模型设置3个监测点,监测边坡顶部、中部和坡脚的位移与速度,监测点并未固定于网格上,而是随粒子进行移动.保持边坡分析模型的高度不变,通过设置不同的长度L,得到不同边坡角β,同时设置黏聚力c为0.69 MPa,1.0 MPa,1.3 MPa,2.27 MPa,研究边坡坡角及强度对边坡稳定性及边坡失稳后滑坡大变形的影响,并将结果与Katz等[14]采用DEM得到的结果进行对比分析.边坡分析模型的物理力学参数见表2.
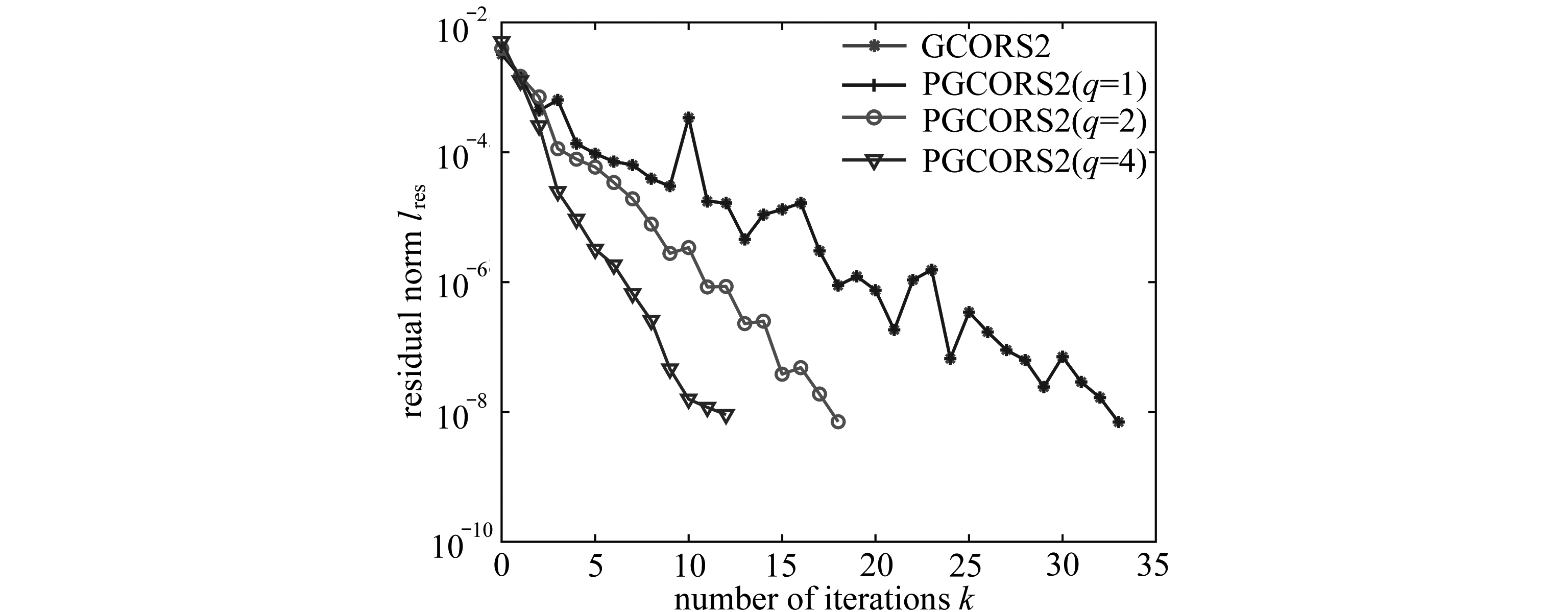
图6 FEMLIP边坡分析模型示意图
Fig. 6 The slope analysis model of the FEMLIP
边坡分析模型的L值从19 m逐渐缩短为3 m,本文共研究了10个不同坡角的边坡破坏情况,限于篇幅,只分析具有代表性的27°,33°,40°,53°和65°共5种坡角的边坡破坏情况.
图7所示为β=53°,不同黏聚力时边坡的滑移面.从图7可以看出利用FEMLIP程序进行边坡稳定性分析时,边坡滑移面呈圆弧形,符合边坡破坏的基本形式.随着黏聚力c值的增大,边坡的滑移量减小,滑移面向坡面方向移动,说明随着边坡强度增大,边坡的滑移量减小,与Katz等[14]采用DEM得到的不同强度下边坡的滑移规律基本相似.
表2 边坡分析模型的材料参数
Table 2 Material parameters of the slope analysis model

itemvalueslope angle β/(°)27,33,40,53,65cohesion c/MPa0.69,1.0,1.3,2.27friction angle φ/(°)31density ρ/(kg/m3)2.5×103elastic modulus E/Pa1.0×108Poisson’s ratio ν0.5coefficient of friction μ0.15
(a) c=0.69 MPa (b) c=1.0 MPa (c) c=1.3 MPa (d) c=2.27 MPa
图7 β=53°时,不同c值边坡的滑移面
Fig. 7 Slip surfaces of the slope with different cohesion values, β=53°
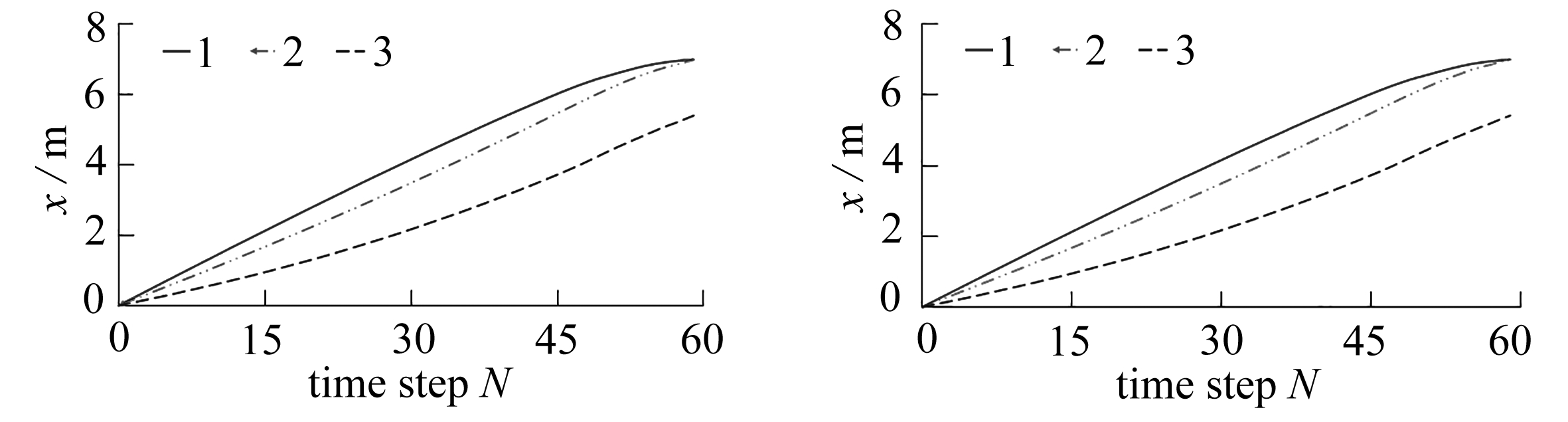
(a) c=0.69 MPa (b) c=1.0 MPa

(c) c=1.3 MPa (d) c=2.27 MPa
图8 β=53°时,不同c值监测点水平位移-时间曲线
Fig. 8 Horizontal displacement-time curves at the monitoring point with different cohesion values, β=53°
图8和图9分别为β=53°,不同黏聚力时监测点水平位移-时间曲线和水平速度-时间曲线图.由图8和图9可以看出,边坡坡角β为53°时,不同黏聚力下边坡滑坡的位移和速度基本相同,这种情况下黏聚力对滑坡的位移和速度的影响较小.由图9可以看出,边坡滑坡时坡脚的水平速度最大,其次为坡中,坡顶的水平速度最小.
从图10数值计算结果可以看出,利用FEMLIP程序进行滑坡模拟,滑移面呈圆弧形,符合边坡破坏的基本形式.随着边坡角度的减小,边坡的滑坡量减小,且滑移面向坡面方向移动,这与Katz等[14]采用DEM得到的不同坡角下边坡的滑移面基本相似.

(a) c=0.69 MPa (b) c=1.0 MPa
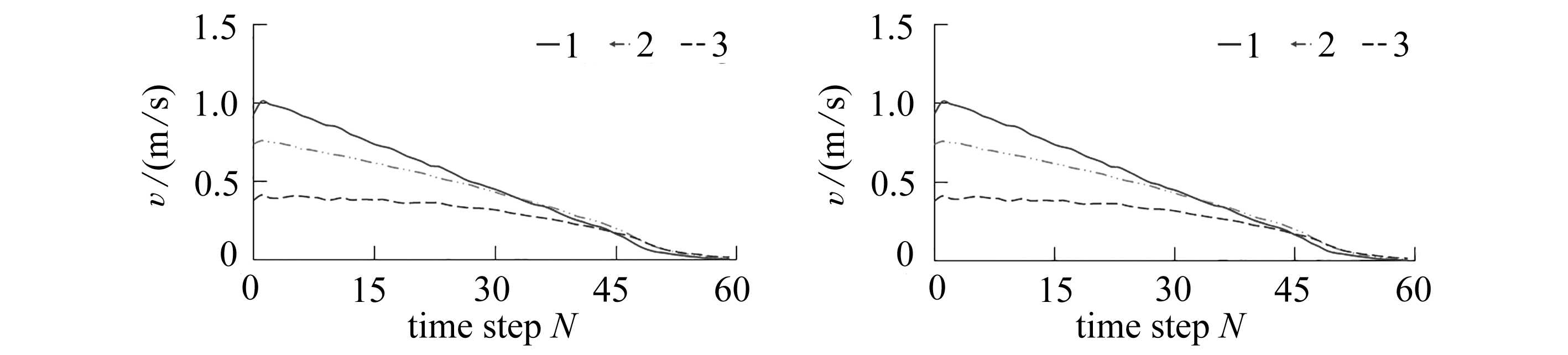
(c) c=1.3 MPa (d) c=2.27 MPa
图9 β=53°时,不同c值监测点水平速度-时间曲线
Fig. 9 Horizontal velocity-time curves at the monitoring point with different cohesion values, β=53°

(a) β=65° (b) β=53° (c) β=40°

(d) β=33° (e) β=27°
图10 黏聚力c=1.0 MPa时,不同坡角下边坡的破坏情况
Fig. 10 Destruction modes of the slope under different slope angles, c=1.0 MPa

(a) Monitoring point 1 (b) Monitoring point 2 (c) Monitoring point 3
图11 c=1.0 MPa时,各监测点水平位移-时间关系曲线
Fig. 11 Horizontal displacement-time curves at the monitoring point, c=1.0 MPa
结合图 11与图 12可以看出,在滑坡开始很短的时间内,边坡顶部、中部、底部监测点的水平方向速度迅速增加到一个较高的水平,此时边坡坡脚水平方向速度最大,坡中次之,顶部最小.随后,边坡水平速度迅速减小,并趋近于0,滑坡停止.通过对比不同坡角的边坡坡脚滑坡水平位移-时间曲线和水平速度-时间曲线,可以得到随着边坡坡角的减小,边坡坡脚的滑坡速度降低、位移减小,边坡角为27°时,边坡滑坡速度最先降为0,位移保持不变,边坡停止滑动.对于边坡的坡中和坡顶,边坡坡角越小,滑坡位移越大,滑坡越早停止,边坡角为40°时,滑坡速度最大.
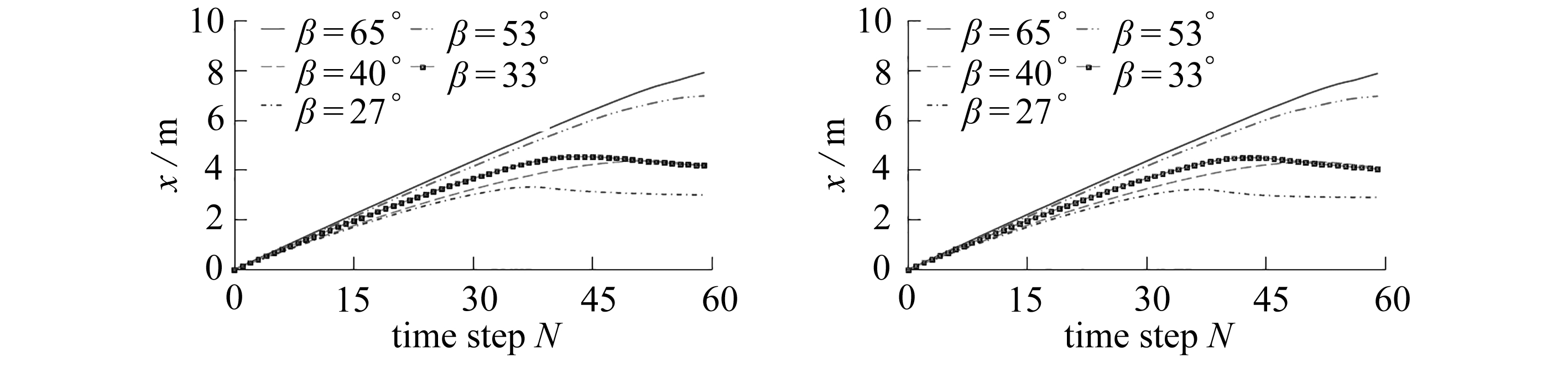
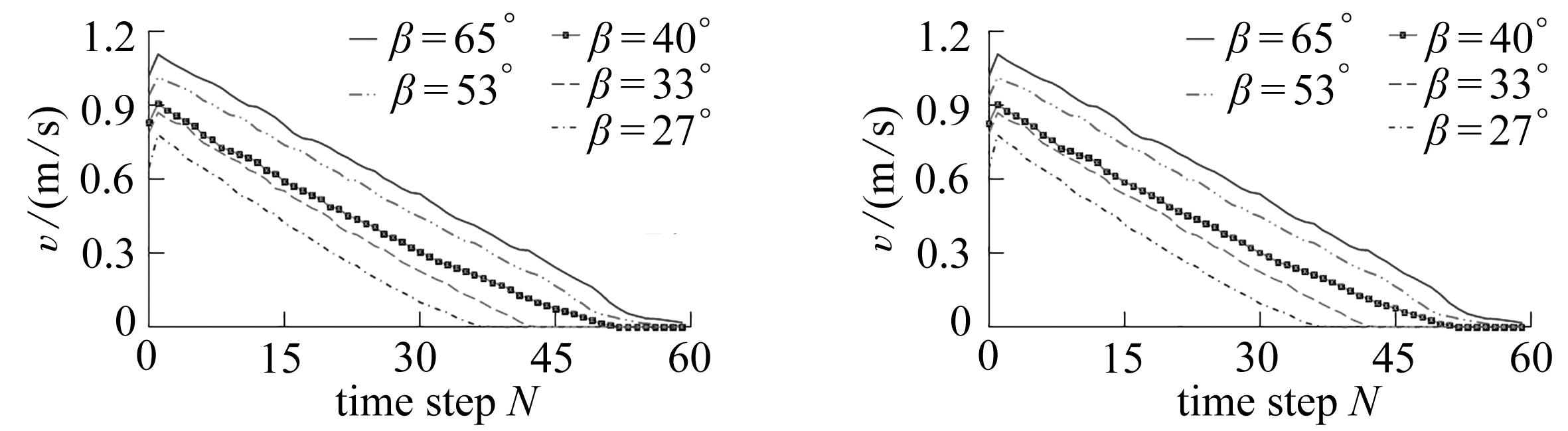
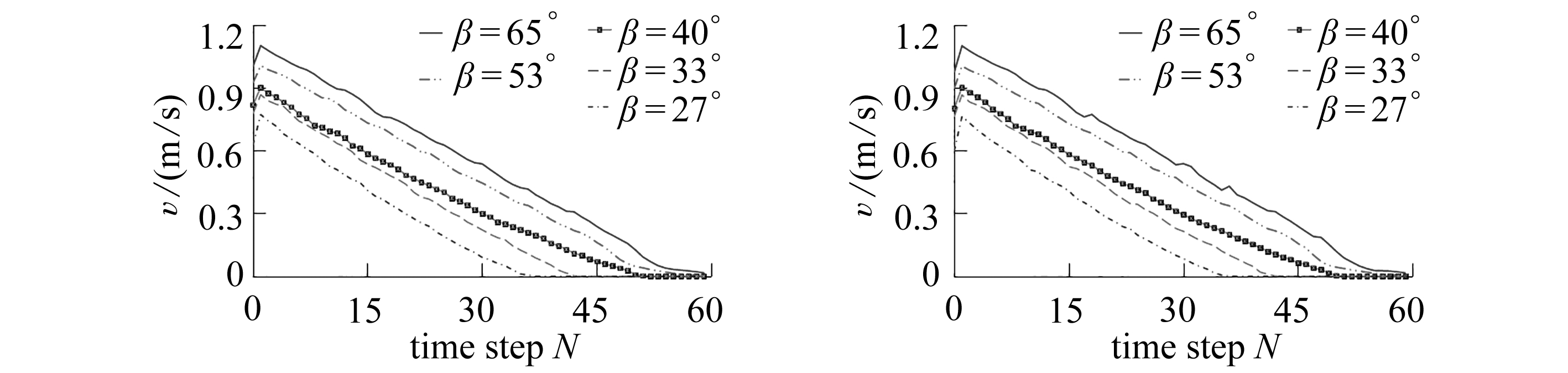
由图13和图14可以看出,在边坡坡角相同时,不同黏聚力下的边坡坡脚的水平位移和水平速度基本相同,表明在边坡破坏后,边坡的黏聚力对边坡的滑坡速度影响较小.在边坡的黏聚力相同时,边坡坡脚的水平位移和水平速度随着边坡坡角的增大而增大,当边坡角度为27°时,边坡坡脚速度最先降为0,滑坡停止.

(a) Monitoring point 1 (b) Monitoring point 2 (c) Monitoring point 3
图12 c=1.0 MPa时,各监测点水平速度-时间关系曲线
Fig. 12 Horizontal velocity-time curves at the monitoring point, c=1.0 MPa
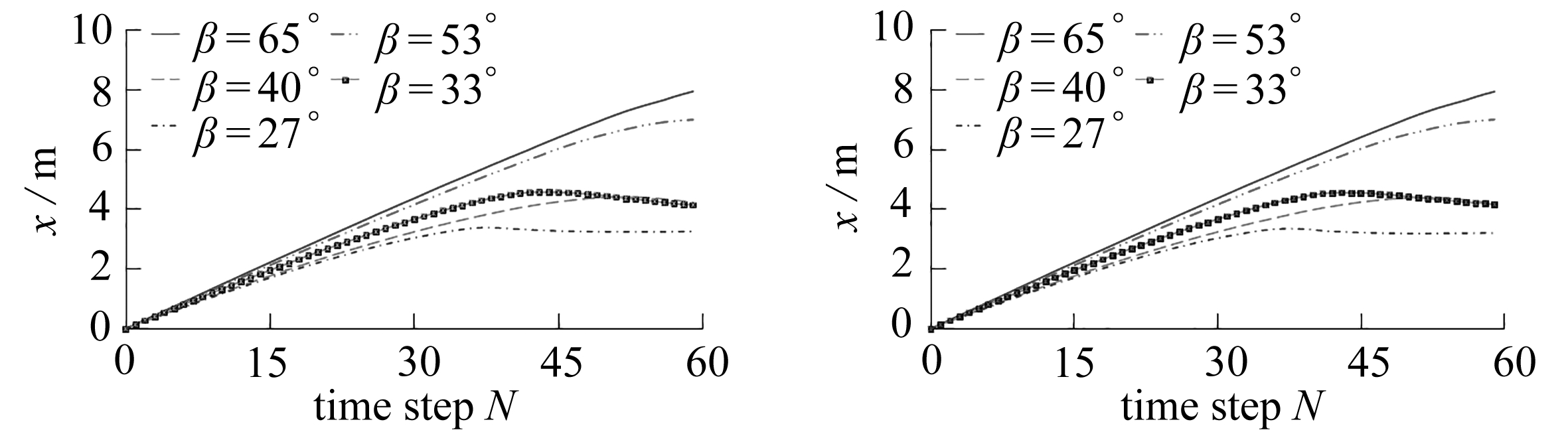
(a) c=0.69 MPa (b) c=1.0 MPa
(c) c=1.3 MPa (d) c=2.27 MPa
图13 不同c值时坡脚水平位移-时间关系曲线图
Fig. 13 Horizontal displacement-time curves at the downhill foot with different cohesion values
(a) c=0.69 MPa (b) c=1.0 MPa
(c) c=1.3 MPa (d) c=2.27 MPa
图14 不同c值时坡脚水平速度-时间关系曲线图
Fig. 14 Horizontal velocity-time curves at the downhill foot with different cohesion values
4 结 论
1) 将一种新型的数值计算方法——FEMLIP,引入到边坡稳定性分析及边坡失稳破坏全过程分析领域,通过一个边坡的典型算例对该方法进行了验证,说明了本文方法的准确性和可行性.
2) 基于FEMLIP,采用Ellipsis 3D计算程序对不同坡角及强度的边坡进行计算分析,并与Katz等[14]采用DEM计算的边坡变形进行了对比分析.结果表明:随着边坡角度的减小和黏聚力c值的增大,边坡的滑移量减小,滑移面向坡面方向移动.滑坡过程中,边坡坡脚水平方向速度最大,坡中次之,顶部最小.在边坡黏聚力相同时,边坡坡脚的水平位移和速度随着边坡坡角的增大而增大.在边坡坡角相同时,不同黏聚力下的边坡坡脚的水平位移和速度基本相同,边坡破坏后,边坡的黏聚力对边坡的滑坡速度影响较小.本文计算结果与Katz等[14]采用DEM得到的不同强度下边坡的滑移规律基本相似.
3) FEMLIP既克服了传统有限元法等仅适用于小变形问题的缺陷,同时对比离散元法也提高了运算效率,弥补了目前常用数值模拟方法在边坡大变形分析中的不足,为边坡失稳后边坡的滑坡分析提供了一种新方法.
[1] PASTOR M, HADDAD B, SORBINO G, et al. A depth-integrated, coupled SPH model for flow-like landslides and related phenomena[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2010, 33(2): 143-172.
[2] 唐宇峰, 施富强, 廖学燕. 基于SPH的土质边坡稳定性及失稳后大变形数值模拟[J]. 地下空间与工程学报, 2018, 14(1): 280-286.(TANG Yufeng, SHI Fuqiang, LIAO Xueyan. Numerical simulation of stability and large deformation of soil slope based on SPH method[J]. Chinese Journal of Underground Space and Engineering, 2018, 14 (1): 280-286.(in Chinese))
[3] FAVIER L, DAUDON D, DONZÉ F, et al. Predicting the drag coefficient of a granular flow using the discrete element method[J]. Journal of Statistical Mechanics Theory & Experiment, 2009, 2009(6): P06012.
[4] FAUG T, CACCAMO P, CHANUT B. Equation for the force experienced by a wall overflowed by a granular avalanche: experimental verification[J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2011, 84(5Pt1): 051301.
[5] 邱家用, 张建良, 孙辉, 等. 并罐式无钟炉顶装料行为的离散元模拟及实验研究[J]. 应用数学和力学, 2014, 35(6): 598-609.(QIU Jiayong, ZHANG Jianliang, SUN Hui, et al. DEM simulation and experimental investigation of burden distribution in the parallel-hopper bell-less top blast furnace[J]. Applied Mathematics and Mechanics, 2014, 35(6): 598-609.(in Chinese))
[6] MORESI L, DUFOUR F, HLHAUS H B. A Lagrangian integration point finite element method for large deformation modeling of viscoelastic geomaterials[J]. Journal of Computational Physics, 2003, 184(2): 476-497.
[7] CUOMO S, PRIME N, IANNONE A, et al. Large deformation FEMLIP drained analysis of a vertical cut[J]. Acta Geotechnica, 2013, 8(2): 125-136.
[8] PRIME N, DUFOUR F, DARVE F. Unified model for geomaterial solid/fluid states and the transition in between[J]. Journal of Engineering Mechanics, 2013, 140(6): 682-694.
[9] PRIME N, DUFOUR F, DARVE F. Solid-fluid transition modelling in geomaterials and application to a mudflow interacting with an obstacle[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(13): 1341-1361.
[10] LI Z H, DUFOUR F, DARVE F. Hydro-elasto-plastic modelling with a solid/fluid transition[J]. Computers and Geotechnics, 2016, 75: 69-79.
[11] LI Z H, DUFOUR F, DARVE F. Modelling rainfall-induced mudflows using FEMLIP and a unified hydro-elasto-plastic model with solid-fluid transition[J]. European Journal of Environmental & Civil Engineering, 2018, 22(4): 491-521.
[12] 蒙伟娟, 陈祖安, 白武明. 地幔柱与岩石圈相互作用过程的数值模拟[J]. 地球物理学报, 2015, 58(2): 495-503.(MENG Weijuan, CHEN Zu’ an, BAI Wuming. Numerical simulation on process of the plume-lithosphere interaction[J]. Chinese Journal of Geophysics, 2015, 58(2): 495-503.(in Chinese))
[13] 白帆, 陈祖安, 白武明. 地幔柱与岩石圈相互作用过程中熔融问题的数值模拟[J]. 地球物理学报, 2018, 61(4): 1341-1351.(BAI Fan, CHEN Zu’an, BAI Wuming. Numerical simulation on the melting process of the mantle plume-lithosphere interaction[J]. Chinese Journal of Geophysics, 2018, 61(4): 1341-1351.(in Chinese))
[14] KATZ O, MORGAN J K, AHARONOV E, et al. Controls on the size and geometry of landslides: insights from discrete element numerical simulations[J]. Geomorphology, 2014, 220: 104-113.
[15] O’NEILL C, MORESI L, MÜLLER D, et al. Ellipsis 3D: a particle-in-cell finite-element hybrid code for modelling mantle convection and lithospheric deformation[J]. Computers & Geosciences, 2006, 32(10): 1769-1779.
[16] MORESI L, DUFOUR F, HLHAUS H B. A Lagrangian integration point finite element method for large deformation modeling of viscoelastic geomaterials[J]. Journal of Computational Physics, 2003, 184(2): 476-497.
[17] MORESI L, SOLOMATOV V. Mantle convection with a brittle lithosphere: thoughts on the global tectonic styles of the earth and venus[J]. Geophysical Journal International, 2008, 133(3): 669-682.
[18] TACKLEY P J. Self-consistent generation of tectonic plates in three-dimensional mantle convection[J]. Earth and Planetary Science Letters, 1998, 157(1): 9-22.
[19] 费康, 张建伟. ABAQUS在岩土工程中的应用[M]. 北京: 中国水利水电出版社, 2009.(FEI Kang, ZHANG Jianwei. Application of ABAQUS in Geotechnical Engineering[M]. Beijing: China Water & Power Press, 2009.(in Chinese))