引 言
由捕食系统和传染病模型结合而成的生态流行病系统，是近些年来生物学一个新的分支．Anderson和May[1]首次将生态系统和传染病系统结合起来并提出了食饵染病的食饵捕食系统．在种群捕食过程中,疾病也得以传播．因此,在传染病系统中研究物种的相互作用效果有实际意义．许多学者研究食饵带疾病的捕食模型[2-4],或捕食者染病的捕食食饵模型[5-7]．另外,也有捕食者系统均染病的捕食食饵模型[8-10]．由于疾病可以在捕食者、食饵群内或群间传播,并且捕食者可选择捕食染病和未染病食饵,从而使这类模型有着丰富的研究内容．
然而,前期的传染病食饵模型,并没有考虑空间分布的不均匀性．即由内竞争与群间躲避和防御等引起的自扩散和交错扩散,这显然不符合实际情形．当捕食者进入食饵密度高的地方捕食时,食饵逃跑或群体防御进攻,从而产生了复杂扩散,相关文章可参考文献[11-14]．文献[13]中研究了一类食饵染病的入侵扩散系统：
(1a)
(1b)
(1c)
(1d)
(X(0,x),S(0,x),I(0,x))=(X0(x),S0(x),I0(x))， x∈Ω，
(1e)
其中Ω是RN(N>1,为正整数)中的有界区域,∂Ω为光滑边界；X是食饵密度，S和I分别代表易感捕食和感染捕食，aX-bX2为logistic项；正常数θ,α,β,c,γ分别代表捕食操作时间,易感捕食者的死亡率，转换率，染病捕食者的死亡率和疾病的传播系数；在扩散项中,d1,d2和d3为自扩散系数,m代表捕食者朝向食饵的一种趋向，且m被称为侵入反应扩散系数．
在此基础上,本文进一步考虑捕食者均染病的入侵扩散捕食系统:
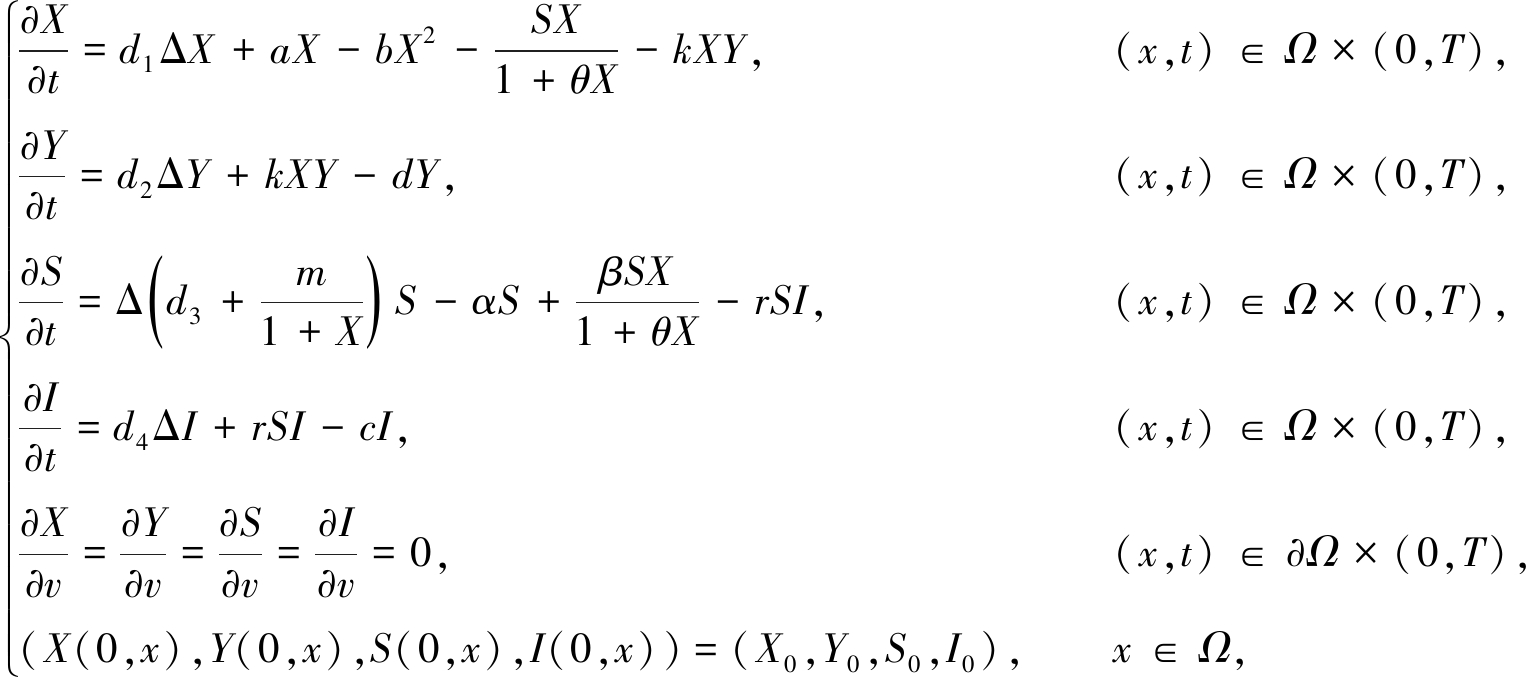
(2)
其中Y为染病食饵，d为染病食饵的死亡率．食饵疾病只在食饵之间传播，初值非负不恒为0．传播率为k,与系统(2)所对应的椭圆系统为
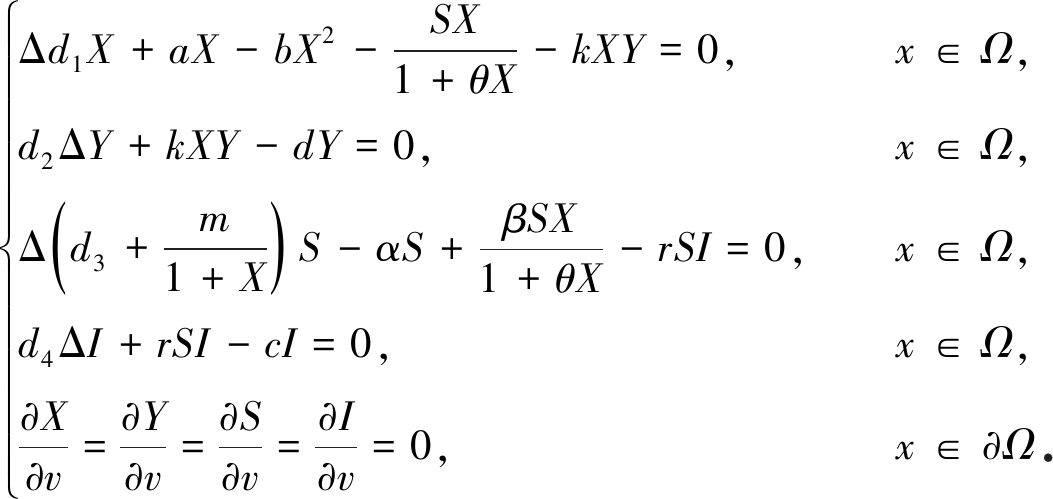
(3)
1 入侵扩散对稳定性的影响
系统(2)有以下非平凡常数平衡点，分布如下．
当满足条件(H1):ak>bd时，存在平衡点
当满足条件(H2):β>θα,a(β-θα)>bβ时，存在平衡点
当满足条件
时，存在平衡点
当满足条件
时，存在平衡点
本文主要分析正常数平衡点E4的稳定性，记
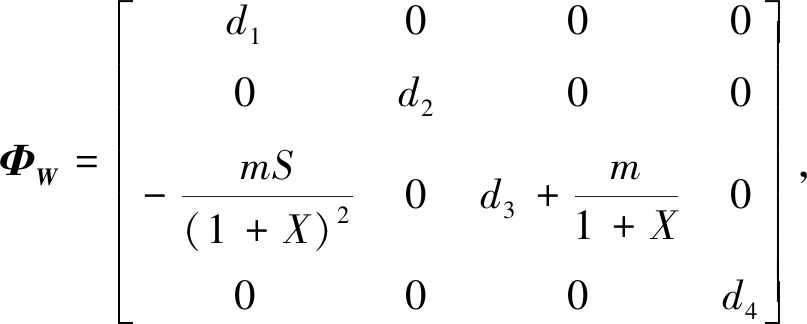
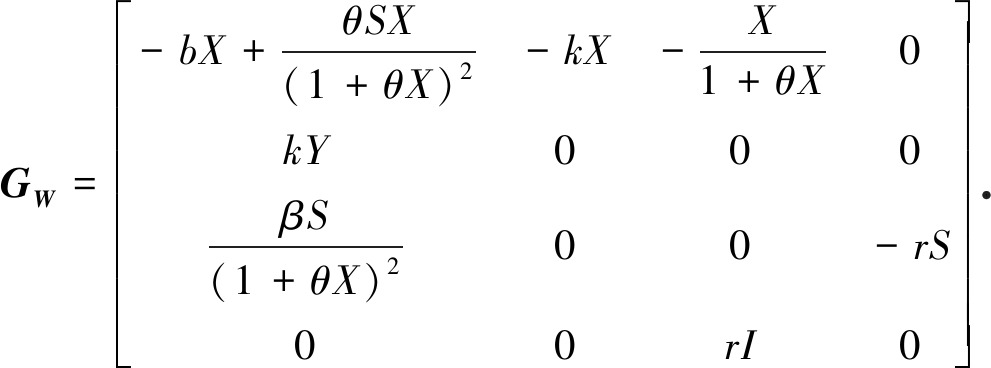
在点E4处，系统(2)的线性化系统为
Wt=ΦW(E4)ΔW+GW(E4)W．
对应的特征方程记为
f(λ)=λ4+A1λ3+A2λ2+A3λ+A4,
其中0=μ0≤μ1≤μ2 ≤…≤μk ≤…,为算子Δ满足齐次Neumann边值条件的特征值．
先证明m=0时的情形，记
定理1 若m=0且r>1，那么正平衡点E4是局部渐近稳定的．
证 当m=0时，为了方便仍然记(X*,Y*,S*,I*)=(X,Y,S,I),此时特征方程为
f0(λ)=λ4+A10λ3+A20λ2+A30λ+A40,
其中
容易得到，当r>1时，f0(0)=A40>0,并且f′0(λ)=4λ3+3A10λ2+2A20λ+A30>0．这说明f0(λ)=0无正实根，下面说明f0(λ)=0无纯虚根． 假设λ=iω(ω>0)是特征方程的特征根,代入方程,则有
(ω40-A20ω2+A40)+i(A30ω-A10ω3)=0．
由上式可得
ω4-A20ω2+A40=0, A30ω-A10ω3=0，
所以有
通过计算可以得出矛盾． 事实上，只要取常数项进行比较．A10A20A30-A302按μk降幂排列，常数项为
而A102A40按μk降幂排列，常数项为
从而特征方程不存在虚根．由文献[15]中定理3.3.1知，特征方程的根均有负实部．即当r>1时,E4具有局部渐近稳定性．
定理2 若m=0且R>1，那么正平衡点E4是全局渐近稳定的．
证 定义Lyapunov函数：
其中h=(1+θX)/β．则
故当R>1时,V(t)≤0,从而正平衡点是全局渐近稳定的．
定理3 若满足
则存在正常数m0,当m>m0，那么正平衡点E4是不稳定的．
证 为了方便，仍然记(X*,Y*,S*,I*)=(X,Y,S,I)．由于
det GW(E4)=
取极限
其中
设μ1(m),μ2(m),μ3(m),μ4(m)为det GW(E4)=0的4个根,且μ1(m)≤μ2(m)≤μ3(m) ≤μ4(m)，则
μ1(m) ·μ2(m) ·μ3(m) ·μ4(m)=k2XY·r2XY>0,
由定理条件可知，B2<0．由连续性可知,存在常数m0,当m>m0时,有
-∞<μ1(m)<μ2(m)<0<μ3(m)<μ4(m)<+∞；
0<μ1(m)<μ2(m)<μ3(m)<μ4(m)<+∞；
因此,存在μk∈(μ3(m),μ4(m)),使得det GW(E4)<0． 这说明此时至少有一正的特征根．故正平衡点E4不稳定．
2 非常数正平衡解的存在性
引理1 存在正常数A,使得系统(3)的解满足
A-1≤(X,Y,S,I)≤A．
证 由极值原理易知
将第一个方程和第二个方程相加，同样由极值原理，有
记
设φ(x0)=max φ(x),由极值原理
从而有
取
下面证明X,Y,S,I下界，记
满足方程
-Δφ1(x)=c(x)φ1(x),
其中
由Harnack[16]不等式可得
从而
同理有
将方程组(3)中第二个和第四个方程积分，由散度定理可得
因此存在x1∈Ω ,使X(x1)=d/k,结合Harnack不等式可得
用同样的方法可证
对于I(x)下界利用反证法,假设存在序列di,k,mk
(i=1,2,3,4),使得k→+∞时，
由Harnack不等式可知，
则Ik(x)→0在Ω一致成立．直接将方程组(3)中第三个方程序列积分，由散度定理可得
令k→+∞并由积分中值定理，存在x2∈Ω,使得
这与条件(H4)矛盾．
利用同样方法可证明Y的下界，引理证毕．
记系统(3)为
-ΔΦ(W)=G(W), B=x∈Ω|A-1≤X,Y,S,I≤A,
将其记为
F(W)=
W-(I-Δ)-1[Φ(W)(W)]-1[G(W)+
W·ΦWW(W) ·W]+W=0,
其中(I-Δ)-1是I-Δ的逆,易证对所有W,det ΦW>0．则
存在,由于算子F(·)是恒等算子I的一个紧干扰算子．对∀W∈∂B有F(W)≠0,则有Leray-Schauder拓扑度deg(F(·),0,B)．直接计算得
DWF(E4)=I-(I-Δ)-1[ΦW(E4)]-1GW(E4)+I,
记
H(μ)=detμI-(ΦW(E4))-1GW(E4)．
由Leray-Schauder定理,有以下引理．
引理2 对所有正整数i都有H(μi)≠0,则
证 由于det [Φ(W)(E4)]-1>0,故只需考虑det[μΦW(E4)-GW(E4)]的符号来判断H(μ)的符号．
定理4 设满足条件(H4)以及
并且μ3(m)∈(μi-1,μi),μ4(m)∈(μj-1,μj), j-i为奇数． 那么存在正常数M,当m>M时,系统(2)至少有一个非常数正平衡解．
证 利用反证法．假设结论不成立，对t∈[0,1],定义
考虑如下方程：
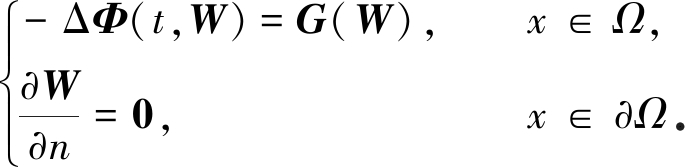
(4)
记
F(t,W)=
W-(I-Δ)-1[ΦW(t,W)]-1[G(W)+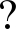W·ΦWW(t,W) ·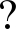W]+W=0．
当t=1时,系统(4)即是系统(3),并且系统(4)只有唯一正常数解E4．由定理条件及引理2可知index(F(1，·),E4)=(-1)σn=-1．
另外,考虑m=0时,
f(λ)=λ4+A10λ3+A20λ2+A30λ+A40，
B10μ4+B20μ3+B30μ2+B40μ+B50，
其中
当满足条件
时，对∀u>0,A40>0．通过计算可得，当满足条件
时，恒有H(μ)>0．因此对任意μ>0,index(F(0，·),E4)=(-1)0=1．
因为由假设，在B中系统(4)只有唯一正常数解E4．因此有
deg(F(0，·),0,B)=index(F(0，·),E4),
deg(F(1，·),0,B)=index(F(1，·),E4)．
这与拓扑度的同伦不变性deg(F(0，·),0,B)=deg(F(1，·),0,B)相矛盾，这说明在B内系统(3)一定有不同于E4的解．证毕．
3 结 论
由文中定理1～3的结论，首先讨论没有入侵扩散时，正常数平衡点的稳定性，得到结论如下：当扩散系数m=0且满足阈值r>1时，平衡点E4是局部渐近稳定的;当扩散系数m=0且满足阈值R>1时，平衡点E4是全局渐近稳定的．而当入侵存在，扩散系数m充分大且满足一定条件时，平衡点E4是不稳定的．这就说明入侵会导致平衡态失稳．进一步地，由定理4的结论可知，当自扩散系数di(i=1,2,3,4)固定且满足一定条件，扩散系数m足够大时，能进一步产生其他非常数正平衡解，此时捕食者和食饵能共存．
[1] ANDERSON R M, MAY R M. Infectious Disease of Humans Dynamics and Control[M]. Oxford: Oxford University Press, UK, 1991.
[2] VENTURINO E. Epidemics in predator-prey models: disease in the prey[J]. Mathematical Population Dynamics: Analysis of Heterogeneity, 1995, 1: 381-393.
[3] XIAO Y, CHEN L. Modeling and analysis of a predator-prey model with disease in the prey[J]. Mathematical Bioscience, 2001, 171(1): 59-82.
[4] CHATTOPADHYAY J, ARINO O. A predator-prey model with disease in the prey[J]. Nonlinear Analysis: Theory, Methods and Applications, 1999, 36(6): 747-766.
[5] 孙树林, 原存德. 捕食者具有流行疾病的捕食-被捕食模型的分析[J]. 生物数学学报, 2006, 21(1): 97-104.(SUN Shuling, YUAN Cunde. On the analysis of predator-prey model with epidemic in the predator[J]. Journal of Biomathematics, 2006, 21(1): 97-104.(in Chinese))
[6] VENTURINO E. Epidemics in predator-prey models: disease in the predators[J]. Mathematical Medicine and Biology: a Journal of the IMA, 2002, 19(3): 185-205.
[7] DAS K P. A study of chaotic dynamics and its possible control in a predator prey model with disease in the predator[J]. Journal of Dynamical and Control Systems, 2015, 21(4): 605-624.
[8] HEISH Y H, HSIAO C K. Predator-prey model with disease infection in both populations[J]. Mathematical Medicine and Biology: a Journal of the IMA, 2008, 25(3): 247-266.
[9] DAS K P, KUNDU K, CHATTOPADHYAY J. A predator-prey mathematical model with both the populations affected by diseases[J]. Ecological Complexity, 2011, 8: 68-80.
[10] DAS K P, CHATTOPADHYAY J. A mathematical study of a predator-prey model with disease circulating in the both populations[J]. International Journal of Biomathematics, 2015, 8(2): 1-27.
[11] 张丽娜, 鲁引儿. 具有Holling-Ⅲ型功能反应的捕食者-食饵扩散模型中避难所的影响[J]. 应用数学, 2017, 30(2): 359-364.(ZHANG Lina, LU Yiner. Effect of a prey refuge on a predator-prey model with diffusion and Holling type Ⅲ response function[J]. Mathematica Applicata, 2017, 30(2): 359-364.(in Chinese))
[12] OKUBO A. Diffusion and Ecological Problems: Mathematical Models[M]. New York: Springer Verlag, 1980.
[13] 李成林. 捕食者带有疾病的入侵反应扩散捕食系统的空间斑图[J]. 应用数学学报, 2016, 39(6): 832-846.(LI Chenling. Spatiotemporal pattern formation of an invasion-diffusion predator-prey system with disease in the predator[J]. Acta Mathematicae Applicatae Sinica, 2016, 39(6): 832-846.(in Chinese))
[14] 祖力, 黄冬冬, 柳扬. 捕食者和食饵均带有扩散的随机捕食-食饵模型动力学分析[J]. 应用数学和力学, 2017, 38(3): 355-368.(ZU Li, HUANG Dongdong, LIU Yang. Dynamics of dual-dispersal predator-prey systems under stochastic perturbations[J]. Applied Mathematics and Mechanics, 2017, 38(3): 355-368.(in Chinese))
[15] YANG K. Delay Differential Equation Application in Population Dynamics[M]. Boston: Academic Press, 1993.
[16] LIN C S, NIW M, TAKAGI I. Large amplitude stationary solutions to a chemotaxis system[J]. Journal of Differential Equations, 1988, 72(1): 1-27.