引 言
欠驱动非线性系统控制问题一直是控制领域的研究热点之一.在实际工程中,欠驱动系统也是典型的非线性系统, 如何用少于自由度的控制输入数来控制系统是具有实际意义的.目前,欠驱动系统在工程实践中的应用有很多[1-3],欠驱动系统动力学和控制研究的主要方法包括线性二次型最优控制方法和部分反馈线性化方法等[4-5].但是在反馈控制的过程中,系统很难持续的稳定在平衡位置.对此,文章使用虚拟约束方法来得到系统稳定的周期解,进而达到使系统稳定于平衡位置的目的.
针对如何设计反馈控制来使欠驱动系统稳定的问题,已有学者进行了广泛研究, Grizzle等以双足机器人为模型证明了欠驱动系统可以得到稳定的周期解[6]; Canudas等论证了在欠驱动系统中计算出运动周期解的可行性[7];随后以Shiriaev为首的学者们提出了虚拟完整约束的理论,并通过实验证明了理论的可行性和有效性[8-11].在此基础上, Consolini和Maggiore将虚拟约束方法的理论做了进一步延伸,并应用到欠驱动自行车模型中[12-13].关于虚拟约束方法国内还鲜有研究,笔者期望通过本文的研究对欠驱动系统的控制问题起到帮助作用.
本文以起重机为研究对象,该系统为典型的欠驱动系统.利用虚拟约束设计反馈控制器以控制重物可以在稳定的平衡位置或以期望的周期轨道运动.该方法首先通过Lagrange(拉格朗日)动力学方程导出系统动力学模型,根据被控制物体的几何约束关系构建虚拟约束;然后定义误差变量,并根据误差变量所表示的关系式得出系统状态方程;最后设计反馈控制器.仿真结果表明,设计的控制器对任意初始值的欠驱动模型都可以稳定到平衡位置或预期轨道.通过研究欠驱动系统,在虚拟约束下通过反馈控制器实现轨道周期稳定的控制,为探索解决欠驱动非线性系统研究探索新的途径和方法.
1 起重机动力学建模
设起重机模型是由小车和重物组成,简化模型如图1所示,期望通过控制小车运动的同时控制重物的运动,显然该系统只有一个输入(施加在小车上的控制力),有两个输出状态量(小车的位移和重物与垂直方向形成的夹角),因此是一典型的欠驱动系统.
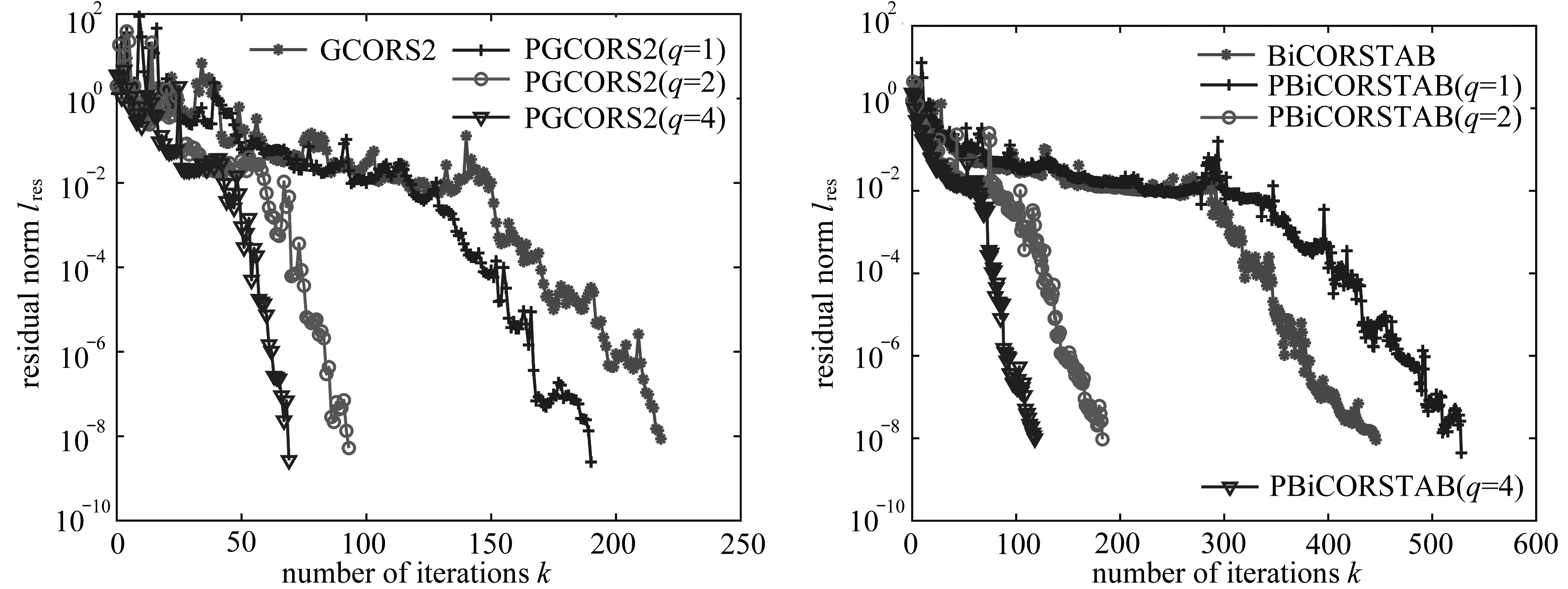
图1 起重机系统的运动模型
Fig. 1 The motion model for the crane system
在图1模型中,设小车质量为M,连接杆长度为l,重物质量为m,θ为连接杆与竖直方向的夹角.选择图中给定的坐标系,用广义坐标(x和θ)表示小车质心位置和重物位形,计算系统动能和势能,利用Lagrange方法建立系统的动力学方程:
(1)
式中f为施加在小车上的水平控制力,![]() 为广义坐标,
为广义坐标,
将式(1)展开可得起重机系统动力学方程:
(2)
2 虚拟完整约束
虚拟约束是指通过选择一个随时间周期函数变化的约束关系作为自变量来设计系统的周期运动.根据欠驱动系统控制量比自由度少的特点,可以建立广义坐标的约束关系,将约束关系代入系统动力学方程可使系统广义坐标缩减,等同于在小车与摆动杆之间添加了虚拟约束关系.由于约束方程不显含速度,因此称为虚拟完整约束.起重机模型的虚拟约束可写为
x+asin θ=b,
(3)
式中a和b为给定的常数.式(3)表示系统维持于稳定位置时x和θ的关系.可以看出,当重物垂直朝下时,x=b.实际上,给定任意欠驱动系统均可以建立起虚拟约束.将式(3)代入到广义坐标φ中可得
(4)
为简化计算,令式(2)中m,M,l为单位量1,则式(2)可简化为
(5)
假设存在一个动态的反馈控制力,可以确保式(3)表示的几何位置不变,将虚拟约束求二阶导数代入到动力学方程(2)中的第二式可得到新的系统方程:
(6)
3 反馈控制器设计
根据系统方程及虚拟约束定义3个误差变量,利用线性二次最优控制器将误差变量逼近于0,误差变量是依据系统预期周期解设计的,因此当误差都为0的时候,系统就会稳定在预期轨道上.
3.1 部分反馈线性化
通过状态的非线性变换和非线性状态反馈将原非线性系统变换成状态方程及输出方程均为线性的可控可观系统.然而,由于欠驱动系统自身的控制输入数目小于自由度数,不能实现完全反馈线性化,因此利用部分反馈线性化.
由于虚拟约束方法将轨道选择的问题完全转换为求微分方程周期解的问题,因此预期轨道幅值和周期的大小完全依赖于常数c的选择.理论上只要常数c在值域内取值,存在无数条周期稳定轨道,c的值域选择可以参考文献[9],将周期解的θ设为θ*,轨道周期为T,存在t使得
θ*(t)=θ*(t+T).
(7)
给定虚拟约束条件和周期解θ*后,开始引入另一个概念:误差变量.因为最终要利用LQR线性二次调节器来设计控制器,因此可以将状态方程的左侧设计为由误差变量构成的向量.由于重物在未达到稳定状态前,x与虚拟约束(3)是有偏差的,利用这一特点,定义向量![]() 即有
即有
η=φ-δ(θ,c),
(8)
其中x偏差量由ε来表示,求出以变量ε表示的广义坐标φ的一、二阶导数:
(9)
(10)
根据反馈线性化理论[8],将输入f转化为关于![]() 的线性化形式.首先,定义
的线性化形式.首先,定义![]() 用u替换式(10)中的
用u替换式(10)中的![]()
(11)
系统动力学方程(1)移项可得
(12)
由式(5)可写出矩阵
将上述矩阵和式(11)代入到式(12)中后,可将控制量f转化为关于u,θ和![]() 的方程,由于θ和
的方程,由于θ和![]() 每一时刻的值都可以测得,因此相当于将f转化为关于u的线性方程
每一时刻的值都可以测得,因此相当于将f转化为关于u的线性方程
(13)
由于系统方程(6)表示的是系统完全在轨道上运动的状态,但初始位置未必处于轨道上,因此式(6)右侧的值并不为0.为求得当前的状态方程,将参数矩阵![]() 以及式(11)代入式(12),可解出起重机模型达到稳定状态前的系统方程:
以及式(11)代入式(12),可解出起重机模型达到稳定状态前的系统方程:
(14)
式中 α(θ)=1-acos2θ, β(θ)=asin θ· cos θ, γ(θ)=gsin θ.
3.2 系统状态方程
设系统初始值为![]() 设计误差变量κ.定义函数σ:
设计误差变量κ.定义函数σ:
(15)
式(15)两边对θ求导,可得dσ与![]() 间的关系:
间的关系:
(16)
将式(15)和(16)代入到系统方程(12)中,以σ替换![]() 和
和![]() 可得
可得
(17)
式(17)可以视为σ关于角度θ的一阶线性非齐次微分方程,其通解形式为
(18)
式中θ0为θ的初始值,
将误差变量κ定义为
(19)
由前面的推导不难看出,当![]() 不在周期轨道上时,σ与
不在周期轨道上时,σ与![]() 是不相等的,误差函数κ值不为0.下面求κ对t的导数,因为κ是一个关于
是不相等的,误差函数κ值不为0.下面求κ对t的导数,因为κ是一个关于![]() 和θ的函数,则有
和θ的函数,则有
(20)
式中![]()
式(20)可写为
(21)
通常情况下,状态向量由满足系统输入输出的常微分程构成,这里设状态向量ζ由误差变量构成,ζ∈R3可以定义为
(22)
式中![]() 为误差变量.联立误差变量的导数表达式,可以得到求周期解所需的状态方程:
为误差变量.联立误差变量的导数表达式,可以得到求周期解所需的状态方程:
(23)
式中A(t)∈R3,B(t)∈R3,其值为
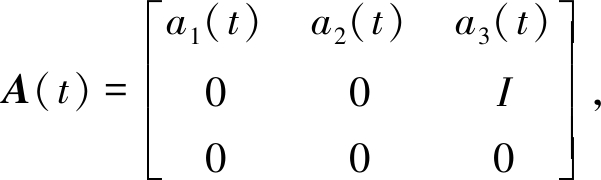
(24)
BT(t)=[b(t),0,I],
(25)
式中I为单位1,ai(t)和b(t)都是以T为周期的周期函数,因此ai(t)=ai(t+T),i=1,2,3;b(t)=b(t+T),具体可表示为
3.3 反馈控制器设计
假设线性系统(23)在[0,T]内是完全可控的.给定一个常数Γ=1和一个3阶的单位矩阵G=GT>0,存在一个3阶的矩阵函数R(t)=R(t+T)并且R(t)=RT(t),符合Riccati方程:
(26)
在[0,T]内存在A(t)和B(t),可以解出反馈控制器u的表达式:
u=-BT(t)R(t)ζ.
(27)
一般来说,非线性系统模型无法通过反馈控制器直接稳定,但可以对反馈控制器稍加修改,结合上文对误差项的推导,设计出一个点对点的反馈控制器,即在任意时刻,系统的每个状态量都有对应的反馈控制量,u可以表示为
(28)
式中R(t)为Riccati方程的稳定解,![]() 为含误差项的状态方程矩阵(25).
为含误差项的状态方程矩阵(25).
4 仿 真 结 果
第2节和第3节详细地展示了在虚拟约束下物体运动周期解的推导过程,接下来的仿真结果验证了虚拟约束方法能够实现起重机持续稳定的平衡状态,也同样要实现欠驱动系统的稳定周期运动.在实验结果中,由于起重机模型只有一个稳定位置,即重物垂直朝下为中心摆动,设置多个初始值来验证预期周期解的存在性,设参数a=0.2,θ与![]() 分别取0.1,0.2,0.3,0.4作为初始值,起重机周期摆动如图2所示,其中选取
分别取0.1,0.2,0.3,0.4作为初始值,起重机周期摆动如图2所示,其中选取![]() 为预期摆动轨道.
为预期摆动轨道.
为了证明系统的稳定性,选择用相位图展示出来,根据非线性系统稳定性判据,当时间t趋于正无穷时,在θ与![]() 所构成的二维平面上的极限环是相空间里的一个闭合的轨迹,系统即是稳定的,如图3所示.图3中原点位置的点表示系统完全稳定时的相位图,即此时重物持续垂直稳定在平衡点上.
所构成的二维平面上的极限环是相空间里的一个闭合的轨迹,系统即是稳定的,如图3所示.图3中原点位置的点表示系统完全稳定时的相位图,即此时重物持续垂直稳定在平衡点上.
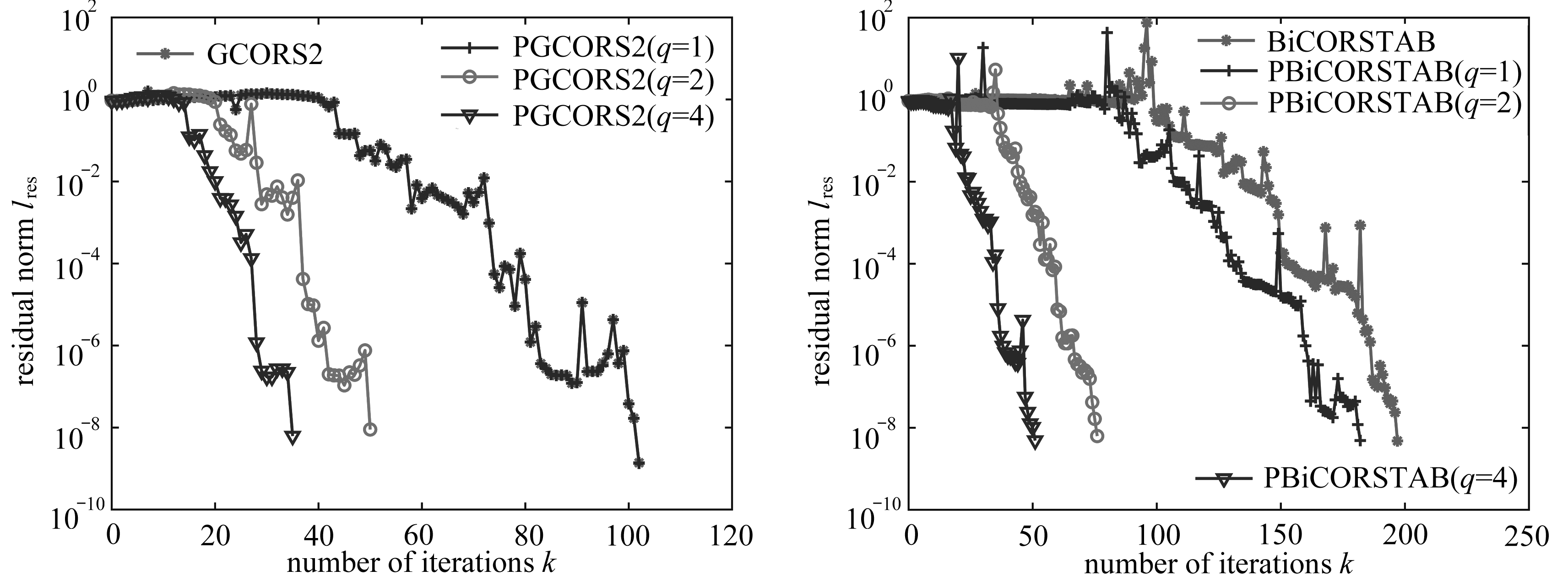
图2 预期周期运动图 图3 周期运动预期相位图
Fig. 2 The expected periodic motion diagram Fig. 3 The expected phase diagram of periodic motion
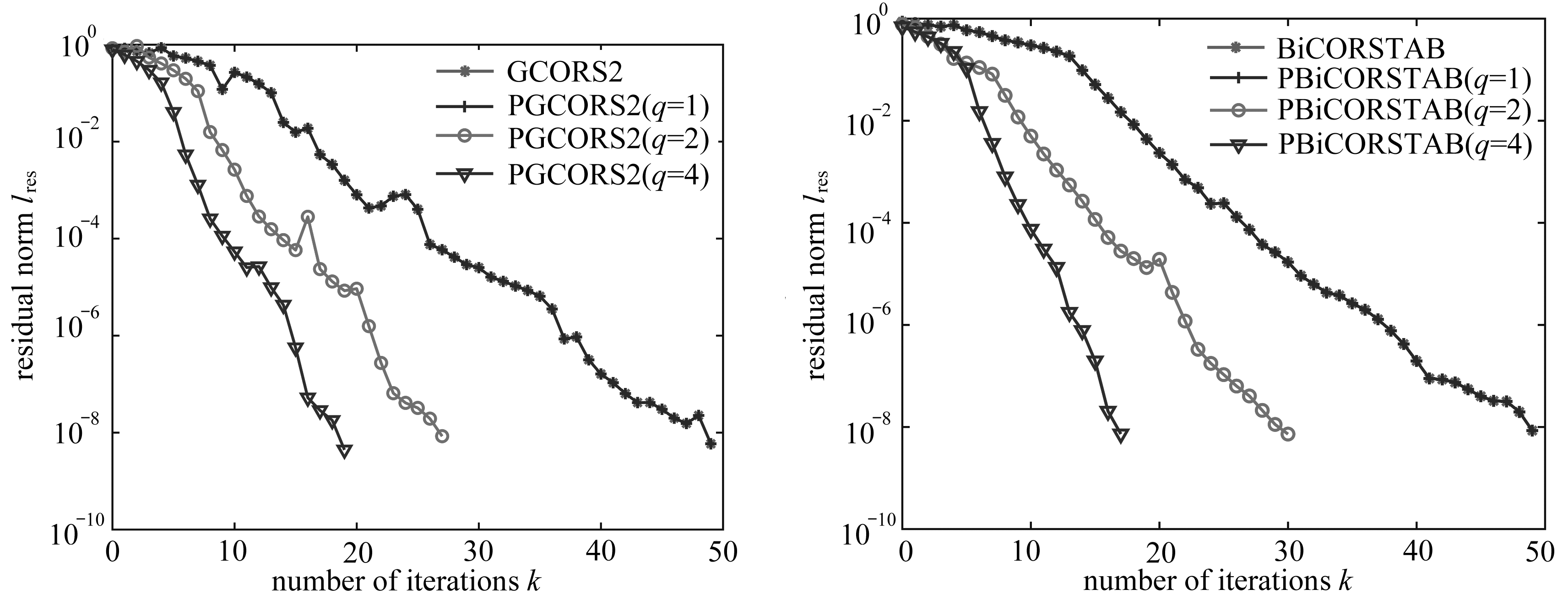
图4 系统在平衡点稳定
Fig. 4 The system is stable at the equilibrium point
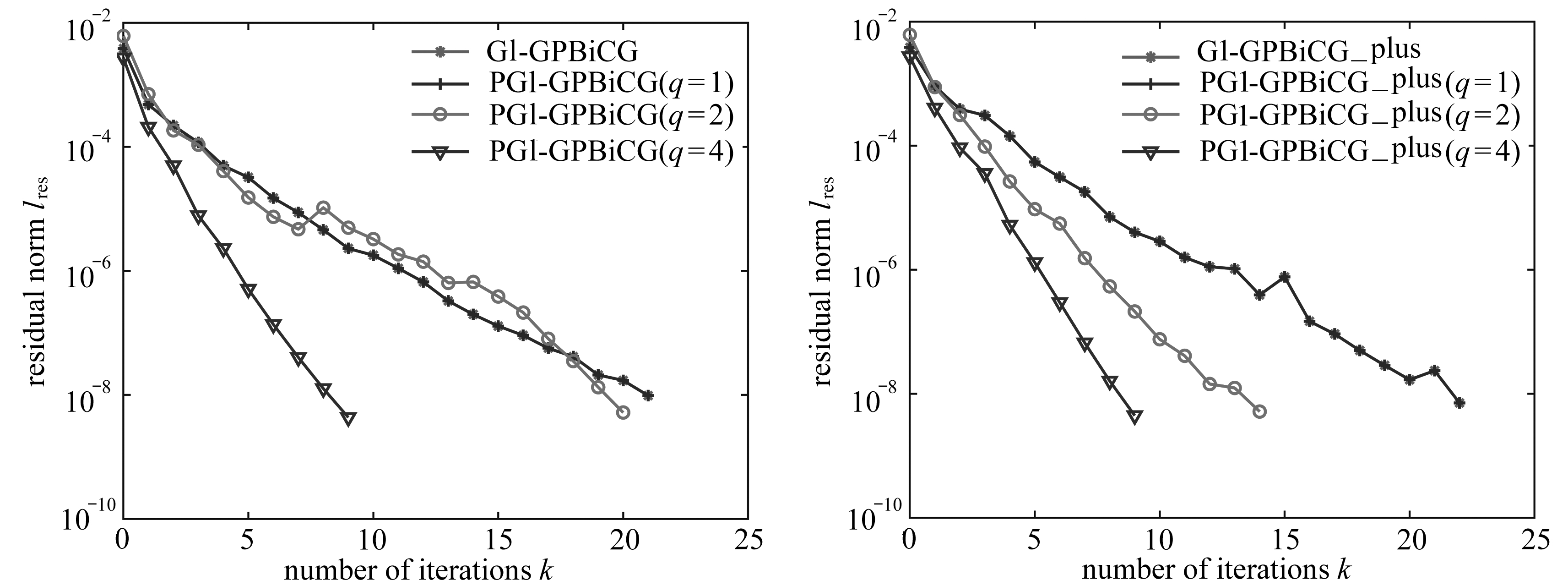
图5 状态方程误差项κ图6 状态方程误差项ε
Fig. 5 State equation error term κFig. 6 State equation error term ε
图4所示的是用虚拟约束方法将系统从θ=0.2的位置上稳定到平衡位置的状态图,图中的角度θ在反馈下最终变为0,表明重物最终稳定于竖直朝下的位置上,证明了该方法可以使重物在反馈控制下稳定于平衡点上.由于3个误差变量都是角度θ的关系式,因此测量角度θ即可得到误差变量,在实际系统中可以通过传感器测量角度的值来确定误差变量的大小.反馈控制器的状态变量,即3个误差变量的值在反馈控制下逼近于0,如图5~7所示.
由图5~7可知,基于虚拟约束方法的反馈控制器在任意初始值下都可以将误差值减小为0.与相位图3相比,系统最终稳定在预期轨道上,对此的直观解释是,选择合适的参数和坐标初始值,使反馈控制器能够找到最快的收敛路线,从而使系统稳定到平衡点上.
图8是θ与![]() 所构成的相位图,图9是角度θ的周期解.对比图3与图4可以看出,在θ=0的初始位置下,虚拟约束方法设计的控制器可以使重物在一段时间后进行周期运动.
所构成的相位图,图9是角度θ的周期解.对比图3与图4可以看出,在θ=0的初始位置下,虚拟约束方法设计的控制器可以使重物在一段时间后进行周期运动.

图7 状态方程误差项![]()
Fig. 7 State equation error term ![]()
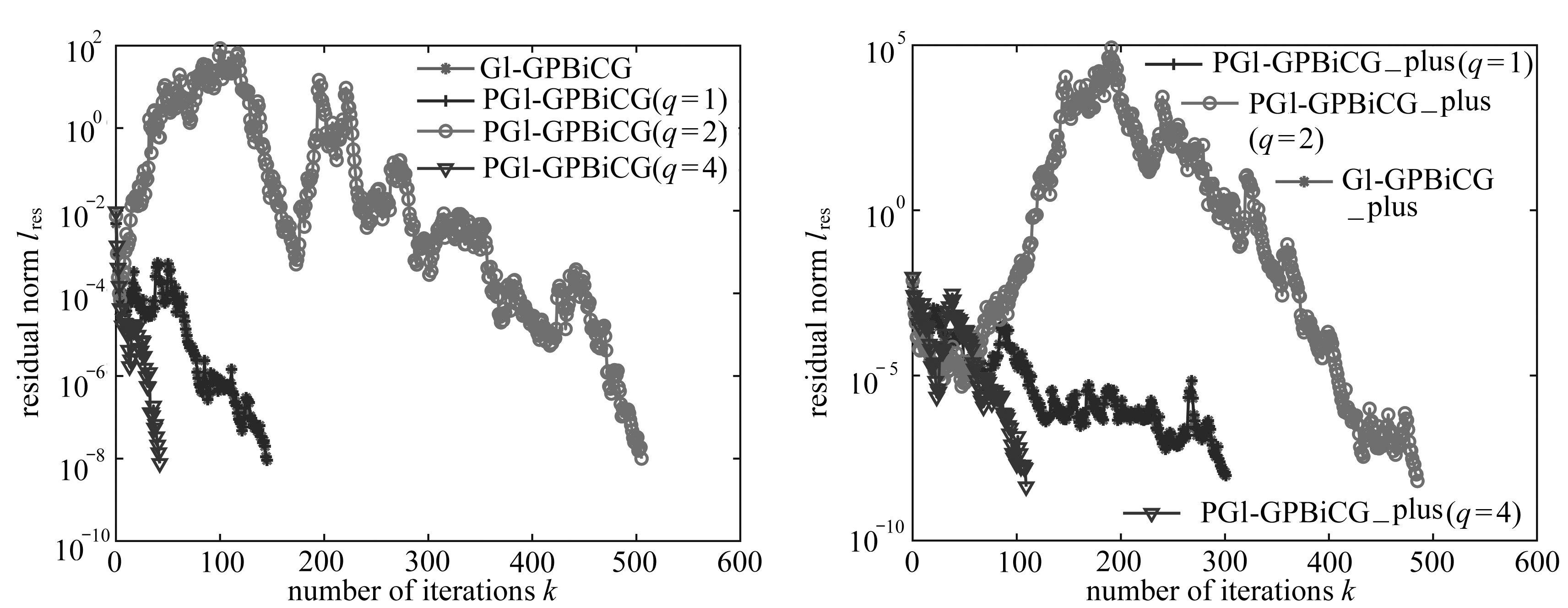
图8 反馈控制下的相位图 图9 系统周期解
Fig. 8 The phase diagram under feedback control Fig. 9 The periodic solution of the system
5 结 论
本文利用虚拟约束方法,在传统动力学方程和非线性欠驱动反馈控制方法的基础上,通过建立虚拟约束作为自变量来设计系统最终的理想运动轨道;并基于误差变量和系统状态方程,构造了一个多预期轨道的反馈控制器,使得欠驱动起重机模型在反馈控制下能够稳定到平衡位置或预期周期轨道;仿真实验验证了该方法的有效性.
[1] MILLER S, MOLINO J A, KENNEDY J, et al. Segway rider behavior: speed and clearance distance in passing sidewalk objects[J]. Transportation Research Record, 2008, 2073: 125-132.
[2] DRAZ M U, ALI M S, MAJEED M, et al. Segway electric vehicle: human transporter[C]//On Robotics and Artificial Intelligence, 2012 International Conference. Pakistan, 2012.
[3] CHWA D. Nonlinear tracking control of underactuate ships based on a unified kinematic and dynamic model[C]//2007 Mediterranean Conference on Control and Automation. Athens, Greece, 2017.
[4] 高丙团, 黄学良. 欠驱动2DTORA基于部分反馈线性化的非线性控制设计[J]. 东南大学学报(自然科学版), 2011, 41(2): 321-325.(GAO Bingtuan, HUANG Xueliang. Nonlinear control design of underactuated 2DTORA based on partial feedback linearization[J]. Journal of Southeast University(Natural Science Edition), 2011, 41(2): 321-325.(in Chinese))
[5] BO L. Approximate linearization of a class of underactuated system and its application in the ball and beam system[J]. International Journal of Control and Automation, 2015, 8(12): 119-130.
[6] GRIZZLE J W, ABBA G, PLESTAN F. Asymptotically stable walking for biped robots: analysis via systems with impulse effects[J]. IEEE Transactions on Automatic Control, 2001, 46(1): 51-64.
[7] CANUDAS DE WIT C, ESPIAU B, URREA C. Orbital stabilization of underactuated mechanical systems[C]//15th IFAC World Congress. Barcelona, Spain, 2002.
[8] SHIRIAEV A, PERRAM J W, CANUDAS DE WIT C. Constructive tool for orbital stabilization of underactuated nonlinear systems: virtual constraints approach[J]. IEEE Transactions on Automatic Control, 2005, 50(8): 1164-1176.
[9] SHIRIAEV A, ROBERTSSON A, PERRAM J, et al. Periodic motion planning for virtually constrained(hybrid) mechanical system[C]//Proceedings of the 44th IEEE Conference on Decision and Control and the 2005 European Control Conference. Seville, Spain, 2005.
[10] SHIRIAEV A S, FREIDOVICH L B, ROBERTSSON A, et al. Virtual-holonomic-constraints-based design of stable oscillations of Furuta pendulum: theory and experiments[J]. IEEE Transactions On Robotics, 2007, 23(4): 827-832.
[11] FREIDOVICH L, ROBERTSSON A, SHIRIAEV A, et al. Periodic motions of the pendubot via virtual holonomic constraints: theory and experiments[J]. Automatica, 2008, 44(3): 785-791.
[12] CONSOLINI L, MAGGIORE M. Virtual holonomic constraints for Euler-Lagrange systems[C]//8th IFAC Symposium on Nonlinear Control Systems. Bologna, Italy, 2010.
[13] CONSOLINI L, MAGGIORE M. Control of a bicycle using virtual holonomic constraints[J]. Automatica, 2014, 49(9): 2831-2839.
[14] CELLINA A. The validity of the Euler-Lagrange equation for solutions to variational problems[J]. Journal of Fixed Point Theory & Applications, 2014, 15(2): 577-586.
[15] PERRAMJ W, SHIRIAEV A, CANUDAS DE WIT C, et al. Explicit formula for a general integral of motion for a class of mechanical systems subject to holonomic constraint[J]. IFAC Proceedings Volumes, 2003, 36(2): 87-92.