引 言
自2013年2月华东地区发现首例人感染新型H7N9流感病毒病例以来[1]，H7N9流感已经在中国出现5波疫情．截至2017年6月，全国已报告1 533人确诊感染H7N9流感病毒，其中592人死亡．疫情迅速蔓延，感染和死亡人数不断增加，引起了全球公共卫生界的警惕．广东省是H7N9流感传播的高危地区[2]，截止2017年6月，广东省共有258例人感染H7N9流感病例，主要发生在每年的10月份到次年4月份．由于目前尚无有效治愈H7N9的方法，死亡率较高，对人群健康和社会经济造成了严重影响，因此研究其传播机制具有十分重要的现实意义．
目前已有部分数学模型从不同的侧重点对H7N9进行研究．例如，2014年，Zhang等[3]建立了一种具有候鸟、居民禽、家禽和人的动力学模型，发现候鸟很可能为长江三角洲地区2013年—2014年疫情的最初感染源，估计基本再生数为4.11～6.02．2016年，Lin等[4]建立了几种传播模型，发现有环境类感染的不含周期效应的模型最适合模拟H7N9的传播模式．同年Lu等[5]采用Bayes(贝叶斯)模型分析人群发病率的时空变化，评估了关闭和重开活禽市场对疫情的影响．2017年，Xing等[6]建立了一种具有候鸟、居民禽、家禽和人的动力学模型，探索温度和周期性关闭活禽市场对H7N9病毒的影响．很多研究表明，接触家禽或者环境中的H7N9病毒是人类感染禽流感的最主要途径[7-8]．为此，我们将进一步考虑禽类、环境中的病毒和人的相互作用，提出一个新的SI-V-SEIR模型．
本文将从理论和数值上分析此模型的动力学行为，并把模型应用于广东省2016年—2017年的禽流感疫情，分析该地区在关闭活禽市场后的基本再生数变化，并讨论不同的模型参数对传播动力学的影响．本文第1节详细叙述模型，给出了基本再生数的表达式，并证明模型的无病平衡点和地方病平衡点的稳定性；第2节给出模型的应用，通过选取广东地区的疫情数据进行数值分析；最后给出结论．
1 数 学 模 型
建立一个简单的H7N9传染病模型．其中，Np(t)和Nh(t)分别表示禽类和人类的总数量，Np(t)分为两个子类：易感禽类Sp(t)和感染禽类Ip(t)；Nh(t)分为4个子类：易感者Sh(t)、潜伏期患者Eh(t)、感染者Ih(t)和康复者Rh(t)．人类和家禽可通过与受感染家禽接触或环境中的病毒(V)感染H7N9病毒．变量V的单位是病毒粒子[9]，用于模拟被感染的家禽向环境中传播H7N9病毒的演变．V源于受感染家禽，存活于环境中[3,9]．疾病传播的流程图如图1示．
图1 H7N9传播模型的流程图
Fig. 1 The flowchart of the H7N9 transmission model
对应的动力学模型可由下列高维微分方程组表示：
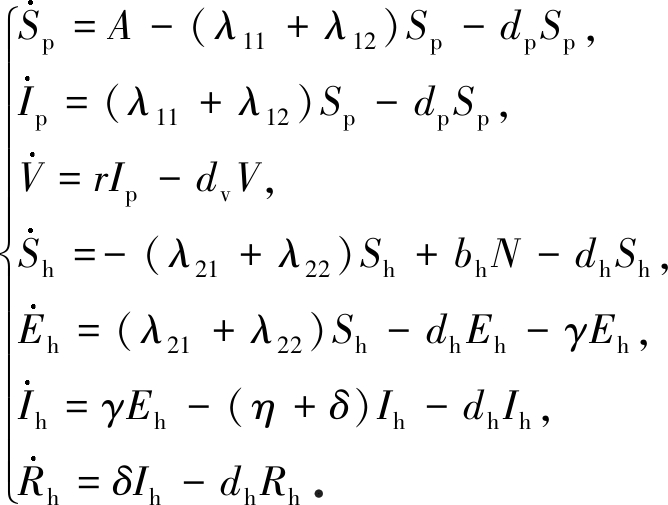
(1)
模型参数定义见表1(具体值对应广东省情况)．感染力λ11，λ12，λ21，λ22定义如下:
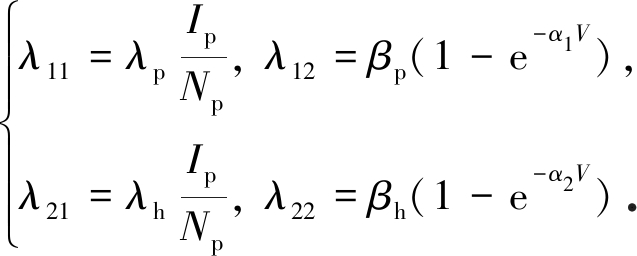
因目前没有直接证据证明H7N9可以人传人[6,10-11]，故假设人类不参与病原体的传播．模型动力学行为主要由下列子系统决定：
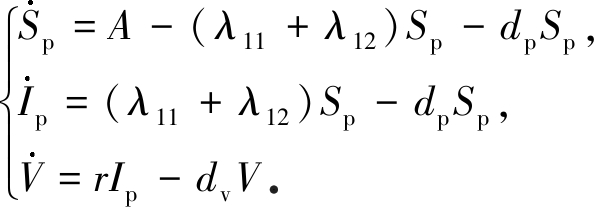
(2)
注意到禽类总数Np满足
故禽类总数的平衡点
是全局渐近稳定，由此获得式(2)的极限系统：
(3)
系统(3)的稳定性决定了系统(1)和(2)的稳定性，因此下面的理论分析主要针对系统(3)．根据模型对应的生物意义及简单计算，方程(3)的正向不变集为
表1 模型参数及取值
Table 1 Parameters and their values
parameterdefinitionvaluenoteArecruitment rate of poultry14 580 000[a]bhbirth rate of human1/(75×52) week-1[b]dhnatural death rate of human(1/(75×52))×0.98 week-1[b]λpbaseline transmission rate among poultryvariableλhbaseline transmission rate from poultry to humanvariableβpbaseline transmission rate from virus in VE to poultryvariableβhbaseline transmission rate from VE to humansvariableα1rescaled constant of environmental infectiousness to poultry0.034 6 week-1estimationα2rescaled constant of environmental infectiousness to humans0.024 4 week-1estimationdprate of screening and culling in poultry1/6 week-1[c]dvelimination rate of VE in natural environment0.961 0 week-1estimationrproduction rate of VE from poultry0.143 3 week-1estimationγreciprocal of the incubation period7/3.3 week-1ref. [3]ηdisease-related death of human0.96 week-1ref. [3]δrecovery rate of infectious human1 week-1ref. [9]
注 [a]为由家禽出栏率估计所得．
[b]为假设人均寿命为75岁．
[c]为由现实中实测估计所得．
Note [a] estimation from the marketing rate of domestic poultry.
[b] with an average life time of human taken as 75 years.
[c] estimation from fild survey.
2 基本再生数与稳定性
基本再生数R0作为衡量疾病爆发或消亡的阈值，有重要的生物意义[12]．根据文献[13]提出的下一代生成矩阵的方法，得
从而
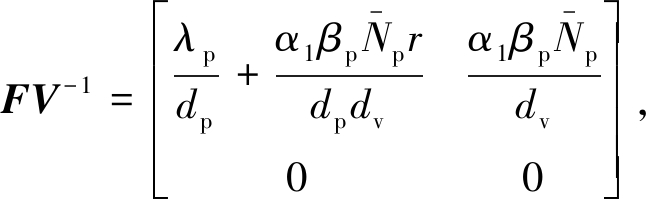
其中
基本再生数是矩阵FV-1的谱半径，因此
2.1 无病平衡点的全局渐近稳定性
令系统(2)的右边为零，求得模型的无病平衡点(Sp,Ip,V)=(A/dp,0,0)，注意到系统(3)的等号右边可看作一个向量值函数：
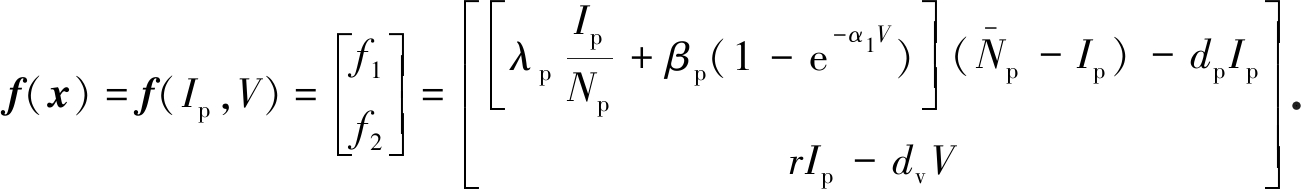
(4)
定理1 当R0<1时，模型(1)的无病平衡点局部渐近稳定．
证明 系统(3)在无病平衡点的Jacobi矩阵为
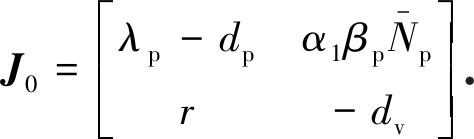
特征方程为
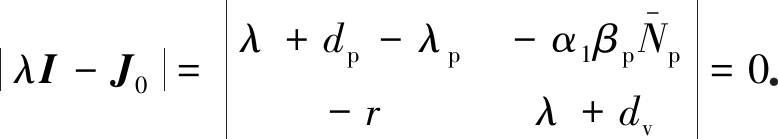
(5)
下面只需证明式(5)的解有负实部即可．
记
则特征方程(5)可简写为
λ2+uλ+v=0．
(6)
方程(6)的解为
且
从而J0的所有特征值均为实数．若要使得特征值都是负数， 应有
即u2<Δ，而u2-Δ=4(mdv-α1βpNp)．另外R0<1等价于
因此当R0<1时，Jacobi矩阵的特征值全为负实数，无病平衡点是局部渐近稳定的．
进一步地有下面的结论．
定理2 当R0<1时，模型(1)的无病平衡点全局渐近稳定，此时疾病灭绝．
证明 由于R0<1，所以
则
令
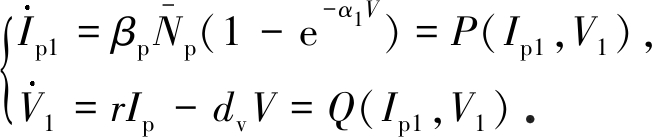
(7)
由于
因此系统(7)只有平衡点(0,0)．由Dulac定理可知，系统(7)是全局渐进稳定的，则当t→∞时，有(Ip1(t),V1(t))→(0,0)．由于Ip(t)≤Ip1(t),V1(t)≤V(t)，所以当t→∞时，有(Ip(t),V(t))→(0,0)．那么系统(2)中Sp(t)→A/dp，即无病平衡点是全局吸引的，同时无病平衡点又是局部稳定的，所以系统(2)中无病平衡点是全局渐近稳定的．证毕．
此时，环境中的病毒和感染禽类的数量均趋向于零，代入系统(1)可知，模型中的感染病人也趋向于零，疾病将灭绝．
2.2 地方病平衡点的全局渐近稳定性
为了分析地方病平衡点的稳定性，需要一个引理(文献[14]中的推论3.2)．
引理1 设函数
连续可微，满足
1) f(x)是协作的，即它的Jacobi矩阵是Metzler矩阵，且∂f(x)不可约；
2) f(0)=0，且对所有的i=1,2,…,n，当xi=0时fi(x)≥0;
3) f(x)严格次线性．
令s(∂f(0))是矩阵∂f(0)的特征值的最大实部，如果s(∂f(0))>0，那么对系统
而言，要么系统的任意解趋向无穷；要么存在唯一的正平衡点，全局渐近稳定．
定理3 若R0>1，模型(2)存在唯一的地方病平衡点且全局渐近稳定，此时病毒将长期存在于禽类、环境和人群中．
证明 1)系统(3)的Jacobi矩阵为
这里的f(x)由式(4)定义，其中
容易看出它的非对角元均非负，因此是Metzler矩阵．令A=df(x)为邻接矩阵，由于A所对应的可达性矩阵Q中全部元素均为1，所以∂f(x)不可约[15]．
2)f(0)=0是显然成立的；当xi=0时，即当Ip,V分别为0时，则
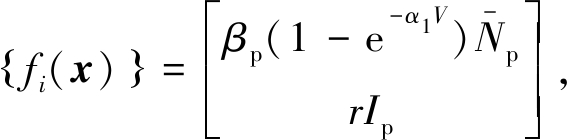
易验证fi(x)≥0,i=1,2．
3) 即对∀α∈(0,1)，有
f2(αx)-αf2(x)=rIp(1-α)>0．
即f(αIp,αV)>αf(Ip,V)，因此是严格次线性的．
注意到∂f(0)=F-V，而文献[13]指出R0>1等价于s(F-V)>0．因为系统(3)有紧正向不变集Ω意味着它的解不会趋向于无穷，故由引理1，系统(3)存在唯一的正平衡点
全局渐近稳定，对应地，系统(2)存在唯一的地方病平衡点
它全局渐近稳定．设地方病平衡点稳定时人类的稳态人口为
于是由平衡点关系获得
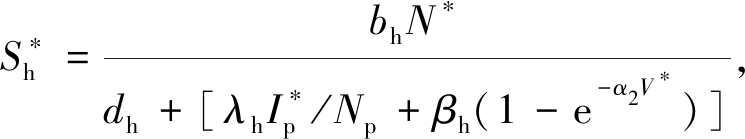
其中
由此可见
的值被唯一确定下来．
以上结论表明，当R0>1时，无病平衡点不稳定，系统(1)存在唯一正平衡点，H7N9病毒感染者将一直存在，并且感染人数逐渐稳定，形成地方病．
3 模 型 应 用
3.1 参数选取
选取广东省2016年11月—2017年6月H7N9的周病例数(从香港特别行政区政府卫生防护中心获取)，在此期间总发病数为63例，发病率为0.057 3/10 000．初值由广东区疫情数据估计而得，模型以周为单位．根据广东省统计信息网，估计禽类的扑杀率dp=1/6和禽类载量A=14 580 000，再利用
假设禽类初始总数Np(0)=17 948 000．从2017年1月开始，政府采取了多种控制措施，特别是加强了对活禽市场管理(如清理和关闭)，从而降低了疾病的传染率，因此将传染率(λp，λh，βp，βh)分成两段代入模型，并利用Markov(马尔科夫)链Monte-Carlo(蒙特卡罗)估计未知参数，得到图2模型的拟合图．可看出， H7N9疫情在2017年1月左右最为严重，随后感染人数逐渐下降，疫情逐渐消失．
3.2 数值分析
运用MATLAB软件进行数值模拟，进一步分析动力学性质．分别对初值Ip(0)和V0(0)以及参数α1,α2,r和dv取不同值，研究初始时刻染病禽类数量和环境病毒载量、以及环境病毒的传染率、染病家禽对病毒生产率和环境病毒的消除率对人群感染的影响，模型其他参数的取值基于广东实际情况进行选取和估计．
分别将初始时刻的病毒数量初值V(0)和感染病毒数Ip(0)视为变量，其他参数不变，感染病人的时间演化图如图3(a)所示．结果发现模型峰值随着Ip(0)和V(0)的不断增大而升高，即感染人数逐渐增多，在2017年1月初达到峰值，之后病例数迅速下降且逐渐趋于零．通过计算估计在2016年11月—2017年1月初期间，模型的基本再生数R0=18.8，这期间疾病流行并迅速蔓延．此时需要对家禽的接种率为V/N=1-1/R0=94.7%，从而可控制H7N9在禽类和环境中的传播．疫情的蔓延使得广东省各地迅速采取了各类措施，如关闭市场和清理环境等，对应的降低了传染力，而后的基本再生数下降为R0=0.140 4<1，此时H7N9疫情随着时间的推移逐渐消亡．
图2 2016年11月—2017年6月广东省H7N9的周病例数和模型的拟合图
Fig. 2 The fitting results of the H7N9 human cases from Nov. 2016 to Jun. 2017 in Guangdong with the model
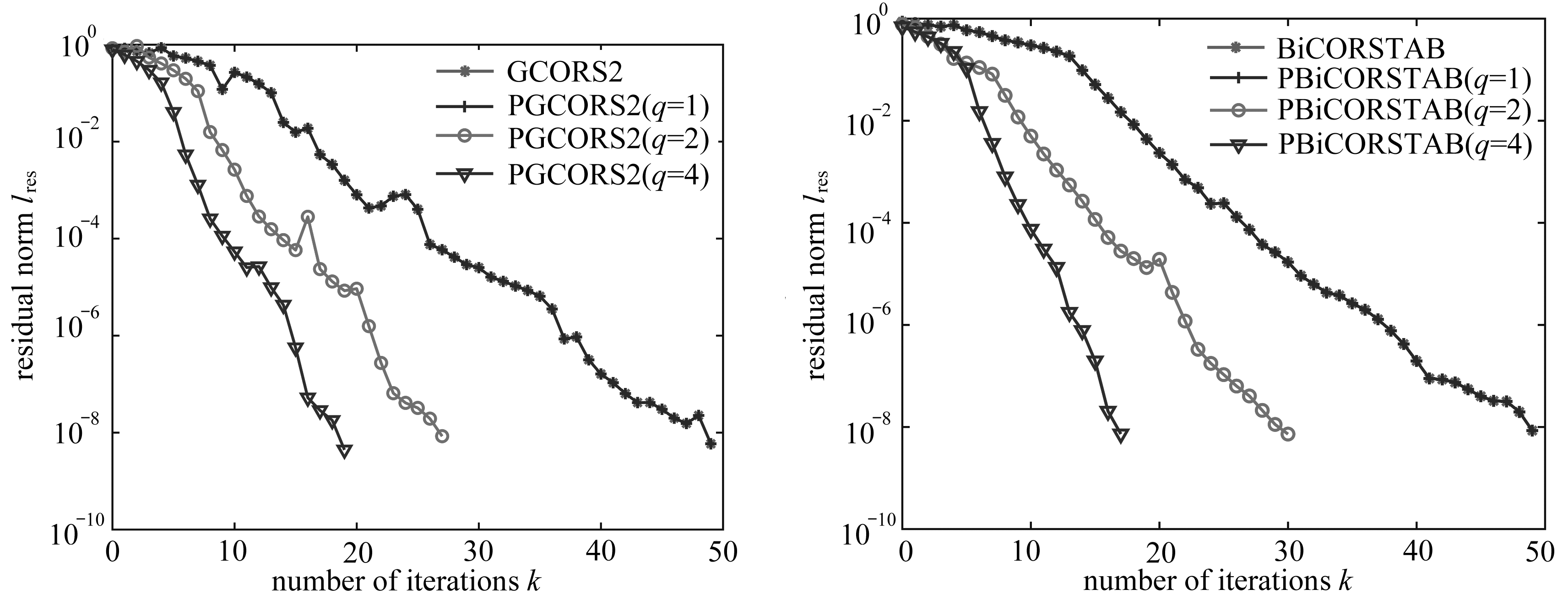
(a) 不同的感染禽类初值的影响 (b) 不同的环境中病毒初值的影响
(a) Different initial values of infected poultry (b) Different initial values of virus in the environment
图3 在不同的初值条件下感染人数的时间演化图
Fig. 3 The time evolution of the infected human number with different initial values
比较图3发现，感染禽类和环境中的病毒初值对感染H7N9人数都有很大的影响，感染禽类比环境中病毒对发病率影响更加显著，这与Breban等[9]分析2009年疫情得到的环境中病毒传播水平较低的结果相符合．
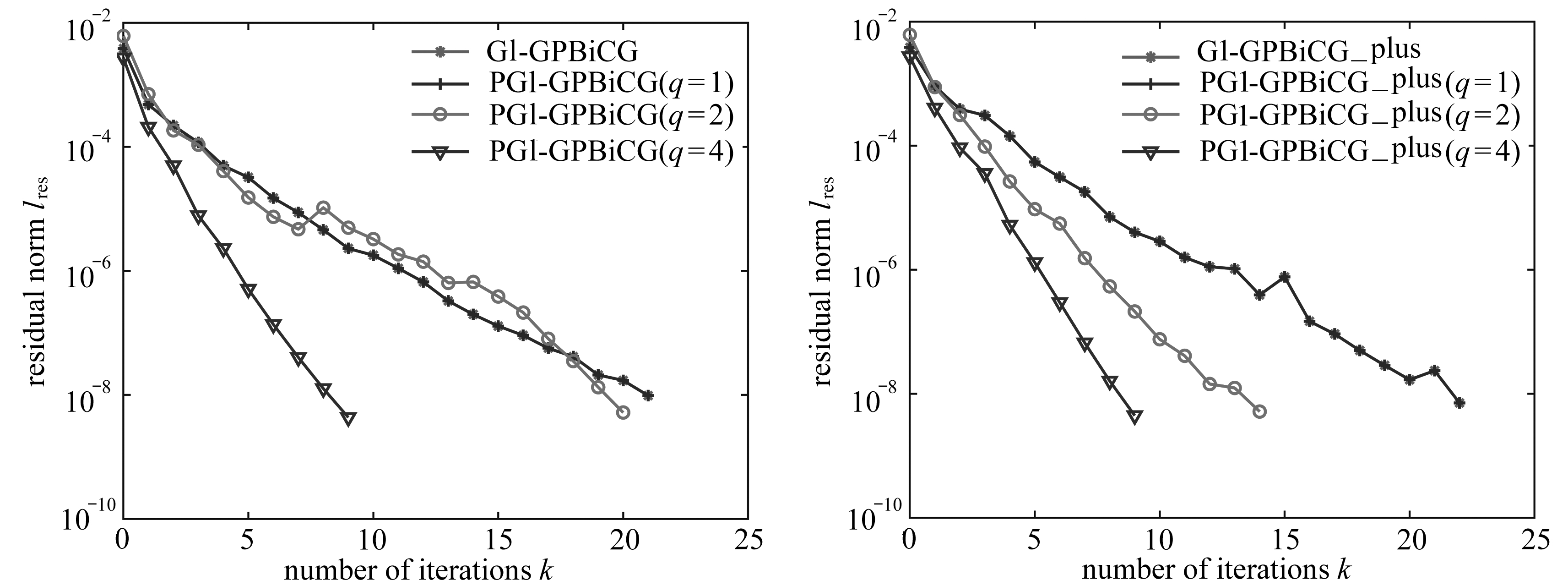
(a) 环境病毒对禽类的传播参数α1对病例数的影响 (b) 环境病毒对人类的传播参数α2对病例数的影响
(a) The effects of parameter α1of rescaled environmental (b) The effects of parameter α2 of rescaled environmental infectiousness to poultry on the human incidence infectiousness to human on the human incidence
(c) 家禽对环境中病毒的生产率r对病例数的影响 (d) 病毒死亡率dv对病例数的影响
(c) The effects of parameter r of VE production rate (d) The effects of parameter dv of VE elimination rate in from poultry on the human incidence natural environment on the human incidence
图4 模型参数对感染人群的影响
Fig. 4 Effects of model parameters on the human incidence
保持初值以及其他参数不变，分别改变α1，α2，r和dv，得到的人群感染数量演化图如图4所示，发现模型峰值随着α1，α2和r的增大及dv的减少而升高，此时感染病例数逐渐增多．
4 结 论
本文提出并分析了一个含有环境中病毒的H7N9传染病模型，运用了微分方程稳定性理论和数值模拟对模型进行讨论．证明了当基本再生数小于1时系统(1)存在无病平衡点且全局渐近稳定，此时疾病随时间的推进将逐渐消亡．若基本再生数大于1，系统(1)存在全局稳定的正平衡点，H7N9传染病将发展为地方病．
通过数值分析发现，降低初始时刻环境中的病毒和感染禽类数量能有效减少人类的感染，但仅仅降低初值还不足够，后期还要通过降低家禽间的传染率(例如对染病禽类进行扑杀)，降低禽类到人类的传染率(例如实施关闭活禽市场)，以及减少环境中病毒对禽类的传染率和对人类的传染率(例如减少去比较密集的地方，离养殖场较近的地方)，减少感染的家禽对环境中病毒的生产率(例如对染病家禽进行焚烧和掩埋，防止病毒进入环境)，均可以有效地减弱H7N9的传播．广东省对控制禽流感实施了许多防控措施，例如，“1110政策”“集中屠宰、冷链配送、生鲜上市”和“定期关闭活禽交易市场”等，使得禽流感疫情得到了有效的控制，但H7N9仍有卷土重来的风险，仍需及时进行风险评估和多加防范．
文中的模型还有许多因素没有考虑，例如温度和湿度等环境因素对H7N9病例数的影响，我们将在以后的工作中做进一步研究与讨论．
[1] GAO R, CAO B, HU Y, et al. Human infection with a novel avian-origin influenza a (H7N9) virus[J]. The New England Journal of Medicine, 2013, 368(20): 1888-1897.
[2] 徐继承, 黄水平, 肖伟伟, 等. 中国大陆地区438例人感染H7N9禽流感空间聚集性分析[J]. 中华流行病学杂志, 2014, 35(11): 1270-1274. (XU Jicheng, HUANG Shuiping, XIAO Weiwei, et al. Spatial aggregation of 438 human infections with avian influenza A (H7N9) in the mainland of China[J]. Chinese Journal of Epidemiology, 2014, 35(11): 1270-1274.(in Chinese))
[3] ZHANG J, JIN Z, SUN G Q, et al. Determination of original infection source of H7N9 avian influenza by dynamical model[J]. Scientific Reports, 2014, 4: 4846. DOI: 10.1038/srep04846.
[4] LIN Q, LIN Z, CHIU A P Y, et al. Seasonality of influenza A (H7N9) virus in China: fitting simple epidemic models to human cases[J]. PloS One, 2016, 11(3): e0151333. DOI: 10.1371/journal.pone.0151333.
[5] LU J, LIU W, XIA R, et al. Effects of closing and reopening live poultry markets on the epidemic of human infection with avian influenza A virus[J]. Journal of Biomedical Research, 2016, 30(2): 112-119.
[6] XING Y, SONG L, SUN G Q, et al. Assessing reappearance factors of H7N9 avian influenza in China[J]. Applied Mathematics and Computation, 2017, 309: 192-204.
[7] ZHOU X, LI Y, WANG Y, et al. The role of live poultry movement and live bird market biosecurity in the epidemiology of influenza A (H7N9): a cross-sectional observational study in four eastern China provinces[J]. Journal of Infection, 2015, 71(4): 470-479.
[8] CHEN L J, LIN X D, GUO W P, et al. Diversity and evolution of avian influenza viruses in live poultry markets, free-range poultry and wild wetland birds in China[J]. Journal of General Virology, 2016, 97(4): 844-854.
[9] BREBAN R, DRAKE J M, STALLKNECHT D E, et al. The role of environmental transmission in recurrent avian influenza epidemics[J]. PLoS Computational Biology, 2009, 5(4): e1000346. DOI: 10.1371/journal.pcbi.1000346.
[10] WEN Y M, KLENK H D. Erratum: H7N9 avian influenza virus: search and re-search[J]. Emerging Microbes & Infections, 2013, 2(5): e26. DOI: 10.1038/emi.2013.26.
[11] ZHOU P, MA J, LAI A, et al. Avian influenza A (H7N9) virus and mixed live poultry-animal markets in Guangdong province: a perfect storm in the making? [J]. Emerging Microbes & Infections, 2015, 4(10): e63. DOI: 10.1038/emi.2015.63.
[12] 马知恩, 周义仓, 王稳地, 等. 传染病动力学的数学建模与研究[M]. 北京: 科学出版社, 2004.(MA Zhien, ZHOU Yicang, WANG Wendi, et al. The Mathematical Modeling and Study of Infectious Disease Dynamics[M]. Beijing: Science Press, 2004.(in Chinese))
[13] VAN DEN DRIESSCHE P, WATMOUGH J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J]. Mathematical Biosciences, 2002, 180(1): 29-48.
[14] ZHAO X Q, JING Z J. Global asymptotic behavior in some cooperative systems of functional differential equations[J]. Canadian Applied Mathematics Quarterly, 1996, 4(4): 421-444.
[15] 王伟贤. 矩阵不可约的充要条件[J]. 数学的实践与认识, 1988(4): 42-46.(WANG Weixian. The necessary condition for the matrix irreducibility[J]. Mathematics in Practice and Theory, 1988(4): 42-46.(in Chinese))