引 言
人造卫星技术是航天科技领域中的关键组成部分．伴随航天科技的飞速发展以及为满足国防和民用等各领域的需求，近些年来，人造卫星技术也在不断地发展．星载天线负责卫星信号的接收与传递，是卫星的核心组成部分．大尺度、高精度和低成本等特点是近些年也是未来卫星天线的主要发展方向[1-2] ．卫星进入轨道后天线在随卫星运行过程中由于尺寸大以及材料柔韧性等自身结构特点，外加复杂的太空环境，如太阳辐射、热激励和微重力等因素，将导致天线产生大幅的非线性振动，严重影响卫星姿态的稳定以及信号精度的控制[3-4] ．因此，卫星天线非线性振动的研究受到国内外许多学者的关注．
Ghosh和Kumar[5]利用有限元方法分析了可移动支撑类型天线在激励作用下产生的非线性响应．Makarov等[6]研究了失稳情形下环形柔性可展天线的非线性动力学行为．赵孟良和关富玲[7]建立了含摩擦的周边桁架式环形天线的动力学模型，分析了桁架单元之间的铰链摩擦以及重力作用等因素对桁架展开的影响．他们设计了四面体构架式的桁架可展开天线、六棱柱单元构架式可展开天线原理样机，并深入研究了所研制的天线结构设计、展开控制、运动特性、动力学特性[8-9]等．胡海岩等[10-11]综述了大型可展天线的研究现状，提出了大型可展天线在结构设计、动力学建模与控制和仿真模拟实验中需要注意的问题，建立了大型可展天线展开后在空中运行的动力学模型并分析了其非线性动力学行为．文献[12]基于Lagrange(拉格朗日)方程建立了可展桁架天线的柔性多体动力学模型，讨论了索网张力对天线桁架的影响，并进行了动态展开分析．Gao等[13]研究了安装两个刚性支承臂的柔性空间天线在3 ∶ 1和2 ∶ 1的内共振情形下的近似解及分叉． Pellicano[14]利用Sanders-Koiter理论将系统简化成圆柱壳并建立了其非线性动力学方程，分析了系统在压缩静力和周期性轴向载荷综合作用下的稳定性．文献[15]将环形桁架卫星天线等效成圆柱壳结构，建立等效圆柱壳结构的呼吸振动形式下的非线性动力学控制方程，并分析了热激励对系统非线性动力学行为的影响．
为研究环形桁架天线在运行中的非线性动力学行为，将环形桁架天线结构简化成力学模型并建立其动力学方程，所建立的动力学方程都可以用高维非线性系统来描述．因此，研究高维非线性动力学方程，不仅对分析卫星天线的非线性动力学行为有重要意义，而且对于研究由工程实际问题所建立的高维非线性动力学方程也具有指导意义．对于高维非线性系统混沌运动的研究从最早的符号动力学、Smale马蹄运动等到现在的能量相位法[16-17]、广义Melnikov方法[18-19]以及数值方法等，研究方法和理论都在不断改进，从而更广泛地适用于研究实际工程问题．目前，为了研究工程实际问题中高维非线性系统的多脉冲混沌运动，研究者将能量相位法不断推广和改进[20-22] ．对于实际工程问题的动力学特性研究还有一些其他的方法，如赵岩等[23]利用虚拟激励法研究了受随机载荷作用下陀螺阻尼系统随机动力响应问题．黎崛珉等[24]在随机激励环境中研究刚度非线性和阻尼非线性对隔振系统在随机激励下力传递率及其概率分布的影响．吴子英等[25]建立了附加线性振子的双稳态电磁式振动能量捕获器的动力学方程，并研究有色噪声激励作用下双稳态能量捕获系统的非线性动力学行为．
卫星天线在轨运行时受到太阳辐射的作用，天线表面在受照区和阴影区的交替过程中温度发生剧烈的冷热交变，引发天线结构热变形、热应力等．因此，环形可展天线的外激励主要为热激励．本文考虑以横向振动为主要振动，对环形桁架天线的动力学方程[15]进行三阶离散，得到系统以呼吸振动为主要振动的三自由度非线性方程．对所得到的三自由度非线性方程即六维非线性方程，选取1 ∶ 4 ∶ 6内共振关系，将推广后适用于分析六维系统的能量相位法[22]进一步地化简并研究环形桁架天线的多脉冲混沌动力学．
1 环形桁架天线的非线性动力学方程和规范型化简
1.1 环形桁架天线的非线性动力学方程
在文献[15]中环形桁架天线被简化成如图1所示的等效圆柱壳模型，R为圆柱壳的面半径，L为轴向长度，h为沿径向壳的厚度．圆柱壳处于变化温度场中，ΔT=T1cos(Ωt)-Tref，Tref为初始温度，T1cos(Ωt)为周期性的热激励扰动项．
根据Reddy一阶剪切变形壳理论、Von Karman非线性应力-应变关系以及Hamilton原理，建立了考虑剪切的等效圆柱壳的非线性动力学方程：
(1a)
(1b)
(1c)
(1d)
(1e)
其中Aij,Bij,Cij(i, j=1,2,…,6)分别代表等效圆柱壳的薄膜刚度、耦合刚度和弯曲刚度，且被定义为
(2a)
(2b)
Gi=
ρ(1,z,z2)dz， i=0,1,2．
图1 等效圆柱壳模型
Fig. 1 The model for the equivalent circular cylindrical shell
考虑如下自由-自由以及固定-固定边界条件：
固定-固定端
v0=w0=φθ=0， θ=0，2π；
(3a)
自由-自由端
Nxx=Nxy=Mxx=Mxy=Qx=0， x=0，L．
(3b)
为便于接下来的定性分析和定量分析不受量纲的影响，对方程进行无量纲化．引入变量和参数的无量纲形式：
考虑以横向振动为主要振动，对方程(1)的w方向进行三阶离散，其余方向一阶离散，得到系统由横向位移表示的呼吸振动的三自由度非线性方程如下：
(4a)
(4b)
(4c)
其中w1(t)，w2(t)和w3(t)分别是第一阶、第二阶和第三阶振动的模态，μ1，μ2和μ3为结构阻尼系数， f1， f2， f3为环形桁架天线的参数激励，F1，F2和F3为环形桁架天线的外激励，方程的其他系数见文献[15]．
利用多尺度法分析等效圆柱壳的非线性呼吸振动方程，考虑如下1 ∶ 4 ∶ 6内共振情形：
(5)
其中σ1，σ2和σ3为三个调谐参数，为简化分析，令
经过计算得到直角坐标系下的平均方程：
(6a)
(6b)
(6c)
(6d)
(6e)
(6f)
1.2 环形桁架天线动力学方程的规范型化简
由于环形桁架天线的平均方程(6)中所含的非线性项复杂，不能对其非线性方程进行直接分析．因此，利用规范型理论对复杂的非线性方程进行化简，而且化简后的方程与原方程是拓扑等价的．
系统(6)在初始平衡点(x1,x2,x3,x4,x5,x6)=(0,0,0,0,0,0)线性部分的Jacobi矩阵为
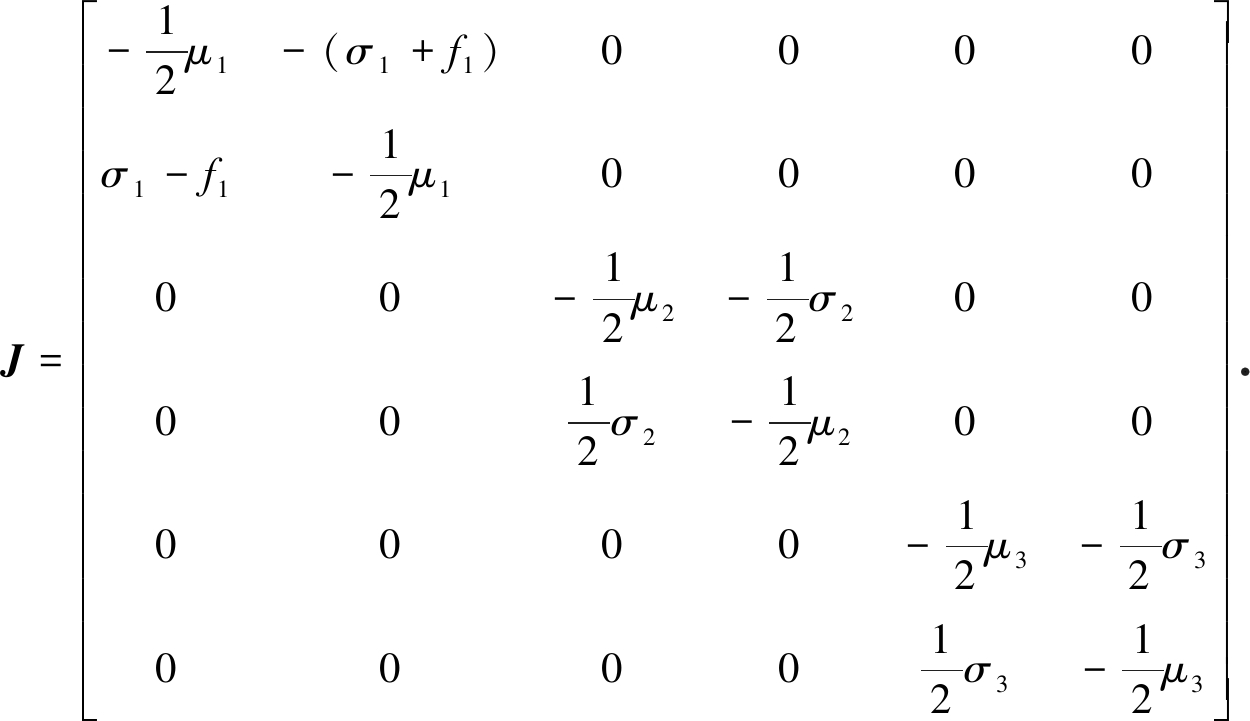
(7)
Jacobi矩阵对应的特征多项式为
(8)
由方程(8)可知，当
时，对应的环形桁架天线的平均方程(6)有一对零特征根和两对纯虚特征根：
(9)
令
将
作为摄动参数，利用MAPLE程序得到系统(6)含参数的三阶规范型：
(10a)
(10b)
(10c)
(10d)
(10e)
(10f)
其中所用的非线性变换见附录．
为便于分析,将系统(10)的后四维方程转化成极坐标形式，即引入如下变换：
y3=I1cos θ1， y4=I1sin θ1， y5=I2cos θ2， y6=I2sin θ2．
(11)
将变换(11)代入到三阶规范型(10)中得到如下的系统：
(12a)
(12b)
(12c)
(12d)
(12e)
(12f)
为将系统(12)化为更简单的形式，引入如下变换：
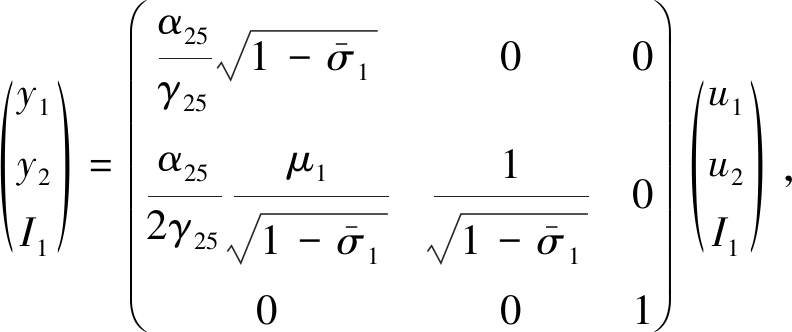
(13)
其中 β23γ22=-2β20γ24．
将变换(13)代入系统(12)中得到三自由度环形桁架天线系统的简单规范型：
(14a)
(14b)
(14c)
(14d)
(14e)
(14f)
其中
为研究阻尼参数对系统非线性动力学的影响，下面对阻尼参数引入扰动项ε：
μ1→εμ1， μ2→εμ2， μ3→εμ3， F2→εF2， F3→εF3．
(15)
因此，系统(14)可以写成带有扰动项的Hamilton系统：
(16a)
(16b)
(16c)
(16d)
(16e)
(16f)
当ε=0时， 未扰系统 (16)是完全可积的Hamilton系统， 其对应的Hamilton函数为如下形式：
(17)
当ε≠0时，系统(16)是耗散扰动系统，其耗散扰动项为如下形式：
(18)
2 未扰系统动力学分析
首先考虑系统未受扰动的情形，即当ε=0时，系统(16)是一个解耦的两自由度未扰动非线性系统．当ε=0时，变量
因此，变量I1和I2为常数，在系统(16)的子空间(u1,u2)中可以看作为参数．系统(16)的前两个方程与后面四个方程是解耦的．下面先研究系统(16)在未扰情形下的前两个方程：
(19a)
(19b)
当c3c4<0时,系统(16)会出现同宿分叉．在此令c3>0,c4<0．当
时，系统(16)只有一个初始平衡点(u1,u2)=(0,0)．通过计算系统(19)在初始平衡点(u1,u2)=(0,0)处Jacobi矩阵可知初始平衡点为中心点．接下来定义临界曲线．令
得到初始平衡点(u1,u2)=(0,0)在原点处发生pitchfork分叉产生三个解，鞍点P1=(0,0)和中心点P2,3=(±B,0)，其中
(20)
在系统中，变量I1，I2和θ1，θ2分别代表系统振动的幅值和相位．所以，变量I1和I2应该满足Ii≥0,i=1,2．在I∈(I1,I2)∉[I11,I12]×[I21,I22]⊂R2中，未扰系统 (19)有两个中心点P2,3=(±B,0)、一个鞍点P1=(0,0)以及一对同宿轨道
且同宿轨道满足limT1→±∞u±i(T1,Ii)=P1,i=1,2，其中T1是定义在二维扰动慢变流形动的相空间上．
未扰系统(19)在相空间(u1,u2)上不同区域内平衡点的相图如图2所示．当时,系统只有一个平衡点且为中心点;当
时,系统有三个平衡点，其中一个鞍点两个中心点且连接鞍点的是一对同宿轨道，而此同宿轨道亦为中心点的外边界．
图2 未扰系统平衡点的相图
Fig. 2 The phase portrait of the equilibrium points of the unperturbed system
在六维相空间中四维正规双曲不变流形定义为如下形式：
M= (u,I,θ)∈R2×R2×S2u=P1,I1<I<I2,0≤θi<2π ,
i=1,2．
(21)
不变流形M有五维稳定流形和不稳定流形分别为Ws(M)和Wu(M)．在系统(21)中由同宿轨道连接的奇点沿五维稳定流形和不稳定流行形成如下五维的同宿流形Γ．其中由连接奇点P1=(0,0)的同宿轨道可知Ws(M)和Wu(M)沿五维同宿流形Γ非横截相交，同宿流形Γ定义为如下形式：
i=1,2．
(22)
对于系统振动的每个幅值I∈(I1,I2)时，二维正规双曲不变圆环θ(I)具有三维稳定流形Ws(θ(I))和不稳定流形Wu(θ(I))重合形成的三维同宿流形，其中六维相空间中流形的结构图如图3所示，γ表示振动相位．
未扰系统(19)的前两维系统定义在二维扰动慢变流形动的相空间上．下面分析限制在流形M上的未扰系统(19)为
(23a)
(23b)
(23c)
(23d)
当
时，系统的解为含有两个参数的二维圆环；当
时，系统的解为不动点圆环，其中
的表达式如下：
(24a)
(24b)
此时使得等式
成立的I值为系统的共振值，记为Ir=(I1r,I2r)．则可得到如下的共振值：
(25a)
(25b)
为计算系统(19)连接双曲鞍点P1=(0,0)的同宿轨道以及相位差Δθ,给出未扰系统(19)未扰动部分的Hamilton函数：
(26)
令
联立鞍点P1=(0,0)和Hamilton函数并化简得到系统(19)的同宿轨道：
(27a)
u2(T1)=∓
(27b)
将轨道(27)代入式(20)中并对式(23b)和(23d)进行积分，得到系统的振动相位θ1和θ2为如下形式：
(28a)
(28b)
其中
和θ02为初始相位角．
图3 六维空间中不变流形M与同宿流形Γ的结构图
Fig. 3 The structure portrait of invariant manifold M and homoclinic manifold Γ in the 6D space
在此定义相位差为如下形式：
Δθi=θ(+∞,Ii)-θ(-∞,Ii), i=1,2．
(29)
当Ii=Iir(i=1,2)时，即共振情况下，di≡0,i=1,2，则相位差为
(30)
3 扰动系统动力学分析
综上分析，得到了未扰系统(19)的同宿轨道、相位差等，并分析了在六维相空间中流形M的几何结构．接下来将研究系统(19)在小扰动影响下的动力学特性．根据文献[16-17]可知，在小扰动下不变流形M沿稳定流形与不稳定流形是不变的，P1仍为鞍点且此时的流形Mε充分接近M，即定义
M=Mε= (u1,u2,I,θ) (u1,u2)=P1,Ii1<I<Ii2,0≤θi<2π,
i=1,2．
(31)
因此将系统(16)限制在流形Mε上，在共振情形下研究系统(16)的动力学特性．首先定义一个四维空间M4=(u1,u2,I1,θ1)为如下形式：
M4=[(u1,u2,I1,θ1)∈R×R×R×S(u1,u2)=P1,
I1∈(I11,I12),0<θ1≤2π]．
(32)
将系统中的变量I2限制在[I2r-ε, I2r+ε]⊂[I21,I22]上，且变量θ2满足θ2∈ (0，2π]．只需研究在共振情形下系统M4=(u1,u2,I1,θ1)的动力学特性，之后让变量I2取遍[I2r-ε,I2r+ε]⊂[I21,I22]上的每个点，从而就可以到到整个六维系统(16)的动力学特性．
为得到系统未扰动部分Hamilton函数，引入如下变换：
(33)
则将变换(33)代入式(16c)和(16d)并化简得到
(34a)
(34b)
未扰系统(34)是Hamilton系统，其对应的Hamilton函数为如下形式：
(35)
当ε=0，在θ1∈(0,2π)区间内得到系统(34)的不动点为
(36)
下面计算在奇点Q1和Q2处的Jacobi矩阵，分析奇点的稳定性，则系统(34)未扰动部分的Jacobi矩阵为
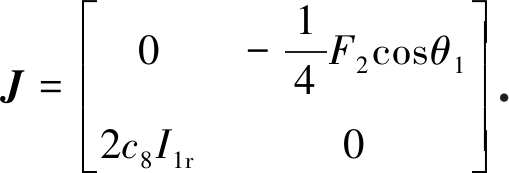
(37)
根据方程 (37)，当
时，系统有一对纯虚特征根，即奇点Q2为中心点；当
时,系统(34)有两个异号的实特征根，即奇点Q1为鞍点且由一对同宿轨道连接．
在小扰动ε下，奇点Q1仍为双曲奇点，扰动后的奇点Qε1仍为鞍点．而奇点Q2在受扰动后将会产生变化，首先考虑系统(34)线性部分的Jacobi矩阵：
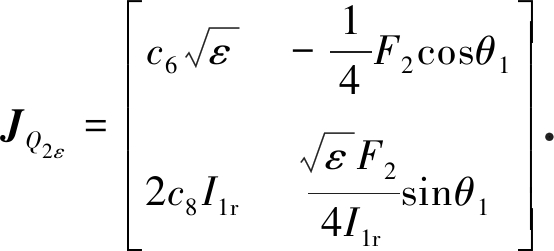
(38)
根据矩阵(38)，我们发现系统(37)线性部分的低阶项在同宿环内小于零．因此，在扰动下奇点Q2变为双曲焦点Qε2．
4 能量相位法
在本节利用Haller和Wiggins[16-17]提出的能量相位法以及改进后的能量相位法，研究环形桁架天线具有Shilnikov同宿轨道的多脉冲混沌运动．计算相空间中快变流行上每个脉冲跳跃所消耗的能量，即能量差分函数的具体表达式以及能量差分函数的横截零点,从而验证系统存在着多脉冲轨道．
首先给出系统(16)的含有耗散项的能量差分函数：
(39)
其中Δθ是相位差，A为在子空间(u1,u2)中由一对同宿轨道围成的区域，∂Al是区域A的边界．由式(39)可知能量差分函数分为四个部分：
为n个脉冲的总能量；
为在(h,θ)平面中未跳起脉冲的能量，即
(40)
为同宿轨道所围成区域的面积，即
(41)
为脉冲沿着同宿轨道的积分，即
(42)
经计算得到系统(16)的能量差分函数的具体表达式:
(43)
接下来计算能量差分函数的横截零点．首先，定义一个包含能量差分函数所有横截零点的集合：
(44)
含耗散项的能量差分函数
的横截零点满足如下条件:
(45)
其中m∈Ζ，并且得到
(46)
在区间
上，当含有耗散项的能量差分函数
满足nΔθ1≠4lπ(l=0,1,2,…)时,能量差分函数有如下两个横截零点：
(47a)
(47b)
由集合(43)可以得出如下关系式：
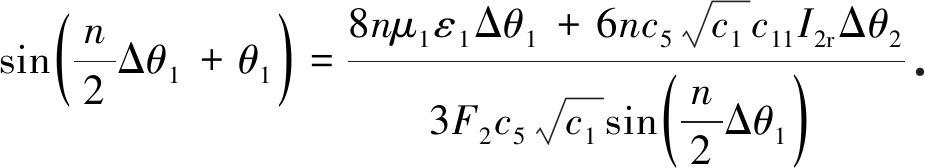
(48)
为研究系统阻尼与激励之间的关系，定义变量d=μ/F2为耗散因子，令μ=μ1=μ2=μ3，则由方程(48)得到耗散因子的上确界：
(49)
同理，可得到脉冲数的上确界
(50)
为分析环形桁架天线系统是否存在Shilnikov型多脉冲轨道，需要验证如下3个条件是否成立：① 系统的Hamilton函数存在非退化零点； ② 在整个六维相空间(u1,u2,I1,I2,θ1,θ2)中，非退化零点是耗散能量差分函数的横截零点且满足非退化条件； ③ 从慢流形上跳起的脉冲轨道最后又落回焦点的吸引域内．
首先由方程(35)得到了Hamilton函数的非退化零点为Q2．
接下来将中心点Q2代入能量差分函数中并计算其零点，即
(51)
化简后得到耗散因子的表达式：
(52)
当耗散因子不为零时，即如下条件成立时，中心点Q2为能量差分函数零点：
nΔθ1≠2kπ, k∈Z+，
(53)
(54)
经验证，在条件(53)情形下，式(51)与(54)不能同时成立，即中心点Q2是能量差分函数的横截零点．
最后，只需验证从慢流形上跳起的脉冲最终又落回到慢流形上中心点Q2的吸引域内．
在慢流形上，我们知道脉冲的起跳点为中心点Q2，其对应的能量函数为
鞍点对应的能量为
在区间(0,2π)上，假设脉冲的落回点为Q，其对应的能量函数为
由于相图的对称性，当落回点与鞍点或中心点距离超过鞍点对应的能量为2kπ时，重新定义落回点为如下形式：
(55)
其中
θ1s=π+arcsin(2dI1r)， θ1c=-arcsin(2dI1r)．
(56)
起跳点处的能量最大，当落回点不断远离起跳点时，能量不断减小，能量最小的落回点为鞍点，当落回点的能量满足如下条件时，落回点就落到了焦点的吸引域内：
(57)
下面以未扰系统的鞍点为吸引域的边界，在区间(0,4π)内定义两个区域：
D1=(π+arcsin(2dI1r),3π+arcsin(2dI1r))，
(58a)
D2=(3π+arcsin(2dI1r),5π+arcsin(2dI1r))．
(58b)
则落回点会落到两个区域中的一个或两个区域平移2kπ后的区域内．如果落回点落入区域D1内，则存在连接鞍点自身的Shilnikov型同宿轨道；如果落回点落入区域D2内，则存在连接两个鞍点的异宿轨道．
5 数 值 模 拟
为了验证上述理论分析，对系统的平均方程(6)进行数值模拟．当系统(6)中的参数
即α14>0时，系统会出现Shilnikov型多脉冲混沌运动．在上述定性分析的基础上发现激励参数在环形桁架天线多脉冲混沌运动中起着重要作用．
图4 系统随激励F2变化的分叉图
Fig. 4 The bifurcation diagram of the system under excitation F2
选择激励参数F2作为系统的控制参数，研究等效圆柱壳的非线性动力学行为．选取系统的初值为x10=0.04，x20=0.15，x30=0.35，x40=0.19，x50=0.01，x60=0.02以及系统的参数值为μ1=0.05，μ2=0.05，μ3=0.05，σ1=0.12，σ2=0.19，σ3=3.12，α14=0.11，α21=0.9，α25=3.9，β15=2.11，β20=7，β23=24，β24=2，γ16=2，γ20=5，γ22=2.5，γ24=2.3，f1=5，F3=17.5，激励F2在F2∈(50,90)区间内环形桁架天线的分叉图如图4所示．从图4中可以看出，当激励F2<80时，系统一直处于周期运动状态；当激励F2>80时，系统进入混沌运动状态．选取激励F2=92.1，得到系统的混沌运动相图，如图5所示．其中图5(a)表示系统在(x1,x2)平面上的相图，图5(b)表示系统在(t,x1)平面上的相图，图5(c)表示系统在(x3,x4)平面上的波形图，图5(d)表示系统在(x6,x5)平面上的波形图，图5(e)表示系统在(x1,x2,x3)平面上的相图，图5(f)表示系统在(x4,x5,x6)平面上的相图．从图5中发现系统的混沌运动轨迹有明显的跳跃现象．
图5 F2=92.1时系统的混沌运动图
Fig. 5 The chaos motion diagram of the system for F2=92.1
6 结 论
本文首次研究了六维系统环形桁架天线Shilnikov型多脉冲混沌运动．选取横向振动为主要振动进行三阶离散，得到环形桁架天线呼吸振动的三自由度非线性方程．利用多尺度法得到1 ∶ 4 ∶ 6内共振关系下环形桁架天线的平均方程．利用规范型理论化简平均方程，根据推广后的能量相位法分析了其拓扑等价方程的非线性动力学行为．通过分析环形桁架天线多脉冲同宿轨道，发现未扰系统中的鞍点存在一条连接自身的同宿轨道，当受到扰动后同宿轨破裂，其中一个分支落入焦点的吸引域内，另一个分支形成了焦点附近吸引域的边界，且焦点产生跳跃的脉冲轨道，最终又回到吸引域内．分析还表明，同宿轨道的存在依赖于能量相位判据．在数值模拟中发现激励参数对天线非线性运动影响较大．当选择一定的参数值和初始条件时，环形桁架天线会出现大幅度的振动．在一定区间内，系统保持稳定的周期运动．随着激励参数的增大，系统进入不稳定的混沌运动状态．本文从多个方面解释和描述了环形桁架天线可以产生Shilnikov型多脉冲混沌运动．综上理论分析与数值模拟，可以为抑制环形桁架天线产生混沌运动或避免大的振动提供参考．
附 录
(A1)
(A2)
(A3)
(A4)
(A5)
(A6)
[1] AKIRA M, AKIO T, NAOKAZU H. Technology status of the 13 m aperture deployment antenna reflectors for engineering test satellite VIII[J]. Acta Astronautica, 2000, 47(2/9): 147-152.
[2] TIBERT G. Deployable tensegrity structures for space applications[D]. PhD Thesis. Stockholm: Royal Institute of Technology, 2002.
[3] 闵桂荣, 郭舜. 航天器热控制[M]. 北京: 科学出版社, 1998.(MIN Guirong, GUO Shun. Spacecraft Thermal Control[M]. Beijing: Science Press, 1998.(in Chinese))
[4] THOMSON M W. AstroMeshTM deployable reflectors for Ku- and Ka-band commercial satellites[C]//20th AIAA International Communication Satellite Systems Conference and Exhibit. Montreal, Quebec, Canada, 2002.
[5] GHOSH A K, KUMAR M R. Dynamic analysis of supporting structure of mobile antenna[J]. Computers & Structures, 1997, 63(3): 633-637.
[6] MAKAROV A L, KHOROSHILOV V S, ZAKRZHEVSKII A E. Spacecraft dynamics due to elastic ring antenna deployment[J]. Acta Astronautica, 2011, 69(7/8): 691-702.
[7] 赵孟良, 关富玲. 考虑摩擦的周边桁架式可展天线展开动力学分析[J]. 空间科学报, 2006, 26(3): 220-226.(ZHAO Mengliang, GUAN Fuling. Deployment dynamic analysis of circular truss deployable antenna with friction[J]. Chinese Journal of Space Science, 2006, 26(3): 220-226.(in Chinese))
[8] YAN X, GUAN F L, CHEN J J, et al. Structural design and static analysis of a double-ring deployable truss for mesh antennas[J]. Acta Astronautica, 2012, 81(2): 545-554.
[9] YAN X, GUAN F L, XU X, et al. Development of a novel double-ring deployable mesh antenna[J]. International Journal of Antennas and Propagation, 2012. DOI:10.1155/2012/375463.
[10] 胡海岩, 田强, 张伟, 等. 大型网架式可展开空间结构的非线性动力学与控制[J]. 力学进展, 2013, 43(4): 390-414.(HU Haiyan, TIAN Qiang, ZHANG Wei, et al. Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes[J]. Advances in Mechanics, 2013, 43(4): 390-414.(in Chinese))
[11] GAO X M, JIN D P, HU H Y. Internal resonances and their bifurcations of a rigid-flexible space antenna[J]. International Journal of Non-Linear Mechanics, 2017, 94: 160-173.
[12] ZHANG Y Q, LI N, YANG G G, et al. Dynamic analysis of the deployment for mesh reflector deployable antennas with the cable-net structure[J]. Acta Astronautica, 2017, 131: 182-189.
[13] GAO X M, JIN D P, HU H Y. Internal resonances and their bifurcations of a rigid-flexible space antenna[J]. International Journal of Non-Linear Mechanics, 2017, 94: 160-173.
[14] PELLICANO F. Dynamic stability and sensitivity to geometric imperfections of strongly compressed circular cylindrical shells under dynamic axial loads[J]. Communications in Nonlinear Science & Numerical Simulation, 2009, 14(8): 3449-3462.
[15] ZHANG W, CHEN J, SUN Y. Nonlinear breathing vibrations and chaos of a circular truss antenna with 1 ∶ 2 internal resonance[J]. International Journal of Bifurcation and Chaos, 2017, 26(5): 1650077. DOI: 10.1142/S0218127416500772.
[16] HALLER G, WIGGINS S. Orbits homoclinic to resonances: the Hamiltonian case[J]. Physica D: Nonlinear Phenomena, 1993, 66(3/4): 298-346.
[17] HALLER G, WIGGINS S. Multi-pulse jumping orbits and homoclinic trees in a modal truncation of the damped-forced nonlinear Schrodinger equation[J]. Physica D: Nonlinear Phenomena, 1995, 85(3): 311-347.
[18] KAPER T J, KOVACIC G. Multi-bump orbits homoclinic to resonance bands[J]. Transactions of the American Mathematical Society, 1996, 348(10): 3835-3887.
[19] CAMASSA R, KOVACIC G, TIN S K. A Melnikov method for homoclinic orbits with many pulses[J]. Archive for Rational Mechanics and Analysis, 1998, 143(2): 105-193.
[20] YAO M H, ZHANG W. Multi-pulse Shilnikov orbits and chaotic dynamics in nonlinear nonplanar motion of a cantilever beam[J]. International Journal of Bifurcation and Chaos, 2005, 15: 3923-3952.
[21] YAO M H, ZHANG W. Multi-pulse homoclinic orbits and chaotic dynamics in motion of parametrically excited viscoelastic moving belt[J]. Chaos, Solitons & Fractals, 2006, 28(1): 42-66.
[22] ZHANG W, GAO M J, YAO M H, et al. Higher-dimensional chaotic dynamics of a composite laminated piezoelectric rectangular plate[J]. Science in China Series G: Physics, Mechanics & Astronomy, 2009, 52(12): 1989-2000.
[23] 赵岩, 李明武, 林家浩, 等. 陀螺系统随机振动分析的辛本征展开方法[J]. 应用数学和力学, 2015, 36(5): 449-459.(ZHAO Yan, LI Mingwu, LIN Jiahao, et al. Symplectic eigenspace expansion for the random vibration analysis of gyroscopic systems[J]. Applied Mathematics and Mechanics, 2015, 36(5): 449-459.(in Chinese))
[24] 黎崛珉, 陆泽琦, 陈立群. 非线性阻尼非线性刚度隔振系统随机动力学特性研究[J]. 应用数学和力学, 2017, 38(6): 613-621.(LI Juemin, LU Zeqi, CHEN Liqun. An investigation on nonlinear-damping and nonlinear-stiffness vibration isolation systems under random excitations[J]. Applied Mathematics and Mechanics, 2017, 38(6): 613-621.(in Chinese))
[25] 吴子英, 牛峰琦, 刘蕊, 等. 有色噪声激励下双稳态电磁式振动能量捕获器动力学特性研究[J]. 应用数学和力学, 2017, 38(5): 570-580.(WU Ziying, NIU Fengqi, LIU Rui, et al. Dynamic characteristics of bistable electromagnetic vibration energy harvesters under colored noise excitation[J]. Applied Mathematics and Mechanics, 2017, 38(5): 570-580.(in Chinese))