引 言
云杉蚜虫又叫云杉食心虫,是一种生活在北美森林的常见昆虫,集中于有黑云杉(白云杉)或香脂冷杉树的地方[1-2].它的幼虫以鲜嫩的芽、嫩枝、叶和植物的其他部分为食物,这对植物造成了严重的影响[3].尽管人们耗费数亿美元购买杀虫剂遏制其增长,但还是导致了云杉蚜虫的周期性爆发,例如在美国的西北太平洋地区以及加拿大的南部地区等[4-6].云杉蚜虫周期性爆发的严重影响就是引起各种疾病广泛的传播,例如杆状病毒[7]等.所以研究云杉蚜虫种群结构模型的动力学行为,对于遏制其疫情的爆发并提供有效的控制措施极为重要.
对于不同种群结构模型的动力学研究成果有许多,如王双明等[8]对寄主种群引入了logistic增长模式,研究了一类带时滞的周期非局部反应扩散传染病模型,并利用次代算子方法定义了模型的基本再生数,进一步给出了疾病持久与消亡的充分条件.在20世纪70年代左右,源于人口结构系统,带有捕食函数的经典logistic云杉蚜虫种群模型[9-10]被提出, 因该模型存在一个稳定的周期轨道被学者广泛研究,如Rasmussen等[11]利用奇异摄动法研究了云杉蚜虫相互作用中的松弛振动.然而,加拿大的新布伦瑞克绿河工程项目人员在实地观察时发现,蚜虫对植物的捕食或者搬运能力并不是导致蚜虫种群周期振动的主要原因[4],同时Hassell等[12-13]也建立了一系列数值模拟方法验证上述观点.此后,Vaidya等[14]把时滞引入模型中,即得到具有时滞的云杉蚜虫种群结构模型,利用图解技术研究了该模型平衡点的存在情况以及周期振动性,并提供了一些控制周期性爆发的有效措施.Xu等[15]在文献[14]模型的基础上又引入反应扩散和生理结构,通过分析模型中特征值的分布以及利用中心流形定理和正规形理论,分别讨论了稳态解的稳定性和Hopf分岔性质等.然而,对于具有时滞的云杉蚜虫种群结构模型正平衡点的存在唯一性,以及分岔周期解的方向和稳定性,笔者至今未见报道.
对于云杉蚜虫的年龄结构种群模型:
其中,N(t,a)表示蚜虫种群在a年龄、t时刻的种群密度,![]() 和Pa分别表示死亡率和捕食率,均与年龄有关.Vaidya和Wu[14]对该模型进行了详细分析(详细过程见文献[14]),并将模型变为
和Pa分别表示死亡率和捕食率,均与年龄有关.Vaidya和Wu[14]对该模型进行了详细分析(详细过程见文献[14]),并将模型变为
这里假设![]() 表示t时刻成熟种群的密度,
表示t时刻成熟种群的密度,![]() 表示成熟的时间延迟;出生函数b(m)=q1me-αm,q1与出生率有关且q1>d,d表示成熟种群的平均死亡率,α>0且1/α表示当出生率达到最大值时其成熟种群量的大小;功能反应函数p(m)m=βm2/(γ2+m2),p=p(m)表示对成熟种群的捕食率,β是捕食的最大水平,γ>0描述在捕食率为β/2时蚜虫的种群量.
表示成熟的时间延迟;出生函数b(m)=q1me-αm,q1与出生率有关且q1>d,d表示成熟种群的平均死亡率,α>0且1/α表示当出生率达到最大值时其成熟种群量的大小;功能反应函数p(m)m=βm2/(γ2+m2),p=p(m)表示对成熟种群的捕食率,β是捕食的最大水平,γ>0描述在捕食率为β/2时蚜虫的种群量.
下面对上述方程进行无量纲化.对出生函数b(m)=q1me-αm的变量做尺度变换![]() 并定义
并定义![]() 为了方便,仍用t表示
为了方便,仍用t表示![]() 即得到本文主要研究的幼年、成年云杉蚜虫结构种群模型:
即得到本文主要研究的幼年、成年云杉蚜虫结构种群模型:
(1)
其中![]() 且
且![]() 均为正数.这里参数A与云杉蚜虫成熟种群的死亡率有关,B和C分别与鸟类的捕食和云杉蚜虫不成熟种群的存活率有关,c>0表示不成熟种群的平均死亡率.
均为正数.这里参数A与云杉蚜虫成熟种群的死亡率有关,B和C分别与鸟类的捕食和云杉蚜虫不成熟种群的存活率有关,c>0表示不成熟种群的平均死亡率.
本文的主要内容安排如下:首先讨论了正平衡点存在且唯一的充分条件,并分析了该平衡点的局部稳定性及Hopf分岔情况;其次,利用正规形理论和中心流形定理研究了分岔周期解的方向和稳定性;最后进行数值模拟,验证了所得结论的正确性.
1 平衡点的存在性及Hopf分岔与稳定性分析
该节分为两部分进行研究,首先讨论模型(1)平衡点的存在性;其次分析正平衡点的Hopf分岔情况及稳定性.
1.1 平衡点的存在性分析
模型(1)的平衡点由如下的方程给出:
显然y=0总是方程(1)的平衡点,并且参数A,B,C的取值决定了是否存在非零平衡点.若![]() 为方程(1)的正平衡点,则
为方程(1)的正平衡点,则![]() 一定满足方程
一定满足方程
(2)
易知,当B≤A时,对任意y∈(0,+∞),
恒成立,这与方程(2)矛盾.因此当B≤A时,方程(1)无正平衡点.
当B>A时,方程(1)可能有1个、2个或3个正平衡点,其正平衡点的个数取决于参数A,B和C的取值,详细内容见文献[14].如果在B>A的条件下假设![]() 成立,即可得方程(1)有唯一的正平衡点.由此可得到下面的定理.
成立,即可得方程(1)有唯一的正平衡点.由此可得到下面的定理.
定理1 若B>A且![]() 则方程(1)除零平衡点外有唯一的正平衡点.
则方程(1)除零平衡点外有唯一的正平衡点.
证明 对方程(2)的等式两边同时乘以eCy有
令
可得
由h1(0)=B-A,B>A,且当y→+∞时,h1(y)→-∞恒成立,又因对任意的![]() 恒成立,则h1(y)为单调减函数且h1(0)>0.
恒成立,则h1(y)为单调减函数且h1(0)>0.
由h2(0)=0,下面只需要证明![]() 对任意y∈(0,+∞)为单调增函数即可.令h3(y)=Cy3-y2+Cy+1,则有
对任意y∈(0,+∞)为单调增函数即可.令h3(y)=Cy3-y2+Cy+1,则有![]() 当
当![]() 时,
时,![]() 恒成立,即h3(y)≥1成立.进一步得到
恒成立,即h3(y)≥1成立.进一步得到![]() 也是成立的,所以当y∈(0,+∞)时,h2(y)为单调增函数.证毕.
也是成立的,所以当y∈(0,+∞)时,h2(y)为单调增函数.证毕.
注1 本文运用了文献[14]中关于云杉蚜虫种群模型的参数值,见表1.从表1中易知![]() 则参数C的假设合理.
则参数C的假设合理.
表1 云杉蚜虫种群模型参数值[14]
Table 1 Spruce budworm population model parameters[14]

symboldescriptionvaluesourceβmax. budworms as prey105 700 (larvae) (hm2·a)-1 (Ludwig et al.,1979), (Ludwig et al.,1978)γrelated to predation function69 748 (larvae) (Ludwig et al.,1979), (Ludwig et al.,1978)τmaturation delay0.75~2 a(Fleming and Shoemaker,1992), (Sheehan et al.,1989), (Royama,1984)cdeath rate of immature population0.95~2.53 (Sheehan et al.,1989), (Royama,1984), calculatedddeath rate of mature population0.30(Sheehan et al.,1989), (Blais,1981), estimatedαrelated to birth function0.000 17estimatedq1related to birth function9.83×105 (Royama,1984), estimated, calculated
1.2 正平衡点的Hopf分岔与稳定性分析
在后面的讨论中,都假设B>A且![]() 是成立的.
是成立的.
为了讨论正平衡点![]() 的稳定性,需将方程(1)在
的稳定性,需将方程(1)在![]() 处进行线性化.首先将平衡点
处进行线性化.首先将平衡点![]() 平移到原点,即做变换
平移到原点,即做变换![]() 从而得到方程(1)在原点处的线性化方程:
从而得到方程(1)在原点处的线性化方程:
(3)
则方程(3)的特征方程为
(4)
令
方程(4)变为
λ=-β0+Bβ1e-λτ.
(5)
当τ=0时,方程(5)化为
λ=Bβ1-β0,
该式表明,若Bβ1<β0成立,方程(5)所有的根具有负实部.
令λ=iw(w>0)是方程(5)的特征根,则有
iw=-β0+Bβ1(cos(wτ)-isin(wτ)).
将上式的实部与虚部分离,可得
β0=Bβ1cos(wτ), w=-Bβ1sin(wτ),
(6)
于是将式(6)中的两式分别平方再相加,有
即
(7)
所以当![]() 时,w存在,记为w0.于是将式(7)代入式(6)中,得到τ的表达式为
时,w存在,记为w0.于是将式(7)代入式(6)中,得到τ的表达式为
(8)
总结起来有下面的引理.
引理1 对方程(5),有
 如果|Bβ1|<β0,则对∀τ≥0,方程(5)所有的根都具有严格负实部.
如果|Bβ1|<β0,则对∀τ≥0,方程(5)所有的根都具有严格负实部.
 如果|Bβ1|>β0,则存在序列
如果|Bβ1|>β0,则存在序列
0<τ0<τ1<…<τk<…
使得当τ=τk(k=0,1,2,…)时,方程(5)有一对纯虚根±iw0.
(a) 若Bβ1<-β0,当τ∈[0,τ0)时,方程(5)的所有根具有严格负实部;当τ=τ0时,除了iw0之外的其他所有根都具有严格负实部;当τ∈(τk,τk+1](k=0,1,2,…)时,方程(5)有k+1对具有正实部的根.
(b) 若Bβ1>β0,则对任意τ≥0,方程(5)至少有一个具有正实部的根.
 如果|Bβ1|=β0,则对∀τ≥0,方程(5)至少有一个零根.
如果|Bβ1|=β0,则对∀τ≥0,方程(5)至少有一个零根.
注2 关于引理1的证明,其过程与文献[16]第二章第1节中结论的证明类似,此处略去.
假设λ(τ)=a(τ)+iw(τ)是方程(5)在τ=τk附近满足a(τk)=0和w(τk)=w0的根,则得到下面的引理,即满足横截性条件.
引理2 a′(τk)>0.
证明 方程(5)两边同时对τ求导,有
因为Bβ1e-λτ=λ+β0,所以解得
故
由此可得
证毕.
结合引理1和引理2立即可得下面关于正平衡点![]() 的稳定性结论.
的稳定性结论.
定理2 对系统(1),有
 若|Bβ1|<β0,则对所有的τ≥0,方程(1)的平衡点
若|Bβ1|<β0,则对所有的τ≥0,方程(1)的平衡点![]() 是渐近稳定的.
是渐近稳定的.
 若Bβ1>β0,则对所有的τ≥0,方程(1)的平衡点
若Bβ1>β0,则对所有的τ≥0,方程(1)的平衡点![]() 是不稳定的.
是不稳定的.
 若Bβ1<-β0,则当τ∈[0,τ0)时,方程(1)的平衡点
若Bβ1<-β0,则当τ∈[0,τ0)时,方程(1)的平衡点![]() 是渐近稳定的;当τ>τ0时,平衡点
是渐近稳定的;当τ>τ0时,平衡点![]() 是不稳定的.并且方程(1)在正平衡点处当τ=τk(k=0,1,2,…)时发生了Hopf分岔.
是不稳定的.并且方程(1)在正平衡点处当τ=τk(k=0,1,2,…)时发生了Hopf分岔.
注3 关于零平衡点稳定性的讨论与此类似,此处略去.
2 分岔周期解的方向和稳定性
该部分内容主要利用中心流形定理和正规形理论,考虑从正平衡点![]() 处分岔出的周期解的方向及稳定性.
处分岔出的周期解的方向及稳定性.
在方程(1)中令![]() 经过尺度变换后得到
经过尺度变换后得到
(9)
其中
为方便起见,在后面的讨论中简单记为f1和f2.则方程(9)的特征方程为
λτ=-τβ0+τBβ1e-λτ,
其中β0和β1见方程(5).
设τ=τk+μ(k=0,1,2,…),μ∈R,则μ=0是方程(9)的Hopf分岔值.下面对方程(9)进行Taylor(泰勒)展开,有
o(x3(0),x3(-1)),
(10)
其中
并记
对于φ∈C[-1,0],设
以及
由Riesz表示定理可知,存在关于θ的有界变差函数η(θ,μ)使得
Lμ(φ)=![]() dη(θ,μ)φ(θ), φ∈C,
dη(θ,μ)φ(θ), φ∈C,
其中θ∈[-1,0],同时定义η(θ,μ)的表达式为
当φ∈C([-1,0])时,定义
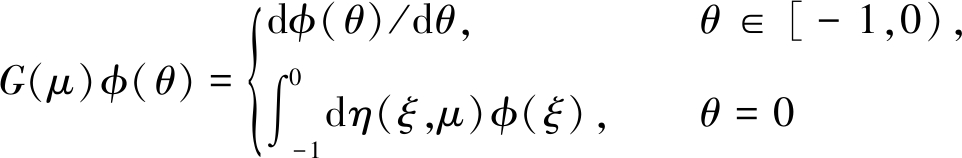
和
则方程(10)变为
其中
xt(θ)=x(t+θ), θ∈[-1,0].
对于ψ∈C1[0,1],定义

其中,G*是G=G(0)的伴随算子, 当ψ∈C[0,1], φ∈C[-1,0]时, 利用双线性形式定义内积
这里![]() 是ψ的共轭.
是ψ的共轭.
显然±iτkw0是G*和G(0)的特征值,易知,q(θ) eiτkw0θ和q*(s)
eiτkw0θ和q*(s) Deiτkw0s分别是G和G*对应于iτkw0和-iτkw0的特征向量,且
Deiτkw0s分别是G和G*对应于iτkw0和-iτkw0的特征向量,且
其中,![]() 是q的共轭,且
是q的共轭,且
D=1/(1+Aτk-iτkw0).
对于方程(10)在μ=0时的解xt,定义
在中心流形£0上![]() 这里
这里![]() 可以表示为z和
可以表示为z和![]() 的幂级数形式:
的幂级数形式:
则方程(10)在中心流形上的流由下面的方程给出:
![]()

![]()
(11)
这里
f0
![]()
下面只需要通过比较系数确定![]() 中相应的系数W20(θ),W11(θ),W02(θ),…,然后代入方程(11)即可得限制在中心流形上的方程,进一步计算出几个重要的量,从而得到相应的定理.
中相应的系数W20(θ),W11(θ),W02(θ),…,然后代入方程(11)即可得限制在中心流形上的方程,进一步计算出几个重要的量,从而得到相应的定理.
将方程(11)改写为限制在中心流形上的约化方程:
其中
![]()

![]()
则应用文献[16]中3.2小节的算法,即可得到
其中
进一步地,可计算出下面几个重要的量:
β2=2Re(c1(0)),
由上面的讨论,根据引理2并结合文献[17],即得到下面的定理.
定理3 假设![]() 且满足引理2,则
且满足引理2,则
 μ2决定分岔周期解的方向:若μ2>0(μ2<0),则从平衡点分岔出的周期解是超临界的(次临界的).
μ2决定分岔周期解的方向:若μ2>0(μ2<0),则从平衡点分岔出的周期解是超临界的(次临界的).
 β2决定分岔周期解的稳定性:若β2<0(β2>0),则分岔周期解是轨道渐近稳定的(不稳定的).
β2决定分岔周期解的稳定性:若β2<0(β2>0),则分岔周期解是轨道渐近稳定的(不稳定的).
 T2决定分岔周期解的周期:若T2>0(T2<0),则随着τ远离τk,分岔周期解的周期是增加的(减少的).
T2决定分岔周期解的周期:若T2>0(T2<0),则随着τ远离τk,分岔周期解的周期是增加的(减少的).
3 数 值 模 拟
该部分主要利用MATLAB作为辅助工具对方程(1)的Hopf分岔现象进行数值模拟,然后分析临界值处的性质.
根据表1中的参数值,并取![]() 时,有B=238 624.882>A≐0.198且C≐
时,有B=238 624.882>A≐0.198且C≐![]() 可知方程(1)满足定理1,即原方程有唯一的正平衡点
可知方程(1)满足定理1,即原方程有唯一的正平衡点![]() ≐1.075.经计算得到β0≐0.661,β1≐-3.43×10-3,则由定理2中的
≐1.075.经计算得到β0≐0.661,β1≐-3.43×10-3,则由定理2中的 ,可知方程(1)中的正平衡点
,可知方程(1)中的正平衡点![]() 在τk≐0.771k+0.203(k=0,1,2,…)处发生了Hopf分岔,且当τ∈[0,τ0)时,正平衡点
在τk≐0.771k+0.203(k=0,1,2,…)处发生了Hopf分岔,且当τ∈[0,τ0)时,正平衡点![]() 是渐近稳定的,当τ>τ0时,正平衡点
是渐近稳定的,当τ>τ0时,正平衡点![]() 是不稳定的(见图1).
是不稳定的(见图1).
下面分析原方程在第一个临界值τ0处的Hopf分岔性质.经计算可得
W11(-1)≐-1.802-10.210i, W20(-1)≐-3.765+3.487i,
E1≐-0.978, E2≐2.559+3.736i,
g20≐-3.585+8.458i, g11≐4.896-7.773i,
g02≐-6.080+6.887i, g21≐-22.845+11.876i.
进一步地,得到
c1(0)≐-32.399-39.092i, μ2≐1.955, β2≐-64.797, T2≐11.721.
因此由定理3可知,从τk分岔出的周期解是超临界的,轨道渐近稳定的,且周期是增加的.
(a) 当τ=0.2 a<τ0时,![]() 当τ=0.4 a>τ0时,方程(1)从
当τ=0.4 a>τ0时,方程(1)从![]() 处 渐近稳定 分岔出稳定的周期解
处 渐近稳定 分岔出稳定的周期解
(a) The local asymptotical stability at positive (b) The stable periodic solution bifurcated at positive equilibrium ![]() τ=0.2 a<τ0 equilibrium
τ=0.2 a<τ0 equilibrium ![]() from eq. (1), τ=0.4 a>τ0
from eq. (1), τ=0.4 a>τ0
图1 Hopf分岔图
Fig. 1 Hopf bifurcation figures
4 结 论
研究不同生物种群模型结构的动力学行为是非常有意义的.本文通过对云杉蚜虫种群阶段结构模型动力学行为的研究,可以预测该种群在何种条件下处于生态平衡,何种条件下该种群会导致虫灾的周期性爆发.例如:当时滞τ大概为0.2年时,满足τ<τ0,由图1(a)可知,正平衡点是渐近稳定的,此时云杉蚜虫种群处于平衡状态;当时滞τ大概为0.4年时有τ>τ0,由图1(b)可知云杉蚜虫种群出现了周期性的爆发.对于后者,必须采取相应的控制措施,例如通过销毁蚜虫卵控制不成熟蚜虫种群量的增长,打农药、鸟类的捕食等都可以有效地控制云杉蚜虫种群的周期性爆发现象,这对于维持生态平衡以及控制虫灾的爆发具有重要作用.
致谢 本文作者衷心感谢河北大学校级研究生创新项目(hbu2018ss46)对本文的资助.
[1] FLEMING R A, SHOEMAKER C A. Evaluating models for spruce budworm-forest management: comparing output with regional field data[J]. Ecological Applications: a Publication of the Ecological Society of America, 1992, 2(4): 460-477.
[2] MAGNUSSEN S, ALFARO R I, BOUDEWYN P. Survival-time analysis of white spruce during spruce budworm defoliation[J]. Silva Fenncia, 2005, 39(2): 177-189.
[3] NIE Z Y, MACLEAN D A, TAYLOR A R. Forest overstory composition and seedling height influence defoliation of understory regeneration by spruce budworm[J]. Forest Ecology and Management, 2018, 409: 353-360.
[4] ROYAMA T. Population dynamics of the spruce budworm choristoneura fumiferana[J]. Ecological Monographs, 1984, 54(4): 429-462.
[5] MEIGS G W, KENNEDY R E, GRAY A N, et al. Spatiotemporal dynamics of recent mountain pine beetle and western spruce budworm outbreaks across the Pacific Northwest Region, USA[J]. Forest Ecology and Management, 2015, 339: 71-86.
[6] ALFARO R I, BERG J, AXELSON J. Periodicity of western spruce budworm in Southern British Columbia, Canada[J]. Forest Ecology and Management, 2014, 315: 72-79.
[7] NEALIS V G, TURNQUIST R, MORIN B, et al. Baculoviruses in populations of western spruce budworm[J]. Journal of Invertebrate Pathology, 2015, 127: 76-80.
[8] 王双明, 张明军, 樊馨蔓. 一类具时滞的周期logistic传染病模型空间动力学研究[J]. 应用数学和力学, 2018, 39(2): 226-238.(WANG Shuangming, ZHANG Mingjun, FAN Xinman. Spatial dynamics of periodic reaction-diffusion epidemic models with delay and logistic growth[J]. Applied Mathematics and Mechanics, 2018, 39(2): 226-238.(in Chinese))
[9] LUDWIG D, JONES D D, HOLLING C S. Qualitative analysis of insect outbreak systems: the spruce budworm forest[J]. Journal of Animal Ecology, 1978, 47: 315-332.
[10] LUDWIG D, ARONSON D G, WEINBERGER H F. Spatial patterning of the spruce budworm[J]. Journal of Mathematical Biology, 1979, 8(3): 217-258.
[11] RASMUSSEN A, WYLLER J, VIK J O. Relaxation oscillations in spruce-budworm interactions[J]. Nonlinear Analysis: Real World Applications, 2011, 12(1): 304-319.
[12] HASSELL D C, ALLWRIGHT D J, FOWLER A C. A mathematical analysis of Jone’s site model for spruce budworm infestation[J]. Journal of Mathematical Biology, 1999, 38(5): 377-421.
[13] SINGH M, EASTON A, CUI G, et al. A numerical study of the spruce budworm reaction diffusion equation with hostile boundaries[J]. Natural Resource Modeling, 2000, 13(4): 535-549.
[14] VAIDYA N K, WU J H. Modeling spruce budworm population revisited: impact of physiological structure on outbreak control[J]. Bulletin of Mathematical Biology, 2008, 70(3): 769-784.
[15] XU X F, WEI J J. Bifurcation analysis of a spruce budworm model with diffusion and physiological structures[J]. Journal of Differential Equations, 2017, 262(10): 5206-5230.
[16] 魏俊杰, 王洪滨, 蒋卫华. 时滞微分方程的分支理论及应用[M]. 北京: 科学出版社, 2012.(WEI Junjie, WANG Hongbin, JIANG Weihua. Bifurcation Theory and Application of Delay Differential Equation[M]. Beijing: Science Press, 2012.(in Chinese))
[17] WAN A Y, ZOU X F. Hopf bifurcation analysis for a model of genetic regulatory system with delay[J]. Journal of Mathematical Analysis and Applications, 2009, 356(2): 464-476.