引 言
凸性和广义凸性在数学规划的研究中起着相当关键的作用.Kazmi[1]给出了向量值情形下的D-预不变凸映射.进一步地,Peng和Zhu[2]建立了D-预不变凸映射的一些性质.Long等[3]讨论了D-半严格预不变凸和D-预不变凸之间的关系.彭再云等[4]提出了D-半预不变真拟凸、D-半严格半预不变真拟凸和D-严格半预不变真拟凸的概念,并建立了这几类广义凸性间的关系.黄应全[5]应用D-上半连续性,*-上半连续性和中间点的D-半预不变真拟凸性,得到了D-半预不变真拟凸映射的两个性质定理.唐莉萍和杨新民[6]分别利用D-半严格半预不变真拟凸性和D-严格半预不变真拟凸性建立D-半预不变凸性的充要条件,最后利用D-半预不变真拟凸性给出了半预不变凸性的刻画.彭建文[7]给出了向量值情形下的D-η-预不变真拟凸映射,并给出了它的一些性质.还有其他一些文献[8-14]对向量广义凸映射进行了研究.随后,文献[15]提出了一类新的向量值广义凸映射:D-η-E-半预不变凸映射,它是D-η-预不变凸映射的真推广,建立了D-η-E-半预不变凸映射与D-η-E-严格半预不变凸映射、D-η-E-半严格半预不变凸映射间的关系,并讨论了D-η-E-半严格半预不变凸映射在一类隐约束向量优化问题中的重要应用.
受文献[6-7]的启发,本文考虑D-η-E-半预不变凸性的新刻画.首先,对文献[15]中提出的条件H给出了一个重要的性质,在此基础上,结合稠密性结果,分别应用D-η-E-半严格半预不变真拟凸性、D-η-E-严格半预不变真拟凸性和D-η-E-半预不变真拟凸性,建立了D-η-E-半预不变凸性的一些充要条件;其次,提出了一类新的广义凸映射:D-η-E-半预不变真拟凸映射,建立了D-η-E-半预不变真拟凸性与D-η-E-半严格半预不变真拟凸性、D-η-E-严格半预不变真拟凸性之间的关系;最后,给出了D-η-E-半严格半预不变真拟凸映射在优化中的应用.
1 预 备 知 识
设X,Y⊂Rn,K⊂X且K≠∅,点闭凸锥D⊂X且D≠∅,
f:K→Y, η:Rn×Rn×[0,1]→Rn, E(·):K→K.
定义1[15] 如果∀x,y∈K,∀α∈[0,1],∀λ∈[0,1],有
E(y)+αη(E(x),E(y),λ) ∈K,
那么,称K⊂X关于η是E-半不变凸集.
本文假设K⊂X是关于η的E-半不变凸集.
定义2[15] 如果∀x,y∈K,∀α∈[0,1],∀λ∈[0,1],有
f(E(y)+αη(E(x),E(y),λ)) ∈αf(E(x))+(1-α)f(E(y))-D,
那么,称f:K→Y关于η是D-η-E-半预不变凸.
定义3 如果∀x,y∈K,∀α∈[0,1],∀λ∈[0,1],有
f(E(y)+αη(E(x),E(y),λ)) ∈f(E(x))-D,
或
f(E(y)+αη(E(x),E(y),λ)) ∈f(E(y))-D,
那么,称f:K→Y关于η是D-η-E-半预不变真拟凸.
定义4 如果∀x,y∈K,x≠y,∀α∈[0,1],∀λ∈[0,1],有
f(E(y)+αη(E(x),E(y),λ)) ∈f(E(x))-int D,
或
f(E(y)+αη(E(x),E(y),λ)) ∈f(E(y))-int D,
那么,称f:K→Y关于η是D-η-E-严格半预不变真拟凸.
定义5 如果∀x,y∈K, f(E(x)) ≠f(E(y)),∀α∈[0,1],∀λ∈[0,1],有
f(E(y)+αη(E(x),E(y),λ)) ∈f(E(x))-int D,
或
f(E(y)+αη(E(x),E(y),λ)) ∈f(E(y))-int D,
那么,称f:K→Y关于η是D-η-E-半严格半预不变真拟凸.
为了讨论D-η-E-半预不变凸的一些性质,将用到下面的条件和引理.
条件H[15] ∀x,y∈K,∀α∈[0,1],∀λ∈[0,1],如果η和E满足关系式:
(H1) η(E(y),E(y)+αη(E(x),E(y),λ),λ)=-αη(E(x),E(y),λ),
(H2) η(E(x),E(y)+αη(E(x),E(y),λ),λ)=(1-α)η(E(x),E(y),λ),
那么,称η满足条件H.
引理1[15] 设η满足条件H,K⊂X关于η是E-半不变凸集,若f:K→Y满足
①f(E(y)+η(E(x),E(y),λ)) ∈f(E(x))-D,∀x,y∈K;
② ∀x,y∈K,∃α∈[0,1],s.t.
f(E(y)+αη(E(x),E(y),λ)) ∈αf(E(x))+(1-α)f(E(y))-D,
则
A=γ∈[0,1]f(E(y)+γη(E(x),E(y),λ)) ∈
γf(E(x))+(1-γ)f(E(y))-D
在[0,1]中稠密.
性质1 设η满足条件H,那么
η(E(y)+α1η(E(x),E(y),λ),E(y)+α2η(E(x),E(y),λ),λ)=
(α1-α2)η(E(x),E(y),λ),
∀x,y∈K, ∀α1,α2∈[0,1], ∀λ∈[0,1].
(1)
证明 分3种情形考虑.
 当α1=α2时,结论明显成立.
当α1=α2时,结论明显成立.
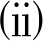 当α1>α2时,
当α1>α2时,
η(E(y)+α1η(E(x),E(y),λ),E(y)+α2η(E(x),E(y),λ),λ)=
η(E(y)+α1η(E(x),E(y),λ),E(y)+α1η(E(x),E(y),λ)+
(α2-α1)η(E(x),E(y),λ),λ)=
η(E(y)+α1η(E(x),E(y),λ),E(y)+α1η(E(x),E(y),λ)+
η(E(y),E(y)+(α1-α2)η(E(x),E(y),λ)),λ)=
-η(E(y),E(y)+(α1-α2)η(E(x),E(y),λ),λ)=
(α1-α2)η(E(x),E(y),λ).
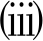 当α1<α2时,
当α1<α2时,
η(E(y)+α1η(E(x),E(y),λ),E(y)+α2η(E(x),E(y),λ),λ)=
η(E(y)+α1η(E(x),E(y),λ),E(y)+α1η(E(x),E(y),λ)+
(α2-α1)η(E(x),E(y),λ),λ)=
-(α2-α1)η(E(x),E(y),λ)=
(α1-α2)η(E(x),E(y),λ).
则式(1)成立.
2 D-η-E-半预不变凸映射
本节将结合性质1和条件H,分别应用D-η-E-半严格半预不变真拟凸性、D-η-E-严格半预不变真拟凸性和D-η-E-半预不变真拟凸性给出D-η-E-半预不变凸性的新刻画.
定理1 f:K→Y关于η是D-η-E-半预不变凸⟺
①f(E(y)+η(E(x),E(y),λ)) ∈f(E(x))-D,∀x,y∈K,∀λ∈(0,1);
②f:K→Y关于η是D-η-E-半严格半预不变真拟凸;
③ ∀x,y∈K,∀λ∈(0,1),∃α∈[0,1],s.t.
f(E(y)+αη(E(x),E(y),λ)) ∈αf(E(x))+(1-α)f(E(y))-D.
证明 必要性明显成立,只需要证明充分性.
(反证法) 设∃x,y∈K,λ∈(0,1),β∈(0,1),s.t.
f(E(y)+βη(E(x),E(y),λ)) ∉βf(E(x))+(1-β)f(E(y))-D.
(2)
根据引理1,∃μ,ω∈A,满足0<μ<β<ω<1,s.t.
f(E(zβ)) ∉μf(E(x))+(1-μ)f(E(y))-D,
(3)
f(E(zβ)) ∉ωf(E(x))+(1-ω)f(E(y))-D,
(4)
其中 E(zβ)=E(y)+βη(E(x),E(y),λ).
令
由条件(H2)和性质1,有
E(zβ)=E(zt1)+μη(E(x),E(zt1),λ), E(zβ)=E(y)+ωη(E(zt2),E(y),λ),
其中 E(zt1)=E(y)+t1η(E(x),E(y),λ), E(zt2)=E(y)+t2η(E(x),E(y),λ).
因μ,ω∈A,故
f(E(zβ)) ∈μf(E(x))+(1-μ)f(E(zt1))-D,
(5)
f(E(zβ)) ∈ωf(E(zt2))+(1-ω)f(E(y))-D.
(6)
分别结合式(3)及式(5),则有
f(E(zt1)) ∉f(E(y))-D,
(7)
f(E(zt2)) ∉f(E(x))-D.
(8)
以下从两个方面来证明:
 f(E(x)) ≠f(E(y)).根据f的D-η-E-半严格半预不变真拟凸性, 结合式(7)及式(8),有
f(E(x)) ≠f(E(y)).根据f的D-η-E-半严格半预不变真拟凸性, 结合式(7)及式(8),有
f(E(zt1)) ∈f(E(x))-int D, f(E(zt2)) ∈f(E(y))-int D.
再分别结合式(5)与式(6),有
f(E(zβ)) ∈f(E(x))-int D, f(E(zβ)) ∈f(E(y))-int D.
则f(E(zβ)) ∈βf(E(x))+(1-β)f(E(y))-int D,与式(2)相矛盾.
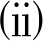 f(E(x))=f(E(y)).由式(2),f(E(zβ)) ≠f(E(y)).由性质1,则
f(E(x))=f(E(y)).由式(2),f(E(zβ)) ≠f(E(y)).由性质1,则
根据f的D-η-E-半严格半预不变真拟凸性和式(7),有f(E(zt1)) ∈f(E(zβ))-int D.结合式(5),有
f(E(zβ)) ∈μf(E(x))+(1-μ)f(E(zβ))-int D,
则
f(E(zβ)) ∈f(E(x))-int D=βf(E(x))+(1-β)f(E(x))-int D=
βf(E(x))+(1-β)f(E(y))-int D,
与式(2)相矛盾.证毕.
根据定义4和定义5,D-η-E-严格半预不变真拟凸一定是D-η-E-半严格半预不变真拟凸,故由定理1,可得到如下的一个推论:
推论1 f:K→Y关于η是D-η-E-半预不变凸⟺
①f(E(y)+η(E(x),E(y),λ)) ∈f(E(x))-D,∀x,y∈K,∀λ∈(0,1);
②f:K→Y关于η是D-η-E-严格半预不变真拟凸;
③ ∀x,y∈K,∀λ∈(0,1),∃α∈[0,1],s.t.
f(E(y)+αη(E(x),E(y),λ)) ∈αf(E(x))+(1-α)f(E(y))-D.
(9)
接下来将应用D-η-E-半预不变真拟凸性给出D-η-E-半预不变凸性的一个新刻画.
定理2 f:K→Y关于η是D-η-E-半预不变凸⟺
①f(E(y)+η(E(x),E(y),λ)) ∈f(E(x))-D,∀x,y∈K,∀λ∈(0,1);
②f:K→Y关于η是D-η-E-半预不变真拟凸;
③ ∀x,y∈K,∀λ∈(0,1),∃α∈[0,1],s.t.
f(E(y)+αη(E(x),E(y),λ)) ∈αf(E(x))+(1-α)f(E(y))-D.
(10)
证明 必要性明显成立,只需要证明充分性.
(反证法) 设∃x,y∈K,λ∈(0,1),β∈(0,1),s.t.
f(E(y)+βη(E(x),E(y),λ)) ∉βf(E(x))+(1-β)f(E(y))-D.
(11)
且∃μ,ω∈A,满足0<μ<β<ω<1,s.t.
E(zβ)=E(z(β-μ)/(1-μ))+μη(E(x),E(z(β-μ)/(1-μ)),λ)E(zβ)=
E(y)+ωη(E(zβ/ω),E(y),λ),
其中
E(zβ)=E(y)+βη(E(x),E(y),λ),
因μ,ω∈A,故
f(E(zβ)) ∈μf(E(x))+(1-μ)f(E(z(β-μ)/(1-μ)))-D,
(12)
f(E(zβ)) ∈ωf(E(zβ/ω))+(1-ω)f(E(y))-D,
(13)
式(12)、(13)分别结合式(5)及式(6),有
f(E(z(β-μ)/(1-μ))) ∉f(E(y))-D,
(14)
f(E(zβ/ω)) ∉f(E(x))-D,
(15)
而
由f的D-η-E-半预不变真拟凸性、式(14)及式(15),则
f(E(z(β-μ)/(1-μ))) ∈f(E(zβ))-D, f(E(zβ/ω)) ∈f(E(zβ))-D.
分别结合式(12)、(13),有
f(E(zβ)) ∈f(E(x))-D, f(E(zβ)) ∈f(E(y))-D,
与式(11)相矛盾.
3 D-η-E-半预不变真拟凸映射
定理3 设E:K→K满射,若
①f:K→Y关于η是D-η-E-半预不变真拟凸映射;
② ∃α∈[0,1],对∀x,y∈K,x≠y,∀λ∈(0,1),s.t.
f(E(y)+αη(E(x),E(y),λ)) ∈f(E(x))-int D,
(16a)
或
f(E(y)+αη(E(x),E(y),λ)) ∈f(E(y))-int D,
(16b)
那么,f:K→Y关于η是D-η-E-严格半预不变真拟凸映射.
证明(反证法) 设f:K→Y关于η不是D-η-E-严格半预不变真拟凸映射,则∃x,y∈K,x≠y,β∈(0,1),s.t.
f(E(y)+αη(E(x),E(y),λ)) ∉f(E(x))-int D,
(17a)
或
f(E(y)+αη(E(x),E(y),λ)) ∉f(E(y))-int D.
(17b)
选取合适的β1,β2,使它们满足0<β1<β2<1,β=αβ1+(1-α)β2.
因为E:K→K是满射,所以∃![]()
因为f:K→Y关于η是D-η-E-半预不变真拟凸映射,所以
或
且
(18a)
或
(18b)
根据条件H有
E(y)+β2η(E(x),E(y),λ)+αη(E(y)+β1η(E(x),E(y),λ),E(y)+
β1η(E(x),E(y),λ)+(β2-β1)η(E(x),E(y),λ),λ)=
E(y)+β2η(E(x),E(y),λ)+
αηE(y)+β1η(E(x),E(y),λ),E(y)+β1η(E(x),E(y),λ)+
E(y)+β2η(E(x),E(y),λ)-
E(y)+βη(E(x),E(y),λ),
即
由式(16)及E:K→K为满射,可得
(19a)
或
(19b)
由式(18)、(19)及D+int D⊂int D,可得
f(E(y)+αη(E(x),E(y),λ)) ∈f(E(x))-int D,
(20a)
或
f(E(y)+αη(E(x),E(y),λ)) ∈f(E(y))-int D.
(20b)
则式(20)与式(17)相矛盾.所以f:K→Y关于η是D-η-E-严格半预不变真拟凸映射.
定理4 设E:K→K满射,若
① ∀x,y∈K, f(E(y)+η(E(x),E(y),λ)) ∈f(E(x))-D;
②f:K→Y关于η是D-η-E-半严格半预不变真拟凸映射;
③ ∃α∈[0,1],对∀x,y∈K,λ∈[0,1],s.t.
f(E(y)+αη(E(x),E(y),λ)) ∈
f(E(x))-Df(E(y)+αη(E(x),E(y),λ)) ∈f(E(y))-D,
(21)
且
f(E(y)+(1-α)η(E(x),E(y),λ)) ∈f(E(x))-D,
(22a)
或
f(E(y)+(1-α)η(E(x),E(y),λ)) ∈f(E(y))-D,
(22b)
那么,f:K→Y关于η是D-η-E-半预不变真拟凸映射.
证明 由假设条件,∀x,y∈K,有
f(E(y)+η(E(x),E(y),λ)) ∈f(E(x))-D且f(E(y)) ∈f(E(y))-D,
则β=0,1时,结果成立.下面证明β∈(0,1)时也成立.
(反证法) 设f:K→Y关于η不是D-η-E-半预不变真拟凸映射,则∃x,y∈K及β∈(0,1),s.t.
f(E(y)+βη(E(x),E(y),λ)) ∉f(E(x))-D,
(23a)
或
f(E(y)+βη(E(x),E(y),λ)) ∉f(E(y))-D.
(23b)
因为E:K→K是满射,则∃z∈K,s.t. E(z)=E(y)+βη(E(x),E(y),λ).
 当f(E(x))≠f(E(y))时,因为f关于η是D-η-E-半严格半预不变真拟凸映射,则
当f(E(x))≠f(E(y))时,因为f关于η是D-η-E-半严格半预不变真拟凸映射,则
f(E(z)) ∈f(E(x))-int D 或 f(E(z)) ∈f(E(y))-int D,
与式(23)相矛盾.
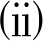 当f(E(x))=f(E(y))时,由式(23),有
当f(E(x))=f(E(y))时,由式(23),有
f(E(z)) ∉f(E(x))-D=f(E(y))-D.
(24)
(a) 当0<β<α<1时,因为E:K→K是满射,则∃z1∈K,s.t.
由条件H,得
E(z1)+(1-α)η(E(y),E(z1),λ)=
E(y)+βη(E(x),E(y),λ)=E(z).
由式(22),得f(E(z)) ∈f(E(y))-D,或f(E(z)) ∈f(E(z1))-D.由式(24),得
f(E(z)) ∈f(E(z1))-D.
(25)
令![]() 则b∈(0,1).由条件H,则
则b∈(0,1).由条件H,则
E(y)+βη(E(x),E(y),λ)+bη(E(x),E(y)+βη(E(x),E(y),λ),λ)=
E(y)+(β+b(1-β))η(E(x),E(y),λ)=
E(z1).
由f的D-η-E-半严格半预不变真拟凸性,则
f(E(z1)) ∈f(E(z))-int D,
或
f(E(z1)) ∈f(E(x))-int D.
由式(24),得f(E(z1)) ∈f(E(z))-int D,与式(25)相矛盾.
(b) 当0<α<β<1时,若![]() 因为E:K→K是满射,则∃z2∈K,s.t.
因为E:K→K是满射,则∃z2∈K,s.t.
由条件H,则
E(z2)+αη(E(x),E(z2),λ)=
E(y)+βη(E(x),E(y),λ)=E(z).
由式(21),则
f(E(z)) ∈f(E(x))-D,
或
f(E(z)) ∈f(E(z2))-D.
由式(24),则
f(E(z)) ∈f(E(z2))-D,
(26)
令![]() 则μ∈(0,1),且
则μ∈(0,1),且
E(z)+(1-μ)η(E(y),E(z),λ)=
E(y)+βη(E(x),E(y),λ)+
(1-μ)η(E(y),E(y)+βη(E(x),E(y),λ),λ)=
E(y)+βμη(E(x),E(y),λ)=
E(z2).
由f的D-η-E-半严格半预不变真拟凸性,有
f(E(z2)) ∈f(E(z))-int D,
或
f(E(z2)) ∈f(E(y))-int D.
由式(24),有f(E(z2)) ∈f(E(z))-int D,与式(26)矛盾.
(c) 当0<α=β<1时,式(21)与式(23)明显矛盾.
所以f:K→Y关于η是D-η-E-半预不变真拟凸映射.
4 D-η-E-半严格半预不变真拟凸映射在优化中的应用
考虑优化问题(VP0):minx∈K f(x).
定义6[15] 令f(E(K))=∪x∈K f(E(x)),E(·):K→K.
 若
若![]() ∅,称
∅,称![]() 是(VP0)的E-全局有效解;若∃x的邻域U,
是(VP0)的E-全局有效解;若∃x的邻域U,![]() ∅,称
∅,称![]() 是(VP0)的E-局部有效解;
是(VP0)的E-局部有效解;
 若
若![]() ∅,称
∅,称![]() 是(VP0)的E-全局弱有效解;若∃x的邻域U,
是(VP0)的E-全局弱有效解;若∃x的邻域U,![]() ∅,称
∅,称![]() 是(VP0)的E-局部弱有效解.
是(VP0)的E-局部弱有效解.
下面给出D-η-E-半严格半预不变真拟凸映射在向量优化中的一个应用.
定理5 设η:K×K→K,E(·):K→K,K⊂X关于η是E-半预不变凸集, f:K→Y关于η是D-η-E-半严格半预不变真拟凸映射,则
① (VP0)的任意E-局部弱有效解是(VP0)的E-全局弱有效解;
② (VP0)的任意E-局部有效解是(VP0)的E-全局有效解.
证明 只需证明第①条.设![]() 是(VP0)的E-全局弱有效解,则∃
是(VP0)的E-全局弱有效解,则∃![]() 的邻域U,
的邻域U,
![]() ∅.
∅.
(27)
假设![]() 不是(VP0)的E-全局弱有效解,则
不是(VP0)的E-全局弱有效解,则![]() ∅.即
∅.即
∃x0∈K, s.t.
因为K关于η是E-半预不变凸集, f: K→Y关于η是D-η-E-半严格半预不变真拟凸映射.则∀α∈(0,1),有![]() 且
且
或
若![]() 则
则
![]() ⊂
⊂
f(E(x0))-int D-int D⊂![]()
故∀α∈(0,1),有
(28)
当α充分小时,![]() 有
有
则式(28)与式(27)矛盾,故![]() 是(VP0)的E-全局弱有效解.同理可以证明第②条亦成立.
是(VP0)的E-全局弱有效解.同理可以证明第②条亦成立.
5 结 论
本文对D-η-E-半预不变凸映射和D-η-E-半预不变真拟凸映射的一些性质进行了研究.讨论了D-η-E-半预不变凸与D-η-E-半严格半预不变真拟凸、D-η-E-严格半预不变真拟凸和D-η-E-半预不变真拟凸之间的关系,以及D-η-E-半预不变真拟凸与D-η-E-半严格半预不变真拟凸和D-η-E-严格半预不变真拟凸之间的关系,分别得到了D-η-E-半预不变凸映射和D-η-E-半预不变真拟凸映射的一些等价刻画.所得结果推广了文献[4,6-7,15]中的相关结果.那么如何建立D-η-E-半预不变凸集值映射的择一性定理,并通过择一性定理研究D-η-E-半预不变凸集值映射向量优化问题的最优性条件、鞍点定理以及对偶定理,这将是有待研究的后续课题.
[1] KAZMI K R. Some remarks on vector optimization problems[J]. Journal of Optimization Theory & Applications, 1998, 96(1): 133-138.
[2] PENG J W, ZHU D L. On D-preinvex type functions[J]. Journal of Inequalities and Applications, 2006, 2006: 1-14.
[3] LONG X J, PENG Z Y, ZENG B. Remark on cone semistrictly preinvex functions[J]. Optimization Letters, 2009, 3(3): 337-345.
[4] 彭再云, 李科科, 唐平, 等. 向量值D-半预不变真拟凸映射的判定与性质[J]. 重庆师范大学学报(自然科学版), 2014, 31(5): 18-25.(PENG Zaiyun, LI Keke, TANG Ping, et al. Characterizations and criterions of D-semiprequasi-invex mappings[J]. Journal of Chongqing Normal University(Natural Science), 2014, 31(5): 18-25.(in Chinese))
[5] 黄应全. 关于向量值D-半预不变真拟凸映射的刻画[J]. 应用数学和力学, 2018, 39(3): 364-370.(HUANG Yingquan. Characterizations of D-properly semi-prequasi-invex mappings[J]. Applied Mathematics and Mechanics, 2018, 39(3): 364-370.(in Chinese))
[6] 唐莉萍, 杨新民. 关于D-半预不变凸性的某些新性质[J]. 应用数学和力学, 2015, 36(3): 325-331.(TANG Liping, YANG Xinmin. A note on some new characteristics of D-semi-preinvexity[J]. Applied Mathematics and Mechanics, 2015, 36(3): 325-331.(in Chinese))
[7] 彭建文. 向量值映射D-η-半预不变真拟凸的性质[J]. 系统科学与数学, 2003, 23(3): 306-314.(PENG Jianwen. Properties of D-η-properly prequasi invex function[J]. Journal of Systems Science and Mathematical Sciences, 2003, 23(3): 306-314.(in Chinese))
[8] 彭建文. 广义凸性及其在最优化问题中的应用[D]. 博士学位论文. 呼和浩特: 内蒙古大学, 2005.(PENG Jianwen. Generalized convexity with application optimization problems[D]. PhD Thesis. Hohhot: Inner Mongolia University, 2005.(in Chinese))
[9] 龙宪军, 毛小红. 关于向量值映射D-η-预不变真拟凸的注记[J]. 云南民族大学学报(自然科学版), 2005, 14(3): 213-215.( LONG Xianjun, MAO Xiaohong. Note on properties of D-η-properly prequasi-invex function[J]. Journal of Yunnan Nationalities University(Natural Sciences Edition), 2005, 14(3): 213-215.(in Chinese))
[10] LUO Hezhi, WU Huixian, ZHU Yihua. New methods for characterizing D-η-properly prequasi-invex functions[J]. Applied Mathematics: A Journal of Chinese Universities, 2006, 21(1): 107-112.
[11] 朱见广. 几类广义凸向量值映射的性质及其在最优化理论中的应用[D]. 硕士学位论文. 重庆: 重庆师范大学, 2008.(ZHU Jianguang. Properties of several kinds of generalized convexity functions with applications in optimization theory[D]. Master Thesis. Chongqing: Chongqing Normal University, 2008.(in Chinese))
[12] ZHOU Mi, WANG Yong, LIU Xiaolan, et al. Properties of D-η-properly prequasi-invex functions[J]. Journal of Hainan Normal University(Natural Science), 2009, 22(4): 365-370, 407.
[13] LI Taiyong, HUANG Min. On the characterizations of D-preinvex functions[J]. Journal of Inequalities and Applications, 2012, 2012: 240. DOI: 10.1186/1029-242X-2012-240.
[14] 彭再云, 王堃颍, 赵勇, 等. D-η-半预不变凸映射的性质及其应用[J]. 应用数学和力学, 2014, 35(2): 202-211.(PENG Zaiyun, WANG Kunying, ZHAO Yong, et al. Characterizations and applications of D-η-semipreinvex mappings[J]. Applied Mathematics and Mechanics, 2014, 35(2): 202-211.(in Chinese))
[15] 彭再云, 李科科, 张石生. 向量D-η-E-半预不变凸映射与向量优化[J]. 应用数学和力学, 2014, 35(9): 1020-1032.(PENG Zaiyun, LI Keke, ZHANG Shisheng. D-η-E-semipreinvex vector mappings and vector optimization[J]. Applied Mathematics and Mechanics, 2014, 35(9): 1020-1032.(in Chinese))