引 言
与常规复合材料性能的分段变化不同,功能梯度材料(FGM)[1-2]的特征在于其微观结构的连续变化.这种材料组成特点,使FGM构件能够消除不同组分材料间的界面效应,因此,此类构件可以同时具有高强度、高韧性、高热阻且可减少应力集中等优越的力学性能.自从FGM问世以来,人们对FGM板壳结构力学行为的研究已经取得了诸多成果[3-8].其中,文献[8]基于Reddy高阶剪切变形板理论,得到的包含剪切变形效应、拉-弯耦合效应和热耦合效应的功能梯度材料平板的广义Kármán型大挠度方程,奠定了功能梯度复合材料板壳结构非线性分析的基础.近年来,人们对FGM梁的静、动力学特性的研究也取得了显著进展.Sankar等[9]假设材料组分沿梁的厚度方向呈指数形式变化,给出了横向荷载以及热荷载作用下FGM弹性梁的二维解,并在平面假设下,对横向荷载以及热荷载作用下FGM Euler-Bernoulli梁的应力进行了研究.仲政等[10]假设材料弹性模量沿厚度按梯度函数分布,并采用弹性力学半逆解法,求得了FGM悬臂梁自由端作用集中力偶和集中力以及在均布荷载作用时的通解.Kadoli等[11]基于高阶剪切变形理论,对FGM梁的静力学特性进行了分析.基于轴线可伸长理论并考虑横向剪切变形效应,李世荣等[12]对横向非均匀升温作用的FGM 梁的热后屈特性进行了分析.Librescu等[13]研究了高温环境下FGM薄壁梁的振动和不稳定性,并分析了体积分数和温度梯度等因素的影响.Bhangale等[14]运用有限元方法对FGM夹层梁的热弹屈曲和振动行为进行了研究.
对于沿高度/厚度方向呈梯度变化的功能梯度梁/板结构,由于其组分材料热物参数的差异,相对初始无应力状态的任意小温度改变,通常会导致结构横截面上产生热弯矩,从而导致结构发生挠曲变形.但对于端部/边界不可移夹紧的情况,在单一升温因素作用下,由于受端部/边界约束弯矩的作用,此类结构呈现出明显的分支点屈曲特性[15-17].据此不难想象,对于热-机械荷载作用的端部不可移夹紧功能梯度梁,由于加载历程的不同,当升温大于热屈曲临界升温之后,对应的梁的荷载-挠度曲线会存在迂回区的情形.在迂回区,梁存在两个稳态构形(仅考虑最低热屈曲模态),梁的稳态构形不但与升温值、机械荷载的大小和方向有关,还与加载历程有关.有些加载过程会导致梁的平衡状态在两个稳态构形之间突然转换(也即“跳跃”)这一非线性系统特有的现象出现.但到目前为止,对功能梯度梁此类几何非线性特性的相关研究还较少见.对于具有迂回特性的荷载-挠度曲线,如果采用逐步加载(这里仅指机械荷载)法,要得到完整的荷载-挠度曲线是比较困难的;如果逐步施加位移[18],则能容易地得到完整的荷载-挠度曲线.基于此,本文采用文献[18]所用的逐步位移加载技术,着重考察了热-机械荷载联合作用下,细长功能梯度梁的双稳态构形及其相互转换的现象.当变温参数为0时,模型退化为功能梯度梁在横向荷载作用下的平面弯曲问题;当横向荷载为0时,模型退化为功能梯度梁在均匀升温时的热屈曲问题,文中分别考察了这两种情况下功能梯度梁的平衡路径,计算了热屈曲临界温度.
1 功能梯度梁
考虑一长度为l,截面宽度为b,高度为h的矩形截面功能梯度梁,坐标系(OXYZ)如图1所示,X轴为梁的轴线,Y和Z轴分别为梁横截面的水平和竖向对称轴.梁在均匀变温T和纵向对称面内的均匀线布荷载q作用下,只会发生XOZ面内的平面弯曲.W=W(X)为梁轴线横向挠度函数,与Z轴正向一致为正;U=U(X)为梁横截面形心的轴向位移函数,与X轴正向一致为正.假定梁的上表面为纯陶瓷,下表面为纯金属,并满足如下体积分数关系[19]:
(1)
式中Vc和Vm分别为陶瓷和金属材料的体积分数,非负指数k为材料的体积分数指数.
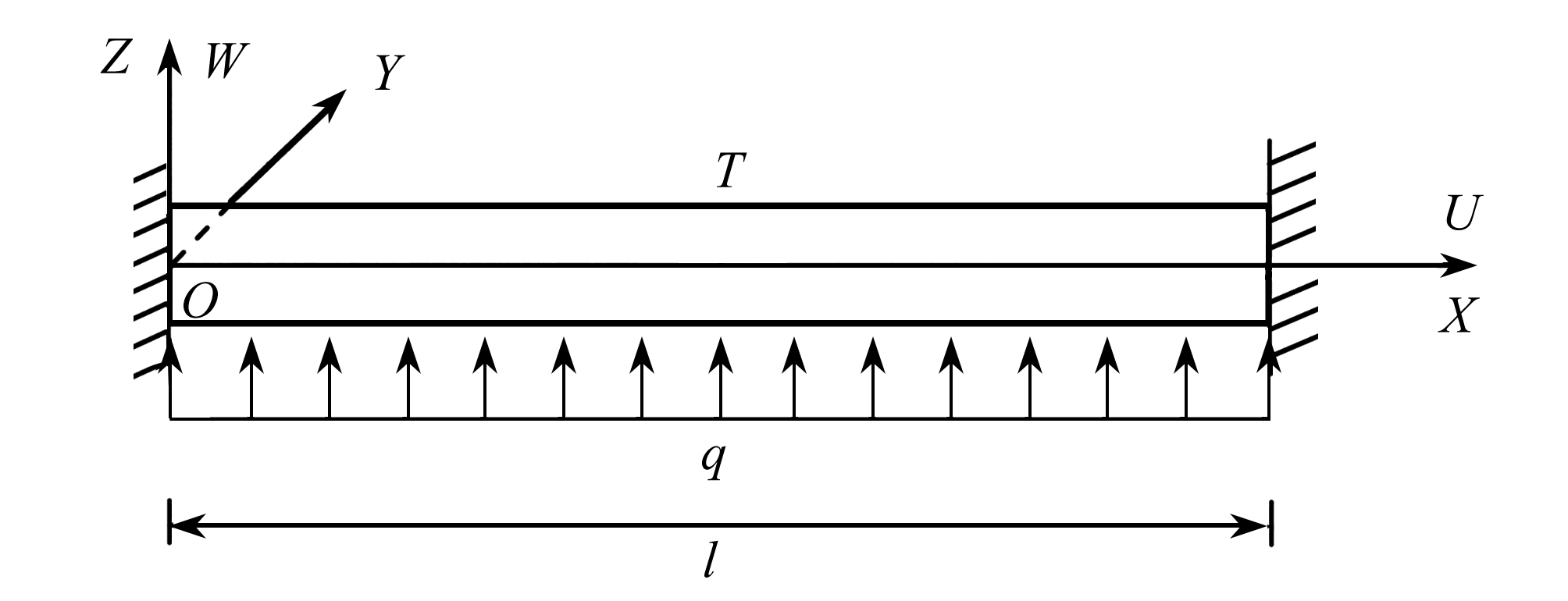
图1 梁的几何坐标
Fig. 1 Geometric coordinates of the beam
由于构成FGM的常见组分材料的材料常数对变温依赖性并不显著,再考虑到本文计算数据所考虑的变温幅度较小,因此,下文中FGM常数Peff不考虑变温的影响,并设其沿厚度方向的变化规律[19]为
Peff(Z)=PcVc(Z)+PmVm(Z),
(2)
式中P为不依赖温度的材料常数,下标c和m分别指陶瓷和金属组分.
由式(1)和式(2)不难得到功能梯度梁的材料弹性模量E、热膨胀系数α如下:
[E(Z),α(Z)]=[Em,αm]+[Ecm,αcm][(2Z+h)/(2h)]k,
(3)
式中Ecm=Ec-Em, αcm=αc-αm.当Z=h/2时,E=Ec, α=αc; 当Z=-h/2时, E=Em, α=αm.另外,假设材料Poisson比ν为常数[19].
2 边 值 问 题
2.1 控制方程
根据经典梁理论,考虑前述坐标系,对称弯曲时梁横截面上任意点(X,Y,Z)的几何非线性应变-位移关系可由文献[20]中的相应关系退化为
(4)
考虑温度应力的应力-应变关系为
σX=E(Z)[εX-α(Z)T],
(5)
式中T为相对初始无应力状态的均匀变温场.
根据虚功原理有
(6)
式中A为梁横截面面积域,q为作用在纵向对称面内的沿轴向均匀线布荷载.
将式(4)、(5)代入式(6),经变分运算(限于篇幅,本文未给出运算过程),并考虑如下无量纲量:
式中w和u分别为无量纲横向和轴向位移,x为无量纲轴向坐标,Q为无量纲横向均匀线布荷载,μ为相对初始无应力状态的无量纲变温,
最终得无量纲形式的位移型几何非线性控制方程如下:
(7)

(8)
2.2 边界条件
不可移夹紧边界条件:
(9)
中心对称条件:
(10)
3 打靶法求解说明
方程(7)、(8),边界条件(9)及中心对称条件(10)为均匀变温场中、横向均匀线布荷载作用的端部不可移夹紧功能梯度梁轴对称弯曲变形的常微分方程两点边值问题,易用打靶法[18]计算得到其数值结果.为了用打靶法求解上述两点边值问题,设
Y=(y1 y2 y3 y4 y5 y6 y7)T=(w w′ w″ w‴ u u′ Q)T.
则原两点边值问题可化为下述初值问题:
式中φi(i=1,2)可以从非线性方程(7)、(8)中得到,不再赘述;
Y(0.5)=(η 0 V1 0 0 V2 V3)T,
式中η为x=0.5处的初始挠度(赋值),Vi(i=1,2,3)为待定参数,由x=1处的边界条件确定.
4 数值结果分析
4.1 功能梯度梁的热屈曲平衡路径
对于本文模型,需要指出的是,当k=0时,模型退化为均质陶瓷梁;当k=+∞时(此种情形与令kc=km,αc=αm的情形相同,为简单起见,下文不再赘述),模型退化为均质铝梁.还需要指出的是,在前述边界条件下,当横向荷载Q=0时,方程(7)、(8)退化为功能梯度梁在均匀变温场中的热屈曲几何非线性控制方程,不但可以分析热屈曲临界升温,还可以分析后屈曲平衡路径.考虑到分析后屈曲平衡路径需要大变形且使梁能在线弹性范围内工作,在端部不可移夹紧边界条件下,通过试算,本文选取长度l=1 500 mm、高度h=10 mm和宽度b=12 mm的细长矩形截面梁,并取组分材料弹性模量Ec=380 GPa和Em=70 GPa,热膨胀系数αc=2.3×10-5 ℃-1和αm=7.4×10-6 ℃-1,Poisson比ν=0.3作为算例进行计算.
已经知道,压杆的Euler临界荷载是在微小弯曲位形上计算的.在小变形时,控制方程(7)、(8)中的非线性项可以略去,方程退化为一个关于挠度w为未知函数的二阶常系数齐次线性微分方程,即方程(7)中的前两项之和等于0(分析热屈曲问题时,横向荷载Q=0).该方程与分析理想轴心受压直杆的Euler临界荷载所用到的无量纲微分方程[21]完全一样.另外,分析热屈曲临界升温时端部不可移夹紧边界条件和分析理想轴心受压直杆的Euler临界荷载时一端固定、另一端夹紧轴向可移边界条件有完全相同的数学形式(挠度及其一阶导数均为0).据此不难判断,所得到的无量纲热屈曲临界升温和无量纲轴向压力在数值上是相等的.用打靶法计算本文边值问题得到的数值结果为39.439(在分支点附近,变形很小,非线性效应可忽略),该值与线性理论的解析解4π2[21]能很好一致.
为了考察材料体积分数指数k对功能梯度梁的热屈曲平衡路径的影响,图2在给定3个指数k=0,0.4,1.0的情况下,给出了梁的无量纲中心挠度w(0.5)与无量纲均匀变温μ的关系曲线.从图中可以看出,当μ<4π2时,梁的中心挠度始终为0;当μ>4π2后,梁的中心挠度迅速增加(两支).这表明,梁在μcr=4π2时发生了分支点屈曲.从图中还可以看出,屈曲后,指数k对无量纲量给出的梁的热屈曲平衡路径有影响,但并不显著.
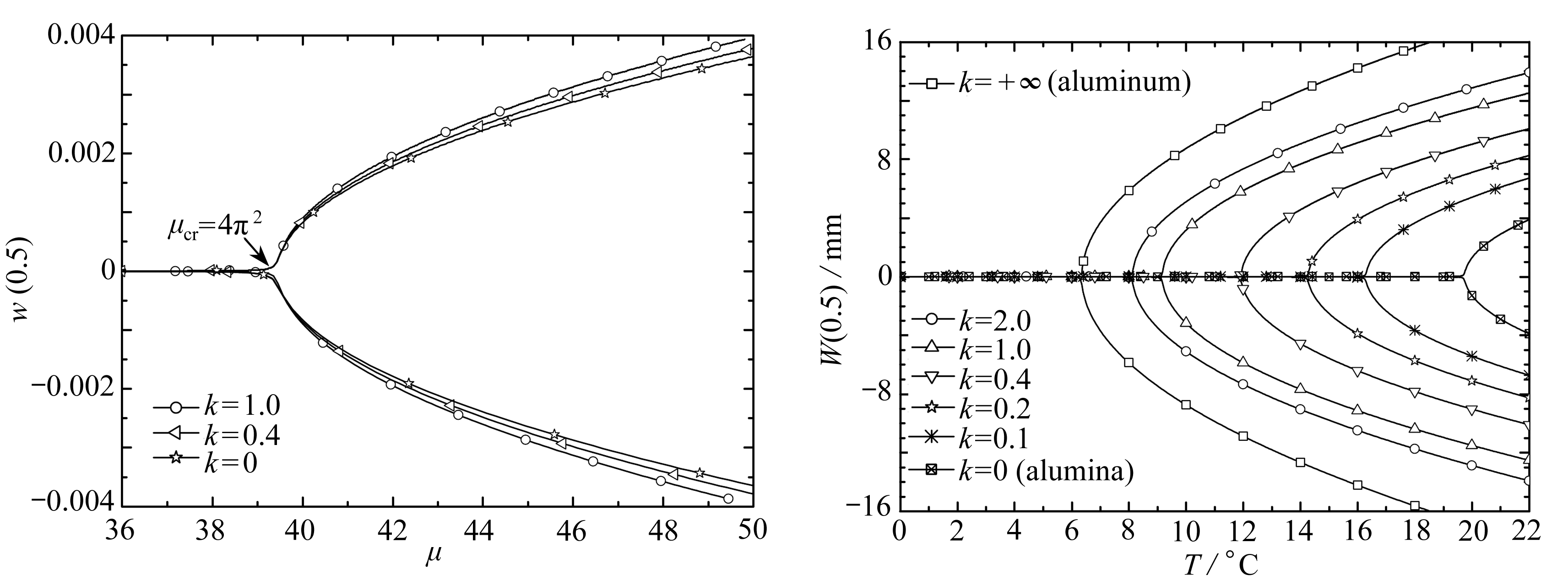
图2 体积分数指数k对FGM梁无量纲图3 体积分数指数k对FGM梁有量纲
热屈曲平衡路径的影响 热屈曲平衡路径的影响
Fig. 2 Effects of volume fraction index k on Fig. 3 Effects of volume fraction index k on the dimensionless thermal buckling the dimensional thermal buckling equilibrium path of the FGM beam equilibrium path of the FGM beam
为了更加直观,图3在给定一组材料体积分数指数k=0,0.1,0.2,0.4,1.0,2.0,+∞的情况下,给出了梁的有量纲热屈曲平衡路径.从图中容易看出,指数k对有量纲量给出的梁的热屈曲平衡路径有非常显著的影响.对于图中给定的指数k,随其增加,梁的有量纲热屈曲临界升温在显著降低,同一升温对应的梁的有量纲后屈曲中心挠度在显著增加.这一现象表明,对于端部不可移夹紧梁,当梁的几何尺寸确定时,可以通过调整指数k来控制梁的有量纲热屈曲临界升温和后屈曲中心挠度.
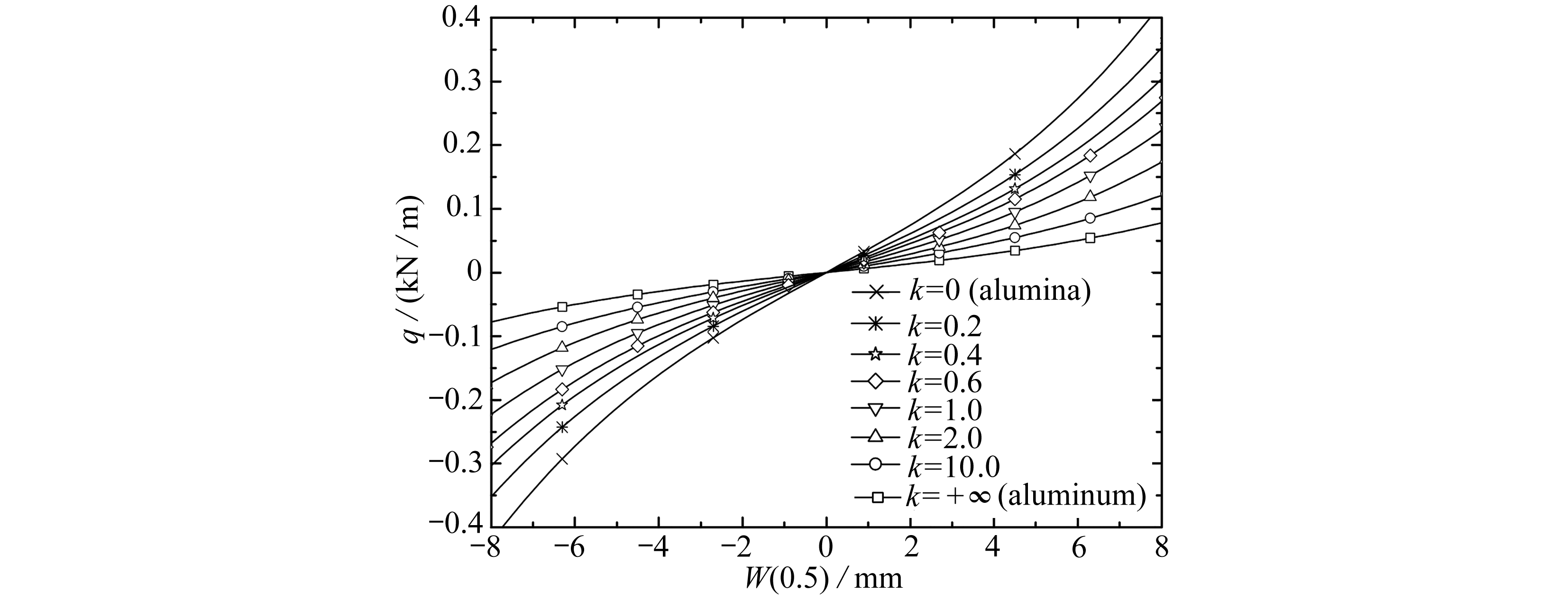
图4 体积分数指数k对FGM梁荷载-挠度曲线的影响
Fig. 4 Effects of volume fraction index k on the load-deflection curves of the FGM beam
4.2 功能梯度梁在机械荷载作用下的响应
当T=0时,方程(7)、(8)退化为功能梯度梁在横向均布荷载作用下的几何非线性弯曲控制方程.为了考察材料体积分数指数k对梁横向弯曲变形的影响,在不变温并给定材料体积分数指数k=0,0.2,0.4,0.6,1.0,2.0,10.0,+∞的情况下,图4给出了不同k值对应的梁的中心挠度与横向均布荷载的关系曲线.从图中容易看出,梁中心挠度W(0.5)是横向均布荷载q的单值函数,且正、反向加载对梁的中心挠度几乎无影响.另外,从图中还可以看出,随指数k的增加,同一荷载对应的梁中心挠度在增加,这是因为随k增加,梁中金属组分含量增加而陶瓷组分含量减少(由于本文给定的金属组分弹性模量小于陶瓷组分弹性模量),因此,指数k增加会导致梁的弯曲刚度显著减小进而导致挠度显著增加.应该指出的是,随指数k的增加,其对挠度影响逐渐减小,这是因为,随着k的增加,其变化对梁中组分材料含量的影响逐渐减小,从而对梁弯曲刚度的影响会显著减弱.此外,从荷载-挠度曲线的凹、凸性可以判断,系统属于硬特性非线性系统,这也与定性分析的结论一致.
4.3 功能梯度梁在热-机械荷载联合作用时的响应
为了考察功能梯度梁在均匀变温场和横向均布荷载联合作用时的响应规律,在k=1时,图5给出了7个变温参数T=40, 30, 20, 9.17, 5, 0,-10 ℃对应的梁的荷载-挠度曲线.从图中看出: ① 变温对荷载-挠度曲线有显著的影响; ② 当T<Tcr=9.17 ℃(线性理论的解析解为9.178 ℃)时,梁中心挠度W(0.5)是均布荷载q的单值函数,这表明随均布荷载q的连续变化,梁的平衡状态是连续变化的; ③ 当T>Tcr之后,在q=0的临近区域内,梁的荷载-挠度曲线出现了迂回区,在该区域,同一个荷载q对应3个跨中挠度W(0.5),多解性导致结构的平衡状态在该区域会发生跳跃,这是典型的非线性现象.以T=20 ℃对应的荷载-挠度曲线为例:当荷载q=0时,对应3个平衡位形(图中O、G和H三点).其中O点对应的未变形位形是不稳定的位形,它仅仅是非线性边值问题(方程(7)~(10))数学上的解,在物理上不能实现;G点(挠曲线凸向Z轴正向)和H点(挠曲线凸向Z轴负向)对应的挠度均是由热屈曲单一因素引起的, 都是稳态位形.从G点开始, 如逐步增大正向荷载, 荷载-挠度曲线会沿着G至C的路径变化.从C端开始,如果逐步减小正向荷载直至荷载变为0,荷载-挠度曲线会沿着C至G变化.从G至D区段,荷载从0开始并沿负方向逐渐增加,但梁跨中挠度依然为正值,表明梁向正向屈曲后,从外凸的一侧逐渐加压(负向),梁的屈曲位形不会立即翻转到负坐标一侧.当沿负向加载至D点(qd=-0.093 58 kN/m,为下文叙述方便,将此类荷载称为下临界荷载)时,梁的平衡位形处于临界不稳定状态,此时,任何微小的扰动都可能使梁的平衡位形由D点跳跃到E点.从E点开始,如果继续增大负向荷载,荷载-挠度曲线会沿着E至F的路径变化.如果从F端开始逐渐减小负向荷载直至为0,荷载-挠度曲线会沿着FEH的路径变化.从H至A区段,从0开始逐渐增大正向荷载,但梁跨中挠度依然为负值,表明梁向负向屈曲后,从外凸的一侧逐渐加压(正向),梁的屈曲位形不会立即翻转到正坐标一侧.当正向加载至A点(qu= 0.093 58 kN/m,为下文叙述方便,将此类荷载称为上临界荷载)时,梁的平衡位形又一次处于临界不稳定状态,此时,任何微小的扰动都可能使梁的平衡位形由A点跳跃到B点.从B点开始,如果继续增大正向荷载,荷载-挠度曲线会沿着B至C路径变化.需要指出的是,当荷载q大于上临界荷载(对应BC段曲线)或小于下临界荷载(对应EF段曲线)时,梁的平衡状态是唯一的,相应的平衡是稳定的.当荷载q界于上、下临界荷载之间(对应BD、EA和AD段曲线)时,边值问题具有3个解,其中BD和EA段曲线对应的梁的平衡状态是稳定的,换句话说,在该区间,一个横向荷载,对应梁的两个稳态位形(双稳态构形),梁究竟处于哪一个位形,与加载历程有关;而AD段曲线仅是数学上的解,梁不会出现此种平衡状态.对其他温度(T>9.17 ℃)的情形,除了上、下临界荷载有变化以外,荷载-挠度曲线响应规律与T=20 ℃对应的荷载-挠度曲线的响应规律完全雷同,不再赘述.
为了比较不同材料体积分数指数k对梁在热-机械荷载联合作用时的荷载-挠度曲线的影响,当k=0.2时,图6给出了7个变温参数T=40,30,14.24,10,5,0,-10 ℃对应的梁的荷载-挠度曲线.与图5中的结果比较可以发现,此时对应的热屈曲临界升温为14.24 ℃,另外,上、下临界荷载发生了一定的变化,其余变化规律与图5中的响应规律完全雷同,不再赘述.
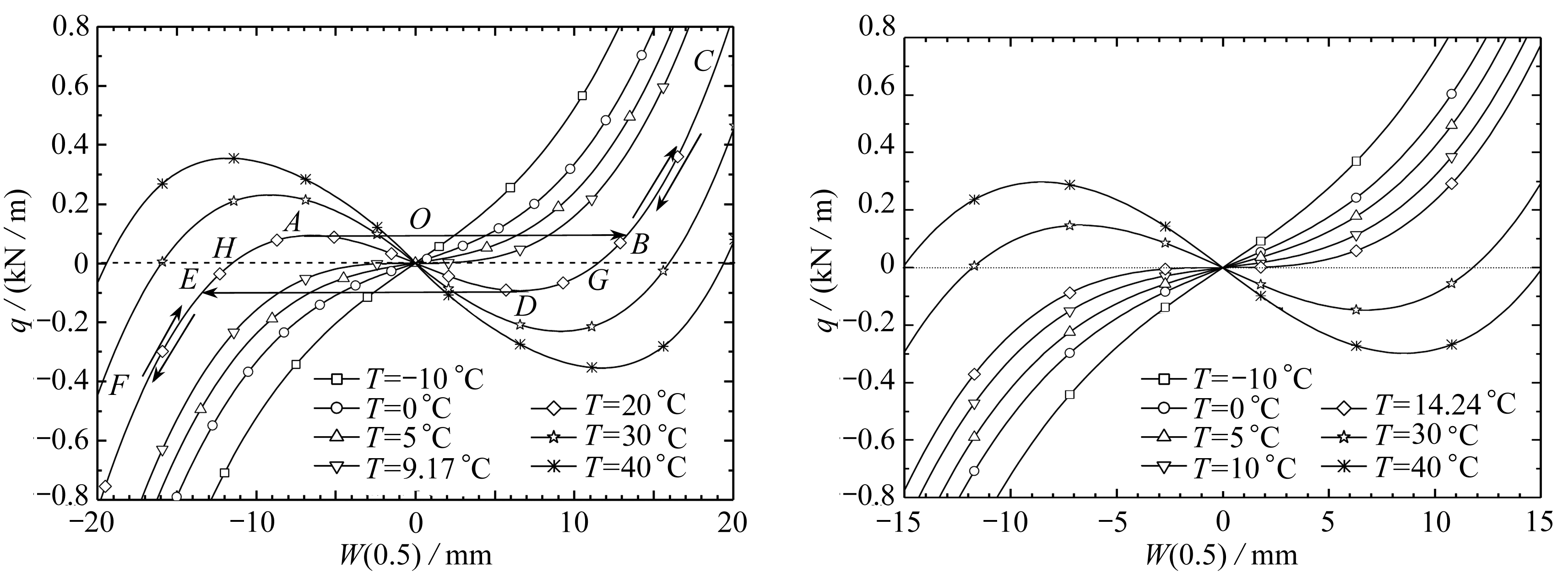
图5 均匀变温场T对FGM梁荷载-挠度图6 均匀变温场T对FGM梁荷载-挠度
曲线的影响(k=1) 曲线的影响(k=0.2)
Fig. 5 Effects of uniform temperature field T on the Fig. 6 Effects of uniform temperature field T on the load-deflection curves of the FGM beam load-deflection curves of the FGM beam (k=1) (k=0.2)

图7 均匀变温场中不同的荷载q对应的FGM梁的平衡构形
Fig. 7 The equilibrium configurations of the FGM beam for different loads q in the uniform temperature field
为了更加直观,对于k=1的功能梯度梁,当T=20 ℃时,针对q=0.2,0.05,0,-0.05,-0.2 kN/m这5个荷载参数,图7给出了对应的8个稳态构形.其中q=0.2 kN/m或-0.2 kN/m时,结构均只有唯一的平衡位形(是稳定的位形).q=0 kN/m对应的两个构形代表的是从正、负两个方向屈曲得到的两个稳态热屈曲构形,形状对称于初始直线位形.q=0.05 kN/m对应的两个稳态构形,其中纵坐标大于0的一支曲线代表梁向正坐标一侧屈曲后,并受到正向(从凹侧指向凸侧)0.05 kN/m的荷载时对应的构形;纵坐标小于0的一支曲线代表梁向负坐标一侧屈曲后,并受到正向(从凸侧指向凹侧)0.05 kN/m的荷载时对应的构形.q=-0.05 kN/m对应的两个稳态构形,其中纵坐标大于零的一支曲线代表梁向正坐标一侧屈曲后,并受到负向(从凸侧指向凹侧)0.05 kN/m的荷载时对应的构形;纵坐标小于0的一支曲线代表梁向负坐标一侧屈曲后,并受到负向(从凹侧指向凸侧)0.05 kN/m的荷载时对应的构形.上述屈曲构形描述的物理现象与定性分析完全一致.
5 结 论
1) 经典理论下的端部不可移夹紧功能梯度梁的热屈曲平衡路径具有明显的分支特征.
2) 随梯度指数的增加,同一几何尺度的端部不可移夹紧功能梯度梁的有量纲热屈曲临界升温在减小.因此,可以通过调整材料体积分数指数来调整此类梁的有量纲热屈曲临界升温.
3) 当均匀升温大于梁的热屈曲临界升温后,在横向均布荷载的一定取值域内,端部不可移夹紧功能梯度梁存在两种稳态构形,梁究竟处于哪一种稳态构形,不但与变温和荷载参数有关,而且与加载历程有关.
[1] KOIZUMI M. FGM activities in Japan[J]. Composites Part B: Engineering, 1997, 28(1/2): 1-4.
[2] 李永, 宋健, 张志民. 梯度功能力学[M]. 北京: 清华大学出版社, 2003.(LI Yong, SONG Jian, ZHANG Zhimin. Gradient Functional Mechanics[M]. Beijing: Tsinghua University Press, 2003.(in Chinese))
[3] MA L S, WANG T J. Relationships between axisymmetric bending and buckling solutions of FGM circular plates based on third-order plate theory and classical plate theory[J]. International Journal of Solids and Structure, 2004, 41(1): 85-101.
[4] REDDY J N, WANG C M, KITIPORNCHAI S. Axisymmetric bending of functionally graded circular and annular plates[J]. European Journal of Mechanics: A/Solids, 1999, 18(2): 185-199.
[5] MOITA J S, ARA JO A L, MOTA SOARES C M, et al. Material and geometric nonlinear analysis of functionally graded plate-shell type structures[J]. Applied Composite Materials, 2016, 23(4): 537-554.
JO A L, MOTA SOARES C M, et al. Material and geometric nonlinear analysis of functionally graded plate-shell type structures[J]. Applied Composite Materials, 2016, 23(4): 537-554.
[6] 胡超, 郑日恒, 孙旭峰, 等. 梯度材料平板弯拉耦合力学的精确化支配方程[J]. 应用数学和力学, 2016, 37(7): 756-765.(HU Chao, ZHENG Riheng, SUN Xufeng, et al. Refined equations for functionally graded material plates under bending-tension coupling[J]. Applied Mathematics and Mechanics, 2016, 37(7): 756-765.(in Chinese))
[7] 张莹, 梅靖, 陈鼎, 等. 功能梯度圆板和环板受周边力作用的弹性力学解[J]. 应用数学和力学, 2018, 39(5): 538-547.(ZHANG Ying, MEI Jing, CHEN Ding, et al. Elasticity solutions for functionally graded circular and annular plates subjected to boundary forces and moments[J]. Applied Mathematics and Mechanics, 2018, 39(5): 538-547.(in Chinese))
[8] SHEN H S. Nonlinear bending response of functionally graded plates subjected to transverse loads and in thermal environments[J]. International Journal of Mechanical Sciences, 2002, 44(3): 561-584.
[9] SANKAR B V, TZENG J T. Thermal stresses in functionally graded beams[J]. AIAA Journal, 2002, 40(6): 1228-1232.
[10] 仲政, 于涛. 功能梯度悬臂梁弯曲问题的解析解[J]. 同济大学学报(自然科学版), 2006, 34(3): 443-447.(ZHONG Zheng, YU Tao. Analytical bending solution of functionally graded cantilever-beam[J]. Journal of Tongji University(Natural Science), 2006, 34(3): 443-447.(in Chinese))
[11] KADOLI R, AKHTAR K, GANESAN N. Static analysis of functionally graded beams using higher order shear deformation theory[J]. Applied Mathematical Modelling, 2008, 32(12): 2509-2525.
[12] 李世荣, 张靖华, 赵永刚. 功能梯度材料Timoshenko梁的热过屈曲分析[J]. 应用数学和力学, 2006, 27(6): 709-715.(LI Shirong, ZHANG Jinghua, ZHAO Yonggang. Thermal post-buckling of functionally graded material Timoshenko beams[J]. Applied Mathematics and Mechanics, 2006, 27(6): 709-715.(in Chinese))
[13] LIBRESCU L, OH S Y, SONG O. Thin-walled beams made of functionally graded materials and operating in a high temperature environment: vibration and stability[J]. Journal of Thermal Stresses, 2005, 28(6/7): 649-712.
[14] BHANGALE R K, GANESAN N. Thermoelastic buckling and vibration behavior of a functionally graded sandwich beam with constrained viscoelastic core[J]. Journal of Sound and Vibration, 2006, 295(1/2): 294-316.
[15] 牛牧华, 马连生. 基于物理中面FGM梁的非线性力学行为[J]. 工程力学, 2011, 28(6): 219-225.(NIU Muhua, MA Liansheng. Nonlinear mechanical behaviors of FGM beams based on the physical neutral surface[J]. Engineering Mechanics, 2011, 28(6): 219-225.(in Chinese))
[16] LIEW K M, YANG J, KITIPORNCHAI S. Postbuckling of piezoelectric FGM plates subject to thermo-electro-mechanical loading[J]. International Journal of Solids and Structures, 2003, 40(15): 3869-3892.
[17] 沈惠申. 功能梯度复合材料板壳结构的弯曲、屈曲和振动[J]. 力学进展, 2004, 34(1): 53-60.(SHEN Huishen. Bending, buckling and vibration of functionally graded plates[J]. Advances in Mechanics, 2004, 34(1): 53-60.(in Chinese))
[18] 赵伟东, 高士武, 马宏伟. 扁球壳在热-机械荷载作用下的稳定性分析[J]. 应用数学和力学, 2017, 38(10): 1146-1154.(ZHAO Weidong, GAO Shiwu, MA Hongwei. Thermomechanical stability analysis of shallow spherical shells[J]. Applied Mathematics and Mechanics, 2017, 38(10): 1146-1154.(in Chinese))
[19] BICH D H, VAN TUNG H. Non-linear axisymmetric response of functionally graded shallow spherical shells under uniform external pressure including temperature effects[J]. International Journal of Non-Linear Mechanics, 2011, 46(9): 1195-1204.
[20] 朱媛媛, 胡育佳, 程昌钧. Euler型梁-柱结构的非线性稳定性和后屈曲分析[J]. 应用数学和力学, 2011, 32(6): 674-682.(ZHU Yuanyuan, HU Yujia, CHENG Changjun. Analysis of nonlinear stability and post-buckling for Euler-type beam-column structure[J]. Applied Mathematics and Mechanics, 2011, 32(6): 674-682.(in Chinese))
[21] 周承倜. 弹性稳定理论[M]. 成都: 四川人民出版社, 1981.(ZHOU Chengti. Elastic Stability Theory[M]. Chengdu: Sichuan People’s Publishing House, 1981.(in Chinese))