引 言
传染病模型是生物数学中一类典型的数学模型,关于传染病模型行波解的存在性研究已有大量的结果[1-10].例如,Wang和Wu[11]研究了一般的Kermack-McKendrick模型行波解的存在性.Li等[12]研究了人口数量变化的非局部时滞SIR传染病模型.文献[13]研究了具有非线性发生率的时滞SIR模型等等.
最近, 邹霞和吴事良[14]研究了以下具有时滞的非局部扩散SIR传染病模型:
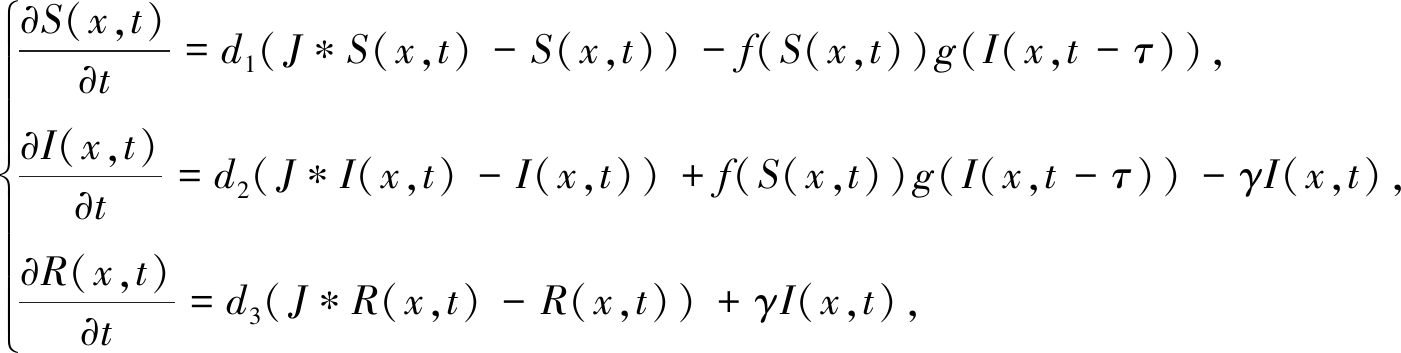
(1)
其中di>0(i=1,2,3)表示扩散系数, γ表示恢复率,τ≥0表示疾病的潜伏时间,J*u(x,t)是关于空间x的标准卷积.J*S(x,t)-S(x,t), J*I(x,t)-I(x,t), J*R(x,t)-R(x,t)分别表示由易感者、感染者、恢复者的扩散导致的净增长率.假设J, f和g满足条件:
(H1) f, g∈C((0,+∞), (0,+∞)), f(0)=g(0)=0, f′(S)>0, ∀S≥0,且g′(I)>0,g″(I)≤0,∀I≥0;
![]() 且J具有紧支撑.
且J具有紧支撑.
在条件(H1)和(H2)下, 邹霞和吴事良[14]证明了当c>max{c*, (3/2)d2σ0}, R0=(f(S-∞)g′(0))/γ>1时, 系统(1)存在满足边界条件S(-∞)=S-∞,I(±∞)=0的行波解, 并得到了当R0≤1或者R0>1,0<c<c*时, 系统(1)不存在行波解的结论, 其中σ0=S-∞![]() J(y)| y |dy.随后, Zhang等[15]也研究了系统(1)的行波解的存在性问题, 他们利用Schauder不动点定理和双边Laplace变换建立了系统(1)的行波解的存在性与不存在性.文献[14]是在大传播速度(即c>max{c*, (3/2)d2σ0})条件下得到系统(1)的行波解的存在性, 文献[15]是在小传播速度(即c>c*)条件下得到行波解的存在性.然而, 文献[14-15]没有讨论当波速c=c*时, 系统(1)的行波解的存在性问题.众所周知, 反应扩散系统在c>c*条件下行波解的存在性已有很多研究, 但当c=c*时行波解的存在性讨论很少, 相关结果可参阅文献[9,16-18], 其中Wu[18]在Fu等[6]研究的基础上,讨论了以下模型临界波的存在性:
J(y)| y |dy.随后, Zhang等[15]也研究了系统(1)的行波解的存在性问题, 他们利用Schauder不动点定理和双边Laplace变换建立了系统(1)的行波解的存在性与不存在性.文献[14]是在大传播速度(即c>max{c*, (3/2)d2σ0})条件下得到系统(1)的行波解的存在性, 文献[15]是在小传播速度(即c>c*)条件下得到行波解的存在性.然而, 文献[14-15]没有讨论当波速c=c*时, 系统(1)的行波解的存在性问题.众所周知, 反应扩散系统在c>c*条件下行波解的存在性已有很多研究, 但当c=c*时行波解的存在性讨论很少, 相关结果可参阅文献[9,16-18], 其中Wu[18]在Fu等[6]研究的基础上,讨论了以下模型临界波的存在性:
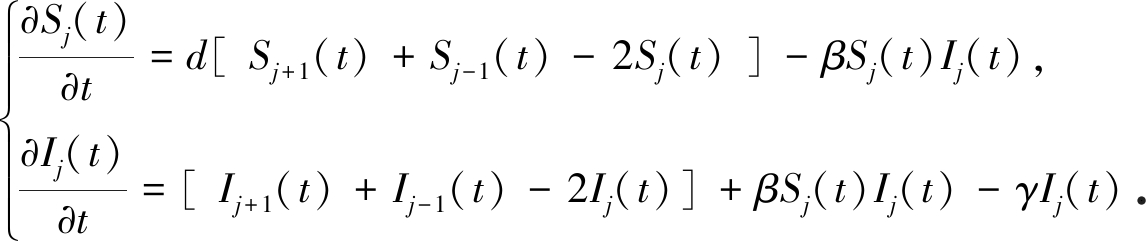
(2)
Wu[18]通过讨论系统(2)中I的有界性, 证得了在波速c>c*条件下行波解的存在性, 从而得到当c=c*时行波解的存在性.最近, Yang等[17]利用文献[18]中的方法建立了以下模型临界波的存在性:
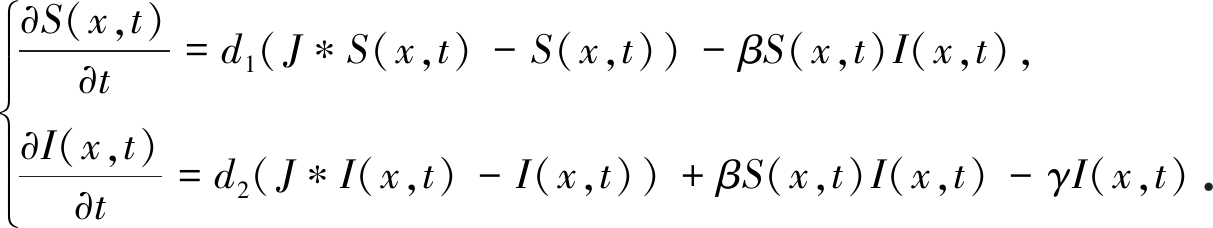
(3)
注意到, 系统(3)是系统(1)的一个特例, 那自然要问:系统(1)是否存在具有临界波速的行波解? 回答是肯定的.
为了研究系统(1)的临界波, 仅需考虑系统(1)的子系统(由于系统(1)的第三个方程与前两个方程不是耦合的):
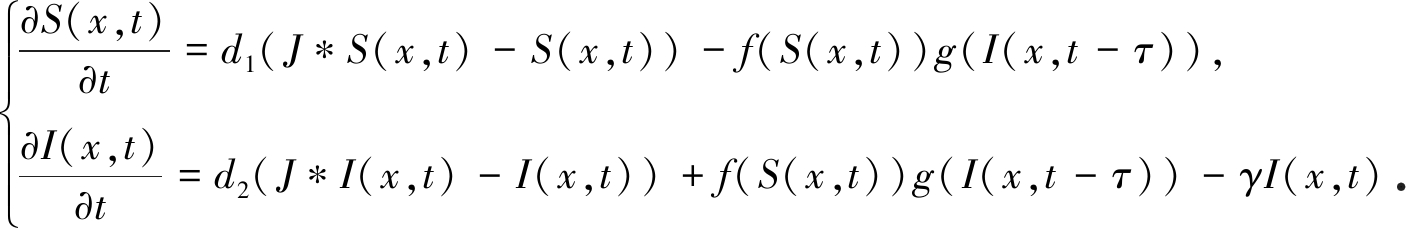
(4)
令(S(x+ct),I(x+ct))=(S(z),I(z)),其中z=x+ct.将其代入系统(4)可得如下相应的行波系统:
(5)
其中边界条件为
(S,I)(-∞)=(S-∞,0), I(+∞)=0,
(6)
且S在+∞处的取值是任意的.
现在, 给定f(S-∞)g′(0)>γ,定义最小传播速度:
c*![]()
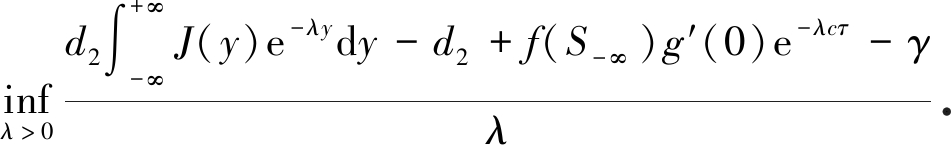
本文受文献[17-18]的启发, 主要研究系统(4)当c=c*时行波解的存在性.因此, 首先利用反证法证明I是有界的, 并根据I的有界性研究波速c>c*时行波解的存在性.其次,利用c>c*时行波的存在性结果证明临界波的存在性.最后, 讨论R0对临界波存在性的影响.
这里需要指出的是,文献[14]在证明行波解的存在性时, 对建立I的有界性附加了一定的条件, 而本文使用文献[17-18]中的技巧, 在没有限制的条件下,利用反证法证明了I的有界性, 进而建立了当c>c*时行波解的存在性.由于时滞的存在和函数g的性质的影响, 在证明I的有界性时, 很多证明细节与文献[17-18]是不同的.
本文的安排如下: 第1节研究当c>c*时行波解的有界性; 第2节证明当c=c*时行波解的存在性; 第3节给出具体实例,验证了所得的临界波结果;最后,对全文内容进行总结.
1 行波解的有界性
本节主要研究系统(4)行波解的有界性. 由文献[14]可得, 当R0>1和c>c* 时, 系统(4)存在满足0<S<S-∞,I>0的解(S,I), 且S(-∞)=S-∞,I(-∞)=0.
引理1 若函数(S,I)是系统(5)波速为c>c*的行波解且0<S<S-∞,I>0,则函数![]() 在R上有界.
在R上有界.
证明 首先, 对方程(5)的第二个方程的两边同时除以I,可得
(7)
因为0<S<S-∞, 可得I′/I的有界性与![]() 的有界性有关.
的有界性有关.
为了方便起见, 记u(z)![]() I′/I和μ=(d2+γ)/c.则式(7)为
I′/I和μ=(d2+γ)/c.则式(7)为
记κ![]()
![]() 和G(z)
和G(z)![]()
![]() 因此, 对G(z)关于z求导, 有
因此, 对G(z)关于z求导, 有
(8)
所以G(z)是非减的且limz→-∞ G(z)=0.由条件(H2)可知,r>0,其中r是supp J的半径.因此, 取0<2r0<r.对方程(8)从-∞到z积分, 可得
则
(9)
然后, 对方程(8)关于x从z-r0到z积分,可得
κr0![]() J(y)eμyG(z-r0-y)dy≥
J(y)eμyG(z-r0-y)dy≥
κr0![]() J(y)eμydyG(z+r0).
J(y)eμydyG(z+r0).
因为r>2r0和![]() J(y)eμydy>0且
J(y)eμydy>0且
ω0![]()
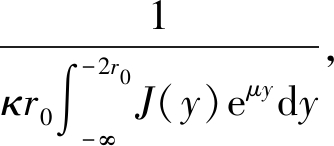
所以, 对任意的ξ∈R,有
G(z+r0)≤ω0G(z).
(10)
由于
结合式(9)和(10)可得
又因为G(z)是非减的,故
G(z)≥G(z-cτ).
整理得
则
因此
(11)
由条件(H1) 知, 对任意的t∈[0,I(z-cτ)],有
f(S-∞)g′(0)exp(μcτ),
则
所以
因此,![]() 和
和![]() 是有界的.
是有界的.
□
下面介绍几个引理用于证明I的有界性.
引理2 任取ck∈(c*,c*+1)且(ck,Sk,Ik)是系统(5)波速为c=ck的一序列行波解, 且0<Sk<S-∞, Ik>0.如果存在一个序列{zk}使得当k→+∞时Ik(zk)→+∞, 则Sk(zk)→0.
证明 反证法.假设不成立, 则存在一个序列{zk}(仍用zk表示) 使得Sk(zk)≥ε, 其中,k∈N和ε>0.由式(5)的第一个方程, 可得S′k(z)≤2d1S-∞/c*.因此,Sk(z)≥ε/2, ∀z∈[zk-δ, zk].由引理1得, 存在实数L1>0 满足|I′k/Ik|≤L1.因此, 对所有的k∈N,有
当k→+∞时, Ik(zk)→+∞,则
Ik(z)≥e-δL1Ik(z k)→+∞.
又因为
因此, 当k→+∞,有
注意到
根据条件(H1)可知0<g′(Ik(z-cτ))<g′(t0)<g′(0).则由式(5)的第一个方程得
这与Sk(z)<S-∞矛盾.证毕.
□
引理3 若(S,I)是系统(5)波速为c>c*时的行波解且0<S(ξ)<S-∞, I>0, 如果lim supz→+∞I(z)=+∞,那么limz→+∞I(z)=+∞.
证明 假设m![]() lim infz→+∞I(z)<+∞.则存在点列{zk
lim infz→+∞I(z)<+∞.则存在点列{zk![]() 满足limk→+∞zk=+∞和I(zk)→m.因此, 对任意的k∈N, 有I(zk)≤m+1.
满足limk→+∞zk=+∞和I(zk)→m.因此, 对任意的k∈N, 有I(zk)≤m+1.
再者,对每一个k∈N,假设存在一个点yk∈[zk,zk+1]使得I(yk)=max z∈[ zk,zk +1 ]I(z).又因为lim supz→+∞I(z)=+∞, 则当k→+∞时, I(yk)→+∞.因为L1是引理1中给定的常数, 所以, 对所有的k∈N, 有I(yk)>(m+1)eL1r, 其中r是supp J的半径.那么, 当|y-yk|≤r时,有
可得[yk-r,yk+r]⊂(zk,zk+1).因此, 由式(5)的第二个方程可得出
0=cI′(yk)=
f(S(yk))g(I(yk-cτ))-γI(yk).
(12)
由limk→+∞I(yk)=+∞和引理2, 所以limk→+∞S(yk)=0.因此, limz→+∞I(z)=+∞.证毕.
□
引理4[19] 假设c>0, B(·)是一个连续函数满足B(±∞)![]() limz→±∞B(z).令Z(z)为一个可测函数且满足
limz→±∞B(z).令Z(z)为一个可测函数且满足
因此,Z是一致连续和一致有界.再者, ψ±![]() limz→±∞Z(z)存在且是方程
limz→±∞Z(z)存在且是方程
的特征根.
定理1 若函数(S,I)是系统(5)波速为c>c*时的行波解且S(-∞)=S-∞,I>0, 则I在R上有界.
证明 反证法.假设I在R上无界, 则lim supz→+∞I(z)=+∞.因此由引理2和引理3,可得I(+∞)=+∞和S(+∞)=0.
记u(x)=I′(x)/I(x).对式(5)的第二个方程两边同除以I,则有
因为S(+∞)=0和S(-∞)=S-∞,所以由引理4可得limz→+∞u(z)存在, 且满足
(13)
定义连续函数:
因此, h满足h(0,c)=-γ<0且
所以方程(13)存在唯一的正根λ0.因为I(z)>0和limz→+∞I(z)=+∞,因此limz→+∞u(z)≥0,则limz→+∞u(z)=λ0.由文献[14], 可得I(z)≤eλ1z,其中0<λ1<λ2是方程
d2![]() J(y)e-λydy-d2-cλ+f(S-∞)g′(0)e-λcτ-γ=0
J(y)e-λydy-d2-cλ+f(S-∞)g′(0)e-λcτ-γ=0
(14)
的两个特征根.将λ2代入方程(14), 整理得
d2![]() J(y)e-λ2ydy-d2-cλ2-γ=-f(S-∞)g′(0)e-λ2cτ<0,
J(y)e-λ2ydy-d2-cλ2-γ=-f(S-∞)g′(0)e-λ2cτ<0,
则0<λ1<λ2<λ0.因为limz→+∞θ(z)=λ0, 从而存在z* 和L满足
I(z)≥Le((λ0+λ2)/2)z*.
这与λ1<(λ2+λ0)/2矛盾.因此,I有界.证毕.
□
正如文献[14]中所描述的, 只要I有界,下面的结果都成立.因此在这里只给出部分证明. 定理2 如果R0>1和c>c*,那么式(5)存在行波解(S(z),I(z))满足0<S(z)<S-∞, 0<I(z), S(+∞)=σ<S(-∞)=S-∞和I(±∞)=0,其中σ>0.同时
证明 由文献[14]中定理2.1,可得式(5)存在一个解(S(z),I(z))且满足0<S(z)<S-∞, 0<I(z), S(+∞)=σ, S(-∞)=S-∞和I(±∞)=0.对任意的φ,υ∈R,有
![]() (J*S(z)-S(z))dz=
(J*S(z)-S(z))dz=
因此
![]()
![]() C0.
C0.
再对式(5)的第一个方程从υ到φ积分, 可得
![]() f(S(z))g(I(z-cτ))dz=
f(S(z))g(I(z-cτ))dz=
d1![]() (J*S(z)-S(z))dz+cS(υ)-cS(φ)≤d1C0+2cS-∞.
(J*S(z)-S(z))dz+cS(υ)-cS(φ)≤d1C0+2cS-∞.
因此
又因I(z)有界, 所以存在实数M使得I(z)≤M成立.对式(5)的第二个方程从ζ到η积分, 有
![]() f(S(z))g(I(z-cτ))dz-c(I(η)-I(ζ)).
f(S(z))g(I(z-cτ))dz-c(I(η)-I(ζ)).
(15)
因此
所以
因为I(z)在R上有界, 所以, 由式(5)的第二个方程可得| I′(z)|<+∞且I(+∞)=0.最后, 类似于文献[14], 可得S(+∞)=σ,其中,σ>0.因此, 定理2成立.证毕.
□
2 临界波行波解的存在性
本节考察当c=c*和R0>1时,系统(5)的行波解的存在性.为了证明当c=c*时的行波解的存在性,取一列严格递减序列{ck}使得limk→+∞ck=c*.不失一般性,假设ck ∈[ c*,c*+1]且(Sk, Ik)是式(5)的行波解.
引理5 {Ik}在R上一致有界.
证明 反证法.假设不成立,则存在一个序列{zk}使得当k→+∞时,有Ik(zk)→+∞.由引理2可得, Sk(zk)→0.又因为对每一个k, 均有Ik(±∞)=0和Ik(z)有界.因此, 假设Ik(zk)=maxRIk(z).则I′k(zk)=0.因此
0=ckI′k(zk)=
f(Sk(zk))g(Ik(zk-cτ))-γIk(zk).
这与足够大的k矛盾, 故{Ik}是一致有界的.证毕.
□
定理3 假设R0>1和c=c*.则方程(5)存在行波解(S*(z),I*(z))满足0<S*(z)<S-∞, I*(z)>0, S*(-∞)=S-∞和I*(±∞)=0, 其中σ≥0.
证明 因为c*<ck<c*+1, 所以0<Sk(z)<S-∞和0<Ik(z)<+∞.并且,Sk(-∞)=S-∞, Ik(±∞)=0和Sk(+∞)=σ<S-∞.又因为(Sk,Ik)满足
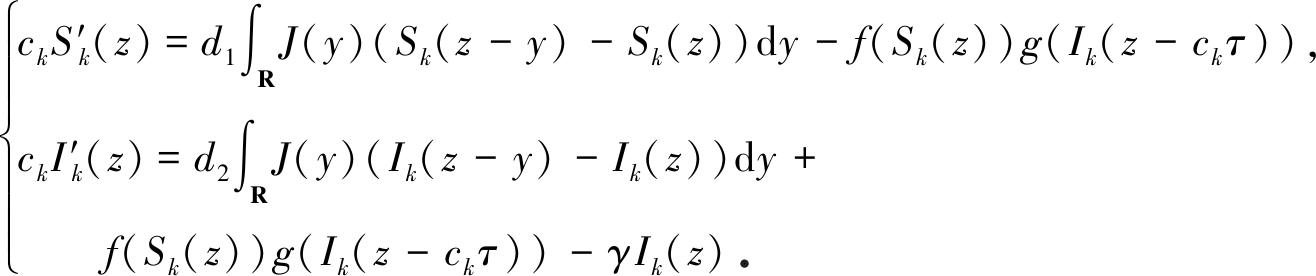
(16)
对式(16)的第二个方程在R上积分, 可得
![]() (f(Sk(z))g(Ik(z-ckτ))-γIk(z))dz=0,
(f(Sk(z))g(Ik(z-ckτ))-γIk(z))dz=0,
则
因为| I′k/Ik|≤K和条件(H1), 因此
又因为Ik是一致有界的, 所以存在一个常数M使得Ik(z-cτ)<M.所以
由条件(H1)可得f(x)是单调递增且f(S-∞)g′(0)>γ, 则存在zk满足f(Sk(zk))=γeckKτ(1/g′(M)).经过平移, 可得f(Sk(0))=γeckKτ(1/g′(M)).又因为0<Sk<S-∞且{Ik} 是一致有界的, 所以{I′k}有界.因此, 根据Arzela-Ascoli定理, 当k→+∞时, 有Sk→S*和Ik→I*在![]() 上成立且满足
上成立且满足
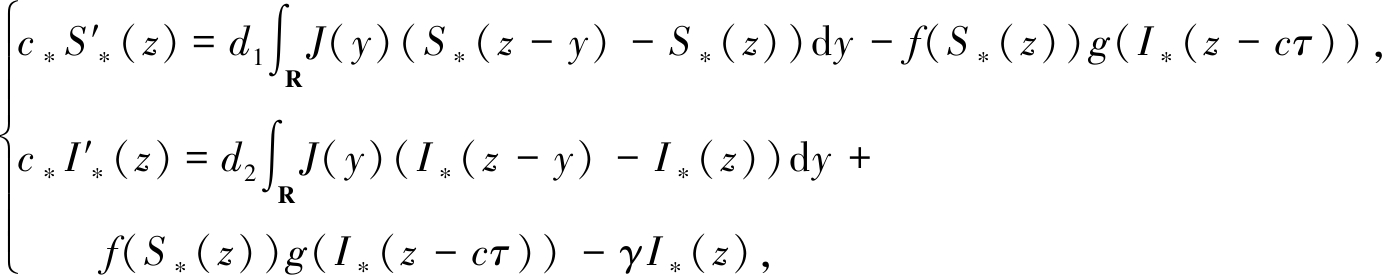
(17)
以及
类似于c >c*,可得I*(±∞)=0.
首先, 证明S* >0.反证法, 假设存在常数y0∈R使得S*(y0)=0成立,则S′*(y0)=0.因此,式(17)的第一个方程为![]() 所以,S*≡0且f(S*)≡0.这与f(Sk(0))矛盾.因此,S*>0.
所以,S*≡0且f(S*)≡0.这与f(Sk(0))矛盾.因此,S*>0.
其次, 证明I*>0.反证法, 假设存在y ∈R使得I*(y)=0成立.类似于S*(z)>0的证明, 可得I*≡0.则式(17)的第一个方程为
(18)
记
H(v)![]()
![]()
因为
因此,H(v)=0有两个实根0和v0.由式(18)、文献[19]中性质3.6和S*(z)在R上有界,可得S*(z)≡C, 其中C∈[0,S-∞].因为f(S*(0))=γec*Kτ(1/g′(M)),因此f(C) ≡γec*Kτ(1/g′(M)).再者, 因为f(S-∞)g′(M) >γec*Kτ>γ,所以, 选择ρk<0使得
成立.
接下来, 证明存在一个正常数T0使得ρk≥-T0.反证法,当k→+∞时, 有ρk→+∞.定义两个函数;
则对每一个k∈N, 有(Uk(z),Vk(z))满足
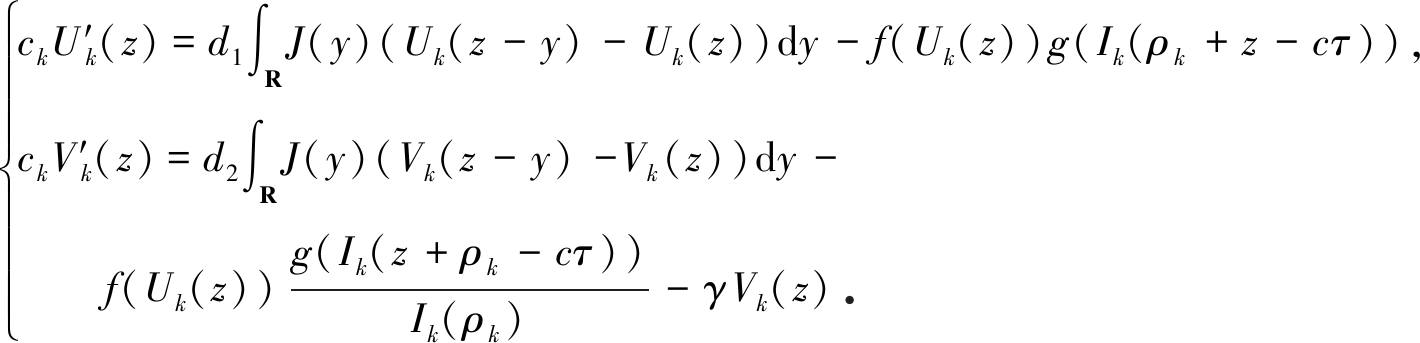
(19)
因为
∀t1∈[0,Ik(z+ρk-cτ)],
则式(19)的第二个方程为
又因为
则Vk(z)在R上局部一致有界.又因为对所有的k∈N,均有Uk(z)<S-∞.因此,当k→+∞时, 有Uk(z)→U+∞(z)和Vk(z)→V+∞(z),其中![]() 因为limk→+∞Ik(ρk)=0, 所以(U+∞(z),V+∞(z))满足
因为limk→+∞Ik(ρk)=0, 所以(U+∞(z),V+∞(z))满足
(20)
f(U+∞(z))g′(0)V+∞(z-cτ)-γV+∞(z).
(21)
类似地, 由文献[19]中性质3.6、式(19)和U+∞(z)有界, 可得U+∞(z) ≡C1成立, 其中C1是任意常数.因为
所以
将f(U+∞(z))代入到方程(21),整理得
令
Q(χ)![]()
![]()
因为Sk(-∞)=S-∞和引理4, 因此, 由式(5)的第二个方程可得
ψk![]()
![]()
存在且是方程
的一个特征根{ψ±},则当k→+∞时, ψ±→ψ*且满足
(22)
因此
γ-(f(S-∞)g′(0)e-ψ*c*τ-γ)≤
f(S-∞)g′(0)e-ψ*c*τ-f(S-∞)g′(0)e-ψ*c*τ=0.
所以Q(χ)=0有两个根χ1, χ2,且0<χ1<χ2.类似地, 再由文献[19]中性质3.6和式(21),可得
V+∞(z)=T3eχ1+T4eχ2,
(23)
其中Tj(j=3,4)是常数.
另一方面, 当k→+∞时,有
则V+∞(z)=eψ*z .因为χ1<ψ*<χ2,这与式(22)矛盾.所以, 存在一个T0>0使得ρk≥-T0成立.因此
![]() ⟹
⟹
这与f(Sk(z)) ≡ec*Kτγ(1/g′(M))矛盾.因此, 可得I*(ξ)>0.
接下来,可证S*(z)<S-∞在R上成立.假设存在实数![]() 使得S*(
使得S*(![]() )=S-∞.从而,S′*(
)=S-∞.从而,S′*(![]() )=0且S*(
)=0且S*(![]() )满足
)满足
0=c*S′*(![]()
![]()
![]() -y)-S*(
-y)-S*(![]() ))dy-f(S*(
))dy-f(S*(![]() ))g(I*(
))g(I*(![]() -cτ))≤
-cτ))≤
-f(S*(![]() ))g(I*(
))g(I*(![]() -cτ)).
-cτ)).
这与I*>0矛盾.
最后, 证明S*(-∞)=S-∞.尽管证明的思想与文献[17]中给定的相似, 但为了文章的完整性还是给出详细的证明.设![]() =lim infx→-∞S*(x)=S-∞.反证法,假设
=lim infx→-∞S*(x)=S-∞.反证法,假设![]() <S-∞, 则存在点列{ηn
<S-∞, 则存在点列{ηn![]() 使得limn→+∞ηn=-∞和limn→+∞S*(ηn)=
使得limn→+∞ηn=-∞和limn→+∞S*(ηn)=![]() 成立.定义函数:
成立.定义函数:
φn(x)![]() S*(x+θn), ψn(x)
S*(x+θn), ψn(x)![]() I*(x+θn), x ∈R.
I*(x+θn), x ∈R.
因此, 当n→+∞ 时, ψn(x)→0.提取子序列(仍然用{θn}表示), 当n→+∞ 时, limn→+∞θn=-∞且φn→φ+∞, 其中![]() 因此φ+∞满足
因此φ+∞满足
所以,φ+∞≡![]() .因此
.因此
![]()
![]() .
.
(24)
又因为(ck,Sk,Ik)是系统(16)的行波解, 所以
(25)
对式(19)的第一个方程从-∞到θn积分, 可得
![]() f(Sk(z))g(Ik(z-cτ))dz,
f(Sk(z))g(Ik(z-cτ))dz,
其中n∈N.又因为Sk(-∞)=S-∞且J(x)=J(-x),可得
因此, 对k取极限, 有
![]() f(S*(z))g(I*(z-cτ))dz.
f(S*(z))g(I*(z-cτ))dz.
因为S*,I* 均有界且![]() 则对n取极限, 有
则对n取极限, 有
0>c*[![]() -S-∞]≥0.
-S-∞]≥0.
因此, S*(-∞)=S-∞.证毕.
□
3 应 用 实 例
这一节主要通过具体的生物模型进一步验证临界波的存在性.
在系统(5)中,令f(S)=S,g(I)=βI/(1+αI),则
那么, 系统(5)就变为如下具有非线性发生率的时滞反应扩散方程:
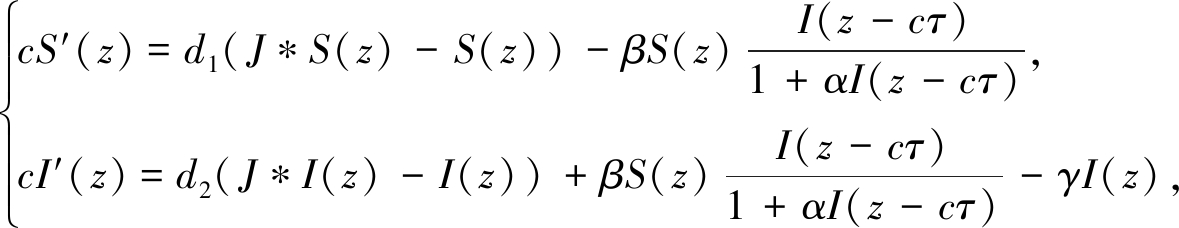
(26)
其中β>0表示感染率, γ表示恢复率,对于系统(26), 条件(H1)和(H2)显然成立.边界条件:(S(-∞),I(-∞))=(S-∞,0)是初始无病平衡点,(S(+∞),I(+∞))=(S+∞,0)是某一个无病平衡点, 且S(+∞)为任意实数.显然,系统(26)是在文献[20]的基础上考虑到霍乱具有潜伏期且易感者与感染者的活动可能是非局部的因素下建立的模型.
对系统(26)的第二个方程在初始无病平衡点线性化, 则特征方程为
cλ=d2![]() J(y)e-λydy-d2+βS-∞e-λcτ-γ.
J(y)e-λydy-d2+βS-∞e-λcτ-γ.
显然, 给定βS-∞>γ,则系统(26)的最小传播速度为
c*![]()
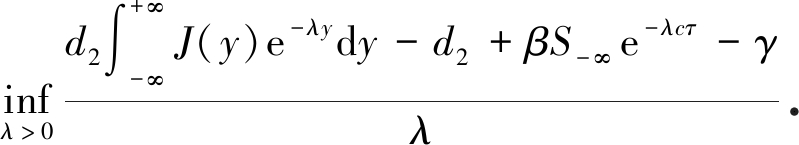
因为g′(I)=β/(1+αI)2,所以g′(I)>0且g′(0)=β.又S(z)≤S-∞, 因此f(S(z))≤ S-∞,则由系统的(26)的第二个方程可得
所以引理1成立.由此可知引理2、引理3和引理4都成立, 则I(z)是有界的, 所以定理1成立.因此, 类似于文献[14]的方法, 易得当波速c>c*时, 系统(26)存在满足边界条件的行波解, 所以定理2成立.
任意选取一列严格递减序列{ck}使得limk→+∞ck=c*.由于当波速c>c*时, 系统(26)存在满足边界条件的行波解.不失一般性, 假设ck ∈[ c*,c*+1]且(Sk, Ik)是系统(26)的行波解.则(Sk, Ik)满足下面的模型:
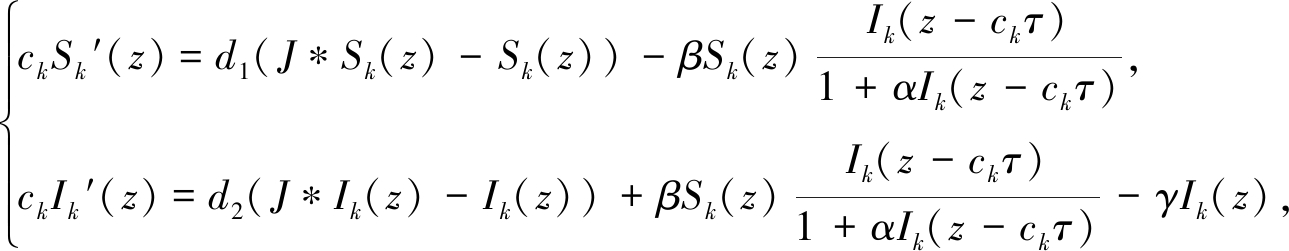
(27)
其中
(Sk(-∞),Ik(-∞))=(S-∞,0), (Sk,Ik)(+∞)=(S+∞,0).
又因为引理2和定理1成立, 所以对每一个k, 都有Ik有界且Ik(±∞)=0,则证得引理5成立, 因而{Ik}是一致有界的, 即总可以找到一个M>0使得Ik≤M.又因为Ik有界, 则由系统(27)的第二个方程可得, |I′k/Ik|有界, 则存在一个常数K>0使得|I′k/Ik|≤K.
因此由理论结果可知, 当R0>(1+αM)2ec*K τ且c=c*时, 系统(26)存在满足边界条件的行波解, 即定理3对于模型(26)依然成立.
4 总 结
本文研究了一类具有非线性发生率与时滞的非局部扩散SIR模型的临界波的存在性, 文献[14-15]中没有讨论当c=c*时, 系统(5)的行波解是否存在.受到文献[17-18]的启发,本文证明了系统(5)在R0>g′(0)ec*Kτ/g′(M)和c=c*时,存在行波解.而对于1<R0≤g′(0)ec*Kτ/g′(M)和c=c*,同样认为其是临界波存在的条件, 这将是笔者下一步需要研究的问题.
[1] VAN DEN DRIESSCHE P, WATMOUGH J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J]. Mathematical Biosciences, 2002, 180(1/2): 29-48.
[2] YANG F Y, LI Y, LI W T, et al. Traveling waves in a nonlocal dispersal Kermack-McKendrick epidemic model[J]. Discrete and Continuous Dynamical Systems(Series B), 2013, 18(7): 1969-1993.
[3] WANG H Y. Spreading speeds and traveling waves for non-cooperative reaction-diffusion systems[J]. Journal of Nonlinear Science, 2011, 21(5): 747-783.
[4] WANG H Y, WANG X S. Traveling wave phenomena in a Kermack-Mckendrick SIR model[J]. Journal of Dynamics & Differential Equations, 2016, 28(1): 143-166.
[5] WANG J B, LI W T, YANG F Y. Traveling waves in a nonlocal dispersal SIR model with nonlocal delayed transmission[J]. Communications in Nonlinear Science & Numerical Simulations, 2015, 27(1/3): 136-152.
[6] FU S C, GUO J S, WU C C. Traveling wave solutions for a discrete diffusive epidemic model[J]. Journal of Nonlinear and Convex Analysis, 2016, 17(9): 1739-1751.
[7] ZHANG T R, WANG W D, WANG K F. Minimal wave speed for a class of non-cooperative diffusion-reaction system[J]. Journal of Differential Equations, 2016, 260(3): 2763-2791.
[8] WANG X S, WANG H Y, WU J H. Traveling waves of diffusive predator-prey systems: disease outbreak propagation[J]. Discrete & Continuous Dynamical Systems, 2017, 32(9): 3303-3324.
[9] LI Y, LI W T, YANG F Y. Traveling waves for a nonlocal dispersal SIR model with delay and external supplies[J]. Applied Mathematics and Computation, 2014, 247: 723-740.
[10] LI Y, LI W T, LIN G. Traveling waves of a delayed diffusive SIR epidemic model[J]. Communications on Pure & Applied Analysis, 2015, 14(3): 1001-1022.
[11] WANG Z C, WU J H. Travelling waves of a diffusive Kermack-McKendrick epidemic model with non-local delayed transmission[J]. Proceedings Mathematical Physical & Engineering Sciences, 2010, 466(2113): 237-261.
[12] LI W T, YANG F Y, MA C, et al. Traveling wave solutions of a nonlocal delayed SIR model without outbreak threshold[J]. Discrete and Continuous Dynamical Systems(Series B), 2014, 19(2): 467-484.
[13] BAI Z G, WU S L. Traveling waves in a delayed SIR epidemic model with nonlinear incidence[J]. Applied Mathematics and Computation, 2015, 263: 221-232.
[14] 邹霞, 吴事良. 一类具有非线性发生率与时滞的非局部扩散SIR模型的行波解[J]. 数学物理学报, 2018, 38(3): 496-513.(ZOU Xia, WU Shiliang. Traveling waves in a nonlocal dispersal SIR epidemic model with delay and nonlinear incidence[J]. Acta Mathematica Scientia, 2018, 38(3): 496-513.(in Chinese))
[15] ZHANG S P, YANG Y R, ZHOU Y H. Traveling waves in a delayed SIR model with nonlocal dispersal and nonlinear incidence[J]. Journal of Mathematical Physics, 2018, 59(1): 011513. DOI: 10.1063/1.5021761.
[16] CHEN Y Y, GUO J S, HAMEL F. Traveling waves for a lattice dynamical system arising in a diffusive endemic model[J]. Nonlinearity, 2016, 30(6). DOI: 10.1088/1361-6544/aa6b0a.
[17] YANG F Y, LI W T. Traveling waves in a nonlocal dispersal SIR model with critical wave speed[J]. Journal of Mathematical Analysis & Applications, 2017, 458(2): 1131-1146.
[18] WU C C. Existence of traveling waves with the critical speed for a discrete diffusive epidemic model[J]. Journal of Differential Equations, 2017, 262(1): 272-282.
[19] ZHANG G B, LI W T, WANG Z C. Spreading speeds and traveling waves for nonlocal dispersal equations with degenerate monostable nonlinearity[J]. Journal of Differential Equations, 2012, 252(9): 5096-5124.
[20] CAPASSO V, SERIO G. A generalization of the Kermack-McKendrick deterministic epidemic model[J]. Mathematical Biosciences, 1978, 42(1/2): 43-61.