引 言
自艾滋病出现以来,其高感染率和死亡率严重威胁着人类的健康,抗HIV药物和疫苗一直在研究当中[1].现阶段,AIDS虽不能完全被治愈,但已成为一个可控的传染病.已有大量文献用数学模型来描述对HIV携带者进行药物治疗或免疫治疗的治疗过程,并进行相应的评价分析[2-15].其中,文献[3-6]均假设药物连续输入,而文献[7-15]则考虑在固定时刻周期性地定量输入药物或免疫因子的情形.通常使用的因子有白细胞介素-2(IL-2)、白细胞介素-7等.其中,IL-2具有促进CD4+T细胞增殖的功能[14-18].基于IL-2的免疫机制,文献[2]建立具有免疫治疗的HIV感染模型:

(1)
其中,T(t)和V(t)分别表示t时刻血浆中单位体积内未被感染的CD4+T细胞和游离的HIV数量,s1表示胸腺等细胞产生CD4+T细胞的速率,μ表示CD4+T细胞的死亡率,k表示CD4+T细胞被HIV感染的速率,c表示HIV的损失率,r(t)是IL-2治疗函数.s2V(t)/(b1+V(t))和gV(t)/(b2+V(t))分别表示HIV对CD4+T细胞增殖的抑制作用和HIV的输入速率,其中,s2表示HIV对CD4+T细胞增殖的最大抑制速率,g表示HIV的最大输入速率,b1和b2表示HIV的半饱和常数,参数均为正常数.
对于模型(1),IL-2的连续输入引起CD4+T细胞的增长率(即r(t)T(t))呈连续性变化.但在临床治疗中,通常所采用的药物输入是间歇性的,其所对应的模型应为脉冲动力系统[7-14,19].同时,模型(1)中并未考虑病毒的自然清除这一客观事实,而文献[3-13]中对其都有刻画和考虑.因此,本文将基于模型(1),既考虑HIV的自然死亡率,又考虑药物治疗按固定时刻定量输入的方式实施,即采用周期性定量注射IL-2的方式以促进体内CD4+T细胞的增加.如此,所得模型为
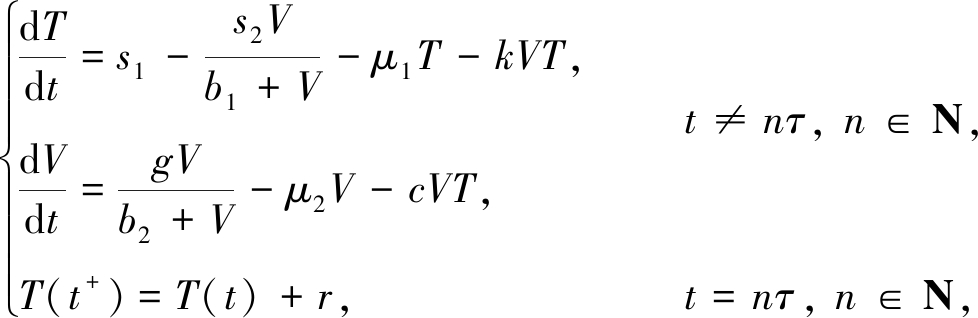
(2)
其中,正数r表示注射一定量的IL-2后体内每次所增加的CD4+T细胞数量,μ1和μ2分别表示CD4+T细胞和HIV的自然死亡率.在HIV感染过程中,文献[20]研究了胸腺等细胞产生CD4+T细胞的速率s1始终大于HIV对CD4+T细胞的最大抑制速率s2的情形.于是,本文假设s1>s2.
本文结构如下: 首先,作为预备知识,介绍了脉冲微分系统和线性齐次周期系数系统等基本理论; 其次,使用Floquet乘子理论和微分方程的比较定理,讨论了系统(2)解的非负性和一致有界性,并给出了无感染周期解局部和全局渐近稳定的阈值条件以及病毒一致持续的充分条件; 最后,通过数值模拟,比较了3种不同治疗方案的治疗效果,验证了脉冲免疫治疗的有效性.
1 预 备 知 识
引理1[12] 脉冲微分系统
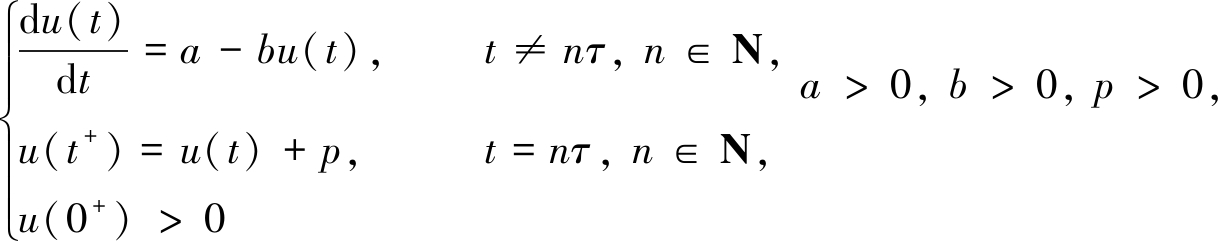
存在唯一全局渐近稳定的正周期解
对于线性齐次周期系数系统
x′=A(t)x, t∈R, x∈Rn,
(3)
其中,A(t)在R上连续并且是以w(w>0)为周期的n×n矩阵函数,即A(t)=A(w+t).
若X(t)是系统(3)的一个基解矩阵,则X(t+w)也是系统(3)的基解矩阵.
定义1[21] 称满足X(t+w)=X(t)M(t∈R)的矩阵M为系统(3)关于X(t)的单值矩阵,其特征根σi(i=1,2,…,n)称为系统(3)的Floquet乘子.
引理2[22] 系统(3)的零解是
1) 稳定的,当且仅当系统(3)的一切Floquet乘子的模都不大于1,并且每个模等于1的Floquet乘子都对应矩阵M的Jordan标准形中的一阶Jordan块;
2) 渐近稳定的,当且仅当系统(3)的一切Floquet乘子的模都小于1.
为了后续讨论HIV病毒的持续性,引入如下定义及引理.
设X是一个以d为度量的局部紧度量空间,F是X的一个闭子集.∂F和int F分别表示集合F的边界和内部.设π是集合F上的一个半动力系统[21].
定义2[23] 如果存在ξ>0,对所有的u∈F\Σ,有limt→+∞d(π(u,t),Σ)>ξ,则称集合F的子集Σ为一致斥子.
对于一个局部紧度量空间的一个闭子集F上所定义的半流,如果F的边界是排斥的,那么半流是一致持续的.由文献[23]引入如下引理.
引理3[23] 设Σ是X的一个紧子集,使得X\Σ是正不变集.Σ为一致斥子的充要条件是存在Σ的一个邻域U和一个连续函数P:X→R+满足
1) P(u)=0当且仅当u∈Σ;
2) 对所有的u∈U\Σ,存在Tu>0使得P(π(u,Tu))>P(u).
2 解的非负性与有界性
定理1 设T(t),V(t)是模型(2)满足初值条件T(0+)≥0,V(0+)≥0的任一解,则对所有t≥0有T(t)≥0,V(t)≥0.
证明 首先考虑模型(2)无脉冲时解的非负性.
先证V(t)的非负性.显然,V(t)=0是模型(2)前两个方程的一个解.由解的存在唯一性得,对所有非负初值V(0+),当t≥0时有V(t)≥0.
再证T(t)的非负性.设当T(0+)≥0时,对所有的t≥0有T(t)≥0.否则存在t1>0,使得T(t1)=0,T′(t1)≤0并且对于t∈[0,t1),有T(t)>0.另外, 在t=t1时刻, 由模型(2)的第一个方程得T′(t1)>0.显然矛盾,故假设不成立.即, 当T(0+)≥0时, 对所有的t≥0有T(t)≥0.
综上可知,模型(2)无脉冲时的解是非负的.
因模型(2)中输入量r>0,而无脉冲时模型(2)的解是非负的.在此基础上,进一步保证了T(t)和V(t)的非负性.证毕.
另外,由模型(2)的第二个方程知
于是,当g≤μ2b2时有limt→+∞V(t)=0.进一步,根据极限系统理论和引理1易知模型(2)存在唯一全局渐近稳定的无感染周期解.因此,下面仅讨论g>μ2b2时模型(2)解的动力学行为.
定理2 模型(2)的解是一致有界的.
证明 由模型(2)的第一个方程得
考虑脉冲微分系统
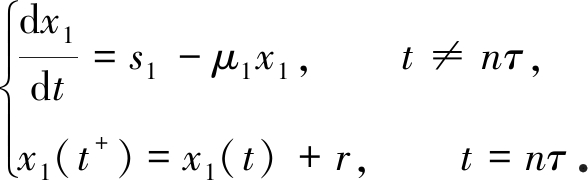
(4)
由引理1知,系统(4)存在唯一全局渐近稳定的正周期解
由脉冲微分方程比较定理,得T(t)≤x1(t).并且存在充分小的ε(>0),当t充分大时,有
成立.
由定理1知T(t)≥0,于是由模型(2)的第二个方程得
有
因此,对于上述ε,当t充分大时,有
令W(t)=T(t)+V(t),则W(t)沿着模型(2)解的全导数满足
记
K=s1+g, δ=min{μ1,μ2}.
于是,由上式及模型(2)的脉冲条件可得如下系统:
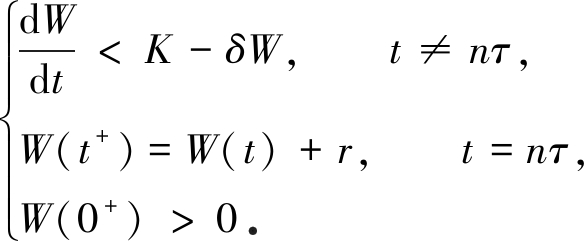
考虑脉冲微分系统

(5)
由引理1知,系统(5)存在唯一全局渐近稳定的正周期解
由脉冲微分方程比较定理,得W(t)<x2(t).并且对于上述ε,当t充分大时,有
成立.因此,模型(2)的解是一致有界的.证毕.
由于ε是任意小的正数,所以当g>μ2b2时,
Ω={(T,V):T≤Tm,V≤Vm,T+V≤Wm}
是模型(2)的一个正不变集.
3 无感染周期解的稳定性
下面考虑模型(2)无感染周期解的存在性.当V(t)≡0时,模型(2)可写为系统(4)的形式.由引理1知,模型(2)总存在唯一的无感染周期解(T*(t),0),其中
记
定理3 当R0<1时,模型(2)的无感染周期解(T*(t),0)是局部渐近稳定的.
证明 令x(t)=T(t)-T*(t),y(t)=V(t),则模型(2)在无感染周期解处的线性化系统为
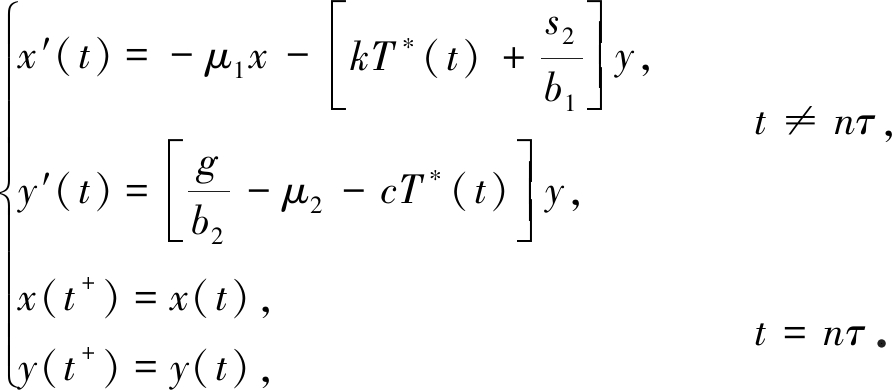
(6)
由系统(6)的后两个方程知x(t)和y(t)均不受脉冲的影响,故考虑如下系统:

(7)
因T*(t)是以τ为周期的周期函数,故系统(7)是一个线性齐次周期系数系统.系统(7)的一个基解矩阵是
其中
显然,Φ(0)是单位矩阵.经验证,Φ(t+τ)也是系统(7)的基解矩阵.于是,相应于Φ(t)的单值矩阵为
显然,M的Floquet乘子为λ1=e-μ1τ<1,λ2=φ22(τ).当R0<1时,有|λ2 |<1.由引理2知,系统(7)的零解是局部渐近稳定的.因此当R0<1时,模型(2)的无感染周期解(T*(t),0)是局部渐近稳定的.证毕.
定理4 当R1<1时,无感染周期解(T*(t),0)是全局渐近稳定的,其中
证明 令
因
故R(x)是[0,+∞)上的增函数,并且R(0)=R0,R(Vm)=R1.由于g>b2μ2,所以Vm>0.由R(x)的单调性可得R(0)<R(Vm),即R0<R1.因此当R1<1时,必有R0<1成立.
因R(Vm)<1,故存在充分小的ε>0使得R(Vm+ε)<1,并且
由模型(2)的第二个方程得
有
对上述ε,存在T1>0,使得当t>T1时,有V(t)<Vm+ε,进而有
当nτ>T1时,考虑
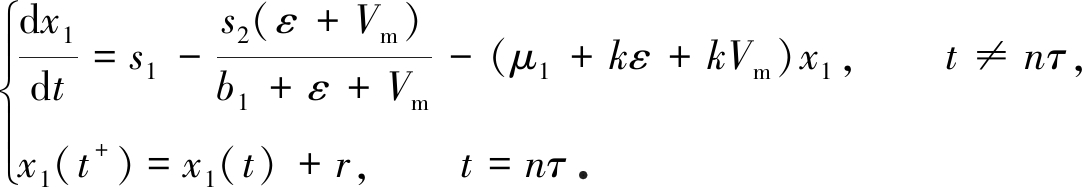
由引理1知,上述系统存在唯一的正周期解
nτ<t≤(n+1)τ,
它是全局渐近稳定的.由脉冲微分方程比较定理得T(t)≥x1(t).并且对于上述ε存在T2>T1,使得当t>T2时,![]() 成立.
成立.
由模型(2)的第二个方程得
当t≥nτ>T2时,有
当R(Vm+ε)<1时,即
对上述ε,因δ<0,所以不等式
成立.于是,
故limt→∞V(t)≤0.结合V(t)的非负性,有limt→∞V(t)=0.因此,由极限系统理论知,脉冲微分系统

有极限系统

由引理1知,上述系统存在全局渐近稳定的正周期解T*(t).于是,当R(Vm+ε)<1时,无感染周期解(T*(t),0)是全局吸引的.由于limε→0 R(Vm+ε)=R1,故当R1<1时,无感染周期解(T*(t),0)是全局吸引的.因R0<R1,故当R1<1时,无感染周期解(T*(t),0)是渐近稳定的.因此,当R1<1时,无感染周期解(T*(t),0)是全局渐近稳定的.证毕.
4 病毒的一致持续性
由于集合Ω是模型(2)的一个正不变集,故对任意的u0=(T0,V0)∈Ω,模型(2)都有定义在R+上,且满足π(u0,0)=u0的唯一解π(u0,t)=(T,V)(t;u0),所以对于t∈R+有π(u0,t)∈Ω且π是Ω内的半动力系统.
下证当R0>1时,Σ={(T,V)∈Ω:V=0}是模型(2)的一个一致斥子,即半动力系统π是一致持续的.
定理5 当R0>1时,病毒V(t)是一致持续的.
证明 由于V=0即Σ是模型(2)的一个不变集,故Ω\Σ也是模型(2)的一个正不变集,并且集合Σ是Ω的一个紧子集.定义P:Ω→ R+为P(T,V)=V,记U={(T,V)∈Ω:P(T,V)<ρ},其中ρ>0充分小,满足
假设存在![]() 使得对每一个t>0都有
使得对每一个t>0都有![]() <ρ,即当t>0时,
<ρ,即当t>0时,![]() 成立.由模型(2)的第一个方程得
成立.由模型(2)的第一个方程得
考虑脉冲微分系统
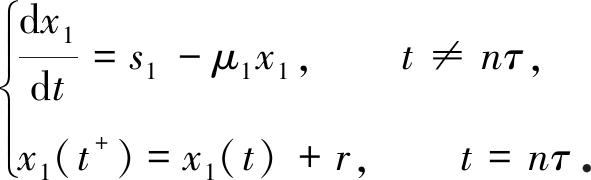
由引理1知,上述系统存在全局渐近稳定的正周期解
由比较定理得T(t)≤x1(t). 对于上述ρ存在t1>0,使得当t>t1时,T(t)<T*(t)+ρ成立.
定义辅助函数L(t)=V(t),则L(t)沿着![]() 的导数为
的导数为
对于V(t)<ρ和t>T1有
因
成立,即
所以limt→∞L(t)=∞.由定理2知,V(t)在Ω上是有界的.因此,上述假设不成立.
于是,对每一个u∈Ω\ Σ且u属于Σ的某个适当的邻域时,都存在一个Tu使得P(π(u,Tu))>P(u).因此,由引理3知,当R0>1时,Σ={(T,V)∈Ω:V=0}是模型(2)的一个一致斥子,故病毒是一致持续的.证毕.
5 数值模拟与讨论
下面借助文献[2,15,20]中的部分参数值和初始值对模型进行一系列数值模拟.显然,g>b2μ2成立.
s1=2 mm3·d-1, s2=1.5 mm3·d-1, c=0.01 mm3·d-1, k=2.5×10-4 mm3·d-1,
g=30 d-1, b1=14 mm3, b2=1 mm3, μ1=0.01 d-1, μ2=3.1 d-1,
T0=1 000 mm-3, V0=1 000 mL-1.
本文已得到如下结论: 当基本再生数R0<1时无感染周期解是局部渐近稳定的,当R1<1时无感染周期解是全局渐近稳定的以及当R0>1时病毒是一致持续的.因为R0<R1,所以当R0<R1<1时病毒被根除,当1<R0<R1时病毒持续存在.对于R0<1<R1的情形,由上述结论可知无感染周期解是局部渐近稳定的但不是全局渐近稳定的.下面通过数值模拟验证上述结论,并分析R0<1<R1情形下无感染周期解的稳定性.
考虑1<R0<R1,R0<1<R1和R0<R1<1这3种情形下,模型(2)中各变量随时间的变化情况.选取药物输入量r=100,服药间隔τ=3,4,5分别进行数值模拟,相应的动力学行为如图1所示.图1表明: 当τ=3时,基本再生数R0=0.761<R1=0.942<1,此时病毒是绝灭的; 当τ=5时,有1<R0=1.223<R1=1.528,此时病毒是持续存在的.显然,上述结论是正确的.对于τ=4,R0<1<R1的情形,数值模拟发现病毒是被根除的,具体理论研究将后续进行.因此,在理论上当R0<R1<1或R0<1<R1时病毒绝灭,当1<R0<R1时病毒持续存在.
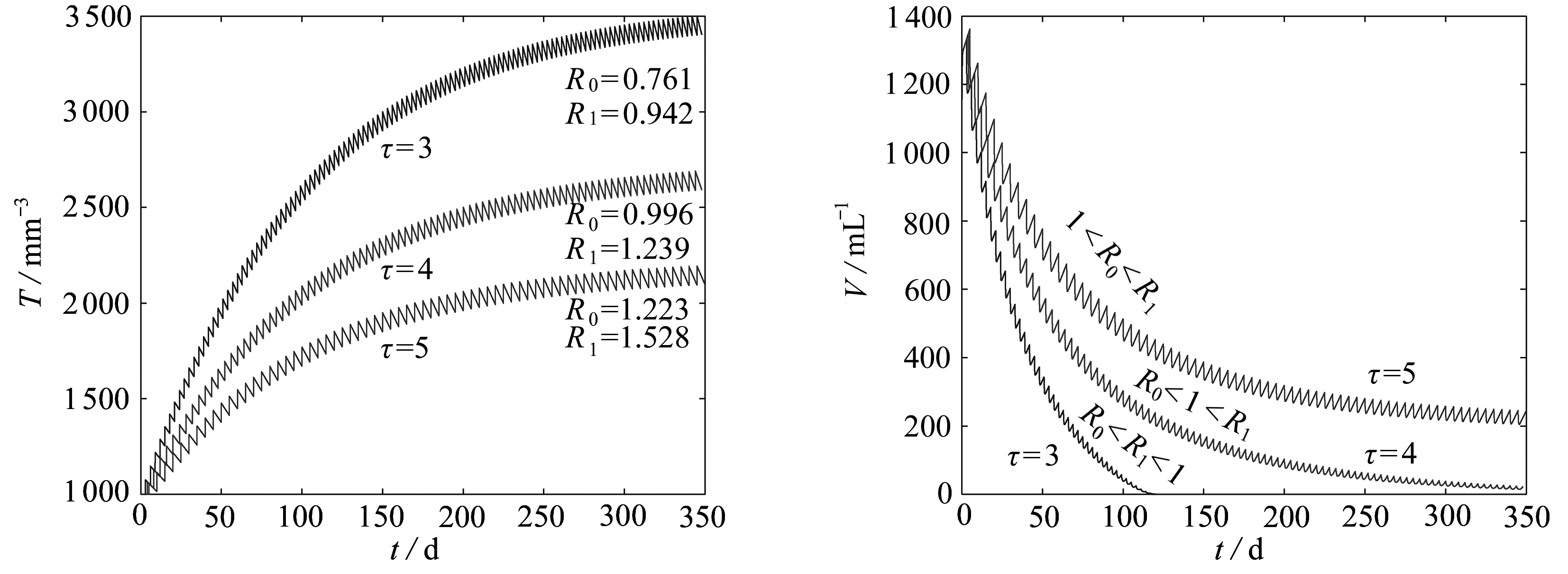
图1 当1<R0<R1,R0<1<R1,R0<R1<1时,模型(2)的动力学行为
Fig. 1 The dynamics of model (2) for 1<R0<R1,R0<1<R1,R0<R1<1
接下来将比较3种不同治疗方案的效果,分别为: 1) 不治疗(即r=0); 2) 服药间隔τ固定,药物输入量r变化; 3) 药物输入量r固定,服药间隔τ变化.
首先,考虑不治疗即r=0时,病人体内CD4+T细胞计数和HIV病毒载量的变化情况.此时,模型(2)是一个常微分方程,基本再生数R0=13.45,表示一个病毒在其生命周期内平均感染13.45个CD4+T细胞.另外,图2刻画了在不治疗情形下,CD4+T细胞计数随时间延长呈递减趋势, HIV病毒载量随时间延长而增加.显然,不治疗时病毒是持续存在的.

图2 无治疗时,模型(2)的动力学行为
Fig. 2 The dynamics of model (2) without therapy
其次,分析服药间隔τ=5,药物输入量r=50和r=60时的脉冲免疫治疗情形.基于上述参数值和初始值,图3分别用深色实线和浅色实线刻画了r=50和r=60时模型(2)的动力学行为.易见,r=50和r=60的基本再生数分别为R0=2.24和R0=1.92.注意到,周期环境和自治传染病模型中所定义的基本再生数的生物意义是不同的.文献[24]将周期环境基本再生数的生物意义解释为“渐近的每代增长率”,在本文中,R0表示每代病毒的增殖速率.也就是说,当r=50时,每代病毒以2.24的速率增殖;r=60时,每代病毒以1.92的速率增殖.显然,药物输入量r越大,病毒的增殖率相对较小,体现了药物对病毒强的抑制作用.另外,因R0>1,由定理5知病毒是持续存在的,与数值模拟的结果是一致的.同时,也说明了r=50和r=60时的药物输入量不够大,不足以将病毒彻底根除,只能将病毒控制到一定水平.
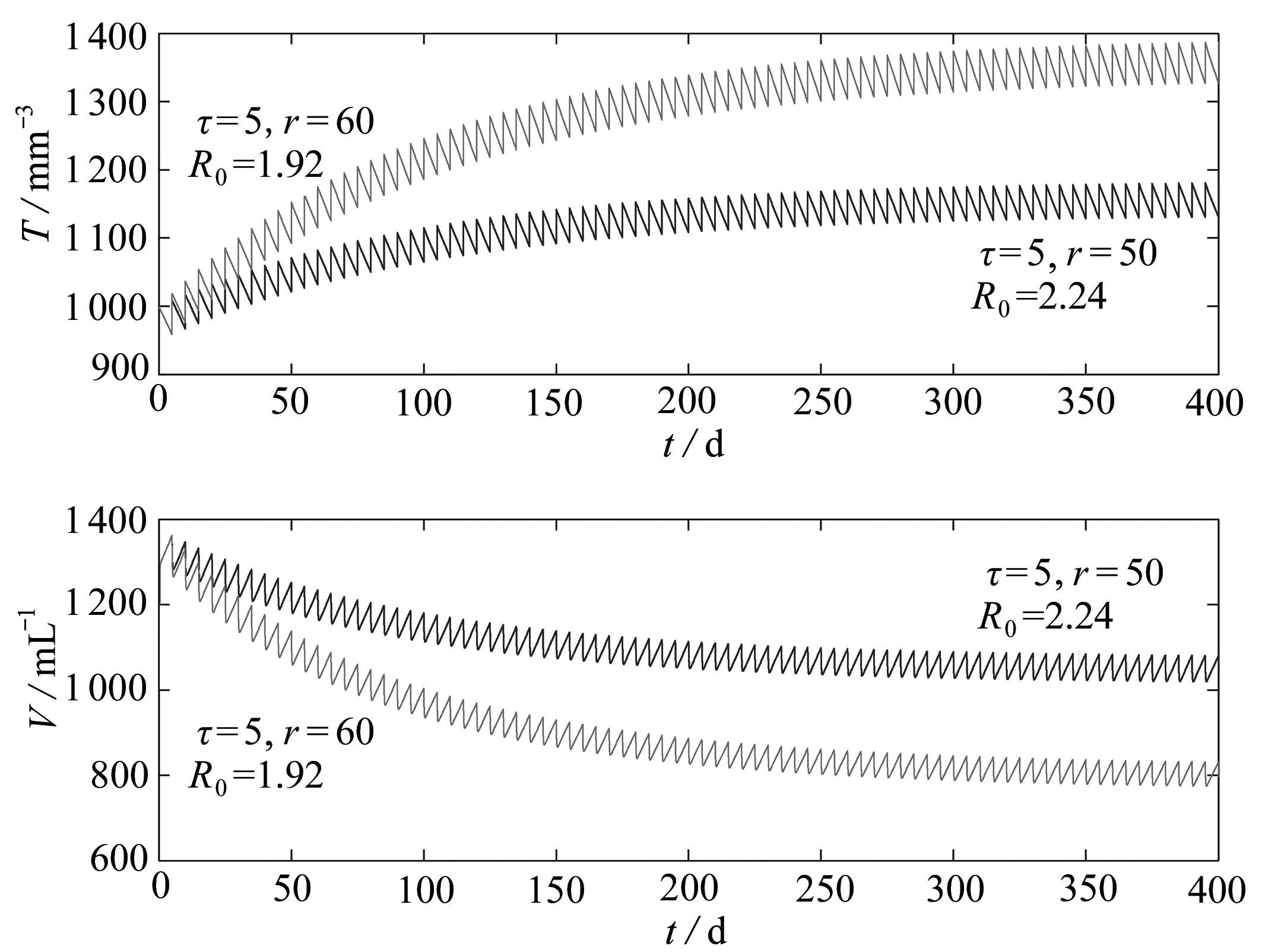
图3 服药间隔τ=5时,模型(2)的动力学行为
Fig. 3 The dynamics of model (2) for dosing interval τ=5

图4 药物输入量r=50时,模型(2)的动力学行为
Fig. 4 The dynamics of model (2) for drug input r=50
最后,讨论药物输入量r=50,服药间隔τ变化的情形.图4用深色实线和浅色实线刻画了τ=5和τ=10时CD4+T细胞和病毒随时间的变化情况.显然病毒和CD4+T细胞的数量随时间延长分别呈递减和递增趋势,最终均维持在某一固定水平.此时,因R0>1,故病毒是持续存在的.对于τ=10 时的脉冲免疫治疗来说,R0=3.84表明每代病毒以3.84的速率增殖.与τ=5相比,服药间隔扩大了两倍后病毒的增殖速率约扩大了1.7倍,体现了服药间隔越长越有利于病毒的生存.因此,当药物输入量固定时,适当短的服药间隔更有利于对病毒的控制.
考虑一种特殊情形,当服药间隔足够短时,系统(2)近似于一种连续治疗模型.数值模拟发现,药物用量固定时,连续治疗的效果优于某一服药间隔下脉冲免疫治疗的效果.但连续服药是不符合常理的,而且药物具有一定的毒副作用,综合考虑连续治疗是不符合实际的,而脉冲免疫治疗更符合实际临床治疗.因此,在治疗HIV过程中,建议采用脉冲疗法.
综上可得,当药物输入量r足够大或服药间隔τ适当短时,从理论上可以有效控制甚至根除病毒,体现了脉冲免疫治疗的有效性.另外,因R0表示“每代病毒的渐近增殖率”,由R0表达式可知: 服药间隔τ越短或药物输入量r越大时,R0越小,即病毒的增殖率越小.这一关系进一步说明了τ适当短或r足够大更有助于病毒载量的控制.同时,与连续治疗相比,脉冲免疫治疗更符合临床HIV的治疗.
6 总 结
通过考虑按固定时刻定量注射IL-2的方式治疗HIV感染,本文建立并分析了一类具有脉冲免疫治疗HIV感染的动力学模型.借助Floquet理论和比较定理等,得到了HIV感染消除的条件,又应用一致斥子理论给出了HIV感染一致持续的相应条件.这些条件对控制HIV的感染具有一定的理论指导作用.同时,通过数值模拟验证了所得的理论结果,并比较了3种不同治疗方案的治疗效果.数值模拟也显示每次注射IL-2的量和用药间隔对治疗效果有着直接的影响.
致谢 本文作者衷心感谢陕西科技大学学术团队项目(2013XSD39)对本文的资助.
[1] AIDS, information on HIV[EB/OL]. [2018-11-29]. https://aidsinfo.nih.gov/clinical-trials.
[2] KIRSCHNER D E, WEBB G F. Immunotherapy of HIV-1 infection[J]. Journal of Biological Systems, 1998, 6(1): 71-83.
[3] PERELSON A S, NELSON P W. Mathematical analysis of HIV-1 dynamics in vivo[J]. Society for Industrial and Applied Mathematics, 1999, 41(1): 3-44.
[4] CALLAWAY D S, PERELSON A S. HIV-1 infection and low steady state viral loads[J]. Bulletin of Mathematical Biology, 2002, 64(1): 29-64.
[5] LEENHEER P D, SMITH H L. Virus dynamics: a global analysis[J]. SIAM Journal on Applied Mathematics, 2003, 63(4): 1313-1327.
[6] HUANG Y X, ROSENKRANZ S L, WU H L. Modeling HIV dynamics and antiviral response with consideration of time-varying drug exposures, adherence and phenotypic sensitivity[J]. Mathematical Biosciences, 2003, 184(2): 165-186.
[7] SMITH R J, WAHL L M. Distinct effects of protease and reverse transcriptase inhibition in an immunological model of HIV-1 infection with impulsive drug effects[J]. Bulletin of Mathematical Biology, 2004, 66(5): 1259-1283.
[8] SMITH R J, WAHL L M. Drug resistance in an immunological model of HIV-1 infection with impulsive drug effects[J]. Bulletin of Mathematical Biology, 2005, 67(4): 783-813.
[9] GAO T, WANG W D, LIU X N. Mathematical analysis of an HIV model with impulsive antiretroviral drug doses[J]. Mathematics and Computers in Simulation, 2012, 82(4): 653-665.
[10] MIRON R E, SMITH R J. Resistance to protease inhibitors in a model of HIV-1 infection with impulsive drug effects[J]. Bulletin of Mathematical Biology, 2014, 76(1): 59-97.
[11] 宋保军, 娄洁, 文清芝. 使用T-20治疗HIV-1患者的不同策略的数学建模与研究[J]. 应用数学和力学, 2011, 32(4): 400-416.(SONG Baojun, LOU Jie, WEN Qingzhi. Modelling two different therapy strategies for drug T-20 on HIV-1 patients[J]. Applied Mathematics and Mechanics, 2011, 32(4): 400-416.(in Chinese))
[12] 韩溢. 具有脉冲免疫因子的HIV模型的稳定性研究[J]. 重庆工商大学学报(自然科学版), 2013, 30(3): 77-82.(HAN Yi. Research on stability for an HIV model with impulsive releasing immune factor[J]. Journal of Chongqing Technology and Business University(Natural Science), 2013, 30(3): 77-82.(in Chinese))
[13] ROY P K, CHATTERJEE A N, LI X Z. The effect of vaccination to dendritic cell and immune cell interaction in HIV disease progression[J]. International Journal of Biomathematics, 2016, 9(1): 1-20.
[14] CHATTERJEE A N, ROY P K. Anti-viral drug treatment along with immune activator IL-2: a control-based mathematical approach for HIV infection[J]. International Journal of Control, 2012, 85(2): 220-237.
[15] JOLY M, ODLOAK D. Modeling interleukin-2-based immunotherapy in AIDS pathogenesis[J]. Journal of Theoretical Biology, 2013, 335(4): 57-78.
[16] ABRAMS D, LEVY Y, LOSSO M H. Interleukin-2 therapy in patients with HIV infection[J]. New England Journal of Medicine, 2009, 361(16): 1548-1559.
[17] BELL C J M, SUN Y L, NOWAK U M, et al. Sustained in vivo signaling by long-lived IL-2 induces prolonged increases of regulatory T cells[J]. Journal of Autoimmunity, 2015, 56: 66-80.
[18] READ S W, LEMPICKI R A, MASCIO M D, et al. CD4 T cell survival after intermittent interleukin-2 therapy is predictive of an increase in the CD4 T cell count of HIV-infected patients[J]. The Journal of Infectious Diseases, 2008, 198(6): 843-850.
[19] 胡晓虎, 唐三一. 血管外给药的非线性房室模型解的逼近[J]. 应用数学和力学, 2014, 35(9): 1033-1045.(HU Xiaohu, TANG Sanyi. Approximate solutions to the nonlinear compartmental model for extravascular administration[J]. Applied Mathematics and Mechanics, 2014, 35(9): 1033-1045.(in Chinese))
[20] KIRSCHNER D E, WEBB G F. A mathematical model of combined drug therapy of HIV infection[J]. Journal of Theoretical Medicine, 2014, 1(1):25-34.
[21] 宋新宇, 郭红建, 师向云. 脉冲微分方程理论及其应用[M]. 北京: 科学出版社, 2011.(SONG Xinyu, GUO Hongjian, SHI Xiangyun. Impulsive Differential Equation Theory and Its Application[M]. Beijing: Science Press, 2011.(in Chinese))
[22] 陆启韶. 常微分方程的定性方法和分叉[M]. 北京: 北京航空航天大学出版社, 1989.(LU Qishao. Qualitative Methods and Bifurcations of Ordinary Differential Equations[M]. Beijing: Beihang University Press, 1989.(in Chinese))
[23] FONDA A. Uniformly persistent semidynamical systems[J]. Proceedings of the American Mathematical Society, 1988, 104(1): 111-116.
[24] 白振国. 周期传染病模型的基本再生数[J]. 工程数学学报, 2013, 30(2): 175-183.(BAI Zhenguo. Basic reproduction number of periodic epidemic models[J]. Chinese Journal of Engineering Mathematics, 2013, 30(2): 175-183.(in Chinese))