引 言
目前,分数阶微积分方程的研究已成为当前数学物理、工程应用、医学研究以及社会经济等各个领域的研究热点[1].分数阶微积分作为一种有效的建模工具,不仅能够有效地描述分形几何、幂率现象等,还能刻画出具有“记忆”和“遗传”特性的材料变化过程.分数阶微分方程产生于一些反常扩散模型,具有深刻的物理背景和丰富的理论内涵.越来越多数学模型的建立需要引入分数阶微积分方程进行描述,例如污染物在土壤中的迁移、湍流[2]和地下水传输[3]等.其中,分数阶扩散方程是分数阶微分方程的一种,它是经典扩散方程(或波方程)的一种推广.在自然界中,分数阶扩散方程可被用来描述具有分形结构的多孔介质中的反常慢扩散现象.
与整数阶微分方程相比,分数阶微积分算子是非局部的,通常难以获得分数阶微分方程的解析解,即使能获得,由于解析解大多含有特殊函数,计算过程也非常困难[4].于是,致力于分数阶扩散方程数值方法的研究越来越多.对于这类方程的数值解,国内外专家学者做了大量的研究.Shen等提出了时间分数阶扩散方程的一个条件收敛和条件稳定的数值解法[5];Chen(陈文)等提出Kansa方法用于求解时间分数阶扩散方程[6];Gorenflo等考虑了一种离散随机行走的方法来求解时间分数阶扩散方程[7].
近些年来,人工神经网络(artificial neural network,ANN)方面的理论已经在众多领域取得成功应用.它是由一些通过权值相连的简单神经元节点构成的一个计算结构系统,通过这些神经单元的相互组合形成网络,并结合相应的算法来解决相关问题.人工神经网络的兴起为解决分数阶微分方程提供了一个新的思路[8].
本文主要根据一般神经网络拓扑结构,设计出一种新型组合神经网络结构,重点利用组合神经网络的逼近性能给出解决时间分数阶扩散方程初边值问题的计算方法,同时给出组合神经网络的学习算法.最后通过一个经典算例,将计算结果与已知方法进行比较,展示出其模型较为简单、计算精度高的特点.
1 预 备 知 识
1.1 组合神经网络结构
人工神经网络简称神经网络(NN),是基于生物学中神经网络的基本原理,在理解和抽象了人脑结构和外界刺激响应机制后,以网络拓扑知识为理论基础,模拟人脑神经系统对复杂信息处理机制的一种数学模型.因其独特的知识表示方式和智能化的自适应学习能力,引起各学科领域的广泛关注[9].
神经网络实际上是一个由大量简单节点(或称神经元)相互连接而成的复杂网络.在神经网络中,进行处理信息的单元主要分为3类:输入单元、输出单元和隐层单元.输入单元接受外部世界的信号与数据;输出单元实现系统处理结果的输出;隐层单元是处在输入和输出单元之间,不能由系统外部观察的单元.在隐层单元中,每一个节点代表一种特定的输出函数,这类输出函数称为激活函数(activation function).同时,每个隐层节点与输出单元之间设有加权值,隐层输出值乘以各自的权重传输到输出层,在输出层中进行求和.我们把这类加权值称之为权重(weight),神经元间的连接权值反映出了单元间的连接强度.神经网络的输出结果则取决于网络的结构、网络的连接方式、权重和激活函数.神经网络就是通过这样的方式来模拟人类的记忆,它具有高度的非线性,能够进行复杂的逻辑操作和非线性关系的实现[10].
为了解决分数阶扩散方程初边值问题,本文构造了一个新型神经网络结构,称之为组合神经网络.它是由传统的RBF神经网络与幂激励前向神经网络结合而成,这两种神经网络在非线性函数逼近方面能够表现出良好的性能.组合神经网络是由两个输入神经元和一个输出神经元组成的四层前馈神经结构,当每个输入值进入隐层后,代入新设定的激励函数得到隐层输出值,然后乘以其各自的权重进行相加,再进入输出层得出结果.根据以上描述,所构造的组合神经网络结构如下:
输入层
(1)
第一隐层
(2)
第二隐层
(3)
输出层
(4)
其结构图如图1所示.
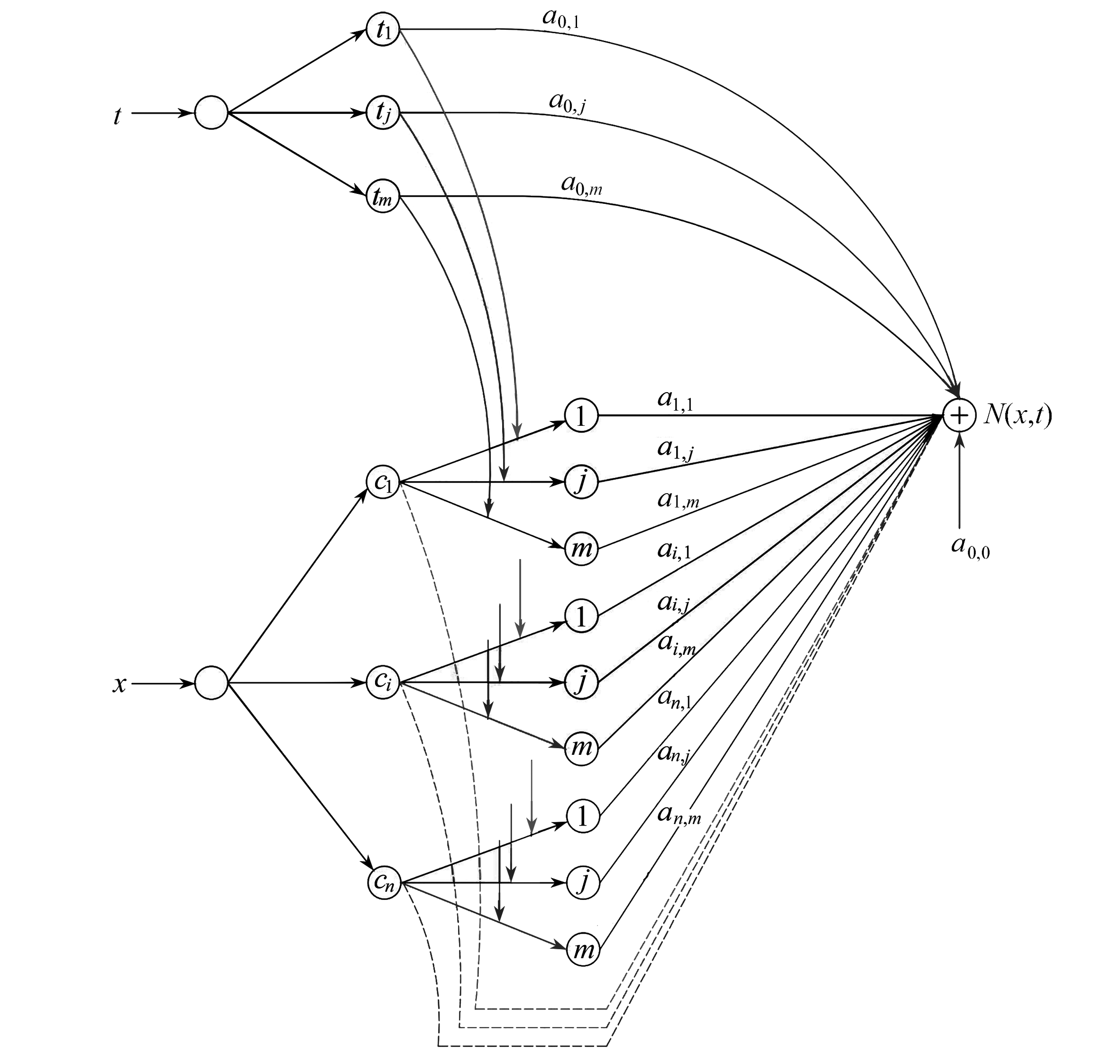
图1 组合神经网络结构图
Fig. 1 Structure diagram of the combined neural network
该网络结构为一般情况下的结构模型,对于分数阶偏微分方程要结合初始条件和边界条件来构造满足相应条件的数值解形式.因此,通过给出一个偏微分方程问题的边界或初始条件,就可以利用该组合神经网络结构来解决问题.
1.2 分数阶微积分相关定义、性质
在利用上述组合神经网络结构来解决时间分数阶扩散方程之前,首先介绍一些分数阶导数的一般概念和基本定义,这些概念和基本定义存在于所解决的问题中.众所周知,随着分数阶微积分理论的发展,研究者们引入了各种各样的定义,常用的有Riemann-Liouville分数阶微分和Caputo分数阶微分.这里,只讨论Caputo提出的最常用的分数阶微分定义[11]:
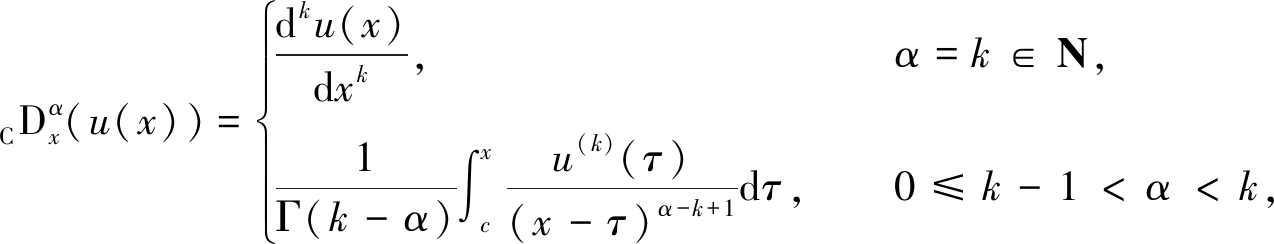
(5)
式中,u(x)是在有限区间[a,b]上k阶连续可导的函数,Γ(·)为Gamma函数.
Caputo分数阶微分的性质如下:
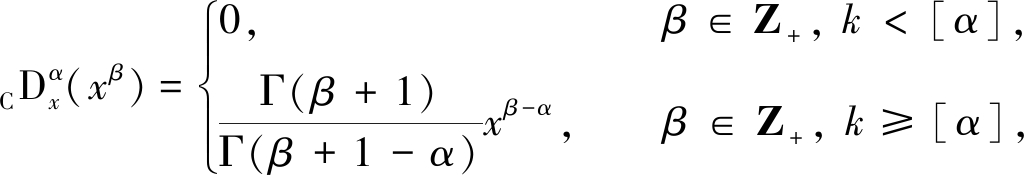
(6)
式中,[α]为大于α的最小正整数.
根据所解决的问题为时间分数阶扩散方程,给出该方程的一般形式为
(7)
初始条件
u(x,0)=g0(x),
边界条件
u(0,t)=h0(t), u(1,t)=h1(t),
式中, f(x,t)为连续实函数.
接下来,将所设计的多层前馈神经网络用于解决时间分数阶扩散方程.
2 组合神经网络一般方法
2.1 数值解形式的构造以及离散化
近十年来,一些幂级数法(power series method)被用于求解具有初始或边界条件的一系列偏微分方程.大量研究表明,这种方法是解决复杂数学问题的有力工具[12-13].如前所述,本文将幂级数法与神经网络相结合,构成幂激励前向型神经网络,同时与传统RBF神经网络相组合,进而求解分数阶扩散方程(7).根据该方法的基本思想,本文将定义在Ω=[0,1]×[0,T]上的解函数u(x,t)用多项式的形式来表示,其中时间项t用幂级数的形式表示,对于空间项x,则用RBF神经网络中的核函数来表示,一般取Gauss函数作为核函数,具体形式如下:
(8)
式中,ai, j为常系数(i=0,1,…,n; j=0,1,…,m),Ai为基函数扩展常数的倒数,ci为中心点.
应当注意的是,当且仅当解函数在开集(0,1)×(0,T)中是可微的时候,解函数可以表示成上述的形式,所以可以合理地利用所设计的神经网络的输出值来表示该多项式.这种组合方法提高了解函数的准确性,从而能够解决更为复杂的关系.
在运用上述多项式来解决时间分数阶扩散方程时,同时要考虑满足初始和边界条件,所以构造如下的测试解形式:
(9)
其中
K(x,t)=(1-x)h0(t)+xh1(t)+g0(x)-[(1-x)g0(0)+xg0(1)],
式中,N(x,t)为神经网络的输出值.
将式(9)代入式(7),则上述时间分数阶对流扩散方程变为如下形式:
(10)
式中
其中
Kx(x,t)=-h0(t)+h1(t)+g′0(x)-g0(0)-g0(1),
Kxx(x,t)=g″0(x).
现在,将设定一组网格点对该方程进行离散化.对于正整数n和m,设Ωp,q为一矩形区域,在矩形区域内存在配点(xp,tq)=(p/n′,q/m′),其中p=0,1,…,n′;q=0,1,…,m′,然后将配点代入上述方程,该问题则简化为以下方程:
(11)
接下来,将利用组合神经网络的方法构造一个迭代过程来求解方程(11).
2.2 误差函数的设定
众所周知,在神经网络中为了得到解决该问题的最优权值ai, j以及各项系数ci,Ai,需要设定一个有效的标准来度量每次网络训练学习所产生的误差,本文采用最小均方函数(LMS)来衡量解的精度[14].对于分数阶扩散方程来说,该误差函数设定为下式:
(xp,tq)∈Ωp,q.
(12)
接下来,通过训练对误差大小的判定,本文将原来正向传播的通路反向传回,并对每个隐层的各个神经元的权值以及各项系数进行修正,以期望误差趋向于0.有关这类技术方法更多的细节可以参见文献[14].
2.3 学习算法的确定
为了使神经网络设定的误差函数不断减小,需要不断地调节初始权值以及其他初始参数,当误差函数最小时,本文将得到最优权值以及最优参数值.本小节将尝试构建一个增量学习算法,它是以最小化误差函数作为目标的一种自我学习机制,称之为梯度下降法.下面将简要介绍该算法.
首先,任意地设置初始权值ai, j(i=0,1,…,n; j=0,1,…,m),以及初始扩展常数倒数Ai和初始中心点ci.然后,设定权值以及其他参数的调整量[8]:
ai, j(r+1)=ai, j(r)+Δai, j(r),
(13)
Ai(r+1)=Ai(r)+ΔAi(r),
(14)
ci(r+1)=ci(r)+Δci(r),
(15)
其中
式中,η,γ分别为学习率和动量项常数,由于算法中梯度下降的特性,在神经网络中反向传播时对学习率和动量常数的取值非常敏感,通常取较小的值,r为循环的次数.上述偏导数项可表示为
(16)
(17)
(18)
因此,通过对每一个点进行循环训练,最终可得到最优结果.下面通过具体的数值算例验证该方法的可行性和有效性.
3 计 算 实 例
本节通过运用计算机软件MATLAB进行编程对算例模拟,进而验证说明本文提出的组合神经网络方法的可靠性和准确性.
首先,为了表明方法数值解的准确性,定义如下的绝对误差、相对误差和平均相对误差:
Eab=|uex(xp,tq)-unum(xp,tq)|,
(19)
(20)
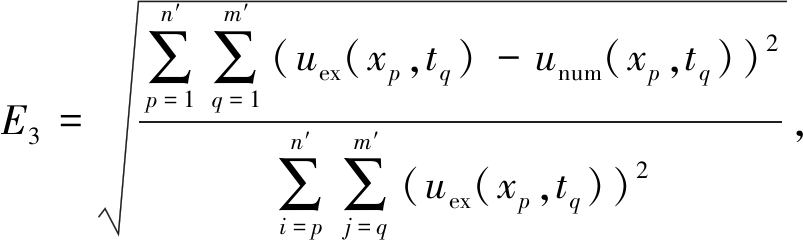
(21)
式中,uex(xp,tq)和unum(xp,tq)分别表示计算点(xp,tq)上物理量的精确解和数值解.
例1 给定时间分数阶对流扩散方程:
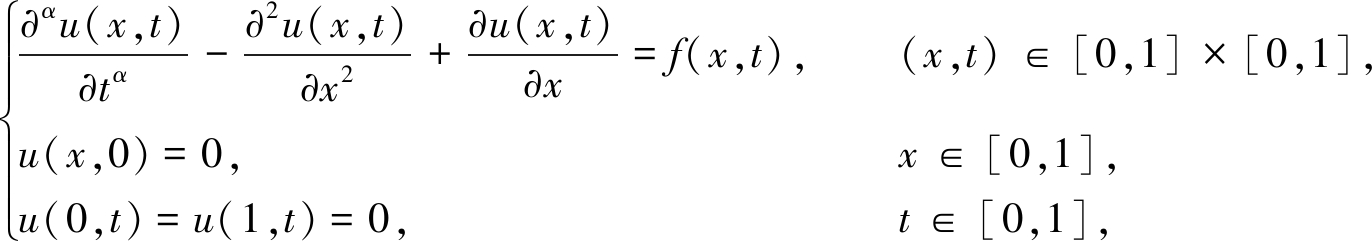
(22)
式中
其精确解为
uex(x,t)=t3+αsin(πx).
设置如下参数:分数阶阶数α=0.2,时间步长为Δt,空间步长为Δh.时间项隐层神经元节点数m=10,空间项隐层神经元节点数n=15,学习率μ=0.001,训练循环次数r=1 000.
图2给出了时间步长与空间步长为Δt=Δh=0.02时的数值解分布,图3和图4给出了相应的绝对误差与相对误差分布情况,由上述图像可以看出数值解与解析解吻合较好.但由于边界点处导数的近似不准确,边界节点处的数值精度相对于中心区域稍微偏低[6].
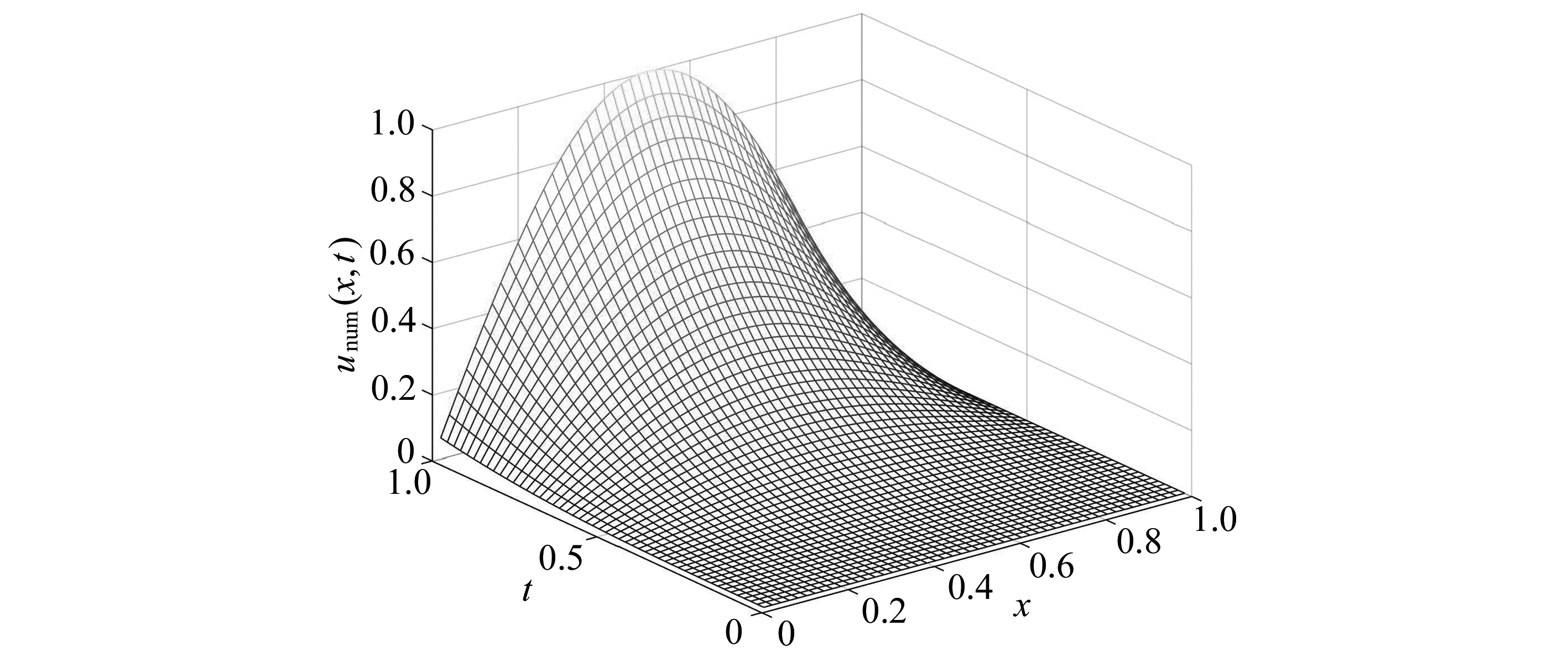
图2 α=0.2,Δt=Δh=0.02时的数值解图像
Fig. 2 Numerical solutions for α=0.2,Δt=Δh=0.02
表1 平均相对误差E3在不同时间步长下的比较
Table 1 Comparison of mean relative error E3 between cases of different time steps

node point xmean relative error E3(Δh=0.02,α=0.2)Δt=0.05Δt=0.020.13.800 0×10-37.187 6×10-30.23.125 8×10-42.730 9×10-40.32.507 4×10-41.730 9×10-40.41.828 9×10-51.509 0×10-50.52.952 8×10-59.762 0×10-60.64.870 9×10-63.380 8×10-60.74.469 3×10-62.478 4×10-60.83.698 7×10-61.997 6×10-60.93.521 9×10-61.785 2×10-6
表1列出了空间步长为Δh=0.02,不同时间步长下,各节点处数值解的平均相对误差.由表1可以看出,当在相同时间步长下,随着节点位置逐渐增大平均相对误差逐渐减小;在相同节点位置处,除x=0.1外,随着时间步长的减小平均相对误差逐渐减小.在配置节点较少的情况下,该方法能获得较满意的结果,同时也验证了该方法是稳定收敛的.
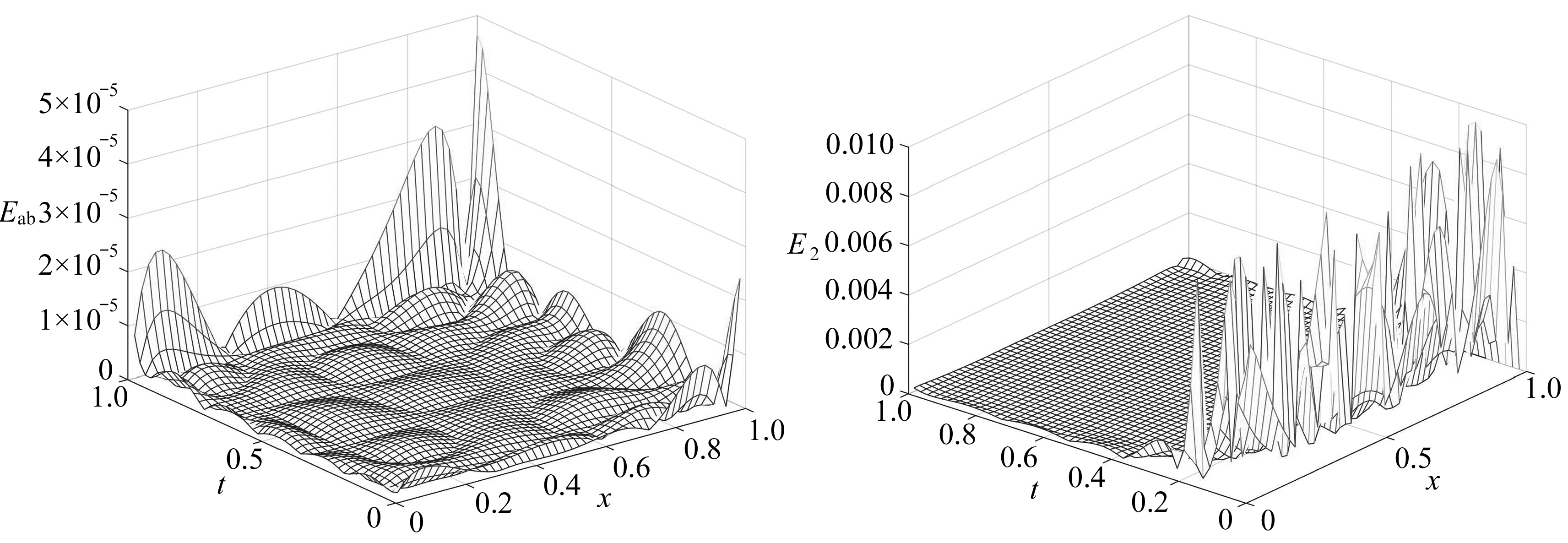
图3 α=0.2,Δt=Δh=0.02时的绝对误差图像图4 α=0.2,Δt=Δh=0.02时的相对误差图像
Fig. 3 Absolute errors between exact and numerical solutions for α=0.2,Δt=Δh=0.02 Fig. 4 Relative errors between exact and numerical solutions for α=0.2,Δt=Δh=0.02
接下来将组合神经网络方法所得结果与文献[15]中近似格式方法所得结果进行比较,其中分数阶阶数为α=0.5,结果如表2所示.
表2 两种方法的最大绝对误差比较
Table 2 Maximum absolute error comparison of the 2 methods

ΔhΔtmaximum absolute error of the combined neural networkref. [15]1201205.610 9×10-43.538 0×10-31401402.796 2×10-41.092 4×10-31801808.674 0×10-53.468 4×10-4116011606.112 6×10-51.128 2×10-4
由表2可知,这两种方法的计算精度均较高,但是在相同的参数下,本文所提出的组合神经网络方法比文献[15]中的方法计算误差更小,结果更加精确,数值结果与理论结果相一致,这进一步说明了本文计算方法的优越性.
4 结 论
本文以人工神经网络理论为基础,通过结合RBF神经网络与幂激励型神经网络,构造出一种新型的网络框架,即组合神经网络.同时结合神经网络梯度下降学习算法,提出了时间分数阶扩散方程初边值问题的组合神经网络算法.
数值算例结果表明,所提出算法得到的结果具有较高的计算精度,除了能得到各节点处的近似值,还可以得到相邻节点间任意指定位置的近似值,此外该方法收敛速度较快,为分数阶微分方程数值计算开辟了一条新的道路,能更好地解决众多领域中面临的分数阶微分方程的问题,具有一定的应用价值.
但是,本文所确定的梯度下降学习算法存在着一定的缺陷,当目标函数更加复杂时,会容易收敛到非最小值点,如何进一步优化学习算法,还有待进一步的研究.
[1] DIETHELM K, FORD N J. Analysis of fractional differential equations[J]. Journal of Mathematical Analysis and Applications, 2002, 265(2): 229-248.
[2] CHEN W. A speculative study of 2/3-order fractional Laplacian modeling of turbulence: some thoughts and conjectures[J]. Chaos, 2006, 16(2): 023126. DOI: 10.1063/1.2208452.
[3] BENSON D A, WHEATCRAFT S W, MEERSCHAERT M M. Application of a fractional advection-dispersion equation[J]. Water Resources Research, 2000, 36(6): 1403-1412.
[4] DE ANDRADE M F, LENZI E K, EVANGELISTA L R, et al. Anomalous diffusion and fractional diffusion equation: anisotropic media and external forces[J]. Physics Letters A, 2005, 347(4/6): 160-169.
[5] SHEN S, LIU F, ANH V, et al. Detailed analysis of a conservative difference approximation for the time fractional diffusion equation[J]. Journal of Applied Mathematics and Computing, 2006, 22(3): 1-19.
[6] CHEN W, YE L, SUN H. Fractional diffusion equations by the Kansa method[J]. Computers & Mathematics With Applications, 2010, 59(5): 1614-1620.
[7] GORENFLO R, MAINARDI F, MORETTI D, et al. Time fractional diffusion: a discrete random walk approach[J]. Nonlinear Dynamics, 2002, 29(1/4): 129-143.
[8] JAFARIAN A, MOKHTARPOUR M, BALEANU D. Artificial neural network approach for a class of fractional ordinary differential equation[J]. Neural Computing and Applications, 2016, 28(4): 765-773.
[9] BASHEER I A, HAJMEER M. Artificial neural networks: fundamentals, computing, design, and application[J]. Journal of Microbiological Methods, 2000, 43(1): 3-31.
[10] HANSS M. Applied Fuzzy Arithmetic: an Introduction With Engineering Applications[M]. Springer, 2010.
[11] 陈文, 孙洪广, 李西成. 力学与工程问题的分数阶导数建模[M]. 北京: 科学出版社, 2010.(CHEN Wen, SUN Hongguang, LI Xicheng. Fractional Derivative Modeling in Mechanical and Engineering Problems[M]. Beijing: Science Press, 2010.(in Chinese))
[12] NUSEIR A S, AL-HASOON A. Power series solutions for nonlinear systems of partial differential equations[J]. Journal of Applied Mathematics, 2017, 6(104/105): 5147-5159.
[13] KURULAY M, BAYRAM M. A novel power series method for solving second order partial differential equations[J]. European Journal of Pure & Applied Mathematics, 2009, 2(2): 268-277.
[14] HASSOUN M H. Fundamentals of Artificial Neural Networks[M]. MIT Press, 1995.
[15] ZHANG J, ZHANG X, YANG B. An approximation scheme for the time fractional convection-diffusion equation[J]. Applied Mathematics and Computation, 2018, 335: 305-312.