引 言
颗粒材料广泛存在于自然界、工业生产和日常生活等诸多领域,并表现出类似于固、液、气不同状态的宏观力学行为[1-2].离散单元法(discrete element method, DEM)是20世纪70年代由Cundall和Strack提出并发展成为一种模拟颗粒材料的重要工具,该方法最初采用二维的圆盘或三维的球体单元,其具有计算简单和易于并行等特点[3-4].然而,自然界或工业中普遍是由非球形颗粒组成的复杂体系,与球形颗粒相比,其在不同空间尺度下的宏细观力学性质均有很大差异[5-6].同时,非球形单元间的接触搜索相比球形颗粒更加复杂,其搜索时间占整个计算时间的比率会显著增加[7].随着对离散元模拟精度和大规模计算需求的提高,非球形颗粒形态的构造及并行计算方法引起了广泛关注[8-9].
非球形颗粒的构造方法主要包括基于规则颗粒的黏结或镶嵌模型[10-11]、基于二次曲面方程的椭球体模型[12-13]、基于连续函数包络的超二次曲面模型[14-15]、基于Minkowski和方法的扩展多面体模型[16-17]、基于球谐函数包络的星型颗粒模型[18-19]、基于水平集算法的任意几何模型[20-21]等.其中,超二次曲面方法能准确地描述自然界中凸面体和凹面体几何模型,通过改变函数方程中3个方向的半轴长和两个形状参数,进而得到不同长宽比和表面尖锐度的颗粒形态[22].Delaney和Cleary[23]通过超二次曲面方法研究了不同单元形状对堆积特性的影响.结果表明,与球形颗粒相比,块状颗粒具有更大的接触面积且颗粒间的面-面接触产生更高的堆积密度.Ma和Zhao[24-25]采用超二次曲面方程构造不同长宽比的椭球体和圆柱体颗粒,分析了单元形状对水平转筒内颗粒材料混合特性的影响规律.Höhner等[26]采用黏结模型、多面体模型和超二次曲面模型研究了料斗中非球形颗粒的流动特性,计算结果与试验结果十分吻合.然而,超二次曲面单元间接触判断的复杂性很大程度上限制了颗粒数量和运行时间,进而难以准确反映大规模非球形颗粒材料的运动规律.
目前,高性能并行计算方法主要包括基于共享内存方式的多线程并行(open multi-processing, OpenMP)方法[27-28]、基于分布式内存模式的消息传递通信(message passing interface, MPI)方法[29-30]和上述两种算法混合使用的MPI-OpenMP方法[31-32].上述方法以CPU为计算核心,各个处理器间相互协同,进而达到加速求解速度或扩大求解规模的目的[33-34].然而,基于CPU并行的计算效率通常依赖于计算节点的数量,导致计算机硬件成本增加且易出现负载不均衡等限制.近年来,以图像处理器(graphics processing unit, GPU)为主要硬件载体的高性能数值算法得到了广泛关注,并逐渐发展成为CPU-GPU协同处理的并行计算架构[35].该方法最早于2007年由NVIDIA提出,并采用统一计算设备架构(computer unified device architecture, CUDA),用于发挥GPU的通用并行计算能力.与CPU相比,GPU拥有一个由数以千计更小且更高效的核心组成的大规模并行架构.这种方式使得GPU拥有强大的并行计算能力,适合于具有较高算术密度且逻辑分支简单的运算,并为大规模颗粒材料的数值计算提供了可靠的硬件基础[36-38].
近年来,基于GPU并行的离散元算法得到广泛发展[39-40].狄少丞和季顺迎[41]采用基于球形颗粒的GPU并行算法模拟了大规模海冰与平台结构的相互作用,分析了海冰的动力破碎特性及结构的冰载荷.Gan等[42]采用GPU并行算法模拟了大规模椭球体颗粒在水平转筒中的混合过程,并研究了不同长宽比对动态休止角的影响.Govender等[43-44]发展了基于分离面方法的多面体GPU并行算法, 同时讨论了不同单元形态和卸料角度对颗粒材料流动特性的影响.然而,目前超二次曲面单元的数值计算普遍采用CPU串行[7]或OpenMP方法[45],而对CUDA-GPU架构下的并行算法研究则相对较少.
本文将在球形颗粒并行算法的基础上发展基于CUDA-GPU架构的超二次曲面单元并行算法.该方法通过核函数创建包围盒的粗判断列表及Newton迭代的细判断列表,同时优化了计算模型和内存访问模式.为检验超二次曲面并行算法的有效性,对块状颗粒的流动过程进行离散元模拟并与试验结果进行对比验证,同时分析了颗粒长宽比和表面尖锐度对颗粒材料流动特性的影响.
1 超二次曲面单元构造及离散元并行算法
1.1 超二次曲面方程的函数形式
超二次曲面方程是数学意义上描述非球形颗粒的普遍方法,其函数形式可定义为[46]
(1)
式中,a, b和c分别表示颗粒沿x, y和z方向的半轴长,n1和n2表示颗粒形状及表面的尖锐度.n1=n2=2得到球体或椭球体颗粒,n1≫n2=2得到类似柱体颗粒,n1=n2≫2得到类似块体颗粒.图1显示在超二次曲面函数方程中改变长宽比和表面尖锐度参数得到不同的单元几何模型.
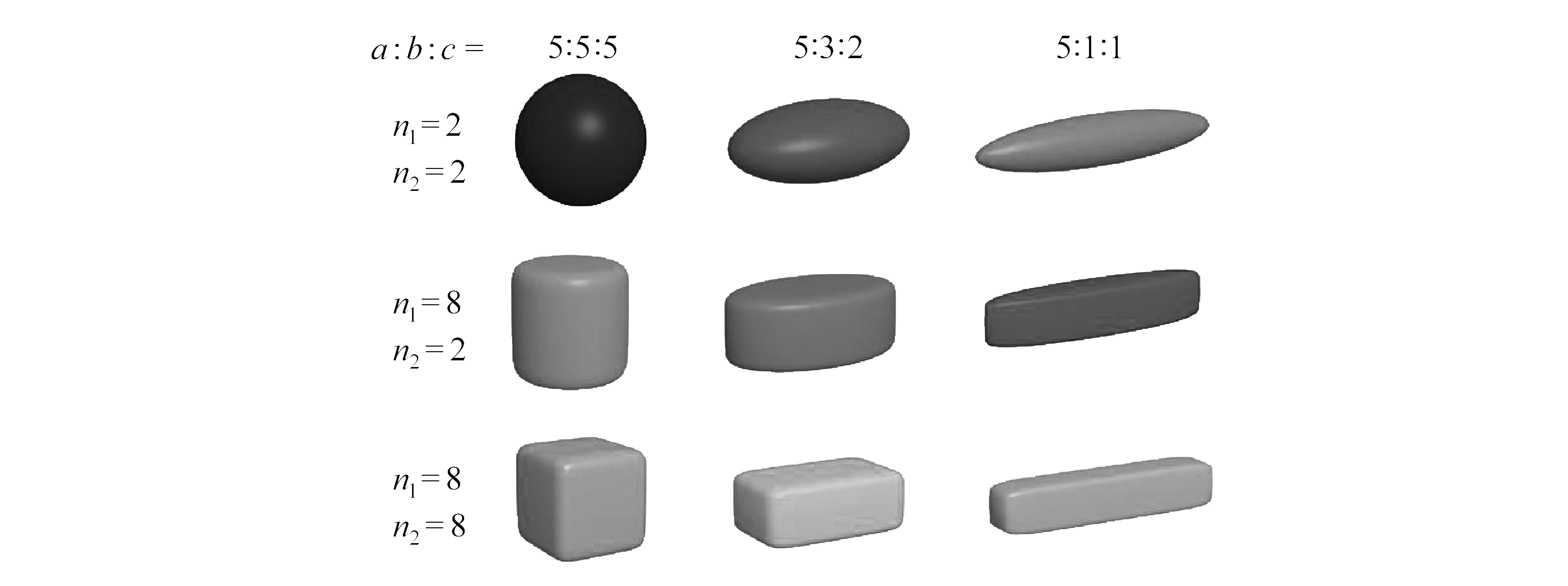
图1 基于超二次曲面的三维非球形颗粒
Fig. 1 Three-dimensional non-spherical particles based on super-quadric equations
1.2 基于GPU并行的离散元算法
针对超二次曲面单元接触搜索的复杂性及GPU并行特点,其接触判断可包括网格划分和邻居搜索、创建包围盒列表和Newton迭代列表、接触力计算和颗粒信息更新.下面将详细介绍离散元算法在GPU并行架构下的计算过程.
1.2.1 背景网格划分和邻居搜索
将计算区域划分为若干个大小相等且稍大于包围球体直径的正方体网格,以颗粒编号作为并行依据,并采用元胞列表法确定颗粒编号与网格编号的对应关系,如图2所示.以颗粒对应的网格编号为基准,通过调用CUDA thrust库中sort_by_key函数直接在GPU上完成对颗粒编号的快速重排序,从而确定超二次曲面单元的新编号,如图3(a)所示.这主要是由于各颗粒单元仅与相同或相邻网格内的颗粒单元发生潜在接触,从而使得空间中潜在接触对的颗粒编号更接近,并有利于采用共享内存模式的GPU快速搜索邻居单元和建立邻居列表[47].同时,对每个网格内颗粒编号的最小值和最大值进行统计,如图3(b)所示.
以颗粒编号为并行依据,即每个线程对应不同的颗粒编号,搜索相同或相邻网格内的颗粒,并采用包围球体作为单元间的第一次粗判断.包围球体半径可以表示为![]() 其接触理论基于传统球体的计算方法.如果两个单元形心的距离小于其半径和,则为接触,从而建立对应每个颗粒编号i的邻居列表Anei[i,Iicell].Iicell对应邻居颗粒编号,其取值范围为0~Nnei,其中,Nnei为超二次曲面单元的最大接触数.本文构造不同形态的颗粒单元,考虑算法的稳定性且假定颗粒长宽比为σ,因此每个颗粒最多可与24σ个邻居单元发生接触.此外,如果邻居颗粒编号小于i,该编号则存储在Anei[i,Iicell]数组的末尾,否则存储在Anei[i,Iicell]数组的开始位置.同时,分别对邻居编号小于i和大于i的数量进行统计,并分别存储在Ijli[i]和Ijgi[i]数组中.
其接触理论基于传统球体的计算方法.如果两个单元形心的距离小于其半径和,则为接触,从而建立对应每个颗粒编号i的邻居列表Anei[i,Iicell].Iicell对应邻居颗粒编号,其取值范围为0~Nnei,其中,Nnei为超二次曲面单元的最大接触数.本文构造不同形态的颗粒单元,考虑算法的稳定性且假定颗粒长宽比为σ,因此每个颗粒最多可与24σ个邻居单元发生接触.此外,如果邻居颗粒编号小于i,该编号则存储在Anei[i,Iicell]数组的末尾,否则存储在Anei[i,Iicell]数组的开始位置.同时,分别对邻居编号小于i和大于i的数量进行统计,并分别存储在Ijli[i]和Ijgi[i]数组中.
通过调用CUDA thrust库中inclusive_scan函数,直接在GPU上完成对数组Ijgi[i]的快速前缀求和,即![]() 每个潜在接触对的编号可表述为Ilist=Isum[i-1]+Iicell(Iicell∈[0,Ijgi[i]-1]),进而创建用于存储单元编号的接触对列表Lpa[Ilist]和Lpb[Ilist].最后,根据Anei[i,Iicell]中颗粒i与所有可能接触的颗粒编号的对应关系,将接触对的编号Ilist存储在参考列表Aref[i,Iicell]中.这有利于后续以颗粒编号为并行依据,在GPU上实现每个颗粒接触力和力矩的快速叠加.
每个潜在接触对的编号可表述为Ilist=Isum[i-1]+Iicell(Iicell∈[0,Ijgi[i]-1]),进而创建用于存储单元编号的接触对列表Lpa[Ilist]和Lpb[Ilist].最后,根据Anei[i,Iicell]中颗粒i与所有可能接触的颗粒编号的对应关系,将接触对的编号Ilist存储在参考列表Aref[i,Iicell]中.这有利于后续以颗粒编号为并行依据,在GPU上实现每个颗粒接触力和力矩的快速叠加.
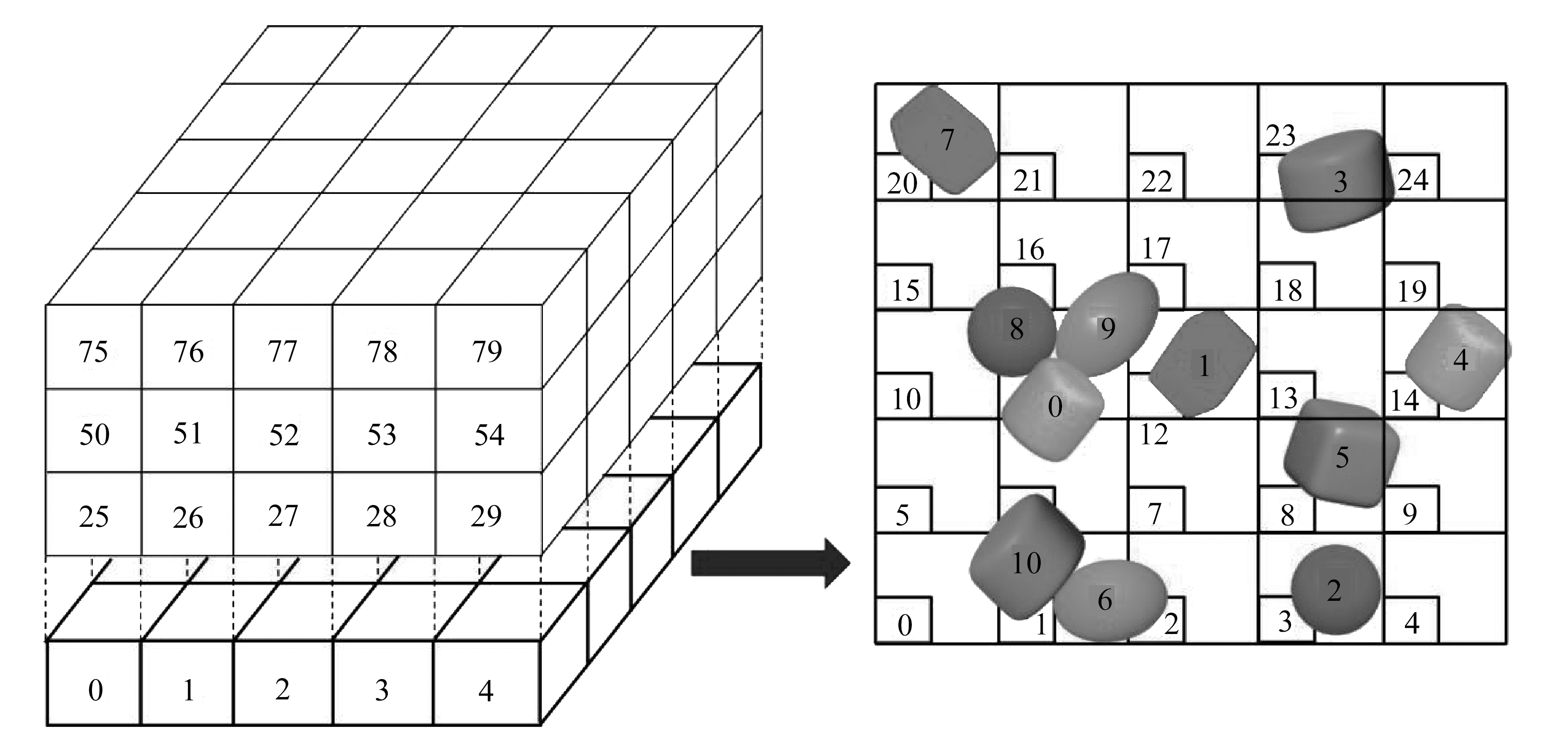
图2 DEM模拟中网格编号与颗粒编号的对应关系
Fig. 2 Relationship between the cell label and the particle label for DEM simulation
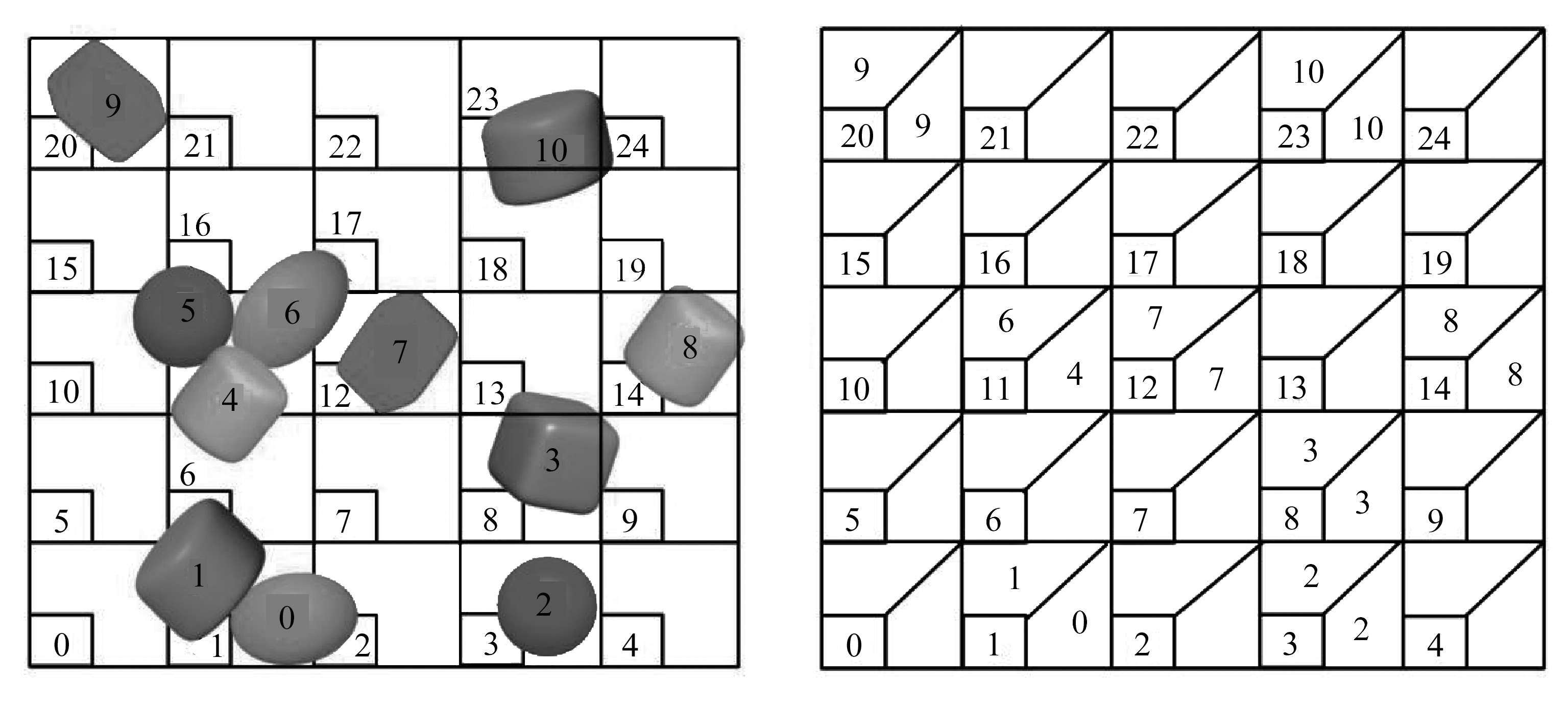
(a) 重新排序后的颗粒编号(b) 网格内的最大和最小颗粒编号
(a) The sorted particle label(b) Maximum and minimum particle labels in each cell
图3 重新排序后颗粒编号与网格编号的关系
Fig. 3 Relation between the cell label and the particle label after sorting
1.2.2 包围盒列表及Newton迭代列表
考虑不同长宽比和方向的颗粒单元,以接触对的编号为并行依据,创建每个接触对对应的包围盒列表Lb.这有利于快速剔除不可能发生碰撞的潜在接触对,提高并行程序的运行效率.根据超二次曲面单元3个主轴方向的半轴长建立最小尺寸的六面体,采用基于分离轴理论的方向包围盒(oriented bounding box, OBB)方法[48],并依次判断两个单元的6个主轴方向和主轴两两叉乘得到的9个矢量方向,从而确定单元间的接触状态.如果两个六面体在空间向量上的投影相交,则在新数组Lb中存储“1”表示接触,否则存储“0”表示分离.
为精确地计算两个超二次曲面单元间的重叠量,以接触对编号为并行依据,对数组Lb中标记为“1”的接触对进行求解.这里采用Newton迭代算法,考虑单元接触时表面法向相互平行且中间点X0到两个单元的几何势能相等 (如图4所示),从而建立四元非线性方程组[45]:
(2)
式中,X=(x,y,z)T,F(X)表示超二次曲面单元的函数方程, F(X)表示函数的一阶导函数方程,下标A和B分别表示两个颗粒编号.因此,计算颗粒间重叠量的Newton迭代公式可以表示为
F(X)表示函数的一阶导函数方程,下标A和B分别表示两个颗粒编号.因此,计算颗粒间重叠量的Newton迭代公式可以表示为
(3)
式中, 2F(X)表示函数的二阶导函数方程.同时,X=X+dX,α=α+dα.
2F(X)表示函数的二阶导函数方程.同时,X=X+dX,α=α+dα.
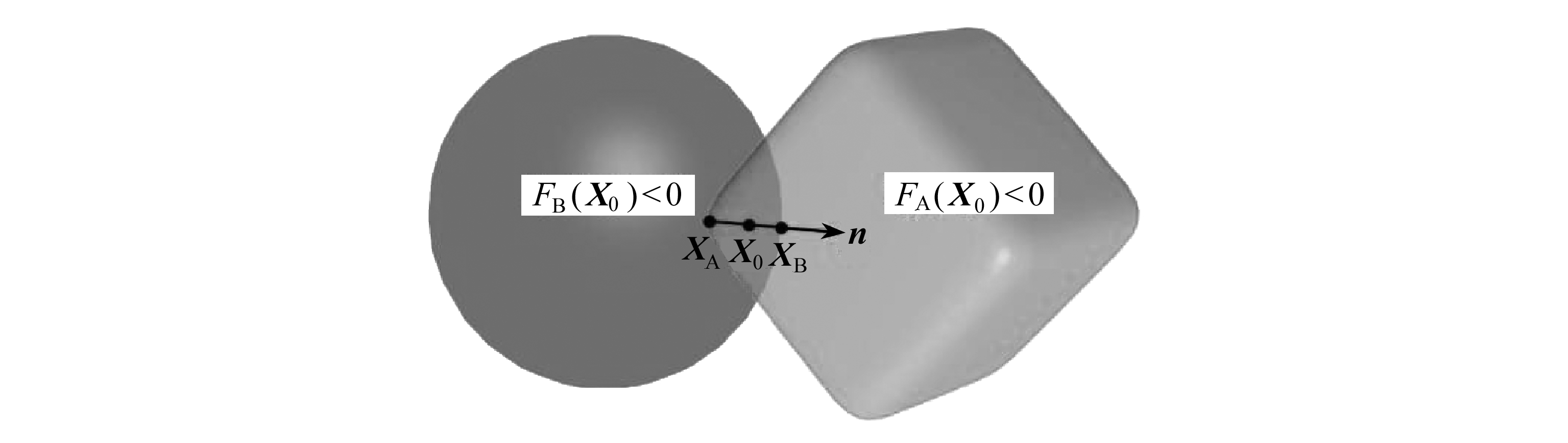
图4 基于Newton迭代算法的单元间接触判断
Fig. 4 Contact detection between particles based on the Newtonian iteration algorithm
如果中间点X0同时满足FA(X0)<0且FB(X0)<0,则两个颗粒发生接触,接触法向向量定义为n= FA(X0)/‖
FA(X0)/‖ FA(X0)‖.考虑两个单元表面点XA和XB可表示为未知参数βA和βB的函数:
FA(X0)‖.考虑两个单元表面点XA和XB可表示为未知参数βA和βB的函数:
XA=X0+βAn, XB=X0+βBn.
同时,βA和βB可通过一元非线性Newton迭代公式计算得到[49]
![]()

![]()

![]()
因此,单元间法向重叠量可表示为δn=XA-XB.
为加快数值迭代的计算效率,这里将中间点X0进行存储并用于下一时间步内Newton迭代的初始预测值.由于在每一时间步的开始会对单元进行排序,单元的编号会被重新设置,因此还需建立单元的新旧编号对应关系以正确传递初始迭代点.
1.2.3 超二次曲面单元间的接触力及颗粒信息更新
在离散元方法中,切向重叠量以增量的方式进行更新.如果该接触对在当前时间步内保持接触,并且在下一时间步内仍为接触,则需根据单元新旧编号的对应关系进而正确传递切向重叠量.这里,每个接触对中颗粒i和j所受接触力和力矩可分别表示为![]() 和
和![]() 以颗粒编号为并行依据,对每个颗粒i所受的合力F[i]和合力矩M[i]进行GPU快速叠加[47]:
以颗粒编号为并行依据,对每个颗粒i所受的合力F[i]和合力矩M[i]进行GPU快速叠加[47]:
(4)
(5)
通过每个颗粒所受的接触力和力矩,根据Newton第二定律,可以计算得到颗粒的速度和角速度,并对颗粒的位置坐标和四元数进行更新,从而进入下一个时间步迭代.
2 超二次曲面单元间的接触模型
考虑超二次曲面单元碰撞时不同形状及表面曲率,采用基于局部接触点处曲率半径的非线性接触模型计算不同接触模式下的作用力[50].因此,单元所受合力主要由法向力和切向力组成,同时合力矩主要由法向力和切向力不穿过单元形心产生的力矩以及单元间发生相对转动时滚动摩擦引起的力矩组成.单元间的法向接触力Fn主要包括弹性力Fcn和黏滞力Fdn,可分别表示为
(6)
(7)
式中
其中,E,ν和Cn分别为非球形颗粒材料的弹性模量、Poisson比和法向阻尼系数;vn,ij为单元间法向相对速度;Ri和Rj分别为单元i和j相互碰撞时局部接触点处的曲率半径,可表示为R=1/Kmean,Kmean为平均曲率,可表示为[51]
(8)
单元间的切向接触力Ft主要包括弹性力Fct和黏滞力Fdt,并考虑Mohr-Coulomb摩擦定律.切向弹性力Fct和黏滞力Fdt可分别表示为
(9)
(10)
式中,μs为单元间的滑动摩擦因数;δt为切向重叠量;δt,max为切向最大重叠量,可表示为δt,max=μs(2-ν)/2(1-ν)·δn;Ct为切向黏滞系数;vt,ij为单元间切向相对速度.
单元间发生相对转动时,由滚动摩擦引起的力矩Mr可表示为
(11)
式中,μr为滚动摩擦因数;![]() 为单元间的相对转动速度,可表示为
为单元间的相对转动速度,可表示为![]()
3 超二次曲面并行算法的试验验证
为检验超二次曲面并行算法的可靠性,这里采用超二次曲面单元构造约为42 000个块状颗粒,在长方体容器中考虑单元的初始随机位置和角度并在重力作用下实现堆积,同时与文献[52]中的试验结果进行对比.超二次曲面方程中函数参数满足2a=0.6~0.71 mm,b/a=0.6~0.85,c/a=0.75~1.0,n1=n2=5,主要的离散元计算参数列于表1.初始生成的颗粒床高约为60 mm,长为40 mm,宽为4 mm,并在宽度方向施加周期性边界条件.容器左侧墙固定,右侧墙以6.11 mm/s的速度缓慢向右移动.由于试验中移动墙的速度非常小且总时间较长,因此采用当前时刻与总时刻的比值,即通过正交时刻描述颗粒的运动规律.
图5显示正交时刻分别为0,0.23,0.67和1.0时超二次曲面颗粒流动过程与试验结果[52]的对比.随着右侧墙的移动,颗粒床在重力作用下缓慢倾斜并最终形成休止角.同时,上层颗粒的流动速度高于下层颗粒.这主要是由于下层颗粒间挤压剧烈并形成较大的摩擦力,进而阻碍颗粒间的相对运动.此外,采用球形颗粒模拟上述颗粒床的流动过程,同时对固定墙和移动墙侧的颗粒床高度分别进行统计,并与试验结果[52]进行对比,如图6所示.可以看出,单元形状显著影响颗粒系统的整个流动过程.与球形颗粒相比,由块状颗粒填充的颗粒床在固定墙侧下降缓慢,而在移动墙侧则下降较快.这主要是由于块状颗粒间接触面积较大,不利于颗粒间的相对平动和转动,从而难以快速地填充颗粒系统中出现的空隙.因此,固定墙侧的颗粒床较为稳定且下降缓慢,而移动墙侧由于空隙不断增加,临近颗粒重新排列进而使得移动墙侧的颗粒床高度快速下降.尽管离散元的数值结果与试验结果存在一定的偏差,但在一定程度上能很好地反映大规模非球形颗粒系统的宏观流动特性,同时表明基于CUDA-GPU架构的超二次曲面并行算法的有效性.
表1 超二次曲面流动过程的计算参数
Table 1 DEM parameters for the flow process of super-quadric particles

parametersymbolvalueYoung’s modulusE1/Pa5×108particle densityρ/(kg·m-3)1 520Poisson’s ratioν0.2friction coefficientμs0.6normal damping coefficientCn0.4tangential damping coefficientCt0.4

(a) tn=0(b) tn=0.23

(c) tn=0.67(d) tn=1.0
图5 不同正交时刻下颗粒床下降过程的试验结果[52](左)和本文离散元数值结果(右)的对比
Fig. 5 Comparison of snapshots of the fall patterns between experiments[52] (left) and present DEM simulations (right) at different normalized moments
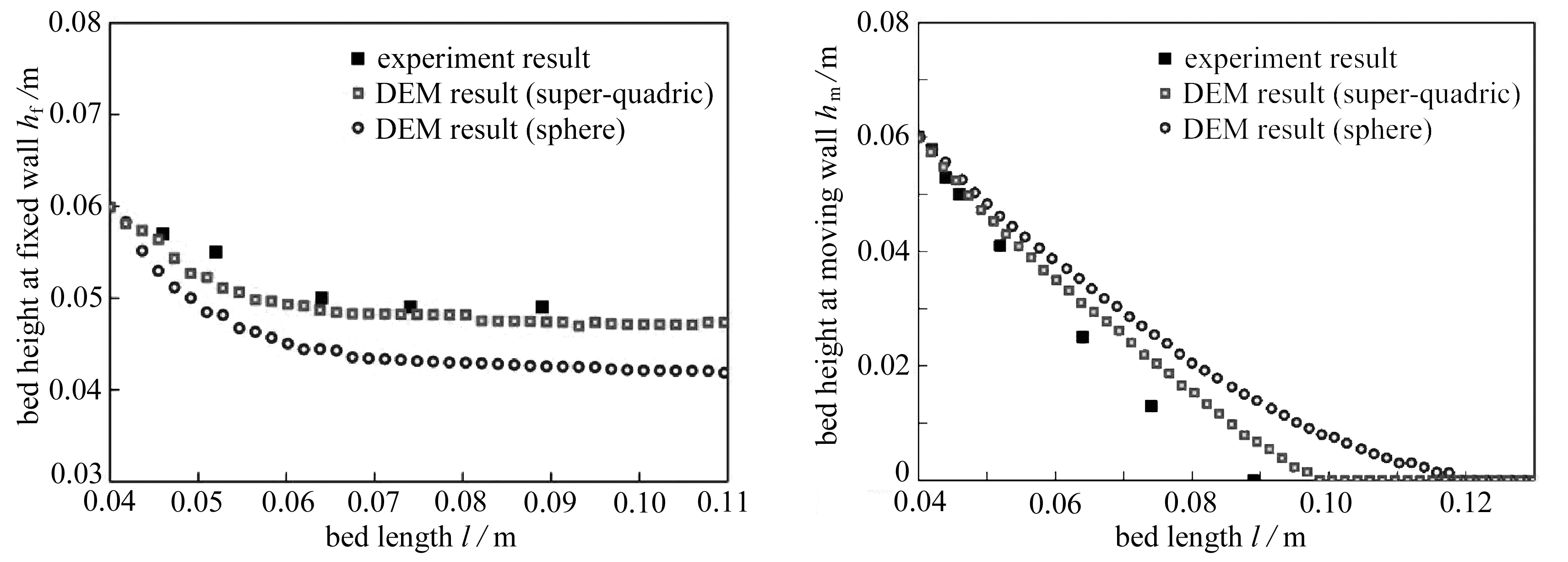
(a) 固定墙侧颗粒床的高度(b) 移动墙侧颗粒床的高度
(a) The height of the granular bed at the fixed wall(b) The height of the granular bed at the moving wall
图6 颗粒床高度随长度的变化关系
Fig. 6 The height of the granular bed varying with its length
4 颗粒形状对流动特性影响的离散元分析
4.1 不同颗粒形态流动过程的离散元模拟
为进一步分析单元形状对颗粒系统宏观流动特性的影响,这里采用超二次曲面方程构造等体积不同形态的颗粒单元以模拟颗粒材料的流动过程,同时考虑单元长宽比和表面尖锐度对宏观堆积和流动特性的影响.超二次曲面方程中函数参数满足σ=c/a(=b)且σ∈[0.5, 2.0].n1=n2=2得到球体或椭球体颗粒,n1=8且n2=2得到类似柱状颗粒,n1=n2=8得到类似块状颗粒.同时,球形颗粒的函数参数满足a=b=c=0.35 mm,其余不同形态的颗粒与球形颗粒体积相等,颗粒总数约为34 000个,离散元的主要参数列于表1.填充的颗粒床高约为60 mm,长为40 mm,宽为4 mm,并在宽度方向施加周期性边界条件.采用超二次曲面单元模拟球体和块体颗粒不同时刻下的流动过程,如图7所示.可以发现,两种形态的颗粒材料具有不同的流动特性,其在最后时刻形成的休止角具有较大差异.下面将进一步通过改变长宽比和表面尖锐度来定量分析颗粒形状对流动特性的影响规律.

图7 不同时刻下块体(上)和球体(下)颗粒床的流动过程
Fig. 7 The flow patterns of the granular beds filled with cubes (top) and spheres (bottom) at different moments
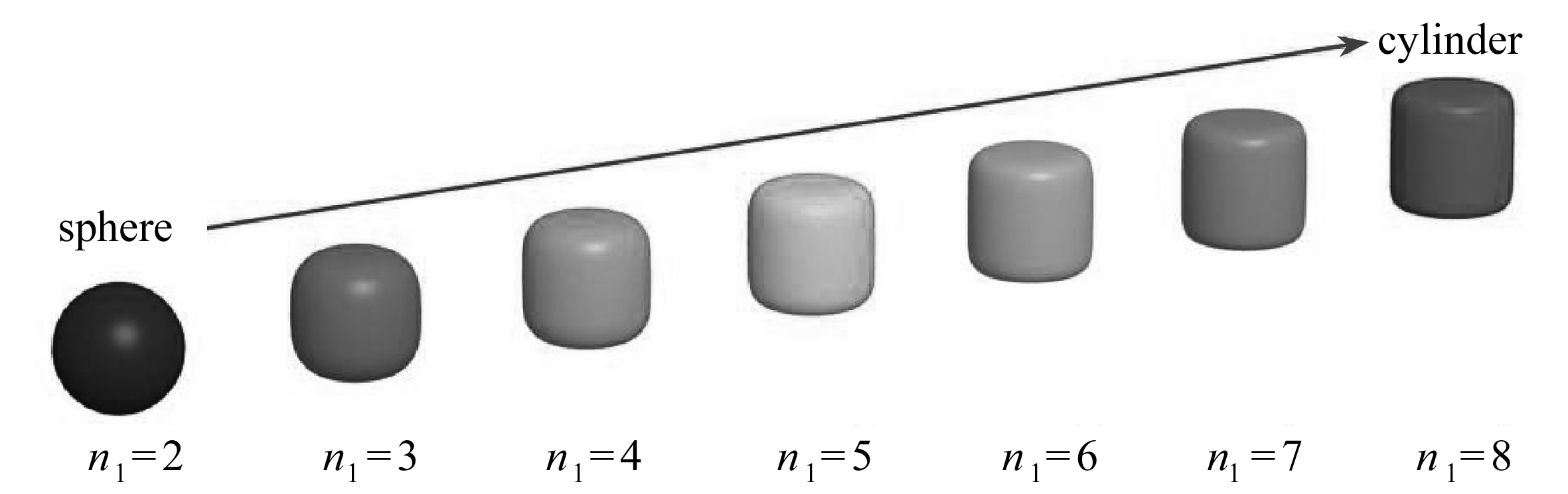
(a) σ=1, n2=2
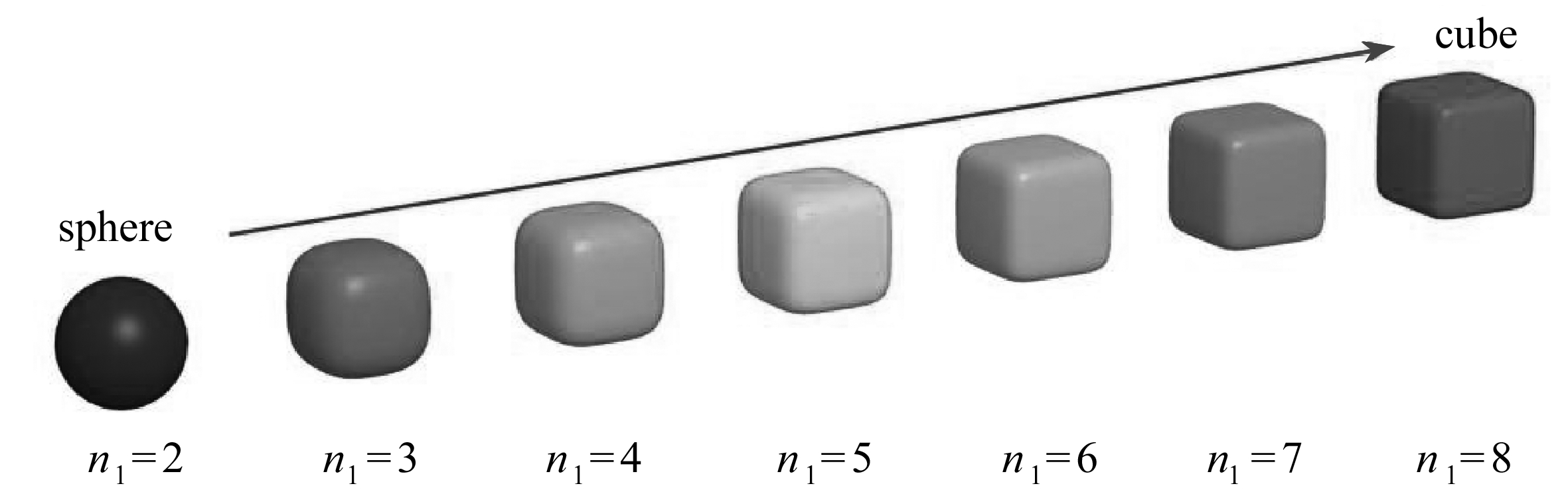
(b) σ=1, n2=n1
图8 不同参数下颗粒的表面尖锐度
Fig. 8 Sharpnesses of particles under different parameters
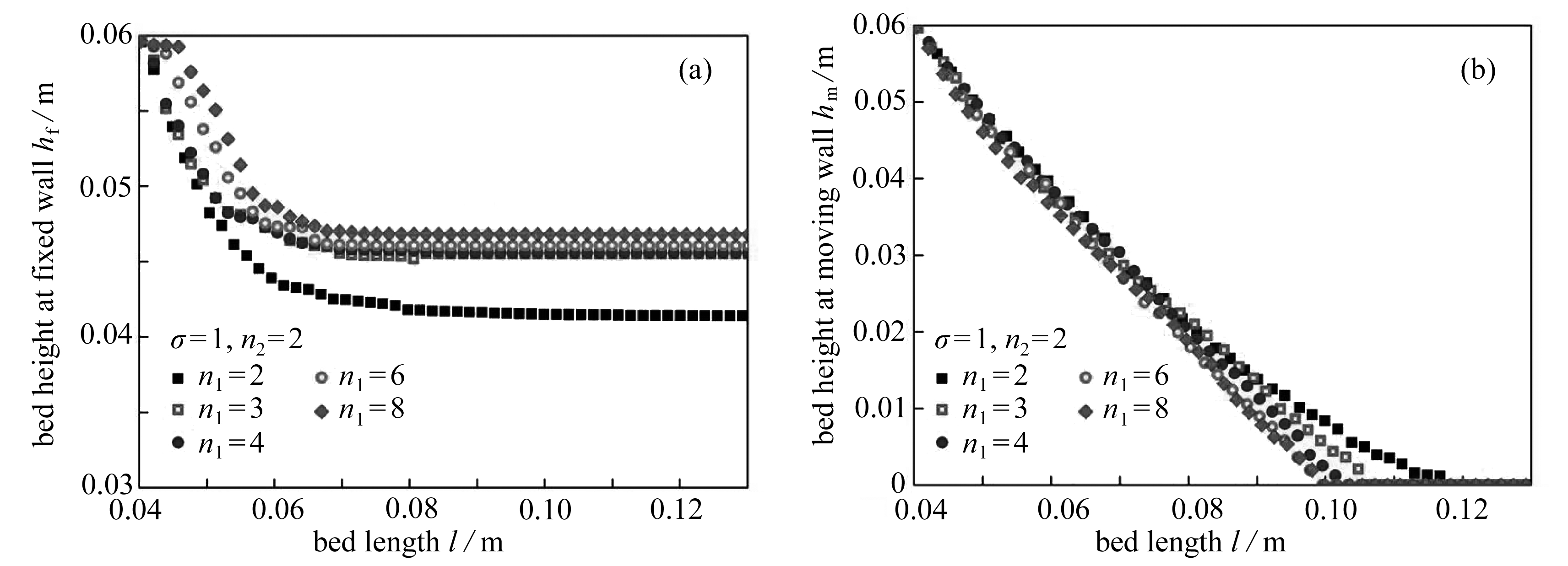
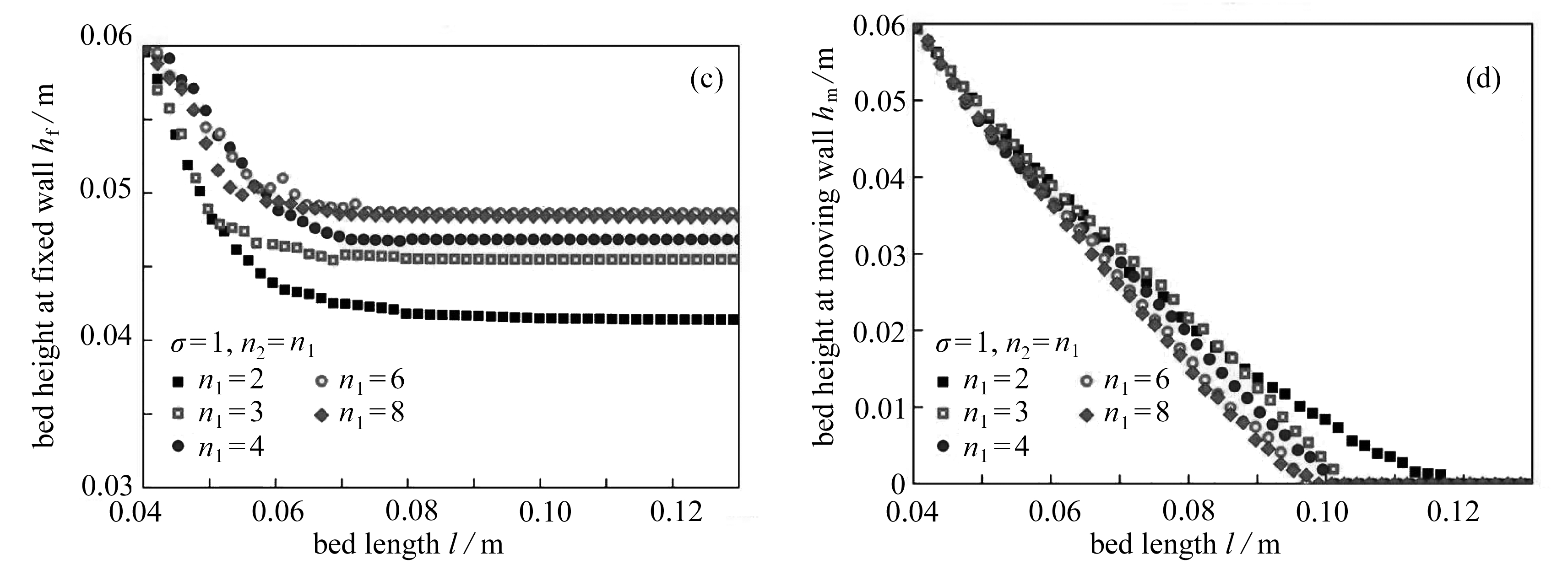
图9 表面尖锐度对颗粒床固定墙侧和移动墙侧高度变化的影响
Fig. 9 The effects of blockiness parameters on the granular bed heights of the fixed wall and the moving wall
4.2 颗粒尖锐度对流动特性的影响
为对比分析不同尖锐度对颗粒材料流动特性的影响,这里选取尖锐度参数分别为2,3,4,5,6,7和8且长宽比σ=c/a(=b)=1的球体、柱体和块体颗粒,如图8所示.对不同单元形态填充的颗粒床统计其固定墙侧和移动墙侧的高度变化,如图9所示,其中图9(a)、(b)为从球体到圆柱体,图9(c)、(d)为从球体到正方体.从图中可以发现,表面尖锐度显著影响颗粒材料的流动特性.随着尖锐度的增加,固定墙侧高度的下降速率均呈减小趋势,而移动墙侧高度的下降速率则均呈增加趋势.此外,对于固定墙侧,球形颗粒床具有最快的下降速率,而块体颗粒的下降速率最慢.与之相反,对于移动墙侧,球形颗粒床具有最慢的下降速率,而块体颗粒的下降速率最快.
对不同表面尖锐度下颗粒床的初始体积分数C0和结束时刻的休止角θ进行统计,如图10所示.可以发现,当尖锐度参数小于4时,初始体积分数和休止角随尖锐度的增加而增加,而当尖锐度参数大于4时,体积分数和休止角不再随尖锐度的增加而显著变化.在颗粒材料随机堆积和流动过程中,表面尖锐度增加了固定墙侧颗粒床的密实度和稳定性,同时阻碍了颗粒间的相对平动和转动,使得固定墙侧的颗粒床下降缓慢.对于移动墙侧颗粒床,表面尖锐度降低了颗粒系统的流动性,当移动墙侧空隙不断增加时,使得临近颗粒重新排列而对整个颗粒系统的影响减小,从而导致移动墙侧的颗粒床高度快速下降,进而形成较大的休止角.

(a) 初始体积分数(b) 最终休止角 (a) The initial packing fraction (b) The final angle of repose
图10 尖锐度参数对初始体积分数和休止角的影响
Fig. 10 The influences of sharpness parameters on the initial packing fraction and the angle of repose
4.3 颗粒长宽比对流动特性的影响
为研究不同长宽比σ=c/a(=b)对颗粒材料流动特性的影响, 这里选取长宽比σ=0.5, 0.75,1.0,1.25,1.5,1.75和2.0的柱状颗粒和块状颗粒,如图11所示.图12为不同长宽比的圆柱形颗粒和长方形颗粒床的高度变化关系,其中图12(a)、(b)为圆柱体,图12(c)、(d)为长方体.可以发现,随着长宽比的增加,固定墙侧和移动墙侧颗粒床高度的下降速率均无显著变化.对不同长宽比下颗粒床的初始体积分数C0和结束时刻的休止角θ进行统计,如图13所示.结果表明,无论增加或减小长宽比,都使得颗粒床的初始体积分数减小,而对休止角的影响较弱.因此,尽管长宽比减小了系统的密集度并在一定程度上阻碍颗粒间的相对滑动或滚动,但对整个颗粒系统的流动性无显著影响.以上结果表明: 表面尖锐度是影响颗粒系统流动特性的主要因素,而长宽比是次要影响因素.
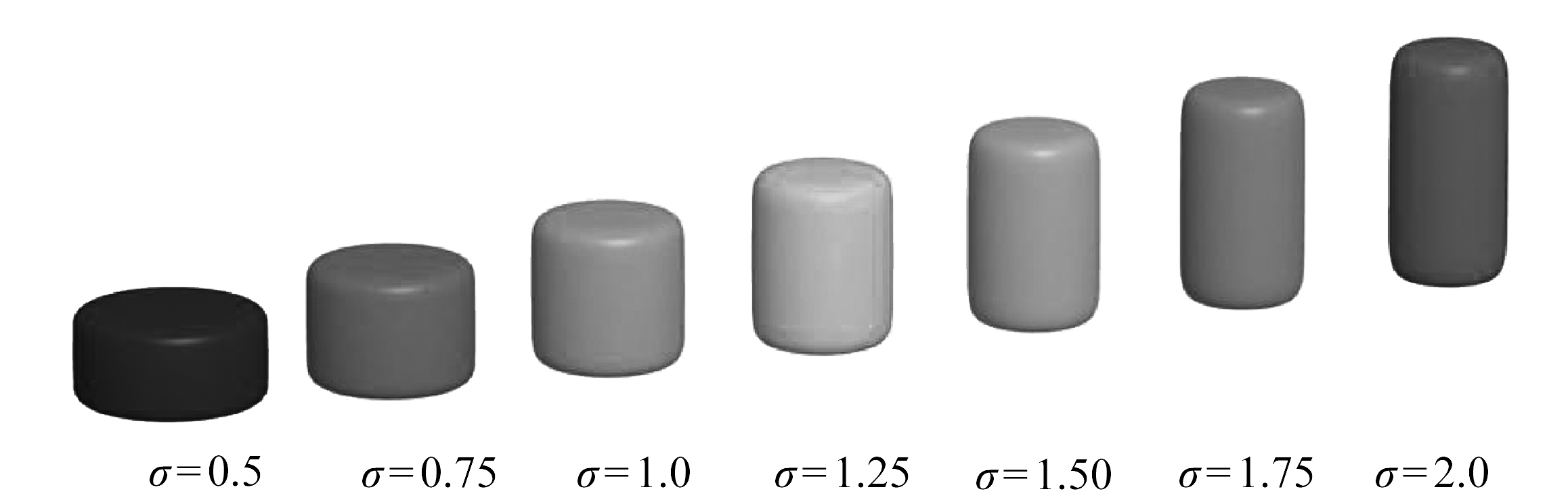
(a) 柱状颗粒(n1=8, n2=2)
(a) Cylinders (n1=8, n2=2)

(b) 块状颗粒(n1=8, n2=8)
(b) Cubes(n1=8, n2=8)
图11 长宽比对单元形态的影响
Fig. 11 The influence of the aspect ratio on the particle shape
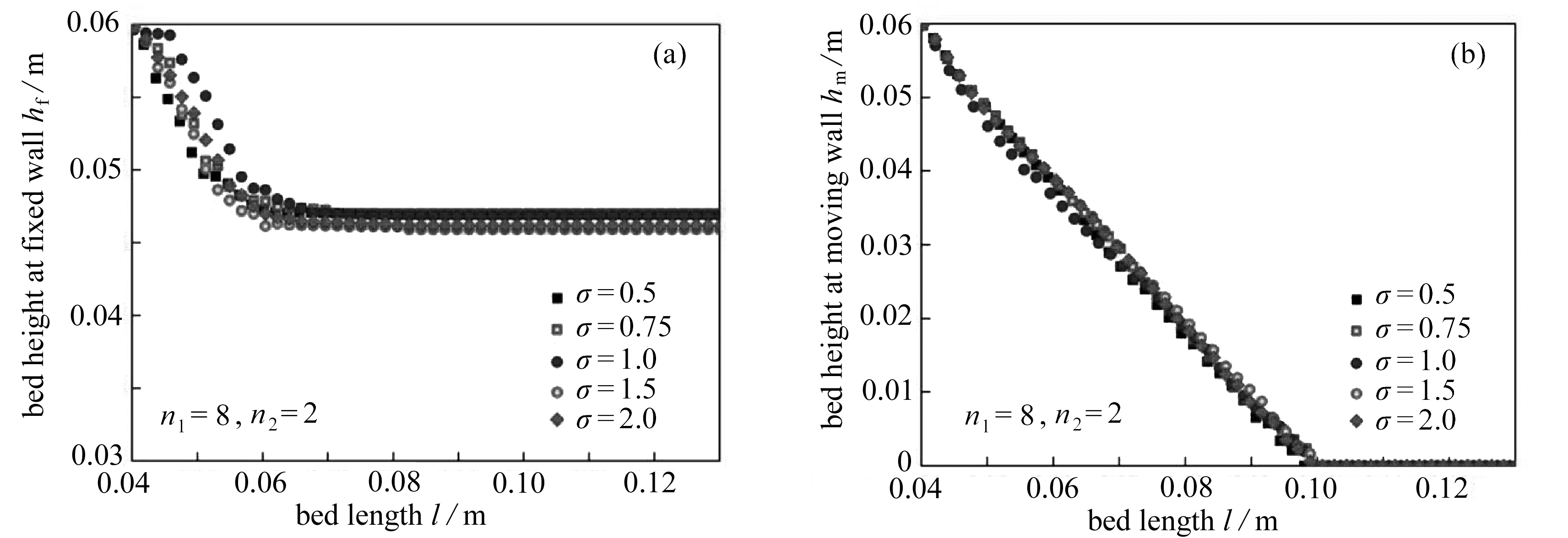
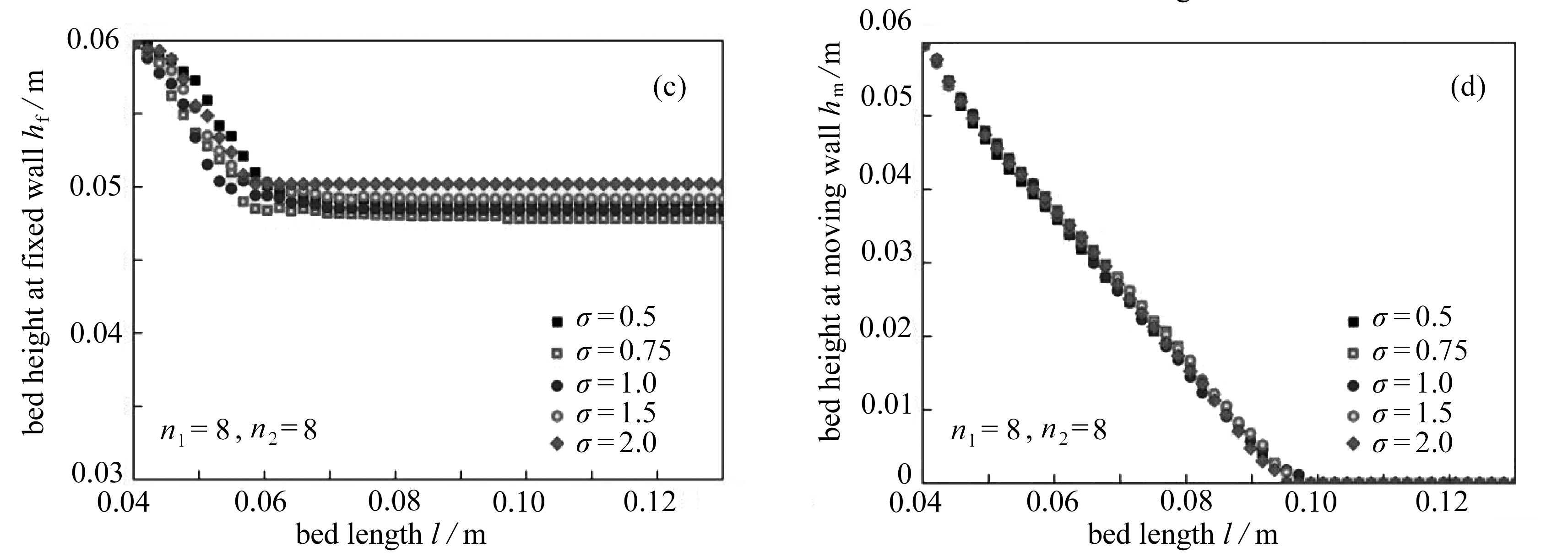
图12 长宽比对颗粒床固定墙侧和移动墙侧高度变化的影响
Fig. 12 The effects of aspect ratios on the granular bed heights of the fixed wall and the moving wall
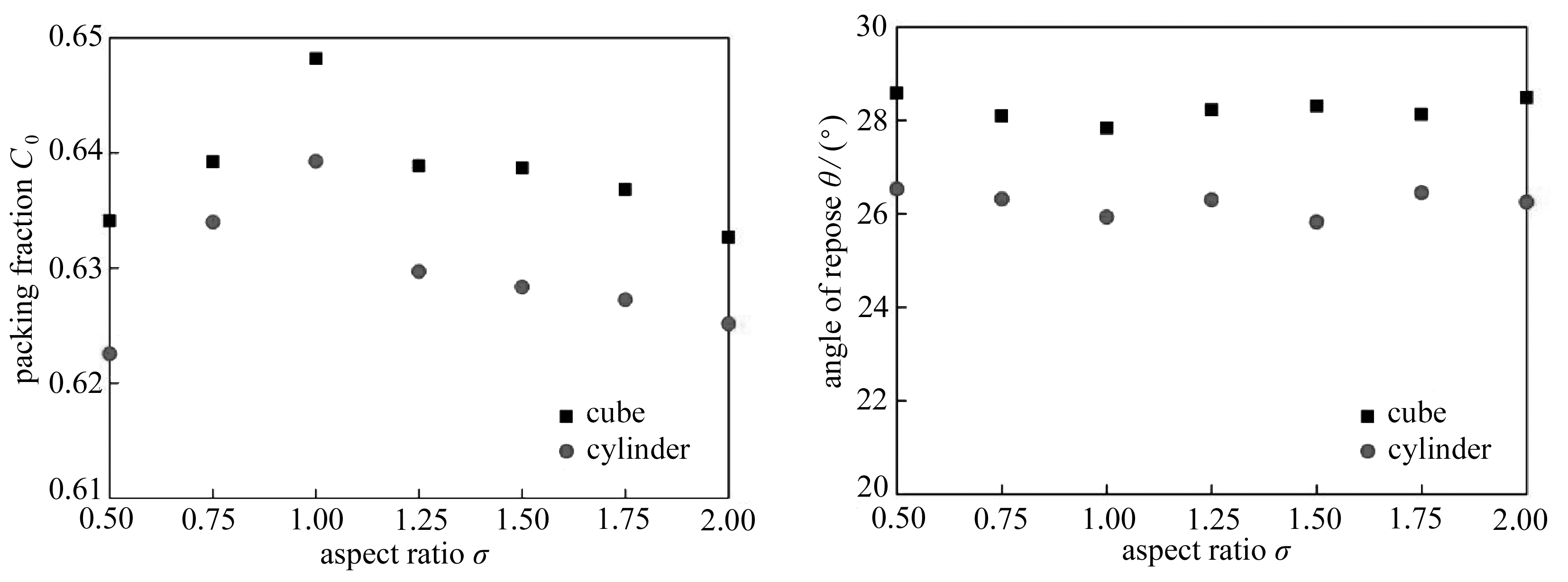
(a) 初始体积分数 (b) 最终休止角 (a) The initial packing fraction (b) The final angle of repose
图13 长宽比对初始体积分数和休止角的影响
Fig. 13 The influences of the aspect ratio on the initial packing fraction and the angle of repose
4.4 单元形态对速度分布的影响
为进一步分析单元形态对颗粒材料流动特性的影响,这里选取球体、正方体和长宽比为2的长方体颗粒,对整个流动过程中的速度分布情况进行统计,如图14所示.从图中可以发现,当处于初始时刻时,整个颗粒系统分为两种状态,即位于左下方的稳定状态和右上方的流动状态.随着容器边界向右侧移动,处于稳定状态的颗粒数目逐渐增加,而处于流动状态的颗粒数目逐渐减小,且主要位于移动墙附近的颗粒床上表面处.与球形颗粒相比,处于流动状态的块体颗粒数目较少,且整个颗粒系统较快地达到稳定状态.这主要是由于表面尖锐度增加颗粒表面的粗糙程度,阻碍单元间的相互运动,从而减弱了颗粒系统的流动性,同时增强了系统的稳定性和耗能特性,并产生较大的休止角.此外,当长宽比为2时,在两种块体颗粒的整个流动过程中速度分布无显著差别.因此,长宽比对颗粒材料流动特性的影响为次要因素,而单元表面的尖锐度是主要的影响因素.

(a) 球形颗粒(n1=n2=2, σ=1)
(a) Spheres(n1=n2=2, σ=1)

(b) 块状颗粒(n1=n2=8, σ=1)
(b) Cubes(n1=n2=8, σ=1)

(c) 块状颗粒(n1=n2=8, σ=2)
(c) Cubes(n1=n8=8, σ=2)
图14 不同单元形态的局部速度分布情况
Fig. 14 Local velocity distributions of differently shaped particles
5 结 论
本文基于超二次曲面方程构造非球形颗粒形态,在球形颗粒并行计算的基础上,发展了基于CUDA-GPU架构的超二次曲面单元并行算法.该方法通过元胞列表法实现颗粒编号重新排序,并调用核函数创建包围盒列表和Newton迭代列表,同时优化了计算模型和内存访问模式.通过与块状颗粒流动过程的试验结果进行对比验证,表明超二次曲面单元并行算法适用于模拟大规模非球形颗粒的堆积和流动过程.在此基础上进一步研究了单元表面尖锐度和长宽比对颗粒系统流动特性的影响.研究结果表明,球形颗粒具有较快的流动速率且较小的休止角,而块状颗粒具有较慢的流动速率且较大的休止角.表面尖锐度增加颗粒的粗糙程度,阻碍单元间的相对平动或转动,从而减小系统的流动性,同时增强系统的稳定性和耗能特性.此外,长宽比是影响颗粒系统流动特性的次要因素,而表面尖锐度是主要的影响因素.
[1] 季顺迎. 非均匀颗粒材料的类固-液相变行为及本构方程[J]. 力学学报, 2007, 39(2): 223-237.(JI Shunying. The quasi-solid-liquid phase transition of non-uniform granular materials and their constitutive equation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(2): 223-237.(in Chinese))
[2] 徐泳, 孙其诚, 张凌, 等. 颗粒离散元法研究进展[J]. 力学进展, 2003, 33(2): 251-260.(XU Yong, SUN Qicheng, ZHANG Ling, et al. Advances in discrete element methods for particulate materials[J]. Advances in Mechanics, 2003, 33(2): 251-260.(in Chinese))
[3] CUNDALL P A, STRACK O D L. A discrete numerical mode for granular assemblies[J]. Géotech-nique, 1979, 29(1): 47-65.
[4] ZHU H P, ZHOU Z Y, YANG R Y, et al. Discrete particle simulation of particulate systems: a review of major applications and findings[J]. Chemical Engineering Science, 2008, 62(13): 3378-3396.
[5] 常晓林, 马刚, 周伟, 等. 颗粒形状及粒间摩擦角对堆石体宏观力学行为的影响[J]. 岩土工程学报, 2012, 34(4): 646-653.(CHANG Xiaolin, MA Gang, ZHOU Wei, et al. Influences of particle shape and inter-particle friction angle on macroscopic response of rockfill[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(4): 646-653.(in Chinese))
[6] 严颖, 赵金凤, 季顺迎. 块石含量和空间分布对土石混合体抗剪强度影响的离散元分析[J]. 工程力学, 2017, 34(6): 146-156.(YAN Ying, ZHAO Jinfeng, JI Shunying. Discrete element analysis of the influence of rock content and rock spatial distribution on shear strength of rock-soil mixtures[J]. Engineering Mechanics, 2017, 34(6): 146-156.(in Chinese))
[7] 崔泽群, 陈友川, 赵永志, 等. 基于超二次曲面的非球形离散单元模型研究[J]. 计算力学学报, 2013, 30(6): 854-859.(CUI Zequn, CHEN Youchuan, ZHAO Yongzhi, et al. Study of discrete element model for non-sphere particles base on super-quadric[J]. Chinese Journal of Computational Mechanics, 2013, 30(6): 854-859.(in Chinese))
[8] LU G, THIRD J R, MÜLLER C R. Discrete element models for non-spherical particle systems: from theoretical developments to applications[J]. Chemical Engineering Science, 2015, 127: 425-465.
[9] ZHONG W, YU A, LIU X, et al. DEM/CFD-DEM modelling of non-spherical particulate systems: theoretical developments and applications[J]. Powder Technology, 2016, 302: 108-152.
[10] 严颖, 季顺迎. 颗粒形态对离散介质剪切强度的影响[J]. 岩土力学, 2009, 30(S1): 225-230.(YAN Ying, JI Shunying. Effects of particle shape on shear strength of discrete media[J]. Rock and Soil Mechanics, 2009, 30(S1): 225-230.(in Chinese))
[11] GUI N, YANG X, TU J, et al. Effect of roundness on the discharge flow of granular particles[J]. Powder Technology, 2017, 314: 140-147.
[12] LIU S D, ZHOU Z Y, ZOU R P, et al. Flow characteristics and discharge rate of ellipsoidal particles in a flat bottom hopper[J]. Powder Technology, 2014, 253: 70-79.
[13] ZHENG Q J, ZHOU Z Y, YU A B. Contact forces between viscoelastic ellipsoidal particles[J]. Powder Technology, 2013, 248: 25-33.
[14] CLEARY P W, SINNOTT M D, MORRISON R D, et al. Analysis of cone crusher performance with changes in material properties and operating conditions using DEM[J]. Minerals Engineering, 2017, 100: 49-70.
[15] CLEARY P W, HILTON J E, SINNOTTO M D. Modelling of industrial particle and multiphase flows[J]. Powder Technology, 2017, 314: 232-252.
[16] 刘璐, 龙雪, 季顺迎. 基于扩展多面体的离散单元法及其作用于圆桩的冰载荷计算[J]. 力学学报, 2015, 47(6): 1046-1057.(LIU Lu, LONG Xue, JI Shunying. Dilated polyhedra based discrete element method and its application of ice load on cylindrical pile[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(6): 1046-1057.(in Chinese))
[17] 孙珊珊, 严颖, 赵春发, 等. 往复荷载下铁路道砟沉降特性的扩展多面体离散元分析[J]. 铁道学报, 2015, 37(11): 89-95.(SUN Shanshan, YAN Ying, ZHAO Chunfa, et al. Dilated polyhedral discrete element analysis of settlement characteristics of railway ballast under cyclic loading[J]. Journal of the China Railway Society, 2015, 37(11): 89-95.(in Chinese))
[18] 许文祥, 孙洪广, 陈文, 等. 软物质系颗粒材料组成、微结构与传输性能之间关联建模综述[J]. 物理学报, 2016, 65(17): 75-98.(XU Wenxiang, SUN Hongguang, CHEN Wen, et al. A review of correlative modeling for transport properties, microstructures, and compositions of granular materials in soft matter[J]. Acta Physica Sinica, 2016, 65(17): 75-98.(in Chinese))
[19] SU D, YAN W M. 3D characterization of general-shape sand particles using microfocus X-ray computed tomography and spherical harmonic functions, and particle regeneration using multivariate random vector[J]. Powder Technology, 2018, 323: 8-23.
[20] KAWAMOTO R, AND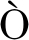 E, VIGGIANI G, et al. All you need is shape: predicting shear banding in sand with LS-DEM[J]. Journal of the Mechanics and Physics of Solids, 2018, 111: 375-392.
E, VIGGIANI G, et al. All you need is shape: predicting shear banding in sand with LS-DEM[J]. Journal of the Mechanics and Physics of Solids, 2018, 111: 375-392.
[21] LIM K W, KAWAMOTO R, AND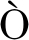 E, et al. Multiscale characterization and modeling of granular materials through a computational mechanics avatar: a case study with experiment[J]. Acta Geotechnica, 2015, 11(2): 243-253.
E, et al. Multiscale characterization and modeling of granular materials through a computational mechanics avatar: a case study with experiment[J]. Acta Geotechnica, 2015, 11(2): 243-253.
[22] 王嗣强, 季顺迎. 基于超二次曲面的颗粒材料缓冲性能离散元分析[J]. 物理学报, 2018, 67(9): 094501. DOI: 10.7498/aps.67.20172549.(WANG Siqiang, JI Shunying. Discrete element analysis of buffering capacity of non-spherical granular materials based on super-quadric method[J]. Acta Physica Sinica, 2018, 67(9): 094501. DOI: 10.7498/aps.67.20172549.(in Chinese))
[23] DELANEY G W, CLEARY P W. The packing properties of superellipsoids[J]. Europhysics Letters, 2010, 89(3): 34002. DOI: 10.1209/0295-5075/89/34002.
[24] MA H, ZHAO Y. Modelling of the flow of ellipsoidal particles in a horizontal rotating drum based on DEM simulation[J]. Chemical Engineering Science, 2017, 172: 636-651.
[25] MA H, ZHAO Y. Investigating the flow of rod-like particles in a horizontal rotating drum using DEM simulation[J]. Granular Matter, 2018, 20(3): 20-41.
[26] HÖHNER D, WIRTZ S, SCHERER V. A study on the influence of particle shape on the mechanical interactions of granular media in a hopper using the discrete element method[J]. Powder Technology, 2015, 278: 286-305.
[27] AMRITKAR A, DEB S, TAFTI D. Efficient parallel CFD-DEM simulations using OpenMP[J]. Journal of Computational Physics, 2014, 256: 501-519.
[28] CHEN J, MATUTTIS H G. Optimization and OpenMP parallelization of a discrete element code for convex polyhedra on multi-core machines[J]. International Journal of Modern Physics C, 2013, 24(2): 1350001. DOI: 10.1142/S0129183113500010.
[29] LEMIEUX M, LÉONARD G, DOUCET J, et al. Large-scale numerical investigation of solids mixing in a V-blender using the discrete element method[J]. Powder Technology, 2008, 181(2): 205-216.
[30] YAN B, REGUEIRO R A. A comprehensive study of MPI parallelism in three-dimensional discrete element method (DEM) simulation of complex-shaped granular particles[J]. Computational Particle Mechanics, 2018, 5(4): 553-577.
[31] LIU H, TAFTI D K, LI T. Hybrid parallelism in MFIX CFD-DEM using OpenMP[J]. Powder Technology, 2014, 259: 22-29.
[32] BERGER R, KLOSS C, KOHLMEYER A, et al. Hybrid parallelization of the LIGGGHTS open-source DEM code[J]. Powder Technology, 2015, 278: 234-247.
[33] 付晓东, 盛谦, 张勇慧. 基于OpenMP的非连续变形分析并行计算方法[J]. 岩土力学, 2014, 35(8): 2401-2407.(FU Xiaodong, SHENG Qian, ZHANG Yonghui. Parallel computing method for discontinuous deformation analysis using OpenMP[J]. Rock and Soil Mechanics, 2014, 35(8): 2401-2407.(in Chinese))
[34] 严成增, 郑宏, 孙冠华, 等. 基于OpenMP的二维有限元-离散元并行分析方法[J]. 岩土力学, 2014, 9(35): 2717-2724.(YAN Chengzeng, ZHENG Hong, SUN Guanhua, et al. Parallel analysis of two-dimensional finite-discrete element method based on OpenMP[J]. Rock and Soil Mechanics, 2014, 9(35): 2717-2724.(in Chinese))
[35] WASHIZAWA T, NAKAHARA Y. Parallel computing of discrete element method on GPU[J]. Applied Mathematics, 2013, 4(1): 242-247.
[36] XU J, QI H, FANG X, et al. Quasi-real-time simulation of rotating drum using discrete element method with parallel GPU computing[J]. Particuology, 2011, 9(4): 446-450.
[37] SEO I S, KIM J H, SHIN J H, et al. Particle behaviors of printing system using GPU-based discrete element method[J]. Journal of Mechanical Science and Technology, 2014, 28(12): 5083-5087.
[38] LONG X, JI S, WANG Y. Validation of microparameters in discrete element modeling of sea ice failure process[J]. Particulate Science and Technology, 2018, 37(5): 546-555. DOI: 10.1080/02726351.2017.1404515.
[39] QI J, LI K, JIANG H, et al. GPU-accelerated DEM implementation with CUDA[J]. International Journal of Computational Science and Engineering, 2015, 11(3): 330-337.
[40] HE Y, EVANS T J, YU A B, et al. A GPU-based DEM for modelling large scale powder compaction with wide size distributions[J]. Powder Technology, 2018, 333: 219-228.
[41] 狄少丞, 季顺迎. 海冰与自升式海洋平台相互作用GPU离散元模拟[J]. 力学学报, 2014, 46(4): 561-571.(DI Shaocheng, JI Shunying. GPU-based discrete element modelling of interaction between sea ice and jack-up platform structure[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(4): 561-571.(in Chinese))
[42] GAN J Q, ZHOU Z Y, YU A B. A GPU-based DEM approach for modelling of particulate systems[J]. Powder Technology, 2016, 301: 1172-1182.
[43] GOVENDER N, WILKE D N, PIZETTE P, et al. A study of shape non-uniformity and poly-dispersity in hopper discharge of spherical and polyhedral particle systems using the Blaze-DEM GPU code[J]. Applied Mathematics and Computation, 2018, 319: 318-336.
[44] GOVENDER N, WILKE D N, KOK S. Collision detection of convex polyhedra on the NVIDIA GPU architecture for the discrete element method[J]. Applied Mathematics and Computation, 2015, 267: 810-829.
[45] SOLTANBEIGI B, PODLOZHNYUK A, PAPANICOLOPULOS S A, et al. DEM study of mechanical characteristics of multi-spherical and superquadric particles at micro and macro scales[J]. Powder Technology, 2018, 329: 288-303.
[46] AH B. Superquadrics and angle-preserving transformations[J]. IEEE Computer Graphics and Applications, 1981, 1(1): 11-23.
[47] NISHIURA D, SAKAGUCHI H. Parallel-vector algorithms for particle simulations on shared-memory multiprocessors[J]. Journal of Computational Physics, 2011, 230: 1923-1938.
[48] PORTAL R, DIAS J, DE SOUSA L. Contact detection between convex superquadric surfaces[J]. Archive of Mechanical Engineering, 2010, 57(2): 165-186.
[49] PODLOZHNYUK A, PIRKER S, KLOSS C. Efficient implementation of superquadric particles in discrete element method within an open-source framework[J]. Computational Particle Mechanics, 2016, 4(1): 101-118.
[50] ZHOU Z Y, ZOU R P, PINSON D, et al. Dynamic simulation of the packing of ellipsoidal particles[J]. Industrial and Engineering Chemistry Research, 2011, 50(16): 9787-9798.
[51] GOLDMAN R. Curvature formulas for implicit curves and surfaces[J]. Computer Aided Geometric Design, 2005, 22(7): 632-658.
[52] OWEN P J, CLEARY P W, MÉRIAUX C. Quasi-static fall of planar granular columns: comparison of 2D and 3D discrete element modelling with laboratory experiments[J]. Geomechanics and Geoengineering, 2009, 4(1): 55-77.