引 言
微分方程数值求解的稳定性是判断数值方法好坏的重要指标之一.20世纪60年代，经过Dahlquist、Widlund、Gear等学者的创新和发展，稳定性理论得到深入发展.Dahlquist[1]以线性方程y′=μy为模型方程提出了A-稳定，即稳定域包含左半复平面.Widlund[2]提出了A(α)-稳定，即稳定域边界与正实轴的夹角为α.Gear[3]提出了刚性稳定，同时将A-稳定概念推广到非线性问题.1975年，Dahlquist[4]提出了单支方法及线性多步法的G-稳定概念.Butcher等[5-6]以非线性方程y′=f(y)为模型方程，研究了Runge-Kutta法的非线性稳定性,建立了Runge-Kutta方法的B-稳定与代数稳定理论，以及一般线性方法的代数稳定准则.Li(李寿佛)[7]建立了一般线性方法的(k,p,q)稳定性理论以及(k,p,q)的弱代数稳定性准则.对于刚性微分方程，希望刚性分量能够尽快衰减，同时稳定域包含左半复平面，仅A-稳定是不够的.Ehle[8]提出了L-稳定，Hairer等[9]指出L-稳定的数值方法会引入阻尼效应，但对抑制高频振荡是很有效的，进而一些学者提出了基于L-稳定求解刚性方程的隐式单步法和多步法，这些方法多基于常微分方程，针对微分-代数方程的L-稳定方法研究相对较少.
多体系统动力学方程的典型形式为微分-代数方程，由常微分运动方程和代数约束方程组成，其数值求解是多体系统动力学研究中的热点和难点.目前微分-代数方程的数值解法主要有直接积分法、精细指数积分法[10]、最优控制保辛算法[11]、Newmark-β类方法等.这些方法针对特定问题表现出了较高的数值精度，例如，精细指数积分法主要求解弱非线性问题，其数值精度要比同阶的Runge-Kutta方法高；最优控制保辛算法在轨迹追踪等方面发挥了很大优势，能较好地与目标轨迹相吻合；Newmark-β类方法在短时间仿真下表现出较好的收敛性，长时间仿真过程中误差累积较为严重[12]，需结合约束投影等方法进行修正[13-14]，这些方法对于稳定性的研究相对较少.本文建立了多体系统动力学微分-代数方程的L-稳定方法一般形式，基于等距节点、Chebyshev节点和Legendre节点给出了具体构造过程，并通过平面双连杆机械臂系统进行验证比较方程的L-稳定方法一般形式，基于等距节点、Chebyshev节点和Legendre节点给出了具体构造过程，并通过平面双连杆机械臂系统进行验证比较.
1 多体系统动力学微分-代数方程
多体系统动力学指标-3的微分-代数方程形式为
(1)
其中q=[q1(t) q2(t) … qn(t)]T为系统的广义坐标，
为广义速度，
为广义加速度， λ=[λ1 λ2 … λm]T是Lagrange乘子，M∈Rn×n是对称正定的质量矩阵，F∈Rn是广义力矢量，Φ=[Φ1 Φ2 … Φm]T 为m个完整的位移约束.
对约束方程Φ关于时间t分别求一、二阶导数，并与方程(1)中的微分方程联立可得如下指标-2、指标-1的微分-代数方程形式：
(2)
(3)
当初值
已知时，可以使用Runge-Kutta法直接求解指标-1(方程(3))，但在选取步长较大的情况下，会导致精度降低，总能量随时间而增大[15]；步长较小，会导致计算效率降低，而且稳定性较差，并且对于指标-3(方程(1))和指标-2(方程(2))，不能使用Runge-Kutta法直接求解.下面构造L-稳定方法，可以用于求解指标-1、-2、-3的多体系统动力学微分-代数方程.
2 微分-代数方程L稳定格式的构造
2.1 L稳定方法的一般形式
1972年，Shampine和Watts[16]提出了求解常微分方程的块隐式单步法，将r个离散时刻做成一个块向量，由一个时刻的输入值得到r个时刻的输出值，并证明了该方法是A-稳定的.这种方法每个块向量中的时间步长是等距的.本文对其进行改进，将块向量对应于单步区间中取点，即在迭代求解过程中，设单步区间[tk,tk+1]，时间步长h=tk+1-tk，选取节点ci(i=1,2,…,r)，tk<c1<c2<…<cr=tk+1，构造微分-代数方程求解格式，其中ci(i=1,2,…,r)可以是等距节点，也可以是非等距节点.以多体系统动力学微分-代数指标-1(方程(3))为例，降阶后可得如下一阶微分方程组：
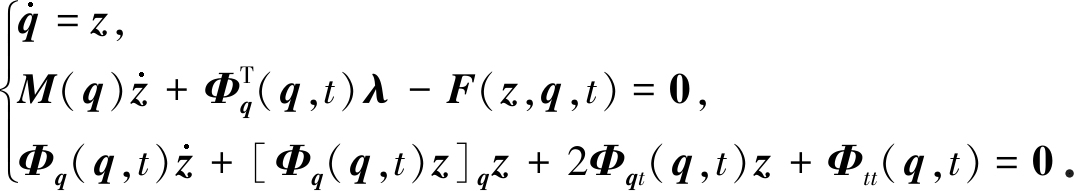
(4)
令
构造求解公式如下：
(5)
其中
为Kronecker积.
将式(5)代入试验方程
(6)
得到稳定性函数为
(7)
其中λ=αh，Ir为r阶单位矩阵,
对稳定性函数R(λ)使用Padé逼近，可以构造L-稳定的求解公式.
定理1(Ehle定理及猜想) 对于(k,j)-Padé逼近，如果k≤j≤k+2，那么此Padé逼近为A-稳定的；如果k<j≤k+2，那么此Padé逼近是L-稳定的[17].
对yi,i=1,2,…,r在tk处进行Taylor展开，设
项系数为待定常数，略去后面的高阶项，即
(8)
其中μi为待定常数，hi=ci-tk.将式(8)代入式(5)可得
(9)
由式(9)可以得到使用待定常数表达的B,d，代入稳定性函数(7)，与相应的Padé逼近形式对比即可得到待定常数μi,i=1,2,…,r的值，从而可以得到B,d的值，代入式(5)可得具体的求解公式形式.
2.2 基于等距节点的L-稳定格式
对于等距节点ci(i=1,2,…,r)，有ci=tk+hi/r,i=1,2,…,r.例如r=3，h=1时，等距节点为ci=tk+i/3,i=1,2,3，此时hi=i/3,i=1,2,3，式(9)变为
(10)
将B,d代入稳定性函数(7)并与(2,3)-Padé逼近进行对比，可求出待定常数
代入B,d的表达式可得
(11)
将上式代入式(5)可得求解公式.使用同样方法可以构造其他r值的L-稳定求解格式.
2.3 基于非等距节点的L-稳定格式
当节点ci(i=1,2,…,r)为Chebyshev多项式的零点时，在区间[tk,tk+1]内，有
(12)
以r=3,h=1为例，此时
代入式(9)得到
(13)
其中
将B,d代入稳定性函数(7)，并与(2,3)-Padé进行对比，得到
从而得到相应的B,d为
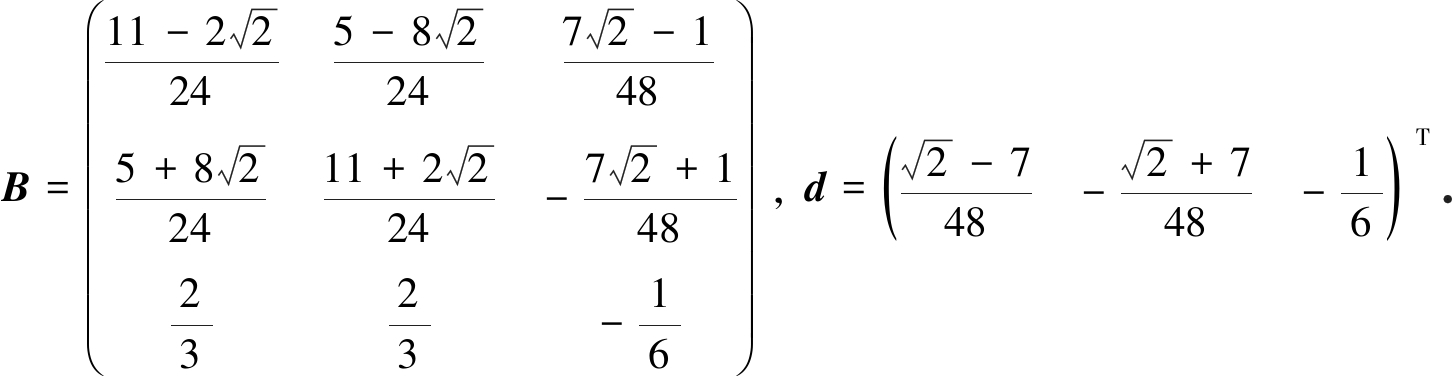
(14)
当节点ci(i=1,2,…,r)为Legendre多项式的零点时，同样以r=3,h=1为例，得到
计算可得
相应的B,d为
(15)
将上式代入式(5)可得求解公式.使用同样方法可以构造其他r值的非等距节点的L-稳定求解格式.
3 数 值 算 例
图1为一个平面双连杆机械臂，其中连杆的长度用L1,L2表示，
质量用m1,m2表示，m1=1 kg,m2=2 kg，转角用θ1,θ2表示，在初始时刻，θ1=π/3,θ2=-π/6，(x1,y1)，(x2,y2)表示两连杆的质心位置坐标.
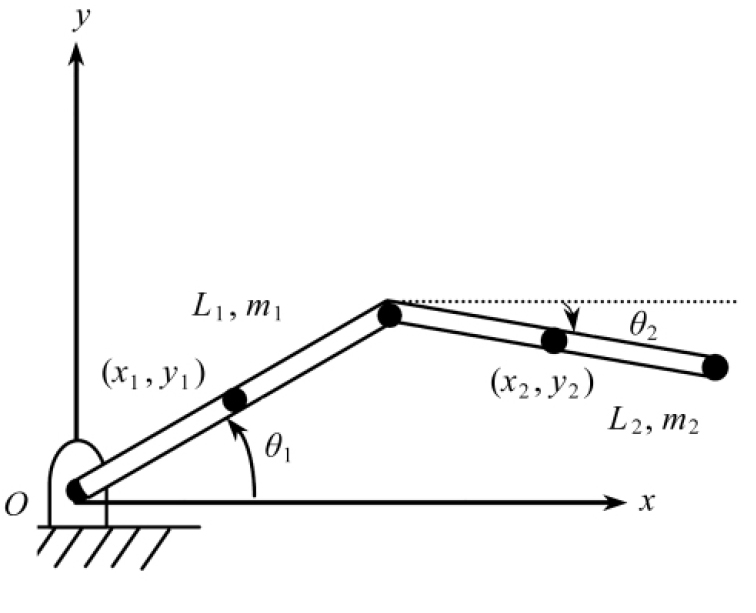
图1 平面双连杆机械臂
Fig. 1 A planar two-link manipulator
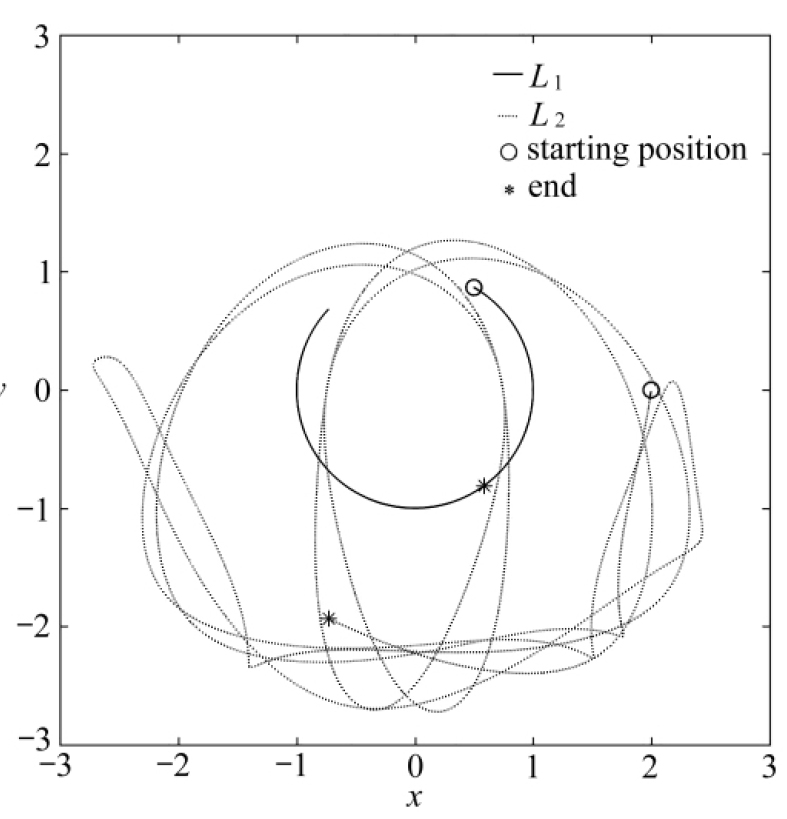
图2 连杆末端轨迹
Fig. 2 The connecting rod end trajectory
根据Lagrange函数建立平面双连杆机械臂动力学微分-代数方程，广义坐标和广义质量矩阵分别为q=(x1,y1,θ1,x2,y2,θ2)T，M=diag(m1,m1,I1,m2,m2,I2)，其中
为连杆转动惯量，F=[0,-m1g,0,0,-m2g,0]T为广义力矢量.
采用(2，4)-Padé逼近，此时r=4，将小区间划分为4等份进行求解，选取步长h=0.01，仿真时间为10 s，使用MATLAB编程，循环求解过程采用Newton迭代法计算，最大容许误差为10-3，可得到连杆末端轨迹如图2，连杆末端起始位置用圆形符号表示，终止位置用星形表示.图3为连杆末端xOy坐标的时间历程图，图4为系统总能量、动能、势能时间历程图，图5为约束函数、速度级约束、加速度级约束时间历程图.
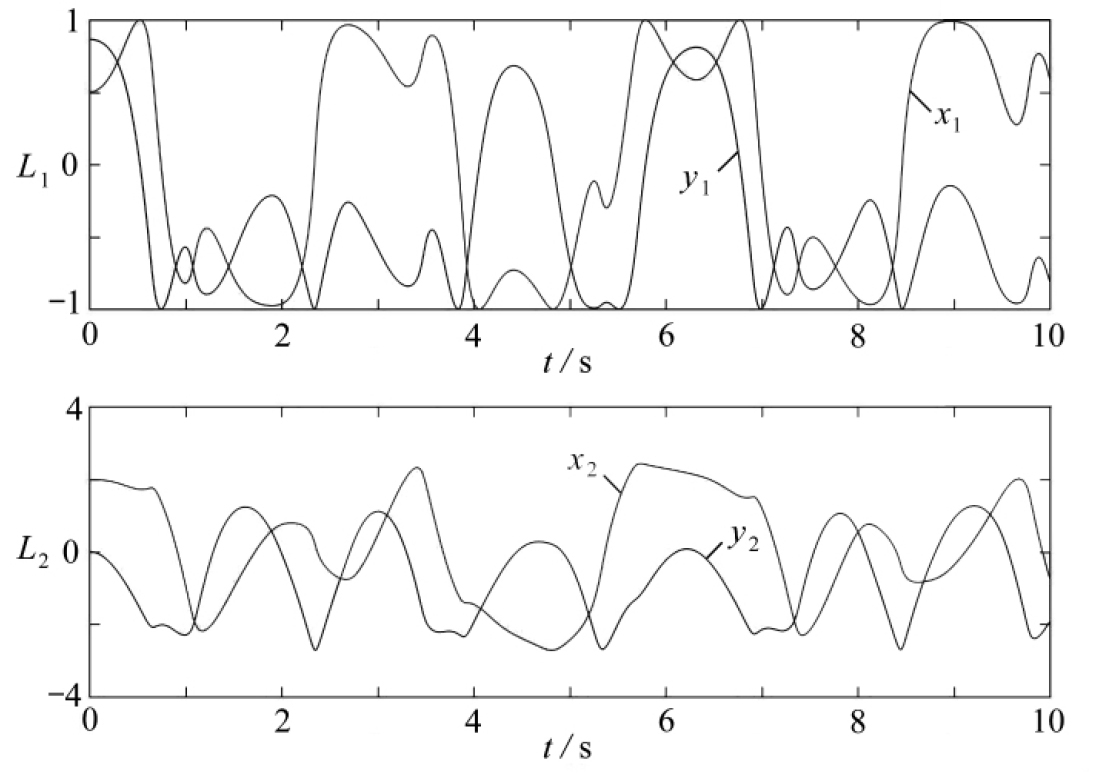
图3 连杆末端xOy坐标时间历程
Fig. 3 Time histories of xOy coordinates at the connecting rod end
图4 系统总能量、动能、势能时间历程
Fig. 4 Total energy, kinetic energy, potential energy time histories of the system
从图2～5可以看出，本文给出的L-稳定方法在仿真过程中能够保持较好的稳定性，总能量误差和各级约束误差均较小，适用于多体系统动力学仿真.下面分不同情况对该方法进行数值验证与比较.
1) 仿真时间为t=10 s，每个时间区间上取相同等距节点数(r=4)，对不同步长结果进行比较，见表1.可以看出，随着步长减小，程序运行所花费的时间增大，最大能量误差|H|max减小，同时约束函数、速度级约束和加速度级约束保持得更好.因此在仿真时间较短的情况下，选择较小的步长有利于提高求解精度和减弱约束违约现象.
图5 约束函数、速度级约束、加速度级约束时间历程
Fig. 5 Time histories of constraint functions and speed-level and acceleration-level constraints
表1 L-稳定方法在不同步长下的结果比较
Table 1 Results of the L-stable method with different steps
stepruntime T/sHmaxconstraint function Φspeed-level constraint Φtacceleration-level constraint Φtth=0.015.890 67.000 7E-56.845 9E-73.748 0E-75.659 5E-12h=0.00510.875 08.807 8E-71.915 4E-96.668 6E-91.984 6E-12h=0.00142.640 65.507 4E-117.676 6E-134.180 0E-131.421 1E-13
表2 L-稳定方法在不同节点数下的结果比较
Table 2 Results of the L-stable method with different node numbers
node numberruntime T/sHmaxconstraint function Φspeed-level constraint Φtacceleration-level constraint Φttr=31.687 50.002 15.821 2E-53.926 7E-46.262 5E-12r=45.890 67.000 7E-56.845 9E-73.748 0E-75.659 5E-12
表3 L-稳定方法与Runge-Kutta法在相同步长下的结果比较(h=0.01)
Table 3 Comparison between the L-stable method and the Runge-Kutta method
with the same step (h=0.01)
runtime T/sHmaxconstraint function Φspeed-level constraint Φtacceleration-level constraint ΦttL-stable5.890 67.000 7E-56.845 9E-73.748 0E-75.659 5E-12Runge-Kutta0.390 60.262 80.008 70.002 19.237 1E-14
2) 仿真时间为t=10 s，固定步长h=0.01，每个时间区间内选择不同的等距节点数进行比较(r=3,4)，见表2.可以看出 ，当r=4时，虽然耗费时间增大，但是最大能量误差、约束函数、速度级约束和加速度级约束均小于r=3时的结果，因此节点数增加可以提高精度.
3) 仿真时间为t=10 s，步长h=0.01，r=4的L-稳定方法与Runge-Kutta法结果比较见表3.可以看出，用L-稳定方法求解微分-代数方程，最大能量误差、约束函数和速度级约束，明显要比Runge-Kutta法的小，虽然加速度级约束精度比Runge-Kutta法稍低，但是L-稳定方法的总能量随时间增加而保持稳定状态，而Runge-Kutta法的总能量随时间一直在快速增加，如图6、7所示.
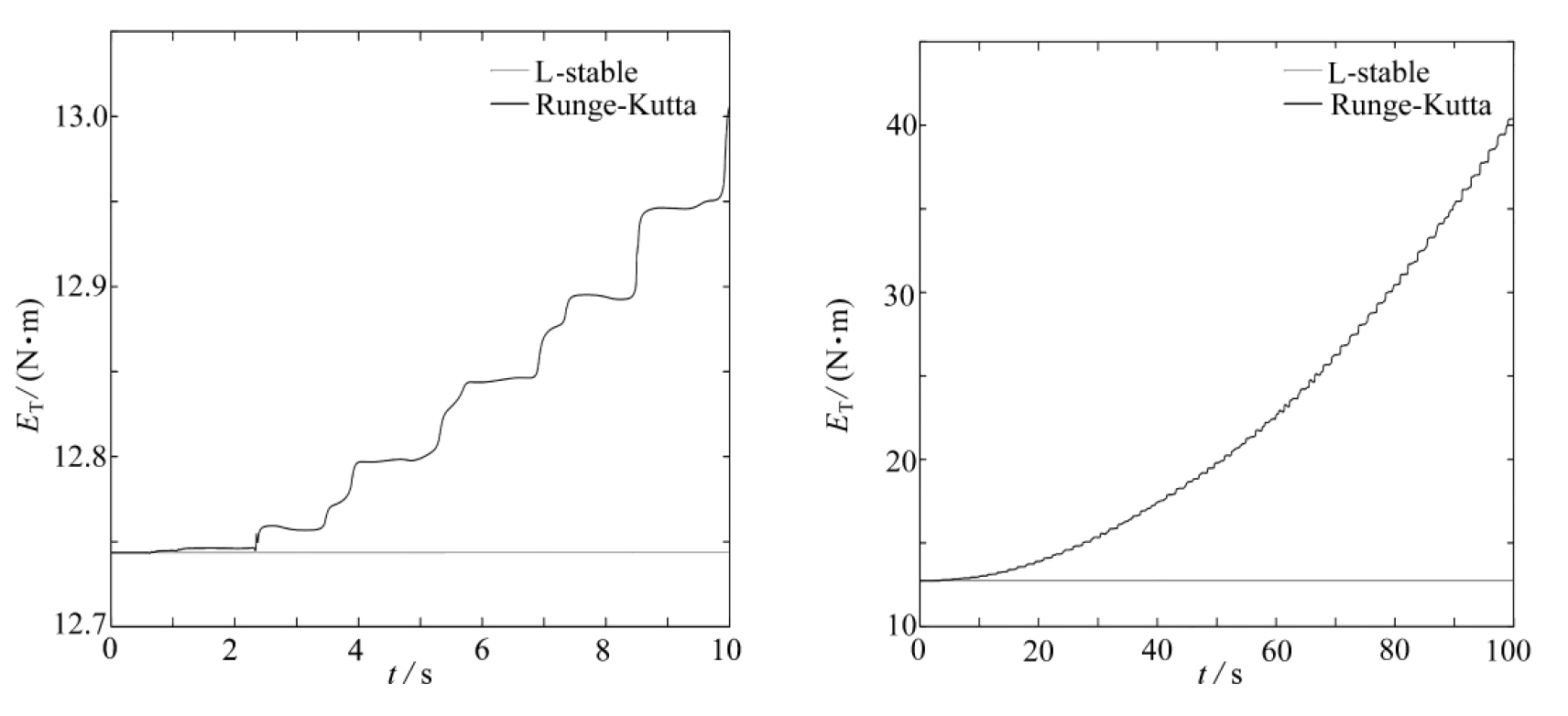
图6 仿真时间10 s时L-稳定方法与Runge-Kutta法的系统总能量时间历程 图7 仿真时间100 s时L-稳定方法与Runge-Kutta法的系统总能量时间历程
Fig. 6 Total energy time histories of the L-stable method and the Runge-Kutta method (t=10 s) Fig. 7 Total energy time histories of the L-stable method and the Runge-Kutta method (t=100 s)
4) 仿真时间为t=10 s，步长h=0.01，相同节点数(r=4)，用L-稳定方法对指标-1、-2、-3的微分-代数方程组进行求解，结果比较见表4.可以看出，L-稳定方法求解指标-1、-2、-3的微分-代数方程组所花费的时间相差不大，指标-1和指标-2的最大能量误差要比指标-3小，指标-3的约束函数误差最小，指标-2的速度级约束误差最小，指标-1的加速度级约束误差最小.综合比较可知，指标-1的整体精度较高.
表4 L-稳定方法求解指标-1、-2、-3的微分-代数方程组结果比较
Table 4 Comparison of indices-1,-2,-3 solutions to differential-algebraic equations with the L-stable method
runtime T/sHmaxconstraint function Φspeed-level constraint Φtacceleration-level constraint Φttindex-15.890 67.000 7E-56.845 9E-73.748 0E-75.659 5E-12index-25.421 93.216 3E-54.394 9E-91.849 8E-140.070 4index-35.609 40.001 12.664 5E-155.940 5E-40.985 4
表5 L-稳定方法取等距节点与非等距节点的结果比较
Table 5 Comparison of the results from the L-stable method with uniform and non-uniform nodes
runtime T/sHmaxconstraint function Φspeed-level constraint Φtacceleration-level constraint Φttuniform nodes5.609 40.001 12.775 6E-155.940 5E-40.985 4Chebyshev nodes5.218 84.324 5E-52.720 0E-151.809 4E-40.688 0Legendre nodes5.109 42.532 7E-42.886 6E-152.904 7E-40.756 0
5) 相同步长下，指标-3的L-稳定方法选取等距节点与非等距节点比较.取步长h=0.01，结果比较见表5.可以看出，当L-稳定方法选择非等距节点时最大能量误差要小于取等距节点时的能量误差，其中Chebyshev节点综合精度较高.
4 精度实验与分析
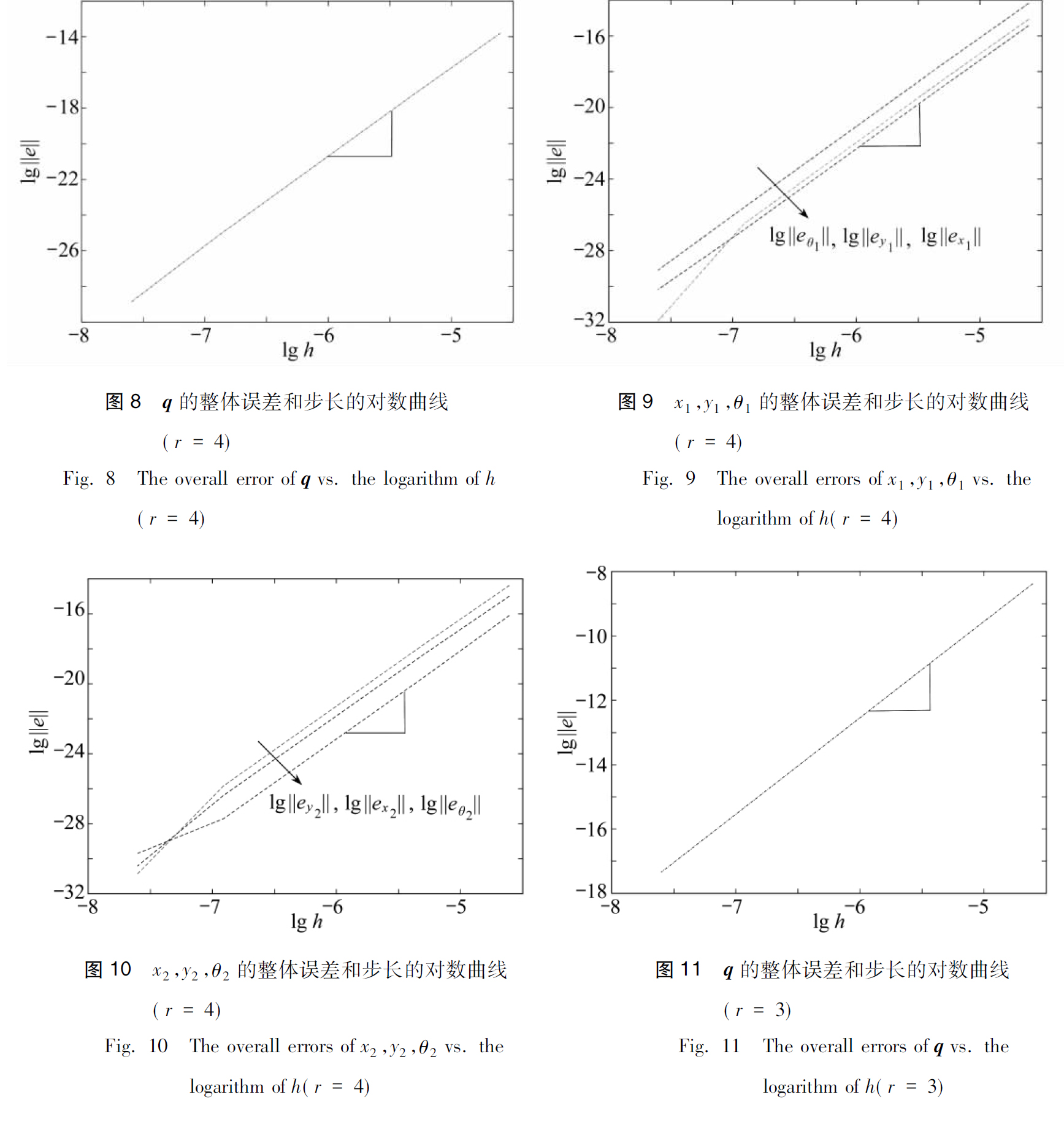
在时间区间t∈[0,1]求解平面双连杆机械臂指标-3的微分-代数方程，取Runge-Kutta法h=0.000 001时的结果作为近似精确解，计算出L-稳定方法在t=1 s,r=4时q的整体误差和步长的对数关系曲线，如图8；q各分量的整体误差和步长的对数关系曲线，如图9、10.r=3时，q的整体误差和步长的对数关系曲线见图11；q各分量的整体误差和步长的对数关系曲线见图12、13.可见当r=4时，L-稳定方法整体误差能够保证四阶精度，r=3时L-稳定方法整体误差能够保证二阶精度，r越大精度越高.
5 结 论
本文构造了求解多体系统动力学微分-代数方程的L-稳定方法，数值结果表明，L-稳定方法在相同节点数情况下，步长越小精度越高；步长固定时，节点数越多精度越高；Chebyshev节点和Legendre节点结果精度高于等距节点.与经典Runge-Kutta法相比较，L-稳定方法数值精度更高，约束违约现象减弱，长时间仿真情况下总能量保持效果更好.该方法数学原理简单、使用方便、编出的程序通用性好，易在计算机中实施，值得研究和推广.如何在保证数值精度的情况下提高计算效率，将是今后需要继续研究的内容.
[1] DAHLQUIST G. A special stability problem for linear multistep methods[J]. BIT Numerical Mathematics, 1963, 3(1): 27-43.
[2] WIDLUND O B. A note on unconditionally stable linear multistep methods[J]. BIT Numerical Mathematics, 1967, 7(1): 65-70.
[3] GEAR C W. The Automatic Integration of Stiff Ordinary Differential Equations[M]. Amsterdam: North Holland Publishing Company, 1963.
[4] DAHLQUIST G. Error Analysis for a Class of Methods for Stiff Non-Linear Initial Value Problems[M]. Berlin: Springer-Verlag, 1975.
[5] BUTCHER J C. A stability property of implicity Runge-Kutta methods[J]. BIT Numerical Mathematics, 1975, 15(4): 358-361.
[6] BURRAGE K, BUTCHER J C. Stability criteria for implicit Runge-Kutta methods[J]. SIAM Journal on Numerical Analysis, 1979, 16(1): 46-57.
[7] LI S F. Nonlinear stability of general linear methods[J]. Journal of Computational Mathematics, 1991, 9(2): 97-104.
[8] EHLE B L. A-stable methods and Pade approximations to the exponential[J]. SIAM Journal on Mathematical Analysis, 1973, 4(4): 671-680.
[9] HAIRER E, WANNER G. Solving Ordinary Differential Equations Ⅱ: Stiff and Differential-Algebraic Problems[M]. 2nd ed. Beijing: Science Press, 2006.
[10] 邓子辰, 李庆军. 精细指数积分法在卫星编队飞行动力学中的应用[J]. 北京大学学报(自然科学版), 2016, 52(4): 669-675.(DENG Zichen, LI Qingjun. Precise exponential integrator and its application in dynamics of spacecraft formation flying[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2016, 52(4): 669-675.(in Chinese))
[11] 彭海军, 李飞, 高强, 等. 多体系统轨迹跟踪的瞬时最优控制保辛方法[J]. 力学学报, 2016, 48(4): 784-791.(PENG Haijun, LI Fei, GAO Qiang, et al. Symplectic method for instantaneous optimal control of multibody system trajectory tracking[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(4): 784-791.(in Chinese))
[12] 阚子云, 彭海军, 陈飙松, 等. 开放式多体系统动力学仿真算法软件研发(Ⅱ): DAEs求解算法对比[J]. 计算力学学报, 2015, 32(6): 707-715.(KAN Ziyun, PENG Haijun, CHEN Biaosong, et al. Study of open simulation algorithm software for multibody system dynamics (Ⅱ): comparison of algorithms for solving DAEs[J]. Chinese Journal of Computational Mechanics, 2015, 32(6): 707-715.(in Chinese))
[13] 丁洁玉, 潘振宽. 多体系统动力学微分-代数方程广义-α投影法[J]. 工程力学, 2013, 30(4): 380-384.(DING Jieyu, PAN Zhenkuan. Generalized-α projection method for differential-algebraic equations of multibody dynamics[J]. Engineering Mechanics, 2013, 30(4): 380-384.(in Chinese))
[14] 徐方暖, 王博, 邓子辰, 等. 基于四元数方法的绳系机器人姿态控制[J]. 应用数学和力学, 2017, 38(12): 1309-1318.(XU Fangnuan, WANG Bo, DENG Zichen, et al. Attitude control of targets captured by tethered space robots based on the quaternion theory[J]. Applied Mathematics and Mechanics, 2017, 38(12): 1309-1318.(in Chinese))
[15] 文立平, 杨春花, 文海洋. 非线性泛函积分微分方程多步Runge-Kutta方法的稳定性和渐近稳定性[J]. 湘潭大学自然科学学报, 2018, 40(1): 1-5.(WEN Liping, YANG Chunhua, WEN Haiyang. Stability and asymptotic stability of multistep Runge-Kutta methods for nonlinear functional-integro-differential equations[J]. Natural Science Journal of Xiangtan University, 2018, 40(1): 1-5.(in Chinese))
[16] SHAMPINE L F, WATTS H A. A-stable block implicit one-step methods[J]. BIT Numerical Mathematics, 1972, 12(2): 252-266.
[17] 袁兆鼎, 费景高, 刘德贵. 刚性常微分方程初值问题的数值解法[M]. 北京: 科学出版社, 2016.(YUAN Zhaoding, FEI Jinggao, LIU Degui. Numerical Solution of Initial Value Problems for Stiff Ordinary Differential Equations[M]. Beijing: Science Press, 2016.(in Chinese))