引 言
穿戴式外骨骼机器人是一种服务性的机器人,可以为行动不便、体力不支的老年人提供有效的帮助,使其行走更加轻松自然.外骨骼机器人的研发可以切实提高老年人的生活质量,减轻家庭和社会的压力.与此同时,外骨骼还可应用到军事、灾害救援、旅游、科考等多个领域,具有广阔的使用前景.
在外骨骼的研究方面,国内外都相继取得了不错的进展.在国外,日本筑波大学研制了世界上第一款商业外骨骼机器人(hybrid assistive limb, HAL),通过附着在下肢屈伸肌表面的肌电和肌肉刚度传感器来控制步行[1].美国加州大学伯克利分校研制的主要用于军事方面的下肢外骨骼(Berkeley lower extremity exoskeleton, BLEEX),其主要以一个步态周期内的单侧人体下肢为研究对象[2].俄罗斯斥巨资研制出“勇士-21”外骨骼机器人.法国某防务公司与法国武器装备总署共同研制出了“大力神”外骨骼机器人[3].美国哈佛大学研制出了一款名为“机器护甲”的柔性化设计的外骨骼机器人.在国内,中科院研制的以电机驱动的外骨骼机器人可以有效地进行负重运动.哈尔滨工业大学的外骨骼机器人可用于抢险和康复,且有望降低成本进行规模化生产.此外,清华大学、东南大学、南京理工大学等科研单位也对外骨骼机器人进行了不同程度的研究[4].
为了实现对外骨骼更好的控制,将人体和外骨骼简化为杆状结构,先对其建立动力学模型,再对力矩进行控制.文献[5]将人体简化为5杆结构,忽略了足部在行走过程中的作用.文献[6]将人体简化成9杆模型,足部和踝关节分别简化为连杆进行分析,随着模型自由度的增加,系统复杂性相应提高.在以往的研究中,大多是直接对人机耦合系统进行建模分析,并没有考虑人体穿戴外骨骼对行走的影响[7-13].少数研究中涉及到了交互力的影响,其中文献[14]中只考虑了大腿处的交互力,但并未将全部交互力考虑完全.文献[15]中讨论了人体和外骨骼在行走过程中的弹性震动导致的二者质心位移,但仅凭两个相互作用连杆之间的角度变化就确定了人体和外骨骼的质心变化位移不够严谨,缺乏一定的说服力.
针对以上问题,为了充分考虑各个关节在行走过程中的作用,同时避免分析过于繁琐,本文分别将外骨骼和人体简化为双足、小腿、大腿及上肢7个部分的杆状结构,构成7杆模型进行分析.建立二者的动力学方程,分析人体和外骨骼的刚性结构在行走周期中所需力矩的同时考虑二者之间的柔性结构.人体和外骨骼之间的柔性结构在行走过程中会有一定的弹性震动,因此可将它们之间的交互力以弹力的形式表现出来,得到下肢外骨骼人机之间的力矩耦合模型.最后建立人机耦合模型,利用ADAMS软件进行仿真分析,验证模型的准确性.
1 建立人体和外骨骼的D-H坐标系
1.1 穿戴式外骨骼及其组成
对于穿戴式外骨骼,从工作过程看,外骨骼系统主要由机械系统、动力系统、传感系统、控制系统构成;从组成机构看,可分为下肢机构(与人体同步行走)、腰部机构(实现身体扭转连接背部和下肢).
图1 穿戴式外骨骼Phoenix系统[16]
Fig. 1 The wearable exoskeleton Phoenix System[16]
由加州大学伯克利分校的人体工程学和机器人实验室开发,suitX公司生产的可穿戴外骨骼Phoenix是一款用于康复的外骨骼.它是一款重量轻、模块化的外骨骼,膝盖、脚踝和臀部可以根据需求单独使用,并可对外骨骼的重量、高度和尺寸参数进行调节以满足不同穿戴者的需求.同时,穿戴者可自主选择外骨骼的行走模式或坐立模式,将人工智能和机械力量进行更加完美的结合.外骨骼Phoenix人机示意图如图1所示[16].
1.2 建立D-H坐标系
人体下肢有3个旋转关节,分别为髋关节、膝关节和踝关节,每个关节的角度都会随行走过程而改变.为了更加准确地表示各个关节在行走过程中的矢量参数,对外骨骼和人体分别建立D-H坐标系[17].外骨骼和人体在每个关节都有相应的局部坐标,同时二者也有共同的基坐标,方便不同坐标之间进行转换[18].
为了用D-H坐标系进行建模,首先要对每一个关节指定一个本地的参考坐标系,即对于每一个关节,指定一个z轴和x轴.若关节是旋转型,则z轴为按右手规则旋转的方向;若关节为滑动型,则z轴为沿直线运动的方向.本文研究的下肢三个关节都为旋转型关节,因此可按照右手规则来确定各个关节的z轴.下肢三个关节之间两两关节的z轴平行,会有无数条公垂线,此时可挑选与前一关节公垂线共线的一条作为x轴来简化模型.在确定好z轴和x轴后,可根据三维坐标系中的右手定则来确定y轴.按照此方法逐步建立好每一个关节的D-H坐标.
根据外骨骼Phoenix的结构将人体和外骨骼分别简化成7杆模型,其中杆件1~7分别表示人体自右向左的右足、右小腿、右大腿、人体上肢、左大腿、左小腿以及左足7个部位.同理,杆件8~14分别表示外骨骼的相应部位.
外骨骼和人体建立的D-H坐标系类似,以外骨骼D-H坐标系(图2)为例说明最终所建立的D-H坐标系.在图2中,li为i杆的长度;黑点处为杆件i质心的位置,用ci表示;杆件的衔接处为下肢的关节,局部坐标Oixiyizi建立在关节i处的位置;ri为质心ci与其相连关节之间的距离;qi是杆件i在运动过程中变化的关节角度,其大小是局部坐标x轴与对应杆件之间的夹角;d1是左右两个髋关节与人体上肢之间的水平距离;O0x0y0z0是坐标轴方向不随人体运动发生变化的基坐标系,该坐标系原点在右足的足尖处.
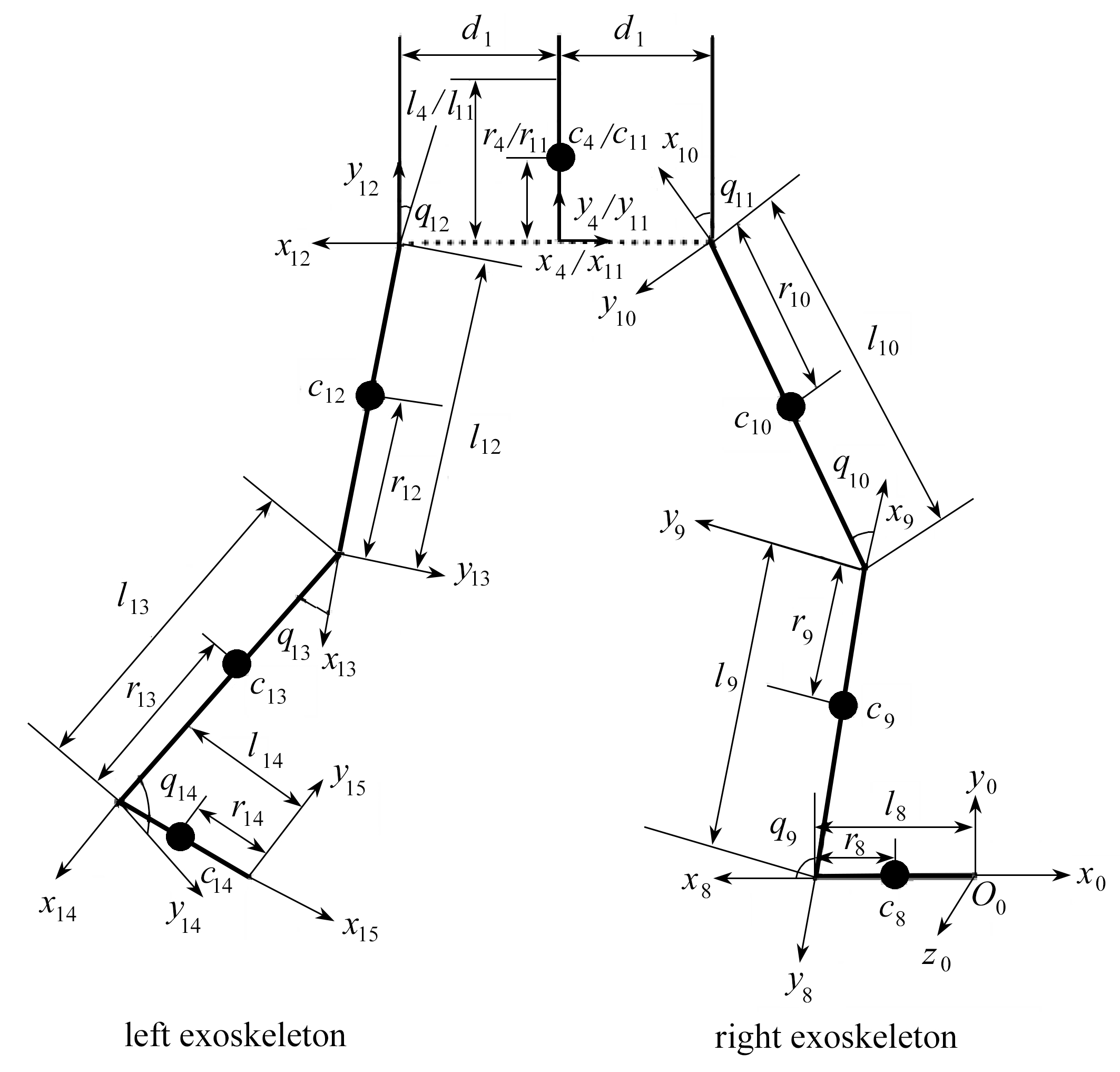
图2 外骨骼单足支撑状态下的D-H坐标
Fig. 2 The D-H coordinates of the exoskeleton supported by a single foot
为了在不同坐标系之间进行转换,需求得各个坐标系之间的变换矩阵.根据D-H参数(令右足足尖与水平方向夹角为q1,具体参数见表1),按照旋转-平移-平移-旋转的顺序可以使坐标系Oi+1xi+1yi+1zi+1转换成坐标系Oixiyizi,其具体的变换矩阵公式为式(1).相邻坐标系之间的转换矩阵右乘得到不相邻坐标系之间的转换矩阵.最终各个关节坐标都可以转换到基坐标当中.
nTn+1=An+1=Rot(z,θn+1)×Tran(0,0,dn+1)×Tran(an+1,0,0)×Rot(x,αn+1)=
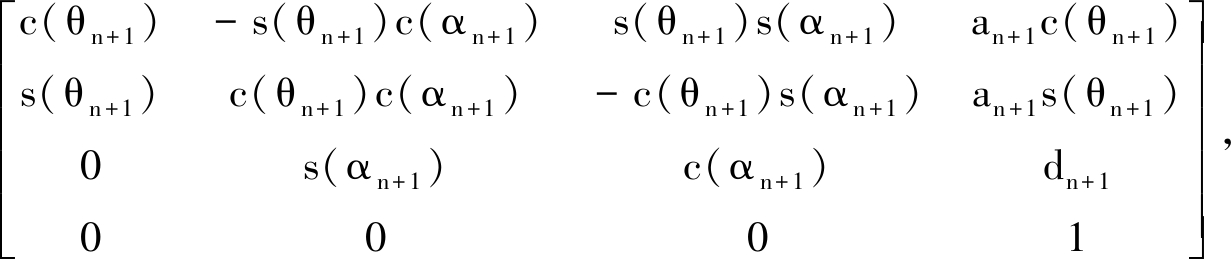
(1)
其中,c(θn+1),s(θn+1)分别表示cos θn+1和sin θn+1.
在求得不同关节坐标与基坐标之间的变换矩阵后,可依次得到各个杆件的质心在基坐标系中的坐标,再对质心坐标进行求导得到其线速度,二次求导得到其线加速度.
表1 D-H参数表
Table 1 D-H parameters

jointθidiaiαi/(°)0π-q80l808-q90l909q100l10010π/2-q110d1180110°0d1012π/2-q120l1218013-q130l13014π-q140l140
2 下肢外骨骼动力学建模
人体下肢的运动是在三维平面中进行的,下肢的运动也是三维的,其三个平面分别划分为:矢状面、冠状面和水平面.考虑到人体下肢的运动主要在矢状面进行,因此本文的动力学模型都是在矢状面上建立并分析.
人体的行走过程是一个周期性的运动,按照行走过程中足部是否与地面接触可将运动周期划分为支撑期和摆动期,人体下肢支撑和摆动过程的交替进行构成了一个完整的行走周期.在一个单侧腿完整行走周期中,摆动期约占总周期的40%,支撑期约占总周期的60%.在一个完整的行走周期中, 人体腿部的状态可划分为双足支撑-单足支撑、 单足摆动-双足支撑-单足摆动、 单足支撑.因此本文将动力学模型分为单足支撑和双足支撑两部分, 分别建立其动力学模型.
2.1 动力学方程式
常用的动力学建模方法有Lagrange法和Newton-Euler法.Lagrange法从系统的能量角度出发,利用系统的动能和势能建立能量函数.而Newton-Euler法是针对机器人的每一个刚体建立相应的Newton-Euler方程,而后将方程联立进行求解,分析的力既有外力,又有内力.考虑到建模过程中要分析下肢和外骨骼之间的相互作用力,所以采用Newton-Euler法建立机理方程.
Newton-Euler动力学方程需要按照倒序递推的原则依次求出杆件14~8的关节力和关节力矩.Newton-Euler动力学方程的力学公式和力矩公式分别为
(2)
M=Icε+ω×Icω.
(3)
人体的腿部和外骨骼之间通过绑带进行连接,具有一定的交互力.在人体和外骨骼静止时绑带的长度最短,为人体髋关节和外骨骼髋关节之间的水平距离.当开始行走时,人体和外骨骼的运动状态并非完全同步,二者之间会产生一定的弹性震动,加大了绑带的拉伸程度,致使二者之间发生了相对位移,产生交互力.不同于人体与外骨骼的其他刚体结构,绑带为一个柔性结构,因此可将该交互力简化为弹力代入到动力学模型当中,增加模型的精确性.
对于连接在人体和外骨骼之间的柔性结构——绑带,太过柔性的布料会沿着腿部轴向没有刚度,而且由于行走时间的累积,布料会变得松弛易从人体和外骨骼的腿部滑落;而布料太过于僵硬,人体佩戴的舒服度又会受到很大影响[19].综上所述,本文将采用宽度为85 mm的尼龙绳作为连接人体和外骨骼的绷带.根据尼龙材料的弹力系数和行走过程中人体和外骨骼之间的实时相对位移得到二者之间的交互力大小.
考虑人体与外骨骼交互力的Newton-Euler方程式为
(4)
M13,14=-r14,c14×F13,14+Ic14ε14+ω14×(Ic14ω14),
(5)
(6)
M12,13=-r13,c13×F12,13-r14,c13×F13,14+Ic13ε13+ω13×(Ic13ω13)-M13,14,
(7)
(8)
M11,12=-r12,c12×F11,12-r13,c12×F12,13+Ic12ε12+ω12×(Ic12ω12)-M12,13,
(9)
(10)
M10,11=-r11,c11×F10,11-r12,c11×F11,12+Ic11ε11+ω11×(Ic11ω11)-M11,12,
(11)
(12)
M9,10=-r10,c10×F9,10-r11,c10×F10,11+Ic10ε10+ω10×(Ic10ω10)-M10,11,
(13)
(14)
M8,9=-r10,c10×F8,9-r10,c9×F9,10+Ic9ε9+ω9×(Ic9ω9)-M9,10,
(15)
其中,Fi-1,i是杆件i-1对杆件i的力,Mi-1,i是杆件i-1对杆件i的力矩,mi是杆件i的质量, g是重力加速度,![]() 是杆件i的质心线加速度,ωi是杆件i的质心角速度, εi是杆件i的质心角加速度, ri+1,ci是坐标系Oi+1xi+1yi+1zi+1的原点到质心ci的距离矢量, Ici为杆件i的惯量张量, F′i是人体和外骨骼之间的交互力.以上各矢量都是在基坐标下进行的.
是杆件i的质心线加速度,ωi是杆件i的质心角速度, εi是杆件i的质心角加速度, ri+1,ci是坐标系Oi+1xi+1yi+1zi+1的原点到质心ci的距离矢量, Ici为杆件i的惯量张量, F′i是人体和外骨骼之间的交互力.以上各矢量都是在基坐标下进行的.
2.2 单足支撑状态下的动力学模型
对于人体左侧小腿和外骨骼小腿之间的交互力F′13进行分析.
为了便于模型的建立,使外骨骼与人体之间绑带的位置都位于二者的质心,在无运动时二者之间的距离为d1-d0(d0是人体髋关节与上肢之间的水平距离).令运动过程中二者之间的位移差为Δ1,其弹力系数为k,则
F′13=kΔ1.
(16)
在行走过程中,人体左小腿质心c6(x6,y6,z6)的坐标和外骨骼左小腿质心c13(x13,y13,z13)的坐标分别为
c6(x6,y6,z6)=
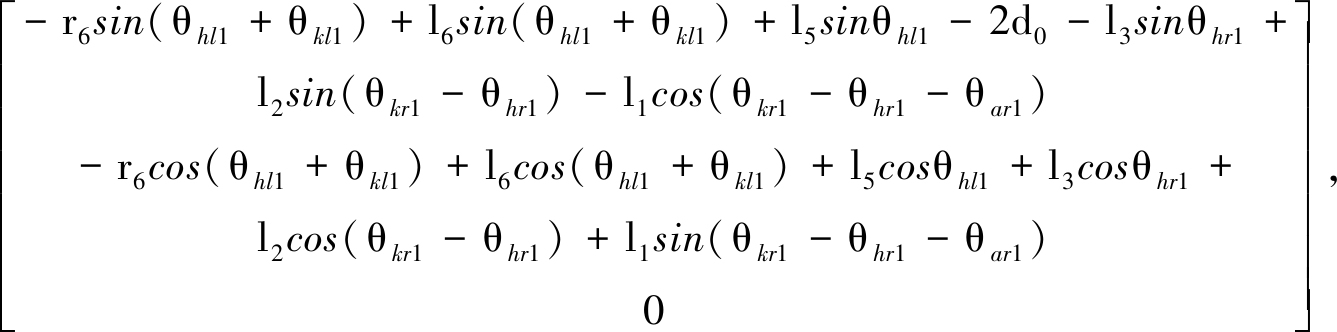
c13(x13,y13,z13)=
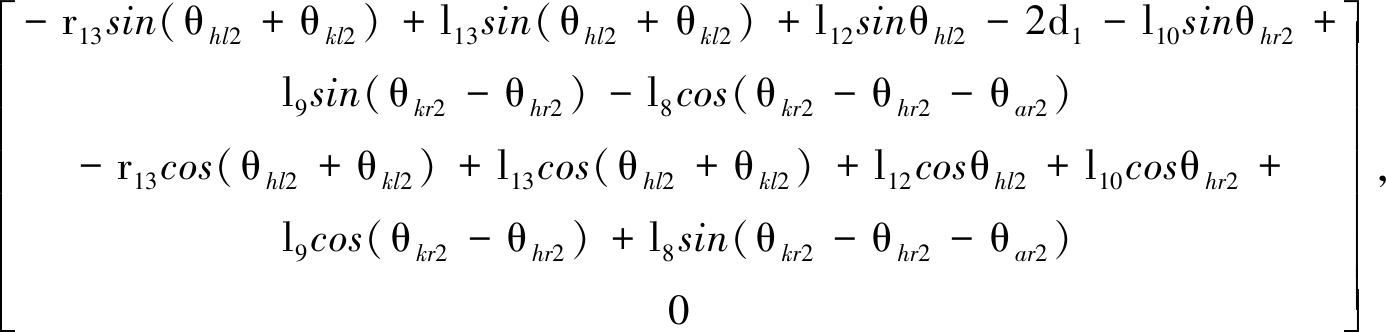
其中,θhl1,θkl1分别为人体左侧的髋关节和膝关节角度;θhr1,θkr1,θar1分别为人体右侧的髋关节、膝关节以及踝关节角度;r6是质心c6到人体踝关节的距离;θhl2,θkl2分别为外骨骼左侧的髋关节和膝关节角度;θhr2,θkr2和θar2分别为外骨骼右侧的髋关节、膝关节和踝关节角度;l6和l5分别为人体左侧的小腿和大腿长度;l3,l2和l1分别为人体右侧的大腿、小腿和足部长度.
分析可得外骨骼和人体左侧小腿的相对位移差为
Δ1=c13(x13,y13,z13)-c6(x6,y6,z6).
(17)
F′12为人体左侧大腿和外骨骼之间的交互力,则
F′12=kΔ2.
(18)
行走过程中,人体左大腿质心c5(x5,y5,z5)的坐标和外骨骼左大腿质心c12(x12,y12,z12)的坐标分别为
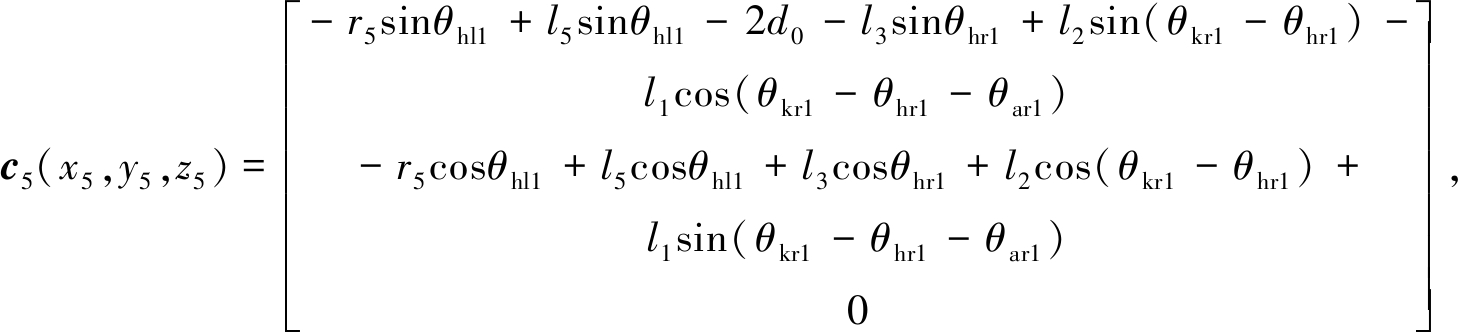
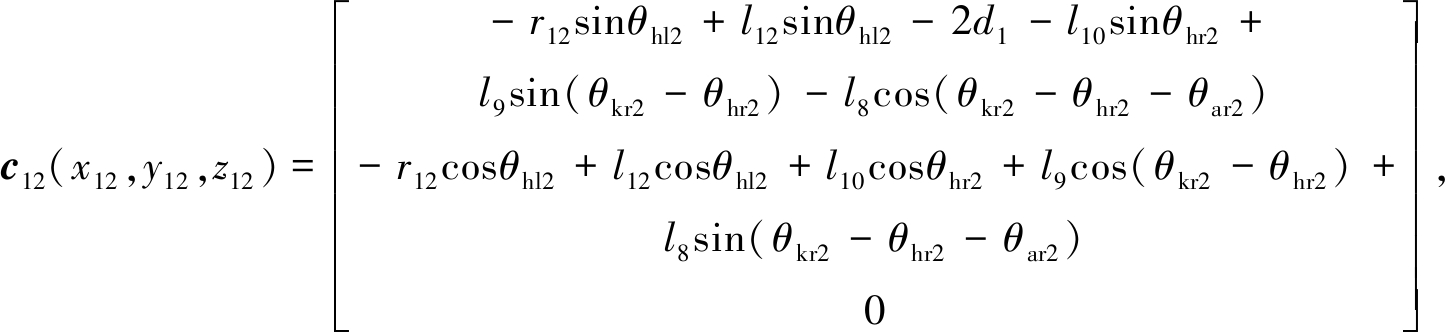
其中,r5为人体左大腿质心c5到膝关节的距离.分析可得
Δ2=c12(x12,y12,z12)-c5(x5,y5,z5).
(19)
杆4是人体上肢,人体在行走过程中,左右下肢担负的上肢质量有所变化,因此根据左右大腿质心位置和人体上肢质心位置的距离之比来确定左右大腿所担负的上肢的质量.人体上肢质心c4(x4,y4,z4)的坐标和外骨骼右大腿质心c10(x10,y10,z10)的坐标分别为
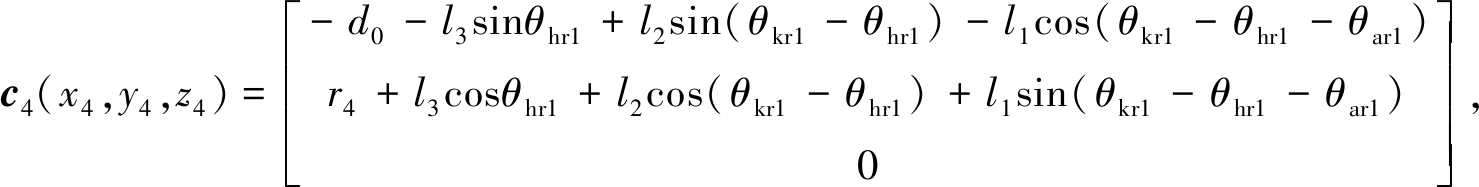
c10(x10,y10,z10)=
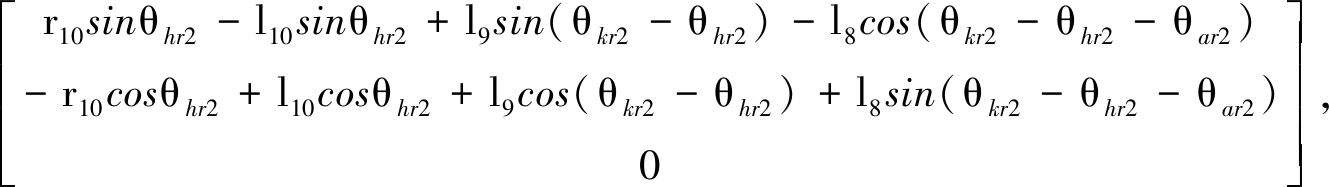
其中,r4是上身躯干质心c4到髋关节的距离.可得
(20)
(21)
令外骨骼左大腿杆12承担的人体上肢的质量为m4L,外骨骼右大腿杆10承担的人体上肢质量为m4R,则
(22)
F′10是人体右大腿与外骨骼之间的交互力,则
F′10=kΔ3,
(23)
行走过程中,人体右大腿质心c3(x3,y3,z3)的坐标为
c3(x3,y3,z3)=
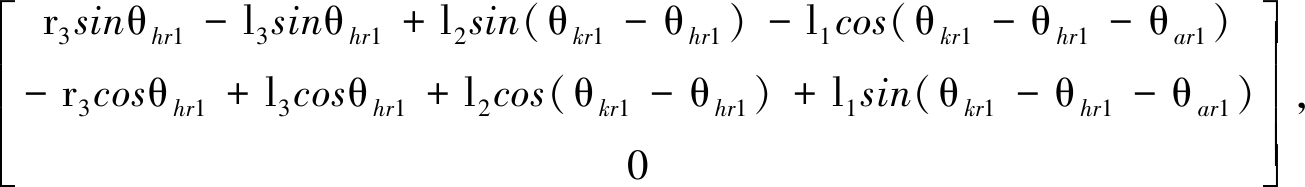
其中
Δ3=c10(x10,y10,z10)-c3(x3,y3,z3).
(24)
F′9为人体右小腿和外骨骼之间的交互力,则
F′9=kΔ4.
(25)
行走过程中,人体右小腿质心c2(x2,y2,z2)的坐标和外骨骼右小腿质心c9(x9,y9,z9)的坐标分别为
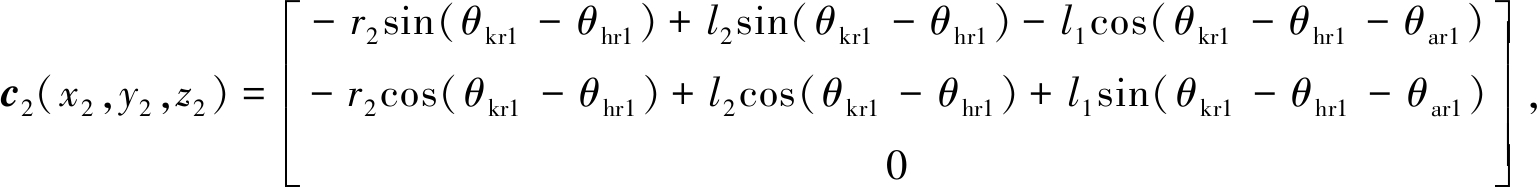
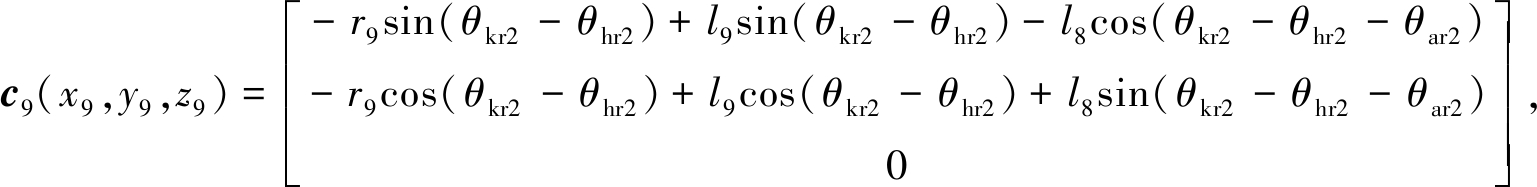
其中,r2是人体右小腿质心c2到右膝关节的距离.则
Δ4=c9(x9,y9,z9)-c2(x2,y2,z2).
(26)
2.3 双足支撑状态下的动力学模型
双足支撑状态下的Newton-Euler方程和单足支撑状态下的方程类似,唯一的不同点就是在外骨骼左足杆14的分析中加入了地面的支持力,即
(27)
3 ADAMS软件仿真
3.1 建立人体和外骨骼模型
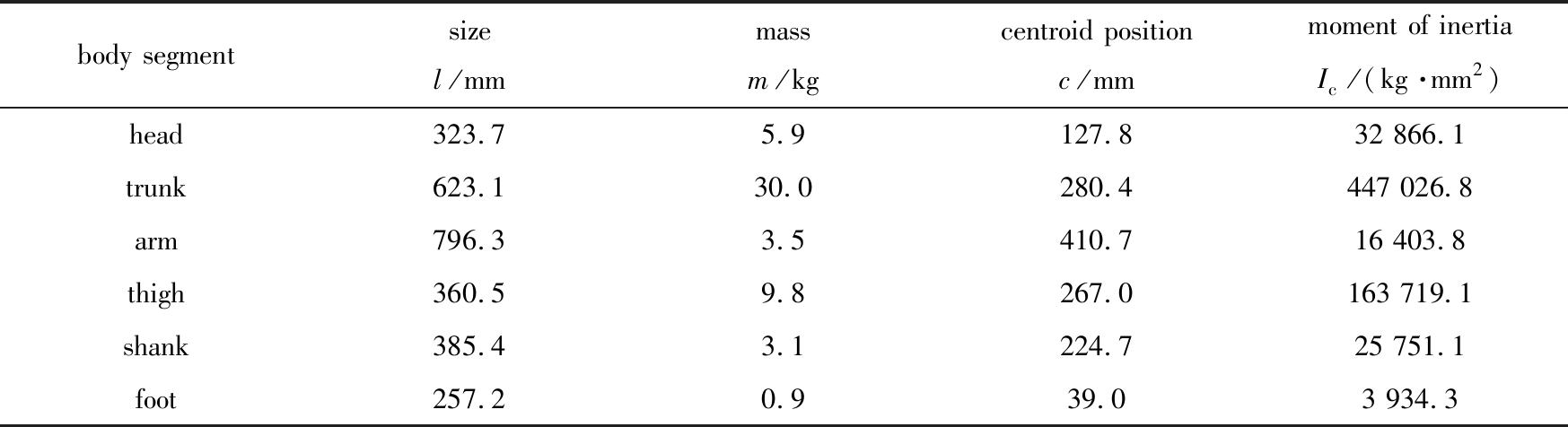
为了实现最终的人-机行走仿真,首先需要在ADAMS中建立人体和外骨骼的三维模型.将人体简化为头部、上躯干、左右臂、左右大腿、左右小腿以及左右足.其中人体各体段长度参考GB 10000—88(中国成年人人体尺寸)设定,人体惯性参数依据 GB/T 17245—2004(成年人人体惯性参数)设定.具体的人体各体段参数设置如表2所示.
3.2 创建运动副和环境参数
创建好系统的各组成部分之后,在ADAMS中添加各种运动副来限制构件之间的相对运动.其中,运动副可分为低副(joint)、基本副(primitive)、耦合副(coupler)和特殊副4类,模型的运动自由度在软件中依靠低副模块来设定.低副模块主要分为固定副(fixed joint)、转动副(revolute joint)、平动副(translational joint)以及球状副(spherical joint)等.由于本文进行的是下肢运动的仿真,所以将上肢的手臂与躯干以转动副的形式连接,实现行走过程中的甩臂,上肢的其他体段均以固定副的形式连接.在人体下肢各关节和外骨骼的各关节处创建旋转副.相对于人体和外骨骼的刚性连接关系,人体和外骨骼之间采用柔性连接,以更好地模拟人-机真实行走状态下的交互作用力.
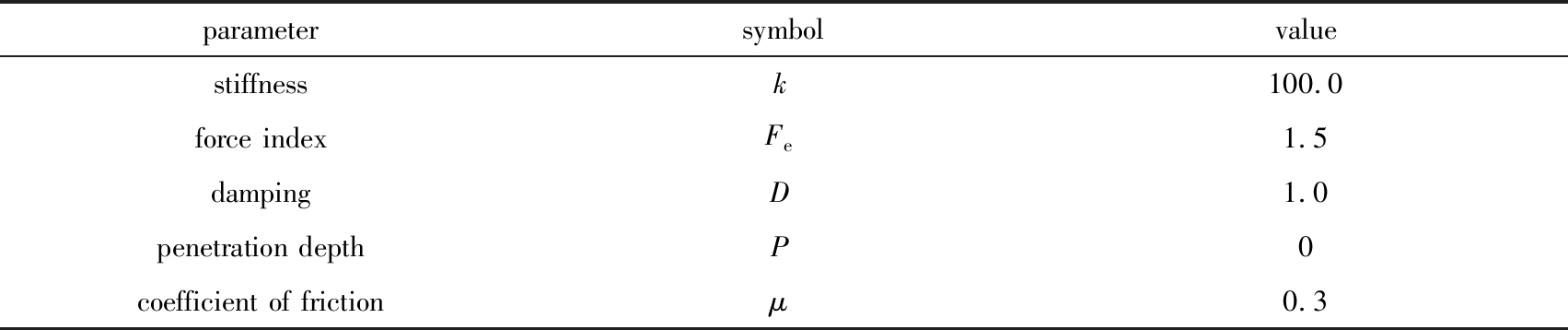
创建好各个连接关系之后需要设置人体与地面的环境参数.通过ADAMS中的contact模块设置足部与地面之间的相关参数,如表3所示,本文着重研究在平地行走状态下的仿真.
表2 人体各体段参数设置
Table 2 Parameters of the body segments
body segmentsize l/mmmass m/kgcentroid position c/mmmoment of inertia Ic/(kg·mm2)head323.75.9127.832 866.1trunk623.130.0280.4447 026.8arm796.33.5410.716 403.8thigh360.59.8267.0163 719.1shank385.43.1224.725 751.1foot257.20.939.03 934.3
表3 仿真模型接触类各参数设置
Table 3 Contact parameters of the simulation model
parametersymbolvaluestiffnessk100.0force indexFe1.5dampingD1.0penetration depthP0coefficient of frictionμ0.3
3.3 仿真实验
将本文建立的Newton-Euler动力学方程式输入到MATLAB仿真软件中,代入行走过程中的关节角度以及表2所示的人体各体段质量、长度等参数值,可得到模型的各关节力矩.将得到的关节力矩导入ADAMS软件中生成样条曲线Spline.在髋关节、膝关节处添加力矩驱动,并用驱动函数CUBSP函数与输入的关节力矩Spline曲线关联起来,进而对关节力矩的准确性进行验证.其中,踝关节通过添加Motion函数用角度进行驱动.

图3 加入髋关节力矩后的行走仿真图4 加入膝关节力矩后的行走仿真
Fig. 3 The simulation of walking with the hip joint torque Fig. 4 The simulation of walking with the knee joint torque
人体的行走是一个周期性的运动,左右腿依次完成同一周期中的不同环节,因此仿真时只考虑单侧右腿在一个完整周期内的运动情况即可.仿真完成后,得到的ADAMS人体-外骨骼模型的行走仿真图如图3、4所示.髋关节和膝关节的理论计算关节角度值和ADAMS仿真后的关节角度值的对比图为图5、6.图7为髋关节和膝关节的关节角度误差.可以看出,髋关节的角度误差范围为-0.5°~1.5°,膝关节的角度误差范围为-2.5°~2.5°,误差范围都较小.仿真结果验证了本文Newton-Euler动力学建模的正确性.
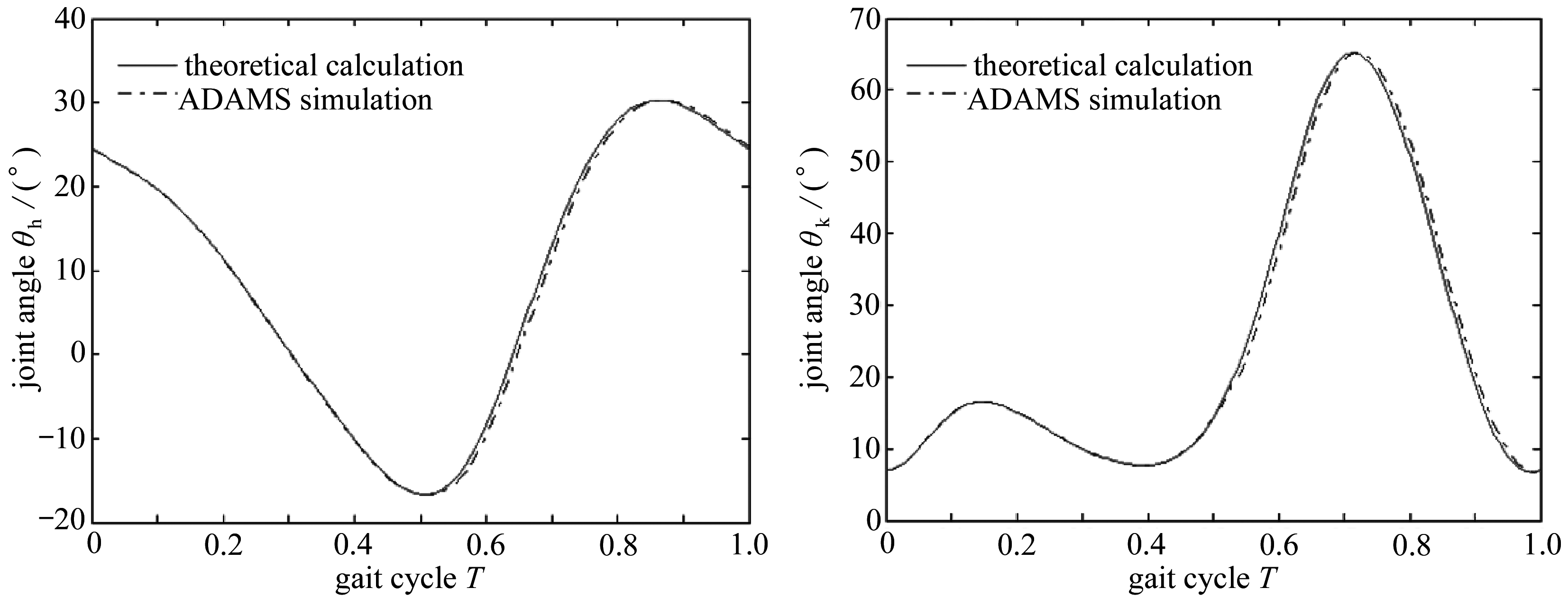
图5 髋关节角度对比图图6 膝关节角度对比图
Fig. 5 The angle comparison chart for the hip jointFig. 6 The angle comparison chart for the knee joint
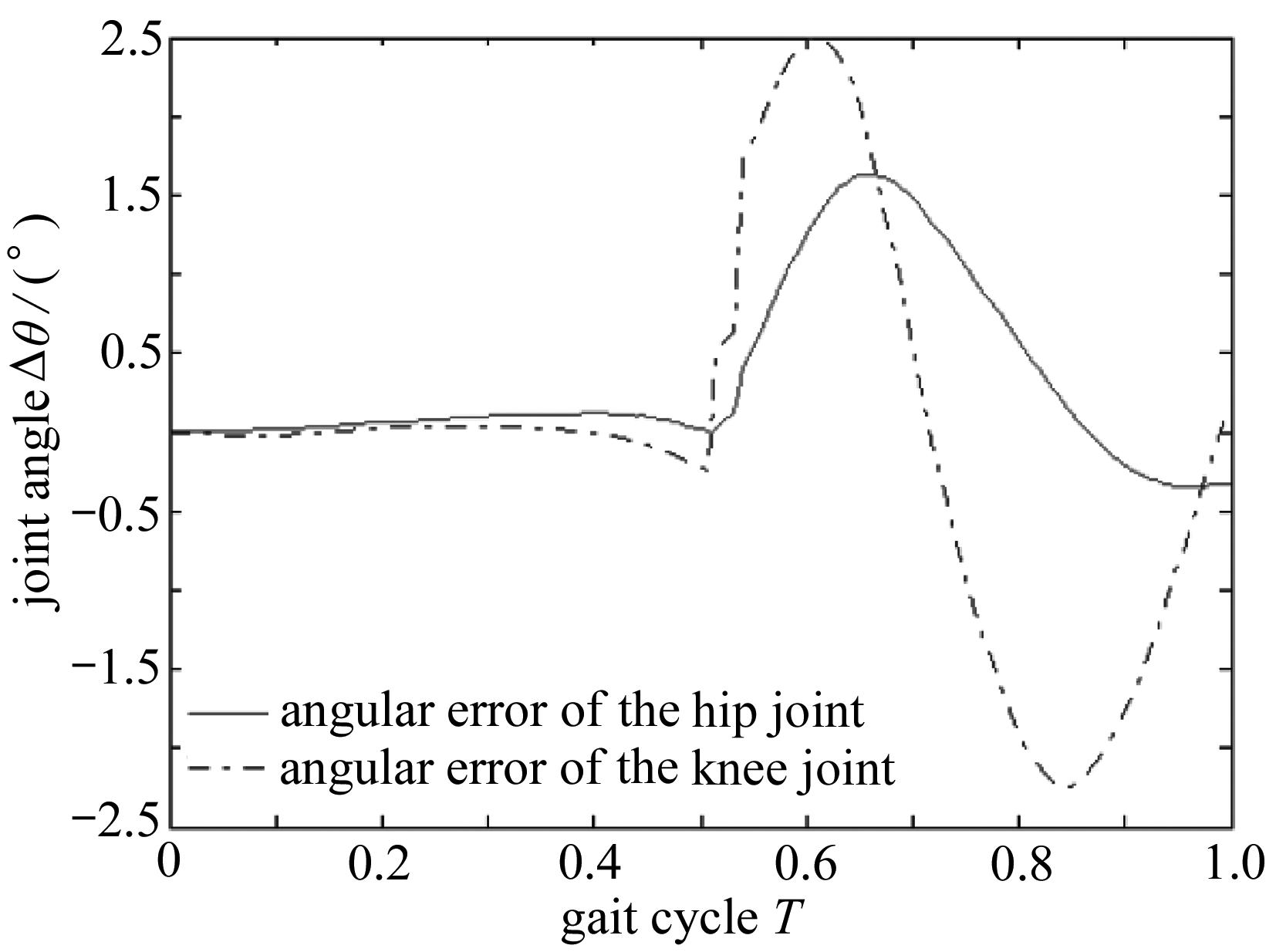
图7 髋关节和膝关节的角度误差
Fig. 7 Angular errors of the hip joint and the knee joint
4 总 结
本文建立了一种包含人机交互力的人体-外骨骼仿真模型.对人体和外骨骼分别采用7连杆的刚体模型进行建模,然后建立其D-H坐标系,得到了其在运动过程中的变化矢量.采用Newton-Euler方程建立动力学方程式,将人机模型之间的交互力简化为弹力,选择合适的绑带材料进而确定了弹力系数.根据运动中人体和外骨骼相应质心之间的距离变化得到其相对位移,从而求得了运动过程中交互力的大小.将交互力代入到方程,得到了包含交互力的动力学方程式.
根据仿真结果可知,仿真得到的关节角度值和理论关节角度值的大小、变化趋势一致,并且二者的角度误差在较小的范围内,仿真结果较为理想.该建模方法能够较准确地表示人体穿戴外骨骼的行走过程,有利于对其进行精确的控制.
[1] SANKAI Y. HAL: hybrid assistive limb based on cybernics[C]//The 13th International Symposium, ISRR. Hiroshima, Japan, 2007.
[2] ZOSS A B, KAZEROONI H, CHU A. Biomechanical design of the Berkeley lower extremity exoskeleton(BLEEX)[J]. IEEE/ASME Transactions on Mechatronics, 2006, 11(2): 128-138.
[3] BOCK T, LINNER T. Construction Robots: Elementary Technologies and Single-Task Construction Robots[M]. Cambridge: Cambridge University Press, 2016.
[4] GUO Z, YU H, YIN Y H. Developing a mobile lower limb robotic exoskeleton for gait rehabilitation[J]. Journal of Medical Devices, 2014, 8(4): 044503.
[5] 杨魏, 张秀峰, 杨灿军, 等. 基于人机5杆模型的下肢外骨骼系统设计[J]. 浙江大学学报(工学版), 2014, 48(3): 430-435.(YANG Wei, ZHANG Xiufeng, YANG Canjun, et al. Design of a lower extremity exoskeleton based on 5-bar human machine model[J]. Journal of Zhejiang University(Engineering Science), 2014, 48(3): 430-435.(in Chinese))
[6] FENG T R, NISHIGUCHI J, LI X, et al. Dynamical analyses of humanoid’s walking by using extended Newton-Euler method[C]//The Twentieth International Symposium on Artificial Life and Robotics 2015. Beppu, Japan, 2015.
[7] 贾山, 韩亚丽, 路新亮, 等. 基于人体特殊步态分析的下肢外骨骼机构设计[J]. 机器人, 2014, 36(4): 392-401.(JIA Shan, HAN Yali, LU Xinliang, et al. Design of lower extremity exoskeleton based on analysis on special human gaits[J]. Robot, 2014, 36(4): 392-401.(in Chinese))
[8] 唐志勇, 谭振中, 裴忠才. 下肢外骨骼机器人动力学分析与设计[J]. 系统仿真学报, 2013, 25(6): 1338-1344.(TANG Zhiyong, TAN Zhenzhong, PEI Zhongcai. Design and dynamic analysis of lower extremity exoskeleton[J]. Journal of System Simulation, 2013, 25(6): 1338-1344.(in Chinese))
[9] 韩亚丽, 王兴松. 下肢助力外骨骼的动力学分析及仿真[J]. 系统仿真学报, 2013, 25(1): 61-67.(HAN Yali, WANG Xingsong. Dynamic analysis and simulation of lower limb power-assisted exoskeleton[J]. Journal of System Simulation, 2013, 25(1): 61-67.(in Chinese))
[10] 陈贵亮, 李长鹏, 赵月, 等. 下肢外骨骼康复机器人的动力学建模及神经网络辨识仿真[J]. 机械设计与制造, 2013(11): 197-200.(CHEN Guiliang, LI Changpeng, ZHAO Yue, et al. Dynamic modeling and neural network identification simulation for lower limbs exoskeletons rehabilitation robot[J]. Machinery Design & Manufacture, 2013(11): 197-200.(in Chinese))
[11] SPENCER A M, KEVIN H H, CLARE H, et al. An assistive control approach for a lower-limb exoskeleton to facilitate recovery of walking following stroke[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2015, 23(3): 441-449.
[12] ZHU Q H, CHEN Z L, LI W D, et al. Structure design and analysis of compliant human-machine interface mechanism for exoskeletons[C]//2017 IEEE Workshop on Advanced Robotics and Its Social Impacts(ARSO). Austin, USA, 2017.
[13] PENG Z Q, MA G W, LUO M D. Modeling and gait generation of powered lower exoskeleton robot[C]//2017 12th IEEE Conference on Industrial Electronics and Applications(ICIEA). Siem Reap, Cambodia, 2017: 1802-1807.
[14] 刘棣斐, 唐志勇, 裴忠才. 基于导纳原理的下肢外骨骼摆动控制[J]. 北京航空航天大学学报, 2015, 41(6): 1019-1025.(LIU Difei, TANG Zhiyong, PEI Zhongcai. Swing motion control of lower extremity exoskeleton based on admittance method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(6): 1019-1025.(in Chinese))
[15] WANG D H, LEE K M, GUO J J, et al. An adaptive knee joint exoskeleton based on biological geometries[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(4): 1268-1278.
[16] PHOENIX medical exoskeleton[EB/OL]. (2016-11-18) [2018-08-03]. https://www.suitx.com/phoenix-medical-exoskeleton.
[17] 易金花, 喻洪流, 张颖, 等. 中央驱动式上肢康复机器人运动学建模与分析[J]. 生物医学工程学, 2015, 32(6): 1196-1201.(YI Jinhua, YU Hongliu, ZHANG Ying, et al. Kinematics modeling and analysis of central-driven robot for upper limb rehabilitation after stroke[J]. Journal of Biomedical Engineering, 2015, 32(6): 1196-1201.(in Chinese))
[18] 赵志刚, 王砚麟, 苏程, 等. 多机器人协调吊运系统逆运动学分析及优化[J]. 应用数学和力学, 2017, 38(6): 643-651.(ZHAO Zhigang, WANG Yanlin, SU Cheng, et al. Analysis and optimization on inverse kinematics for multi-robot parallel lifting systems[J]. Applied Mathematics and Mechanics, 2017, 38(6): 643-651.(in Chinese))
[19] 王阳, 宋遒志, 王晓光. 下肢外骨骼机器人人机腿部约束分析[J]. 现在制造技术与装备, 2016(1): 50-52.(WANG Yang, SONG Qiuzhi, WANG Xiaoguang. Research of a lower extremity exoskeleton for human-machine leg restriction[J]. Manufacturing Technology and Equipment, 2016(1): 50-52.(in Chinese))