引 言
近年来，分数阶微分方程(fractional differential equation，FDE)因其非局部特性，在研究具有历史记忆性的过程和具有遗传特性的材料方面得到了广泛的应用[1-3].而分布阶FDE作为FDE的一种，最早是由Caputo在20世纪60年代提出的，用于模拟滞弹性介质中的应力-应变行为[4].不同于常数阶FDE和多项FDE，分布阶FDE是通过把FDE中分数阶导数的阶在某个给定区间上积分得到的，这类方程可以看作是前面提到的两类FDE的推广.分布阶FDE的典型应用是模拟减速的次扩散过程[5-7]，在这类过程中，粒子束的均方位移关于时间以对数增长，最终将形成超慢扩散.近年来，分布阶FDE还被应用于控制和信号过程[8]、电介质感应和扩散的模拟[9]以及识别系统[10]等多个研究领域.
由于分布阶FDE的广泛应用，方程的求解就成为一个重要问题.在大多数情况下，要求得解析解非常困难，甚至是不可能的，因此，研究可靠而有效的数值解法就势在必行.数值求解分布阶FDE的相关研究目前还处于初始阶段，其中，有限差分法以其格式便于构造、编程方便等优点成为采用较多的一种方法.Ford等[11]提出了一种求解时间分布阶扩散方程的隐式差分格式.Gao(高广花)等[12]采用Grünwald-Letnikov公式，并应用外推技术提高近似精度，提出了两种求解一维分布阶FDE的差分格式；而在文献[13]中，他们又采用加权-平移的Grünwald-Letnikov公式，得到了求解分布阶扩散方程的两种高阶差分格式，其收敛速率分别为O(τ2+h2+Δβ2)和O(τ2+h4+Δβ4)，这里τ,h和Δβ分别表示时间、空间和分布阶三个方向的步长.文献[14]提出了求解带有非线性源项的二维和三维时间分布阶波动方程的差分格式，并对解进行了模拟.本文基于复化Simpson公式和复化两点Gauss-Legendre公式，提出了求解一维时间分布阶扩散方程的两种高阶差分格式.不同于以往文献中提出的时间一阶或二阶格式，本文提出的格式在时间方向可达到三阶精度，而且在分布阶和空间方向都具有四阶精度.本文在第3节中列出的数值结果表明，所提出的两种格式是稳定且收敛的，并且通过与文献[13]和文献[11]中的算法对比,得出其更为高效.
1 准 备 工 作
1.1 数值积分
先介绍两个关键的数值积分公式：复化Simpson公式和复化两点Gauss-Legendre公式.设J是正整数，
Δβ=1/J， βl=lΔβ， l=0,1,…,J;
l=0,1,…,J-1.
引理1(复化Simpson公式) 设h(β)∈C4([0，1])，有
引理2[15](复化两点Gauss-Legendre公式) 设h(β)∈C4([0，1])，有
1.2 时间离散
接下来考虑时间导数的离散.时间分布阶扩散方程的时间导数是Caputo型分数阶导数，为了使构造的格式在时间方向达到三阶精度，本文采用一种离散左Riemann-Liouville分数阶导数的加权-平移Grünwald-Letnikov公式[16]离散时间导数.
下面叙述左Riemann-Liouville分数阶导数的定义以及它和Caputo分数阶导数的关系.设β∈(n-1,n)，对于t∈R，函数u(t)的β阶左Riemann-Liouville导数定义为
特别地，若t∈(0,T]，有
若β∈(0,1)，Caputo分数阶导数和左Riemann-Liouville分数阶导数有下列关系[1]：
设
是f(t)的Fourier变换，记
设f∈C3+β(R)，对于t∈R，有三阶近似精度的加权-平移Grünwald-Letnikov公式[16]
其中
系数
且有如下递推关系：
若β=0，规定
若f∈C([0,T])，可先考虑定义在R上的函数
如下:
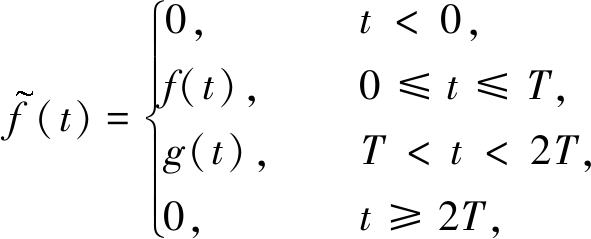
其中g(t)是光滑函数，且满足条件g(k)(T)=f(k)(T)，g(k)(2T)=0，k=0,1,…,4.假定
对于任意的t∈[0,T]，有
(1)
1.3 空间离散
设M是一个正整数，h=L/M是空间步长，
是空间网格点.u={ui|0≤i≤M}表示定义在
上的网格函数，定义记号：
关于空间二阶导数离散，有以下结论：
设函数u(x)∈C6([xi-1,xi+1])，xi+1=xi+h，xi-1=xi-h，且ζ(s)=(1-s)3[5-3(1-s)2]，那么有[17]
2 高阶格式的构造
考虑时间分布阶扩散方程及其初始和边界条件如下：
(2)
u(x,0)=0, x∈Ω,
(3)
u(x,t)=φ(x,t), x∈∂Ω, t∈[0,T],
(4)
其中Ω=(0,L)，∂Ω是Ω的边界，G(x,t)是源项.方程(2)中的分数阶导数是Caputo型的，即
不失一般性，假定u(x,0)=0.若u(x,0)=ψ(x)≠0，可令v(x,t)=u(x,t)-ψ(x)，然后考虑关于函数v(x,t)的问题(2)～(4)即可.
接下来，在点(xi,tn)处考虑方程(2)，有
(5)
由Caputo导数和左Riemann-Liouville导数的关系及等式(1)，整理可得方程(5)中时间导数的如下离散格式[18]：
(6)
其中
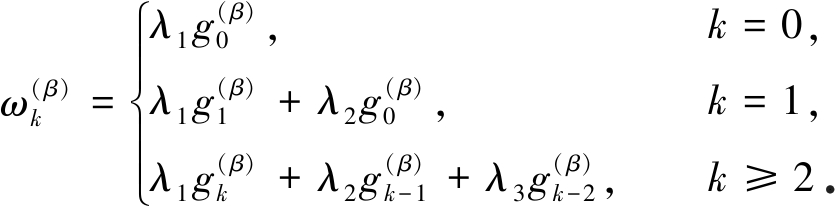
记
基于引理1和引理2，方程(5)分别可写为如下两种形式：
(7)
(8)
由式(6)，方程(7)等价于
(9)
方程(8)等价于
(10)
为书写简便起见，引入记号
接下来用算子H作用方程(9)和(10)两端，分别可得
(11)
(12)
在式(11)和(12)中去掉高阶项，并用u(xi,tn)的近似值
代替
得到方程(2)的两个近似方程，截断误差均为O(τ3+h4+Δβ4)，它们是基于不同的数值积分公式得到的，即复化Simpson公式和复化两点Gauss-Legendre公式.结合初始条件和边界条件，可得问题(2)～(4)的两个高阶差分格式，格式的收敛速率为O(τ3+h4+Δβ4)，本文将在下一节通过数值算例进行验证.下面把这两个格式写成便于计算的形式，即把第n时间层的待求函数值放在等号的左边，之前的各层函数值和已知量放在等号的右边，得到
(13)
(14)
(15)
以及
(16)
(17)
(18)
3 数 值 实 验
为了验证本文所提出的两种差分格式的稳定性、收敛性，计算下面的例子.在以下算例中，采用L∞范数表示误差，即
三个方向的收敛速率通过下面的公式计算：
例1 在初边值问题(2)～(4)中取L=π，T=0.5，p(β)=Γ(4-β)，G(x,t)=8[6(t3-t2)/ln t+t3]sin x.精确解为u(x,t)=8t3sin x.
图1和图2分别给出了应用格式(13)～(15)和(16)～(18)计算例1的逐点绝对误差曲线，这些曲线直观地表明了两种算法的收敛性.
(a) t=0.2(b) t=0.4
图1 基于离散格式(13)～(15)的数值解在t=0.2和0.4时刻的绝对误差
Fig. 1 Absolute errors of solutions at t=0.2 and 0.4 obtained with discrete schemes (13)～(15)
(a) t=0.2(b) t=0.4
图2 基于离散格式(16)～(18)的数值解在t=0.2和0.4时刻的绝对误差
Fig. 2 Absolute errors of solutions at t=0.2 and 0.4 obtained with discrete schemes (16)～(18)
下面验证两种算法在各个方向的收敛速率.首先考虑时间方向.为此，固定足够小的空间步长和分布阶步长，令时间步长依次减半，使得计算误差的变化主要由时间步长的变化产生.从表1的计算结果可以看出，格式(13)～(15)和格式(16)～(18)是稳定的、收敛的，在时间方向具有三阶收敛速率，这和预期的结果是一致的.而且，当三个方向的步长分别相等时，即计算网格相同时，格式(13)～(15)和格式(16)～(18)的误差也基本相同，但是格式(16)～(18)耗时更少，效率更高.
表1 格式(13)～(15)和格式(16)～(18)在t=0.5时刻的误差和时间方向的收敛速率以及计算时长
Table 1 Errors, temporal convergence rates and time consumptions of
schemes (13)～(15) and (16)～(18) at t=0.5
τschemes (13)～(15)(h=π/100, Δβ=1/100)E(τ,h,Δβ)RτCPU time T/sschemes (16)～(18)(h=π/100, Δβ=1/100)E(τ,h,Δβ)RτCPU time T/s1/409.879 0E-5-0.221 79.879 0E-5-0.171 01/801.382 7E-52.836 90.965 31.382 7E-52.836 90.650 31/1601.884 6E-62.875 23.553 91.884 6E-62.875 22.456 31/3202.516 7E-72.904 714.585 02.516 7E-72.904 79.933 81/6403.309 9E-82.926 758.398 33.309 9E-82.926 740.379 61/128 04.304 1E-92.943 0231.453 24.304 1E-92.943 0160.863 9
然后，验证空间方向的收敛速率.此处固定足够小的时间步长和分布阶步长，让空间步长依次减半，使计算误差的变化主要由空间步长的变化造成.从表2所列的结果可以看出，两个格式都是稳定的、收敛的，在空间方向都具有四阶收敛速率，这和预期的结果一致.而且，当剖分的网格相同时，格式(16)～(18)更省时间，剖分越细，耗时的差异越明显.
表2 格式(13)～(15)和格式(16)～(18)在t=0.5时刻的误差和空间方向的收敛速率以及计算时长
Table 2 Errors, spatial convergence rates and time consumptions of
schemes (13)～(15) and (16)～(18) at t=0.5
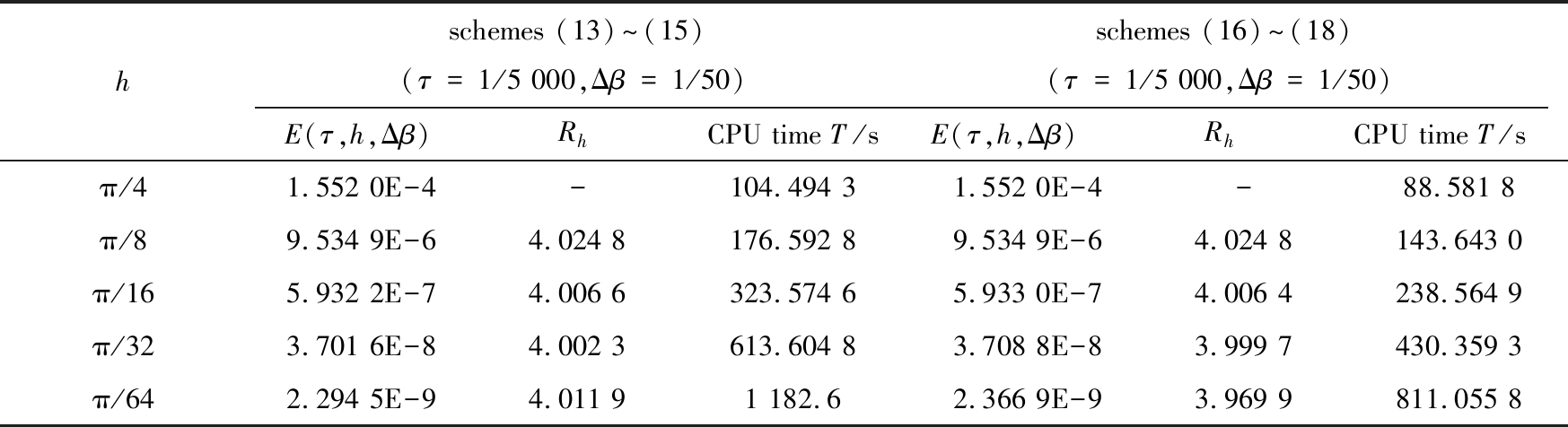
hschemes (13)～(15)(τ=1/5 000,Δβ=1/50)E(τ,h,Δβ)RhCPU time T/sschemes (16)～(18)(τ=1/5 000,Δβ=1/50)E(τ,h,Δβ)RhCPU time T/sπ/41.552 0E-4-104.494 31.552 0E-4-88.581 8π/89.534 9E-64.024 8176.592 89.534 9E-64.024 8143.643 0π/165.932 2E-74.006 6323.574 65.933 0E-74.006 4238.564 9π/323.701 6E-84.002 3613.604 83.708 8E-83.999 7430.359 3π/642.294 5E-94.011 91 182.62.366 9E-93.969 9811.055 8
表3 格式(13)～(15)、(16)～(18)和格式(3.30)～(3.32)[13]在t=0.5时刻关于误差以及分布阶收敛速率的比较
Table 3 Comparisons of errors and convergence rates in distributed orders obtained with
schemes (13)～(15), (16)～(18) and (3.30)～(3.32)[13] at t=0.5
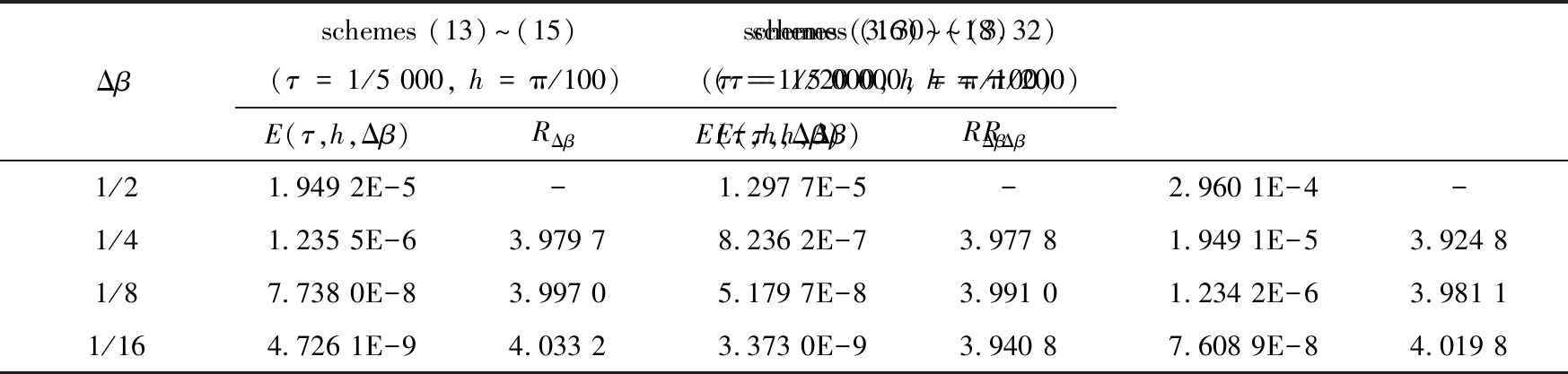
Δβschemes (13)～(15)(τ=1/5 000, h=π/100)E(τ,h,Δβ)RΔβschemes (16)～(18)(τ=1/5 000, h=π/100)E(τ,h,Δβ)RΔβschemes (3.30)～(3.32)(τ=1/20 000, h=π/200)E(τ,h,Δβ)RΔβ1/21.949 2E-5-1.297 7E-5-2.960 1E-4-1/41.235 5E-63.979 78.236 2E-73.977 81.949 1E-53.924 81/87.738 0E-83.997 05.179 7E-83.991 01.234 2E-63.981 11/164.726 1E-94.033 23.373 0E-93.940 87.608 9E-84.019 8
接下来验证分布阶的收敛速率.类似前面的方法，固定充分小的时间步长和空间步长，让Δβ依次减半，计算误差和收敛速率，同时，列出文献[13]中相应的数值结果做对比.表3的数据表明，格式(13)～(15)、格式(16)～(18)和文献[13]中格式(3.30)～(3.32)关于分布阶的收敛速率都大致等于4，但是格式(13)～(15)和(16)～(18)在较粗的网格上产生的数值误差反而更小，因此效率更高.
下面选取文献[11]中的例2做测试，并把本文两个格式的计算结果与文献[11]中的结果做对比.
例2 在初边值问题(2)～(4)中取
L=1， T=1， p(β)=Γ(5/2-β)，
精确解为u(x,t)=x2(1-x)4t3/2.
在计算例2时，取优化的步长比例，即在数值上取Δβ=h，τ=h4/3.表4的数值结果表明，本文两个格式的收敛速率为O(τ3+h4+Δβ4).另外,与文献[11]的算法在优化步长比例下(Δβ=h，τ=h2)的计算结果做对比可以看出，本文算法的误差更小，精度更高.
表4 在优化的步长比例下格式(13)～(15)、(16)～(18)和文献[11]中格式在t=1时刻关于误差和收敛速率的比较
Table 4 Comparisons of errors and convergence rates obtained with schemes (13)～(15), (16)～(18) and
schemes in ref. [11] with an optimal step size ratio for τ, h and Δβ at t=1
hschemes (13)～(15)E(τ,h,Δβ)Rhschemes (16)～(18)E(τ,h,Δβ)Rhschemes in ref. [11]E(τ,h,Δβ)Rh1/20.014 3-0.014 3-8.40E-3 -1/40.001 23.574 90.001 23.574 92.45E-31.781/87.251 2E-54.048 77.251 2E-54.048 76.36E-41.951/164.956 4E-63.870 94.956 4E-63.870 91.62E-41.98
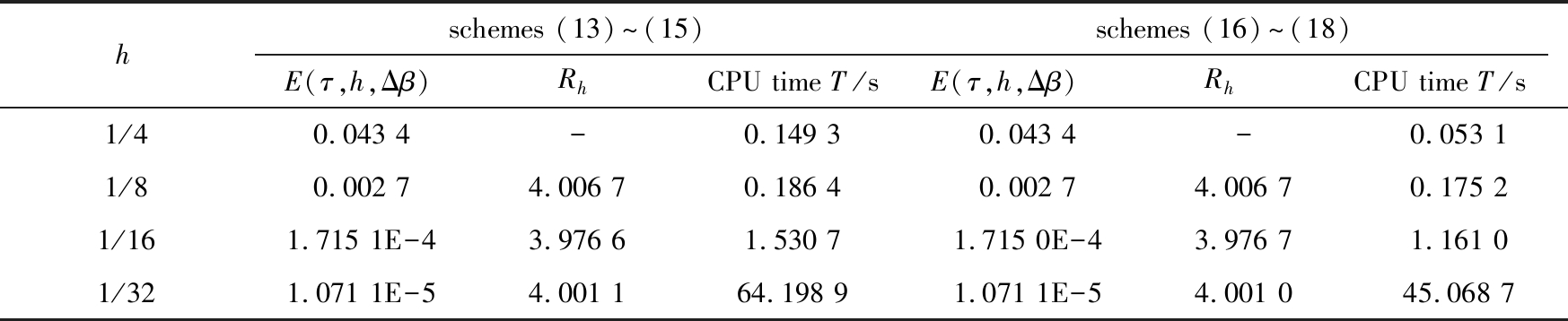
表5 在优化的步长比例下格式(13)～(15)、(16)～(18)在t=10时刻的误差和收敛速率以及计算时长
Table 5 Errors, convergence rates and time consumptions of schemes (13)～(15) and (16)～(18)
with an optimal step size ratio for τ, h and Δβ at t=10
hschemes (13)～(15)E(τ,h,Δβ)RhCPU time T/sschemes (16)～(18)E(τ,h,Δβ)RhCPU time T/s1/40.043 4-0.149 30.043 4-0.053 11/80.002 74.006 70.186 40.002 74.006 70.175 21/161.715 1E-43.976 61.530 71.715 0E-43.976 71.161 01/321.071 1E-54.001 164.198 91.071 1E-54.001 045.068 7
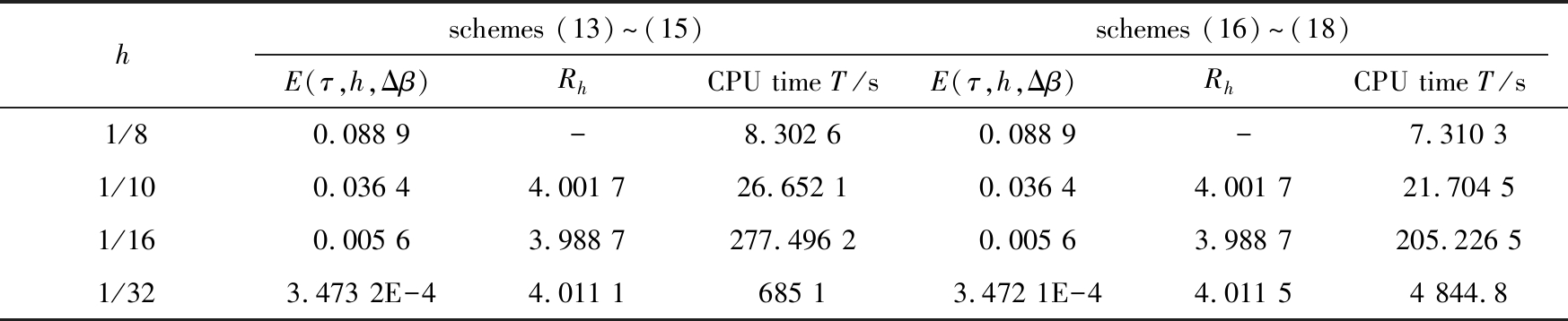
表6 在优化的步长比例下格式(13)～(15)、(16)～(18)在t=100时刻的误差和收敛速率以及计算时长
Table 6 Errors, convergence rates and time consumptions of schemes (13)～(15) and (16)～(18)
with an optimal step size ratio for τ, h and Δβ at t=100
hschemes (13)～(15)E(τ,h,Δβ)RhCPU time T/sschemes (16)～(18)E(τ,h,Δβ)RhCPU time T/s1/80.088 9-8.302 60.088 9-7.310 31/100.036 44.001 726.652 10.036 44.001 721.704 51/160.005 63.988 7277.496 20.005 63.988 7205.226 51/323.473 2E-44.011 1685 13.472 1E-44.011 54 844.8
最后，通过例2测试了较长时间(分别取T=10和100)的计算效果，数值结果见表5和表6.计算时仍然取优化的步长比例，即Δβ=h，τ=h4/3.从数值结果可以看出，两种算法是稳定的、收敛的，而且格式(16)～(18)比格式(13)～(15)耗时要少，网格越细，差异越明显.另外，与表4的结果做对比可以发现，当计算时长大幅度增加时，积累的误差也有所增加，但是算法仍然是可靠和有效的.
4 结 论
文章基于复化Simpson公式和复化两点Gauss-Legendre公式， 构造了两个求解分布阶扩散方程的高阶差分格式， 在时间、 空间和分布阶三个方向的收敛速率分别可达到3，4，4.通过数值实验， 验证了算法的稳定性、 收敛性以及收敛速率， 并比较了两种算法的效率；同时，也将本文的两种算法与文献中求解相同问题的算法做对比.数值结果表明， 本文的算法误差更小， 具有更高的收敛精度.在进一步的工作中， 笔者考虑将此高阶格式推广用以解决相应的多维空间问题.
[1] PODLUBNY I. Fractional Differential Equations: an Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications[M]. San Diego: Academic Press, 1999.
[2] 张平奎, 杨绪君. 基于激励滑模控制的分数阶神经网络的修正投影同步研究[J]. 应用数学和力学, 2018, 39(3): 343-354.(ZHANG Pingkui, YANG Xujun. Modified projective synchronization of a class of fractional-order neural networks based on active sliding mode control[J]. Applied Mathematics and Mechanics, 2018, 39(3): 343-354.(in Chinese))
[3] 杨旭, 梁英杰, 孙洪广, 等. 空间分数阶非Newton流体本构及圆管流动规律研究[J]. 应用数学和力学, 2018, 39(11): 1213-1226.(YANG Xu, LIANG Yingjie, SUN Hongguang, et al. A study on the constitutive relation and the flow of spatial fractional non-Newtonian fluid in circular pipes[J]. Applied Mathematics and Mechanics, 2018, 39(11): 1213-1226.(in Chinese))
[4] CAPUTO M. Elasticità e Dissipazione[M]. Bologna: Zanichelli, 1969.
[5] SINAI Y G. The limiting behavior of a one-dimensional random walk in a random medium[J]. Theory of Probability & Its Applications, 1983, 27(2): 256-268.
[6] CHECHKIN A V, KLAFTER J, SOKOLOV I M. Fractional Fokker-Planck equation for ultraslow kinetics[J]. Europhysics Letters, 2003, 63(3): 326-332.
[7] KOCHUBEI A N. Distributed order calculus and equations of ultraslow diffusion[J]. Journal of Mathematical Analysis and Applications, 2008, 340(1): 252-281.
[8] JIAO Z, CHEN Y,PODLUBNY I. Distributed-Order Dynamic Systems: Stability, Simulation, Applications and Perspectives[M]. London: Springer, 2012.
[9] CAPUTO M. Distributed order differential equations modelling dielectric induction and diffusion[J]. Fractional Calculus and Applied Analysis, 2001, 4(4): 421-442.
[10] HARTLEY T T, LORENZO C F. Fractional system identification: an approach using continuous order-distributions: NASA/TM-1999-209640[R]. USA: NASA, 1999.
[11] FORD N J, MORGADO M L, REBELO M. An implicit finite difference approximation for the solution of the diffusion equation with distributed order in time[J]. Electronic Transactions on Numerical Analysis, 2015, 44: 289-305.
[12] GAO G H, SUN Z Z. Two unconditionally stable and convergent difference schemes with the extrapolation method for the one-dimensional distributed-order differential equations[J]. Numerical Methods for Partial Differential Equations, 2016, 32(2): 591-615.
[13] GAO G H, SUN H W, SUN Z Z. Some high-order difference schemes for the distributed-order differential equations[J]. Journal of Computational Physics, 2015, 298: 337-359.
[14] HU J H, WANG J G, NIE Y F. Numerical algorithms for multidimensional time-fractional wave equation of distributed-order with a nonlinear source term[J]. Advances in Difference Equations, 2018(1): 352. DOI: 10.1186/s13662-018-1817-2.
[15] 郭晓斌, 尚德泉. 复化两点Gauss-Legendre公式及其误差分析[J]. 数学教学研究, 2010, 29(4): 49-51.(GUO Xiaobin, SHANG Dequan. Composite two-point Gauss-Legendre formula and the error analysis[J]. Research of Mathematic Teaching-Learning, 2010, 29(4): 49-51.(in Chinese))
[16] TIAN W, ZHOU H, DENG W. A class of second order difference approximations for solving space fractional diffusion equations[J]. Mathematics of Computation, 2015, 84(294): 1703-1727.
[17] SUN Z Z. The Method of Order Reduction and Its Application to the Numerical Solutions of Partial Differential Equations[M]. Beijing: Science Press, 2009.
[18] ZHU Y, SUN Z Z. A high-order difference scheme for the space and time fractional Bloch-Torrey equation[J]. Computational Methods in Applied Mathematics, 2018, 18(1): 147-164.