引 言
对于大型喷雾机，一个重要的考虑因素是实现高精度喷射操作.喷嘴和冠层距离影响喷雾质量，距离过小或过大，液滴都不能均匀喷洒在农作物上，喷雾机在行进运动中喷杆会发生有害振动[1].因此，精准控制喷雾机喷杆位置对均匀喷洒农药具有重要意义.
喷雾机喷杆系统的位置调节多使用被动弹簧缓冲技术和PID控制策略[2-6].文献[2]针对喷杆连接机构采用钢索、弹簧等柔性连接来减轻喷杆有害振动，但未进行主动控制；文献[6]设计基于超声波传感器的PID控制喷杆位姿系统，当外部干扰作用于系统时，控制器难以满足精度要求.电液伺服系统具有控制精度高、负载能力强、响应速度快等特点，已逐步被应用在大型智能喷雾机喷杆伺服跟踪领域，但喷杆系统本身具有强非线性和参数不确定性，严重影响系统的控制精度与效果.
目前，为了提高电液伺服系统的控制精度与稳定性能，国内外学者做了大量的研究，并取得了一些研究成果[7-17].文献[9]提出了基于反馈线性化技术的方法，文献[10-11]将鲁棒自适应方法应用于电液伺服系统控制.反步控制可以较好地处理非线性系统，文献[12-15]提出了基于反步法的非对称液压缸控制方法，取得了良好的控制效果，文献[16]针对一类具有外部扰动的非线性系统，基于反步法进行干扰补偿.传统反步设计需要对虚拟控制量重复微分，增加了算法复杂性.而动态面算法对反步法中虚拟量进行一阶滤波，简化了控制器设计.
基于上述分析，本文针对以喷雾机喷杆为负载的电液伺服系统，提出了一种自适应动态面控制方法.考虑喷杆系统结构并建立完整数学模型，采用RBF网络逼近非线性函数，通过阻尼项补偿干扰对系统的影响，结合动态面方法，避免了传统反步的“膨胀”问题，简化控制器结构.最后将设计控制器应用到某喷雾机喷杆系统进行仿真，验证了所提方法的合理性与有效性.
1 电液伺服系统建模
电液伺服系统数学模型主要由液压缸运动学方程和流量方程组成，系统示意图如图1所示.
图1 电液伺服系统
Fig. 1 The electro-hydraulic servo system
系统运动学方程为
(1)
式中，P1,P2为液压腔压力；A1,A2为液压腔作用面积；xp为喷杆位移；m为喷杆质量；Bp为活塞摩擦因数；ks为弹性系数；FL为作用在活塞外负载力、摩擦力和难以建模的阻力等.
忽略外泄漏影响，系统流量方程为
(2)
式中,βe为弹性模量；Ctm为内泄漏系数；V1=V10+A1xp，V2=V20-A2xp，V10和V20为液压两腔初始容积；Q1为流入无杆腔流量，Q2为流出有杆腔流量.
流量Q1和Q2为
(3)
其中
(4)
(5)
为阀口流量系数，w为伺服阀开口梯度，ρ为液压油密度；Ps和Pr为供油压力和回油压力；xv为阀芯位移，与输入电压u之间近似为比例环节，即xv=kvu，系数kv>0.选取状态变量
转化为严格反馈形式，定义新系统变量
可得
(6)
式中
D1和D2为系统中的复合干扰；Δfi(x)和Δbi(i=1, 2)表示由参数摄动引起的不确定性；d=
-FL/m为外部扰动.参数βe，Bp，ks，Ctm，Cd和ρ具有不确定性，m不能精确已知，外负载力FL是时变的.仅考虑参数m，βe，Cd和FL存在不确定性.
2 基 本 假 设
根据实际系统，不失一般性，考虑如下假设： 1) 参考输入信号
和
存在且有界； 2) f1(x)和f2(x)为非线性光滑函数，复合干扰D1和D2均有界； 3) 增益函数g(x)的符号已知，假设为正.存在常数g1,g3≥0，使得g1≤g(x)≤g3成立.
引理1[17] 一个n输入单输出且中间层有N个神经元的RBF神经网络可以表示为y=θTξ(x)，其中x∈Rn是输入向量，y∈R是输出量，θ∈RN是可调权值向量，ξ(x)∈RN是非线性函数且ξ(x)=[β1(x),β2(x),…,βN(x)]T，βi(x),i=1,2,…,N是Gauss基函数，形如βi(x)=exp(-‖x-zi‖2/2v2),其中，zi∈Rn,i=1,2,…,N为第i个Gauss基函数中心，v>0为Gauss基函数宽度.
f(x)=θ*Tξ(x)+σ*, x∈Ω,
(7)
式中,σ*为误差且满足|σ*|≤σM；θ*有界且未知,存在已知正数θM使‖θ*‖≤θM.
3 动态面控制器设计
3.1 控制器设计
采用动态面方法设计喷杆位置伺服控制器.设计分为3步，前2步分别设计虚拟控制量和自适应律，最后一步设计实际控制律.
第1步 定义第一个误差面S1=x1-x1d,求导得
(8)
设计虚拟控制量
(9)
其中，c1>0为可调控制参数.
取x2d为
低通滤波器1/(τ2s+1)输出，定义
满足
(10)
第2步 定义第二个误差面S2=x2-x2d，求导得
(11)
构造RBF网络逼近非线性函数
(12)
其中，
为逼近误差，
为理想权值，
定义向量
(13)
其中,c2>0为可调控制参数；ε为正数；
为阻尼项，用于补偿D1.
设计虚拟控制量
(14)
其中，
是θ1的估计值.
设计自适应律为
(15)
其中，Γ1为正定对称矩阵，η1为正实数.
取x3d为
低通滤波器1/(τ3s+1)输出，满足
(16)
第3步 定义第三个误差面S3=x3-x3d，求导得
(17)
构造RBF网络逼近非线性函数
(18)
其中，
为逼近误差，
为理想权值，
定义向量
(19)
其中，c3>0为可调控制参数；ε为正数；
为阻尼项，用于补偿D2.
设计实际控制量
(20)
其中，
是权值θ2的估计.
自适应律为
(21)
其中，Γ2为正定对称矩阵，η2为正实数.
3.2 稳定性分析
定理1 对于电液伺服闭环系统，在满足假设1)～3)的条件下和初始条件V(0)≤p(p为任意正常数)，采用动态面算法和基于稳定性理论分析可得：① 闭环系统是稳定的; ② 喷杆系统位置跟踪误差S1=x1-x1d及各参数估计误差一致有界; ③ 当t充分大时，跟踪误差收敛于Q/(2r).
证明 定义虚拟控制量误差为
(22)
可得
(23)
定义RBF网络权值误差
分别对各项误差面和虚拟控制量求导整理得
(24)
(25)
存在非负上界连续函数B2，B3，且有
(26)
(27)
则
(28)
选取整个系统的Lyapunov函数
V=V1+V2+V3，
(29)
其中
(30)
由
和
整理得
(31)
由Young不等式及
整理得
(32)
控制参数选取如下：
r为待设计正数.
考虑假设1)～3)及
整理得
(33)
其中
(34)
当V≤p成立时，Bi≤Mi成立；当V=p时，即V≤-2rp+Q≤0，故选取r≥Q/(2p).
解不等式可得
(35)
因此，喷杆闭环系统内所有信号均有界，且当t充分大时，V(t)≤Q/(2r).定理1得证.
4 仿 真
为验证设计控制器性能，采用仿真软件对控制系统仿真.伺服系统参数选择如下所示：
Ps=9 MPa， Pr=0 MPa， A1=3.14×10-4 m2， A2=2.355×10-4 m2，
V10=8.5×10-5 m3， V20=5.36×10-5 m3， βe=690 MPa，
Ctm=1×10-5 m3/(s·MPa)， ρ=870 kg/m3， m=40 kg，
τv=0.000 8 s， kv=0.25 A-1， Cd=0.65， w=π/6×10-3 m2/m.
设定理想跟踪轨迹x1d=0.8sin t，取D1=0.01sin(2t)，D2=0.2cos(2t)，初始状态为
第一个RBF网络结构取2输入8隐层1输出.网络输入为x1,x2，网络权值初始化均为0，根据输入范围基函数中心分布在[-9,9]范围，宽度取10.第二个RBF网络结构取2输入8隐层1输出.网络输入为x2,x3，网络权值初始化均为0，根据输入范围基函数中心分布在[-9,9]范围，宽度取10.控制参数选取如下：ρ1=0.1,ρ2=0.05,r=0.01，c1=1.5,c2=2,c3=1，η1=0.05,η2=0.01，Γ1=diag(5),Γ2=diag(10)，τ2=τ3=0.05.
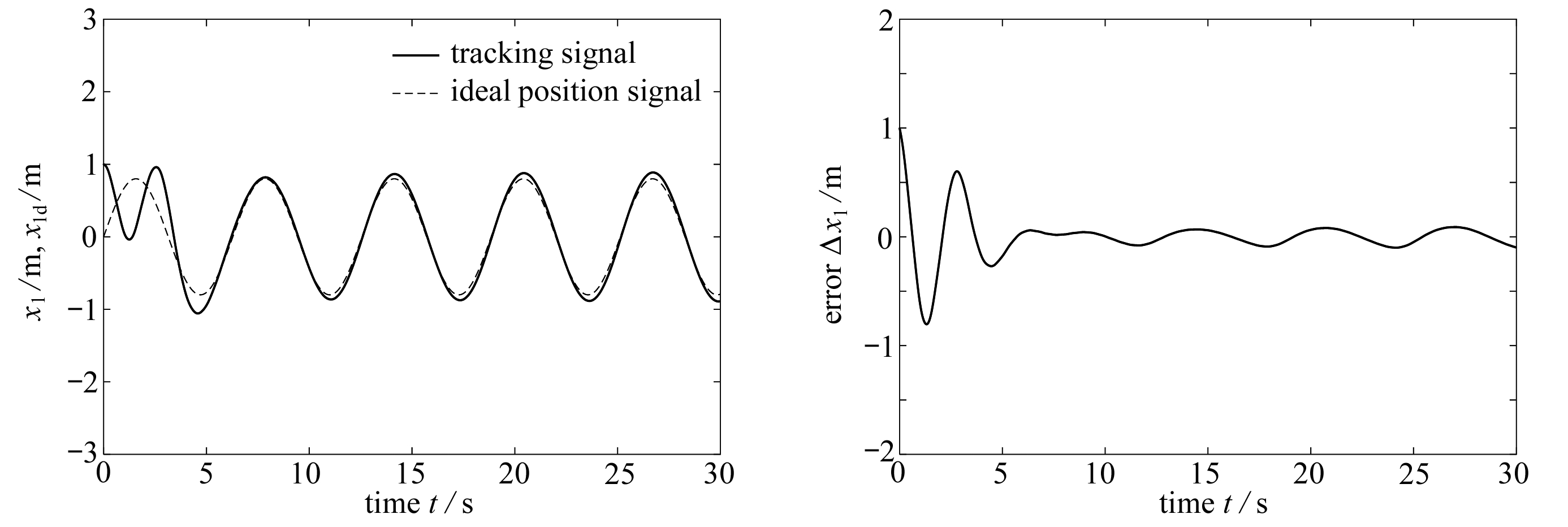
图2 位置跟踪曲线及跟踪误差
Fig. 2 The position tracking curve and the tracking error
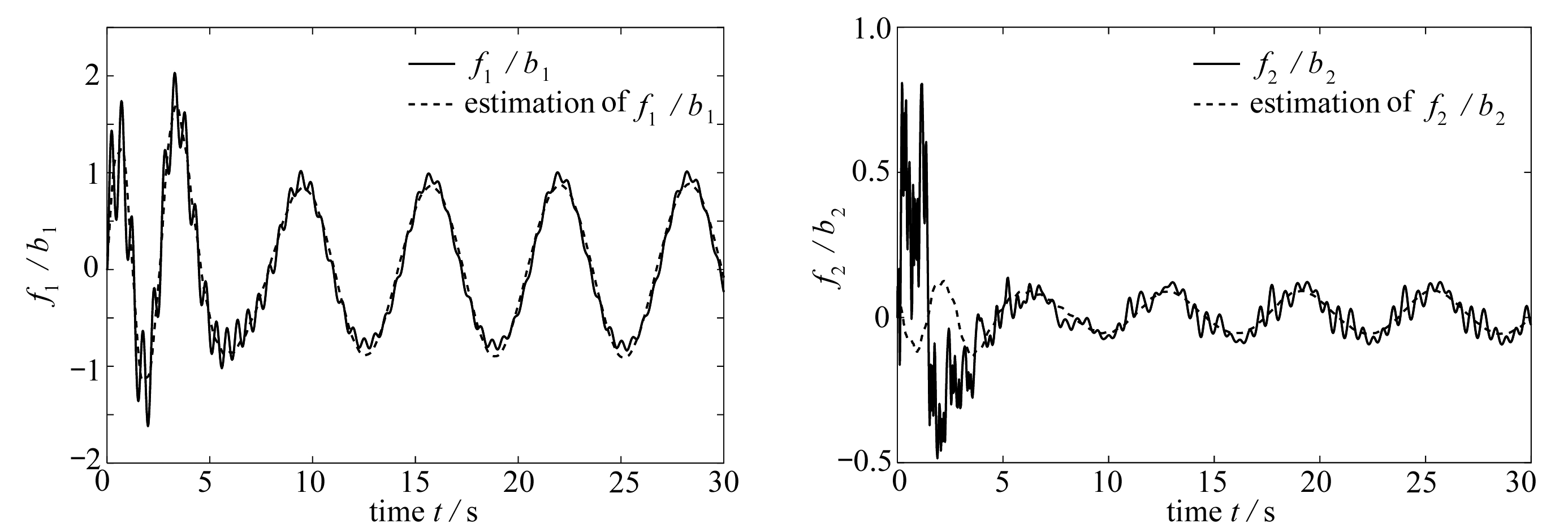
图3 逼近曲线
Fig. 3 The approximation curves
图2表示喷杆位置系统在控制输入信号作用下，喷杆实际输出位置高度能够较好地仿形跟踪给定参考冠层高度值，且跟踪误差逐渐减小，保持在较小的区域范围内且满足喷杆喷洒的精度要求.图3表示RBF网络逼近整个喷杆位置系统的非线性函数效果图，可以看出RBF网络对非线性函数逼近效果良好、误差较小.仿真验证了设计的喷杆位置伺服控制器具有良好的仿形跟踪控制性能和稳定性能，对植保机喷杆位置的升降调节起到了良好的控制效果.
5 结 论
为了实现喷雾机喷杆快速稳定而又精准地伺服跟踪植物冠层高度，选用电液伺服系统作为其位置调节装置，提出了一种采用RBF网络自适应动态面控制方法.建立完整数学模型，采用RBF网络逼近非线性函数，加入阻尼项补偿干扰对系统的影响，结合动态面方法进行控制器设计.避免了传统反步控制中“膨胀”的问题，简化控制器结构.仿真结果表明设计的控制器性能良好、精度较高，很好地克服了参数不确定性、外界干扰以及强非线性特性对系统的影响.
[1] 陈晨, 薛新宇, 顾伟, 等. 喷雾机喷杆结构形状及截面尺寸优化与试验[J]. 农业工程学报, 2015, 31(9): 50-56.(CHEN Chen, XUE Xinyu, GU Wei, et al. Experiment and structure shape and section size optimization of spray boom[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(9): 50-56.(in Chinese))
[2] 陈树人, 韩红阳, 陈刚, 等. 喷杆喷雾机机架动态特性分析与减振设计[J]. 农业机械学报, 2013, 44(4): 50-53.(CHEN Shuren, HAN Hongyang, CHEN Gang, et al. Dynamic characteristic analysis and vibration reduction design for sprayer frame[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(4): 50-53.(in Chinese))
[3] 陈双, 宗长富, 张立军, 等. 主动悬架平顺性和侧倾姿态综合控制策略[J]. 吉林大学学报(工学版), 2011, 41(2): 59-64.(CHEN Shuang, ZONG Changfu, ZHANG Lijun, et al. Research on integrated control strategy of ride and roll attitude via active suspension[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(2): 59-64.(in Chinese))
[4] 吴吉麟, 苗玉斌. 不同激励源下宽幅喷雾机喷杆的动态特性分析[J]. 农业工程学报, 2012, 28(4): 39-44.(WU Jilin, MIAO Yubin. Dynamic characteristic analysis of boom for wide sprayer with different exciting sources[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(4): 39-44.(in Chinese))
[5] 陈文坊, 邱白晶, 杨宁, 等. 基于超声波传感器的喷杆位姿控制系统[J]. 农机化研究, 2013, 34(3): 84-87.(CHEN Wenfang, QIU Baijing, YANG Ning, et al. Spray boom position control system based on ultrasonic sensors[J]. Journal of Agricultural Mechanization Research, 2013, 34(3): 84-87.(in Chinese))
[6] 魏新华, 邵菁, 缪丹丹, 等. 喷杆式喷雾机喷杆高度及平衡在线调控系统[J]. 农业机械学报, 2015, 46(8): 66-71.(WEI Xinhua, SHAO Jing, MIAO Dandan, et al. Online control system of spray boom height and balance[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(8): 66-71.(in Chinese))
[7] 石胜利, 李建雄, 方一鸣. 具有输入饱和的电液伺服系统反步位置跟踪控制[J]. 中南大学学报(自然科学版), 2016, 47(10): 3369-3374.(SHI Shengli, LI Jianxiong, FANG Yiming. Backstepping position tracking control for electro-hydraulic servo system with input saturation[J]. Journal of Central South University(Science and Technology), 2016, 47(10): 3369-3374.(in Chinese))
[8] SUN Y B, GUO Q D. Feedback linearization speed-tracking control of linear servo system based on sliding mode observer[J]. Journal of Control Theory and Applications, 2014, 21(6): 391-397.
[9] 俞珏, 庄健, 于德弘. 采用李雅普诺夫函数的电液伺服系统反馈线性化控制[J]. 西安交通大学学报, 2014, 48(7): 71-76.(YU Jue, ZHUANG Jian, YU Dehong. Feedback linearization control for an electro-hydraulic servo system using Lyapunov functions[J]. Journal of Xi’an Jiaotong University, 2014, 48(7): 71-76.(in Chinese))
[10] 杨四阳, 韩江, 张魁榜, 等. 电液位置伺服系统的鲁棒自适应控制[J]. 应用数学和力学, 2017, 38(6): 676-684.(YANG Siyang, HAN Jiang, ZHANG Kuibang, et al. A robust adaptive backstepping control method for electro-hydraulic position servo systems[J]. Applied Mathematics and Mechanics, 2017, 38(6): 676-684.(in Chinese))
[11] 陈光荣, 王军政, 汪首坤, 等. 自适应鲁棒控制器设计新方法在电液伺服系统中的应用[J]. 自动化学报, 2016, 42(3): 375-384.(CHEN Guangrong, WANG Junzheng, WANG Shoukun, et al. Application of a new adaptive robust controller design method to electro-hydraulic servo system[J]. Acta Automatica Sinica, 2016, 42(3): 375-384.(in Chinese))
[12] 方一鸣, 许衍泽, 李建雄. 具有输入饱和的电液伺服位置系统自适应动态面控制[J]. 控制理论与应用, 2014, 31(4): 511-518.(FANG Yiming, XU Yanze, LI Jianxiong. Adaptive dynamic surface control for electro-hydraulic servo position system with input saturation[J]. Control Theory & Applications, 2014, 31(4): 511-518.(in Chinese))
[13] 吴忠强, 夏青, 彭艳, 等. 高阶非线性液压辊缝系统的Backstepping动态面控制[J]. 仪器仪表学报, 2012, 33(4): 949-954.(WU Zhongqiang, XIA Qing, PENG Yan, et al. Backstepping dynamic surface control for high-order nonlinear hydraulic roll gap system[J]. Chinese Journal of Scientific Instrument, 2012, 33(4): 949-954.(in Chinese))
[14] WONHEE K, SHIN D, WON D, et al. Disturbance observer based position tracking controller in the presence of biased sinusoidal disturbance for electrohydraulic actuators[J]. IEEE Transactions on Control Systems Technology, 2013, 21(6): 2290-2298.
[15] SHI S L, FANG Y M, LI J X, et al. Adaptive position tracking control for electro-hydraulic servo system with input saturation[J]. ICIC Express Letters, 2012, 6(10): 2699-2704.
[16] WEN C Y, ZHOU J, LIU Z T, et al. Robust adaptive control of uncertain nonlinear systems in the presence of input saturation and external disturbance[J]. IEEE Transactions on Automatic Control, 2017, 56(7): 1672-1678.
[17] 张天平, 施枭铖, 沈启坤. 具有未建模动态的自适应神经网络动态面控制[J]. 控制理论与应用, 2013, 30(4): 475-481.(ZHANG Tianping, SHI Xiaocheng, SHEN Qikun. Adaptive neural-network dynamic surface-control with unmodeled dynamics[J]. Control Theory & Applications, 2013, 30(4): 475-481.(in Chinese)