引 言
微生物形体微小、结构简单,却是自然中非常重要的一类物种.它在生物化工、农业发展、能源环保等领域都发挥着非常重大的作用,例如用于药物制备、污水处理、生产生物燃料和肥料等.早在20世纪早期, Wager [1]等科学家就已经观测到生物对流现象.与自然对流相似,生物对流指在重力条件下由微生物运动引起的对流现象.微生物富集过程会受其趋光或者趋氧等生物学因素影响,微生物会自主运动向液体上层聚集.由于微生物的密度通常比流体的密度大,当聚集体的浓度变得足够大时,就会因重力原因形成生物对流.趋旋性[2]是微生物运动过程中的常见特性之一,其发生机理是某些微生物在结构上都是重心位于底部,导致其在流体中游动时同时受重力矩和黏力矩而产生回旋.
在过去十多年中,生物对流这一实验现象越来越受到理论研究工作者的重视. Kuznetsov等[3]对多孔介质中趋旋性微生物的对流稳定性进行了研究,验证了多孔介质对生物对流的阻碍作用,并确定了使生物对流能够产生的临界渗透率.Nield等[4]采用线性稳定性分析方法研究了趋旋性微生物悬浮液中热-生物对流的震荡不稳定性.Zhao等[5]研究了非震荡热-生物对流稳定性,并分析了热Rayleigh数、Lewis数和细胞偏心率对生物对流稳定性的影响.
近些年来,幂律流体作为一类工程中应用广泛的非Newton流体,得到了越来越多学者的关注[6-10].其中Barletta 等[7]研究了幂律流体垂直渗流的热对流稳定性,得到了在不同流速下的幂律对流稳定性规律.实际上,在微生物实验中,因为添加培养液的缘故,容易整体呈现出典型的非Newton流体特征.鉴于此,本文的目的是研究趋旋性微生物在幂律流体饱和水平多孔层中的热-生物对流稳定性.利用线性稳定性分析以及Galerkin数值方法,得到了不同情况下的生物Rayleigh数,分析生物对流系统的稳定性条件以及各物理参数,如热Rayleigh数、幂律指数、对流Péclet数、生物Péclet数、生物Lewis数等对生物对流系统稳定性的影响.此研究结果可以为非Newton流体中的生物对流实验提供理论支持.
1 力 学 模 型
1.1 控制方程
考虑一个厚度为H,水平放置的饱和多孔层,如图1所示.其中充满了幂律流体以及均匀分布的趋旋性单细胞微生物.采用直角坐标系来表示流体的状态,z轴的方向与重力方向相反.为研究方便,该多孔层在上下边界处是等温和半渗透的.顶部和底部温度分别为T0和T0+ΔT,其中ΔT是正值,代表底部温度高于顶部温度.流体可以透过上下边界,微生物则无法通过.层间的微生物平均数量密度为![]()
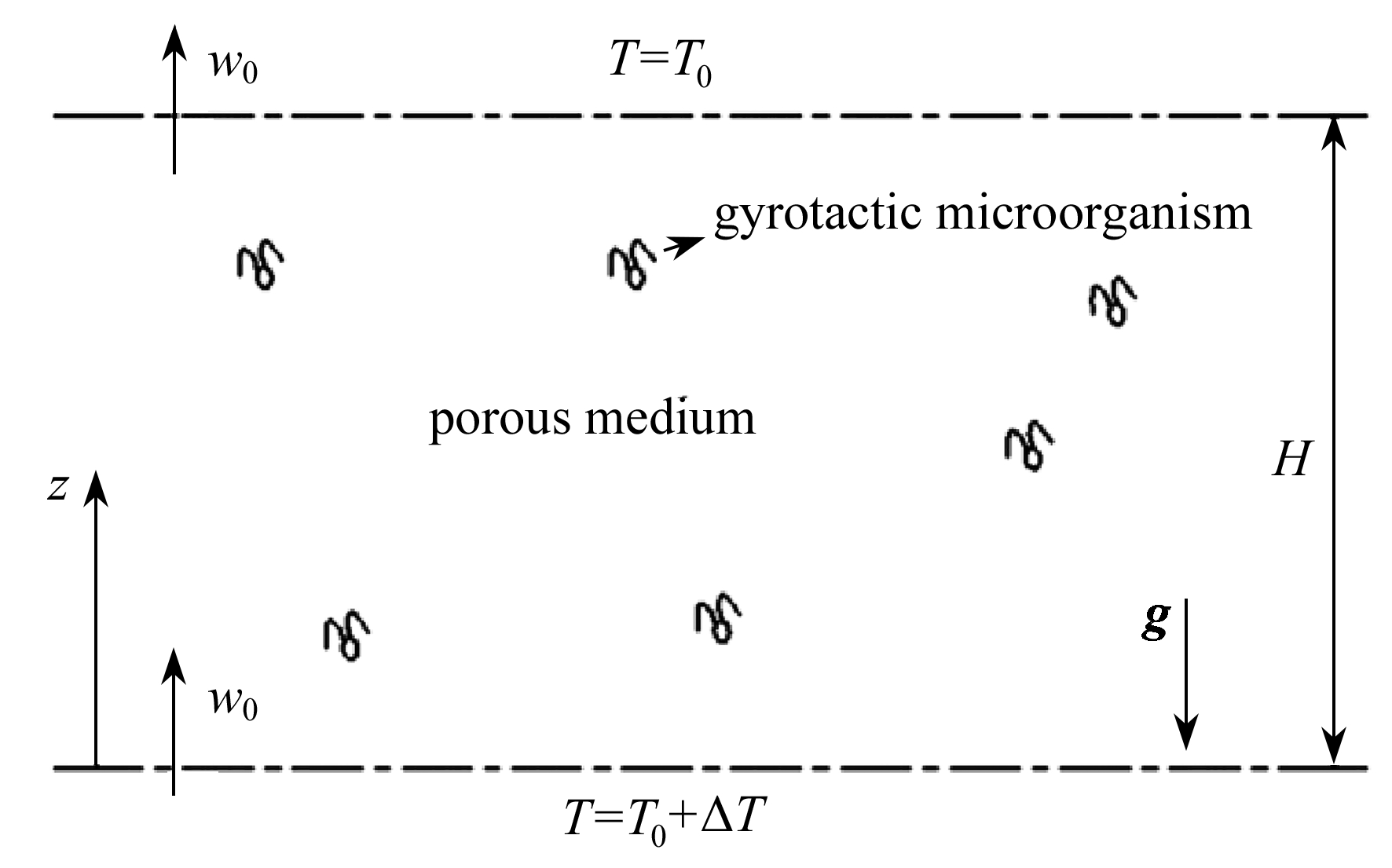
图1 对流模型示意图
Fig. 1 Schematic of the convection model
内部的幂律流体遵循的剪切公式[11]为
(1)
其中τ是剪应力,μ是动力黏度,![]() 是剪切速率即流速梯度,n是幂律指数(n>0).当n=1时是Newton流体,其剪应力和剪切速率是线性关系;当n<1时是假塑性流体,也称剪切变稀流体,它的表观黏度随着剪切速率增大而降低;反之当n>1时,代表的是膨胀性流体,也称剪切变稠流体.
是剪切速率即流速梯度,n是幂律指数(n>0).当n=1时是Newton流体,其剪应力和剪切速率是线性关系;当n<1时是假塑性流体,也称剪切变稀流体,它的表观黏度随着剪切速率增大而降低;反之当n>1时,代表的是膨胀性流体,也称剪切变稠流体.
根据Kuznetsov等[3]和Barletta等[7]的研究,结合幂律流体的剪切特性和微生物的随机游动模型,忽略多孔介质黏性耗散,采用Boussinesq近似[12],得到以下控制方程:
连续性方程
 ·u=0,
·u=0,
(2)
其中u是流体渗流速度,它有3个分量u,v,w.
动量方程
![]()
 P-ρ0gβT(T-T0)+NυΔρg,
P-ρ0gβT(T-T0)+NυΔρg,
(3)
这里的Ca是加速度系数,ρ0是流体密度,μe是幂律流体等效动力黏度,K是多孔介质渗透率,P是压强,g是重力加速度,βT是流体热膨胀系数,T是温度,T0是参考温度,N是微生物数量密度,υ 是微生物的平均体积,Δρ是微生物和流体的密度差.
能量方程
![]()
 T=κ
T=κ 2T,
2T,
(4)
其中γ是相对比热容,κ是流体的热扩散系数.
微生物数量的平衡方程可基于Fick定律表述:
![]()
 ·j,
·j,
(5)
其中φ 是多孔介质的孔隙率,j 是微生物通量,其具体数值为
![]()
 N,
N,
(6)
其中Ws是微生物平均运动速度,![]() 是细胞平均运动方向,Dm是微生物的质量扩散系数.
是细胞平均运动方向,Dm是微生物的质量扩散系数.
1.2 边界条件
考虑水平多孔层在水平方向是无限长的,因此可以忽略水平方向分量的影响.考虑上下边界是半渗透的,即水可以流通而微生物无法通过.流体在上下边界的渗流速度均为w0,微生物在边界上垂直方向的通量为0.此外,下边界的温度比上边界高,且分别保持恒温.
由此可得边界条件的表达式为
(7)
其中ez是z方向的单位向量.
1.3 无量纲化
为了避免计算时单位换算的不便,现对方程进行无量纲化处理.由相似原理,无量纲化之后的方程仍然反映了原各物理量之间的关系,定义如下无量纲变量:
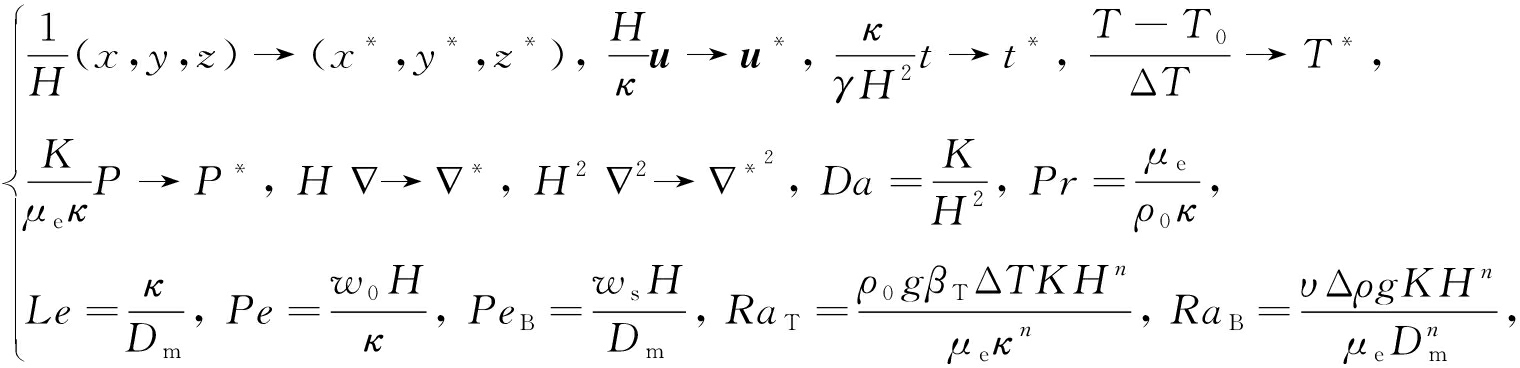
(8)
其中Da是Darcy数,表征了多孔介质的渗透率;Pr是Prandtl数,反映了流体物理性质对生物对流传热过程的影响;Le是微生物的Lewis数,表示热扩散系数和生物质量扩散系数之比;Pe是Péclet数,反映了流体流动的速度;PeB是生物Péclet数,反映了生物的平均运动速度;RaT是热Rayleigh数,反映了多孔层间的温度梯度;RaB是生物Rayleigh数,反映了生物对流稳定性.为了表达方便,去掉上标“*”,无量纲化之后的控制方程为
![]()

![]()
(9)
![]()
 T=
T= 2T,
2T,
(10)
![]()

![]()
(11)
无量纲化后的边界条件为
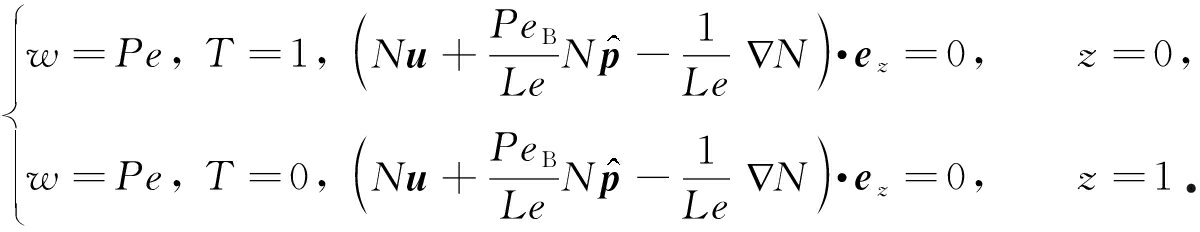
(12)
1.4 稳态解
当系统处于稳定状态时,取一个垂直的均匀流作为该问题的稳态解,此时微生物运动方向竖直向上,则有
(13)
其中下标b表示稳态解.将式(13)代入方程(10)、(11)并结合边界条件式(13),可得温度的稳态解为
(14)
(15)
浓度的稳态解为
(16)
Nb(z)=N0e(LePe+PeB)z.
(17)
由式(17)可得,底层的细胞数量密度为N0,多孔层中的细胞平均数量密度为![]() 那么
那么
(18)
于是得出
(19)
2 线性稳定性分析
扰动法是指在系统达到稳定后,对系统的物理量施加一个微小扰动,通过分析扰动后的流动情况来研究对流系统的稳定性.于是有
u=ub(z)+u′(t,x,y,z),
(20)
T=Tb(z)+T′(t,x,y,z),
(21)
N=Nb(z)+N′(t,x,y,z),
(22)
(23)
其中上标“′”表示扰动量.
Pedley等[13]通过研究微生物趋旋性对其游动的定向作用,提出了一种趋旋性运动的扰动方式:
(24)
(25)
(26)
(27)
(28)
其中B是微生物调整游动方向所需的时间尺度,α⊥是趋旋性的一个系数,h是微生物细胞质心和形心的距离,α0是细胞的偏心率.
将扰动量(20)~(23)和稳态解(13)~(19)代入到控制方程(9)~(11)中,忽略二次扰动项,得到z方向的扰动方程如下:
(29)
![]()
 2T′,
2T′,
(30)
![]()
 2N′,
2N′,
(31)
其中
(32)
同理,代入扰动后扰动量的边界条件为
(33)
在线性稳定性分析中,扰动可以用正则模式的叠加形式来表示,即
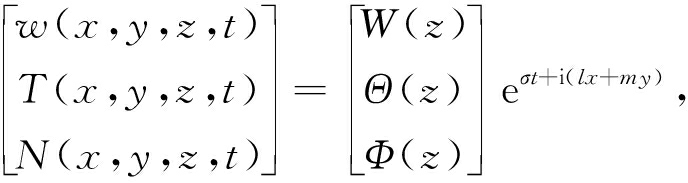
(34)
其中σ为扰动的时间增长率,l和m分别为x和y方向的波数[14].为了表达方便,上式中去掉了扰动量的上标.一般来说,式(34)中的σ为复数.但本文仅就流体非振荡对流情况下的线性稳定性进行分析,因此限定选取σ为实数.将式(34)代入到扰动方程(29)~(31)中可得扰动方程的特征值问题,其解就是可反映对流稳定性的Rayleigh数RaT和RaB.由线性稳定性分析法,上述特征值问题可简化为
(35)
(36)
(37)
其中
α2=l2+m2, Q=LePe+PeB,
(38)
这里α的物理意义是扰动的波数.边界条件为
(39)
利用Galerkin方法对上述控制方程进行数值求解.选取满足边界条件(39)的试函数为
W1=z(1-z), Θ1=z(1-z), Φ1=Q2z2+(2Q-Q2)z+(2-Q).
(40)
近似解为试函数与待定系数的线性组合.将近似解和试函数代入到方程组(35)~(37)中,分别进行积分运算后,联立消去待定系数即可得到RaB与RaT的关系.
3 结果与讨论
在自然对流的问题研究中,通常用热Rayleigh数表征由温度梯度引起的流体对流稳定性,温度梯度越大则热Rayleigh数越大.式(35)~(37)中的热Rayleigh数RaT为系统稳定的前提下可容许的热Rayleigh数最大值,在同等条件下RaT越大说明对流越稳定.对于生物对流的稳定性问题,类比采用生物Rayleigh数RaB来表示其对流稳定性.进一步地,引入临界生物Rayleigh数![]() 来表示临界波数下的对流稳定性,若超过
来表示临界波数下的对流稳定性,若超过![]() 该生物对流系统就会失
该生物对流系统就会失![]() 是RaB在波数α取不同值时的最小值,此时对应的波数就是临界波数,用公式表述为
是RaB在波数α取不同值时的最小值,此时对应的波数就是临界波数,用公式表述为
(41)
其余参数默认设置为RaT=10, Pe=0.1, Le=5, PeB=0.1, B=1, α0=0.2, ![]()
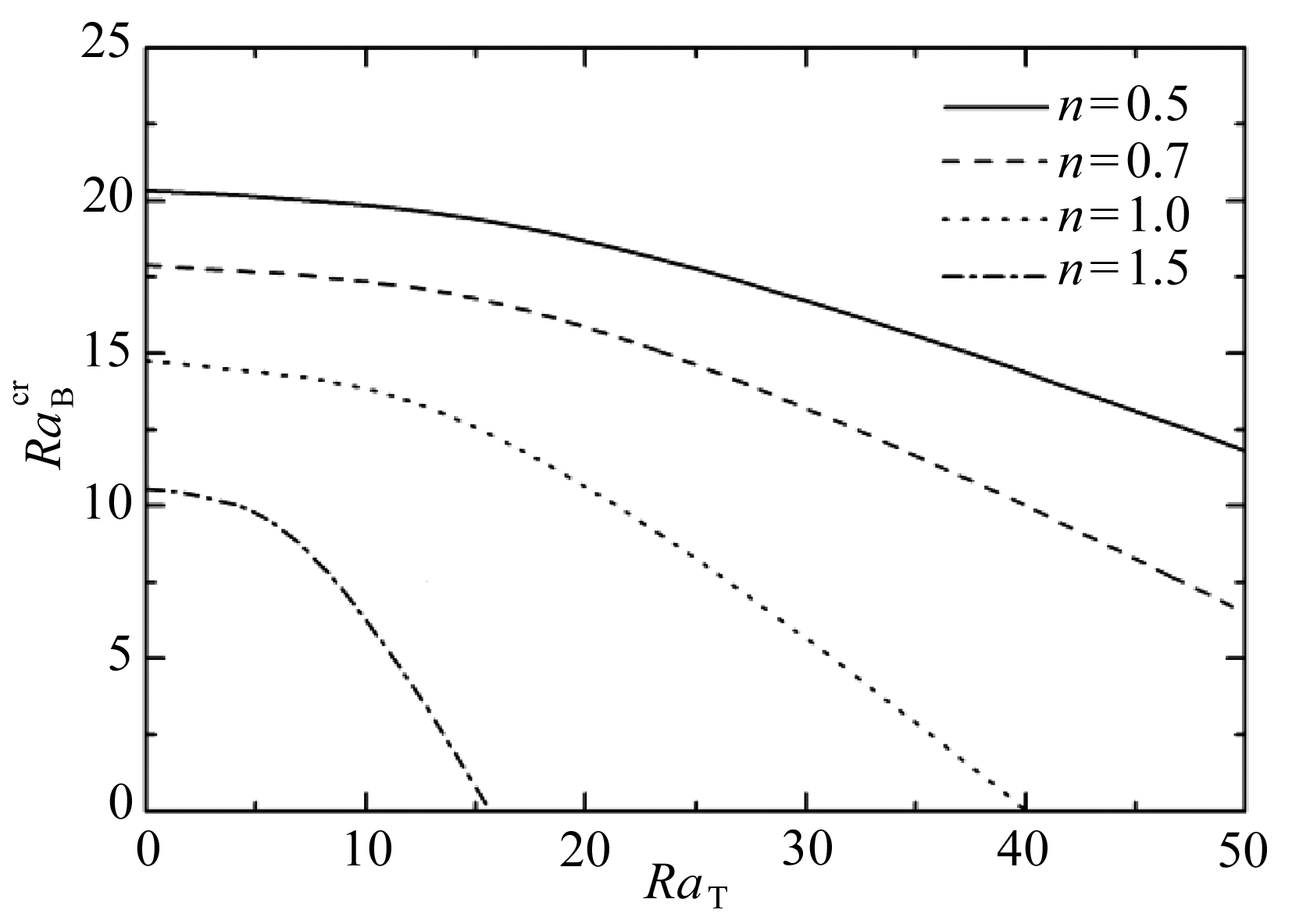
图2 不同n下,![]() 随RaT的变化曲线
随RaT的变化曲线
Fig. 2 Effects of n on ![]() variation with RaT
variation with RaT
图2描述了不同幂律指数n条件下,热Rayleigh数RaT对临界生物Rayleigh数![]() 的影响.随着非Newton指数n增大,流体逐渐从假塑性流体变成Newton流体再到膨胀性流体.可以得出,无论是上述哪种流体,
的影响.随着非Newton指数n增大,流体逐渐从假塑性流体变成Newton流体再到膨胀性流体.可以得出,无论是上述哪种流体,![]() 都随着RaT的增大而减小,也就是说温度梯度越大生物对流越不稳定.类比双扩散对流[15]进行分析,由于本研究中温度梯度和生物运动对对流的影响都是向上的,所以RaT和RaB的作用是相反的.
都随着RaT的增大而减小,也就是说温度梯度越大生物对流越不稳定.类比双扩散对流[15]进行分析,由于本研究中温度梯度和生物运动对对流的影响都是向上的,所以RaT和RaB的作用是相反的.
图3显示了在不同的Pe和RaT条件下,幂律指数n对生物对流稳定性的影响.当Pe=0.1和Pe=0.3时,随着n的增大,![]() 先开始增大,到达一个最大值后再逐渐减小.而且RaT越小,最大值所对应的n值就越大.当Pe逐渐增大时,最大值所对应的n值越大.当Pe=0.5时,在n=0~3范围内,曲线逐渐开始变成单调递增;当Pe=1时,所有曲线均变成单调递增,即当Pe较大时,n对稳定性的影响均是促进作用.其物理解释为,当Pe较小且RaT较大时,生物对流在假塑性流体中比在膨胀性流体中更稳定;当Pe较大时,生物对流在膨胀性流体中比在假塑性流体中更稳定.在Pe增大过程中,稳定性有一个最高点,也就是存在一个使n对稳定性影响发生变化的过渡区间.另外,从图3可以看出,当Pe增大或者RaT减小时,这个过渡区间对应的n值越大.为进一步研究这个过渡区间,本文分析了
先开始增大,到达一个最大值后再逐渐减小.而且RaT越小,最大值所对应的n值就越大.当Pe逐渐增大时,最大值所对应的n值越大.当Pe=0.5时,在n=0~3范围内,曲线逐渐开始变成单调递增;当Pe=1时,所有曲线均变成单调递增,即当Pe较大时,n对稳定性的影响均是促进作用.其物理解释为,当Pe较小且RaT较大时,生物对流在假塑性流体中比在膨胀性流体中更稳定;当Pe较大时,生物对流在膨胀性流体中比在假塑性流体中更稳定.在Pe增大过程中,稳定性有一个最高点,也就是存在一个使n对稳定性影响发生变化的过渡区间.另外,从图3可以看出,当Pe增大或者RaT减小时,这个过渡区间对应的n值越大.为进一步研究这个过渡区间,本文分析了![]() 随Pe增大时的变化,如图4所示.
随Pe增大时的变化,如图4所示.
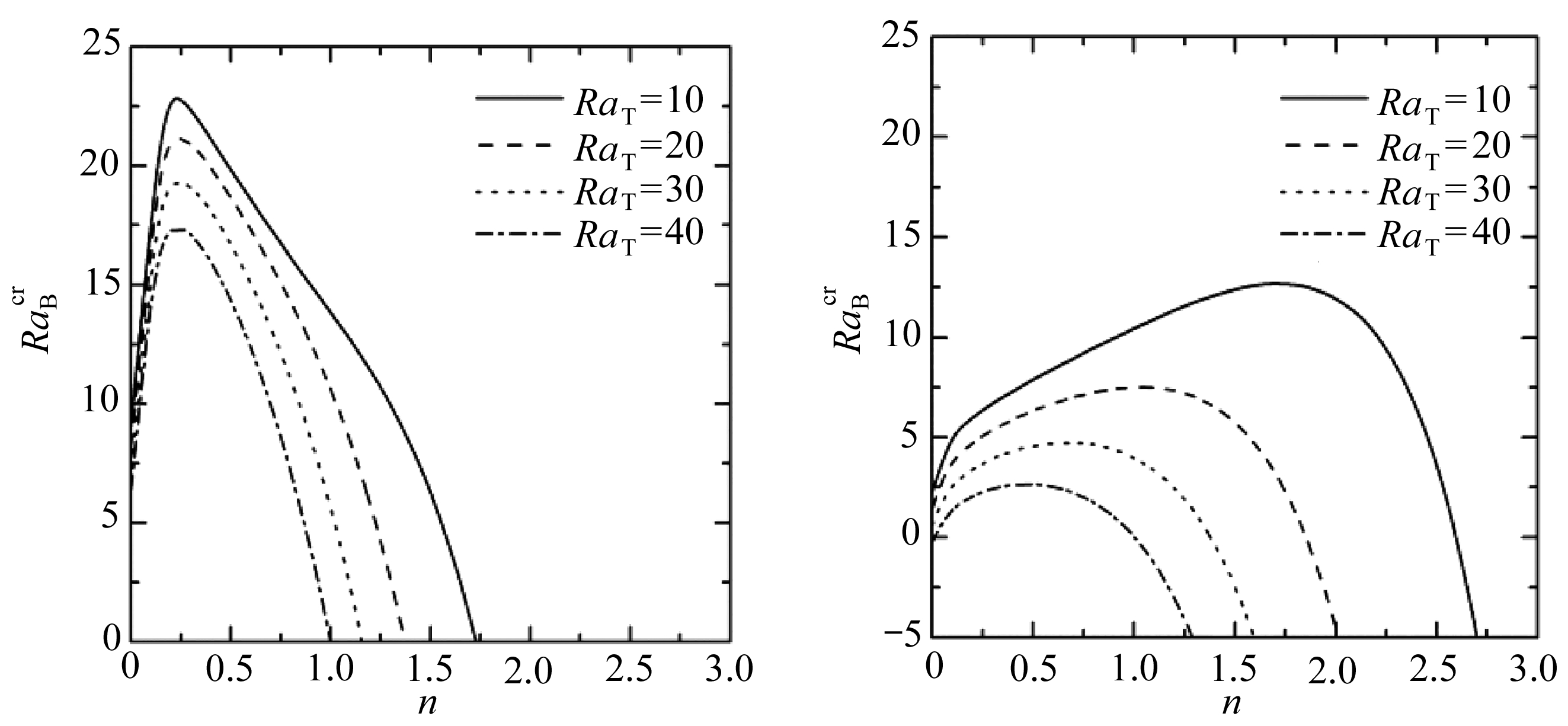
(a) Pe=0.1(b) Pe=0.3
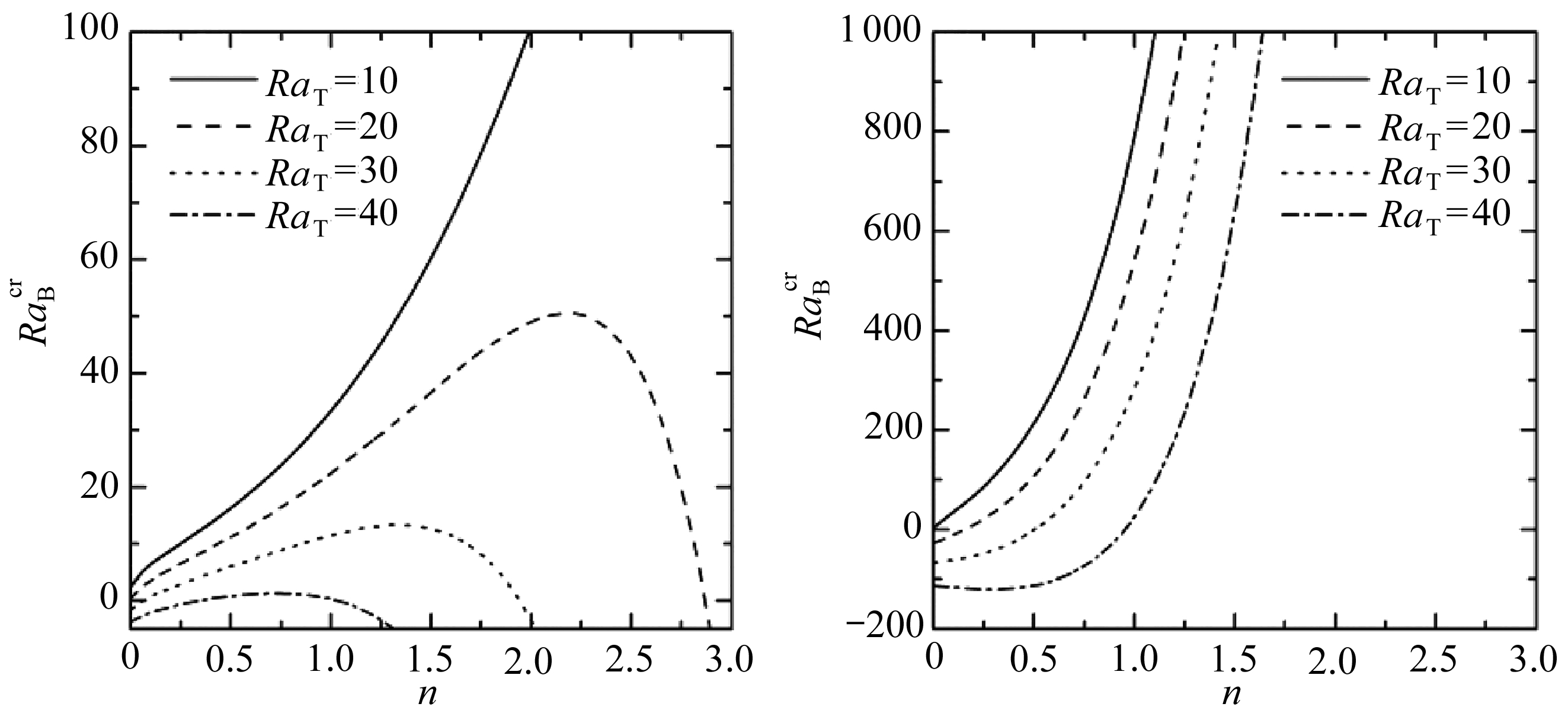
(c) Pe=0.5(d) Pe=1
图3 不同Pe和RaT下,![]() 随n的变化曲线
随n的变化曲线
Fig. 3 Effects of RaT on ![]() variation with n for different Pe numbers
variation with n for different Pe numbers
从图4可以看出,不同n对应的曲线会相交于一点附近.这也说明了,当Pe较小时,随着幂律指数n的取值增大,生物对流系统变得愈发不稳定;当Pe较大时,随着n增大,生物对流系统则趋于稳定.曲线相交的区域正是上文提到的过渡区间.此外我们还注意到,过渡区间还与Le有关.Le越小,过渡区间对应的Pe越大,也就是需要更大的Pe来保证系统稳定性随n增大而增强.因此,可以通过改变Le来调节Pe对系统稳定性的影响.
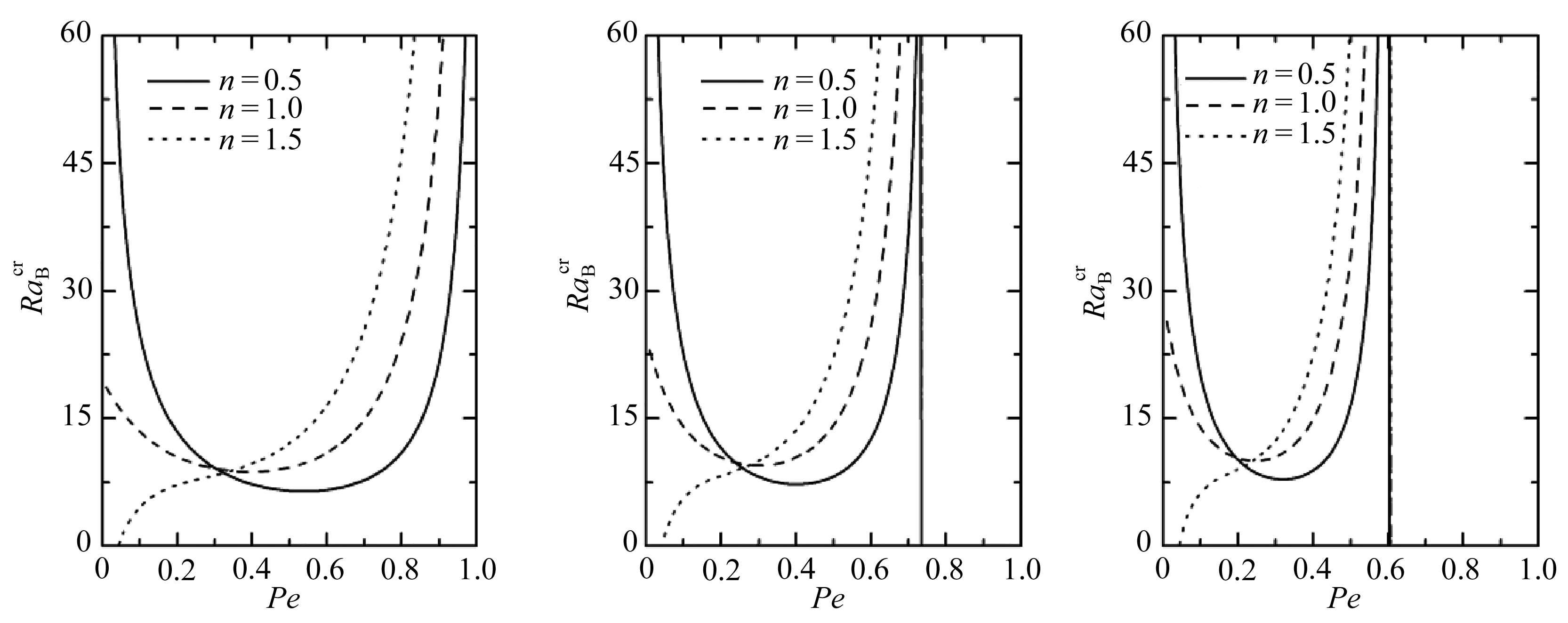
(a) Le=3 (b) Le=4(c) Le=5
图4 不同Le和n下,![]() 随Pe的变化曲线
随Pe的变化曲线
Fig. 4 Effects of n on ![]() variation with Pe for different Le numbers
variation with Pe for different Le numbers
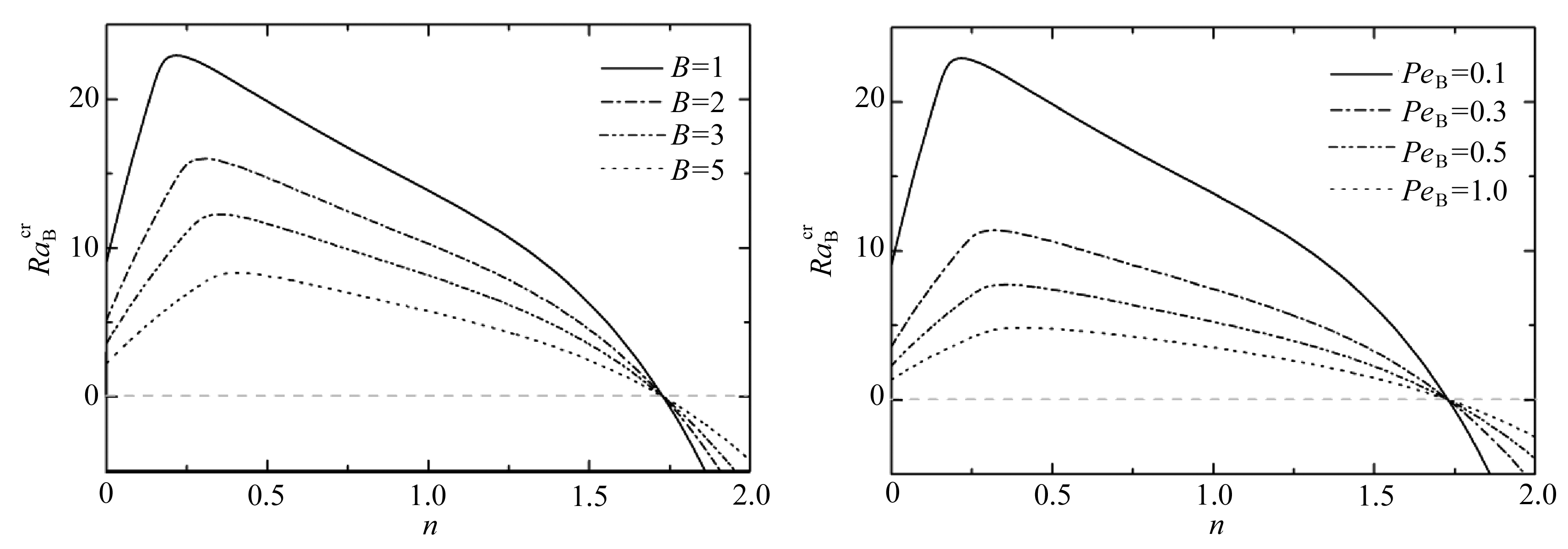
图5 不同B下,![]() 随n的变化曲线 图6 不同PeB下,
随n的变化曲线 图6 不同PeB下,![]() 随n的变化曲线
随n的变化曲线
Fig. 5 Effects of B on ![]() variation with nFig. 6 Effects of PeB on
variation with nFig. 6 Effects of PeB on ![]() variation with n
variation with n
图5给出了微生物趋旋性参数B对稳定性的影响.B=0时微生物运动方向竖直向上,表明微生物不具有趋旋性,B越大表明微生物运动过程中的趋旋性特征越明显,相应地生物的活性也就越高.由图5可得,在![]() 的条件下,无论幂律指数n<1或n>1,随着B增大,临界生物Rayleigh数
的条件下,无论幂律指数n<1或n>1,随着B增大,临界生物Rayleigh数![]() 减小,而且不会改变
减小,而且不会改变![]() 零点的位置,即无论哪种幂律流体,生物对流系统会随着生物趋旋性能力增大而变得更加不稳定.通过比较各数值曲线还可以发现,当B增大时,
零点的位置,即无论哪种幂律流体,生物对流系统会随着生物趋旋性能力增大而变得更加不稳定.通过比较各数值曲线还可以发现,当B增大时,![]() 最大值对应的n越大.由此可得,对于趋旋性较强的微生物,减小流体的假塑性更利于稳定.
最大值对应的n越大.由此可得,对于趋旋性较强的微生物,减小流体的假塑性更利于稳定.
图6给出了微生物平均游动速度PeB对稳定性的影响.结果表明,在![]() 的条件下,随着PeB增大,
的条件下,随着PeB增大,![]() 逐渐减小,生物对流越不稳定.而且和趋旋性参数B一样,PeB的变化不会改变
逐渐减小,生物对流越不稳定.而且和趋旋性参数B一样,PeB的变化不会改变![]() 零点的位置,它对稳定性的影响不受流体幂律指数n的影响.
零点的位置,它对稳定性的影响不受流体幂律指数n的影响.
4 结 论
本文研究了幂律流体饱和水平多孔层中的热-生物对流稳定性,获得了不同幂律指数n下的稳定性变化规律,结论如下:
1) 当底部温度高于顶部时,生物Rayleigh数RaB会随着热Rayleigh数RaT的增大而减小,从而导致生物对流越不稳定.幂律流体的类型不影响热稳定性和生物对流稳定性之间的关系.
2) 当Péclet数Pe较小且RaT较大时,生物对流在假塑性流体中比在膨胀性流体中更稳定.当Pe较大时,生物对流在膨胀性流体中比在假塑性流体中更稳定.
3) 当Péclet数Pe较小时,幂律指数n越大,生物对流稳定性先增大后减小.在Pe增大过程中,存在一个稳定性变化的过渡区间,Pe越大或者RaT越小,过渡区间对应的n值越大.通过改变生物Lewis数Le,可以调节Pe对系统稳定性的影响.
4) 在同一幂律指数n下,微生物趋旋性越大,生物对流越不稳定.对于趋旋性较大的微生物,适当增大n值可增强其对流稳定性.
[1] WAGER H. On the effect of gravity upon the movements and aggregation of euglena viridis, ehrb, and other microorganisms[J]. Philosophical Transactions of the Royal Society B: Biological Sciences, 1911, 201(1): 333-390.
[2] KESSLER J O. Hydrodynamic focusing of motile algal cells[J]. Nature, 1985, 313(5999): 218-220.
[3] KUZNETSOV A V, AVRAMENKO A A. Stability analysis of bioconvection of gyrotactic motile microorganisms in a fluid saturated porous medium[J]. Transport in Porous Media, 2003, 53(1): 95-104.
[4] NIELD D A, KUZNETSOV A V. The onset of bio-thermal convection in a suspension of gyrotactic microorganisms in a fluid layer: oscillatory convection[J]. International Journal of Thermal Sciences, 2006, 45(10): 990-997.
[5] ZHAO M, XIAO Y, WANG S. Linear stability of thermal-bioconvection in a suspension of gyrotactic micro-organisms[J]. International Journal of Heat and Mass Transfer, 2018, 126: 95-102.
[6] BARLETTA A, NIELD D A. Linear instability of the horizontal throughflow in a plane porous layer saturated by a power-law fluid[J]. Physics of Fluids, 2011, 23(1): 013102.
[7] BARLETTA A, STORESLETTEN L. Linear instability of the vertical throughflow in a horizontal porous layer saturated by a power-law fluid[J]. International Journal of Heat and Mass Transfer, 2016, 99: 293-302.
[8] 罗艳, 李鸣, 杨大勇. 微通道内电渗压力混合驱动幂律流体流动模拟[J]. 应用数学和力学, 2016, 37(4): 373-381.(LUO Yan, LI Ming, YANG Dayong. Simmulation of mixed electroosmotic and pressure-driven flows of power-law fluids in microchannels[J]. Applied Mathematics and Mechanics, 2016, 37(4): 373-381.(in Chinese))
[9] 田兴旺, 王平, 徐士鸣. 颗粒堆积多孔介质内幂律流体的流动阻力特性[J]. 哈尔滨工业大学学报, 2017, 49(1): 126-132.(TIAN Xingwang, WANG Ping, XU Shiming. Flow resistance characteristics of power law fluid flow through granular porous medium[J]. Journal of Harbin Institute of Technology, 2017, 49(1): 126-132.(in Chinese))
[10] 杨旭, 梁英杰, 孙洪广, 等. 空间分数阶非Newton流体本构及圆管流动规律研究[J]. 应用数学和力学, 2018, 39(11): 1213-1226.(YANG Xu, LIANG Yingjie, SUN Hongguang, et al. A study on the constitutive relation and the flow of spatial fractional non-Newtonian fluid in circular pipes[J]. Applied Mathematics and Mechanics, 2018, 39(11): 1213-1226.(in Chinese))
[11] CHRISTOPHER R H, MIDDLEMAN S. Power-law flow through a packed tube[J]. Industrial & Engineering Chemistry Fundamentals, 1965, 4(4): 422-426.
[12] GRAY D D, GIORGINI A. The validity of the Boussinesq approximation for liquids and gases[J]. International Journal of Heat and Mass Transfer, 1976, 19(5): 545-551.
[13] PEDLEY T J, KESSLER J O. The orientation of spheroidal microorganisms swimming in a flow field[J]. Proceedings of the Royal Society of London, 1987, 231(1262): 47-70.
[14] NARAYANA M, SIBANDA P, MOTSA S S, et al. Linear and nonlinear stability analysis of binary Maxwell fluid convection in a porous medium[J]. Heat and Mass Transfer, 2012, 48(5): 863-874.
[15] WANG S, TAN W. Stability analysis of double-diffusive convection of Maxwell fluid in a porous medium heated from below[J]. Physics Letters A, 2008, 372(17): 3046-3050.