引 言
流体中固体与固体碰撞在工业中广泛存在,比如输运管道中固体颗粒对管道的冲蚀磨损,流体机械中固体颗粒对水轮机叶片的冲击,海洋工程中流体诱导海洋立管之间的碰撞以及坠物对海底管道的撞击等.由于碰撞的大变形和非线性特性以及流体域网格拓扑结构的变化,采用界面解析直接数值模拟方法研究流体中固体与固体之间的碰撞具有很大的挑战,因此尚未得到广泛的研究.
传统的流固耦合数值方法通常是基于贴体网格,最典型的例子是任意Lagrange-Euler(ALE)界面跟踪方法[1],该方法已得到了广泛的应用.在这种方法中,由于网格服从结构形状,可以很容易地定义流固耦合边界;此外,还可以对固体表面附近的网格进行局部细化,在耦合界面附近的数值模拟精度较高,该方法的缺点是在处理大变形和动态边界问题时需要不断更新网格,并在新旧网格上交换各种数据,不仅增加了计算量,而且降低了求解的精度和稳定性.在具有复杂几何形状的三维空间中,这个过程会相当复杂,特别是当流体中存在固体间接触和碰撞问题时,会出现负体积网格,导致计算终止.而基于固定网格的流动求解方法为此提供了一个有效的解决途径,如浸入边界法[2]和虚拟区域法[3],其中浸入边界法在近年来得到了更多的关注和应用,它是一种使用简单且流体域网格不需要重构的求解方法,适用于复杂和移动边界问题,但存在固体边界与流体网格线不一致的问题,需对浸入边界附近的控制方程进行局部修正,这些修正在一定程度上施加了流体域中所需的边界条件,也是控制计算误差的主要措施.在原始的浸入边界法[4]中,移动边界对流场的影响是通过连续函数来实现的,导致了边界条件在界面处的扩散.近年来,一类清晰界面浸入边界法被用于避免扩散问题[5],在这些方法中,移动边界对流体的影响可以通过修改网格的局部形状考虑[6];或者直接施加离散函数到离散方程组[7];或者用插值格式重构浸入边界附近的边界条件[8].
随着各种改进的浸入边界法被提出[9],应用领域得到了快速扩展,如宫兆新[10]用浸入边界法对二维与三维细胞在剪切流的运动进行了研究,分析了细胞的运动特性和相关参数的影响;郝栋伟和王文全[11]采用浸入边界法分析了鱼自主游动的水动力学特征和鱼体运动特征,揭示了影响鱼游动速度的关键因素及其力学机理;及春宁等[12]采用浸入边界法对串列双圆柱流致振动进行了数值模拟,分析了两圆柱间的耦合机制.采用浸入边界方法模拟颗粒流的碰撞问题也已成为可能[13-15],颗粒的刚体运动和碰撞由Newton方程和软球模型进行求解.在固体动力学分析中,有限元法是分析物体运动、几何非线性、材料非线性和接触非线性的主要方法,可用于结构的安全设计、强度校核和寿命预测等,但在涉及固体间碰撞问题的流固耦合研究中,清晰界面浸入边界法与有限元法相结合还未见应用.
本文的创新之处是将清晰界面浸入边界法与有限元法相结合,以分域耦合方式实现流体域和固体域的耦合求解,建立了流体中固体与固体碰撞的数值模拟方法,通过与球形颗粒和壁面正碰撞以及斜碰撞实验数据的对比,证明了本文所建立的数值模拟方法的正确性.
1 控制方程和数值求解方法
1.1 求解流动问题的浸入边界法
在采用浸入边界法求解流固耦合问题时,流体域处理为连续体,其中不可压缩黏性流体的连续性方程和动量方程可表示为
(1)
(2)
其中ui代表速度分量,ρf是流体密度,p为流体压力,ν是动力黏度.控制方程的离散采用同位网格方法将所有原始变量存储于单元中心,采用分步方法对控制方程进行时间推进.分步方法由3个子步骤组成,在第一个子步骤中,求解动量方程,得到了中间速度u*.在这一步中只考虑对流项与扩散项,对流项采用二阶Adams-Bashforth格式离散,扩散项采用隐式Crank-Nicolson格式离散,离散方程为
(3)
其中![]() 为当前时间步的节点速度,Uj为沿j方向的节点速度线性平均值计算得到的界面中心速度.方程(3)采用迭代法进行求解.在第二个子步骤中,由Poisson方程得到压力的近似解:
为当前时间步的节点速度,Uj为沿j方向的节点速度线性平均值计算得到的界面中心速度.方程(3)采用迭代法进行求解.在第二个子步骤中,由Poisson方程得到压力的近似解:
(4)
在第三个子步骤中,得到n+1时刻的更新速度为
(5)
采用清晰界面浸入边界法[8]模拟流固界面解析时浸入的固体边界将切割流体网格,如图1所示,流体域计算节点根据相对于边界的位置可分为3类: 1) 流体域中的节点; 2)浸入固体域中的流体节点; 3) 浸入边界附近的流体(NB)节点.在NB节点上,用插值公式代替动量方程和连续性方程.NB节点的切向速度沿边界法向方向由固体边界(IB)点的切向速度(应用无滑移条件)与流体(IF)点的切向速度之间的线性插值计算得到,在每个时间步重复该过程,并将其值用作求解流体域的边界条件.IB点的速度由固体域求解得到,IF点的速度由其周围流体域中的节点1~4(如图1所示)通过双线性插值求得,如下式所示:
(6)
其中ui为流体域中节点速度,αi为线性插值系数.

图1 清晰界面浸入边界法示意图
Fig. 1 The schematic diagram of the sharp interface immersed boundary method
假定近壁面边界区域壁面剪切应力为常数,基于壁面距离来计算NB节点的切向速度,
(7)
其中(uIB)Tang和(uIF)Tang分别为IB点和IF点的切向速度,μNB和μIF分别是NB节点和IF点的动力黏度,yIF是IF点和IB点之间的距离,yNB是NB节点和IB点之间的距离.假定NB节点的法向速度与浸没边界上IB点处法向速度相同,则NB节点的速度可表示为
uNB=(uIB)Norm+(uNB)Tang.
(8)
将动量方程(2)投影到浸入边界法线方向,得到浸入边界上压力场的Neumann边界条件:
![]()
 u,
u,
(9)
其中n为浸入边界法向单位向量,则IB点的压力沿浸入边界法向近似确定为
(10)
针对动边界问题,浸入固体域中的流体节点在下一时间步会变为流体域中的节点,而此节点速度在空间上是不连续的,通过限制时间步,使单个时间步长内浸入边界的移动距离不超过一个网格单元长度,则新出现的浸入固体域中的流体节点会成为NB节点,并由式(8)得到其速度,从而保证了算法的鲁棒性.当流体域中浸入多个固体时,在最不利的情况下即只有一个或没有NB节点可用时,插值方程(7)无法建立,在这种情况下,速度可能是不准确的,可通过加密网格来减小这种行为,因此并不会给计算带来很多误差.
1.2 求解固体运动与碰撞问题的有限元法
对于包含接触界面的固体力学问题的泛函可表示为
π=U-W+G,
(11)
其中U是应变能,W为外力功,G为固-固接触约束对应的泛函.采用罚函数法将固-固接触的约束条件引入泛函中,得到
(12)
其中g′=diag(g′1,g′2,g′3),g′1和g′2分别为沿两个切向的滑动位移,g′3是法向的运动位移;Λ′=diag(a′1,a′2,a′3)为罚系数.于是可以得到
(13)
其中![]() 和
和![]() 分别为接触节点的作用力和反作用力.
分别为接触节点的作用力和反作用力.
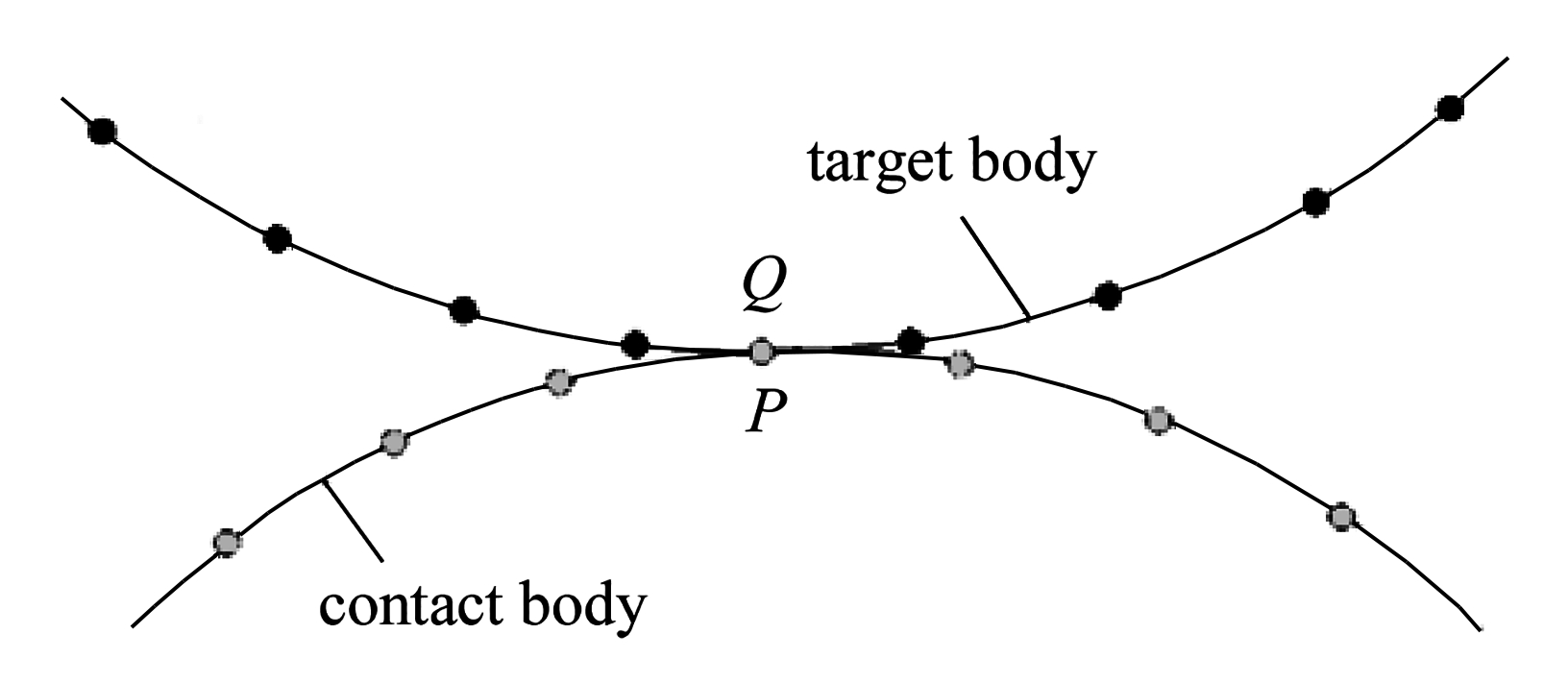
图2 接触点对示意图
Fig. 2 The schematic diagram of a contact point pair
当两个物体接触时,主动接触物体上的节点P和目标物体上的点Q形成接触对,如图2所示.因为Q点一般不是单元节点,其坐标和位移需由所在接触点上节点的坐标和位移插值得到,根据形函数矩阵及坐标系转换,可得在局部坐标系下一个接触点对的接触力引起的等效节点力向量为
(14)
其中T为坐标转换矩阵,Nc为形函数矩阵,dc为P点与Q点的相对位移矩阵.整体坐标系中等效接触力的矢量可表示为
(15)
上式可进一步写成
(16)
其中![]() 是接触节点的接触刚度矩阵,
是接触节点的接触刚度矩阵,![]() 是接触节点的接触力.将各接触点的接触刚度和接触力进行组合拼装,得到整个系统的等效节点接触力,并将它们代入动力学方程,最终得到浸没在流体中的固体碰撞的动力学方程为
是接触节点的接触力.将各接触点的接触刚度和接触力进行组合拼装,得到整个系统的等效节点接触力,并将它们代入动力学方程,最终得到浸没在流体中的固体碰撞的动力学方程为
(17)
其中M是固体的质量矩阵,C是阻尼矩阵,K是刚度矩阵,Kc(t)是接触刚度矩阵,Ff(t)为流固耦合界面上的流体力,Fc(t)为碰撞时的接触力,Fs(t)为固体所受到的其他外力.采用Newmark-β法和Newton-Raphson迭代法相结合完成动力学方程(17)的求解[16].由于描述固-固接触碰撞特征时间尺度通常远小于流固耦合时间步长Δt,在固体域中将时间步长Δt分为若干子步来捕捉固体间接触碰撞状态.最小子步步长比耦合时间步长Δt小两个数量级,由于固体域子步非常小,假定流体力在子步计算中是恒定的.
1.3 分域流固耦合方法
流固耦合求解采用分域耦合方法,假定在流固耦合界面ΓFSI上没有滑移和穿透,各物理量应满足位移、速度协调及力平衡条件.在流固耦合分析中,流体作用力会影响固体的位移,同时固体的位移和速度又影响流场的形态,所以流固耦合求解是非线性问题,因此需要采用迭代的方法得到某一时刻的解.一般根据力、位移、速度来检查迭代的收敛性,耦合界面上归一化的收敛准则如下所示:
(18)
其中t是当前时间步;jk是当前时间步内的耦合迭代步数;i=f,s分别为流体域、固体域中的流固耦合界面;![]() 为归一化的收敛值;
为归一化的收敛值;![]() 为从流体域或固体域界面获得的新物理量;
为从流体域或固体域界面获得的新物理量;![]() 为当前耦合迭代步中施加的界面物理量;
为当前耦合迭代步中施加的界面物理量;![]() 为收敛容差;流固耦合界面物理量为
为收敛容差;流固耦合界面物理量为![]() 分别为流体域或固体域在耦合界面处的位移、速度及力向量.为保证交错迭代的数值稳定性,下一个耦合迭代步传递的界面物理量为
分别为流体域或固体域在耦合界面处的位移、速度及力向量.为保证交错迭代的数值稳定性,下一个耦合迭代步传递的界面物理量为
(19)
其中α为引入的松弛因子.
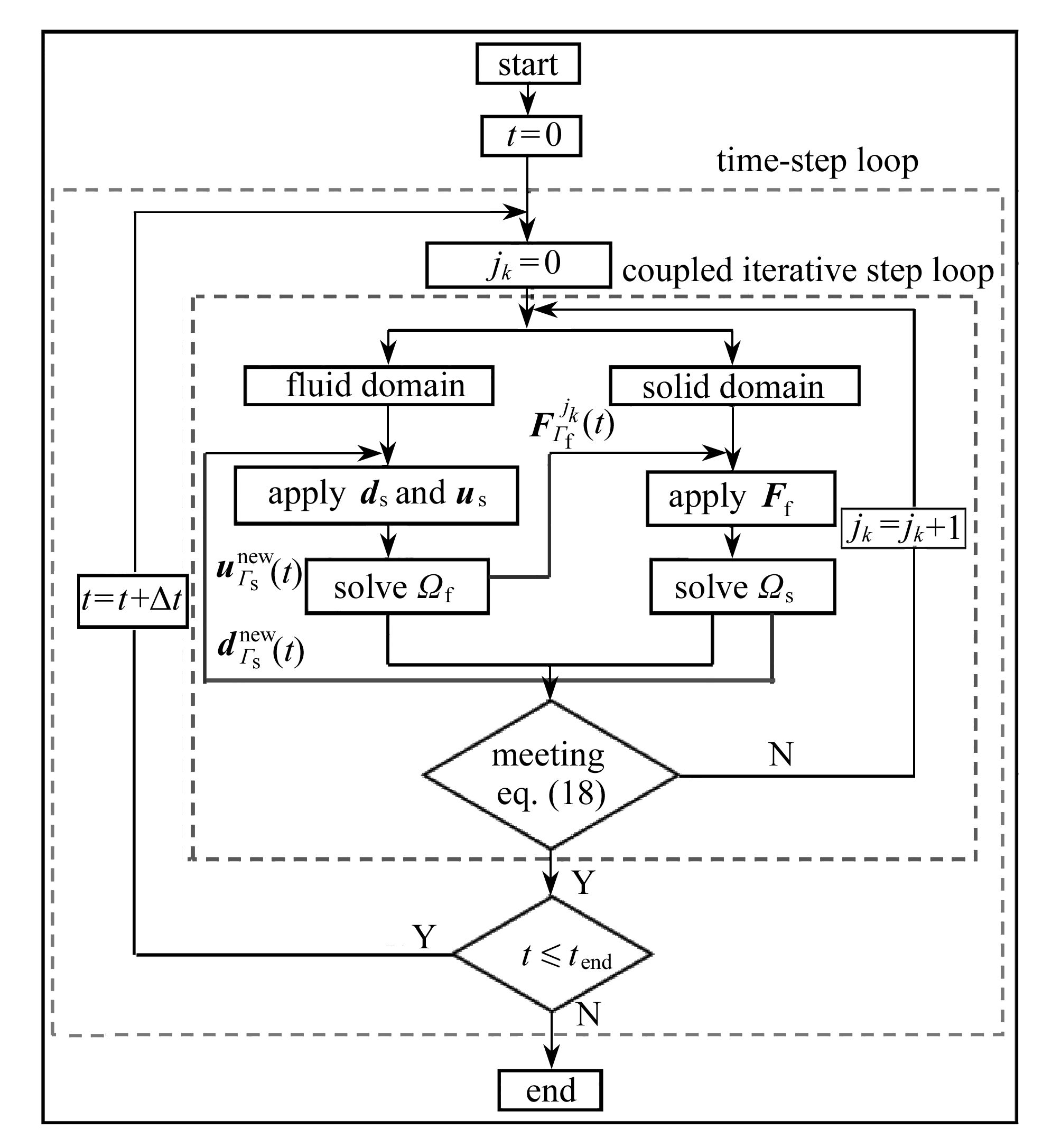
图3 分域耦合迭代框图
Fig. 3 The total frame diagram of partitioned coupling
在流固耦合分域求解过程中,分为域内部循环、耦合迭代步循环和时间步循环,图3为分域求解总迭代框图,其迭代过程简述如下:
1) 建立固体域模型及流体域模型,定义边界条件,假设时间步t已经完成;
2) 令jk=0;
3) 令jk=jk+1,将方程(3)~(8)在流体域内求解并保持![]() 和
和![]() 恒定,由更新后的流场通过式(10)进一步得到耦合界面载荷
恒定,由更新后的流场通过式(10)进一步得到耦合界面载荷![]()
4) 将![]() 传递到固体域,将方程(17)在固体域内求解并保持
传递到固体域,将方程(17)在固体域内求解并保持![]() 恒定,得到耦合界面位移
恒定,得到耦合界面位移![]() 和速度
和速度![]()
5) 将![]() 和
和![]() 传递到流体域,将方程(3)~(8)在流体域内求解并保持
传递到流体域,将方程(3)~(8)在流体域内求解并保持![]() 和
和![]() 恒定,得到新的耦合界面荷载
恒定,得到新的耦合界面荷载![]()
6) 根据收敛准则式(18), 如果位移、 速度和力不能同时满足收敛准则, 则返回迭代步3)~5);
7) 如果位移、速度和力能同时满足收敛准则式(18),则令t=t+Δt;
8) 如果t≤tend,则返回迭代步2)~6),否则,迭代结束.
2 流固耦合碰撞数值模拟方法验证
2.1 颗粒与壁面正碰撞
对流体中球形颗粒在重力作用下与壁面正碰撞和反弹的过程进行了数值模拟,并与Gondret等[17]的实验数据进行了对比.流体计算域取为Lx×Ly×Lz=40 mm×40 mm×300 mm,网格离散为Nx×Ny×Nz=125×125×1 000.为了准确模拟球形颗粒与壁面碰撞和反弹的过程,在底部壁面处采用平滑过渡方法进行了局部网格加密,壁面处第一层网格高度为0.01 mm,边界层增长率为1.1;球形颗粒和底部玻璃板采用有限元实体单元划分网格,球形颗粒表面共有1 276个网格节点,玻璃板厚度为12 mm,划分了4层单元,玻璃板底面为固定约束,球形颗粒在重力作用下由静止开始下落,流体在初始时刻是静止的,本文数值模拟中的球形颗粒和流体的物理参数同Gondret等[17]的实验,如表1所示.
表1 球形颗粒和流体的物理参数
Table 1 Physical parameters of the particles and fluids
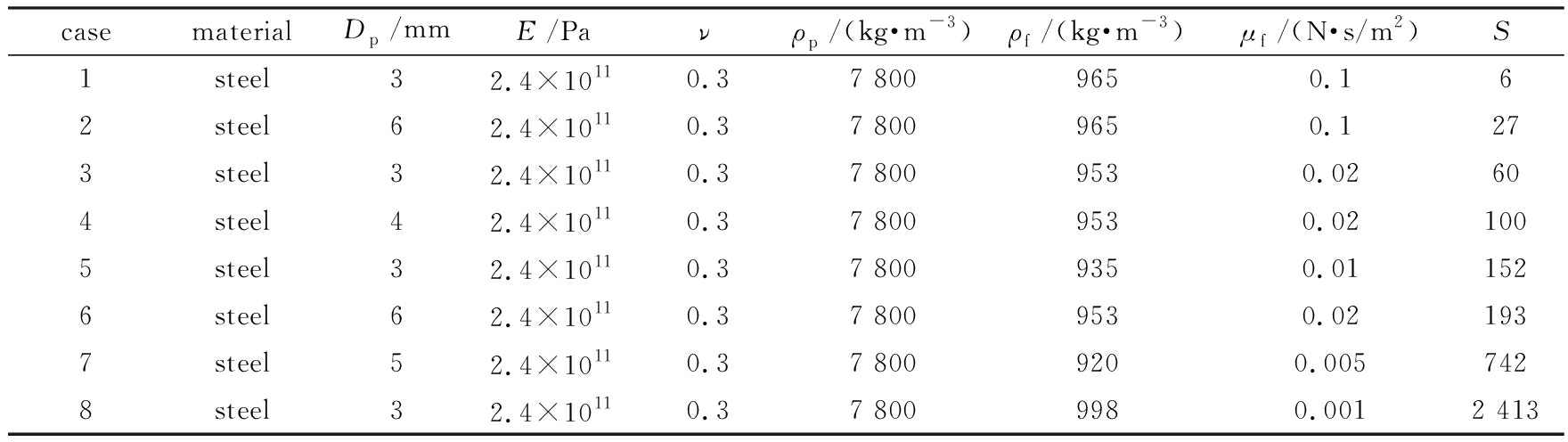
casematerialDp/mmE/Paνρp/(kg·m-3)ρf/(kg·m-3)μf/(N·s/m2)S1steel32.4×10110.37 8009650.162steel62.4×10110.37 8009650.1273steel32.4×10110.37 8009530.02604steel42.4×10110.37 8009530.021005steel32.4×10110.37 8009350.011526steel62.4×10110.37 8009530.021937steel52.4×10110.37 8009200.0057428steel32.4×10110.37 8009980.0012 413
图4为工况1~8球形颗粒的恢复系数e与Stokes数S的关系曲线,并与Gondret等 [17]的实验数据进行了对比.从图中可以看出,在S≈10以下时,颗粒不反弹,随着S的逐渐增大,恢复系数逐渐趋向于球形颗粒干碰撞时的恢复系数.数值模拟与实验数据吻合较好表明本文建立的数值方法对流体中固体与固体碰撞的模拟是可行的.
图5(a)为工况5球形颗粒与玻璃壁面碰撞和反弹过程中位移随时间变化曲线,取时间t=0 s为球形颗粒与玻璃壁面第一次碰撞时间.由于流体黏性耗散和材料阻尼导致动能损失,后续的反弹高度越来越低,Stokes数由第一次碰撞S=152分别减小为79,40和22,数值模拟能够很好地展现该工况的运动趋势并且与实验数据吻合,表明本文建立的数值方法对流体中固体与固体正碰撞的模拟是准确的.图5(b)为壁面处网格对工况5第一次碰撞后颗粒运动位移的影响,壁面局部加密网格在底部壁面附近计算得到的流体阻力大于均匀网格,使得局部加密网格的反弹高度小于均匀网格并且与实验结果更加贴近,最大高度相对误差为1.4%,而均匀网格与实验结果最大高度相对误差为6.7%.

图4 球形颗粒的恢复系数与Stokes数S的关系曲线
Fig. 4 Coefficients of restitution for different Stokes numbers

(a) 整体 (b) 局部网格影响
(a) The whole (b) The local mesh effect
图5 工况5颗粒运动位移随时间变化曲线
Fig. 5 The particle position and velocity vs. time in case 5
图6为工况5球形颗粒与壁面正碰撞和反弹过程中涡量场随时间变化云图.当球形颗粒下降时,由于速度逐渐增大尾迹涡环也逐渐增大,在t=-0.014 s时,颗粒距壁面较远,颗粒仍处在加速过程中;在t=-0.004 s即球形颗粒与壁面距离约为颗粒半径时,流体被挤出间隙,壁面处产生与颗粒尾迹涡环方向相反的涡量;当t=0 s时,颗粒第一次与壁面碰撞;在t=0.009 s时,反弹过程中的颗粒通过主尾迹环向上运动并形成方向相反的二次涡环;在t=0.039 s时,颗粒第一次反弹到最大高度,由于黏性耗散,颗粒周围的初始涡环减小;在t=0.086 s时,颗粒回落并第二次与壁面碰撞.

(a) t=-0.014 s(b) t=-0.004 s(c) t=0 s
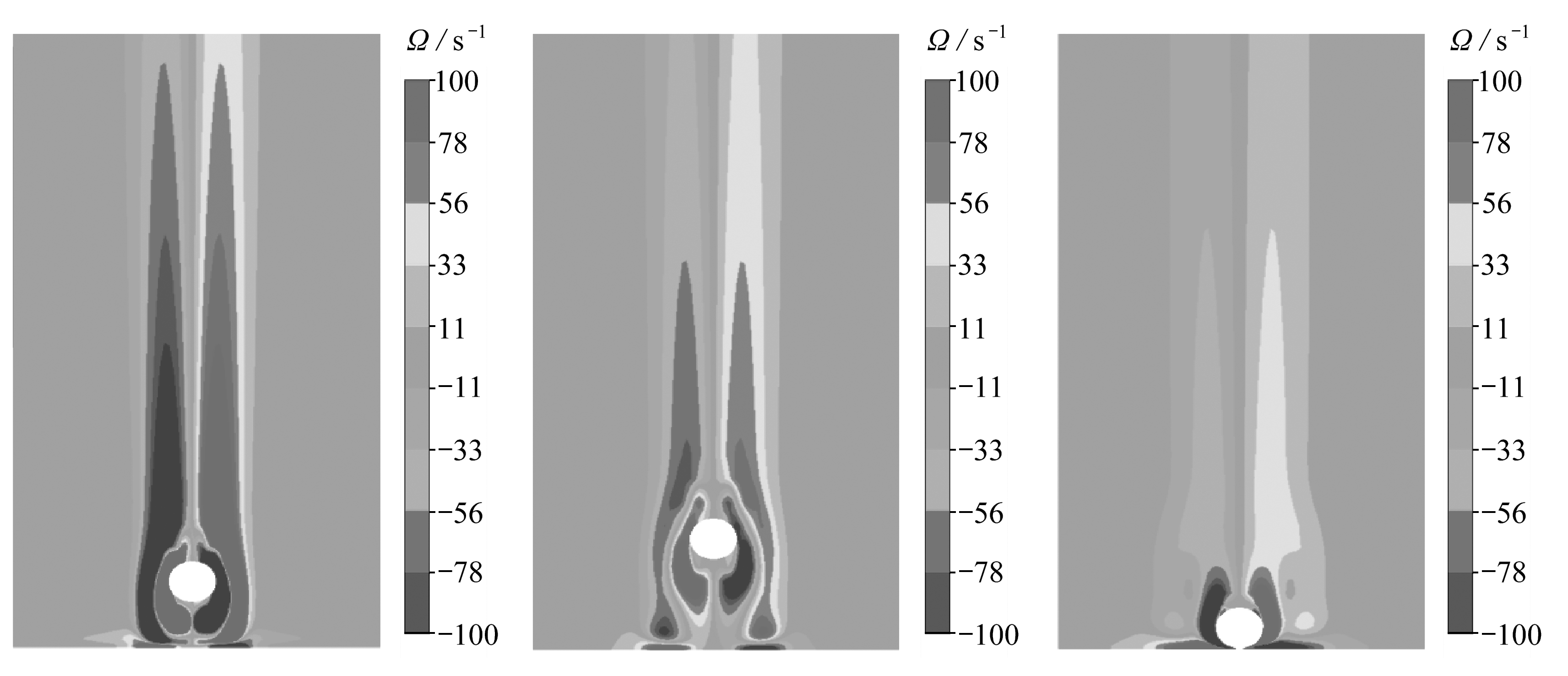
(d) t=0.009 s(e) t=0.039 s(f) t=0.086 s
图6 正碰撞涡量场随时间变化云图
Fig. 6 The time evolution contours of the normal collision vorticity
注 为了解释图中的颜色,读者可以参考本文的电子网页版本,后同.
图7为工况5颗粒和玻璃板第一次碰撞时的Mises应力云图.为了对比分析,将真空中干碰撞同等参数下得到的Mises应力云图一并给出,从图中可以看出两者的分布状态基本相同,但由于有流体阻力的存在,使湿碰撞的Mises应力比真空中干碰撞的Mises应力小3倍左右.表2为工况5前三次碰撞时颗粒的速度和碰撞力,并与真空中的干碰撞力进行了对比,从表中可以看出真空中的干碰撞力比湿碰撞力大3倍左右.
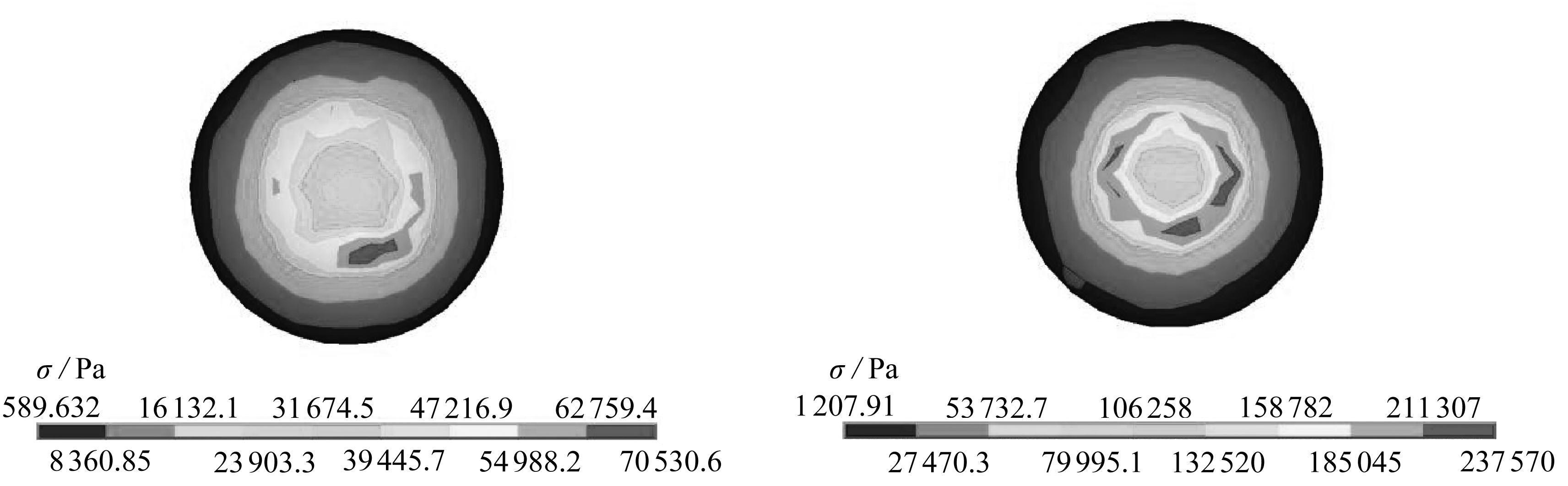
(a) 颗粒湿碰撞应力云图 (b) 颗粒干碰撞应力云图
(a) The stress contour of the particle in silicon oil RV10 (b) The stress contour of the particle in vacuum
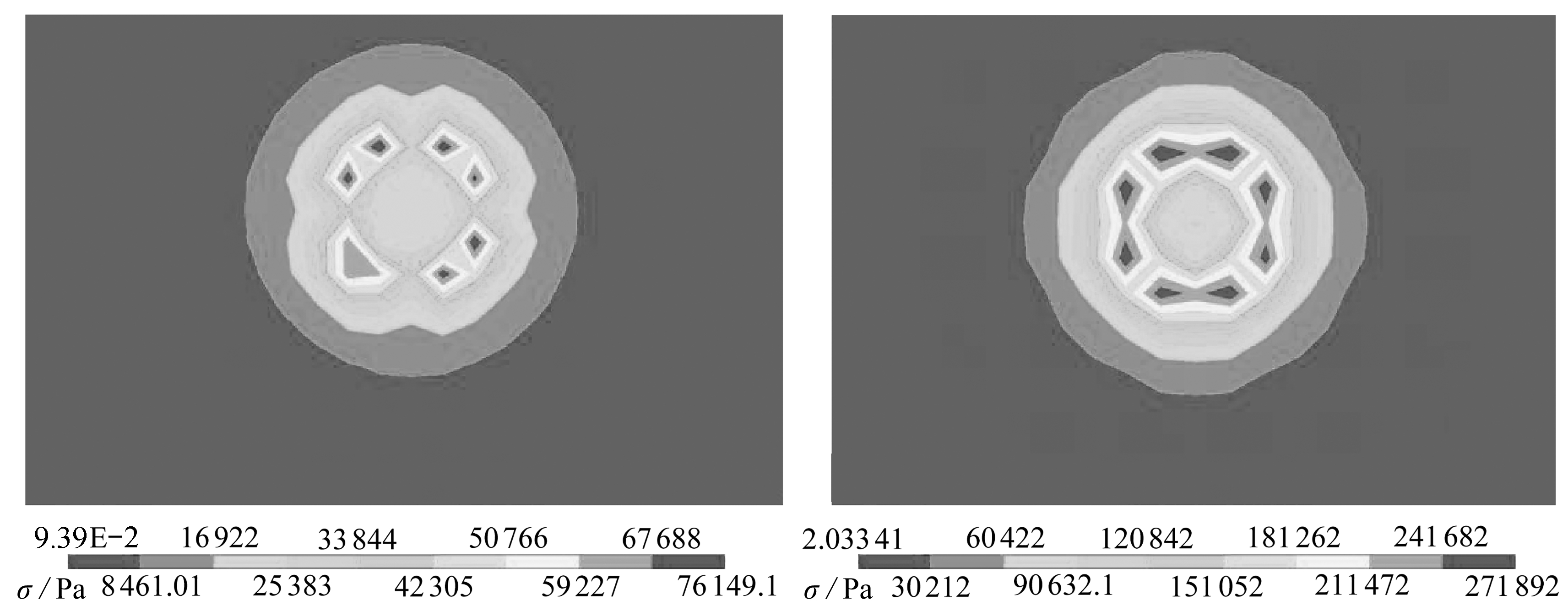
(c) 玻璃板湿碰撞应力云图 (d) 玻璃板干碰撞应力云图
(c) The stress contour of the bottom wall in silicon oil RV10 (d) The stress contour of the bottom wall in vacuum
图7 工况5颗粒和玻璃板干湿碰撞应力云图
Fig. 7 The stress contours of the particle and the glass plate in case 5
表2 工况5前三次碰撞时干湿碰撞接触力对比
Table 2 Comparison of dry and wet contact forces in the 1st 3 collisions in case 5

parameter of collision1st2nd3rdvelocity u/(m/s)0.5740.2980.172dry force Fdry/N0.3730.1960.113wet force Fwet/N0.1200.0660.039Fdry/Fwet3.112.972.90
2.2 颗粒与壁面斜碰撞
对流体中球形颗粒与壁面斜碰撞和反弹过程进行了数值模拟,并与Joseph和Hunt[18]的实验数据进行了对比.流体计算域取为Lx×Ly×Lz=60 mm×60 mm×100 mm,网格离散为Nx×Ny×Nz=192×192×320.在预碰撞壁面处采用平滑过渡方法进行了局部网格加密,壁面处第一层网格高度为0.01 mm,边界层增长率为1.1;球形颗粒直径为12.7 mm,表面共有2 100个网格节点,数值模拟与Joseph和Hunt[18]实验中使用的颗粒和黏性流体的物理参数如表3所示,颗粒加速度方向为eg=sin(θin) ·g·ey-cos(θin) ·g·ez,通过调整角度θin来改变球体入射角度,加速度g=9.81 m/s2,流体在初始时刻是静止的.
表3 球体和流体的物理参数
Table 3 Physical parameters of the particles and fluids

materialDp/mmedryμdryρp/(kg·m-3)ρf/(kg·m-3)μf/(N·s/m2)steel12.70.970.117 8009980.001
图8为球形颗粒在水中与壁面斜碰撞数值模拟得到的无量纲化入射角和反弹角关系曲线,并与Joseph和Hunt[18]的实验数据进行了对比,从图中可以出,数值模拟结果趋势与实验数据吻合较好,表明本文建立的数值模拟方法对流体中斜碰撞的数值模拟也是适用和准确的.

图8 斜碰撞无量纲化入射角和反弹角关系曲线
Fig. 8 The relationship between the normalized incidence and rebound angles
图9为θin=45°时球形颗粒与壁面斜碰撞和反弹过程中涡量场随时间的变化云图.从t=-0.04 s到t=0 s时的涡量场与球形颗粒与壁面正碰撞非常相似,但是倾斜了一定角度;在t=0.005 s球形颗粒反弹时,下落时尾迹的初始涡环以相同的角度撞击壁面,并在颗粒周围出现一个新的涡环;在t=0.04 s时,球形颗粒在反弹后达到其最大高度;从t=0.04 s到t=0.06 s时,部分初始涡环会随着球形颗粒一起移动.

(a) t=-0.04 s(b) t=-0.005 s

(c) t=0 s(d) t=0.005 s

(e) t=0.04 s(f) t=0.06 s
图9 斜碰撞涡量场随时间的变化云图
Fig. 9 The time evolution contour of the oblique collision vorticity
3 结论和展望
本文通过分域耦合的方法,将清晰界面浸入边界法与有限元法相结合,建立了流体中固体与固体碰撞界面解析直接模拟方法.所建立的数值模拟方法主要特点是将流体区域离散在简单且固定网格上,在求解大变形和动边界问题时不需要更新网格,提高了计算效率,避免了传统流固耦合方法求解流体中存在固体间碰撞问题时出现负体积网格的问题,并且对于在流体中碰撞的固体,通过本文建立的动力学模型可以得到应力和接触力等结果,这对于评价结构的强度和寿命等是非常重要的.通过与静止流体中球形颗粒与壁面正碰撞和斜碰撞实验数据的对比,验证了建立的数值模拟方法的正确性.未来,我们将把该数值模拟方法应用到流体流动环境中,如固体颗粒对管道的冲蚀、流体诱导海洋立管之间的碰撞、坠物对海底管道的撞击等.
致谢 本文作者衷心感谢东北石油大学研究生教育创新工程项目(JYCX_CX04_2018)对本文的资助.
[1] FABIAN D, RAUL G, SRINIVASAN N. Arbitrary Lagrangian-Eulerian method for Navier-Stokes equations with moving boundaries[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(45/47): 4819-4836.
[2] PESKIN C S. Flow patterns around heart valves: a numerical method[J]. Journal of Computational Physics, 1972, 10(2): 252-271.
[3] GLOWINSKI R, PAN T W, HESLA T I, et al. A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: application to particulate flow[J]. Journal of Computational Physics, 2001, 169(2): 363-426.
[4] PESKTH C S. The immersed boundary method[J]. Acta Numerica, 2002, 11: 479-517.
[5] MITTAL R, IACCARINO G. Immersed boundary methods[J]. Annual Review of Fluid Mechanics, 2005, 37: 239-261.
[6] UDAYKUMAR H S, MITTAL R, SHYY W. Computation of solid-liquid phase fronts in the sharp interface limit on fixed grids[J]. Journal of Computational Physics, 1999, 153(2): 535-574.
[7] LE D V, KHOO B C, PERAIRE J. An immersed interface method for viscous incompressible flows involving rigid and flexible boundaries[J]. Journal of Computational Physics, 2006, 220(1): 109-138.
[8] GILMANOV A, SOTIROPOULOS F. A hybrid Cartesian/immersed boundary method for simulating flows with 3D, geometrically complex, moving bodies[J]. Journal of Computational Physics, 2005, 207(2): 457-492.
[9] 王文全, 梁林, 闫妍. 基于投影浸入边界法的流固耦合计算模型[J]. 北京工业大学学报, 2014, 40(6): 819-824.(WANG Wenquan, LIANG Lin, YAN Yan. Numerical investigation of fluid-structure interaction using projected immersed boundary method[J]. Journal of Beijing University of Technology, 2014, 40(6): 819-824.(in Chinese))
[10] 宫兆新. 浸入边界法及其在细胞力学中的应用[D]. 博士学位论文. 上海: 上海交通大学, 2010.(GONG Zhaoxin. Research on the immersed boundary method and its application on cell mechanics[D]. PhD Thesis. Shanghai: Shanghai Jiao Tong University, 2010.(in Chinese))
[11] 郝栋伟, 王文全. 某型仿生鱼自主直线巡游速度的影响因素研究[J]. 应用数学和力学, 2014, 35(6): 674-683.(HAO Dongwei, WANG Wenquan. Parametric study on the straight-line cruising velocity of an auto-swimming robotic fish[J]. Applied Mathematics and Mechanics, 2014, 35(6): 674-683.(in Chinese))
[12] 及春宁, 陈威霖, 黄继露, 等. 串列双圆柱流致振动的数值模拟及其耦合机制[J]. 力学学报, 2014, 46(6): 862-870.(JI Chunning, CHEN Weilin, HUANG Jilu, et al. Numerical investigation on flow-induced vibration of two cylinders in tandem arrangements and its coupling mechanisms[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(6): 862-870.(in Chinese))
[13] KEMPE T, FRÖHLICH J. Collision modelling for the interface-resolved simulation of spherical particles in viscous fluids[J]. Journal of Fluid Mechanics, 2012, 709: 445-489.
[14] IZARD E, BONOMETTI T, LACAZE L. Modelling the dynamics of a sphere approaching and bouncing on a wall in a viscous fluid[J]. Journal of Fluid Mechanics, 2014, 747(4): 422-446.
[15] COSTA P, BOERSMA B J, WESTERWEEL J, et al. Collision model for fully resolved simulations of flows laden with finite-size particles[J]. Physical Review E, 2015, 92(5): 053012.
[16] 刘巨保, 罗敏. 有限单元法及应用[M]. 北京: 中国电力出版社, 2013.(LIU Jubao, LUO Min. Finite Element Method and Application[M]. Beijing: China Electric Power Press, 2013.(in Chinese))
[17] GONDRET P, LANCE M, PETIT L. Bouncing motion of spherical particles in fluids[J]. Physics of Fluids, 2002, 14(2): 643.
[18] JOSEPH G G, HUNT M L. Oblique particle-wall collisions in a liquid[J]. Journal of Fluid Mechanics, 2004, 510: 71-93.