引 言
大气运动是由一系列方程所描述的，主要包括热力学方程、连续性方程、状态方程、动量方程以及能量方程等．由于方程精确形式的复杂性，研究者试图寻求各种近似方法用来简化方程组，如浅水模式近似、静力近似等．浅水模式近似是常用的近似方法之一，其忽略了动量方程中四项度量项，更重要的是忽略了动量方程中Coriolis力水平分量项, 称之为“传统近似”[1]．“传统近似”将动量方程简化为二维问题，且还能够保持一些基本物理原理，如角动量守恒[2-4]．在“传统近似”下，大气Rossby孤立波的产生或者影响因子是很多学者关心的问题[5-15]．目前，考虑完善的Coriolis力水平分量的研究还不是很多．
对于中高纬地区大气运动，从定量角度而言，“传统近似”是合适的．Kasahara指出忽略垂直方向的加速度比忽略Coriolis水平分量所带来的误差可能更大[16]．但是就动力学角度而言，“传统近似”是有争议的[17], 因此建议在弹性近似中包含Coriolis水平分量项，称为“非传统近似”．Gerkema和Shrira从含有完整Coriolis力的基本方程组出发，考虑了“非传统近似”下的近惯性波[18]．Dellar和Salmon通过变分原理得到具有完整Coriolis力作用的位涡守恒方程[19]．
对于正压流体，Long在1964年做了开创性的研究，得到在β平面近似下Rossby波振幅演变满足Korteweg-de Vries方程[20]．随后罗德海和张永利等还分别研究了Rossby波振幅演变下的Schrödinger方程[21-22]．Boyd用多重尺度法，从基本方程导出在正压流体中小振幅Rossby孤立波振幅演变满足非线性KdV方程和mKdV方程．笔者从能量的角度出发分别研究了正压模式和正压准地转模式下的能量守恒问题[23-24]．但是大气空间等压面和等密度面是相交割的，亦即大气是斜压的，常常为了使问题简化，将大气看做是一种理想化的大气状态分布(正压大气)；对于斜压大气的研究，有从大尺度环流指数结合大气的斜压性讨论了温带气旋和风暴轴20世纪变化的可能原因[25]．郝世峰等[26]证明了采用半解析方法求解大气原始方程组是可行的，为大气数值模拟的构建提供了一个新的思路．滕代高等[27]对斜压大气中台风涡旋自组织的问题进行了初步研究，研究表明和正压大气的结果类似．这些结果都是对斜压大气实际应用很好的补充与推广，但是对斜压大气理论方面的认识并不多．
Rossby波在大气大尺度循环中扮演着至关重要的角色，对于Rossby波的研究将是今后大气动力学方面的一个重点．本文在考虑了完整Coriolis力的情况下，从最原始的大气基本方程组出发，得到了斜压大气下Rossby波振幅所满足的KdV方程，并且进一步分析了Coriolis力对Rossby波的影响．
1 大气动力学方程组的摄动展开
将垂直方向的气压梯度力与压力表示成扰动气压梯度与浮力之和，并采用Boussinesq近似，此时，大气运动的基本方程组为
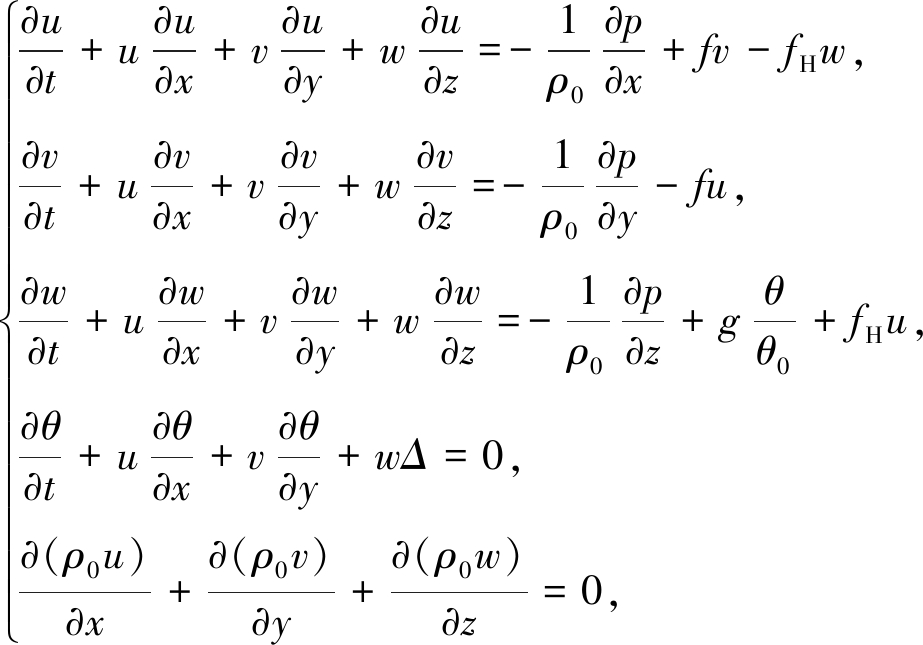
(1)
其中，θ0，ρ0分别是环境流场的位温与密度，它们只是高度的函数，
(2)
再将各变量写成其特征尺度与无量纲的乘积：
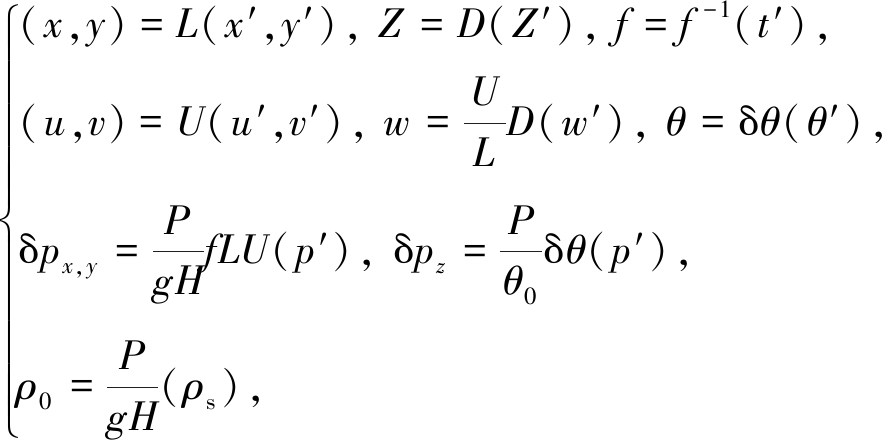
(3)
其中，H是均值大气的高度，P是地面的特征尺度，δpx,y表示水平方向的气候变化，δpz则是其垂直方向的变化，“′”表示无量纲量．
将式(3)代入式(1)，可以得到如下方程组：
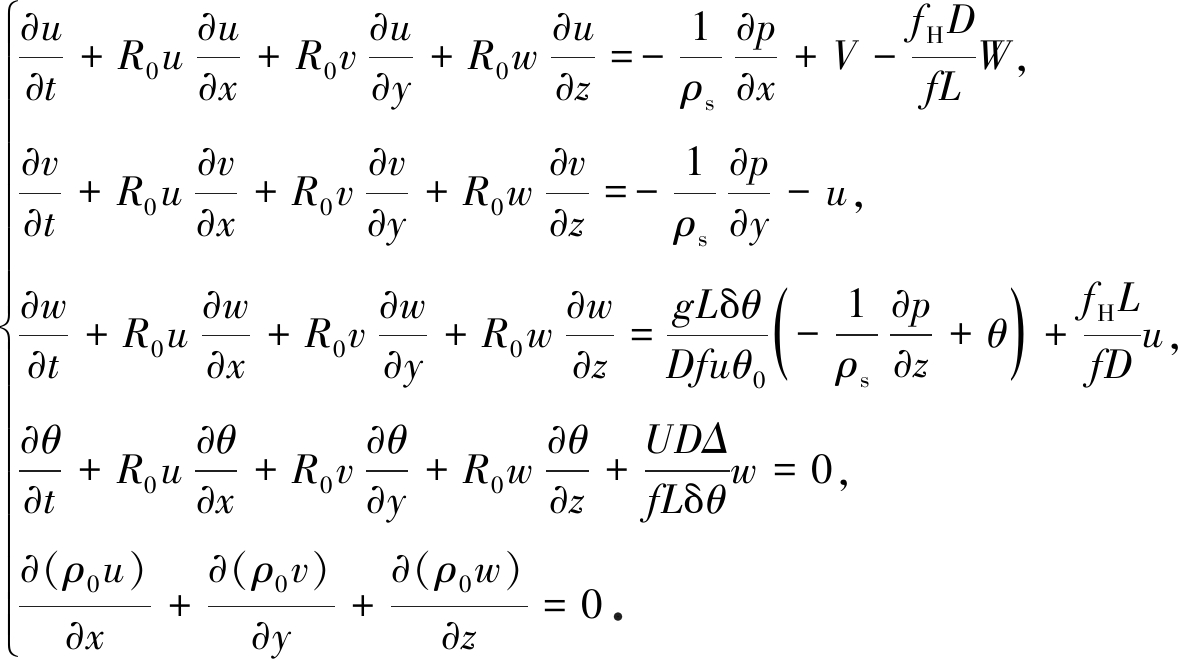
(4)
如下定义形态比：δ=D/L． 定义Coriolis水平分量与垂直分量比为：γ=fH/f且假设δ·γ≪γ/δ≪1，这样做是符合要求的．由于式(4)中第四式第二项比较小，为了量纲上的平衡，故有
(5a)
(5b)
由于R0=U/(fL)为Rossby数，考虑中尺度大气，则R0～o(1)，从而有
(6)
其中，gΔ/θ0=N2是Brunt-Väisälä频率．记ε=f2/N2，则ε≪1，在如上的假设及定义下，方程组(4)变为如下形式：
(7)
记 α=δγ,β=γ/δ 表征带有水平分量的方程项系项．
2 多重尺度法、摄动展开法
为了导出KdV方程，作如下的G-M变换，令
(8)
则有
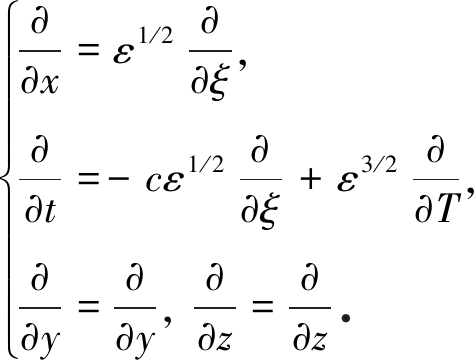
(9)
将u,v,w,p,θ按参数ε展开，得到
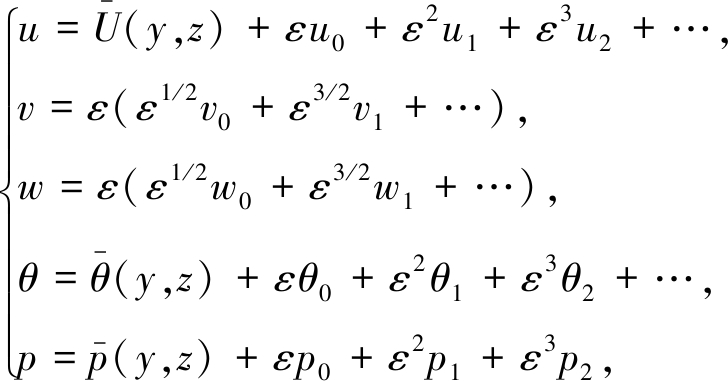
(10)
这里的
分别是基本气流的速度、位温和气压场，它们只是y,z的函数．将式(9)、(10)代入到式(7)，得到如下的方程组：
(11)
ε的零级近似，
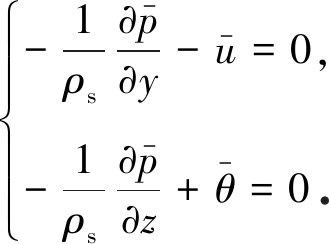
(12)
上式表明基本气流是地转平衡和静力平衡，对基本气流还可以进一步假设
(13)
ε的一级近似，
(14)
(15)
(16)
(17)
(18)
ε的二级近似，
(19)
(20)
(21)
(22)
(23)
3 KdV方程的导出
引入新的变量：
ρsu0=u′0, ρsv0=v′0, ρsw0=w′0, ρsθ0=θ′0, p0=p′0，
(24)
ρsu1=u′1, ρsv1=v′1, ρsw1=w′1, ρsθ1=θ′1, p1=p′1．
(25)
于是，可将方程(14)～(18)、(19)～(23)写为
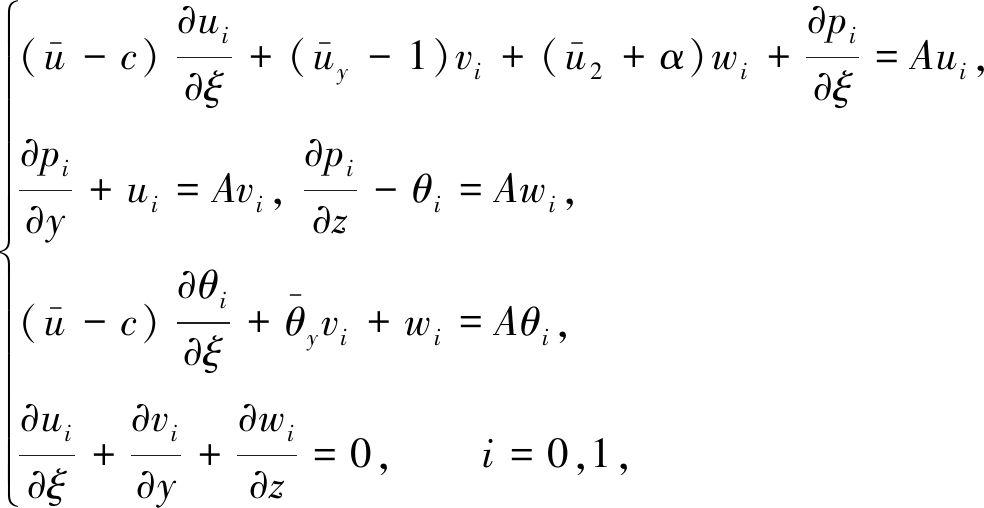
(26)
其中
(27)
(28)
(29)
Aw1=βu0，
(30)
(31)
下面将对方程(26)进行消元，得到
(32)
当i=0时，方程(32)右端
记
(33)
则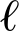 
y,p(∂p0/∂ξ)=0． 方程(32)是一个变量可分离的方程，设其解为
(34)
从而有
(35)
在一定条件下可以解出
与特征值c，并进而求得全部解为
(36)
其中，n0(T,ξ)为已知．将式(31)代入式(28)～(31)，得
(37)
(38)
(39)
(40)
由于上述两级方程的齐次部分均相同，从而当i=1时，方程(32)有解的条件可以归结为
(41)
将方程(41)整理后，得到
(42)
其中
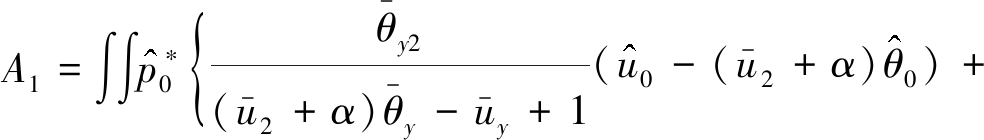
(43)
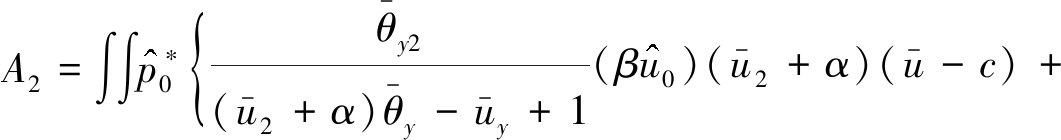
(44)
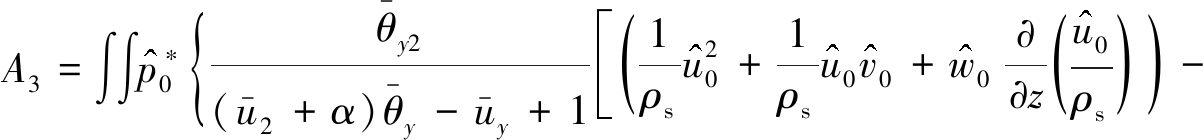
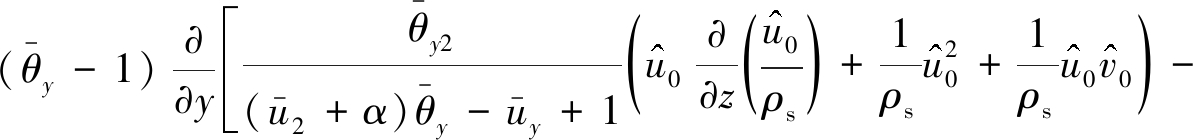
(45)
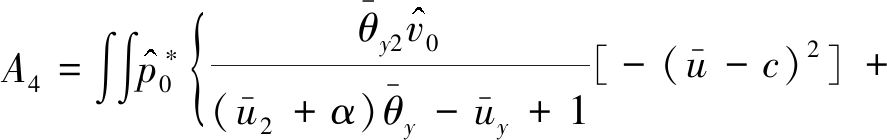
(46)
是
的共轭方程的解，由下式定义:
(47)
上述得到的关于振幅n0(T,ξ)的非线性方程为推广的KdV方程(即方程(42))，利用椭圆函数展开法，能够得到孤立波解为
它包含了频散过程和非线性过程．特别注意系数A2，说明Coriolis力的水平分量也是影响赤道大气Rossby孤波的一个重要因子，会影响孤立波的频率特征，这里不需要借助于地形作用，也可以得到类似的结论．同时方程(42)中的A2项表征由于Coriolis水平分量参数所得的项，这是与以往任何方程所不同的地方，亦即我们得到了带有水平分量的描述斜压大气的Rossby波动问题，这是以前所没有的结果．
4 结 论
本文从大气运动基本方程组出发，研究了完整Coriolis力作用下的中高纬非线性Rossby波振幅的演化规律，说明Coriolis水平分量也是产生赤道大气孤立波的重要因子，指出Coriolis力水平分量能够影响波动传播的频率特征．孤立波解也表明Coriolis水平分量对赤道非线性波动的影响．
需要指出的是，从直观上讲，由于本文对热力作用和摩擦作用没有考虑，无疑会造成与观测上的不同，所以这些需要进一步的讨论．
[1] ECKART C. Chapter Ⅳ: the field equations[J]. Hydrodynamics of Oceans and Atmospheres, 1960, 14(8): 52-63.
[2] PHILLIPS N A. The equations of motion for a shallow rotating atmosphere and the traditional approximation[J]. Journal of the Atmospheric Sciences, 2010, 27(5): 504-505.
[3] WHITE A A, BROMLEY R A. Dynamically consistent, quasi-hydrostatic equations for global models with a complete representation of the Coriolis force[J]. Quarterly Journal of the Royal Meteorological Society, 2010, 121(522): 399-418.
[4] GERKEMA T, ZIMMERMAN J, MAAS L. Geophysical and astrophysical fluid dynamics beyond the traditional approximation[J]. Reviews of Geophysics, 1977, 46(2): 1-33.
[5] ROBERT R L. Solitary waves in the one- and two-fluid systems[J]. Tellus, 1956, 8(4): 460-471.
[6] REDEKOPP L G. On the theory of solitary Rossby waves[J]. Journal of Fluid Mechanics, 1977, 82: 725-745.
[7] WADATI M. The modified Korteweg-de Vries equation[J]. Journal of the Physical Society of Japan, 1973, 34(5): 1289-1296.
[8] CHARNEY J G, STRAUS D M. Form-drag instability, multiple equilibria and propagating planetary waves in baroclinic, orographically forced, planetary wave systems[J]. Journal of the Atmospheric Sciences,1980, 6: 1205-1216.
[9] BODY J P. Equatorial solitary waves, part Ⅰ: Rossby solitons[J]. Journal of Physical Oceanography, 1980, 10: 1699-1718.
[10] BOYD J P. Equatorial solitary waves, part 2: envelope solitons[J]. Journal of Physical Oceanography, 2010, 13(3): 428-449.
[11] LUO D H, JI L R. A theory of blocking formation in the atmosphere[J]. Science in China (Series B), 1989, 33(3): 323-333.
[12] 刘式适, 谭本馗. 考虑β变化下的Rossby波[J]. 应用数学和力学, 1992, 13(1): 35-44.(LIU Shikuo, TAN Benkui. Rossby waves with the change of β[J]. Applied Mathematics and Mechanics, 1992, 13(1): 35-44.(in Chinese))
[13] SONG J, YANG L G. Force solitary Rossby waves with beta effect and topography effect in stratified flows[J]. Acta Physica Sinica, 2010, 59(12): 221-226.
[14] SONG J, YANG L G, LIU Q S. Solitary Rossby waves with beta effect and topography effect in a barotropic atmospheric model[J]. Progress in Geophysics, 2012, 27(2): 393-397.
[15] SONG J, LIU Q S, YANG L G. Algebraic solitary Rossby wave excited slowly changing topography and beta effect[J]. Progress in Geophysics, 2013，28(4): 1684-1688.
[16] KASAHARA A J. Use of precipitation data for diabatic initialization to improve the tropical analysis of divergence and moisture[J]. Meteorology and Atmospheric Physics, 1996, 60(1/3): 143-156.
[17] PHILLIPS N A. The equations of motion for a shallow rotating atmosphere and the traditional approximation[J]. Journal of the Atmospheric Sciences, 1966, 23(5): 626-628.
[18] GERKEMA T, SHRIRA V I. Near-inertial waves in the ocean: beyond the ‘traditional approximation’[J]. Journal of Fluid Mechanics, 2005, 529: 195-219.
[19] DELLAR P J, SALMON R. Shallow water equations with a complete Coriolis force and topography[J]. Physics of Fluids, 2005, 17(10): 106601.
[20] LONG R R. Solitary waves in the westerlies[J]. Journal of the Atmospheric Sciences, 1964, 3: 197-200.
[21] 罗德海. 大气中非线性Rossby波包的传播[J]. 成都气象学院学报, 1991(2): 1-6.(LUO Dehai. Propagation of nonlinear Rossby wave packet in atmosphere[J]. Journal of Chengdu Institute of Information Engineering, 1991(2): 1-6.(in Chinese))
[22] 张永利, 杨联贵. 正压大气模式中在地形效应和beta效应作用下的非线性Rossby包络孤立波[J]. 地球物理学进展, 2016, 31(6): 1381-1386.(ZHANG Yongli, YANG Liangui. Nonlinear Rossby envelope solitary waves with topographic effect and β effect in the barotropic atmospheric model[J]. Progress in Geophysics, 2016, 31(6): 1381-1386.(in Chinese))
[23] 张永利, 杨联贵, 宋健. 地形效应下正压模式方程组的能量守恒[J]. 内蒙古大学学报(自然科学版), 2016, 47(2): 140-144.(ZHANG Yongli, YANG Liangui, SONG Jian. Conservation of energy for positive pressure model system under topographic effect[J]. Journal of Inner Mongolia University (Natural Science Edition), 2016, 47(2): 140-144.(in Chinese))
[24] 张永利, 杨联贵. 地形效应下正压准地转模式的能量守恒[J]. 应用数学和力学, 2016, 37(9): 936-944.(ZHANG Yongli, YANG Liangui. Conservation of energy in the barotropic quasi-geostrophic model under orographic effects[J]. Applied Mathematics and Mechanics, 2016, 37(9): 936-944.(in Chinese))
[25] 张颖娴. 北半球温带气旋的气候学及其变率研究[D]. 博士学位论文. 南京: 南京信息工程大学, 2012.(ZHANG Yingxian. A climatology and variation research of extratropical cyclones in the North Hemisphere[D]. PhD Thesis. Nanjing: Nanjing University of Information Science & Technology.(in Chinese))
[26] 郝世峰, 楼茂园, 杨诗芳, 等. 干斜压大气拉格朗日原始方程组的半解析解法和非线性密度流数值试验[J]. 物理学报, 2015, 64(19): 194702.(HAO Shifeng, LOU Maoyuan, YANG Shifang, et al. Semi-analytical solution of the dry baroclinic atmosphere primitive equations and nonlinear experiment of a non-liner density currente[J]. Acta Physica Sinica, 2015, 64(19): 194702.(in Chinese))
[27] 滕代高, 罗哲贤, 李春虎, 等. 斜压大气中台风涡旋自组织的研究[J]. 气象学报, 2008, 66(1): 71-80.(TENG Daigao, LUO Zhexian, LI Chunhu, et al. Typhoon vortices self-organization in a baroclinic environment[J]. Acta Meteorologica Sinica, 2008, 66(1): 71-80.(in Chinese))