引 言
由固相、液相、气相以及其他相相互作用所形成的物质叫做多孔介质.在我们生活中多孔介质普遍存在,例如岩石、煤炭[1]等,所以对多孔介质性能的研究具有重大的意义和实用价值.
多孔介质的固相类似于人体的骨架支撑着整个空间,液相类似于人体的血液,气相以及其他相存在于固液两相之间.通常将除了固相以外的其他物质空间叫做孔隙,而多孔介质中的孔隙尺寸一般都极其微小,并且比表面积很大.多孔介质中的孔隙一般也分3类,分别为互相连通的孔隙、部分连通的孔隙和相互不连通的孔隙,在连通的孔隙中流体的运动一般是以渗流[2-3]方式为主.关于多孔介质的理论研究最早见于Terzaghi的研究,Biot继承了Terzaghi的思想,把多孔介质的固结理论从一维扩展到了二维和三维,建立了比较完善的固结理论,给出了相应的微分方程组,李向约和李向维[4]研究了饱和多孔介质的热固结理论.
通解是指满足全部基本方程的各种解的集合,是解决具体工程问题的一种有效的数学工具,国内外学者对各种类型基本方程的通解进行了研究.郭时光[5]研究了Poisson方程3类问题的通解;王敏中和黄克服[6]研究了半空间的热弹性问题弹性通解及其应用;沈惠川[7]研究了弹性动力学的通解;陈伟球和丁皓江[8]研究了横观各向同性三维热弹性力学通解及其势理论法;徐颖等[9]研究了双孔介质弹性动力学通解及其完备性;Unger和Aifantis[10]研究了双孔材料通解的完备性;Zhao和Lu[11]研究了各向同性多孔介质的热弹性稳态通解.
本文求解了二维多孔介质的通解,第1节通过引入4个物理量,将基本方程转化成Cauchy-Riemann方程组的形式,并将方程分解为膨胀波和扭转波两部分;第2节利用Lur’e算子矩阵理论[12]推导出二维各向同性多孔介质的动力学通解;第3节将动态解退化时间项后,获得稳态通解,并证明了稳态通解的完备解;第4节对通解进行了讨论.
1 基 本 方 程
在二维直角坐标系下,固体骨架的位移场和流体的速度场有如下形式:
(1)
其中,i, j是x,y方向的单位向量,u为固体位移,V表示流体的流速.
根据Zinkiewicz等[13]的研究,对饱和多孔介质来说,在低频的情况下,可忽略流体相对于骨架运动的惯性项和流体的可压缩性,其满足下列基本方程:
固体骨架的运动方程
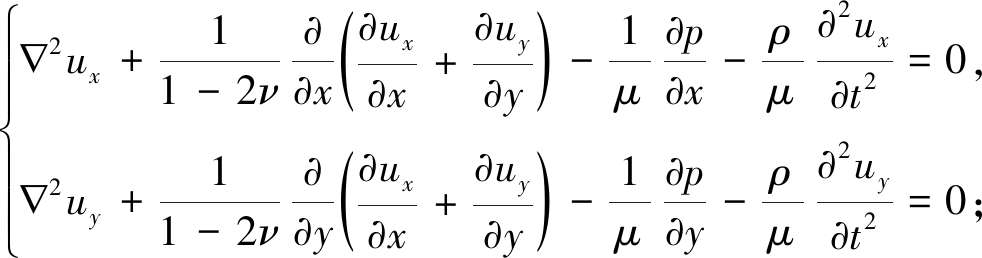
(2)
流体的运动方程

(3)
流体的连续性方程
(4)
式中
ν为Poisson比,p为液体压力的变化量,ρ为固体颗粒的密度,μ为剪切模量,ρf为流体的密度,k为渗透系数,由于本文研究的多孔介质为均质材料,故k与坐标无关,n为流体黏度系数,忽略流体黏度n随压力的变化.
为了更好地对基本方程进行分析,此处引入4个与x,y,t相关的函数vx,vy,wx,wy,令
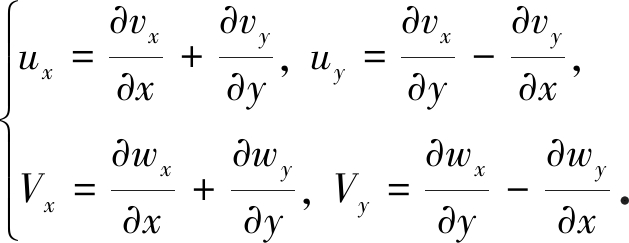
(5)
由方程(2)~(4)可得
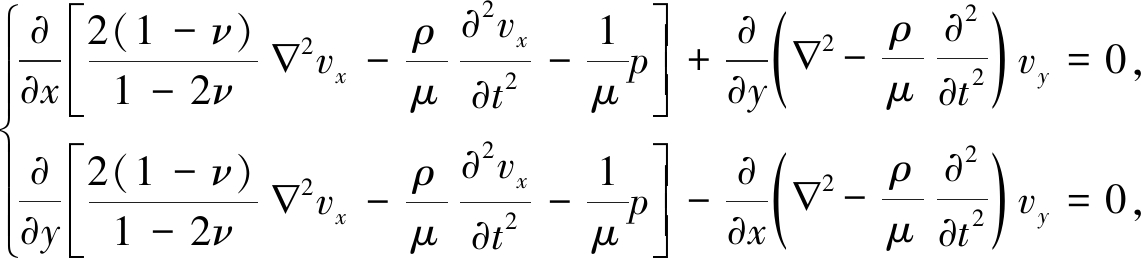
(6)
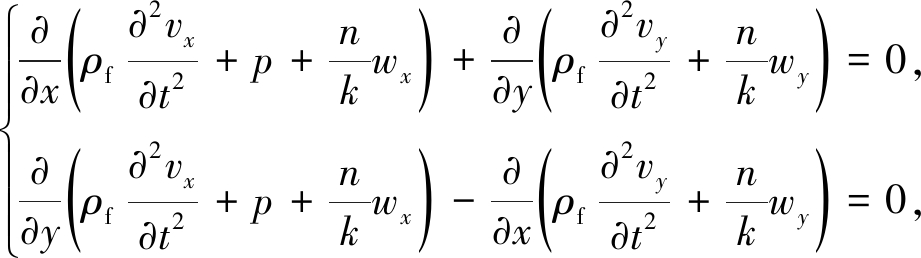
(7)
![]()
 2wx=0.
2wx=0.
(8)
由于式(6)和(7)均为Cauchy-Riemann方程组,则其可改写为
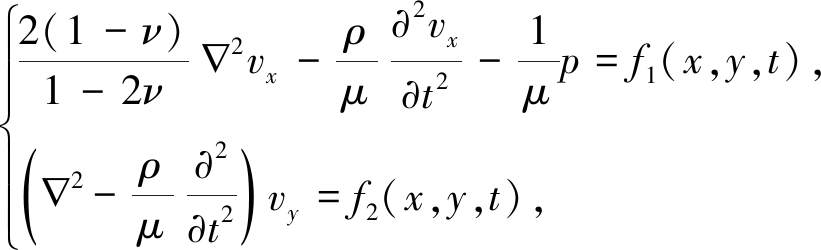
(9)
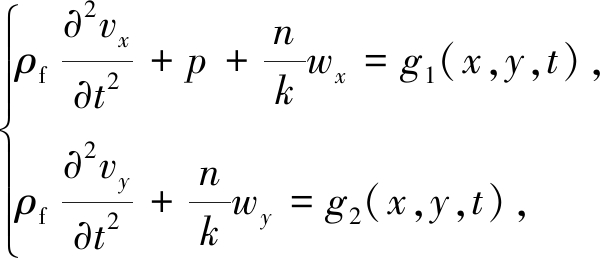
(10)
其中f1(x,y,t),f2(x,y,t),g1(x,y,t),g2(x,y,t)满足
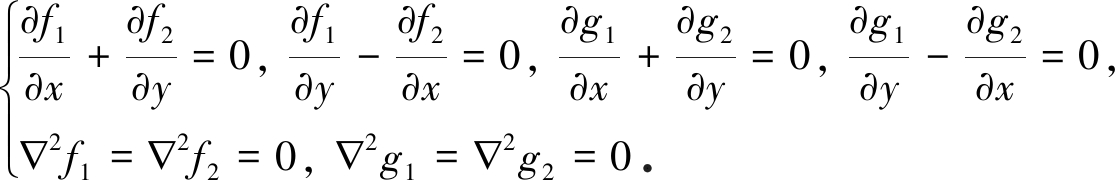
(11)
方程(9)和(10)有如下特解:
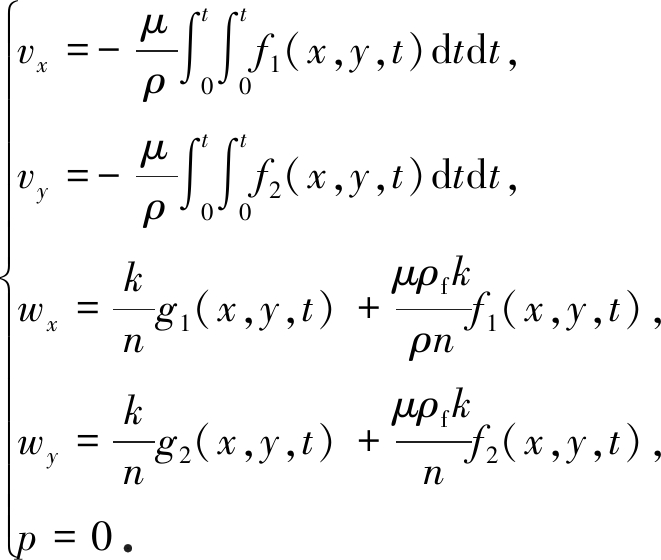
(12)
把特解(12)代入式(2)可知,特解(12)不影响流场和位移场同时满足流体的连续性方程,故可舍去.即以下方程组成立:
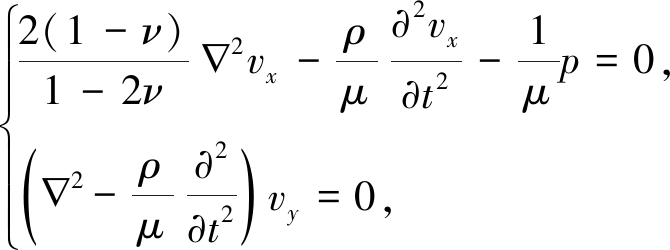
(13)
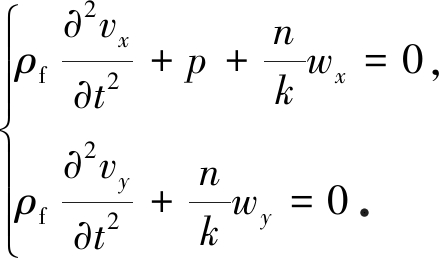
(14)
根据式(5)可以看出vx,wx和p与膨胀有关,其波动属于膨胀波,而vy和wy与扭转有关,其波动属于扭转波,两部分方程相互解耦,下面分别进行求解.
2 动力学通解
方程(13)第一式、方程(14)第一式、方程(8)属于膨胀波方程,可写成如下形式:
Aη=0,
(15)
其中
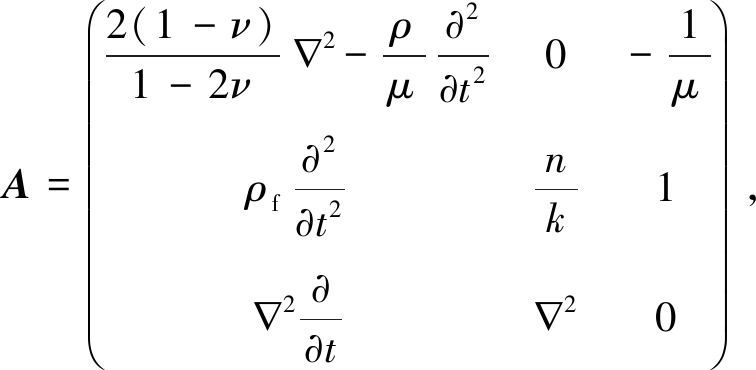
(16)
η=(vx,wx,p)T.
(17)
根据Lur’e算子理论[12]可知方程的解有如下形式:
η=Bφ,
(18)
其中,φ=(φ1,φ2,φ3)T,满足方程
|A|φi=0, i=1,2,3,
(19)
其中,B是算子矩阵A的伴随矩阵, |A|为算子矩阵A的行列式,满足
(20)
伴随矩阵B的各分量为
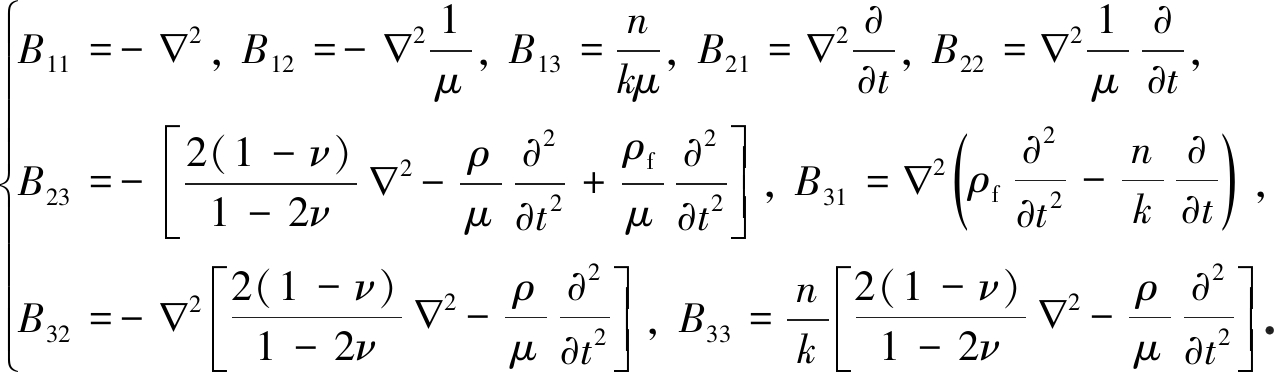
(21)
将式(21)代入式(18)可得

(22)
将式(20)代入式(19)可得
(23)
令
(24)
由式(23)可知
(25)
(26)
根据式(23),通解(22)可改写为
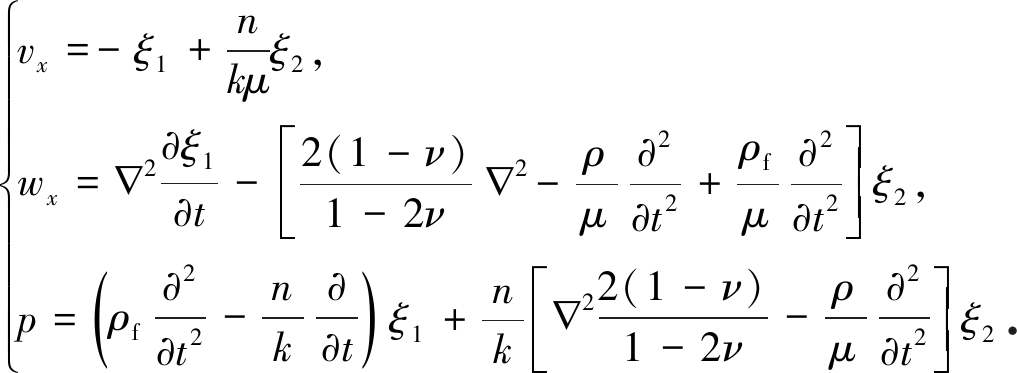
(27)
vy和wy满足方程(13)第二式和方程(14)第二式,这些方程属于扭转波方程,令
ξ3=vy.
(28)
根据方程(13)第二式和方程(14)第二式,可知
(29)
(30)
从式(25)、(26)、(30)可以看出,退化时间项后,ξi(i=1,2,3)具有调和函数或双调和函数,为了有所区分,称之为类调和函数.
将式(27)~(29)代入式(5),可以整理出动力学通解:
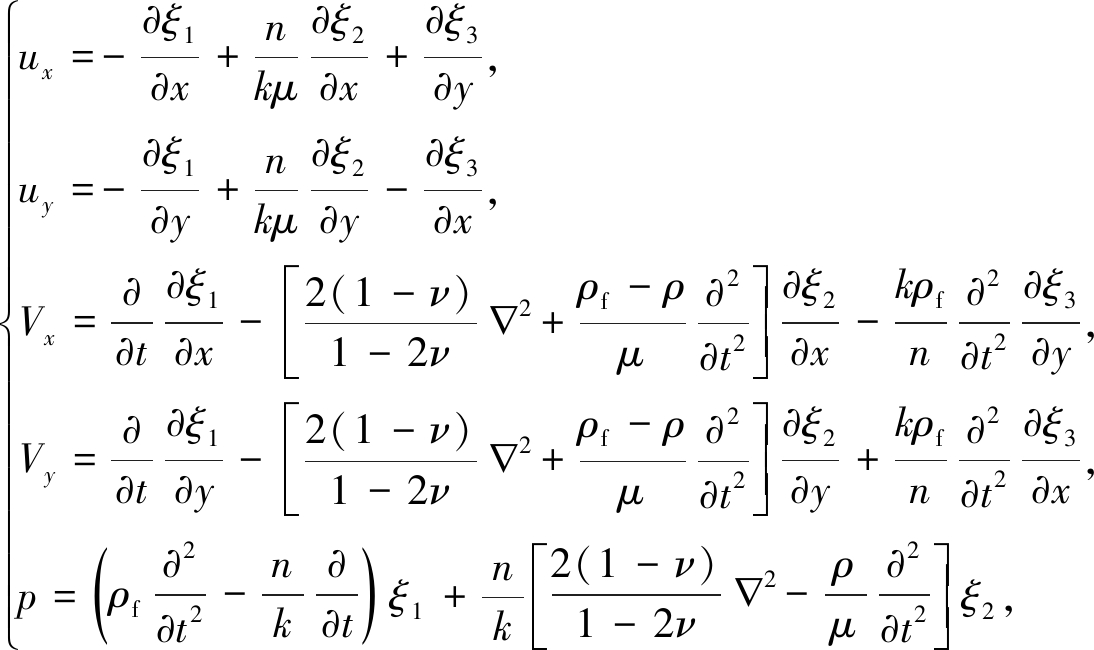
(31)
其中,ξ1,ξ2和ξ3分别满足方程(25)、(26)和(30).把方程(31)代入固体骨架的运动方程(2)、流体的运动方程(3)、流体的连续性方程(4),方程皆成立,故方程(31)为弹性动力学通解.
3 稳态通解及完备性
将动力学通解(31)中的时间项退化,可得其稳态通解:

(32)
其中
 2ξ1=0,
2ξ1=0,  2
2 2ξ2=0,
2ξ2=0,  2ξ3=0.
2ξ3=0.
(33)
由式(3)和(4)可知
 2p=0.
2p=0.
(34)
对任意p总可以找到ξ2使
![]()
 2ξ2,
2ξ2,
可获一组特解:
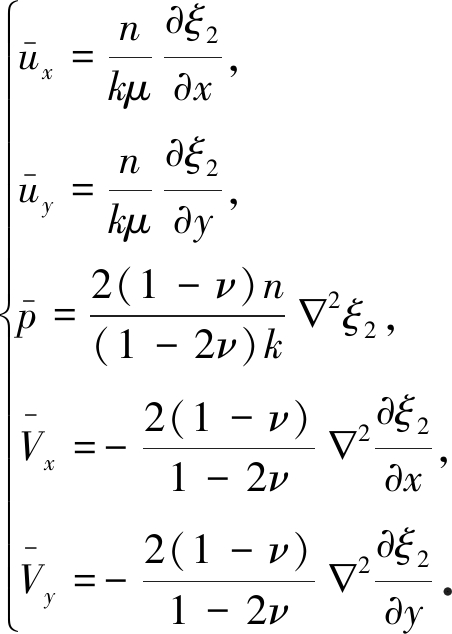
(35)
令
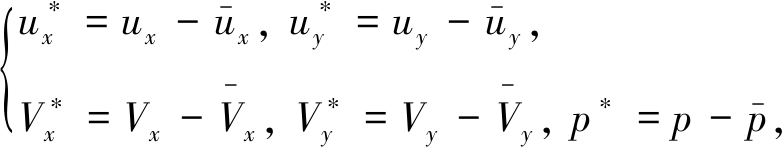
(36)
由式(32)、(33)可知
把式(36)代入式(2)中得
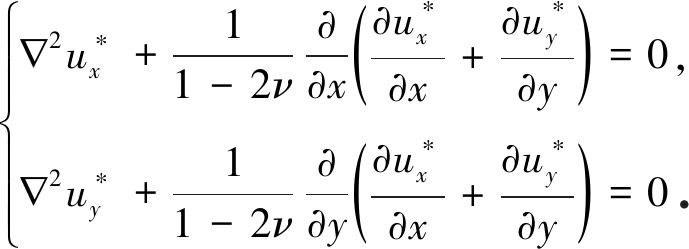
(37)
式(37)为二维弹性位移方程,与第三方向无关,如将这两个方程中的第二项系数1/(1-2ν)替换为由横观各向同性材料常数表示的(C12+C66)/C66,在数学形式上与横观各向同性材料在各向同性面内的平面应变问题的方程一致,故方程(37)的解具有二维Elliott-Lodge通解的形式:
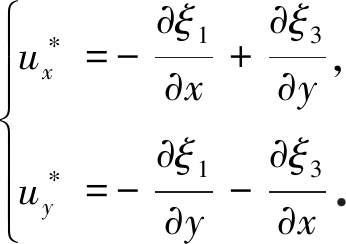
(38)
Wang等[14]证明了Elliott-Lodge通解的完备性,即对任意位移场![]() 和
和![]() 总可找到满足式(32)和(33)的ξ1和ξ3,故二维各向同性稳态通解(32)是完备的.
总可找到满足式(32)和(33)的ξ1和ξ3,故二维各向同性稳态通解(32)是完备的.
4 结果与讨论
4.1 讨论
本文给出了二维多孔介质的动力学通解(31),利用本构关系

(39)
可以得到利用类调和函数ξi(i=1,2,3)表示的应力场:
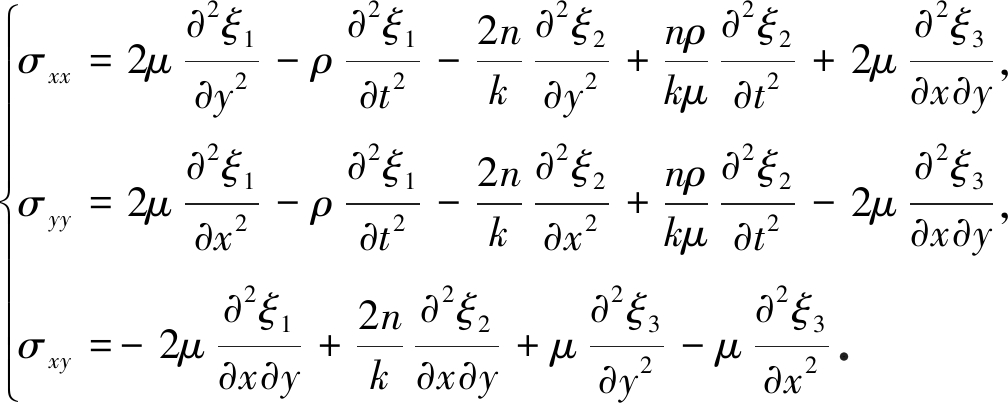
(40)
将时间项退化后,可以得到
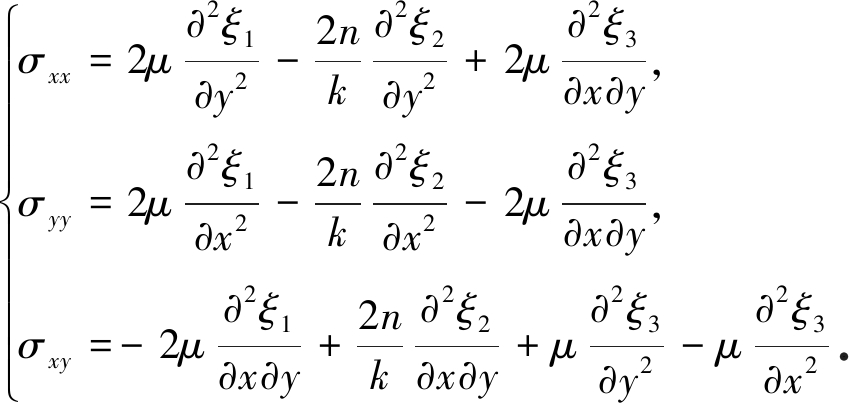
(41)
此时的各类调和函数退化为(双)调和函数,满足式(33).
令
H1=![]() ξ3(x,ζ)dζ,
ξ3(x,ζ)dζ,
其中,y0(x)是研究区域边界上一点,它是关于x的函数[15].
可以知道
(42)
根据式(36)和式(33)的第三个方程,可以推导出
(43)
该方程与y无关.令
(44)
根据式(36)和(37)可知ξ4(x,y)=H1(x,y)-H2(x)满足
![]()
 2ξ4=0.
2ξ4=0.
(45)
则式(41)可以改写为

(46)
其中括号内为双调和函数,与平面应变问题的应力场一致.
4.2 结论
本文给出了二维各向同性多孔介质的弹性动力学通解,该通解退化时间项后可以获得稳态通解,可以证明该稳态通解具有完备性.这些通解的获得将大大降低求解二维多孔介质边值问题的工作量和难度,可以为多孔介质在油气田开采、岩石加固、地下水迁移引起的地基沉降变形、部分软骨组织在多场作用下的膨胀、聚合物胶体的溶胀等重要研究领域的应用提供必要且有效的理论支持.
[1] 李子文, 林柏泉, 郝志勇, 等. 煤体多孔介质孔隙度的分形特征研究[J]. 采矿与安全工程学报, 2013, 30(3): 437-442.(LI Ziwen, LIN Boquan, HAO Zhiyong, et al. Fractal characteristics of porosity for porous media in coal mass[J]. Journal of Mining and Safety Engineering, 2013, 30(3): 437-442.(in Chinese))
[2] 李飞, 袁梅. 多孔介质渗流场数值模拟分析[J]. 矿业研究与发展, 2012, 32(1): 101-102.(LI Fei, YUAN Mei. Numerical simulation analysis of porous media seepage field[J]. Mining Research and Development, 2012, 32(1): 101-102.(in Chinese))
[3] 徐鹏, 郁伯铭, 邱淑霞. 裂纹型多孔介质的平面径向渗流特性研究[J]. 华中科技大学学报, 2012, 40(1): 101-103.(XU Peng, YU Boming, QIU Shuxia. Study on the characteristics of planar radial seepage in cracked porous media[J]. Journal of Central China University of Science and Technology, 2012, 40(1): 101-103.(in Chinese))
[4] 李向约, 李向维. 饱和多孔介质的热固结理论[J]. 固体力学学报, 1990, 11(4): 330-338.(LI Xiangyue, LI Xiangwei. Thermosetting theory of saturated porous media[J]. Journal of Solid Mechanics, 1990, 11(4): 330-338.(in Chinese))
[5] 郭时光. Poisson方程三类问题的通解[J]. 四川理工学院学报(自然科学版), 2014, 27(6): 75-79.(GUO Shiguang. General solution to three problems of Poisson equation[J]. Journal of Sichuan Institute of Technology(Natural Science edition), 2014, 27(6): 75-79.(in Chinese))
[6] 王敏中, 黄克服. 半空间的热弹性问题: 弹性通解方法的应用[J]. 应用数学和力学, 1991, 12(9): 795-806.(WANG Minzhong, HUANG Kefu. Thermoelastic problems in the half space: an application of the general solution in elasticity[J]. Applied Mathematics and Mechanics, 1991, 12(9): 795-806.(in Chinese))
[7] 沈惠川. 弹性动力学的通解[J]. 应用数学和力学, 1985, 6(9): 791-796.(SHEN Huichuan. General solution of elastic dynamics[J]. Applied Mathematics and Mechanics, 1985, 6(9): 791-796.(in Chinese))
[8] 陈伟球, 丁皓江. 横观各向同性三维热弹性力学通解及其势理论法[J]. 力学学报, 2003, 35(5): 578-583.(CHEN Weiqiu, DING Haojiang. Three-dimensional general solution of transversely isotropic thermoelasticity and the potential theory method[J]. Acta Mechanica Sinica, 2003, 35(5): 578-583.(in Chinese))
[9] 徐颖, 王敏中. 双孔介质弹性动力学通解及其完备性[J]. 北京大学学报(自然科学版), 1994, 30(3): 339-342.(XU Ying, WANG Minzhong. Genneral solutions and completeness on elastodynamics with double porosity[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 1994, 30(3): 339-342.(in Chinese))
[10] UNGER D J, AIFANTIS E C. Completeness of solutions in the double porosity theory[J]. Acta Mechanica, 1998, 75(1/4): 269-274.
[11] ZHAO B S, LU G X. General steady-state solution for thermo-poroelastic material[J]. Acta Mechanica, 2014, 225(9): 245-2652.
[12] LUR’E A I. Three-Dimensional Problems of the Theory of Elasticity[M]. New York: Interscience Publishers, 1964.
[13] ZINKIEWICZ O C, CHANG C T, BETTESS P. Drained, undrained, consolidating and dynamic behavior assumption soil[J]. Géotechnique, 1980,30(4): 385-395.
[14] WANG M Z, WANG W. Completeness and nonuniqueness of general solutions of transversely isotropic elasticity[J]. Create Account Sign in International Journal of Solids and Structures, 1995, 32(3/4): 501-513.
[15] 王敏中. 高等弹性力学[M]. 北京: 北京大学出版社, 2002.(WANG Minzhong. Advanced Elastics[M]. Beijing: Peking University Press, 2002.(in Chinese))