引 言
自适应求解是有限元法的一种新型求解方式.对于常规有限元法,用户根据经验和定性分析输入计算网格,得到该网格上的计算结果,该结果的精度如何需另行判断;而基于有效误差估计的自适应有限元法(adaptive finite element method,AFEM),用户只需输入解答精度需要满足的误差限,算法会自动划分网格并进行误差估计,最终得到按某种方式度量满足该误差限的解答[1-2].AFEM以常规FEM为基础,以误差估计和网格划分为核心技术,自提出以来备受学者们的关注[3-4],除在固体静力学问题中得以应用外,也逐渐被推广至与时间相关的结构动力学等问题[5-6].
结构受迫振动是结构动力学的基础性问题之一.常规FEM求解时,往往采用半离散的思想,对空间域进行有限元(finite element,FE)离散,得到关于时间的二阶常微分方程组(ordinary differential equations,ODEs)初值问题(以下简称离散系统的运动方程组)[3],对该方程组采用中心差分法、Newmark-β法、Wilson-θ法、广义α法、精细积分法等[7]进行求解.相关的自适应分析研究常常只对空间域或只对时间域展开[8-9],可以对时间域和空间域同时进行自适应求解的方法一般都是基于间断Galerkin法(discontinuous Galerkin method,DGM)的,如文献[5]采用了SPR(super-convergent patch recovery)法以能量模对误差进行估计,实现时空网格划分.SPR法[2]是由Zienkiewicz和Zhu提出的一种较为流行的有限元超收敛算法.
超收敛算法可以给出收敛阶更高的超收敛解,超收敛解可以用以估计常规有限元解的误差并指导网格划分,是自适应分析成功的关键环节.单元能量投影法[10-11]也是高效的有限元超收敛算法之一.对于一维杆件静力问题,它能够给出按最大模度量、至少比常规有限元解精度高一阶的超收敛解答.以EEP超收敛解估计误差并指导网格划分的有限元自适应求解算法已成功应用于各类一维线性和非线性问题[12-13]、二维线性问题[14]、三维线性问题[15]及工程实际中的路面结构静力分析[16].
基于EEP法的离散系统线性运动方程组的自适应分析也随之取得成功[17].它以Galerkin弱型式的时域FEM[18-19]为基础算法,构建时域上的EEP超收敛解来估计误差并指导网格划分, 建立了一种有效的时域AFEM, 能自动划分时间网格并给出在时间定义域内任一点的动位移, 该位移按最大模度量满足给定误差限, 此后其中的线性元格式也得到了进一步的深入研究[20-21].
基于EEP自适应分析在杆件静力问题和运动方程组中取得的成功,本文以直杆轴向受迫振动为例,研究并建立了一种在时间域和一维空间域同时实现自适应分析的方法.根据半离散的思想,首先由空间有限元离散将偏微分控制方程转化为离散系统运动方程组,对该方程组进行时域有限元的自适应求解;然后,基于空间域超收敛计算的EEP解再对空间域进行自适应,直至最终的时空网格下动位移解答与超收敛解之间的误差逐点满足给定误差限要求.本文首先介绍模型问题和Galerkin有限元求解方法;然后给出整体求解思想并对时域有限元自适应和空间域EEP超收敛公式这两项关键技术进行了阐述,归纳整体策略;最后通过典型算例展示了该算法的有效性和适用性,其中包括El Centro地震波输入下的轴向受迫振动问题的结果.该法同时也适用Euler梁和Timoshenko梁横向受迫振动以及黏弹性梁的振动问题[22-24].
1 问题描述及Galerkin有限元解
1.1 模型问题
如图1所示,考虑如下变截面直杆有阻尼轴向受迫振动问题的一般形式:

(1)
其中,杆件的轴向振动位移u=u(x,t)及外荷载f=f(x,t)是空间坐标x和时间坐标t的二元函数;p=p(x),m=m(x),c=c(x)分别是杆件的抗拉刚度、分布质量和阻尼系数;记![]() 且L为上式定义的线性微分算子.
且L为上式定义的线性微分算子.
1.2 Galerkin有限元解
本文的特点之一是时-空均采用连续的Galerkin有限元进行求解.下面首先由杆长方向的Galerkin有限元离散导出运动方程组,然后简介运动方程组的Galerkin有限元解.
式(1)模型问题的求解域可视为图2(a)所示的区域Ω=(0,l]×(0,tf].求解该问题可转化为求![]() 使得
使得
(2)
其中
(3)
特别地,试探函数空间为![]() 而检验函数空间取
而检验函数空间取![]() 这里
这里![]() 中的v(x,tf)=0这一条件由Galerkin弱型式分部积分得到,相当于Hamilton原理中位移在任一时间间隔的末时刻,其一阶变分为0.
中的v(x,tf)=0这一条件由Galerkin弱型式分部积分得到,相当于Hamilton原理中位移在任一时间间隔的末时刻,其一阶变分为0.
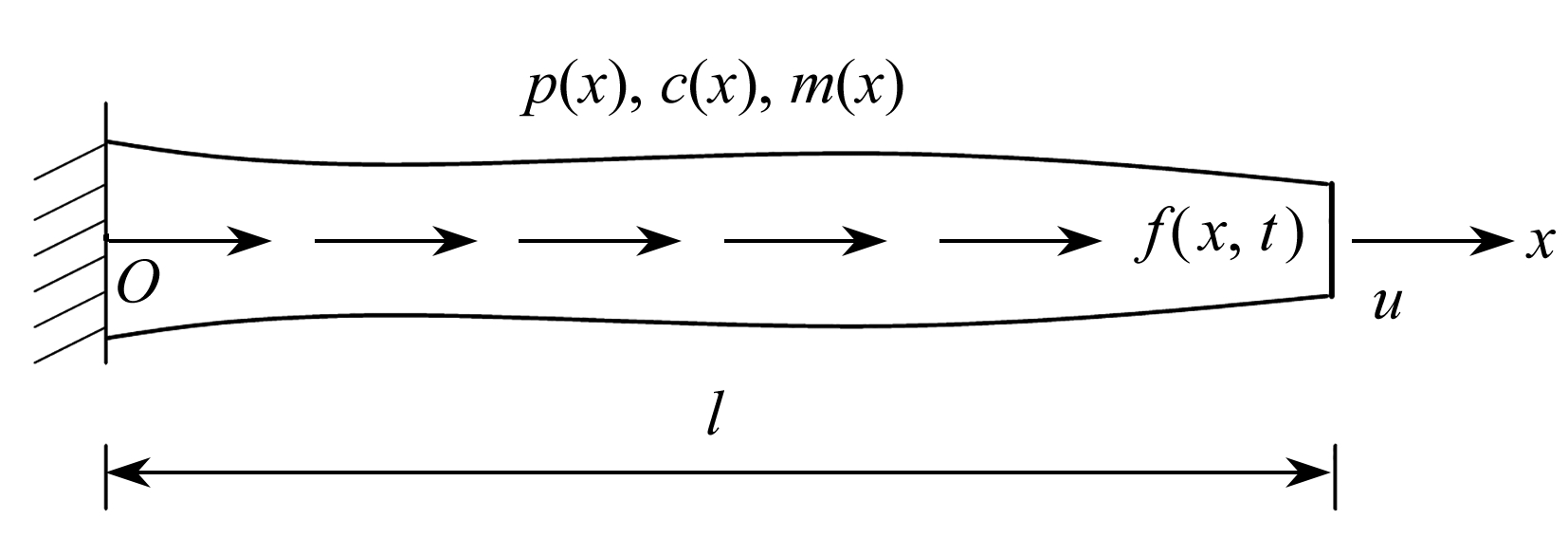
图1 杆件轴向受迫振动模型
Fig. 1 The model for the bar under axial forced vibration

(a) 求解区域 (b) 典型空间单元 (c) 典型时间单元
(a) The solution domain (b) A typical space element (c) A typical time element
图2 求解区域和典型单元示意图
Fig. 2 Schematic illustration of the solution domain and the typical elements
沿杆长方向经有限元离散划分为Nes个空间单元,其中典型空间单元![]() 如图2(b)所示,其试探函数和检验函数分别为
如图2(b)所示,其试探函数和检验函数分别为
(4)
其中,m为空间单元次数;N=[N1,N2,…,Nm+1]为单元形函数矩阵,Ni(i=1,2,…,m+1)为m次Lagrange插值形函数;![]() 这里
这里![]() 为空间单元结点上的动位移,以下称为单元结点动位移;
为空间单元结点上的动位移,以下称为单元结点动位移;![]()
令式(2)在空间单元e上积分,将式(4)代入其中,整理之后由vhe的任意性可得
(5)
其中
(6)
依次为单元质量阵、单元阻尼阵、单元刚度阵和单元荷载向量.将其集成为整体阵和整体荷载向量,可得如下离散系统的运动方程:
(7a)
(7b)
其中d是以时间t为自变量的整体结点动位移向量,Lt是按式(7a)定义的微分算子.
应用时域Galerkin有限元法求解式(7)的离散系统运动方程组,如文献[17-19]所述,将时间定义域划分为Net个单元,典型时间单元![]() 如图2(c)所示,该单元上可类似地得到Galerkin弱型式:
如图2(c)所示,该单元上可类似地得到Galerkin弱型式:
(8)
将时间单元上的试探函数和检验函数也表示成m次Lagrange形函数插值的形式,即
(9)
其中,![]() 分别为
分别为![]() 的第j个分量;
的第j个分量;![]() 分别为
分别为![]() 在时间单元上第i个结点处的值.将式(9)代入式(8)即可生成整体时域有限元求解的代数方程组,从而求得运动方程组的Galerkin有限元解.
在时间单元上第i个结点处的值.将式(9)代入式(8)即可生成整体时域有限元求解的代数方程组,从而求得运动方程组的Galerkin有限元解.
这种求解离散系统运动方程组的方法也被称为基于Galerkin弱型式的时间积分法[18],文献[18]对m=1,2,3次时算法的数值稳定性进行了详细分析,指出常规计算时该算法是有条件稳定的,并给出了稳定区间.按照类似的思路,本文对m=4,5次单元的稳定区间进行了推导计算,推导过程这里暂不赘述,结果汇总于表1,其中,Δt为时间单元长度,Tp为所求问题的最高阶模态对应周期.同时, 文献[19]指出, 如果在计算刚度系数矩阵时不采用精确积分, 而采用减缩Gauss积分时, 该方法是无条件稳定的, 进而保证了这一方法的通用性.本文按较为不利的有条件稳定算法(即各项均采用精确积分)进行计算,无条件稳定算法的结果与此类似或更好.
表1 Galerkin时域FEM的数值稳定性条件
Table 1 Stability conditions for the time-dependent Galerkin FEM

degree of elements mstability condition1Δt/Tp≤0.551 32Δt/Tp≤0.503 3, 0.551 3≤Δt/Tp≤1.232 83Δt/Tp≤0.500 1, 0.503 3≤Δt/Tp≤1.031 4, 1.232 8≤Δt/Tp≤2.075 94Δt/Tp≤1.003 6, 1.031 5≤Δt/Tp≤1.608 4, 2.075 9≤Δt/Tp≤3.103 55Δt/Tp≤1.000 2, 1.003 7≤Δt/Tp≤1.520 1, 1.608 5≤Δt/Tp≤2.253 5, 3.103 5≤Δt/Tp≤4.326 2
2 基于EEP法的自适应求解方法
2.1 整体思路
综合1.2小节所述,对模型问题式(1)实施了空间和时间两个方向的有限元离散,得到如图3所示的典型时空单元![]() 为单元内任一点.一个较为直接的自适应分析思路是,根据半离散的思想,在当前的空间网格下,对运动方程组式(7)进行时域有限元自适应求解,得到结点动位移向量的自适应解
为单元内任一点.一个较为直接的自适应分析思路是,根据半离散的思想,在当前的空间网格下,对运动方程组式(7)进行时域有限元自适应求解,得到结点动位移向量的自适应解![]() 然后将dh代入式(4)得到单元内任一点Q的动位移有限元解,在空间维度上计算精度更高的EEP超收敛解,根据ZZ法(Zienkiewicz-Zhu method)[2]以该解估计动位移有限元解的误差,对不满足误差限的单元进行细分,得到新的空间网格,该空间网格上的运动方程组更接近原模型问题的振动性质;往复上述过程直至全求解域Ω内逐点的动位移EEP解和有限元解的误差满足给定误差限,计算停止.
然后将dh代入式(4)得到单元内任一点Q的动位移有限元解,在空间维度上计算精度更高的EEP超收敛解,根据ZZ法(Zienkiewicz-Zhu method)[2]以该解估计动位移有限元解的误差,对不满足误差限的单元进行细分,得到新的空间网格,该空间网格上的运动方程组更接近原模型问题的振动性质;往复上述过程直至全求解域Ω内逐点的动位移EEP解和有限元解的误差满足给定误差限,计算停止.
可见,时域上离散系统运动方程组的Galerkin自适应有限元分析和空间维度上的EEP超收敛位移解的计算公式是其中的两个关键环节.
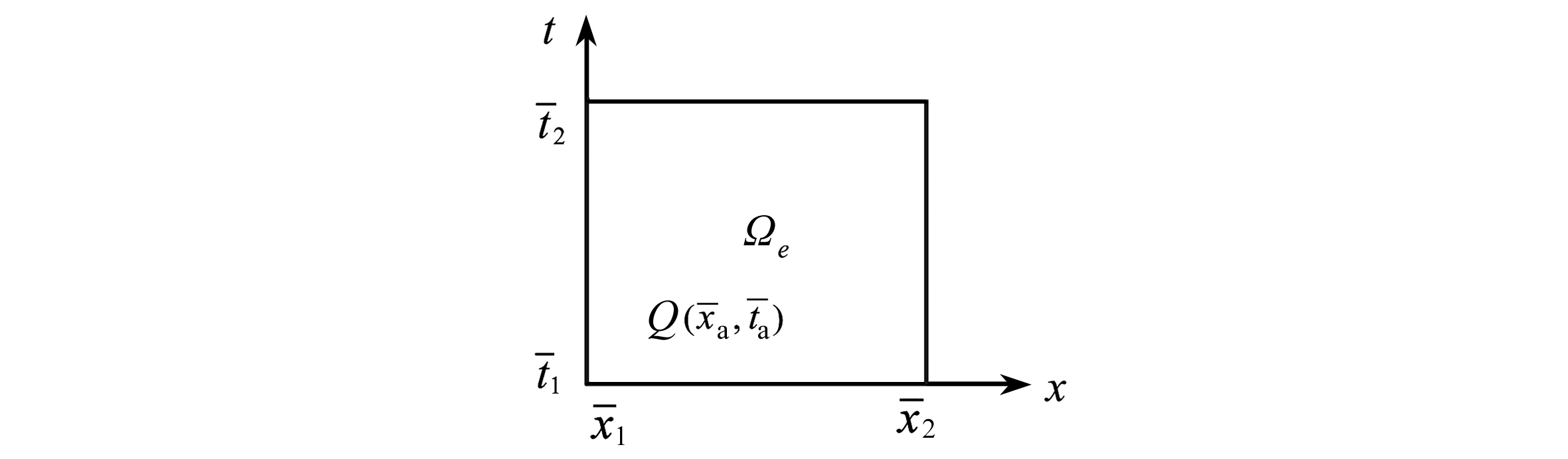
图3 典型时空单元示意图
Fig. 3 Schematic illustration of a typical space-time element
2.2 运动方程组的Galerkin时域自适应算法
对于空间离散得到如式(7)所示的离散系统运动方程组,文献[17]给出了其自适应分析的详细方法和实施步骤,归纳为以下三步:
1) 有限元解 在当前时域网格(按表1中m次单元的最小稳定区间将全域均分作为初始网格)下进行时域Galerkin有限元计算,得到运动方程组式(7)的有限元解dh.
2) 超收敛解 逐单元采用下式计算单元内任一时刻![]() 式(7)的EEP超收敛解d*:
式(7)的EEP超收敛解d*:
(10)
其中下标“a”代表在![]() 时刻的值,
时刻的值,![]() 为线性Lagrange形函数.
为线性Lagrange形函数.
3) 网格细分 用具有更高收敛阶的EEP超收敛解估计和控制有限元解的误差,逐单元检验是否满足下式的误差控制准则:
(11)
其中,Tl为预先给定的误差限,![]() 分别为d*,dh的第j个分量,n为向量d*和dh的维数(本文中n=mNes+1).对所有不满足式(11)的单元使用均差法[17]进行二分,得到新的时域网格,返回步骤1),直至整个时域所有单元上的位移解均满足式(11).
分别为d*,dh的第j个分量,n为向量d*和dh的维数(本文中n=mNes+1).对所有不满足式(11)的单元使用均差法[17]进行二分,得到新的时域网格,返回步骤1),直至整个时域所有单元上的位移解均满足式(11).
2.3 一维空间域上动位移的EEP超收敛公式
时域自适应得到d(t)后,原问题式(1)的位移有限元解uh(x,t)可由式(4)插值得到,下面给出uh(x,t)的EEP超收敛解计算公式.对于受轴向荷载的静力杆,假设其数学理论中的投影定理在单个杆件单元上也近似成立,已推导出其逐点具有高一阶精度的EEP超收敛解的计算公式[10],并给出了其收敛阶的数学证明[25].仿照这一思路,可以推导出轴向动荷载作用下的位移超收敛计算公式.
记eh=u-uh,由式(2)可容易得到全域上精确成立的整体投影定理:
(12)
假设该投影定理在单个空间单元上仍近似成立,即式(12)的积分区间取在单元![]() 上得
上得
(13)
取检验函数vh为线性函数
(14a)
(14b)
代入式(13)进行分部积分,认为边界项高阶收敛进行一定的舍略后,得到单元内任一点动位移的EEP公式:
(15)
其中u*为超收敛解,rh≡Leh=f-Luh.
3 自适应算法策略
自适应求解的目标为:寻找一个优化的时-空网格π*,使得该网格上的有限元解uh相对于真解u的误差按最大模满足事先给定的误差限Tl;由于精确解事先未知,以EEP超收敛解u*代替精确解,即全域Ω=(0,l]×(0,tf]上满足
(16)
基于常规的Galerkin时空FEM,整体自适应求解策略总结如下:
1) 给定误差限Tl以及杆件自适应分析的初始空间网格π0s(通常整个杆件取1个单元即可),令当前网格πs=π0s,其杆单元总数为Nes.
2) 在当前网格πs上,逐单元由式(6)计算单元阵Me,Ke,Ce和单元荷载向量Pe,并集成为整体阵M,K,C和整体向量P,得到形如式(7)的离散系统运动方程组.
3) 对上一步得到的离散系统运动方程组按以下步骤进行自适应求解:
(3a) 给定初始时间网格π0t(按表1中m次单元的最小稳定区间将全域均分作为初始时间网格),令πt=π0t.
(3b) 有限元解 在当前网格πt上进行时域Galerkin有限元计算,得到有限元解dh.
(3c) 超收敛解 逐单元用式(10)计算其EEP简约格式超收敛解d*.
(3d) 网格细分 逐单元逐分量检验是否满足式(11).对于所有不满足的单元,使用均差法进行时间网格细分,得到新的时间网格,并设此新网格为πt,返回步骤(3b);直到所有分量均满足式(11).
4) 空间域有限元解 将dh代入式(4)插值得到有限元解uh.
5) 空间域超收敛解 逐空间单元将uh代入式(15)求得杆单元上的超收敛解u*.
6) 空间网格细分 逐空间单元检验是否满足式(16).对所有不满足的单元,使用均差法进行空间网格细分,生成新的空间网格,令此新网格为当前网格πs,返回步骤2);若所有单元均满足式(16),则停止,此时网格πs及πt构成最终的自适应时空网格π*.
4 数 值 算 例
基于上述自适应策略,以FORTRAN90编制了杆件轴向受迫振动的自适应求解程序,进行了数值试验,本节给出其中3个典型算例以显示本算法的效果.前两个算例给定真解的表达式,将其代入式(1)导出荷载f(x,t),再假设真解未知进行自适应分析,将最终结果与真解比较,以验证本法的可靠性;第三个算例将El Centro地震波作为轴向荷载作用于一等截面混凝土杆件,将本文自适应结果与SAP2000计算结果进行对比.
例1和例2采用无量纲计算.以下空间上的初始网格取1个单元,时域上的初始网格按表1中m次单元的最小稳定区间将全域均分得到;hmax,hmin分别表示自适应网格π*中时间单元或空间单元的最大、最小尺寸,![]() 为全域动位移的最大绝对误差;时间网格被加密一次称为一步时域自适应,空间网格被加密一次称为一步空间域自适应.
为全域动位移的最大绝对误差;时间网格被加密一次称为一步时域自适应,空间网格被加密一次称为一步空间域自适应.
例1 常截面杆件无阻尼轴向受迫振动.一根x=0端固定、x=1端自由的均质等截面杆件,轴向作用不均匀干扰力,设其动位移的解析表达式为
(17)
刚度p和质量m均取1,荷载f(x,t)由式(1)导出,误差限取为Tl=10-3,求解时长tf=10 s.m=2~4次单元自适应计算结果列于表2,图4给出了3次、4次单元下有限元解与真解式(17)相比的误差分布.可见,杆件各点在各时刻的动位移有限元解的精度均满足误差限.
表2 例1各次单元自适应求解的结果
Table 2 Results of the adaptive solution for example 1
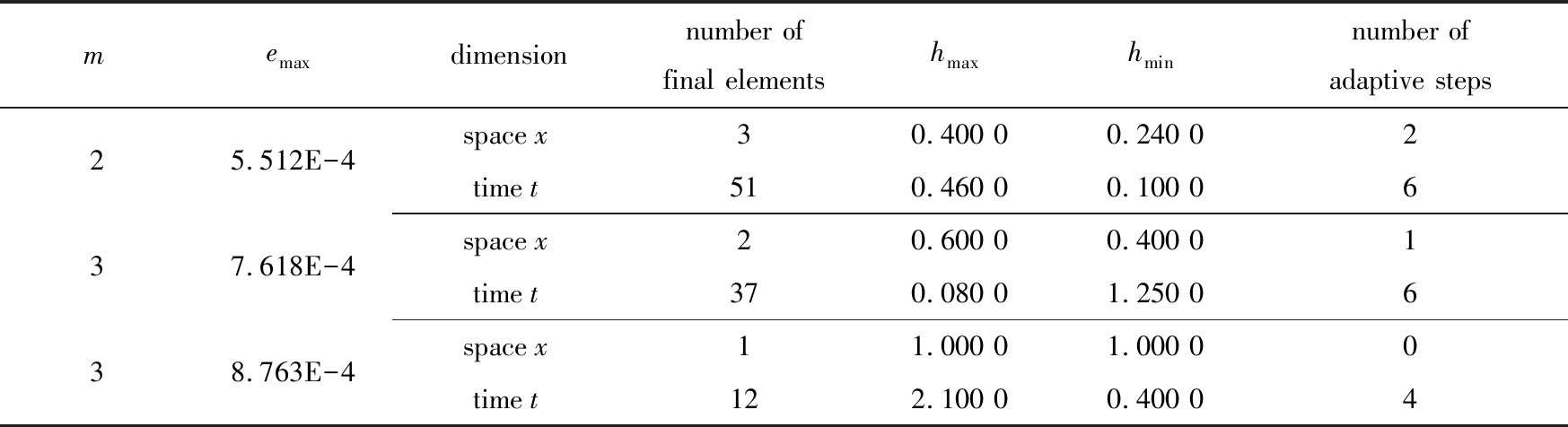
memaxdimensionnumber of final elementshmaxhminnumber of adaptive steps25.512E-4space x30.400 00.240 02time t510.460 00.100 0637.618E-4space x20.600 00.400 01time t370.080 01.250 0638.763E-4space x11.000 01.000 00time t122.100 00.400 04
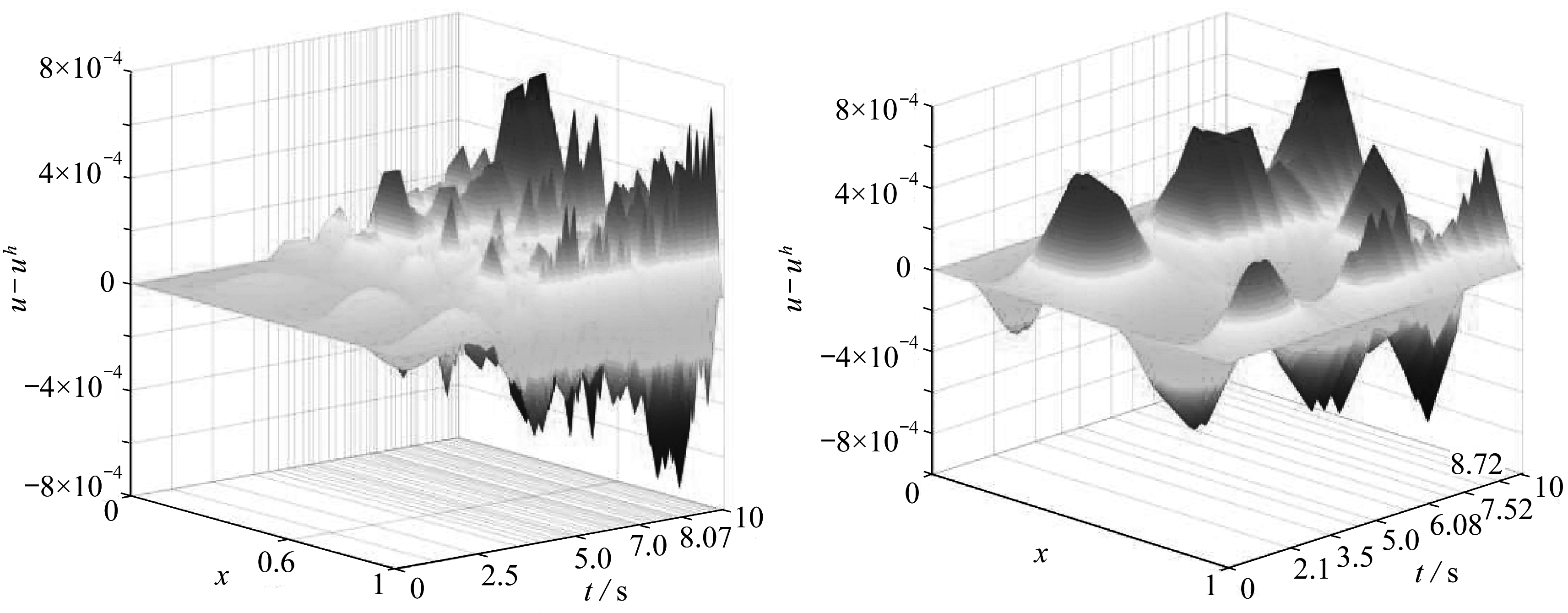
(a) 3次单元解误差分布 (b) 4次单元解误差分布
(a) Error distribution for m=3 (b) Error distribution for m=4
图4 例1自适应有限元解与真解的误差分布图(m=3,4)
Fig. 4 The error distributions of the adaptive finite element solution for example 1 (m=3,4)
例2 变截面杆件有阻尼轴向受迫振动.取刚度p(x)=1-x、质量m(x)=2-x、阻尼系数c(x)=x,杆长为1.设其动位移响应的解析表达式为
u=(cos(2πt)-1)sin(πx), 0<x<1, 0<t<tf.
(18)
误差限取为Tl=10-3,求解时长tf=4 s.采用m=2~4次单元进行自适应求解,结果列于表 3,图 5给出了3次、4次单元下自适应有限元解的误差分布情况.结果再次显示,杆件各点在各时刻的动位移有限元解相比于真解的误差均满足给定误差限.
表3 例2各次单元自适应求解的结果
Table 3 Results of the adaptive solution for example 2

memaxdimensionnumber of final elementshmaxhminnumber of adaptive steps28.262E-4space x110.140 00.050 06time t770.060 00.050 0737.809E-4space x50.280 00.090 03time t320.125 00.125 0549.539E-4space x20.600 00.400 01time t160.250 00.250 04

(a) 3次单元解误差分布 (b) 4次单元解误差分布
(a) Error distribution for m=3 (b) Error distribution for m=4
图5 例2自适应有限元解与真解的误差分布图(m=3,4)
Fig. 5 The error distributions of the adaptive finite element solution for example 2(m=3,4)

图6 例3的混凝土杆件示意图 图7 El Centro地震波
Fig. 6 The concrete bar in example 3 Fig. 7 The El Centro earthquake wave
例3 图6中左端固定的等截面混凝土杆,长600 ft,即182.88 m,截面为中空圆环形,外直径50 ft,壁2.5 ft,混凝土的弹性模量Ec为3.6×106 lbf/in2,密度为4.69 lbf·s2/ft4,换算为国际单位并计算出其抗拉刚度EA=5.98×109 N,线密度为8.33×104 kg/m.不考虑阻尼,沿杆件轴向输入El Centro地震波(图7).计算时长取tf=5 s,误差限取Tl=10-2.
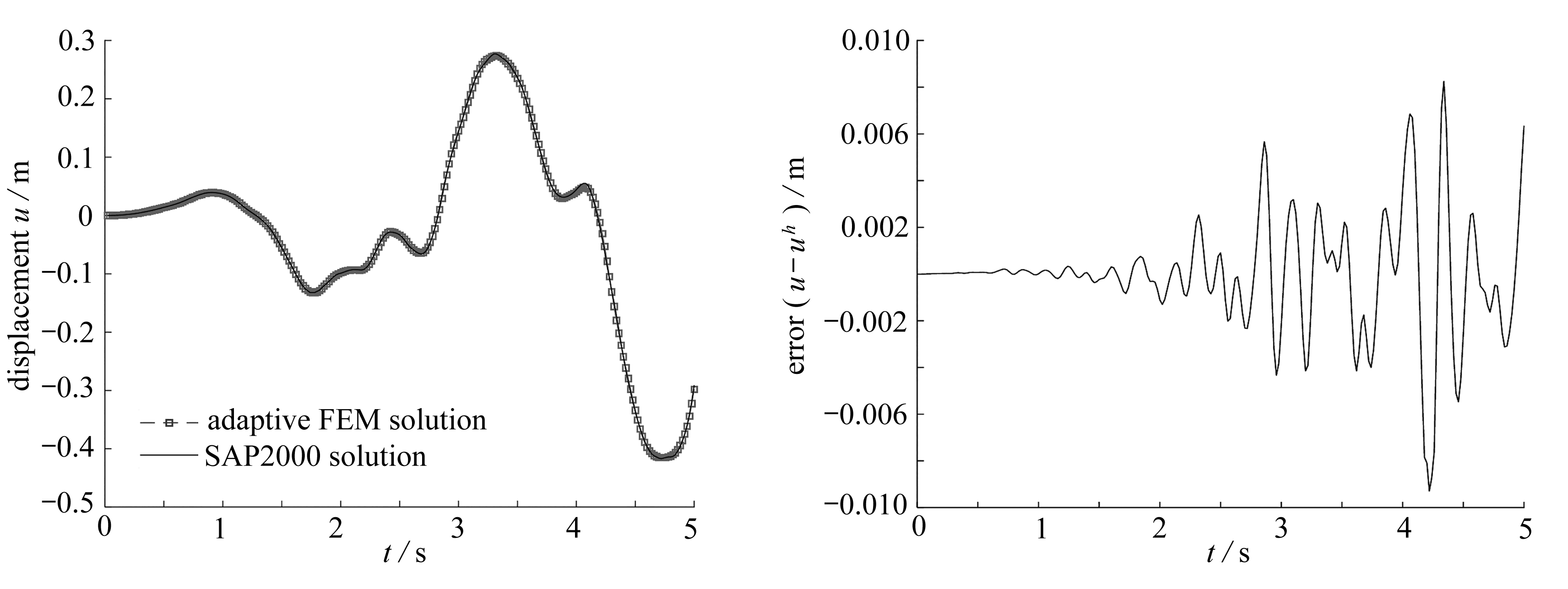
(a) 自适应有限元解和SAP2000解 (b) 自适应有限元解和SAP2000解的误差
(a) The adaptive solution and the (b) Errors between the adaptive solution SAP2000 solution and the SAP2000 solution
图8 混凝土杆件自由端的自适应有限元解、SAP2000解及二者误差分布
Fig. 8 The adaptive FE solution, the SAP2000 solution and the errors between the 2 solutions at the free end of the concrete bar
使用有限元商用软件SAP2000对该问题进行计算,杆件划分为300个等分单元,用此密集网格下的SAP2000位移解作为该算例的比较解.本法中采用三次元进行自适应求解,最终杆长度方向划分为4个等分单元、时域上划分为1 966个单元,最短的时间单元长度为0.001 25 s,最长的时间单元长度为0.02 s;将其给出的自适应有限元解与上述SAP2000的解进行比较,全域内最大绝对误差为9.29×10-3 m,满足给定误差限要求.图8给出该杆件右端点上动位移的本文解与SAP2000解,以及两解之间的误差图.可见,该算法在地震波这样的复杂荷载下依然适用.
5 结 语
本文以直杆轴向受迫振动问题为模型,提出了一种对时域和一维空间区域同时进行EEP自适应分析的算法.该法在时空两个维度均采用常规Galerkin有限元法求解,两个维度上的EEP超收敛计算公式基本一致,求得的杆件各点各时刻的自适应有限元解通常都满足给定误差限的要求,具有精度保证.该算法也对梁的横向振动、杆系结构振动等问题同样适用,可以推广应用.从数值算例结果中可以发现,最终给出的自适应时间网格往往略显密集,这是由于本算法目前根据半离散思想,首先对时域进行自适应分析造成的,本文方法仍可进一步深入研究以取得更好的结果.
[1] BABUSKA I, RHEINBOLDT W C. Error estimates for adaptive finite element computations[J]. SIAM Journal on Numerical Analysis, 1989, 15(4): 746-754.
[2] ZIENKIEWICZ O C, ZHU J Z. A simple error estimator and adaptive procedure for practical engineering analysis[J]. International Journal for Numerical Methods in Engineering, 1987, 24(2): 337-357.
[3] ZIENKIEWICZ O C, TAYLOR R L, ZHU J Z. The Finite Element Method: Its Basis and Fundamentals[M]. 7th ed. Singapore: Elsevier, 2013.
[4] BANGERTH W, RANNACHER R. Adaptive Finite Element Methods for Differential Equations[M]. Springer, 2013.
[5] LI X D, WIBERG N E. Implementation and adaptivity of a space-time finite element method for structural dynamics[J]. Computer Methods in Applied Mechanics & Engineering, 1998, 156(1/4): 211-229.
[6] THOMPSON L L, HE D T. Adaptive space-time finite element methods for the wave equation on unbounded domains[J]. Computer Methods in Applied Mechanics & Engineering, 2005, 194(18): 1947-2000.
[7] 张雄, 王天舒, 刘岩. 计算动力学[M]. 2版. 北京: 清华大学出版社, 2015.(ZHANG Xiong, WANG Tianshu, LIU Yan. Computational Dynamics[M]. 2nd ed. Beijing: Tsinghua University Press, 2015.(in Chinese))
[8] BLUM H, RADEMACHER A, SCHRÖDER A. Space adaptive finite element methods for dynamic Signorini problems[J]. Computational Mechanics, 2008, 44(4): 481-491.
[9] MAYR M, WALL W A, GEE M W. Adaptive time stepping for fluid-structure interaction solvers[J]. Finite Elements in Analysis and Design, 2018, 141: 55-69.
[10] 袁驷, 王枚. 一维有限元后处理超收敛解答计算的EEP法[J]. 工程力学, 2004, 21(2): 1-9.(YUAN Si, WANG Mei. An element-energy-projection method for post-computation of super-convergent solutions in one-dimensional FEM[J]. Engineering Mechanics, 2004, 21(2): 1-9.(in Chinese))
[11] 王枚, 袁驷. Timoshenko梁单元超收敛结点应力的EEP法计算[J]. 应用数学和力学, 2004, 25(11): 1124-1134.(WANG Mei, YUAN Si. Computation of super-convergent nodal stresses of Timoshenko beam elements by EEP method[J]. Applied Mathematics and Mechanics, 2004, 25(11): 1124-1134.(in Chinese))
[12] 袁驷, 邢沁妍, 王旭, 等. 基于最佳超收敛阶EEP法的一维有限元自适应求解[J]. 应用数学和力学, 2008, 29(5): 533-543.(YUAN Si, XING Qinyan, WANG Xu, et al. Self-adaptive strategy for one-dimensional finite element method based on EEP method with optimal super-convergence order[J]. Applied Mathematics and Mechanics, 2008, 29(5): 533-543.(in Chinese))
[13] YUAN S, DU Y, XING Q Y, et al. Self-adaptive one-dimensional nonlinear finite element method based on element energy projection method[J]. Applied Mathematics and Mechanics(English Edition), 2014, 35(10): 1223-1232.
[14] YUAN Si, DONG Yiyi, XING Qinyan, et al. Adaptive finite element method of lines with local mesh refinement in maximum norm based on element energy projection method[J]. International Journal of Computational Methods, 2019, 18(3): 195008.
[15] YUAN S, WU Y, XING Q Y. Recursive super-convergence computation for multi-dimensional problems via one-dimensional element energy projection technique[J]. Applied Mathematics and Mechanics (English Edition), 2018, 39(7): 1031-1044.
[16] LIU P F, XING Q Y, DONG Y Y, et al. Application of finite layer method in pavement structural analysis[J]. Applied Sciences, 2017, 7(6): 611.
[17] 邢沁妍, 杨杏, 袁驷. 离散系统运动方程的Galerkin有限元EEP法自适应求解[J]. 应用数学和力学, 2017, 38(2): 133-143.(XING Qinyan, YANG Xing, YUAN Si. An EEP adaptive strategy of the Galerkin FEM for dynamic equations of discrete systems[J]. Applied Mathematics and Mechanics, 2017, 38(2): 133-143.(in Chinese))
[18] 邢向华, 张雄, 陆明万. 基于Galerkin法弱形式的时间积分法[J]. 工程力学, 2006, 23(7): 8-12.(XING Xianghua, ZHANG Xiong, LU Mingwan. A time integration method based on the weak form Galerkin method [J]. Engineering Mechanics, 2006, 23(7): 8-12.(in Chinese))
[19] BORRI M, GHIRINGHELLI G L, LANZ M, et al. Dynamic response of mechanical systems by a weak Hamilton formulation[J]. Computers & Structures, 1985, 20(1/3): 495-508.
[20] 袁驷, 袁全, 闫维明, 等. 运动方程自适应步长求解的一个新进展: 基于EEP超收敛计算的线性有限元法[J]. 工程力学, 2018, 35(2): 13-20.(YUAN Si, YUAN Quan, YAN Weiming, et al. A new development of solution of equations of motion with adaptive time-step size: linear FEM based on EEP super-convergence technique[J]. Engineering Mechanics, 2018, 35(2): 13-20.(in Chinese))
[21] 袁全, 袁驷, 李易, 等. 线性元时程积分按最大模自适应步长公式的证明[J]. 工程力学, 2018, 35(8): 9-13.(YUAN Quan, YUAN Si, LI Yi, et al. Proof of adaptive time-step size formula based on maximum norm in time integration of linear elements[J]. Engineering Mechanics, 2018, 35(8): 9-13.(in Chinese))
[22] 杨杏. 基于EEP法的杆件受迫振动有限元自适应分析[D]. 硕士学位论文. 北京: 清华大学, 2016.(YANG Xing. Adaptive analysis of FEM for forced vibrations of bars based on EEP super-convergent method[D]. Master Thesis. Beijing: Tsinghua University, 2016.(in Chinese))
[23] 陆琛宇. 基于EEP法的平面直杆系受迫振动自适应分析的研究[D]. 硕士学位论文. 北京: 清华大学, 2018.(LU Chenyu. Adaptive analysis of forced vibrations for skeletal systems based on EEP super-convergent method[D]. Master Thesis. Beijing: Tsinghua University, 2018.(in Chinese))
[24] XING Q Y, LU C Y, YANG X, et al. Adaptive finite element analysis for forced vibration of Euler beams in transverse direction with EEP method[C]//Proceeding of the 15th East Asia-Pacific Conference on Structural Engineering and Constrcution. Xi’an, China, 2017.
[25] 袁驷, 邢沁妍. 一维Ritz有限元超收敛计算的EEP法简约格式的误差估计[J]. 工程力学, 2014, 31(12): 1-3.(YUAN Si, XING Qinyan. A direct derivation and proof of super-convergence of EEP displacement of simplified form in one-dimensional Ritz FEM[J]. Engineering Mechanics, 2014, 31(12): 1-3.(in Chinese))