引 言
近年来以非线性能量汇(NES)为基础的减振设计引起了研究人员的广泛关注,与线性减振装置相比,NES具有减振频率宽、振动能量单向传递等优点,因此具备强大的减振能力和广泛的应用前景.Gendelman和Vakakis等呈现和研究了带有NES的系统中能量单向、不可逆转移的现象[1-2].近年来,国内学者也开展了关于NES的大量研究.熊怀和孔宪仁等研究了NES的参数设计问题和阻尼对NES的影响[3-4];李继伟等考察了多个NES组合接连的吸振效果[5];孙敏等对比了并联和串联NES的吸振效能[6];王菁菁等设计了一种轨道型的NES并考察其减振性能[7];刘中坡等研究了NES的刚度优化问题并开展了振动台试验[8];孙斌等研究了NES在民用航空发动机减振方面的可行性[9];Yang等将NES应用于设计整星减振装置[10] . 惯容器的概念首先由剑桥大学的学者Smith提出[11].惯容器的主要特点是其两端自由、两端可以受力、两端的力与两端的加速度差值之比为定值,这个比值被称为惯容器的惯质系数(也称惯容系数).由于这一特性,惯容器得到了广泛的关注和研究.Salvi等进行了带惯容器的线性减振器整合能量采集器的概念研究[12]; Luo等考察了带惯容器的线性减振器整合了能量采集器后在建筑领域的应用[13];刘彦探索了惯容器与传统的线性机械振动被动控制系统串、并联的特点[14];在车辆悬架领域,惯容器得到了成功的应用[15];杨晓峰等研究了惯质系数对惯容器减振效果的影响[16];Zhang等使用复化平均法分析了惯容器与NES系统结合的效果[17].
在航天工程领域,受限于外部能源的稀缺,如果能采集振动的能量并转化为电能,有望为设备提供额外的能源供应,因此将能量采集装置整合进减振装置是很有前景的.目前振动能量采集器主要有电磁式、压电式和静电式等几种形式,基于超磁致伸缩材料(GMM)的能量采集器就是一种电磁式振动能量采集器.刘蕊等提出并研究了附加非线性振子的双稳态电磁式振动能量捕获器的特性[18];Fang等[19]和Li等[20]分别考察了将电磁式和压电式能量采集器整合进NES减振装置的问题.
由于惯容器的独有特性,惯容器的惯质系数可以在一定条件下“充当”惯性元件的质量[11,21],而且惯质系数与惯容器自身的实际质量没有必然联系,所以惯容器能以自身较小质量替代大质量的惯性元件,有望在实现相同减振效果的同时减少减振装置本身的重量,这对发射质量有严格要求的航天工程意义重大.本文首次用惯容器替代NES的质量元件,并与GMM能量采集器结合,组成NES-I-GMM减振和能量采集一体化装置,在整星减振的实际工程背景下,以数值方法分析了该装置的减振和能量采集效果.
1 建 立 模 型
图1是一个附加有NES的整星减振与GMM能量采集一体化系统.其中代表卫星结构的主系统包括:质量为m1,m2的质量块,m1,m2之间平行安置的刚度为k1的线性弹簧和阻尼为c1的黏性阻尼, m2通过平行安置的刚度为k2的线性弹簧和阻尼为c2的黏性阻尼与基座相连.NES-I-GMM装置包括:惯质系数为b的惯容器、适当的阻尼c3和非线性刚度为k3的非线性弹簧以及GMM能量采集器,其中NES部分起主要减振作用.NES元件和惯容器平行安置于m2和GMM之间,惯容器并联设置的原因在于:在确保惯容器和弹簧、阻尼等元件能够正常发挥性能的情况下[22],使附加在主结构上的装置最简单,以达到整星减振设计的减重要求.GMM可以简单描述为由Terfenol-D棒外围环绕着拾取线圈组成,拾取线圈通过一个电阻R组成闭合电路,电阻R的功率可以反映能量采集情况.GMM上端和NES元件和惯容器下端相连,下端与基座固定相连.
图1中的x1,x2用于描述在外部位移激励u作用下质量块m1,m2的位移,x3表示惯容器下端的位移.同时由于惯容器上端和m2固连、下端和GMM固连,所以x2也表示惯容器上端的位移,x3也表示GMM上端的位移.
根据Newton定律,上述系统的控制方程为
(1)
(2)
(3)
(4)
其中FNES为GMM上端所受NES和惯容器的合力,σ为GMM内的应力,σ0为施加在GMM上的预应力,dGMM为GMM的直径.
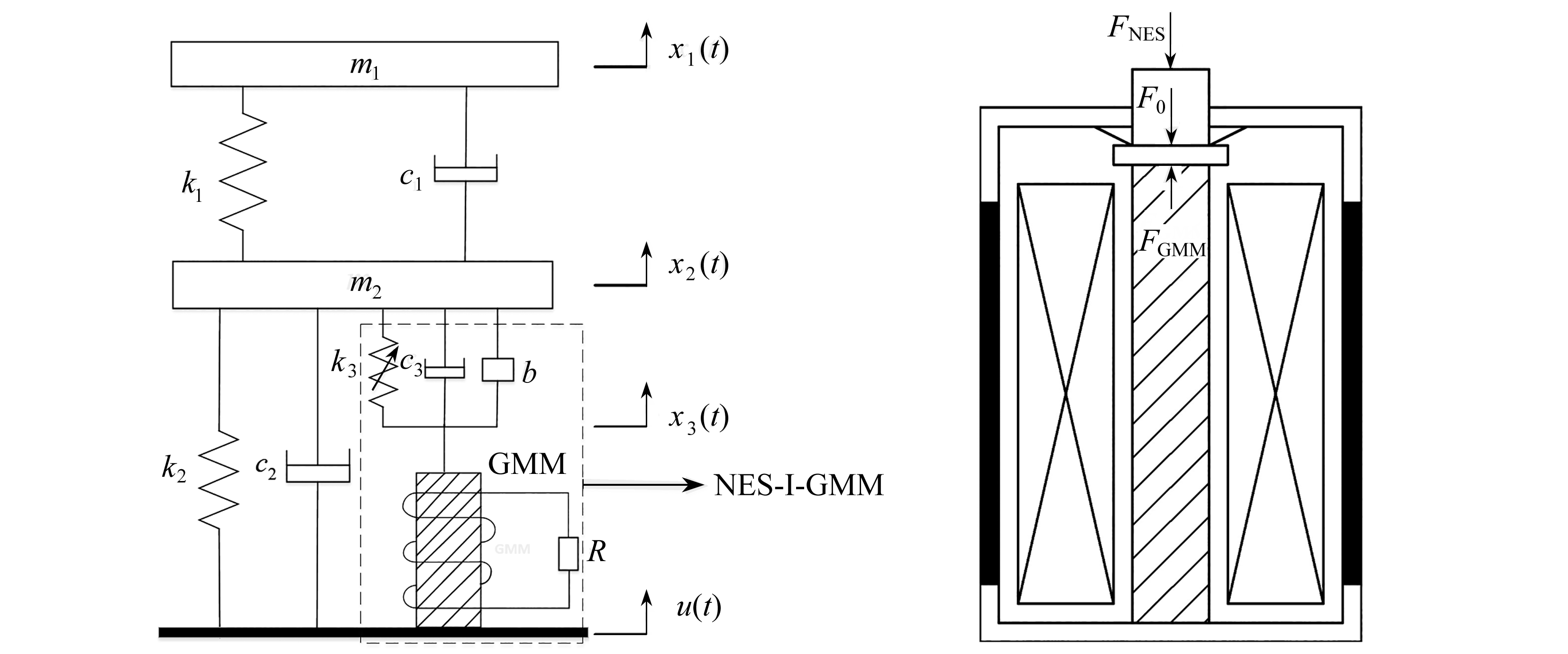
(a) 附带NES-I-GMM装置的两自由度整星模型 (b) GMM结构图
(a) Schematic diagram of the 2-DOF whole spacecraft model(b) The GMM structure
图1 动力学模型
Fig. 1 Schematic diagrams of the dynamic prototype
式(3)和(4)可以化简得到
(5)
激励采用简谐位移激励:
u=Ausin(2πft),
(6)
其中f为位移激励的频率,Au为激励幅值.
表1 系统参数
Table 1 Parameters of the system
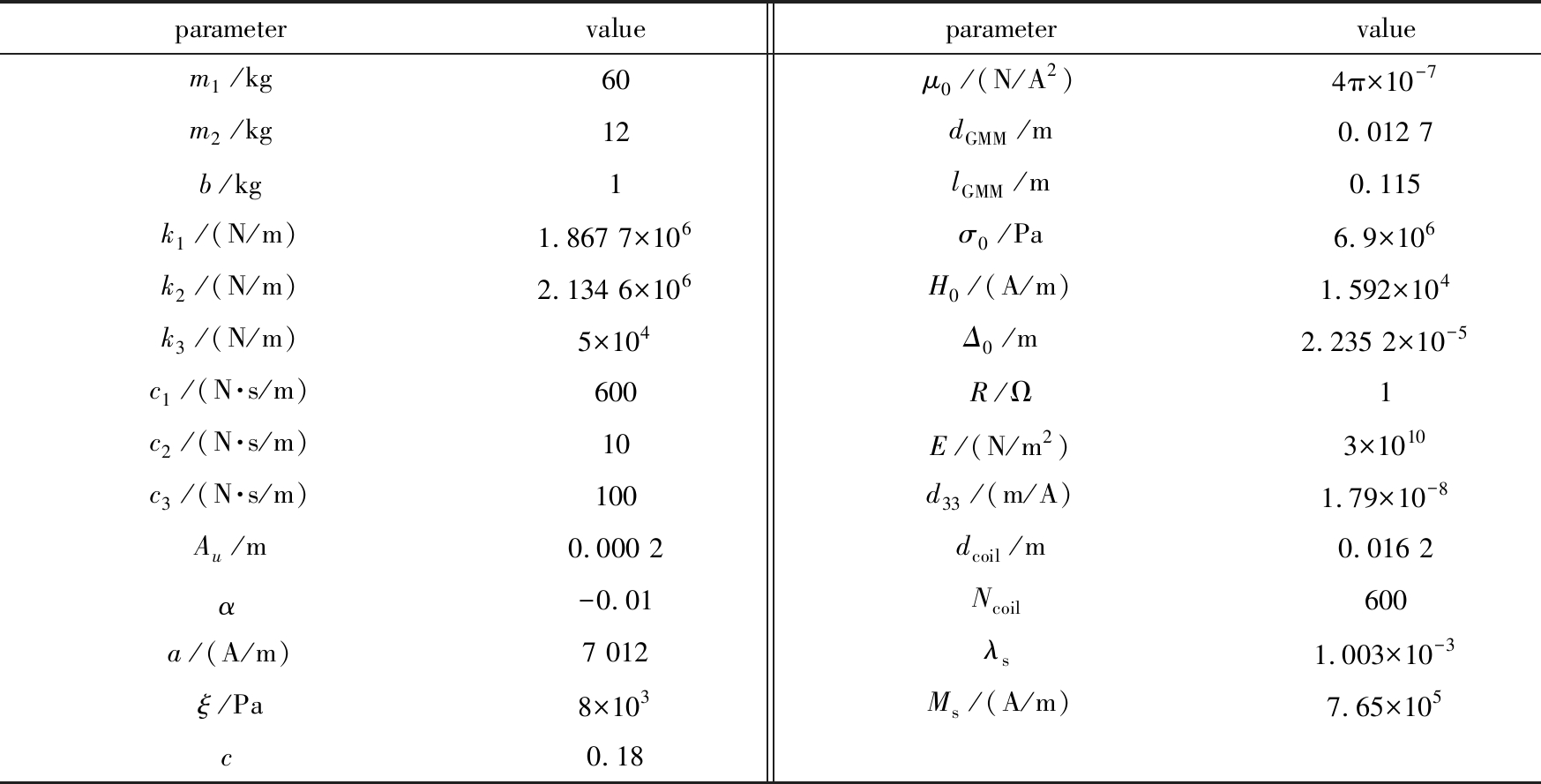
parametervalueparametervaluem1/kg60μ0/(N/A2)4π×10-7m2/kg12dGMM/m0.012 7b/kg1lGMM/m0.115k1/(N/m)1.867 7×106σ0/Pa6.9×106k2/(N/m)2.134 6×106H0/(A/m)1.592×104k3/(N/m)5×104Δ0/m2.235 2×10-5c1/(N·s/m)600R/Ω1c2/(N·s/m)10E/(N/m2)3×1010c3/(N·s/m)100d33/(m/A)1.79×10-8Au/m0.000 2dcoil/m0.016 2α-0.01Ncoil600a/(A/m)7 012λs1.003×10-3ξ/Pa8×103Ms/(A/m)7.65×105c0.18
根据描述GMM的磁滞行为的Jiles-Atherton模型和参考文献[19],还可以推导得到一个σ满足的方程:
(7)
其中λs为饱和磁致伸缩系数,H0为偏置磁场强度,Ms为饱和磁化强度,a为无磁滞磁化强度的形状系数,c为可逆系数,E为GMM的弹性模量,Δ0为由于施加在GMM上的预应力而引起的位移,lGMM为GMM的长度,![]() 由公式
由公式![]() 定义,此处α为畴壁相互作用系数,μ0为真空磁导率,ξ为单位体积能量耦合系数.
定义,此处α为畴壁相互作用系数,μ0为真空磁导率,ξ为单位体积能量耦合系数.
上述方程中x1, x2, x3和σ是未知变量,式(1)、(2)、(5)和(7)构成了一个包含4个方程和4个未知数的方程组,即为系统的动力学方程组.系统中具体参数取值如表1所示.
2 频 域 分 析
确定动力学方程并选定若干基本参数后,采用Runge-Kutta算法对动力学方程组进行求解,具体采用MATLAB的Ode15s求解器进行求解,并进行数值仿真.
首先考察系统的频域特征,同时画出带和不带NES-I-GMM装置的f-x1曲线图(系统幅频曲线图),如图2所示,图中的振幅表示在该频率下x1的最大振幅.可以看出,在两个共振频率附近,加装NES-I-GMM装置可以大幅降低系统共振时的振幅.
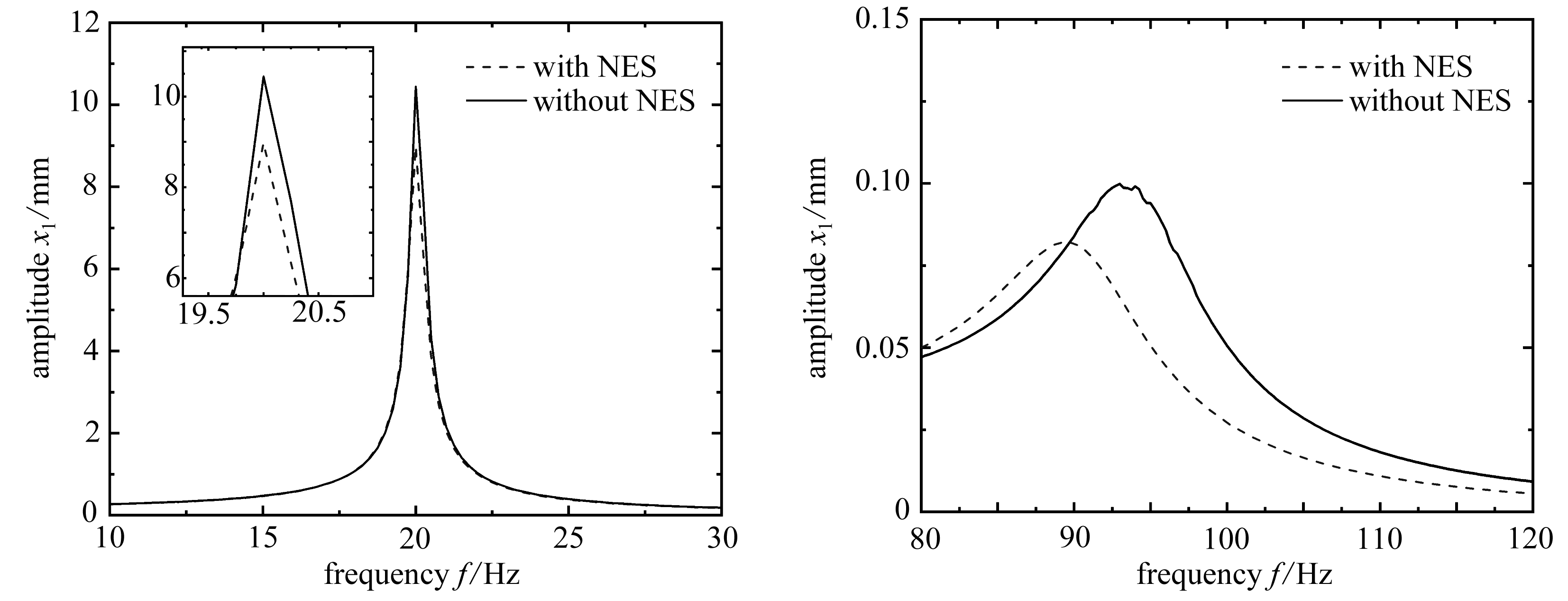
(a) 系统一阶固有频率附近的f-x1曲线 (b) 系统二阶固有频率附近的f-x1曲线
(a) The f-x1 curves around 1st-order natural frequency(b) The f-x1 curves around 2nd-order natural frequency
图2 系统幅频响应曲线
Fig. 2 The amplitude-frequency response curves
从图2(a)可以看出系统的一阶固有频率约为20 Hz,这一频率与不带NES-I-GMM装置的系统固有频率基本一致,这印证了NES装置对系统固有频率影响很小的特性[23],从图2(b)可以看出系统的二阶固有频率约为94 Hz,加入NES-I-GMM装置对系统二阶固有频率产生了少许影响,加入NES-I-GMM装置后的系统二阶固有频率减小为约89 Hz.但是二阶固有频率附近振幅已经很小,仅有一阶固有频率的1%左右,所以二阶固有频率的改变影响很小.
3 参 数 分 析
逐步改变NES-I-GMM装置各参数和激励幅值,考察主系统幅频响应变化,本文所设计的装置在二阶固有频率处的振动幅值已经很小,而且系统在高频率处主要受阻尼影响,其他参数变化在高阶处对系统不会产生重大影响,所以以下仅考察本系统在一阶固有频率附近受参数变化的影响.图3给出了参数变化下的主系统幅频响应曲线.
从图3可以看出:1) 图3(a)显示主系统振幅对非线性刚度k3变化很不敏感,非线性刚度变化对主系统振幅影响很小; 2) 图3(b)显示NES阻尼对主系统的振幅影响十分显著,随着阻尼c3由小增大,主系统振幅随之逐步减小; 3) 图3(c)显示惯质系数对主系统的振动影响有两方面,一是随着惯容器惯质系数b的减小,主系统振幅略微减小,二是随着惯容器惯质系数b的减小,系统共振频率略微增大; 4) 图3(d)显示了激励幅值对主系统振幅的影响,随着激励幅值Au由小增大,主系统振动幅值也随之成比例增大.
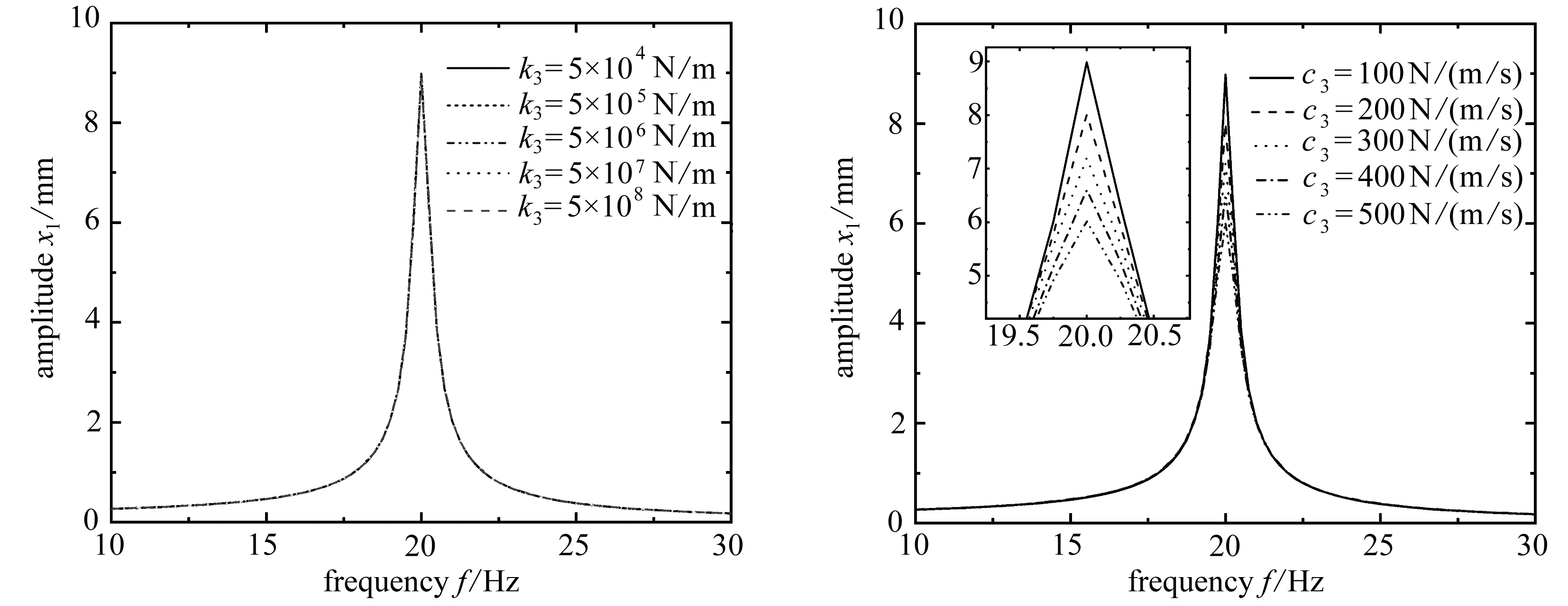
(a) NES非线性刚度k3变化 (b) NES阻尼c3变化
(a) NES nonlinear stiffness k3 changes (b) NES damping c3 changes
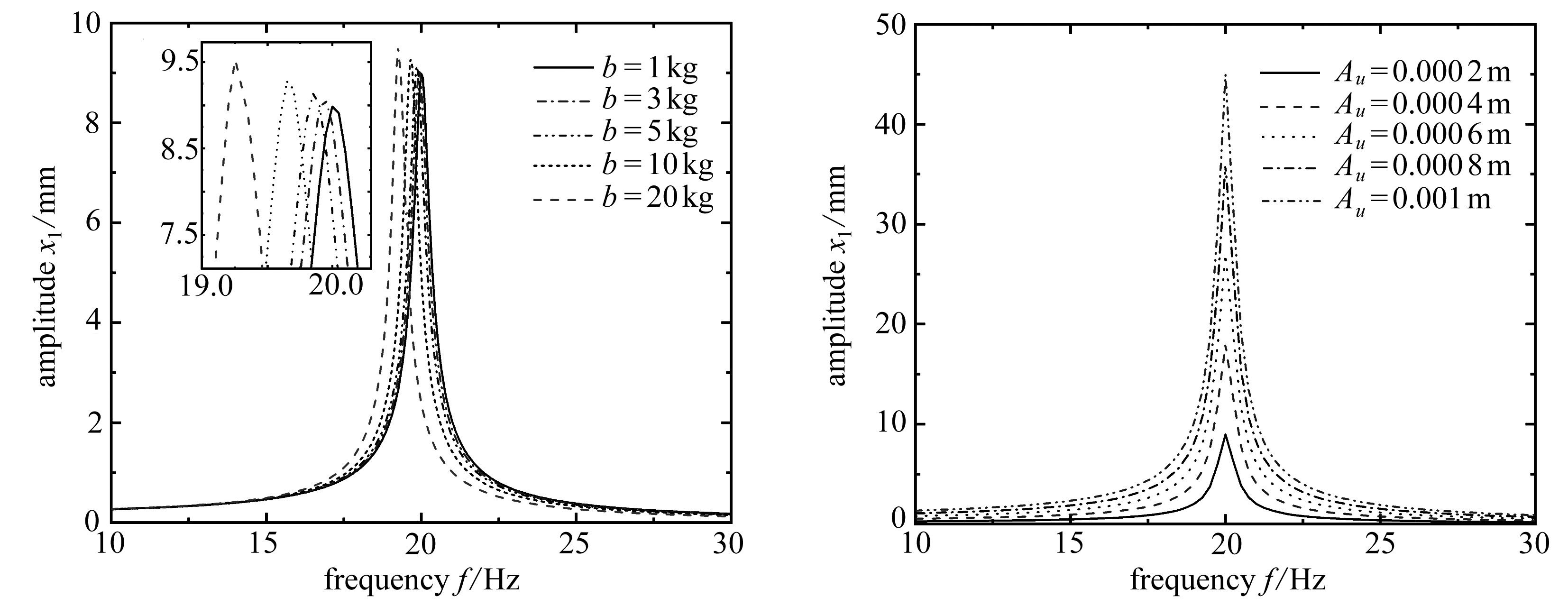
(c) 惯容器惯质系数b变化 (d) 激励幅值Au变化
(c) Inertial coefficient b changes of the inerter (d) Excitation amplitude Au changes
图3 参数变化下的主系统幅频响应曲线
Fig. 3 The amplitude-frequency response curves with variable parameters
4 能 量 分 析
在进行能量分析前,先要考察GMM元件上的最大应力,GMM元件抗压能力较强,抗拉能力很弱,所以要预加压应力,使得GMM元件上的应力始终为正.计算在工作频率范围内的GMM的最大和最小应力如图4所示.从图4可以看出GMM元件上的应力始终为正,预加应力有效避免了出现拉(负)应力,所以GMM在工作中不会损坏,能够有效采集能量.
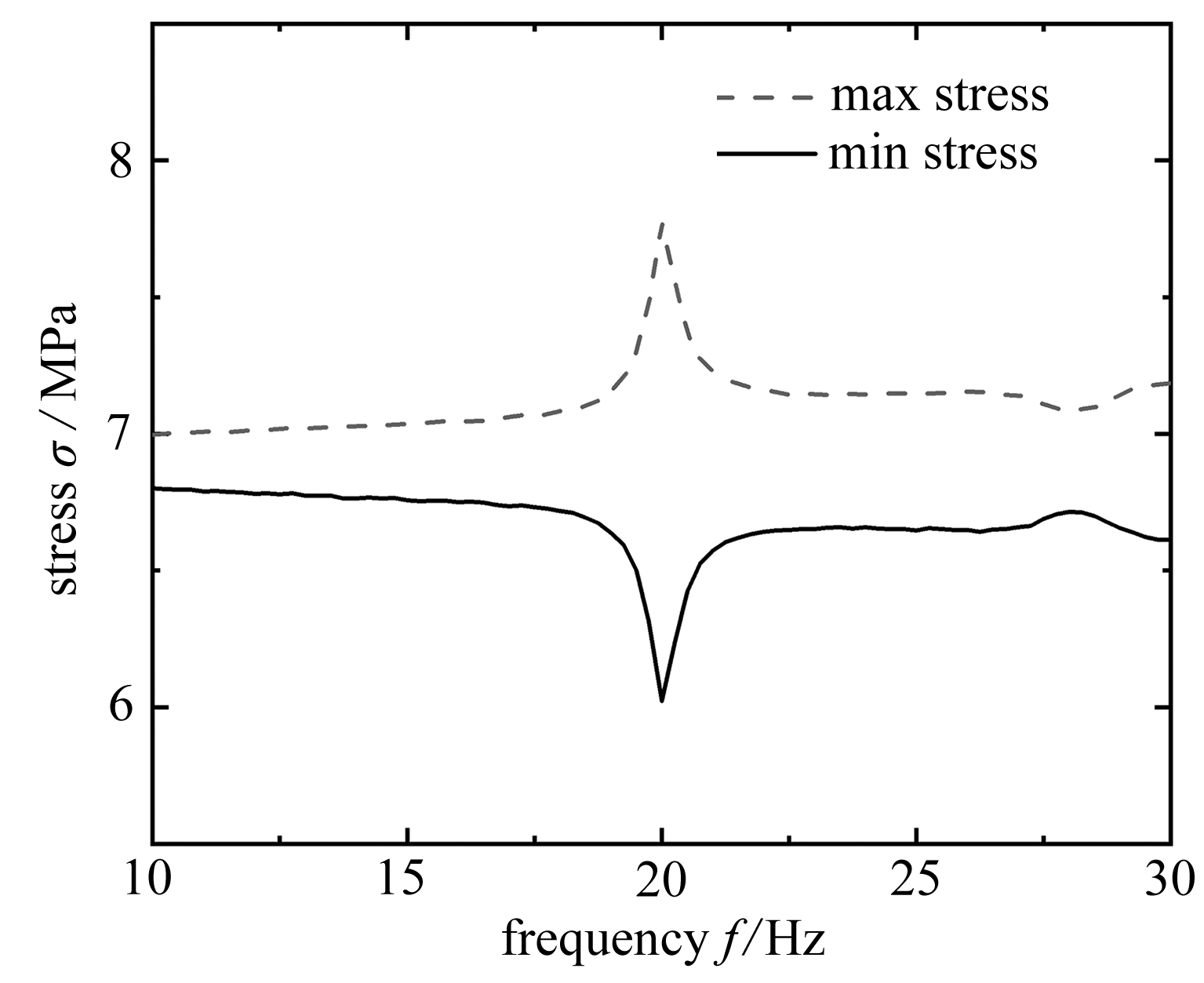
图4 GMM的最大和最小应力
Fig. 4 The maximum and minimum stresses of GMM
计算一阶固有频率前后、15~25 Hz范围内GMM能量采集器采集到的最大电压和最大电功率,如图5所示.
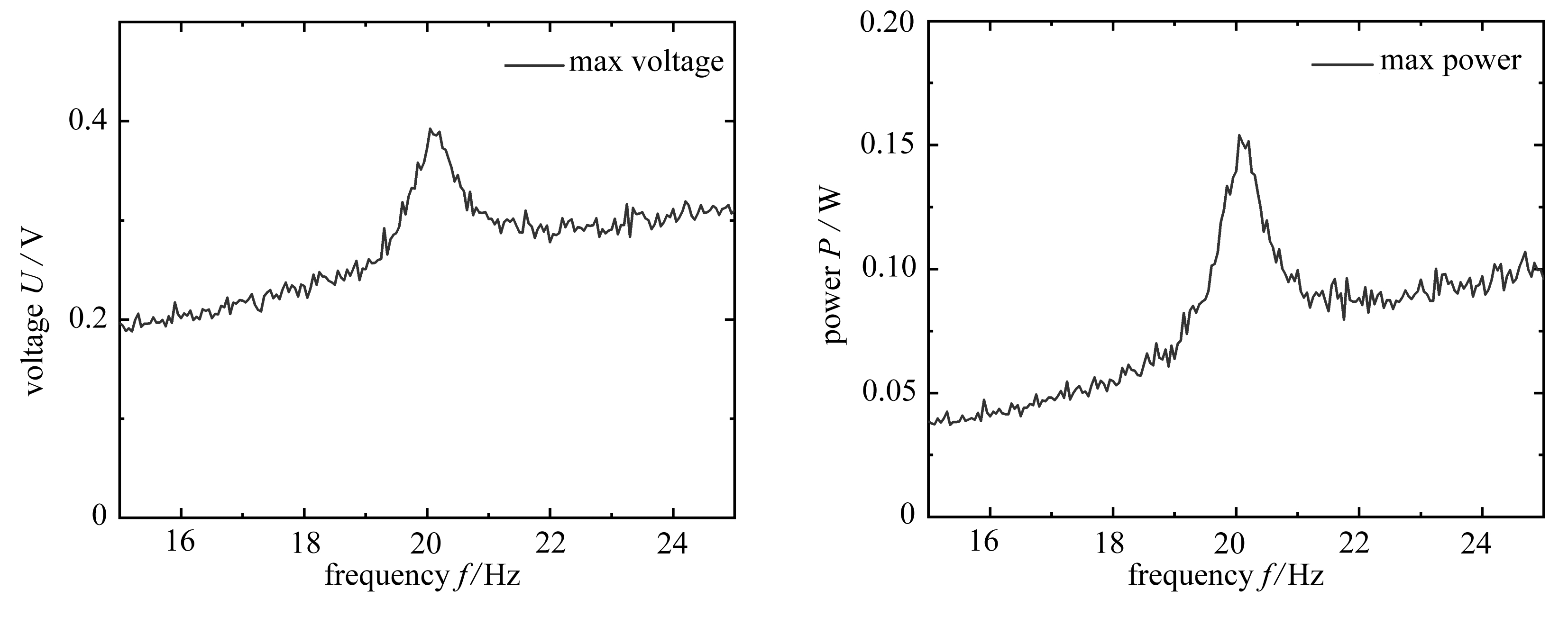
(a) GMM的最大电压 (b) GMM的最大电功率
(a) The maximum voltage of GMM (b) The maximum electrical power of GMM
图5 GMM的最大电压和最大电功率
Fig. 5 The maximum voltage and maximum electrical power of GMM
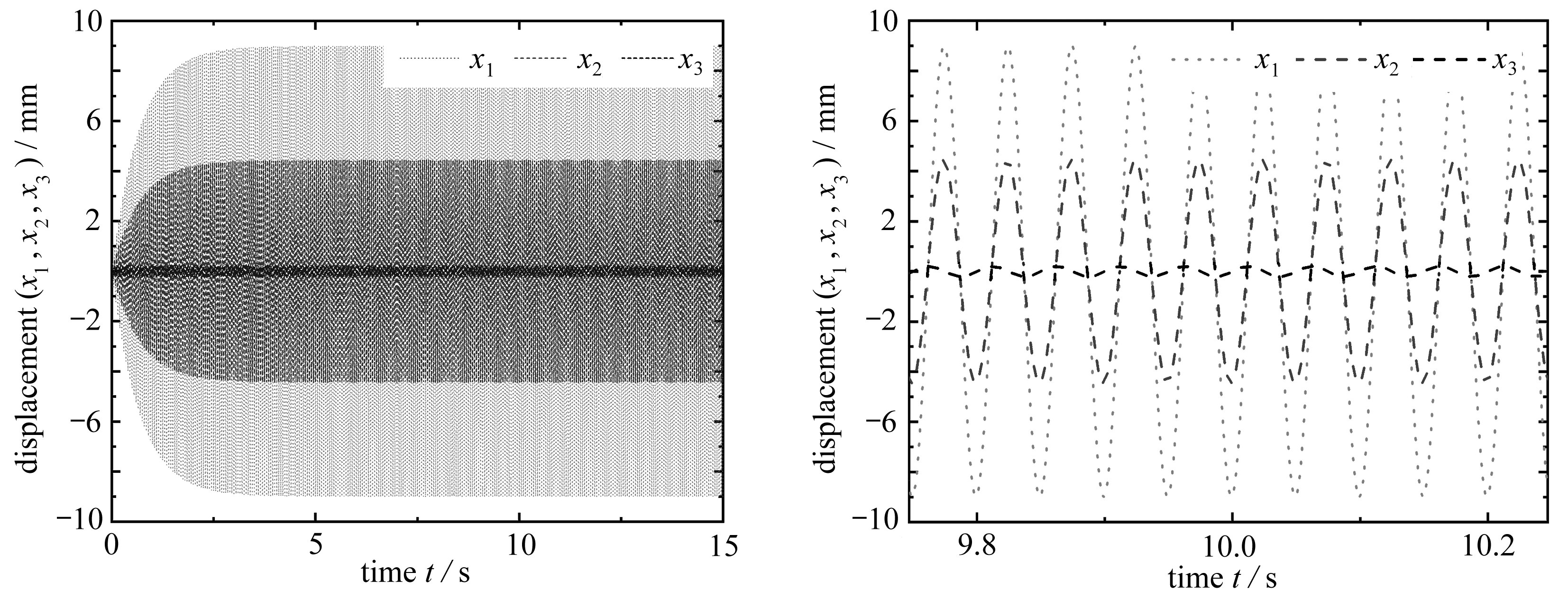
图6 20 Hz时x1,x2,x3的时域响应
Fig. 6 The time-domain responses of x1,x2,x3 at 20 Hz
从图5看出,在给定频率范围内,GMM在共振频率处采集到的电压最大,约为0.4 V,同时产生最大电功率,约为0.15 W.
考虑到系统在一阶共振频率处(约20 Hz)的振幅最大,能量采集效果也最好,所以考察系统在20 Hz频率下具体的时域表现,如图6、7所示.
从图6的x1,x2,x3时域响应可以看出系统中3个自由度振动的细节:主系统的两个自由度x1,x2的响应趋势一致,x2振幅大约是x1的一半,NES下端自由度x3的振幅相比主系统两个自由度较小,且在相位上x3领先主系统的两个自由度四分之一个周期.
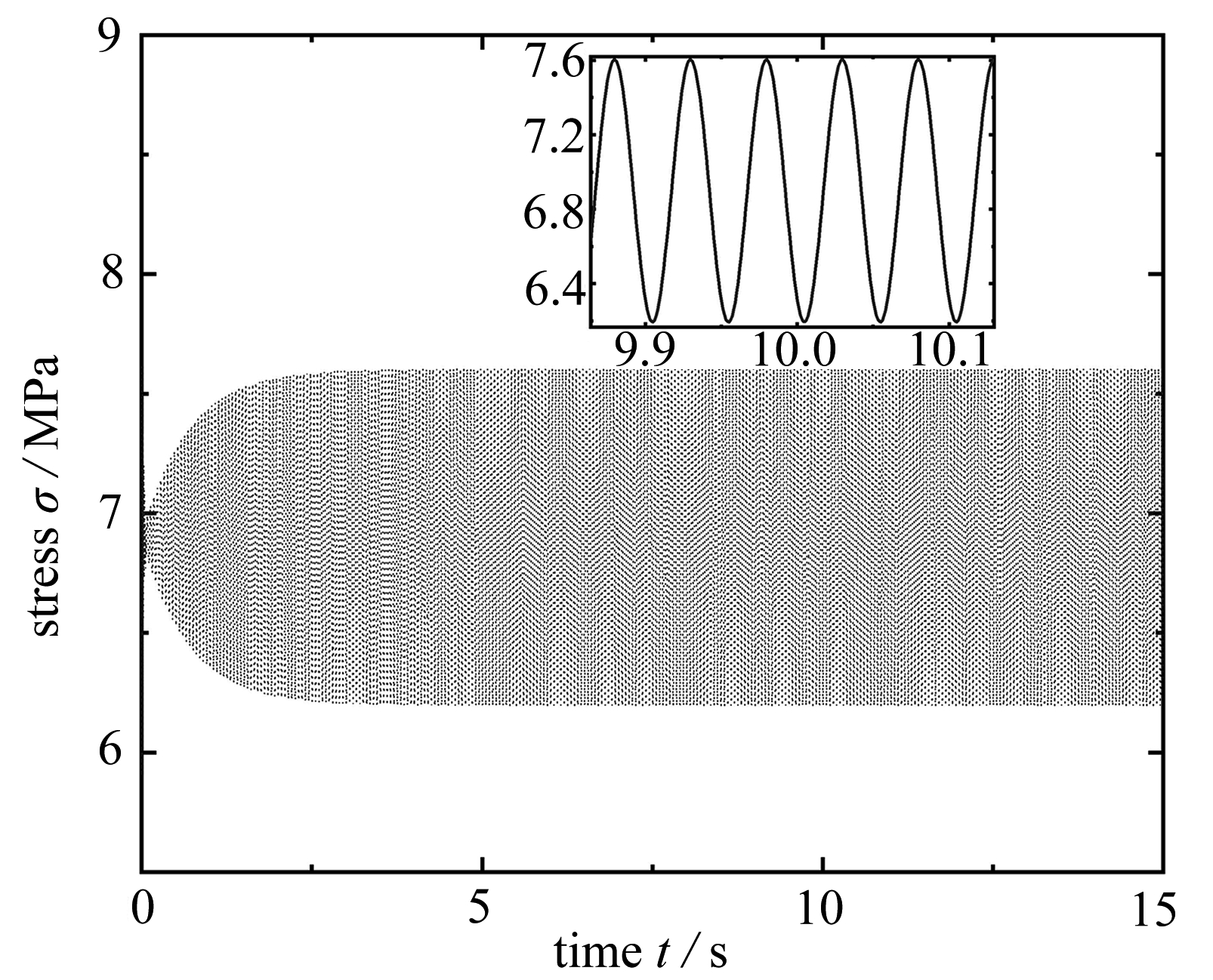
(a) 瞬时应力
(a) The instantaneous stress
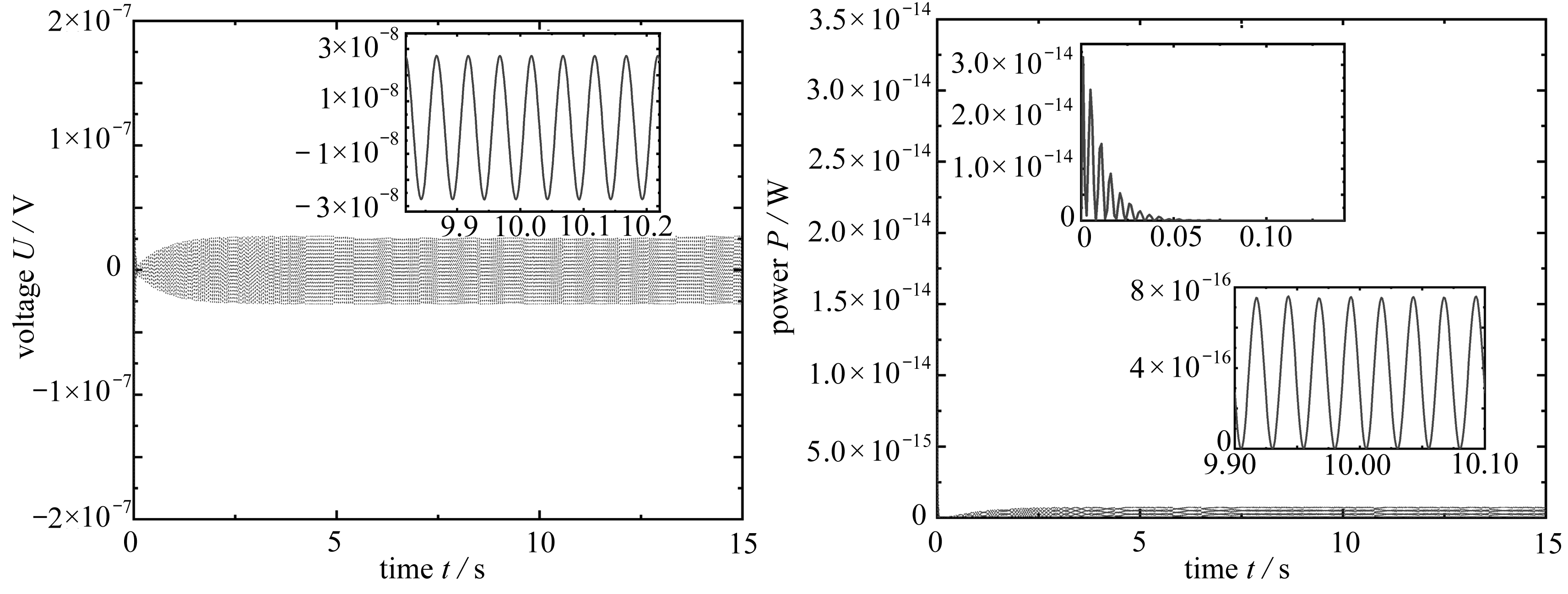
(b) 瞬时电压 (c) 瞬时电功率
(b) The instantaneous voltage(c) The instantaneous electrical power
图7 20 Hz时GMM的应力、电压和电功率
Fig. 7 The stress, voltage and electrical power of GMM at 20 Hz
从图7可以看出,在共振频率处GMM上的应力、电压和电功率均在初始阶段启动时会产生一个峰值,随后迅速减小,然后再从小逐渐增大,最后稳态呈简谐波形态,且最后稳态的振幅小于初始时的最大值.系统进入稳态响应后,对瞬时电功率进行积分,可以得到GMM采集到的能量,进而还可以得到GMM的平均电功率等.下面列出了系统中各部分能量的表达式.
式(8)给出了主系统的能量Epr(t)的表达式:
Epr(t)=T1(t)+T2(t)+V1(t)+V2(t)+Wc1(t)+Wc2(t)=
(8)
其中T1(t)和T2(t)分别代表质量块m1,m2的动能,V1(t)和V2(t)分别代表弹簧k1,k2的弹性势能,Wc1(t)和Wc2(t)分别代表阻尼c1,c2耗散的能量.
式(9)给出了NES的能量ENES(t)的表达式:
ENES(t)=V3(t)+Wc3(t)=
(9)
其中V3(t)代表非线性弹簧的弹性势能,Wc3(t)代表NES阻尼c3耗散的能量.值得注意的是,由于用惯容器取代了NES的质量元件,所以NES的能量中没有动能.
式(10)给出了惯容器的能量Einerter(t)的表达式,由于不同惯容器的结构不同,零件更是千差万别,所以想要直接计算出惯容器的能量十分困难,这里采用机械能守恒的思想,式中Fb表示惯容器两端受到的力的大小,通过分析系统动力学方程组可得力Fb的表达式,根据做功公式W=FS并积分可得惯容器两端外力对惯容器所做的功——在理想状况下即为惯容器的能量:
Einerter(t)=![]() Fb(x3-x2)dτ=
Fb(x3-x2)dτ=
(10)
式(11)~(13)给出了GMM能量采集器中的能量:
(11)
(12)
(13)
其中Eh(t)代表GMM采集到的电能,Em(t)代表瞬时磁场能,Es(t)代表瞬时应变能,这里
式(14)给出了系统总输入能量Ein(t)的表达式,由能量守恒定律推导得到
Ein(t)=Epr(t)+ENES(t)+Einerter(t)+Eh(t)+Em(t)+Es(t).
(14)
由于采集到的能量与激励形式和幅值直接相关,所以考察能量传递和回收的比例更有实际意义,式(15)给出了计算系统各部分能量占比的表达式:
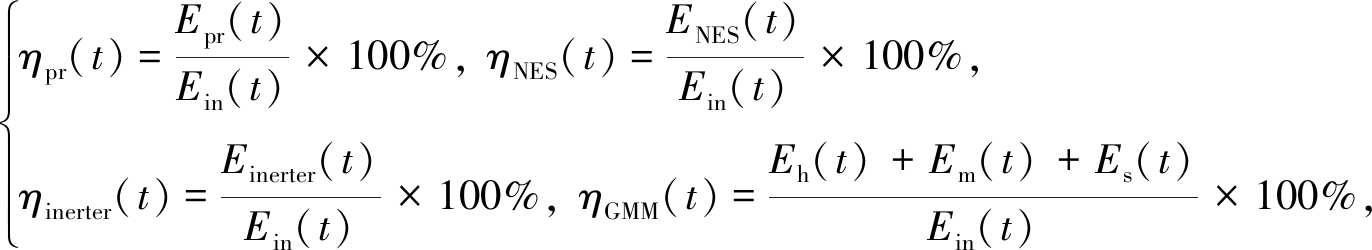
(15)
其中ηpr(t),ηNES(t),ηinerter(t)和ηGMM(t)分别代表主系统能量占比、NES能量占比、惯容器能量占比和GMM能量占比,计算结果如图8所示.
从图8可以看出,在振动开始时,能量100%集中在GMM能量采集器中,采集的能量比例极高,这也与图7中振动开始时采集到的大电压和大功率相印证,之后能量迅速转移进主系统和NES中,达到稳定响应阶段后,主系统中能量约占全部能量的87%,NES中能量约占全部能量的13%,GMM的能量约占全部能量的0.1%,惯容器中的能量一直很小,说明惯容器基本没有储能作用,输入惯容器的能量又几乎全部从惯容器流出.
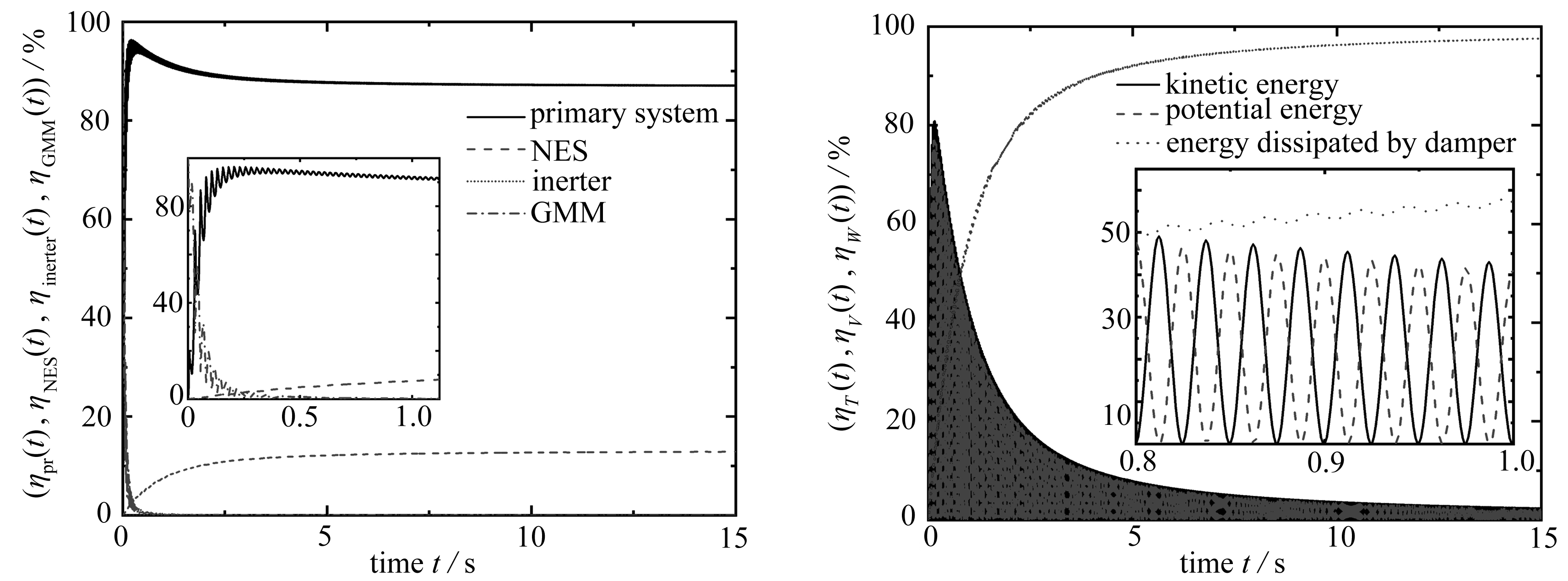
图8 系统各部分能量占比 图9 系统主要的能量转换过程
Fig. 8 Energy ratios of the system Fig. 9 The main energy conversion process of the system
进一步分析系统主要的能量转换过程,按照式(16)分别计算系统中的动能、势能和阻尼耗散掉的能量分别占总能量的比例,它们随时间变化的情况如图9所示.
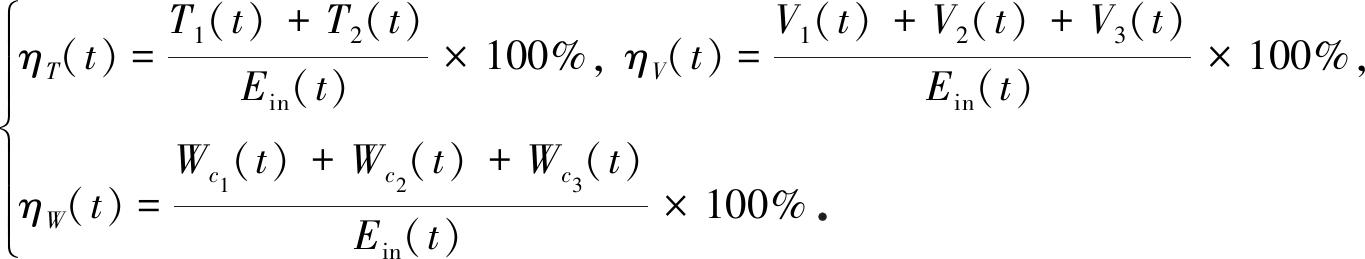
(16)
从图9可以看出,系统中动能和势能所占总能量的比例在振动开始时从0%跃升到约80%,随后呈下降趋势,最终保持在一个较小的比例;振动开始时,阻尼耗散的能量占比很小,随后阻尼耗散的能量占比快速提高,并在进入稳态响应阶段后占到系统能量的大部分,这说明系统中大部分的能量最终被阻尼耗散掉.
5 结 论
1) 本文设计并考察了一种NES-I-GMM减振和能量采集一体化装置,将本文的减振装置与以往文献中的NES减振装置的减振效果进行对比可以得知,本文中以并联方式连接的惯容器可以替代传统NES装置中的惯性元件,同样能够起到减振作用.
2) 通过参数分析得知,NES减振效果受NES的阻尼和惯容器惯质系数影响明显,优化各项参数可以达到更好的减振效果.NES减振能力受NES阻尼影响比较明显,大阻尼有着比小阻尼更好的减振效果.NES减振能力也受惯容器惯质系数的影响,与NES并联的惯容器的惯质系数减小时,系统的振幅略微减小,同时系统固有频率亦受惯质系数影响,惯质系数增大时,系统固有频率略微减小.所以并联使用惯容器可以调节系统的固有频率.值得指出的是,惯容器的惯质系数与惯容器的结构有关,与惯容器的自身质量没有必然关系,所以可以考虑设计并选用合适惯容器,以达到所需要的惯质系数.
3) 通过能量分析发现,本文所设计NES-I-GMM装置中的能量采集器能够实现稳定的振动能量的回收和利用,采集能量的比例在振动开始时的比例很高,在激励发生的短时间内能够采集到可观的电压和功率.本文所设计装置的实际工程背景是在轨运行的卫星,对于在太空中很难获得外界能源的卫星或其他航天器,回收的振动能量有望为航天器的传感器等低能耗元件供电,若进一步优化GMM能量采集器的参数,有望进一步提高能量采集的效率,整星减振和能量采集一体化装置具有良好的发展前景.
[1] GENDELMAN O, MANEVITCH L I, VAKAKIS A F, et al. Energy pumping in nonlinear mechanical oscillators, part Ⅰ: dynamics of the underlying Hamiltonian systems[J]. Journal of Applied Mechanics, 2001, 68: 34-41.
[2] VAKAKIS A F, GENDELMAN O. Energy pumping in nonlinear mechanical oscillators, part Ⅱ: resonance capture[J]. Journal of Applied Mechanics, 2000, 68: 42-48.
[3] 熊怀, 孔宪仁, 刘源. 阻尼对耦合非线性能量阱系统影响研究[J]. 振动与冲击, 2015, 34(11): 116-121.(XIONG Huai, KONG Xianren, LIU Yuan. Influence of structural damping on a system with nonlinear energy sinks[J]. Journal of Vibration and Shock, 2015, 34(11): 116-121.(in Chinese))
[4] 熊怀, 孔宪仁, 刘源. 一类立方非线性吸振器的能量传递和耗散研究及参数设计[J]. 振动工程学报, 2015, 28(5): 785-792.(XIONG Huai, KONG Xianren, LIU Yuan. Energy transfer and dissipation of a class of nonlinear absorber and its parameter design[J]. Journal of Vibration Engineering, 2015, 28(5): 785-792.(in Chinese))
[5] 李继伟, 丁旺才, 李国芳. 多自由度非线性吸振器的连接方式及吸振效果[J]. 兰州交通大学学报, 2017, 36(1): 96-101. (LI Jiwei, DING Wangcai, LI Guofang. Connection and performance of a vibration system with multi-degree of freedom nonlinear energy sink[J]. Journal of Lanzhou Jiaotong University, 2017, 36(1): 96-101. (in Chinese))
[6] 孙敏, 陈建恩, 陈焕林. 并联和串联非线性能量阱的吸振效能对比研究[J]. 哈尔滨工程大学学报, 2018, 39(10): 1727-1732. (SUN Min, CHEN Jian’en, CHEN Huanlin. Comparison on vibration absorption efficiency of parallel and series nonlinear energy sinks[J]. Journal of Harbin Engineering University, 2018, 39(10): 1727-1732.(in Chinese))
[7] 王菁菁, 浩文明, 吕西林. 轨道非线性能量阱阻尼对其减振性能的影响[J]. 振动与冲击, 2017, 36(24): 30-34.(WANG Jingjing, HAO Wenming, LÜ Xilin. Influence of track nonlinear energy sink damping on its vibration reduction performance[J]. Journal of Vibration and Shock, 2017, 36(24): 30-34.(in Chinese))
[8] 刘中坡, 吕西林, 王栋, 等. 非线性能量阱刚度优化计算与振动台试验[J]. 振动与冲击, 2017, 36(7): 26-33.(LIU Zhongpo, LÜ Xilin, WANG Dong, et al. Stiffness optimization and shaking table tests for nonlinear energy sink[J]. Journal of Vibration and Shock, 2017, 36(7): 26-33. (in Chinese))
[9] 孙斌, 吴志强. 基于非线性能量阱的双频激励非线性系统减振[J]. 应用数学和力学, 2017, 38(11): 1240-1250.(SUN Bin, WU Zhiqiang. Vibration suppression of nonlinear systems under dual-frequency excitations with nonlinear energy sink[J]. Applied Mathematics and Mechanics, 2017, 38(11): 1240-1250.(in Chinese))
[10] YANG K, ZHANG Y W, DING H, et al. Nonlinear energy sink for whole-spacecraft vibration reduction[J]. Journal of Vibration and Acoustics, 2017, 139(2): 021011. DOI: 10.1115/1.4035377.
[11] SMITH M C. Synthesis of mechanical networks: the inerter[J]. IEEE Transactions on Automatic Control, 2002, 47(10): 1648-1662.
[12] SALVI J, GIARALIS A. Concept study of a novel energy harvesting-enabled tuned mass-damper-inerter(EH-TMDI) device for vibration control of harmonically-excited structures[J]. Journal of Physics: Conference Series, 2016, 744(1): 012082. DOI: 10.1088/1742-6596/744/1/012082.
[13] LUO Y F, SUN H X, WANG X Y, et al. Wind induced vibration control and energy harvesting of electromagnetic resonant shunt tuned mass-damper-inerter for building structures[J]. Shock and Vibration, 2017: 4180134. DOI: 10.1155/2017/4180134.
[14] 刘彦. 基于惯容器的机械振动被动控制系统传递特性分析[J]. 中国舰船研究, 2016, 11(1): 108-113, 120.(LIU Yan. Analysis of the transmission characteristics of mechanical passive control systems with the inerter[J]. Chinese Journal of Ship Research, 2016, 11(1): 108-113, 120.(in Chinese))
[15] 毛明, 王乐, 陈轶杰, 等. 惯容器及惯容器-弹簧-阻尼器悬架研究进展[J]. 兵工学报, 2016, 37(3): 525-534.(MAO Ming, WANG Le, CHEN Yijie, et al. Research progress in inerter and inerter-spring-damper suspension[J]. Acta Armamentarii, 2016, 37(3): 525-534.(in Chinese))
[16] 杨晓峰, 杜毅, 刘雁玲, 等. 惯质系数对车辆ISD悬架系统频率特性的影响研究[J]. 振动与冲击, 2018, 37(7): 240-246.(YANG Xiaofeng, DU Yi, LIU Yanling, et al. Influences of inertial mass coefficient on frequency characteristics of ISD suspension systems[J]. Journal of Vibration and Shock, 2018, 37(7): 240-246.(in Chinese))
[17] ZHANG Y W, LU Y N, ZHANG W, et al. Nonlinear energy sink with inerter[J]. Mechanical Systems and Signal Processing, 2018, 125: 52-64.
[18] 刘蕊, 吴子英, 叶文腾. 附加非线性振子的双稳态电磁式振动能量捕获器动力学特性研究[J]. 应用数学和力学, 2017, 38(4): 432-446.(LIU Rui, WU Ziying, YE Wenteng. Dynamics research of bistable electromagnetic energy harvesters with auxiliary nonlinear oscillators[J]. Applied Mathematics and Mechanics, 2017, 38(4): 432-446.(in Chinese))
[19] FANG Z W, ZHANG Y W, LI X, et al. Integration of a nonlinear energy sink and a giant magnetostrictive energy harvester[J]. Journal of Sound and Vibration, 2017, 391: 35-49.
[20] LI X, ZHANG Y W, DING H, et al. Integration of a nonlinear energy sink and a piezoelectric energy harvester[J]. Applied Mathematics and Mechanics(English Edition), 2017, 38(7): 1019-1030.
[21] 昝浩, 温华兵, 范紫岩. 含惯容器的多层隔振系统动态性能研究[J]. 江苏科技大学学报(自然科学版), 2015, 29(2): 131-137.(ZAN Hao, WEN Huabing, FAN Ziyan. Study of dynamic property of multi stage vibration isolation system with inerter[J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition), 2015, 29(2): 131-137.(in Chinese))
[22] 陈龙, 杨晓峰, 汪若尘, 等. 改进的ISD三元件车辆被动悬架性能的研究[J]. 汽车工程, 2014, 36(3): 340-345.(CHEN Long, YANG Xiaofeng, WANG Ruochen, et al. A study on the performances of vehicle passive suspension with modified inerter-spring-damper three-element structure[J]. Automotive Engineering, 2014, 36(3): 340-345.(in Chinese))
[23] ZANG J, ZHANG Y W, DING H, et al. The evaluation of a nonlinear energy sink absorber based on the transmissibility[J]. Mechanical Systems and Signal Processing, 2018, 125: 99-122.