引 言
自1981年Carne开始研究集中阻尼弦的振动以来,集中阻尼弦本征解的性质就受到了持续关注[1-3].这些研究主要考虑阻尼位于弦端附近的情况,通过数值手段求取近似解,在处理工程索结构的振动问题上取得了显著成效[3-6].
在各种激励下,索结构易产生大幅振动,因此,工程索结构常采用阻尼器进行减振[7-8].通过引入若干假设,索结构与阻尼器构成的系统可简化为带有集中阻尼的弦[5,9].弦是连续系统,与弦相连的集中阻尼则是离散系统.连续弦和离散阻尼相结合,构成了同时包含连续子系统和离散子系统的混合动力学系统,其本征解的性质是其动力学的基本问题.
在解析求解方面,2002年,美国霍普金斯大学的Main等将集中阻尼弦在阻尼处进行分段,各段分列方程,然后在分段处(即阻尼位置)引入位移协调条件,求解了单集中阻尼弦的本征问题[6].对于多个集中阻尼的一般情况,由于各分段处均需引入位移协调条件,这种做法在数学处理上会变得较为困难和繁琐.本文通过引入Dirac δ函数,对集中阻尼弦的动力学方程在其全域进行统一列式,求解了一般集中阻尼弦在两端固支条件下的本征问题,并对单集中阻尼弦本征解的性质进行了讨论.
1 集中阻尼弦的本征解
含任意有限n项集中线性黏性阻尼的张紧弦系统如图1所示.该张紧弦具有单位长度l、单位分布质量密度m和单位张力T,其位置坐标、时间、挠曲函数、第i项阻尼和该阻尼的位置坐标分别用x,t,w(x,t),ci和xi表示,i=1,2,…,n.
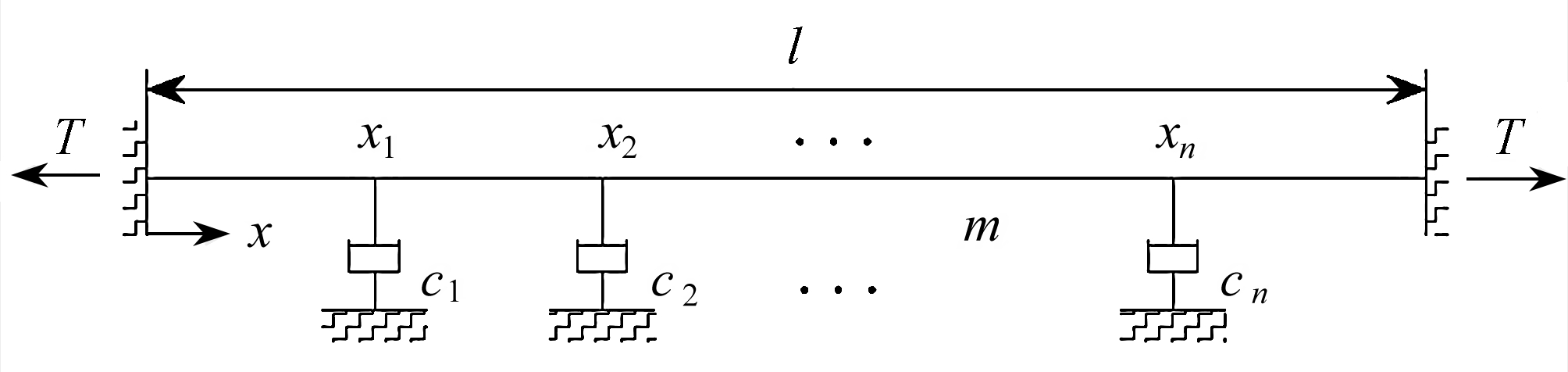
图1 含n项黏性阻尼的张紧弦
Fig. 1 A taut string with n concentrated viscous damping dashpots
1.1 动力学平衡方程与分离变量
通过引入Dirac δ函数,图1所示混合系统的动力学平衡方程可在其全域统一表示为
(1)
设φ(x)为w(x,t)的本征函数,采用分离变量法,由式(1)可得如下的常微分方程:
(2)
1.2 加权和函数形式的本征函数
本征函数φ(x)的非齐次常微分方程(2)的右端项为Dirac δ函数的加权和函数形式,故φ(x)可设为Green函数Gi(x; xi,ci,p)的加权和函数形式,即
(3)
式(3)中,Gi(x;xi,ci,p)是以x为自变量,带有xi,ci和p三个参数的Green函数,可简写为Gicp(x).参数p是系统的本征值;φ(xi)是本征函数φ(x)在第i项阻尼位置处的函数值.所有的φ(xi)构成一个n维向量,可称其为系统的本征向量,用φ表示.一般地,Green函数Gicp(x)应满足如下非齐次常微分方程:
-G″icp(x)+p2Gicp(x)=ciδ(x-xi).
(4)
对式(4)进行Laplace变换,再进行Laplace逆变换,得
(5)
式中,i=1,2,…,n,Gicp(0)和G′icp(0) 由边界条件确定, μ(x-xi)为单位阶跃函数,即
(6)
1.3 位移协调条件、本征方程组与频率方程
由式(3),在阻尼位置xr(r=1,2,…,n)处,有位移协调条件:
(7)
式(7)即为本征方程组,可进一步简化.利用Kronecker符号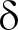 ir将式(7)左端写为求和形式,右端的Gicp(xr)简写为Gircp,得
ir将式(7)左端写为求和形式,右端的Gicp(xr)简写为Gircp,得
(8)
将式(8)右端项移到左端,整理得
(9)
式(9)即为系统的本征方程组,r=1,2,…,n,共n个方程,其矩阵形式为
(I+H)φ=0.
(10)
式(10)中,I为n阶单位矩阵,列向量φ为本征向量,矩阵H和本征值p均与Green函数在阻尼位置处的取值Gircp有关,i, r=1,2,…,n,H由下式定义:
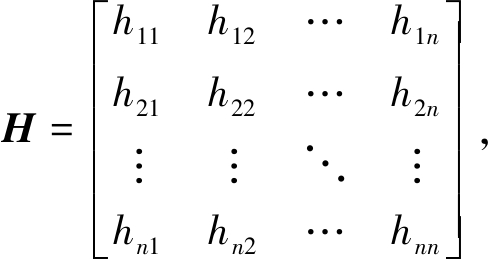
(11a)
hir=pGircp.
(11b)
式(10)有非平凡解的条件是其系数矩阵I+H的行列式为0,即
det(I+H)=0.
(12)
式(12)是关于本征值p的超越方程.
一般地,本征值p可由超越方程(12)通过数值算法解得.因本征值p的虚部为系统的圆频率,也称式(12)为系统的频率方程.由式(12)解得系统的任意一阶本征值p后,式(10)就变为代数方程组,可由其解得对应的本征向量φp.
2 单集中阻尼弦的本征解
上一节已导出了一般集中阻尼弦的本征方程组、频率方程和求解方法.本节将对其进一步化简,以具体求得仅设置一个集中阻尼器的单集中阻尼弦的本征解为例,并讨论其性质.当阻尼仅有1项时,式(2)、式(3)和式(12)分别简化为
-φ″(x)+p2φ(x)=-pφ(x)cδ(x-x1),
(13)
φ(x)=-pG1cp(x)φ(x1),
(14)
1+pG1cp(x1)=0.
(15)
上述三式依次为单集中阻尼弦系统本征函数的常微分方程、本征函数的一般表达式和频率方程.
2.1 边界条件与Green函数的待定系数
本征函数的一般表达式(14)中Green函数G1cp(x) 的一般形式为式(5),其中含有两个待定常数G1cp(0)和G′1cp(0),需由边界条件给定.设边界条件为弦在左右两端位移均为0,可解得
G1cp(0)=0,
(16)
G′1cp(0)=c1sinh(p(1-x1))/sinh p.
(17)
Green函数G1cp(x) 的两个待定常数G1cp(0)和G′1cp(0)已由式(16)和式(17)确定,将两者代入Green函数的一般表达式(5),得
(18)
式(18)即为零边界条件单集中阻尼弦系统的Green函数.
2.2 频率方程
令Green函数式(18)在x=x1处取值,此时sinh(p(x-x1))为0,则该式右端第2项为0,式(18)变为
(19)
将式(19)代入式(15),当c1不为0时,可得单集中阻尼弦频率方程的一般形式为
(20)
对任意的x1>0和c1>0,式(20)中的本征值p一般可用数值方法解得具体数值.
2.3 本征向量与和本征函数
注意到单集中阻尼弦只有一项阻尼,因此,系统的本征向量(即本征函数在阻尼位置处的取值)只有一个元素.对于该元素的取值,如阻尼位置不是本征函数的驻点,则可取1,即φ =[φ1]=[1];如阻尼位置是本征函数的驻点,则该元素值必为0,即φ =[φ1]=[0].
此处先讨论阻尼位置不是本征函数的驻点,即φ =[φ1]=[1]的情况,对于阻尼位置是本征函数驻点的情况,则将在本文第4节中讨论.由于φ1=1,将式(18)代入式(14),可得带有参数p的本征函数φ(x)的具体形式为
(21)
3 中点集中阻尼弦本征解的性质
频率方程式(20)为超越方程,其阻尼位置坐标x1可在0(弦左端)和1(弦右端)之间的任意点取值.因此,对于阻尼位置的一般情况,由频率方程求解本征值p仍需要采用数值解法.但当阻尼位于某些特殊位置时,例如阻尼位于弦中点,即x1=1/2的情况,则可由频率方程解得本征值p的显式解.以下对此做进一步讨论.
3.1 本征值
将x1=1/2代入频率方程(20),该式简化为
tanh(p/2)=-2/c1.
(22)
由式(22)解得
(23)
式(23)即为中点集中阻尼弦本征值的解析解,其右端项需取对数,因此,本征值p一般应采用复数形式表示,即p=σ+jω,j为虚数单位.
3.2 本征函数
将x1=1/2代入本征函数式(21),得
(24)
由于本征函数乘以非零常数仍为本征函数, 故上式中c1可约去, 并可表示为分段函数的形式:
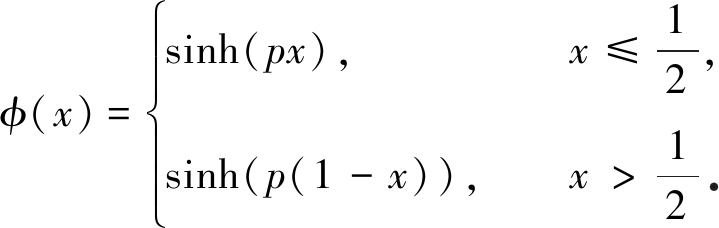
(25)
由式(25)易知,本征函数φ(x)关于弦中点对称.因此,除特别说明外,下文讨论相关问题时,只考虑x≤1/2的部分.将本征值的复数形式p=σ +jω代入式(25)右端,得
φ(x)=sinh(σx)cos(ωx)+jcosh(σx)sin(ωx).
(26)
式(26)给出了中点集中阻尼弦在零边界条件下本征函数的一般表达式(根据对称性,只考虑x≤1/2的部分).
3.3 本征值与本征函数的性质
当阻尼c1取值不同时,本征值p、本征函数φ(x)及系统运动的特性都将随之变化,以下分为大阻尼、适中阻尼和特征阻尼3种情况进行讨论.
3.3.1 大阻尼(c1>2)
阻尼c1>2时,由本征值与阻尼的关系式(23)得
pk=ln|(c1-2)/(c1+2)|+j·2sπ, s=0,±1,±2,….
(27)
式(27)中,本征值阶次k由整数s确定,当s≤0时,k=2|s|,当s>0时,k=2s-1.
由式(27)得本征值pk的实部和虚部分别为
σ=ln|(c1-2)/(c1+2)|,
(28)
ωk=2sπ, s=0,±1,±2,±3,….
(29)
由式(27)和后文式(34a)知,当c1>0且c1≠2时,均有σ < 0,可绘出衰减率-σ随系统阻尼c1的变化情况,如图2所示.
1) 频率
由式(29)可知,阻尼c1>2时,系统存在虚部为0的本征值p0,此时p0=σ,系统的频率为0,表明系统的0阶运动无震荡特性.
除0阶外,系统还有1阶及以上无穷多阶本征值,即这些本征值的虚部ω为2sπ,s=±1, ±2, ±3,…,系统的频率为|s|.注意到,c1>2时,由式(29)可以看出:系统频率与其阻尼无关,这是该混合系统区别于一般的离散系统或连续系统的一个独特性质,可称为性质Ⅰ.
2) 衰减率
从式(28)可以看出,当c1>2时,包括0阶在内的系统各阶本征值的实部均相等,表明所有各阶运动均具有相同的衰减率,即均为-σ.衰减率与本征值的阶次无关,这是该混合系统区别于一般的离散系统或连续系统的又一个独特性质,可称为性质Ⅱ.
特别地,令式(28)中c1趋于+∞,得
(30)
此时,衰减率-σ趋于无穷小.注意到,由于衰减率趋于无穷小,表明此时系统趋于无阻尼运动.
3) 本征函数
阻尼c1>2时,本征函数的一个显著特点在于具有非震荡的0阶本征函数,记为φ0(x),且φ0(x)为实函数.由于0阶本征值的虚部ω为0,由式(26)可得0阶本征函数为
φ0(x)=sinh(σx).
(31)
由式(31)可知,0阶本征函数φ0(x)为实双曲正弦函数.
特别地,当c1趋于+∞时,σ趋于负无穷小(0-).令本征函数一般表达式(26)中的σ趋于负无穷小,得
σxcos(ωkx)+jsin(ωkx).
(32)
注意到式(32)中ωk取值为2sπ,于是由式(32)可知,本征函数实部接近于σxcos(2sπx),为一阶无穷小量;虚部接近于函数sin(2sπx).实部与虚部相比,一般为一阶无穷小量,但0阶本征函数则是一个例外:由式(31)可知,0阶本征函数φ0(x)趋于σx,仍为一阶无穷小量,但其虚部严格为0.
图3绘出了不同阻尼下0阶本征函数φ0(x)的图形(其中x>1/2的部分由图形关于x=1/2的对称性作出,图中本征函数已利用中点函数值进行了归一化处理).从图3可以看出,随着阻尼增大,0阶本征函数φ0(x)的形状逐渐接近于函数σx;随着阻尼趋近于2,本征函数在弦中点以外的位置迅速衰减为0.
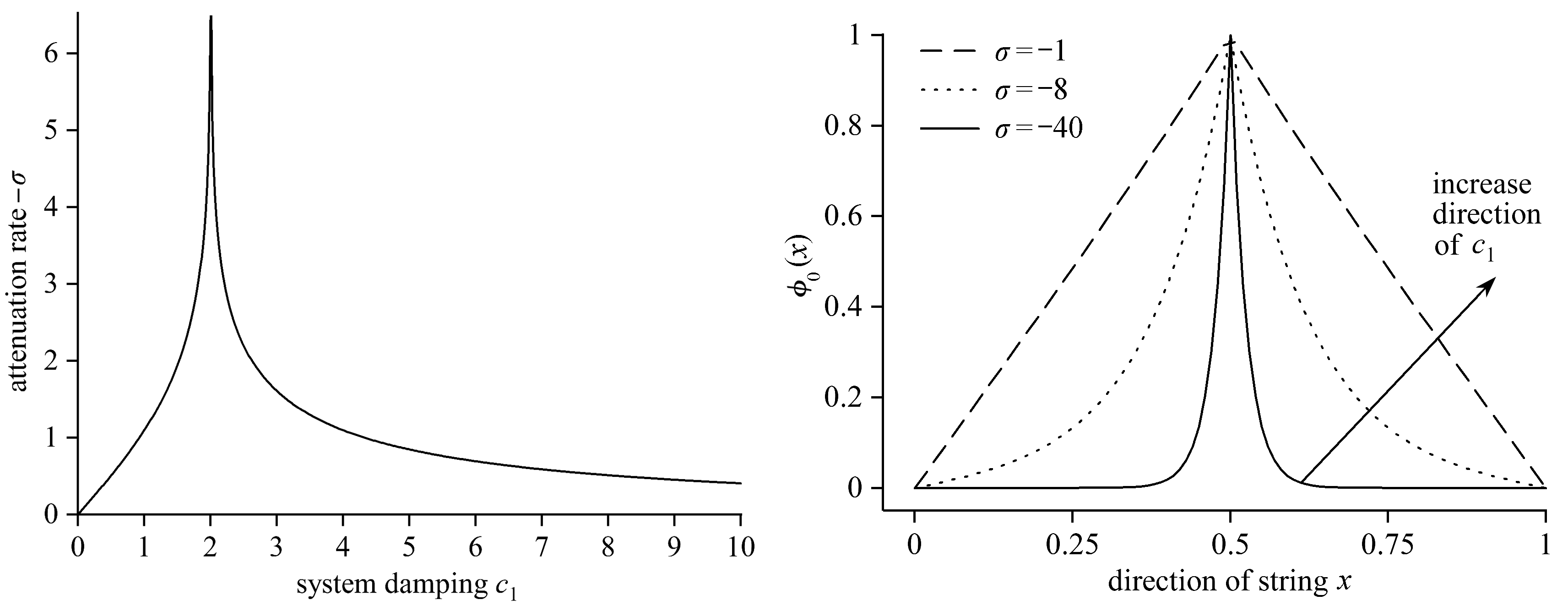
图2 衰减率-σ随系统阻尼c1变化 图3 当c1>2时系统的0阶本征函数
Fig. 2 Variation of attenuation rate σ with Fig. 3 The 0th order eigenfunction of the system damping c1 system for c1>2
图4(a)~4(c)分别给出了1阶本征函数φ1(x)及不同阻尼下φ1(x) 的实部和虚部的图形(x>1/2的部分由关于x=1/2的对称性做出,φ1(x)的实部和虚部均由其峰值进行了归一化处理).
从图4(b)~4(c)可以看出,随着阻尼从2开始增大,1阶本征函数φ1(x)的实部形状逐渐接近于-xcos(2πx),虚部形状接近于sin(2πx).
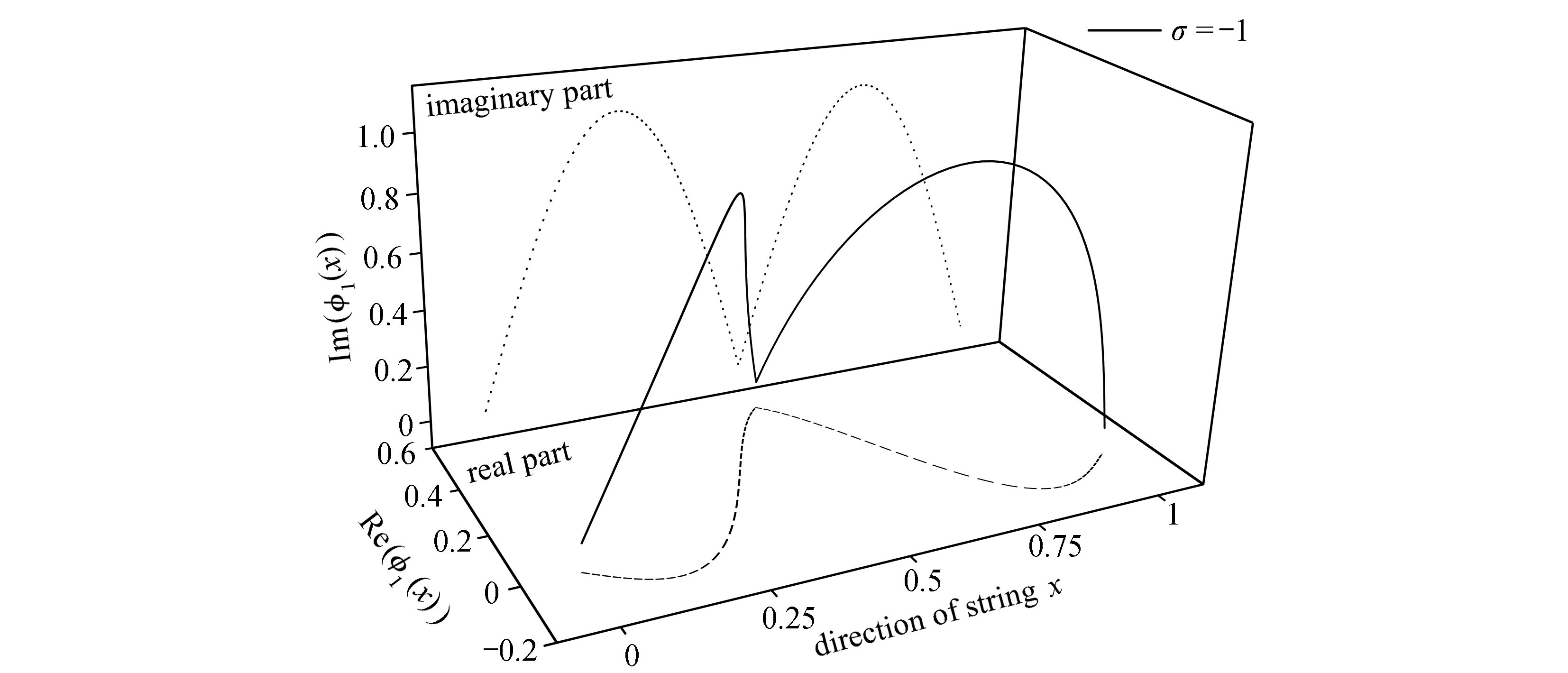
(a) 本征函数的空间曲线及其实部、虚部投影
(a) The space curve of the eigenfunction and its real part and imaginary part projections
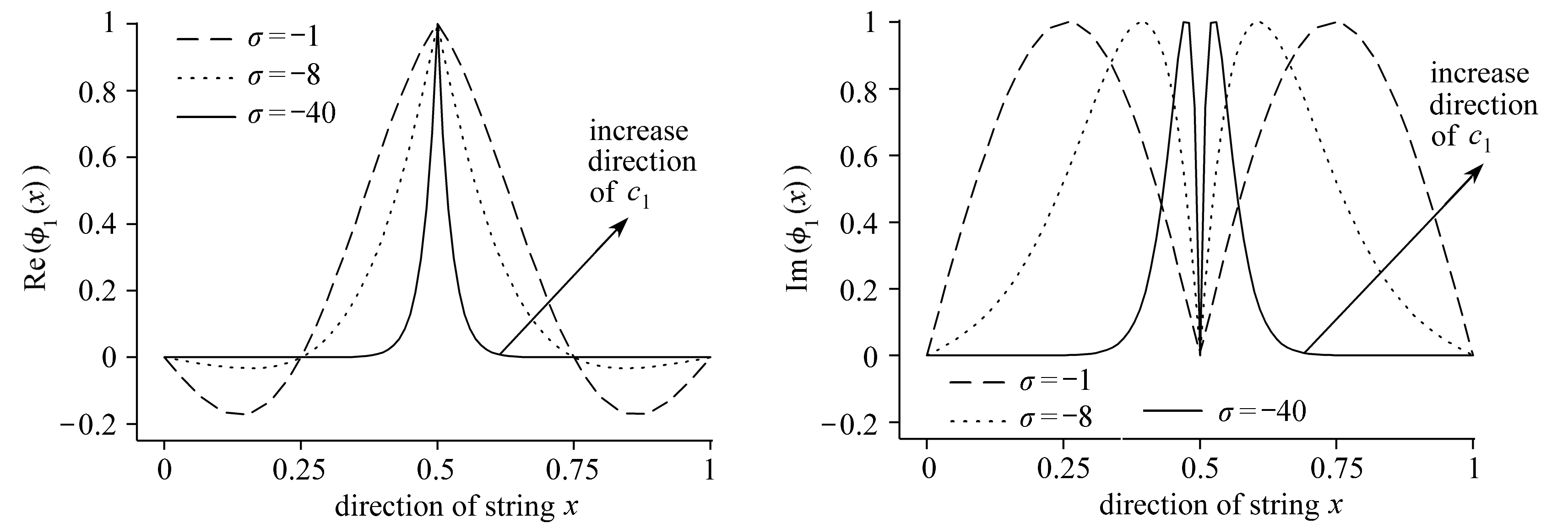
(b) 实部形状随c1变化 (c) 虚部形状随c1变化
(b) The real part shape varying with c1 (c) The imaginary part shape varying with c1
图4 当c1>2时系统的1阶本征函数
Fig. 4 The 1st order eigenfunction of the system for c1>2
3.3.2 适中阻尼(0<c1<2)
当0<c1<2时,由本征值与阻尼的关系式(23)得
pk=ln|(c1-2)/(c1+2)|+j(2s+1)π, s=0,±1,±2,….
(33)
式(33)中,本征值p的阶次k由整数s确定,当s<0时,k=2|s|,当s≥0时,k=2s+1.
由式(33)可知,当0<c1<2时,本征值p是复数,p的实部和虚部分别为
σ=ln|(c1-2)/(c1+2)|,
(34a)
ωk=(2s+1)π, s=0,±1,±2,….
(34b)
1) 频率
由式(34b)知,当0<c1<2时,各阶本征值的虚部ω为(2s+1)π,s=0,±1,±2,±3,…,系统的频率为|s+1/2|.式(34b)还表明,系统频率仍与其阻尼无关,再次表现出该混合系统的性质Ⅰ.
2) 衰减率
由式(34a)可知, 对0<c1<2的情况, 所有各阶本征值的实部σ都相同, 表明各阶本征函数在单位时间内的衰减率都相同, 衰减率与本征值的阶次无关, 再次表现出该混合系统的性质Ⅱ.
特别地,当c1大于且趋于0时,得
(35)
此时,衰减率-σ趋于无穷小.应注意到,衰减率趋于无穷小,表明该混合系统趋于无阻尼振动.
3) 本征函数
不论阻尼如何取值,本征函数均可统一表达为式(26).上文提到,当c1>2时,系统存在虚部为0的本征值,其对应的0阶本征函数为实双曲正弦函数.但对于0<c1<2的情况,由式(34b)可知,系统各阶本征值虚部均不可能为0,故任何本征函数都不能再退化为实函数.
特别地,由式(35)可知,当c1大于且趋于0时,σ趋于负无穷小.令本征函数式(26)中的σ趋于负无穷小,得
σxcos(ωkx)+jsin(ωkx).
(36)
同时注意到式(34b)中ωk取值为(2s+1)π,于是由式(36)可知,本征函数的实部接近σxcos((2s+1)πx),为无穷小量;虚部接近于sin((2s+1)πx);本征函数的实部与虚部相比,一般为一阶无穷小量.
图5绘出了不同阻尼下1阶本征函数φ1(x)的实部和虚部的图形(x>1/2的部分由关于x=1/2的对称性做出,φ1(x)的实部和虚部均由其峰值进行了归一化处理).从图5可以看出,随着阻尼从2开始减小至0,1阶本征函数φ1(x)的实部形状逐渐接近于xcos(πx),其虚部形状接近于sin(πx).

(a) 实部形状随c1变化 (b) 虚部形状随c1变化
(a) The real part shape varying with c1 (b) The imaginary part shape varying with c1
图5 当0<c1<2时系统的1阶本征函数
Fig. 5 The 1st order eigenfunction of the system for 0<c1<2
3.3.3 特征阻尼(c1=2)
由本征值与阻尼的一般关系式(23)知,当阻尼值取2时,由于式(23)右端需对0取对数,即使在复域,这个对数都无意义(无定义).但该混合动力学系统(中点集中阻尼弦)本身并不能排斥阻尼值取2的情况,因此,有必要从极限角度对此问题进行讨论.
不论从大于2的方向还是从小于2的方向,当c1趋于2时,由式(23)可得本征值实部的极限为
(37)
此时,σ趋于负无穷大.本征值的虚部ω则与c1是否大于2有关:c1>2时,ω=2sπ;c1<2时,ω=(2s+1) π;s均为整数,s= 0,±1, ±2, ±3,….
1) 频率
如前所述,当阻尼c1从两个不同的方向趋于2时,本征值虚部ω取值不同,表明其左右极限不同.
2) 衰减率
如前所述,c1不论从哪个方向趋于2,本征值实部σ均趋于负无穷大,即系统衰减率-σ趋于无穷大.从数学上看,这表明各阶本征函数所表征的运动会在瞬时衰减为0,可以理解为系统的有阻尼运动(包括震荡和非震荡两种有阻尼运动)被完全抑制,系统不能发生任何有阻尼振动,这是该系统区别于一般的离散系统或连续系统的再一个独特性质,可称为性质Ⅲ.
3) 本征函数
如前所述,当c1趋于2时,σ趋于负无穷大.因此,可令本征函数统一表达式(26)中的σ趋于负无穷大,得
e-σx(-cos(ωkx)+jsin(ωkx))/2=
-e-σxe-jωkx/2.
(38)
式(38)表明:当σ趋于负无穷大时,本征函数在所有非0点的取值趋于无穷大.
这将得到如下推论:若c1趋于2,则在采用叠加法确定挠曲函数w(x,t)中任意一阶本征函数φk(x)的系数时,由于φk(x)在除x=0点以外,处处趋于无穷大, φk(x)的系数在任何能量有限的初始条件下都将趋于无穷小.这意味着当阻尼为特征阻尼时,有阻尼运动都将被完全抑制.因此,从本征函数的角度分析,系统此时也不能发生任何有阻尼振动,这和上文从衰减率角度分析得到的结论一致,再次表现出该混合系统的性质Ⅲ.
4 无衰减自由振动(第二类本征解)
对单阻尼设置于弦中点的情况,集中阻尼弦存在一类特殊的自由振动,这类振动对应弦中点恰好为无阻尼自由振动驻点的那一部分本征解.由于这类本征解在阻尼处取值为0,因此其对应的振动不受阻尼的影响,其自由振动无衰减.
此种情况下,本征函数φ(x)在阻尼位置处(x1=1/2)应满足
φ(x1)=0,
(39)
则阻尼力恒为0.因此,φ(x)的常微分方程(13)变为
-φ″(x)+p2φ(x)=0.
(40)
同时,φ(x)尚需满足两端的零边界条件:
φ(0)=φ(1)=0.
(41)
易看出,式(40)及式(41)与两端固支无阻尼弦本征函数满足的常微分和边界条件完全一致,易解得本征值和本征函数为
p=jsπ,
(42)
φ(x)=sinh(px),
(43)
式(42)中,s为非0整数.
注意到,式(43)中的φ(x)尚应满足式(39),应做进一步讨论.令N=2,引入记号α表示无阻尼弦,sα= ±N,±2N,±3N,…;sα<0时,q=2|sα|, sα>0时,q=2sα-1,易知无阻尼弦自由振动第q阶本征解pαq和φαq(x)除了满足式(40)及式(41),还将同时满足式(39).因此,pαq和φαq(x)同时也分别为集中阻尼弦的无衰减自由振动的本征值pβv和本征函数φβv(x),记号β表示集中阻尼弦,记号v表示本征值阶次.则集中阻尼弦的无衰减自由振动的本征值阶次v应按照系统频率从小到大的方式编号.当同时考虑集中阻尼弦的无衰减和有衰减振动时,应对两类本征解的阶次统一编号.此时,编号规则仍然应是本征值阶次随频率(绝对值)的递增而增加.
由以上推导可知,中点集中阻尼弦的自由振动存在这样一类本征解:阻尼位置(此处即弦中点)处于本征函数的驻点处.这类解实际上就是无阻尼弦的本征解中,在弦中点为驻点的那一部分解.
1) 频率
由式(42)知,本征值p的虚部ω为2sπ,表明系统频率为s(s=±1,±2,±3,…).
2) 衰减率
显然,由于这类本征解与无衰减自由振动相对应,可知衰减率为0,这与式(43)中本征解的实部均为0是对应的.
3) 本征函数
显然,这类本征函数关于弦中点反对称,且与无阻尼弦系统相应的反对称本征函数完全一致,其本征函数为
φv(x)=sin(2sπx), s=±1,±2,±3,….
(44)
5 中点集中阻尼弦自由振动的一般表达式
中点集中阻尼弦的本征解一般由无衰减自由振动、有衰减自由振动和有衰减的0阶非震荡运动组成,因此,可将其表示为如下通用形式:
(45)
式(45)中,右端三项依次为非震荡的0阶本征运动、有衰减自由振动和无衰减自由振动;φk(x)是由式(26)给出的复函数;Ck为复常数,Av,Bv为实常数,这些常数须由初始条件确定.
6 结果与讨论
本文利用Dirac δ函数,在全域建立并求解集中阻尼弦的动力学方程, 导出了其本征方程组、 频率方程和本征函数的一般形式, 分析了中点阻尼对张紧弦本征解的影响,得到的结果如下:
1) 集中阻尼弦有三个既区别于连续系统,又区别于离散系统的独特性质:系统频率与阻尼值无关(性质Ⅰ),阻尼振动的衰减率均相等(性质Ⅱ),及当阻尼为特定值时,有衰减振动被完全抑制,系统只存在无衰减振动(性质Ⅲ).
2) 当阻尼小于特定值时,系统只有震荡的运动;当阻尼大于特定值时,系统则可同时有震荡运动和非震荡运动.
3) 中点集中阻尼弦的无衰减振动均关于中点反对称,有衰减运动(包括0阶的非震荡运动和1阶及以上阶次的震荡运动)均关于中点对称.
对于理论推导,给出系统本征解的一般形式及分析本征解的性质仍然是不够的.在此基础上,还需根据初始条件确定本征解叠加时的待定系数,这是理论推导应该解决的问题,此问题将在后续论文中研讨.
[1] CARNE T G. Guy cable design and damping for vertical axis wind turbines: SAND 80-2669[R]. Albuquerque, New Mexico, US: Sandia National Laboratories, 1981.
[2] YONEDA M, MAEDA K. A study on practical estimation method for structural damping of stay cable with damper[C]//Proceedings of the Canada-Japan Workshop on Bridge Aerodynamics. Ottawa, Canada, 1989.
[3] PACHECO B M, FUJINO Y, SULEKH A. Estimation curve for modal damping in stay cables with viscous damper[J]. Journal of Structural Engineering, 1993, 119(6): 1961-1979.
[4] TABATABAI H, MEHRABI A B. Design of mechanical viscous dampers for stay cables[J]. Journal of Bridge Engineering, 2000, 5(2): 114-123.
[5] YU Z, XU Y L. Mitigation of three-dimensional vibration of inclined sag cable using discrete oil dampers, Ⅰ: formulation[J]. Journal of Sound and Vibration, 1998, 214(4): 659-673.
[6] MAIN J A, JONES N P. Free vibrations of taut cable with attached damper, Ⅰ: linear viscous damper[J]. Journal of Engineering Mechanics, 2002, 128(10): 1062-1071.
[7] BATTINI J M. Analysis of dampers for stay cables using nonlinear beam elements[J]. Structures, 2018, 16: 45-49.
[8] CHEN L, SUN L M, NAGARAJAIAH S. Cable vibration control with both lateral and rotational dampers attached at an intermediate location[J]. Journal of Sound and Vibration, 2016, 377(1): 38-57.
[9] LAZAR F, NEILD S A, WAGG D J. Vibration suppression of cables using tuned-inerter-dampers[J]. Engineering Structures, 2016, 122(1): 62-71.