引 言
悬索桥是大跨度桥梁的常见桥型,由于其刚度偏小,动力响应往往成为设计的控制性因素.随着有限元技术的高度发展,数值分析已成为悬索桥等大型结构动力分析的首选方法.但是,经典悬索桥振动微分方程理论对于深层次理解结构的动力特性仍具有不可替代的学术价值.同时,在结构的方案设计阶段,利用经典振动微分方程可以进行大量的参数比较分析,同样具有非常重要的工程实用价值.
悬索桥的竖向自由振动对于研究车桥耦合振动[1-5]与气动稳定[6-8]等动力学问题有重要的学术价值.李国豪[9]给出了悬索桥竖向自由振动的微分方程组,该方程组由一个微分方程和一个积分方程构成,且二者成耦合关系,并采用Galerkin法对该微分方程组进行了近似求解.
传递矩阵法是在微分方程求解的基础上发展起来的一种数值方法[10-14].对于变截面和变刚度问题,传递矩阵法具有内存消耗小、计算速度快及解析精度高等优点.对于采用钢箱梁作为加劲梁的大跨度悬索桥,为了提高其气动稳定性,钢箱梁往往采用分离式结构.这时,加劲梁刚度沿跨度方向不再为常数,对于这一问题可以方便地用传递矩阵方法加以解决.
本文通过数学推演,直接给出了悬索桥竖向自由振动的解析解,相比Galerkin法等半解析数值手段,具有精度更高等优点.并且在此基础上,本文引入传递矩阵方法,得到悬索桥竖向自由振动的传递矩阵解.通过算例分析,验证了本文方法的有效性.同时,本文分析了某分离式钢箱梁大跨度悬索桥的竖向自由振动问题,讨论了加劲梁刚度变化对结构自振特性的影响.
1 悬索桥竖向自由振动微分方程解析解
文献[9]给出了如图1所示的悬索桥,其自由振动方程为
(1)
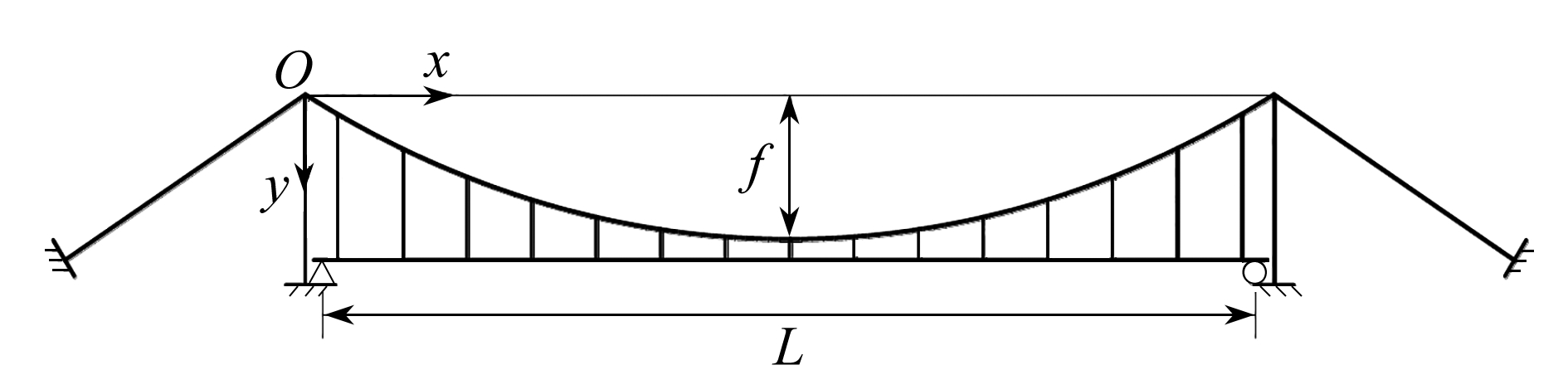
图1 单跨悬索桥
Fig. 1 A single-span suspension bridge
![]()
(2)
其中
(3)
(4)
式中,E是加劲梁弹性模量,I是加劲梁惯性矩,η是加劲梁竖向挠度,m是加劲梁线容重,Hp是大缆水平拉力, f是大缆垂度,ΔL是大缆因Hp=1引起的伸长量,L是跨度,y是按照抛物线方程确定的大缆线形.
Timoshenko等[15]给出式(2)中ΔL的表达式为
(5)
式中,φ是大缆与水平x轴的夹角,Ec是大缆弹性模量,Ac是大缆截面积.
对于自由振动,可以令
η=η0sin(ωt),
(6)
其中,ω和η0分别为自由振动的频率和振型.将式(6)代入式(1)可得
(7)
在式(7)中,由于存在积分项,过去的研究中一般采用Galerkin法的近似方法进行求解[9].本文采用如下方法对式(7)进行求解.首先,将积分项移至方程右端得
(8)
式中,方程左端的第一项为加劲梁振动的弹性力,第二项为恒载作用下大缆水平拉力对弹性力的贡献,第三项为惯性力.方程右端代表了振动引起的大缆水平拉力变化对弹性力的影响,由于振动引起的大缆水平拉力变化远小于恒载引起的水平拉力,本文将其移至右端,转化为一个非齐次方程进行求解.
式(8)的通解为
(9)
式中
(10)
(11)
在已知η的情况下,由式(2)可知,Hp为一常数,因而其对应的特解也为一常量,只是其值的大小一直在发生改变.对于常量而言,其二阶导数和四阶导数均为0,所以,式(8)中的第一项与第二项均不参与特解的求解.由式(9)所示的通解求出第一步特解![]()
(12)
则式(8)的解可以写为
(13)
将式(13)代入式(2)和(8)可得第二步迭代解为
(14)
其中
(15)
由上述过程可知,方程的第i步迭代解为
(16)
上式右端从第二项到第i项为一等比数列,从物理意义上讲,式(8)有稳态解而不发散,需满足δ<1.则式(16)取无穷阶级数后的等比数列求和解为
(17)
从数学意义上讲,式(17)可视为式(8)的解析解.将式(9)与(12)代入式(17)中,可得式(8)的解析式为
(18)
从式(18)可以看出,虽然本文将自由振动转化为一个非齐次微分方程进行求解,但是可以发现该非齐次方程的特解项仍然与待定系数C1~C4有关.因此,本文的数学求解方法并未根本上改变自由振动的特征值求解问题.
由式(18)求出悬索桥自由振动加劲梁转角、弯矩及剪力的解析式为
(19)
(20)
(21)
2 悬索桥竖向自由振动传递矩阵解
采用传递矩阵求解时,需将悬索桥划分为若干个单元,记第i个单元左右两端的状态向量为
(22)
(23)
式中,上标1和2分别代表单元的左右两端.将x=0,li代入式(18)~(21)可得

(24)
由上式进一步推导得
(25)
式中,Ti为单元i的单元传递矩阵.
应用传递矩阵原理,将所有首尾相连的单元传递矩阵连乘,得到总体传递矩阵:
(26)
然后引入边界条件,得到相应的特征方程, 求解此特征方程, 即可求得悬索桥竖向自由振动的自振频率和振型.
3 算 例
3.1 等截面加劲梁悬索桥[9]
某跨度L=750 m、大缆垂度f=87.3 m的公铁两用悬索桥,恒载集度g=500 kN/m,大缆弹性模量Ec=16 000 N/mm2,截面面积Ac=1.15 m2,加劲梁弹性模量E=21 000 N/mm2,抗弯惯性矩I=13.5 m4.
采用本文的传递矩阵计算方法(TMA)与ANSYS有限元分析得到的频率结果对比如表1所示,前6阶振型结果对比如图2所示.
表1 频率计算结果(等截面)
Table 1 Frequency calculation results(uniform-cross-section)
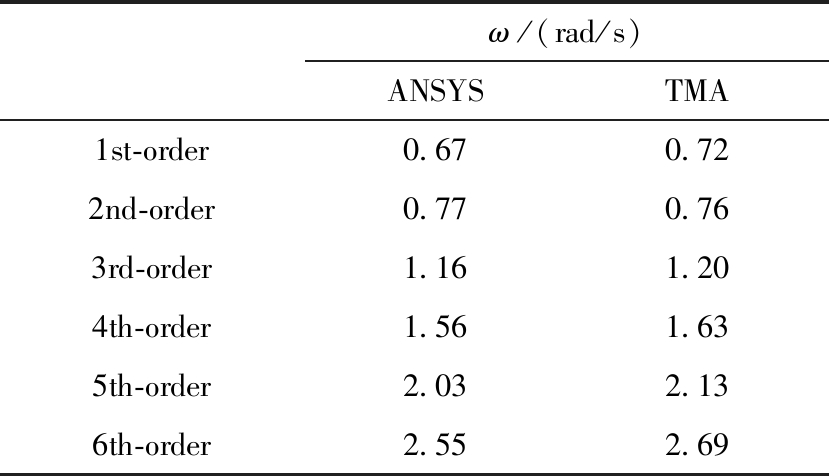
ω/(rad/s)ANSYSTMA1st-order0.670.722nd-order0.770.763rd-order1.161.204th-order1.561.635th-order2.032.136th-order2.552.69
表2 频率计算结果(变截面)
Table 2 Frequency calculation results(nonuniform-cross-section)
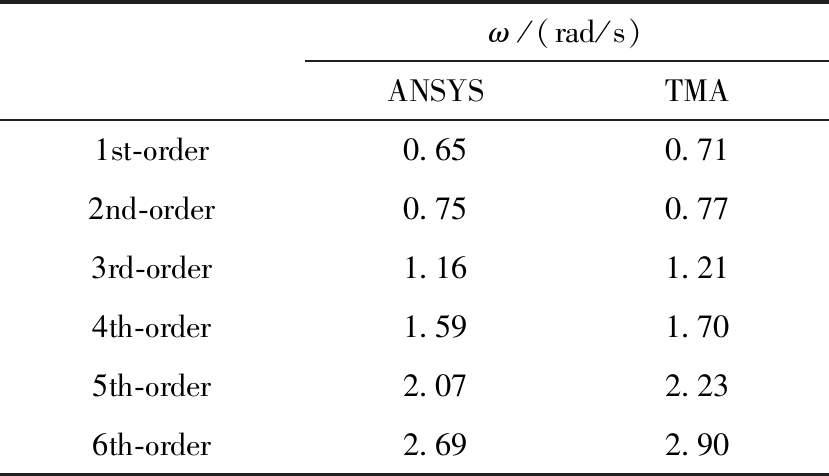
ω/(rad/s)ANSYSTMA1st-order0.650.712nd-order0.750.773rd-order1.161.214th-order1.591.705th-order2.072.236th-order2.692.90

(a) 第一阶振型 (b) 第二阶振型
(a) The 1st-order mode shape (b) The 2nd-order mode shape
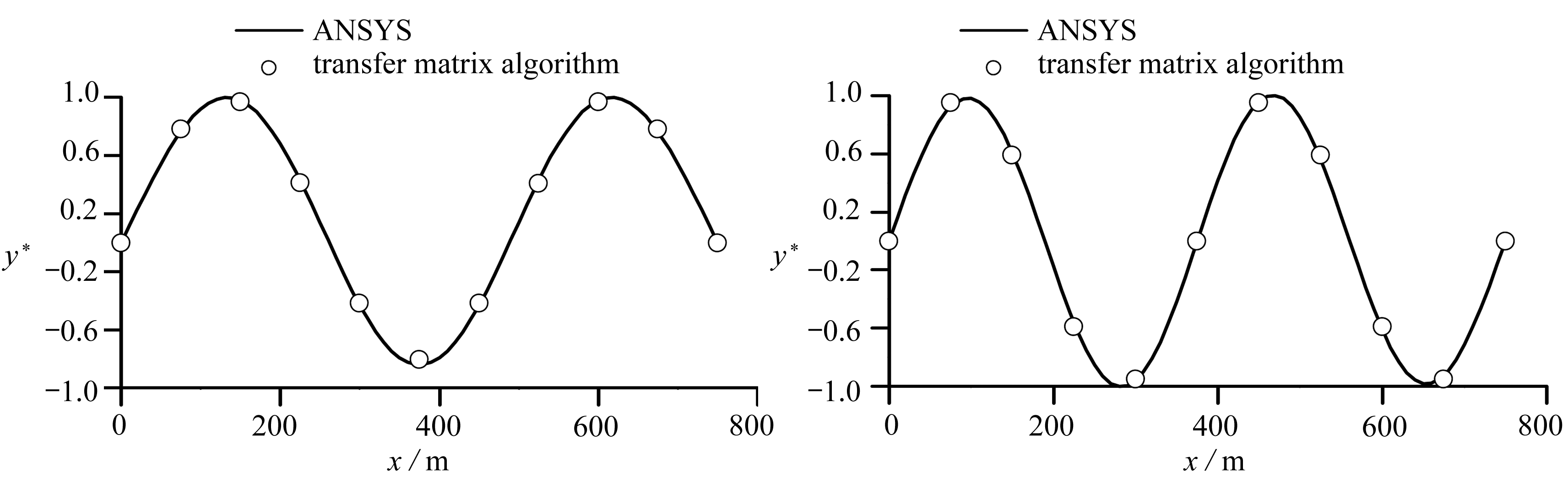
(c) 第三阶振型 (d) 第四阶振型
(c) The 3rd-order mode shape (d) The 4th-order mode shape

(e) 第五阶振型 (f) 第六阶振型
(e) The 5th-order mode shape (f) The 6th-order mode shape
图2 振型计算结果(等截面)
Fig. 2 Calculation results of vibration mode shapes(uniform-cross-section)
对比图2可以发现,传递矩阵解与有限元解吻合良好,证明了本文方法的有效性.同时,传递矩阵法具有计算方便快速的优点,在悬索桥方案设计阶段可以进行大量的参数比选.
3.2 变截面加劲梁悬索桥[16-17]
目前,为了减轻大跨度悬索桥加劲梁的重量和保持其空气动力学稳定性,有采用分离式钢箱梁作为加劲梁的趋势.对于分离式钢箱梁,其抗弯刚度沿桥长不再是一个定值.
仍以3.1小节中的悬索桥为例,研究分离式钢箱梁悬索桥的自由振动问题.除箱梁的抗弯惯性矩外,其余参数取值同3.1小节.当x=60~90,210~240,360~390,510~540,660~690 m的范围内为分离式箱梁,其抗弯惯性矩I1=19.433 m4,其余部分为整体式箱梁,其抗弯惯性矩I2=21.533 m4.
采用本文的传递矩阵计算方法与ANSYS有限元分析得到的频率结果对比如表2所示,前6阶振型结果对比如图3所示.
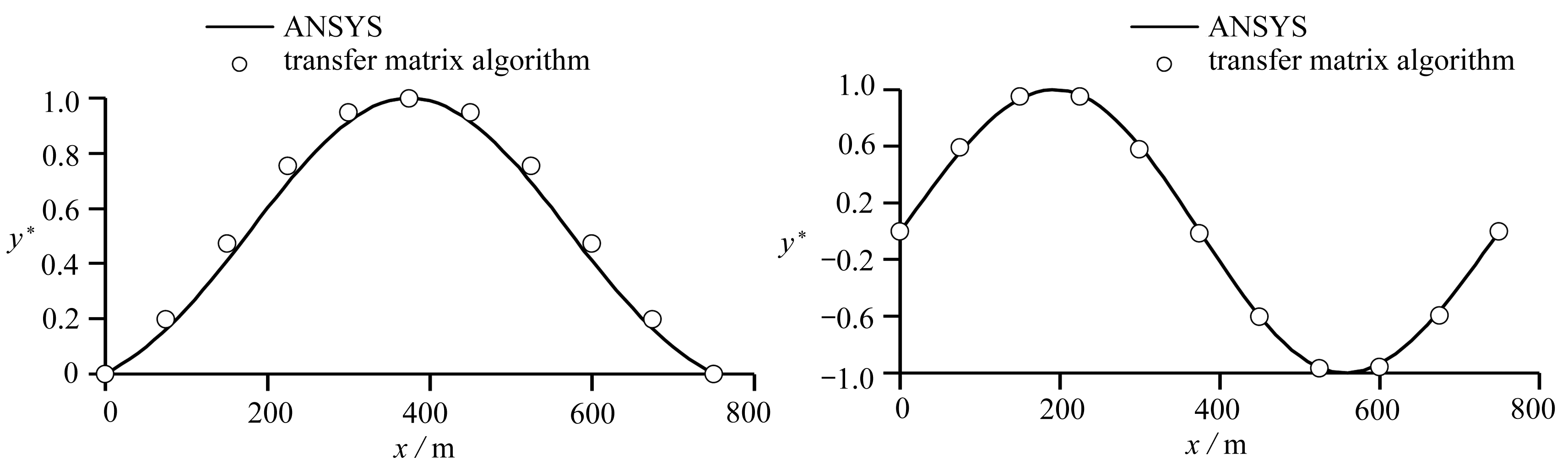
(a) 第一阶振型 (b) 第二阶振型
(a) The 1st-order mode shape (b) The 2nd-order mode shape
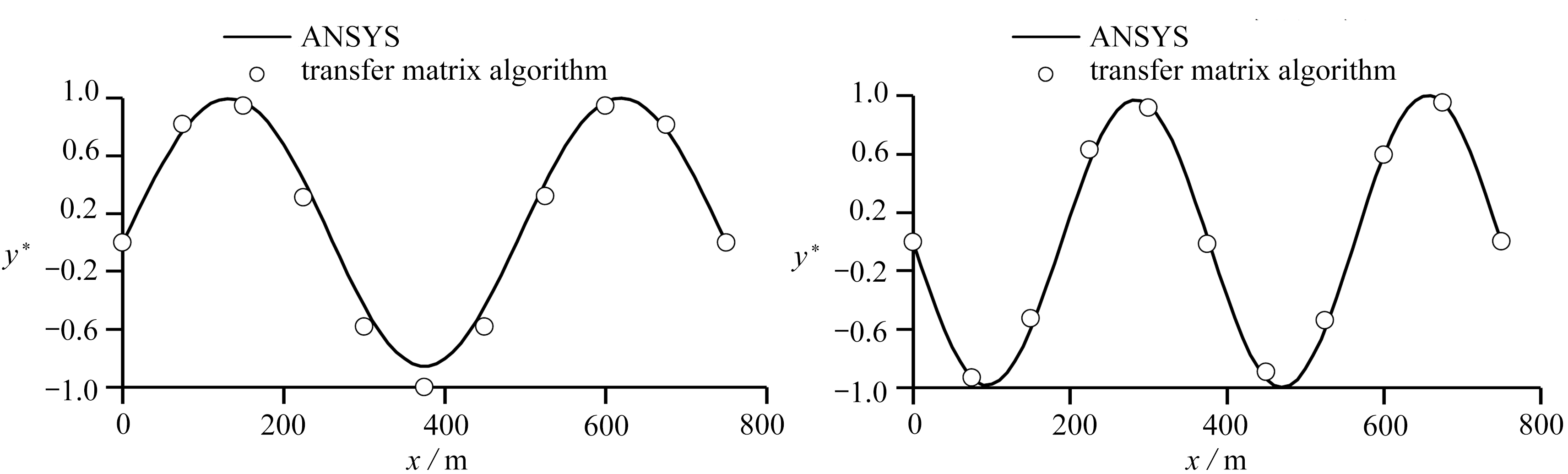
(c) 第三阶振型 (d) 第四阶振型
(c) The 3rd-order mode shape (d) The 4th-order mode shape

(e) 第五阶振型 (f) 第六阶振型
(e) The 5th-order mode shape (f) The 6th-order mode shape
图3 振型计算结果(变截面)
Fig. 3 Calculation results of vibration mode shapes(nonuniform-cross-section)
对比图3可以发现,变截面悬索桥中的传递矩阵解也与有限元解吻合良好.
作为参数分析,本文研究了分离式钢箱梁设置方式对悬索桥自振特性的影响.保持其余参数不变,分别计算分离式箱梁无连接处的宽度为0,15,35 m三种情况下的悬索桥前6阶自振频率.计算结果如图4所示.
由图4可以看出,当分离式箱梁无连接处宽度为0 m(方案1)和15 m(方案2)时,两种情况的结构竖向自振频率基本一致,表明在此范围内,箱梁竖向抗弯刚度的变化对结构自振特性影响甚小.进一步增大无连接处宽度,可以发现,结构自振频率明显降低,且随着振型阶数的提高,频率降低越明显.
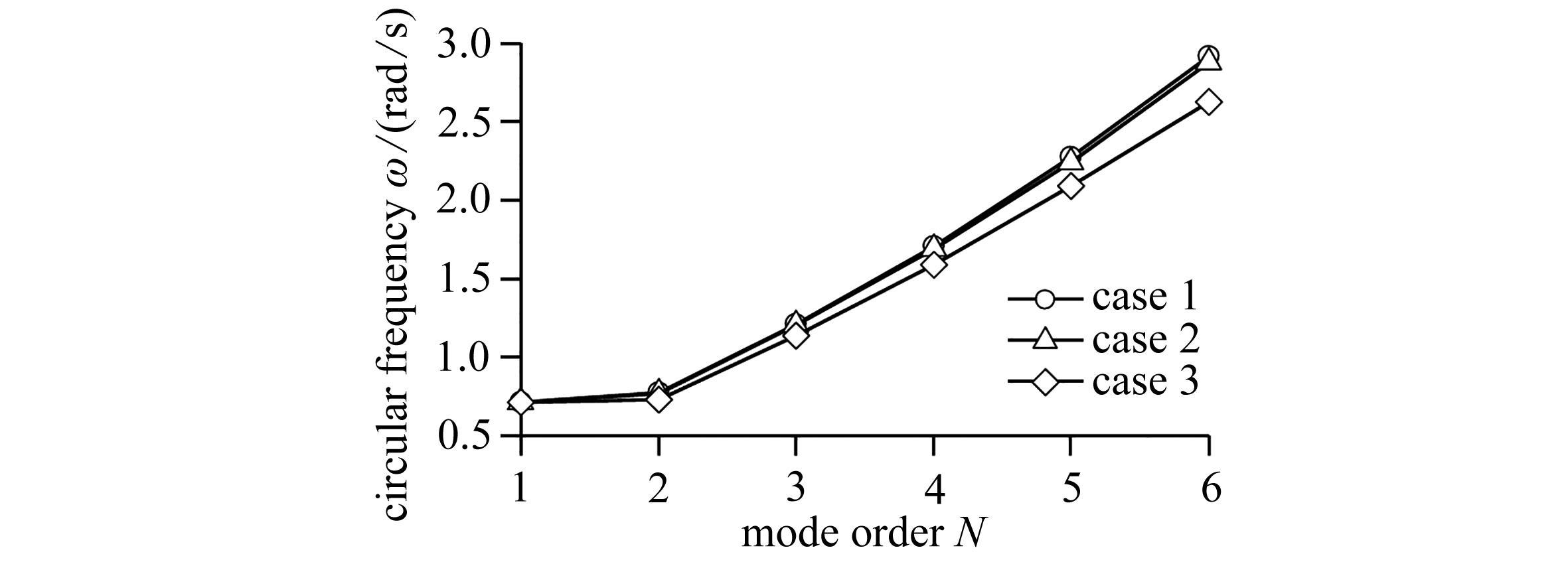
图4 频率随无连接宽度变化规律
Fig. 4 Frequency variation with the unconnected width
4 结 论
本文主要研究了悬索桥的竖向自由振动微分方程的解析解问题,并通过传递矩阵方法求解等截面与变截面悬索桥的竖向自由振动问题,通过研究发现以下结论:
1) 本文在数学理论上进一步研究了悬索桥竖向自由振动的求解问题,直接给出了解析解,相比于在悬索桥经典理论中常采用的数值分析方法,解析方法更具有理论价值.
2) 在微分方程求解的基础上,本文引入传递矩阵方法求解悬索桥自由振动问题,并通过与有限元的对比,证明传递矩阵解的可行性与精确性.利用该方法把研究对象从等截面悬索桥扩展到变截面悬索桥,研究了分离式钢箱梁悬索桥的竖向自由振动问题.本文所做的研究对于悬索桥初步设计阶段的动力问题分析有工程应用价值.
3) 本文在悬索桥竖向自由振动微分方程求解及传递矩阵方法应用中所得到的技术方法,还可应用于悬索桥扭转以及横向振动的解析分析,笔者将在进一步的研究中对这一问题进行深入探讨.
4) 本文根据悬索桥竖向振动的经典微分方程,得到其数学解析解,并将其应用于传递矩阵求解,能用于桥梁方案设计阶段的参数比选分析.同时,由于悬索桥竖向振动的微分方程在建立时引入了一些假设,如吊杆为刚性的,以及主缆线形为抛物线等,这些假设的引入使得微分方程解只是数学解析解,而非真实的精确解,在进一步的研究中,有必要继续探讨引入的简化条件对微分方程数学解析解的计算准确性的影响.
[1] XIANG T Y, ZHAO R D, XU T F. Reliability evaluation of vehicle-bridge dynamic interaction[J]. Journal of Structural Engineering, 2007, 133(8): 1092-1099.
[2] YANG Y B, WU Y S. A versatile element for analyzing vehicle-bridge interaction response[J]. Engineering Structures, 2001, 23(5): 452-469.
[3] LU F, LIN J H, KENNEDY D, et al. An algorithm to study non-stationary random vibrations of vehicle-bridge systems[J]. Computers and Structures, 2009, 87(3/4): 177-185.
[4] 李慧乐, 夏禾. 基于车桥耦合随机振动分析的钢桥疲劳可靠度评估[J]. 工程力学, 2017, 34(2): 69-77.(LI Huile, XIA He. Fatigue reliability evaluation of steel bridges based on coupling random vibration analysis of train and bridge[J]. Engineering Mechanics, 2017, 34(2): 69-77.(in Chinese))
[5] 苏成, 钟春意, 周立成. 车桥耦合系统随机振动的时域显式解法[J]. 应用数学和力学, 2017, 38(1): 99-108.(SU Cheng, ZHONG Chunyi, ZHOU Licheng. Random vibration analysis of coupled vehicle-bridge systems with the explicit time-domain method[J]. Applied Mathematics and Mechanics, 2017, 38(1): 99-108.(in Chinese))
[6] LI Y L, TOGBENOU K, XIANG H Y, et al. Simulation of non-stationary wind velocity field on bridges based on Taylor series[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2017, 169: 117-127.
[7] 项海帆, 葛耀君. 悬索桥跨径的空气动力极限[J]. 土木工程学报, 2005, 38(1): 60-70.(XIANG Haifan, GE Yaojun. On aerodynamic limits to suspension bridges[J]. China Civil Engineering Journal, 2005, 38(1): 60-70.(in Chinese))
[8] 李春光, 张志田, 陈政清, 等. 桁架加劲梁悬索桥气动稳定措施试验研究[J]. 振动与冲击, 2008, 27(9): 40-43.(LI Chunguang, ZHANG Zhitian, CHEN Zhengqing, et al. Experimential study on the aerodynamic stability measure of a suspension bridge with truss stiffening girder[J]. Journal of Vibration and Shock, 2008, 27(9): 40-43.(in Chinese))
[9] 李国豪. 桥梁结构稳定与振动[M]. 北京: 中国铁道出版社, 1992.(LI Guohao. Stability and Vibration of Bridge Structure[M]. Beijing: China Railway Publishing House, 1992.(in Chinese))
[10] 周欣竹, 郑建军, 姜璐. 弹性地基上变厚度环板分析的传递矩阵法[J]. 浙江工业大学学报, 2005, 33(1): 8-12.(ZHOU Xinzhu, ZHENG Jianjun, JIANG Lu. Transfer matrix method for the analysis of annular plates with variable thickness on an elastic foundation[J]. Journal of Zhejiang University of Technology, 2005, 33(1): 8-12.(in Chinese))
[11] 杨海根, 芮筱亭. 多体系统传递矩阵法分布式并行计算研究[J]. 振动工程学报, 2014, 27(1): 9-15.(YANG Haigen, RUI Xiaoting. Study on distributed parallel computing of transfer matrix method for multibody systems[J]. Journal of Vibration Engineering, 2014, 27(1): 9-15.(in Chinese))
[12] 宫建国, 马宇山. 汽车消声器声学特性的声传递矩阵分析[J]. 振动工程学报, 2010, 23(6): 636-641.(GONG Jianguo, MA Yushan. Numerical analysis on acoustic characteristics of automotive exhaust muffler by transfer matrix method[J]. Journal of Vibration Engineering, 2010, 23(6): 636-641.(in Chinese))
[13] 王渊, 沈锐利, 王路. 变截面梁动力响应的频域传递矩阵计算方法[J]. 力学季刊, 2018, 39(1): 191-200.(WANG Yuan, SHEN Ruili, WANG Lu. The calculating method of dynamic analysis of beam with variable cross-section based on the frequency-domain transfer matrix method[J]. Chinese Quarterly of Mechanics, 2018, 39(1): 191-200.(in Chinese))
[14] 鞠海燕, 扶名福, 徐斌. 基于传递矩阵法的周期性圆柱壳体振动特性分析[J]. 应用数学和力学, 2018, 39(3): 278-285.(JU Haiyan, FU Mingfu, XU Bin. Vibration characteristics analysis of periodic cylindrical shells based on the transfer matrix method[J]. Applied Mathematics and Mechanics, 2018, 39(3): 278-285.(in Chinese))
[15] TIMOSHENKO S P, YOUNG D H. Theory of Structures[M]. 2nd ed. Beijing: Tsinghua University Press, 2002.
[16] 李永乐, 陈科宇, 王斌, 等. 钝体分离式双箱梁涡振优化措施研究[J]. 振动与冲击, 2018, 37(7): 116-122.(LI Yongle, CHEN Keyu, WANG Bin, et al. Optimal measures for vortex-induced vibration of a bluff girder with separated twin-box[J]. Journal of Vibration and Shock, 2018, 37(7): 116-122.(in Chinese))
[17] 李翠. 悬索桥分离式箱形加劲梁力学特性研究[D]. 硕士学位论文. 成都: 西南交通大学, 2008.(LI Cui. Mechanical performance research on slotted steel box-girder of suspension bridge[D]. Master Thesis. Chengdu: Southwest Jiaotong University, 2008.(in Chinese))