引 言
在过去的几十年里,偏微分方程(PDEs)的研究受到了数学家和物理学家的广泛关注.Navier-Stokes方程的求解和解的非线性动力学特性是流体力学家最为关注的.然而,对于一般的三维Navier-Stokes方程组而言,其理论解的存在性和唯一性尚未被证明[1].因此,复杂流动的研究变得极为困难,例如湍流.降维方法是研究偏微分方程的有效方法之一,它的基本思想是将偏微分方程这一无穷维动力系统投影到常微分方程(ODEs)这一有限维动力系统上[2],从而最大化地保留偏微分方程动力系统的主要特性.通过这一方式,有限维模型就可以表现出偏微分方程的无穷维动力系统的部分动力学特性和长期行为.除此之外,为了研究湍流拟序结构[3],了解低维湍流模型的动力学行为是非常重要的.
目前,降维方法主要分为先验方法和后验方法两类.先验方法不依赖于偏微分方程,例如基于Fourier分解[4]或广义Fourier展开的Galerkin方法、局部Taylor展开方法[5]、中心流形和惯性流形方法、能量稳定性分析方法和建模[6]等.相反,后验方法依赖于具体的偏微分方程,例如特征正交分解(POD)方法.Poje、Berkooz、Lumley等[6-7]率先将POD方法引入湍流研究,其主要贡献是在POD基函数上构造Navier-Stokes方程的Galerkin投影[8],从而得到一系列低维模型,用它们来分析流场的特性.
POD基有许多很好的性质.首先,从数学的角度,POD基被证明是均方意义(能量)下的最优降维方法,因此POD基能够客观地逼近未知流动数据库.其次,根据惯性流形能够掌控变量的思想,高阶模态的影响可以被低阶模态包含.并且,用POD方法来降维偏微分方程可以抑制数值不稳定现象[8]和节省计算资源[9-12].然而,有必要指出POD方法的三个缺陷: 第一,此方法只能被用于内积型最优化问题;第二,投影误差无法被避免;第三,POD基必须从已知的数据库中获得.
另一方面,最优化和最优控制方法在流体力学领域被广泛使用.为了利用POD方法的优点,并弥补它的不足,Wu[13]提出了建立最优低维动力系统(以下简称“最优动力系统”)的新理论.与上述方法(如广义Fourier展开等)相比,这一新理论的主要思想是假设用于谱展开的基函数是未知的,需要通过最优化方法求得.通过这一方式,基于最优基函数的低维动力系统将会最优地逼近原偏微分方程的特性.
最优动力系统理论有三个发展阶段.第一阶段中,Wu和Shi[14]提出了流动数据库分析和低维动力系统建模的最优化理论,它不仅仅是POD方法的拓展和修正,而是一个更广泛的、全新的理论,在一定程度上包含了POD方法;随后,吴锤结和赵红亮[15]提出了直接从偏微分方程构建最优动力系统的理论,进一步弥补了POD方法的不足.然而,最优泛函是在余量极小的意义下得到的,这一假设在某些情况下是不适用的.在第二阶段中,Wu和Wang[16]用最小残差构造了最优泛函,并使用了全局最优化方法.然而,在研究Burgers方程时发现,当以残差为收敛准则时,误差可能会不可控.为了解决这一问题,在第三阶段中,Peng等[17-18]用最小加权残数构造了最优泛函,并将该理论应用于三维不可压缩Navier-Stokes方程和基于螺旋波分解的Navier-Stokes方程,很好地克服了上述不足.
然而,根据我们最近的研究,发现第三阶段的最优动力系统理论只能满足时间平均意义下的弱解边界条件,且速度的不可压缩性条件并未采用任何措施进行满足,同时加权残数最优泛函与Galerkin投影等价,可以略去.
本文基于最优动力系统的理论框架,提出了一种可以同时满足任意速度边界条件和速度不可压缩性的最优动力系统理论,将其应用于三维不可压缩Navier-Stokes方程,并对该最优动力系统的动力学特性进行了分析.本文的概要如下:第1节详细阐述了建立最优动力系统的理论基础.第2节中,将该理论应用于三维不可压缩Navier-Stokes方程,得到满足任意速度边界条件和速度不可压条件的最优动力系统模型,并详细介绍了边界条件的处理.第3节中,基于方柱绕流算例,运用多尺度全局最优化方法获得全局最优基函数,得到具体的最优动力系统模型.第4节中,对该最优动力系统的动力学特性进行了分析.最后,第5节中,总结了本研究并得出结论.
1 最优动力系统建模理论基础
1.1 一般理论框架
对于一般的非线性初边值偏微分方程问题,其控制方程、初始条件和边界条件为
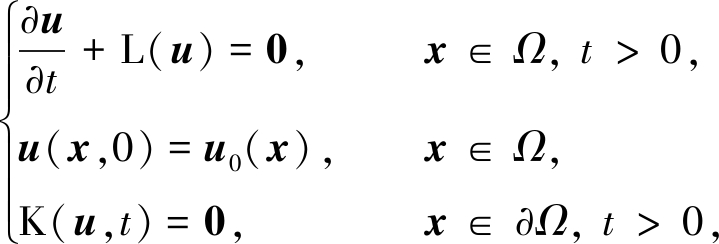
(1)
其中,Ω⊂Rn,t∈[0,T],u(x,t)可以是任意的标量、矢量或张量函数,L和K是u(x,t)的线性算子或非线性矢量算子.因此方程(1)的边界条件可以是线性、非线性或其他复杂边界条件.
假设该问题被定义在Sobolev空间,即
u(x,t)∈Wm,p(ΩT),
(2)
指标m,q与u的光滑性有关,且m,q∈N+,p=2q,N+是所有正整数集合,ΩT=Ω×[0,T].在Sobolev空间Wm,p(ΩT)中,范数的定义为
(3)
其中,Dαu是α阶广义微分,且Ip(ΩT)是ΩT中的p阶可积函数的集合.如果u=(u1,u2,…,uN)T,它的范数可以表示为
(4)
下面在Sobolev空间中定义基函数集合ξk(x)(k=1,2,…,∞),它张成的空间B满足如下条件:
(5)
注意,ξk是未知的.方程(1)的精确解基于ξk(x)的谱展开形式为
(6)
它对应于无穷维动力系统.
接下来, 将问题进一步限定在N维Hilbert空间HN中, 其中基函数应该满足正交性条件.由这些基函数张成的函数空间BN的定义为
(7)
其中,(·)是HN(Ω)中的I2内积运算,定义为
(8)
对方程(6)的前N项进行截断,得到u(x,t)在空间BN中的低维近似表达式:
(9)
其中,uR(x,t)是余项,ak(t)和ξk(x)都是未知的待求函数,且它们之间满足
ak=(u,ξk).
(10)
将方程(9)代入方程(1),并将得到的结果在任意未知基函数ξk上投影[2],得到如下的Galerkin投影方程组:
(11)
Galerkin投影方程组是方程(1)的低维模型,也被称为低维动力系统,可以写为
![]()
 ξk,…),
ξk,…),
(12)
其中,![]() 代表ak的时间导数,
代表ak的时间导数, ξk代表ξk的一阶空间导数,“…”代表ξk的高阶空间导数.至此实现了方程(1)的降维近似.如果动力系统建立在最优基
ξk代表ξk的一阶空间导数,“…”代表ξk的高阶空间导数.至此实现了方程(1)的降维近似.如果动力系统建立在最优基![]() 上,那么就被称为最优动力系统.可见,最优基的获得是建立最优动力系统的核心.因此,基于合适的最优条件,可以建立出目标泛函并得到如下的最优化问题:
上,那么就被称为最优动力系统.可见,最优基的获得是建立最优动力系统的核心.因此,基于合适的最优条件,可以建立出目标泛函并得到如下的最优化问题:
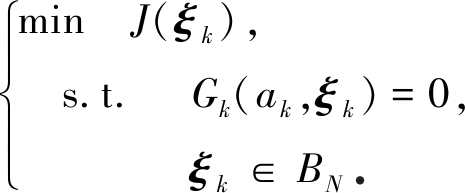
(13)
综上所述,最优动力系统的构建依赖于以下因素:
1) 函数空间B或BN的类型;
2) 目标泛函J(ξk)的具体形式;
3) 具体问题,包括控制方程、初始条件和边界条件;
4) 截断阶数N.
1.2 广义目标泛函及最优动力系统模型方程
为将约束优化问题转化为无约束优化问题,可以通过Lagrange乘子法或罚函数法对约束条件进行转化,使得转化后的约束条件与目标泛函J共同组成广义目标泛函Jg.通过对Jg求变分,便可得到最优动力系统模型方程:
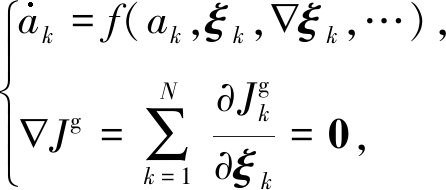
(14)
其中,![]() 是Jg的第k项,被称为Hamilton函数.最优基
是Jg的第k项,被称为Hamilton函数.最优基![]() 通过联立求解方程组(14)得到.
通过联立求解方程组(14)得到.
1.3 多尺度全局优化方法
由于方程(14)是通过对空间BN中Jg的局部极值点的变分得到的,因此求得的最优基![]() 不是整个空间中的全局最优基.然而,根据全局最优化理论[19],一般情况下,全局极值点无法通过有限次搜索得到.同理,本问题中,最后的收敛结果依赖于初始迭代基
不是整个空间中的全局最优基.然而,根据全局最优化理论[19],一般情况下,全局极值点无法通过有限次搜索得到.同理,本问题中,最后的收敛结果依赖于初始迭代基![]() 因此,当且仅当初始基位于全局极值点附近时,才能得到全局最优基.
因此,当且仅当初始基位于全局极值点附近时,才能得到全局最优基.
因此,应采用多尺度全局最优化方法[17]来得到最优基.其基本思想是,基于粗粒化的分析,局部极值点将会被光滑化,可以迅速定位到全局极值点.以双尺度方法为例,具体步骤见参考文献[17, 20].
需要强调的是,这一方法虽然用到了粗糙数据库,但是数据库仅被用来生成初始基函数,后续优化过程中不再用到数据库.因此,最终得到的最优基仍然是不依赖于数据库的.
2 不可压缩Navier-Stokes方程最优动力系统建模与分析
出于简洁性的考虑,在本节中,所有的公式都用指标记号[21]表示.指标i和j对应于物理空间中的坐标,满足i, j=1,2,3;指标标k,l和m对应于函数空间BN中的坐标,满足k,l,m=1,2,…,N.除非特别说明,任意指标成对出现时,则构成哑指标,满足Einstein求和约定.
2.1 建模理论
对于一般的三维流体力学问题,无量纲Navier-Stokes方程、连续性方程和初边值条件为
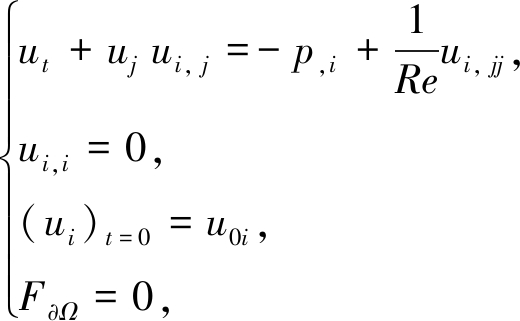
(15)
其中,p为压力,Re为Reynolds数,F∂Ω表示各种边界条件,具体形式见后文.
基函数ξki的函数空间定义为
(16)
ξki二阶可微.
ui在函数空间BN中的低维近似表达式为
ui=ak(t) ξki(xi)+uRi≈ak(t) ξki(xi),
(17)
其中,k=1,2,…,N,N为截断阶数,在后文中省略.
将方程(17)代入方程(15)得到
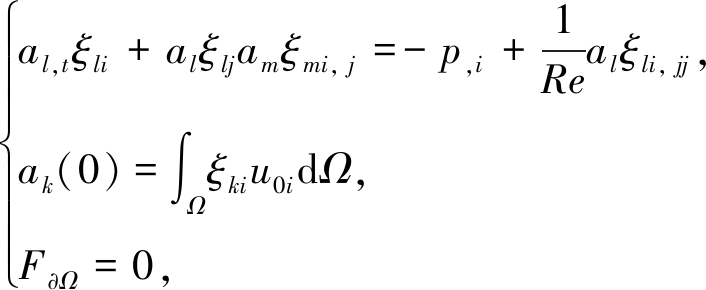
(18)
其中,由基函数定义式(16)可知,方程(15)中的连续方程已自动满足.
对方程组(18)中第一式构造Galerkin投影方程,在投影时引入边界条件:
(19)
其中,(akξki)b的具体形式由边界条件决定,得到满足边界条件的Galerkin投影方程:
(20)
其中
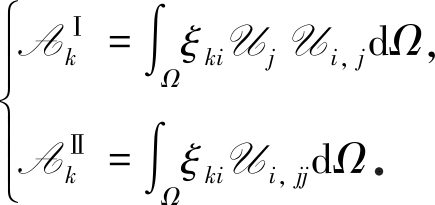
(21)
至此,偏微分方程定解问题(18)便转化为常微分方程(动力系统)定解问题:

(22)
需要着重说明的是,上述定解问题中,边界条件通过积分项![]() 和
和![]() 中边界处的Ui和边界附近的导数Ui, j,Ui, jj与内部流场耦合起来.动力系统方程求解完毕后,内部速度场由基函数及其系数给出,而边界处的速度由边界条件给出.
中边界处的Ui和边界附近的导数Ui, j,Ui, jj与内部流场耦合起来.动力系统方程求解完毕后,内部速度场由基函数及其系数给出,而边界处的速度由边界条件给出.
下面结合速度的不可压缩条件,建立速度不可压缩性目标泛函:
(23)
速度的不可压缩性是指速度的散度为零,即速度场是无源场,满足速度不可压缩性条件的流体的声速是无穷大的.
同时引入罚函数μ来转化正交性约束条件,使之与目标泛函J共同组成广义目标泛函Jg:
(24)
其中
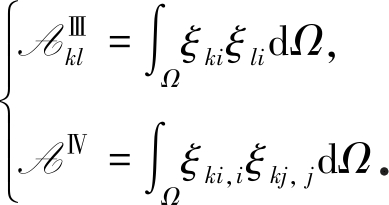
(25)
通过对方程(24)的变分运算,得到三维不可压缩Navier-Stokes方程的最优动力系统模型方程.
1) 关于ak,t的动力系统方程

(26)
2) 广义目标泛函梯度方程
在Ω内
(27)
在边界∂Ω上
ξkj, jni=0,
(28)
其中,ni为边界的单位外法向向量.
至此,即可用共轭梯度优化算法对最优动力系统模型进行求解.
2.2 速度边界条件的数值实现
传统 Galerkin 谱方法虽然精度很高,但使用条件非常苛刻,即要求基函数满足边界条件,因此只能被用来求解具有简单边界条件的物理问题.本文提出的方法,可以将 Galerkin 谱方法推广到任意速度边界条件的问题中,主要思想是在物理空间中满足速度边界条件.
下面讨论各类常见边界条件F∂Ω的数值实现.
 滑移边界条件
滑移边界条件
设边界处的局部坐标系由正交单位方向向量ni,si和ti组成,其中ni指向边界的外法向,si和ti分别指向与边界相切但互相正交的两个方向,则有
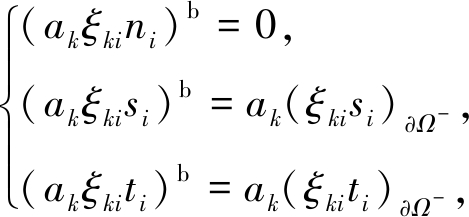
(29)
其中,上标b表示边界网格,下标∂Ω-表示与边界相邻的一层网格.
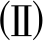 无滑移边界条件
无滑移边界条件
(akξki)b=0.
(30)
 入流边界条件
入流边界条件
(akξki)b=ubi,
(31)
其中,ubi为入口速度分布函数.
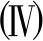 连续出流边界条件
连续出流边界条件
(akξki)b=ak (ξki)∂Ω-.
(32)
 周期边界条件
周期边界条件
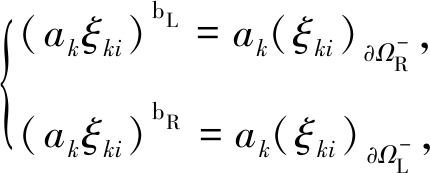
(33)
其中,以左右周期边界为例,上标bL,bR分别代表左、右边界网格,下标![]() 分别表示与左、右边界相邻的一层网格,其他方向的周期边界条件设置方式与此类似.
分别表示与左、右边界相邻的一层网格,其他方向的周期边界条件设置方式与此类似.
根据以上边界条件的定义,方柱绕流问题的边界条件F∂Ω如下:
1) 左边界 入流边界和无滑移边界的混合;
2) 右边界 连续出流边界;
3) 前后上下边界 滑移边界.
3 最优动力系统的数值分析
3.1 数值算例和POD分析
本小节中,以三维方柱绕流问题为例,进行最优动力系统的数值分析.整个计算域的无量纲尺寸为Ω=50.0×8.0×20.0,左边界由方柱和来流共同组成,方柱部分为无滑移边界条件,方柱的特征尺寸为2.0;非方柱部分为入流边界条件,无量纲来流速度为uB=(1.0, 0.0, 0.0);流向四周的边界皆为滑移边界条件,Reynolds数为Re=100.
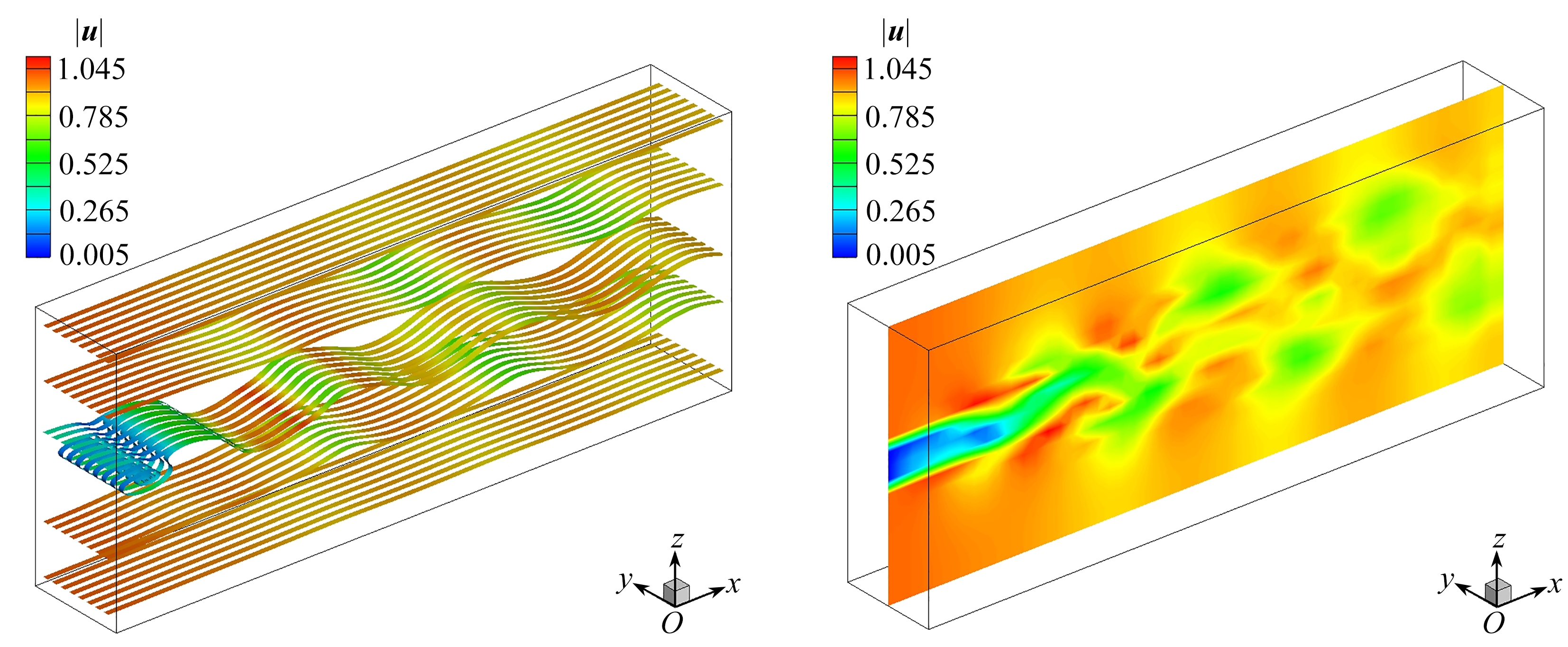
(a) 带状流线 (b) 速度模值云图 (a) Ribboned streamlines(b) The velocity contour
图1 t=700.0粗糙流场
Fig. 1 The coarse velocity field for t=700.0
注 为了解释图中的颜色,读者可以参考本文的电子网页版本,后同.
该算例通过NASA-VOF3D程序[22]计算. 粗糙网格数为50×8×20, 无量纲网格尺寸为Δx=Δy=Δz=1.0,无量纲时间步长为Δt=0.05 .图1展示了t=700.0无量纲时刻速度场的带状流线(用速度模值|u|对流线进行着色)和速度模值|u|的云图.
表1 POD基能量分布
Table 1 The energy distribution of POD bases

orderenergy of kth basis ek/%energy of first k bases ∑ek/%197.717 97697.717 97621.093 829 298.811 80531.013 126 399.824 93140.079 726 199.904 65850.077 336 099.981 99460.008 924 499.990 91870.008 616 899.999 53580.000 228 499.999 76390.000 223 899.999 987100.000 004 999.999 992
选取无量纲时间t=700.0~740.0的流体数据库来提取POD基.令无量纲时间步长Δt=0.2,通过snapshots方法[23]获得200个POD基.表1列出了前10阶基函数捕捉的能量(动能)的比例,从中可以看出,前3阶基捕获了几乎100%的能量,所以选取前 3 阶基函数来拟合原始流场.同时,根据动力系统的理论,为了表征一个真实的流体动力系统,至少需要三个基函数,其中,第一阶基反映的是平均流动的特征;第二阶基反映流动的线性特征;第三阶反映流动的非线性特征.因此,选取前三阶基函数来构造最优动力系统是合理的.
3.2 全局最优化与最优基
采用双尺度全局最优化方法.首先,将前三阶基插值到密一倍的网格上,密网格尺寸为Δx′=Δy′=Δz′=0.5.然后,将这些密基函数作为迭代初始基,代入共轭梯度优化算法进行计算,即可得到近似全局最优基![]() 图2展示了式(24)中的广义目标泛函值Jg的收敛曲线,该值反映了对全局最优的速度不可压缩性和基函数正交性的逼近程度.
图2展示了式(24)中的广义目标泛函值Jg的收敛曲线,该值反映了对全局最优的速度不可压缩性和基函数正交性的逼近程度.
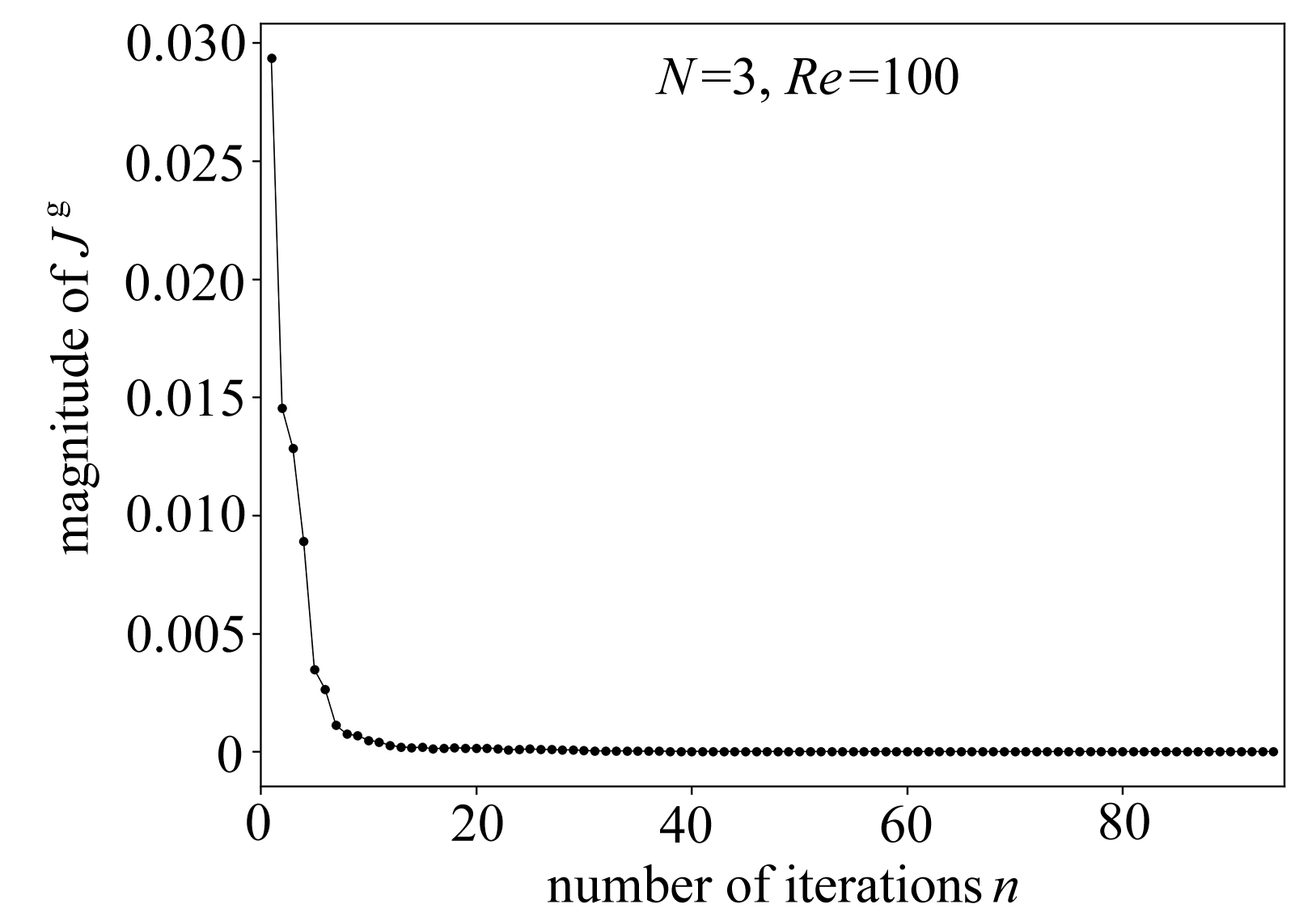
图2 Jg的收敛曲线
Fig. 2 The convergence curve of Jg
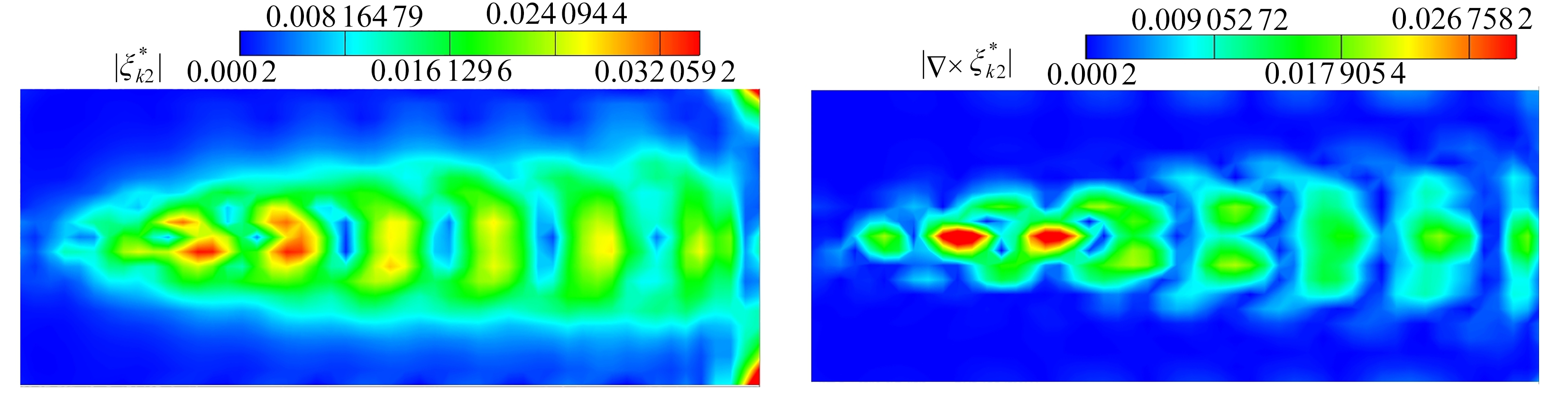
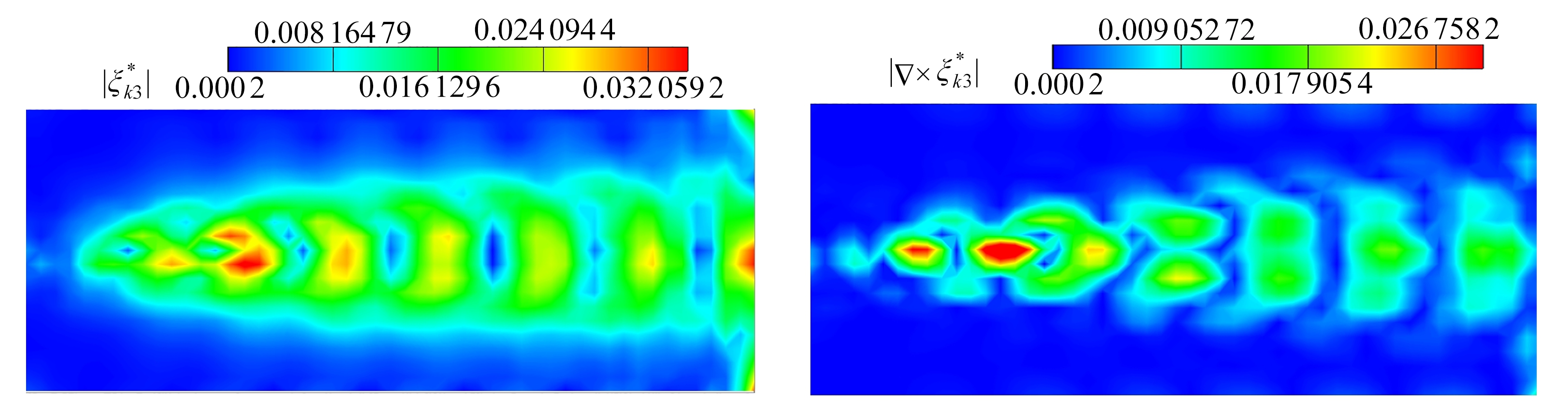
已知速度的旋度即为涡量,涡量可以反映流场的涡结构.类似地,通过对最优基求旋度,即可从物理上反映出最优基中的涡结构特点.图3展示了流向中截面上最优基![]() 的模
的模![]() 的云图和最优基旋度
的云图和最优基旋度
![]() 的模|
的模|
![]() 的云图.图3中的最优基包含了真实流场的典型物理结构,如周期涡结构.随着阶数的升高,最优基的结构越来越复杂,即低阶基反映了流场的大尺度结构,高阶基反映了小尺度结构.最优基与POD基最大的区别是,基函数的个数(即截断阶数N)不同时,优化后的最优基就不同,这是因为最优基是真实流体动力系统的内禀量,与所选取的函数空间的种类和维度密切相关.如图3所示,最优基流形的拓扑结构还具有数学上的拉伸对称性,具体的表达式可以通过群论[24]得到.
的云图.图3中的最优基包含了真实流场的典型物理结构,如周期涡结构.随着阶数的升高,最优基的结构越来越复杂,即低阶基反映了流场的大尺度结构,高阶基反映了小尺度结构.最优基与POD基最大的区别是,基函数的个数(即截断阶数N)不同时,优化后的最优基就不同,这是因为最优基是真实流体动力系统的内禀量,与所选取的函数空间的种类和维度密切相关.如图3所示,最优基流形的拓扑结构还具有数学上的拉伸对称性,具体的表达式可以通过群论[24]得到.
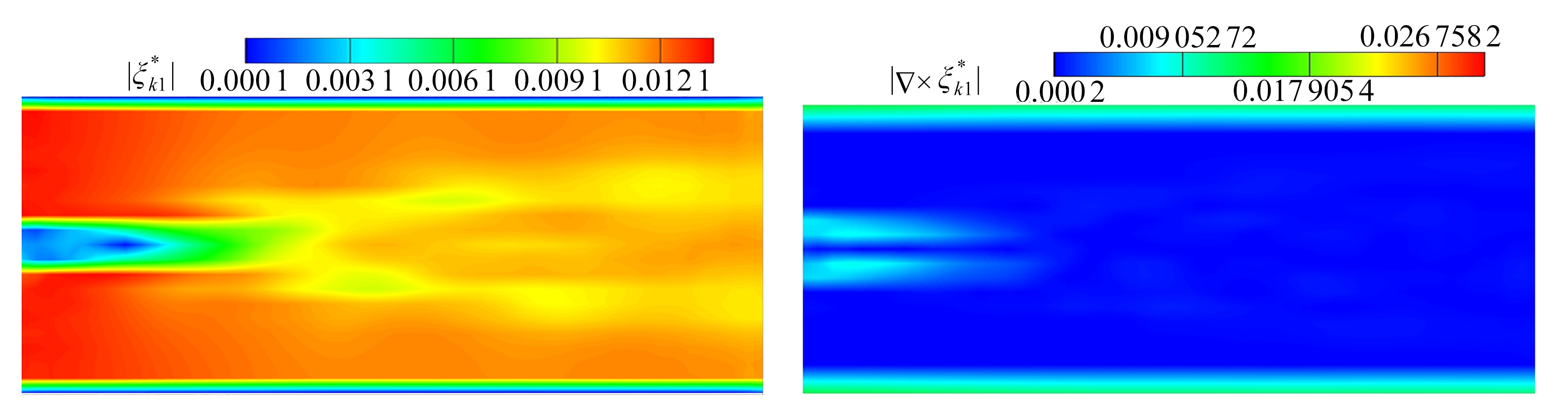
(a) 第一阶最优基模值 (b) 第一阶最优基旋度模值 (a) The 1st-order optimal basis (b) The 1st-order optimal basis curls
(c) 第二阶最优基模值 (d) 第二阶最优基旋度模值 (c) The 2nd-order optimal basis (d) The 2nd-order optimal basis curls
(e) 第三阶最优基模值 (f) 第三阶最优基旋度模值 (e) The 3rd-order optimal basis (f) The 3rd-order optimal basis curls
图3 流向中截面上的最优基模值云图和最优基旋度模值云图
Fig. 3 The contours of the optimal basis magnitudes and curls in the streamwise middle section
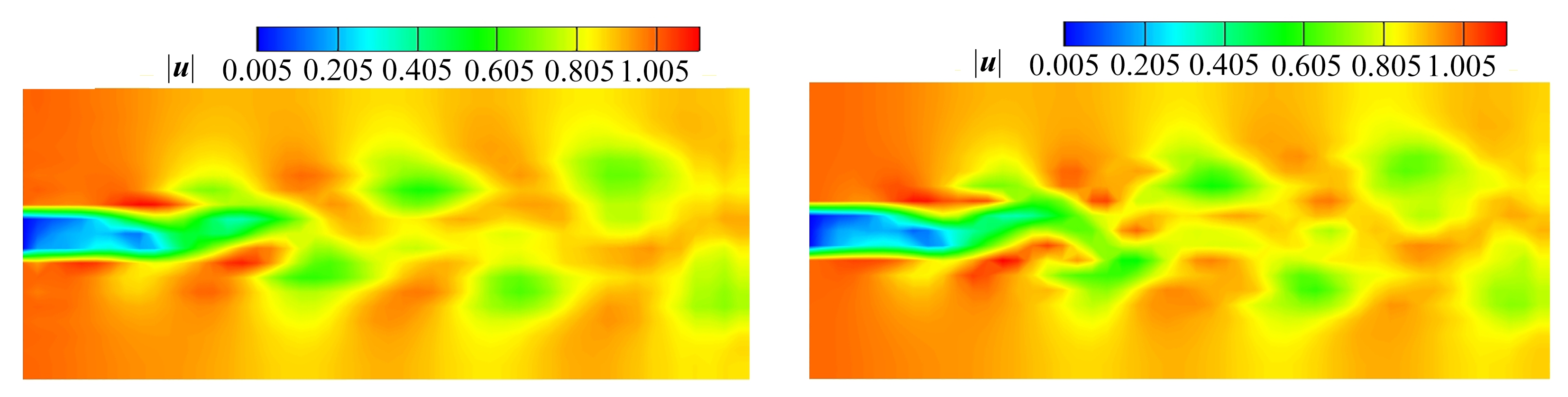
(a) t=700.0最优动力系统流场 (b) t=700.0数据库流场 (a) The optimal dynamical system for t=700.0 (b) The database for t=700.0
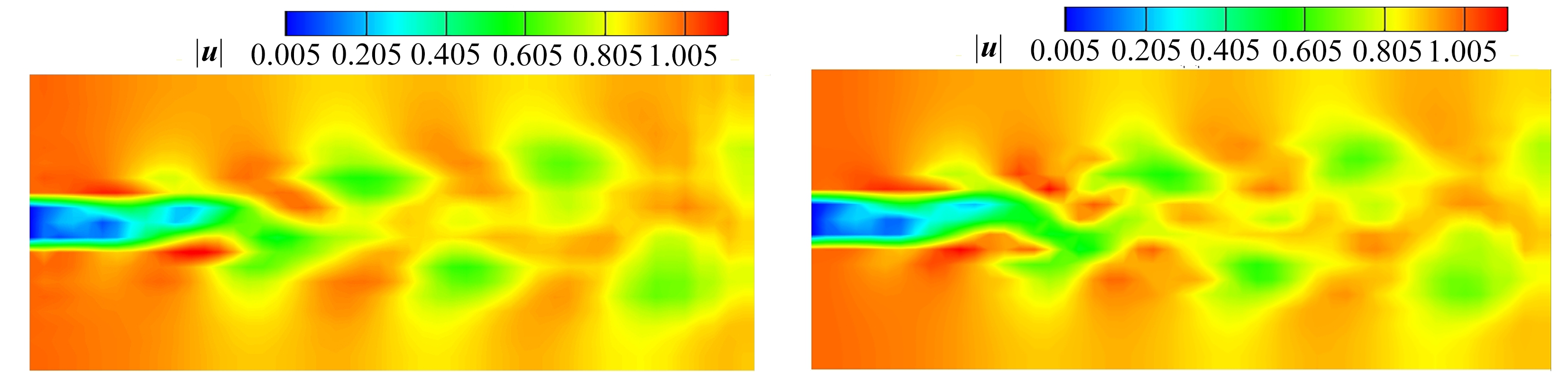
(c) t=713.0最优动力系统流场 (d) t=713.0数据库流场 (c) The optimal dynamical system for t=713.0 (d) The database for t=713.0
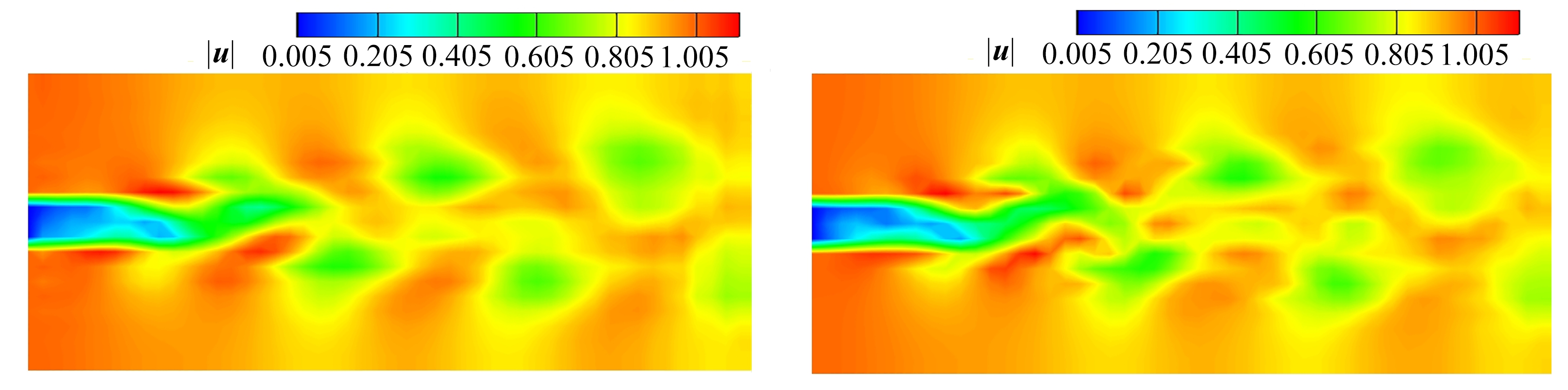
(e) t=720.0最优动力系统流场 (f) t=720.0数据库流场 (e) The optimal dynamical system for t=720.0 (f) The database for t=720.0
图4 最优动力系统速度模值和数据库速度模值比较
Fig. 4 The comparison of the velocity magnitudes between the optimal dynamical system and the database
3.3 最优基对流场的拟合
图4展示了前三阶最优基拟合的的近似流场的中截面速度模值云图与数据库流场的中截面速度模值云图的对比,可以发现拟合的流场抓住了流动的所有主要特征.
4 最优动力系统的动力学特性分析
下面对不可压缩 Navier-Stokes 方程最优动力系统的相空间轨道、Poincaré截面、功率谱、Lyapunov指数集和分岔等特性进行分析.
4.1 相空间轨道
首先观察最优动力系统在相空间中的轨迹,如图5所示,其反映了最优动力系统的周期性特征,这对应了图3和图4中的周期性流场结构.图5(a)为系统在三维相空间中的轨迹,图5(b)、5(c)、5(d)依次为系统在上述三维相空间的三个二维子空间中的轨迹.
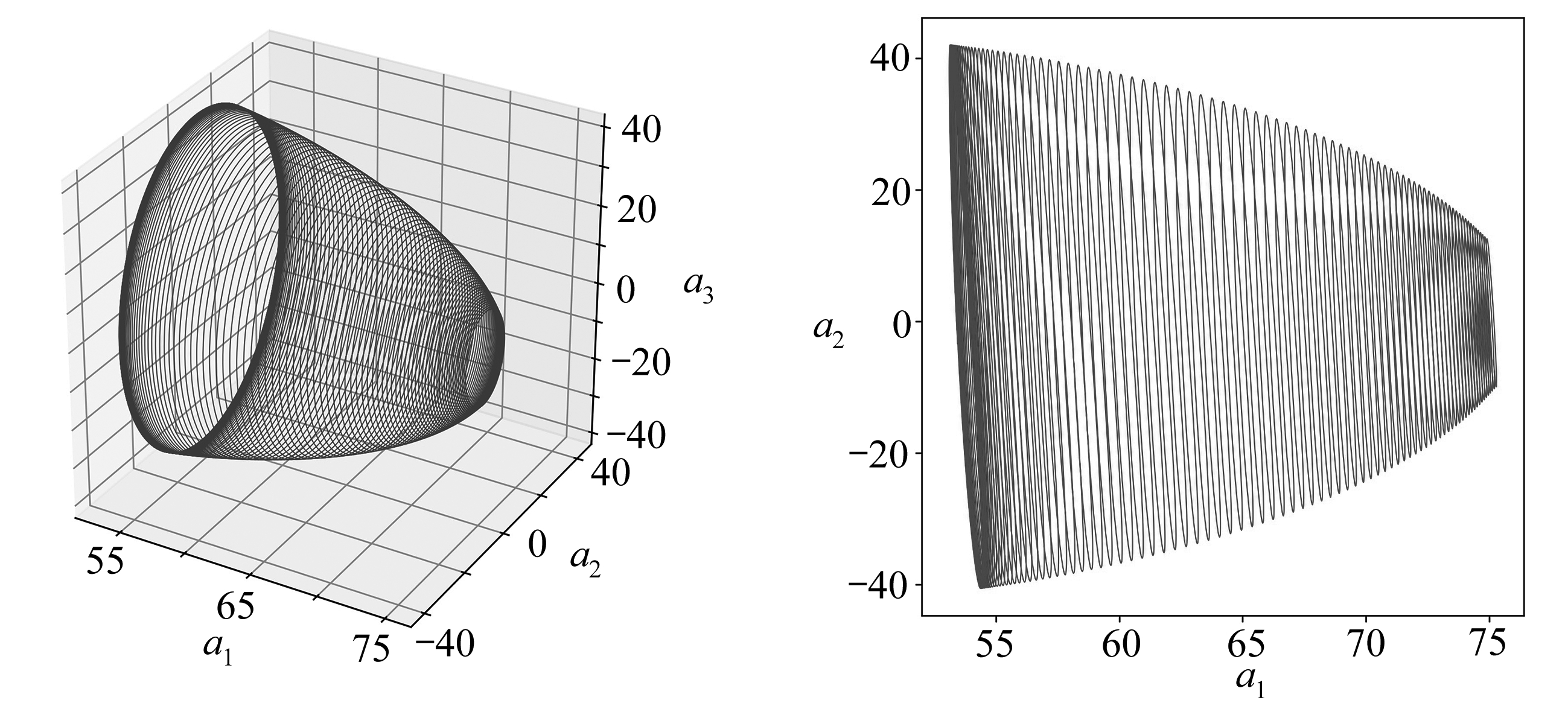
(a) a1-a2-a3 (b) a1-a2
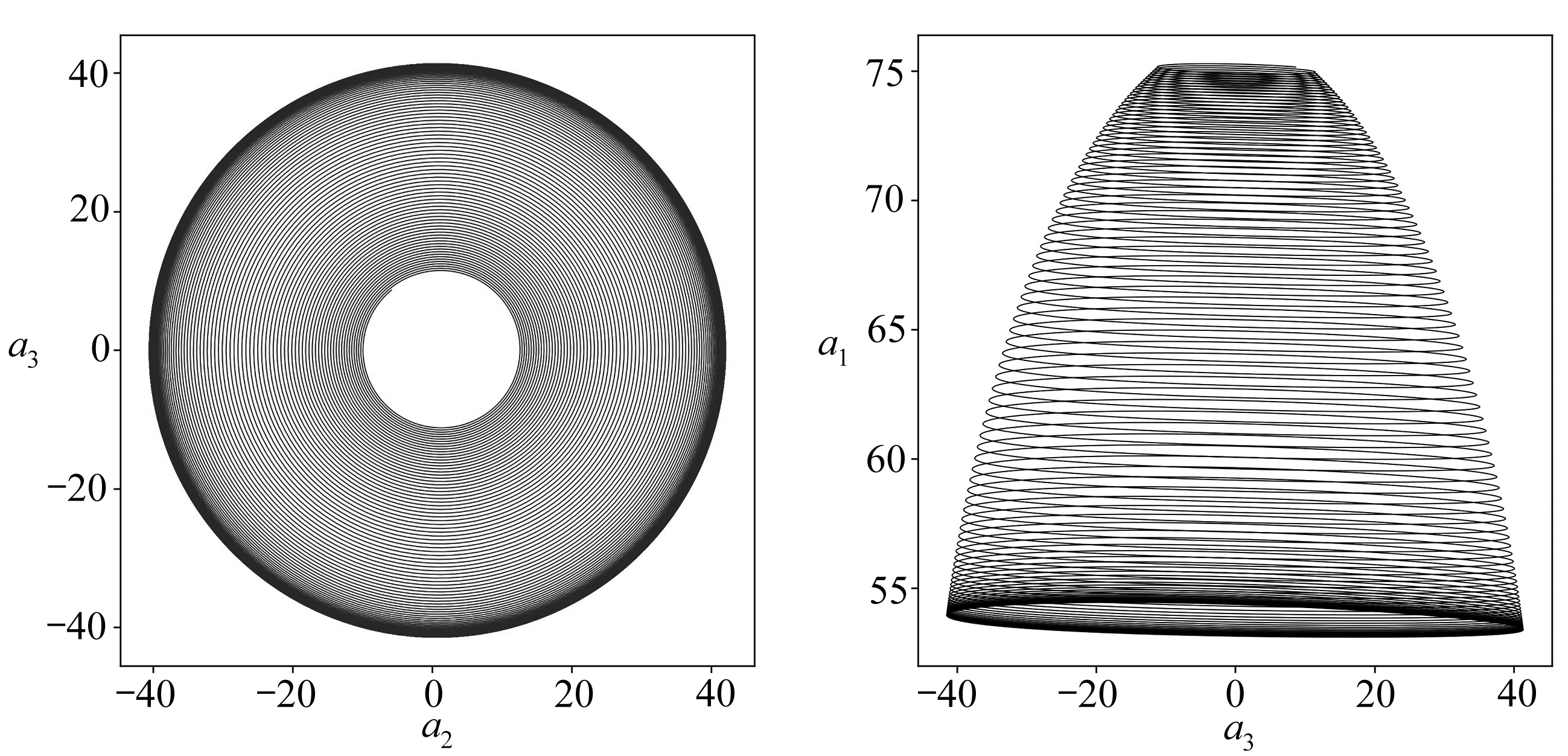
(c) a2-a3 (d) a3-a1
图5 最优动力系统相空间轨道
Fig. 5 Phase portaits of the optimal dynamical system
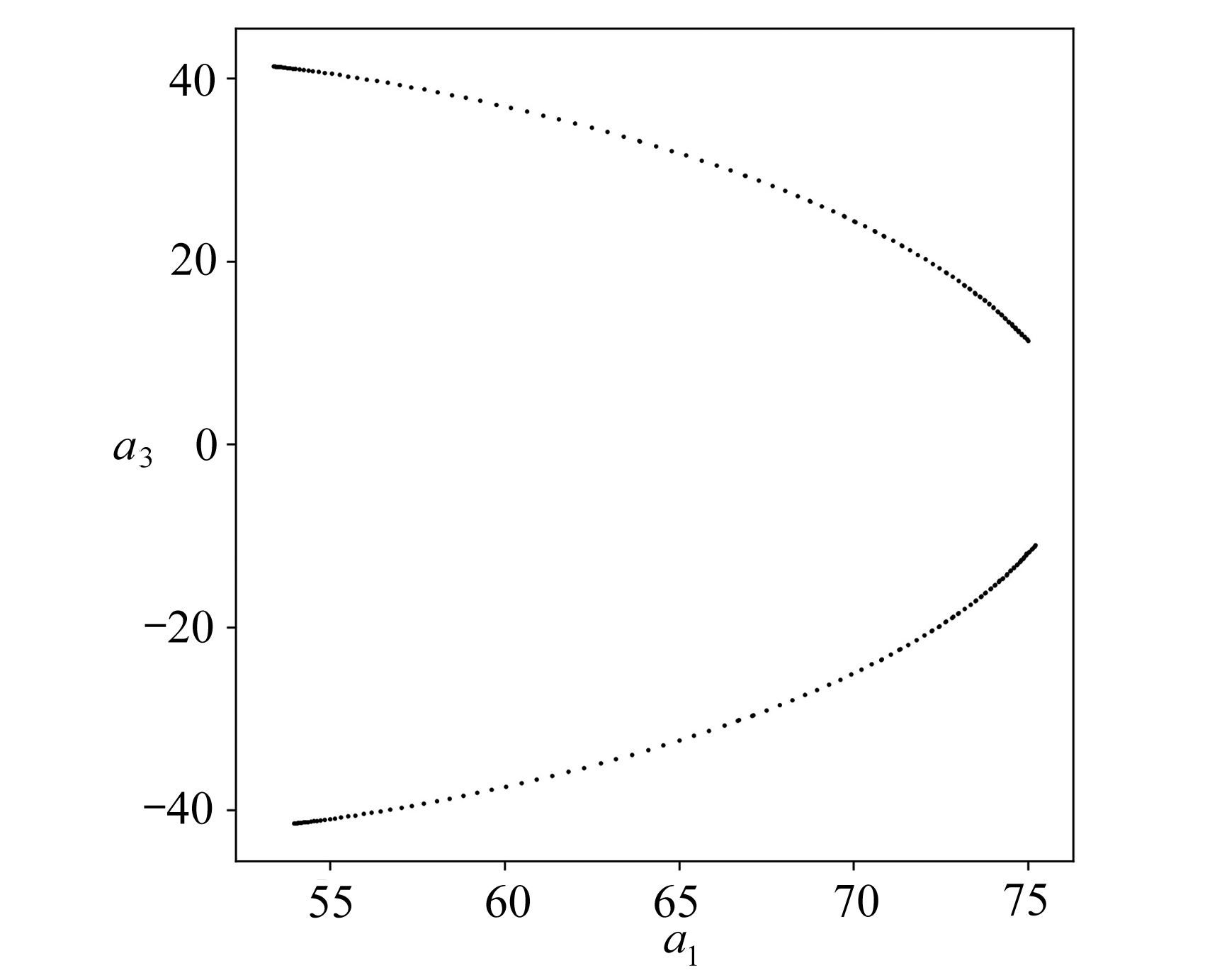
图6 相空间轨迹经过a2=0平面时的Poincaré截面
Fig. 6 The Poincaré section formed with the phase portrait intersecting plane a2=0
4.2 Poincaré截面
Poincaré截面是一种分析高维动力系统的有效方法,可以看作是一种离散的动力系统.图6是最优动力系统在相平面a2=0上的Poincaré截面,右端的点对应初始时刻,左端的点对应于末端时刻,结合图5的相轨迹,可以断定此系统在Re=100时的长期动力学特性是极限环.
4.3 功率谱分析
下面采用功率谱分析的方法来对最优动力系统的结果进行分析.取无量纲时间t=700.0~20 700.0的最优动力系统时间序列,一共M=105个点.首先,计算该序列的自相关函数:
(34)
其次,对Ci进行离散Fourier变换,得到功率谱:
(35)
在实际操作中,离散Fourier变换由FFT方法代替,且假设动力系统时间序列的总时长为1,根据采样定理,频率范围仅仅取为0~0.5,结果如图7所示,其中横坐标为频率ω,纵坐标率谱Pω.
理论上,功率谱中的尖峰代表周期运动,而宽峰和噪声背景代表混沌运动.由图7可知,a1的功率谱在0.01附近有两个主频,而a2和a3在0.01附近有三个主频,且存在宽峰.
4.4 Lyapunov指数
动力系统的众多特性中,Lyapunov指数扮演了很重要的角色,它可以定量地反映相邻轨道的分离程度,因此是一个可被用来衡量系统是否可以被预测的定量指标.Lyapunov指数为正时,反映出系统中存在正的不稳定能量,它会使得两个原本在一起的质点的运动轨迹逐渐分离;Lyapunov指数为负时,运动轨迹规则;Lyapunov指数为0时,质点轨迹不收缩也不发散.
在高维动力系统中,系统的混沌程度可以用Lyapunov指数集来描述,混沌程度与动力系统中正的Lyapunov指数个数正相关.对于Hamilton系统,混沌的特征是Lyapunov指数有正有负.对于非保守动力系统,动力学行为更混沌,因为正的Lyapunov指数可能有多个.Lyapunov指数在数学中的定义为
(36)
其中,J是动力系统的的Jacobi行列式,i=1,2,…,k,k为动力系统维数.该定义反映了动力系统在相空间中各个正交方向上的轨迹距离随指数变化情况的平均.
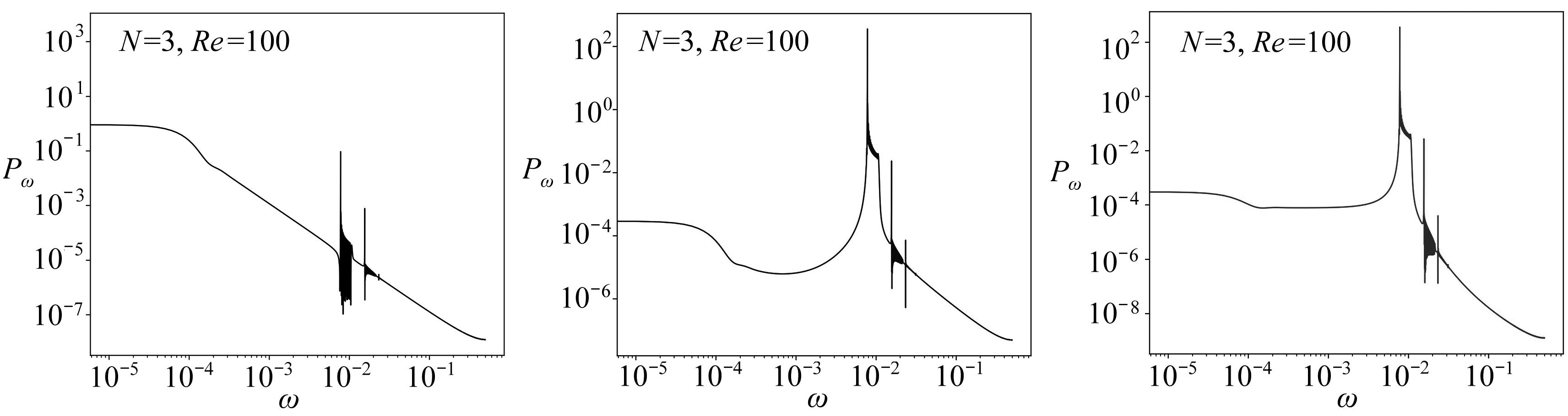
(a) a1的功率谱 (b) a2的功率谱 (c) a3的功率谱 (a) The power spectrum of a1(b) The power spectrum of a2(c) The power spectrum of a3
图7 最优动力系统轨迹的功率谱
Fig. 7 The power spectra of the portraits of optimal dynamical systems
Lyapunov指数的计算可以根据动力系统方程的右端项计算出Jacobi行列式而直接求出,但对于本文的最优动力系统,Jacobi行列式无法直接求出,这是因为对于为了使动力系统在任意时刻都满足边界条件,其右端项是随时间变化的,且不易求导,因此采用中心差分公式[25]来计算Jacobi行列式,即
(37)
其中,i=1,2,…,k, δ是一个与机器精度相关的小量.
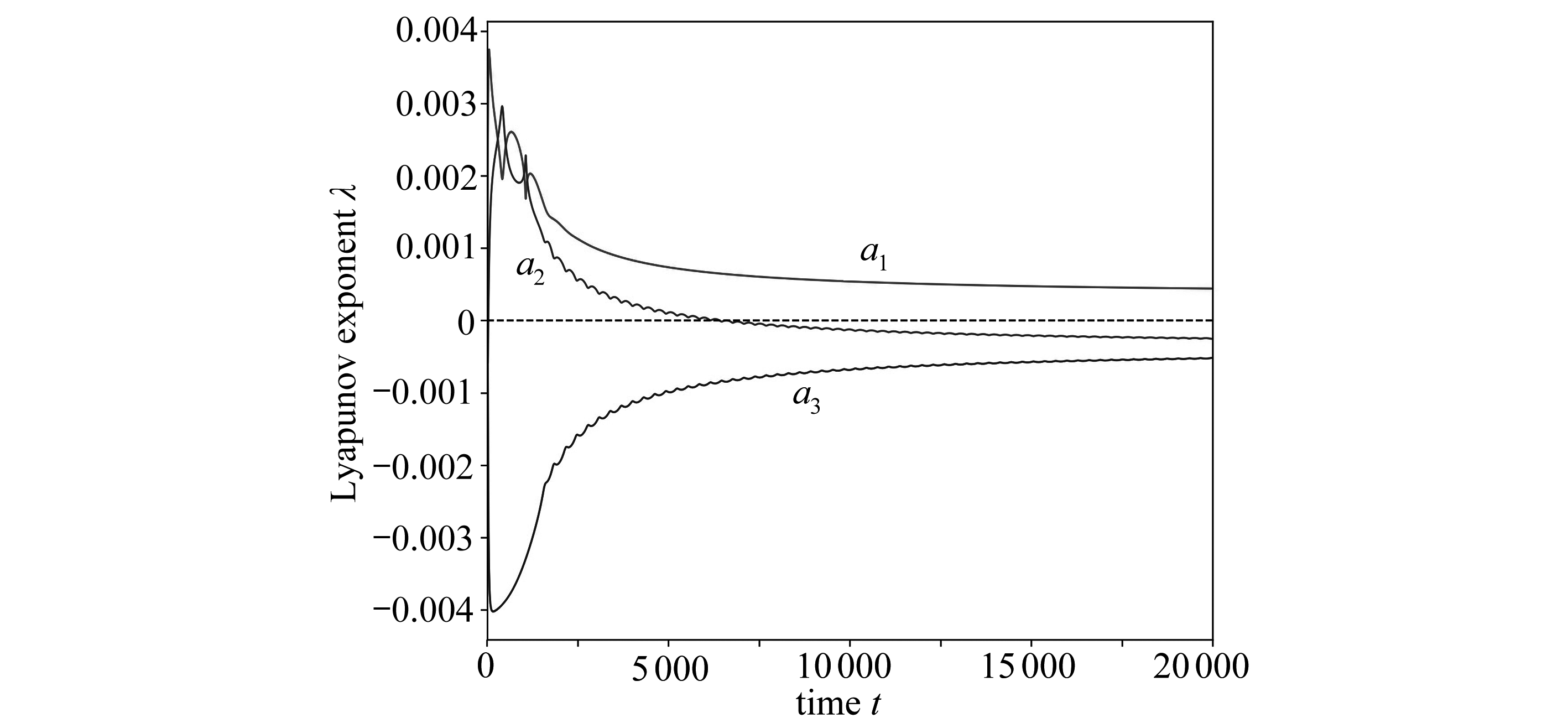
图8 最优动力系统 Lyapunov 指数集的演化
Fig. 8 The evolution of the Lyapunov exponent spectrum of the optimal dynamical system
采用上述方法对最优动力系统在t=700.0~20 700.0无量纲时段内的动力学行为进行Lyapunov指数集分析.假设动力系统起始时间为t=0.0,结果如图8所示,三个Lyapunov指数分别为0.000 440 58,-0.000 252 29和-0.000 519 03,即一个为正,两个为负,三者之和为负,反映出此最优动力系统为耗散系统,且长期动力学行为趋于稳定,与4.2小节中根据Poincaré截面得出的动力系统长期行为是极限环的结论相符合.
4.5 分岔特性
分岔图可以帮助全面了解最优动力系统在不同参数下的动力学特性,此前所描述的最优动力系统的动力学特性是在Re=100下的特殊情形,它们仅仅是分岔图的横轴上这一固定参数所具有的动力学特性.因此,下面研究最优动力系统随Reynolds数Re变化的分岔特性.需要说明,图9为分叉图,图中的横轴代表Reynolds数Re,纵轴代表a1,图中的点代表t=2 700.0~4 700.0无量纲时段内,最优动力系统轨迹与a2=0相平面相交时,在该Poincaré截面上的位置,无量纲时间步长为0.2.

(a) Re=100~300 (b) Re=250~300
图9 最优动力系统分岔图
Fig. 9 The bifurcation diagrams of the optimal system
图9(a)给出了Re=100~300之间的最优动力系统分岔特性,Re步长取为2;图9(b)给出了Re=250~300之间更为精细的最优动力系统分岔特性,Re步长取为0.1.可见,当Re=100~250时,最优动力系统的动力学特性为极限环或不动点; 当260<Re<279时,最优动力系统出现分岔;当Re≈280时,最优动力系统的动力学特性恢复为极限环;当Re>285时,最优动力系统再次出现分岔.
5 结 论
本文在最优动力系统的框架下,建立了满足任意速度边界条件和速度不可压条件的三维不可压缩Navier-Stokes方程的最优动力系统.其中,速度边界条件是通过满足物理空间的速度边界条件来实现的.以方柱绕流算例为例,对最优动力系统进行了数值分析和动力学特性分析,从相轨迹、Poincaré截面以及Lyapunov指数集可以发现,方柱绕流最优动力系统的动力学特性为极限环.当改变参数Re时,从分岔图可以看出,该系统的动力学特性随着Re的增大,分岔特性呈现间歇性的变化.由于仅包含了三个最优基函数的最优动力系统,就能很好地描述方柱绕流算例所有主要的流场特征和该问题的动力学特性,故本文提出的建模方法是一种能够用最少的基函数最大限度地描述复杂流体问题及其动力学特性的方法.
[1] POPE S B. Turbulent Flows[M]. Cambridge: Cambridge University Press, 2000.
[2] HOLMES P, LUMLEY J L, BERKOOZ G. Turbulence, Coherent Structures, Dynamical Systems and Symmetry[M]. Cambridge: Cambridge University Press, 1996.
[3] 是勋刚. 湍流[M]. 天津: 天津大学出版社, 1994.(SHI Xungang. Turbulence[M] Tianjin: Tianjin University Press, 1994.(in Chinese))
[4] SHRIER H N. Nonlinear Hydrodynamic Modeling: a Mathematical Introduction[M]. Berlin: Springer-Verlag, 1987.
[5] DANIELSON T J, OTTINO J M. Structural stability in two-dimensional model flows: Lagrangian and Eulerian turbulence[J]. Physics of Fluids A: Fluid Dynamics, 1990, 2(11): 2024-2035.
[6] POJE C, LUMLEY J L. A model for large scale structures in turbulence shear flows[J]. Journal of Fluid Mechanics, 1995, 285: 349-369.
[7] BERKOOZ G, HOLMES P, LUMLEY J L. The proper orthogonal decomposition in analysis of turbulent flows[J]. Annual Review of Fluid Mechanics, 1993, 25(1): 539-575.
[8] KALASHNIKOVA I, WAANDERS B V, ARUNAJATESAN S, et al. Stabilization of projection-based reduced order models for linear time-invariant systems via optimization-based eigenvalue reassignment[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 272: 251-270.
[9] LUO Z D, YANG X Z, ZHOU Y J. A reduced finite difference scheme based on singular value decomposition and proper orthogonal decomposition for Burgers equation[J]. Journal of Computational and Applied Mathematics, 2009, 229(1): 97-107.
[10] ALONSO D, VELAZQUEZ A, VEGA J M. A method to generate computationally efficient reduced order models[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198(33/36): 2683-2691.
[11] WANG X L, JIANG Y L. Model order reduction methods for coupled systems in the time domain using Laguerre polynomials[J]. Computers and Mathematics With Applications, 2011, 62(8): 3241-3250.
[12] AMMAR A, MOKDAD B, CHINESTA F, et al. A new family of solvers for some classes of multidimensional partial differential equations encountered in kinetic theory modeling of complex fluids[J]. Journal of Non-Newtonian Fluid Mechanics, 2006, 139(3): 153-176.
[13] WU C J. Large optimal truncated low-dimensional dynamical systems[J]. Discrete and Continuous Dynamical Systems (Series A), 1996, 2(4): 559-583.
[14] WU C J, SHI H S. An optimal theory for an expansion of flow quantities to capture the flow structures[J]. Fluid Dynamics Research, 1995, 17(2): 67-85.
[15] 吴锤结, 赵红亮. 不依赖数据库的最优动力系统建模理论及其应用[J]. 力学学报, 2001, 33(3): 289-300.(WU Chuijie, ZHAO Hongliang. A new database-free method of constructing optimal low-dimensional dynamical systems and its application[J] Acta Mechanica Sinica, 2001, 33(3): 289-300.(in Chinese))
[16] WU C J, WANG L. A method of constructing a database-free optimal dynamical system and a global optimal dynamical system[J]. Science in China(Series G): Physics, Mechanics & Astronomy, 2008, 51(7): 905-915.
[17] PENG N F, GUAN H, WU C J. Research on the optimal dynamical systems of three-dimensional Navier-Stokes equations based on weighted residual[J]. Science China: Physics, Mechanics & Astronomy, 2016, 59(4): 644-701.
[18] PENG N F, GUAN H, WU C J. Optimal dynamical systems of Navier-Stokes equations based on generalized helical-wave bases and the fundamental elements of turbulence[J]. Science China: Physics, Mechanics & Astronomy, 2016, 59(11): 114713. DOI: 10.1007/s11433-016-0247-3.
[19] TÖRN A, ZILINSKAS A. Global Optimization[M]. Berlin: Springer-Verlag, 1989.
[20] 叶庆凯, 王肇明. 优化与最优控制中的计算方法[M]. 北京: 科学出版社, 1986.(YE Qingkai, WANG Zhaoming. Computational Methods of Optimization and Optimum Control[M]. Beijing: Science Press, 1986.(in Chinese))
[21] 黄克智, 薛明德, 陆明万. 张量分析[M]. 北京: 清华大学出版社, 2003.(HUANG Kezhi, XUE Mingde, LU Mingwan. Tensor Analysis[M]. Beijing: Tsinghua University Press, 2003.(in Chinese))
[22] TORREY M D, MJOLSNESS R C, STEIN L R. NASA-VOF3D: a three-dimensional computer program for incompressible flows with free surfaces[R]. Nasa Sti/Recon Technical Report N, 1987.
[23] SIROVICH L. Turbulence and the dynamics of coherent structures, part Ⅲ: dynamics and scaling[J]. Quarterly of Applied Mathematics, 1987, 45(3): 561-571.
[24] CARBONE F, AUBRY N. Hierarchical order in wall-bounded shear turbulence[J]. Physics of Fluids, 1996, 8(4): 1061-1075.
[25] KAUFMAN E H, LEEMING D J, TAYLOR G D. An ODE-based approach to nonlinearly constrained minimax problems[J]. Numerical Algorithms, 1995, 9(1): 25-37.