引 言
考虑如下连续的Sylvester矩阵方程:
AX+XB=F,
(1)
其中A∈Cm×m,B∈Cn×n,F∈Cm×n,且A,B,F均为稀疏矩阵,A,B为正定矩阵.作为矩阵方程中极其重要的一类方程,连续Sylvester方程在工程计算等诸多领域都有着广泛的应用,如控制与系统理论[1-2]、图形恢复[3]、信号处理[4]等方面,因此求解连续Sylvester方程具有非常重要的实际工程意义和学术价值.
对于连续Sylvester方程(1)的求解,目前主要有两种方式进行处理,第一种是将Sylvester矩阵方程(1)进行拉直,转化为形如![]() 的形式求解,其中
的形式求解,其中![]() 分别是阶数为n和m的单位矩阵;第二种是直接对Sylvester方程(1)进行迭代求解.然而当Sylvester方程(1)的阶数较大时,会导致线性方程系数矩阵
分别是阶数为n和m的单位矩阵;第二种是直接对Sylvester方程(1)进行迭代求解.然而当Sylvester方程(1)的阶数较大时,会导致线性方程系数矩阵![]() 的维数急剧增大,一方面会引发病态方程的产生,另一方面会造成计算机存储量的增大,计算时间的增加.因此,直接对连续的Sylvester矩阵方程(1)的求解成为了当前众多学者关注的热点.
的维数急剧增大,一方面会引发病态方程的产生,另一方面会造成计算机存储量的增大,计算时间的增加.因此,直接对连续的Sylvester矩阵方程(1)的求解成为了当前众多学者关注的热点.
目前直接法和迭代法是求解连续Sylvester矩阵方程(1)的主要工具.直接法主要用于矩阵方程(1)阶数较小的情况,如Bartels-Stewart和Hessenberg-Schur方法[5-6].迭代法一般用于矩阵阶数较大或系数矩阵为稀疏矩阵的情况.近些年,众多学者基于系数矩阵分裂的思想提出了大量有效可行的算法[7-13]:如Bai提出了求解连续Sylvester方程(1)的HSS迭代算法(Hermitian and skew-Hermitian splitting),该算法是求解线性方程![]() 的HSS算法的拓展[7].为了提高HSS算法的收敛性,修正HSS(MHSS)算法避免了HSS算法每次迭代求解复线性矩阵方程的过程,而只需在每次迭代中求解两个实线性子系统,进而大大加速了算法的收敛性,减少迭代时间[8].之后,由于预处理技术的引入,相继提出预处理HSS(PHSS)算法、非交错PHSS(NPHSS)算法、非精确PHSS(IPHSS)算法以及非精确NPHSS(INPHSS)算法[9],大大改善了原HSS算法的收敛速度.然而,上述的分裂迭代算法均面临一个最优迭代参数选取的问题,并且由于最优迭代参数的选取并没有一个统一的公式去定性计算,这在一定程度上增加了此类分裂迭代算法计算的复杂性.
的HSS算法的拓展[7].为了提高HSS算法的收敛性,修正HSS(MHSS)算法避免了HSS算法每次迭代求解复线性矩阵方程的过程,而只需在每次迭代中求解两个实线性子系统,进而大大加速了算法的收敛性,减少迭代时间[8].之后,由于预处理技术的引入,相继提出预处理HSS(PHSS)算法、非交错PHSS(NPHSS)算法、非精确PHSS(IPHSS)算法以及非精确NPHSS(INPHSS)算法[9],大大改善了原HSS算法的收敛速度.然而,上述的分裂迭代算法均面临一个最优迭代参数选取的问题,并且由于最优迭代参数的选取并没有一个统一的公式去定性计算,这在一定程度上增加了此类分裂迭代算法计算的复杂性.
为了避免最优迭代参数的选取,本文借鉴上述分裂迭代算法的思想,拟采用内外迭代进行处理,通过将连续的Sylvester矩阵方程(1)的系数矩阵A和B分裂为对称矩阵和反对称矩阵,使内迭代过程转化为复对称矩阵方程组的求解.而近些年来对于复对称线性方程组的求解已有大量丰富的学术成果,从宏观角度出发,主要分为分裂迭代法[14-19]和Krylov子空间迭代法[20-24]两大类.但基于最优迭代参数选取的考虑,现主要针对Krylov子空间迭代法进行研究,如共轭正交共轭梯度(COCG)法[20-21]、共轭A-正交共轭残量(COCR)法[21-22]、复对称矩阵的双共轭梯度(SCBiCG(Г,m))法[23]以及复对称矩阵的双共轭残量(SCBiCR(Г,m))法[24]等Krylov子空间迭代法.COCG法和COCR法分别是共轭梯度(CG)法和共轭残量(CR)法的延拓,但在实际应用中由于COCG法有时会导致不规则的收敛行为,因此COCR法相较于COCG法具有更好的鲁棒性.SCBiCG(Г,m)法和SCBiCR(Г,m)法分别由双共轭梯度(BiCG)法和双共轭残量(BiCR)法推导得到,但相较于SCBiCG(Г,m)法,SCBiCR(Г,m)法克服了SCBiCG(Г,m)法需要确定系数ci的不足,大大提高了收敛速度.此外,丰富的预处理技术应用也大大加快了Krylov子空间迭代法的收敛速度[21].
基于上述的调研,本文主要针对连续的Sylvester矩阵方程(1)的求解,提出了一种新型的分裂迭代算法,该算法采用内外迭代方式进行求解,外迭代基于分裂思想,将系数矩阵A,B分裂为一个对称矩阵和一个反对称矩阵,该分裂方式区别于HSS一类方法的分裂方式(Hermitian矩阵和反Hermitian矩阵);内迭代采用复对称线性方程组的求解算法,有效地避免了最优迭代参数的选取.基于这样一种新型的分裂迭代算法,可有效地加快连续的Sylvester矩阵方程(1)的收敛速度.
文中内积定义:若X,Y∈Cm×n,则其内积为〈X,Y〉=tr(XHY),由此导出矩阵的Frobenius范数为![]() 表示X的转置矩阵,
表示X的转置矩阵,![]() 表示X的共轭矩阵,XH表示X的共轭转置矩阵,ρ(X)表示矩阵X的谱半径,
表示X的共轭矩阵,XH表示X的共轭转置矩阵,ρ(X)表示矩阵X的谱半径,![]() 表示矩阵X的拉直,X⊗Y表示矩阵X与Y的直积或Kronecker积.若x∈C,Re(x)表示x的实部,Im(x)表示x的虚部.
表示矩阵X的拉直,X⊗Y表示矩阵X与Y的直积或Kronecker积.若x∈C,Re(x)表示x的实部,Im(x)表示x的虚部.
1 分裂迭代算法
针对连续Sylvester矩阵方程(1)的求解,拟基于分裂迭代思想,采用内外迭代格式进行处理,其中外迭代主要对系数矩阵进行分裂,内迭代执行复对称矩阵方程组的求解,以下给出详细的推导过程.
1.1 外迭代格式
首先将连续Sylvester矩阵方程(1)的系数矩阵A和B分裂为
A=M1-N1, B=M2-N2,
(2)
其中
M1=(AT+A)/2, N1=(AT-A)/2, M2=(BT+B)/2, N2=(BT-B)/2,
(3)
满足![]() 故矩阵方程(1)等价于
故矩阵方程(1)等价于
M1X+XM2=N1X+XN2+F.
(4)
然后根据矩阵方程(4),建立相应的分裂迭代格式.
给定初始矩阵X0∈Cm×n,外迭代格式如下:
M1Xk+1+Xk+1M2=N1Xk+XkN2+F.
(5)
令![]() 则有
则有
(6)
计算Xk+1∈Cm×n,k=0,1,2,…,直至迭代序列{Xk![]() 收敛.
收敛.
通过上述外迭代格式的分析,可知外迭代过程已将连续Sylvester矩阵方程(1)的求解转化为复对称矩阵方程组(6)的求解,相应地,内迭代过程主要针对这一问题进行处理.
1.2 内迭代格式
基于文献调研,大量的研究成果主要针对复对称线性方程组![]() 的形式进行求解,其中
的形式进行求解,其中![]() 故为了有效求解复对称矩阵方程(6),本文拟通过线性变换形式,将求解
故为了有效求解复对称矩阵方程(6),本文拟通过线性变换形式,将求解![]() 的可行算法进行延拓.
的可行算法进行延拓.
1.2.1 复对称线性变换
首先给出复对称线性变换的定义.
定义1 设T是酉空间V上的线性变换,对于任意X,Y∈V,满足
(7)
则称T为酉空间V中一个对称变换.
根据复对称线性变换的定义,给出相应的复对称线性变换方程:
T(X)=C,
(8)
其中T(X)=MX+XN, M∈Cm×m,N∈Cn×n,X∈Cm×n,且M=MT,N=NT.
下面验证酉空间V上的线性变换T(X)=MX+XN为复对称变换.
根据酉空间的内积定义满足![]() 则
则
故线性变换T(X)=MX+XN为酉空间V中一个对称变换.
1.2.2 算法延拓
为了提升分裂迭代算法的收敛性,这里仅针对文献中收敛性较好的3种算法进行代表性阐明拓展,即COCR算法[21-22]、COCG算法[20-21]以及CCC of SCBiCR算法(简记为CCC_SCBiCR算法)[24].如下给出求解复对称线性变换方程(8)的3种拓展算法.
首先给出求解复对称线性变换方程(8)的COCR算法.
第1步 给定初始矩阵X0∈Cm×n,计算R0=C-T(X0),置P0=R0,U0=T(P0),S0=U0,k![]() 0.
0.
第2步 若‖Rk‖F≤ε‖R0‖F,计算停止,其中ε∈R+;否则,计算
第3步 置k![]() k+1,转第2步.
k+1,转第2步.
其次给出求解复对称线性变换方程(8)的COCG算法.
第1步 给定初始矩阵X0∈Cm×n,计算R0=C-T(X0),置P0=R0,k![]() 0.
0.
第2步 若‖Rk‖F≤ε‖R0‖F,计算停止,其中ε∈R+;否则,计算
第3步 置k![]() k+1,转第2步.
k+1,转第2步.
最后给出求解复对称线性变换方程(8)的CCC_SCBiCR算法.
第1步 给定初始矩阵X0∈Cm×n,计算R0=C-T(X0),置P0=R0,U0=T(R0),S0=U0,k![]() 0.
0.
第2步 若‖Rk‖F≤ε‖R0‖F,计算停止,其中ε∈R+;否则,计算
Pk+1=Rk+1+βkPk, Sk+1=Uk+1+βkSk.
第3步 置k![]() k+1,转第2步.
k+1,转第2步.
1.3 分裂迭代算法
通过内外迭代格式的推导,如下给出整体的分裂迭代算法.
第1步 给定一个初始矩阵X0∈Cm×n,通过式(3),计算M1,M2,N1,N2,R0=F-AX0-X0B,置k![]() 0.
0.
第2步(外迭代) 若‖Rk‖F≤ε‖R0‖F,计算停止,其中ε∈R+;否则,计算
第3步(内迭代) 采用COCR、COCG及CCC_SCBiCR中任意一种方法求解
计算Rk+1=F-AXk+1-Xk+1B.
第4步 置k![]() k+1,转第2步.
k+1,转第2步.
为了后续描述方便,采用不同内迭代方法的分裂迭代算法分别记作TS_COCR算法、TS_COCG算法以及TS_CCC_SCBiCR算法.
2 收敛性分析
针对文中所提出的分裂迭代算法,给出其相应的收敛性质.
定理1 假定A∈Cm×m是正定矩阵,且AM-N,其中M=(AT+A)/2,N=(AT-A)/2.若对于任意的x∈Cm且x≠0,满足![]() 则ρ(M-1N)<1.
则ρ(M-1N)<1.
证明 设M-1N的特征值为λ,相应的特征向量为x,则满足M-1Nx=λx,等价于λMx=Nx.故|λ|=|xHNx|/|xHMx|.又由于M=MT,N=-NT,所以
(9)
而若要满足![]() <1,则需满足
<1,则需满足![]() 而
而
则如果对任意的x∈Cm且x≠0,满足![]() 则ρ(M-1N)<1. 证毕.
则ρ(M-1N)<1. 证毕.
□
定理2 假定连续的Sylvester方程AX+XB=F中的A∈Cm×m,B∈Cn×n是正定矩阵,且A=M1-N1,B=M2-N2,其中M1=(AT+A)/2,N1=(AT-A)/2,M2=(BT+B)/2,N2=(BT-B)/2.若对任意的X∈Cm×n且X≠0,满足![]() 则ρ((M1⊗In+Im⊗M2)-1(N1⊗In+Im⊗N2))<1.
则ρ((M1⊗In+Im⊗M2)-1(N1⊗In+Im⊗N2))<1.
证明 将连续的Sylvester方程AX+XB=F两端拉直,可得
(10)
其中![]() 由A=M1-N1,B=M2-N2可知,方程(10)等价于
由A=M1-N1,B=M2-N2可知,方程(10)等价于
(11)
令![]() 则满足
则满足
(12)
(13)
由定理1可知, 对于任意的![]() 且
且![]() 满足
满足![]() 则
则![]() 而
而
(14)
故对任意的X∈Cm×n且X≠0,当满足![]() 时,
时,
ρ((M1⊗In+Im⊗M2)-1(N1⊗In+Im⊗N2))<1.
证毕.
□
3 数值算例与结果分析
对于连续Sylvester矩阵方程(1)的求解,分别采用INPHSS算法[9]、CGS算法[25]、TS_COCR算法、TS_COCG算法和TS_CCC_SCBiCR算法进行对比分析,以此验证本文所提出分裂迭代算法的可行性和有效性.本文算例主要针对稀疏复线性方程组.算例中,初始矩阵X0=0∈Cm×n,Rk=F-AXk-XkB,其中Xk表示第k步迭代矩阵,Rk表示第k步迭代误差,终止条件满足‖Rk‖F/‖R0‖F≤10-8,即算法中提及的ε=10-8.此外对于INPHSS算法中所涉及的矩阵P1和P2满足P1=Im,P2=βIn/α,其中α=β,Im和In分别为m阶和n阶单位矩阵.内迭代过程采用求解Hermite正定方程组的CG算法.CGS算法中选取![]() 算例中k,t分别表示计算近似解的迭代次数和迭代时间,且算例中的迭代次数k表示的是INPHSS算法、TS_COCR算法、TS_COCG算法及TS_CCC_SCBiCR算法的外迭代次数.
算例中k,t分别表示计算近似解的迭代次数和迭代时间,且算例中的迭代次数k表示的是INPHSS算法、TS_COCR算法、TS_COCG算法及TS_CCC_SCBiCR算法的外迭代次数.
本文所有算例均使用双精度浮点运算并在MATLAB R2017b平台上运行,电脑配置为PC-Intel(R) Core(TM) i7-6700 CPU 3.40 GHz,16 GB内存.
例1 考虑连续Sylvester矩阵方程(1),且m=n,方程(1)中系数矩阵为
A=MA+2qNA+100I/(n+1)2, B=MB+2qNB+100I/(n+1)2,
其中三对角矩阵MA,NA,MB,NB∈Rn×n,满足
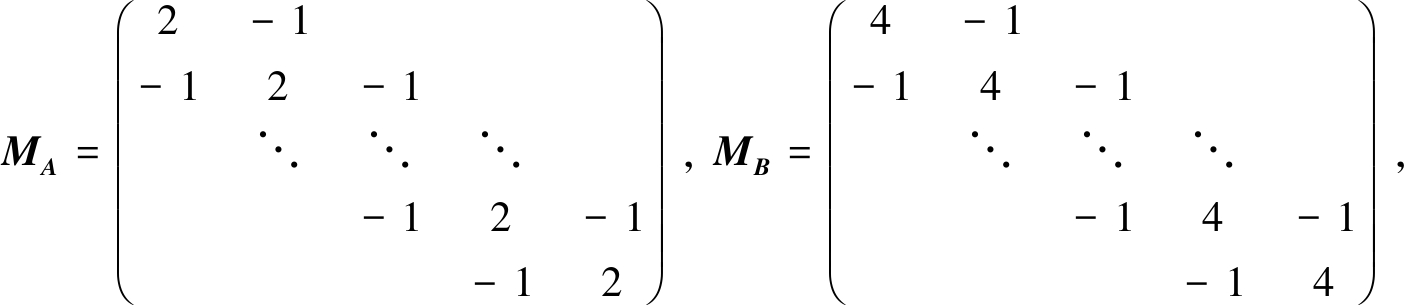
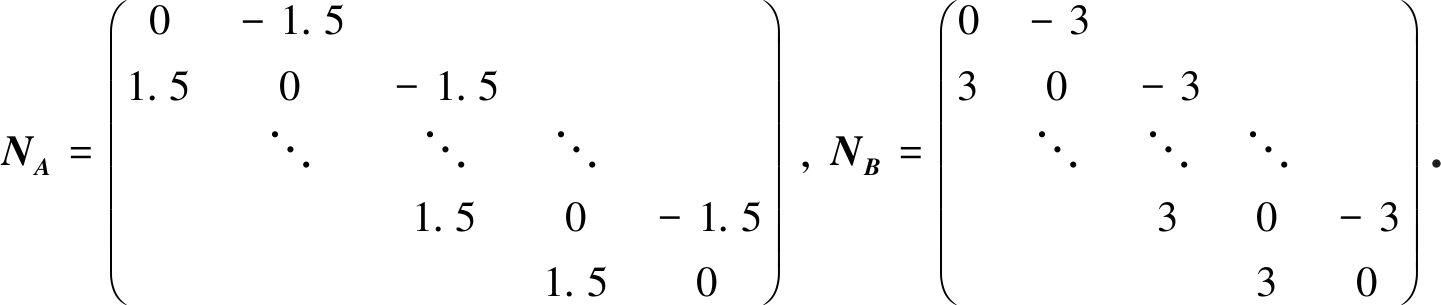
右端项F选取随机稀疏矩阵.该算例的系数矩阵来源于文献[9].针对该算例,INPHSS算法的理论最优迭代参数α如表1所示[9],INPHSS算法、CGS算法、TS_COCR算法、TS_COCG算法及TS_CCC_SCBiCR算法的计算结果对比详见表2.
表1 INPHSS的理论最优迭代参数
Table 1 The theoretical quasi-optimal iteration parameters for INPHSS

nαq=0.05q=0.1q=0.2800.033 00.131 90.527 61600.033 60.134 20.536 8
表2 INPHSS、CGS、TS_COCR、TS_COCG及TS_CCC_SCBiCR求解例1的数值结果
Table 2 Numerical results of example 1 obtained with the INPHSS,CGS,TS_COCR,TS_COCG
and TS_CCC_SCBiCR methods
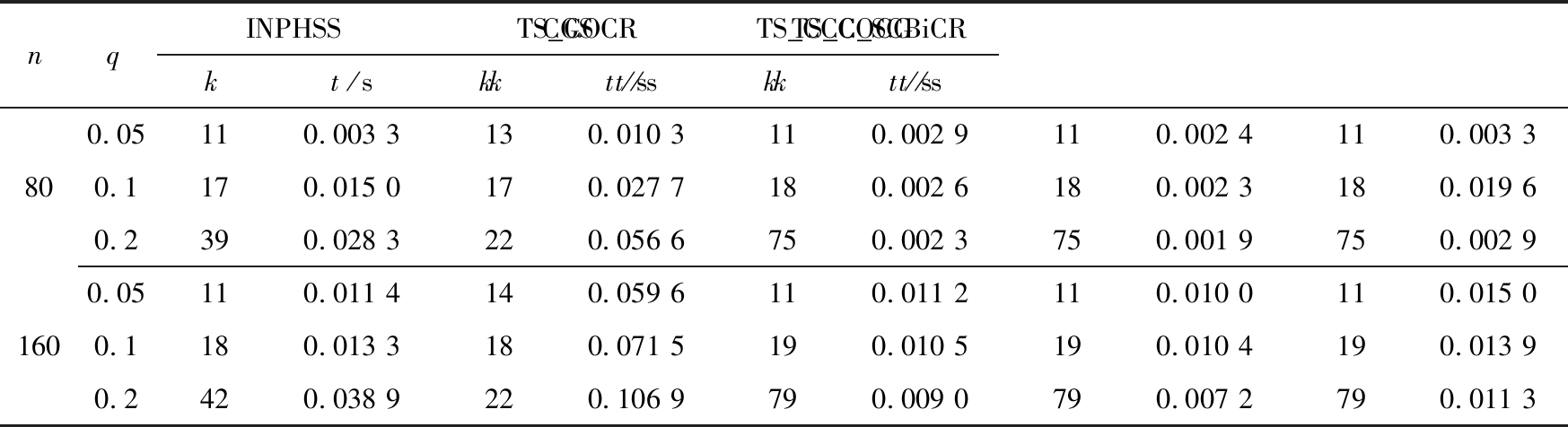
nqINPHSSkt/sCGSkt/sTS_COCRkt/sTS_COCGkt/sTS_CCC_SCBiCRkt/s800.05110.003 3130.010 3110.002 9110.002 4110.003 30.1170.015 0170.027 7180.002 6180.002 3180.019 60.2390.028 3220.056 6750.002 3750.001 9750.002 91600.05110.011 4140.059 6110.011 2110.010 0110.015 00.1180.013 3180.071 5190.010 5190.010 4190.013 90.2420.038 9220.106 9790.009 0790.007 2790.011 3
例2 考虑连续Sylvester矩阵方程(1),且m=n,方程(1)中系数矩阵为
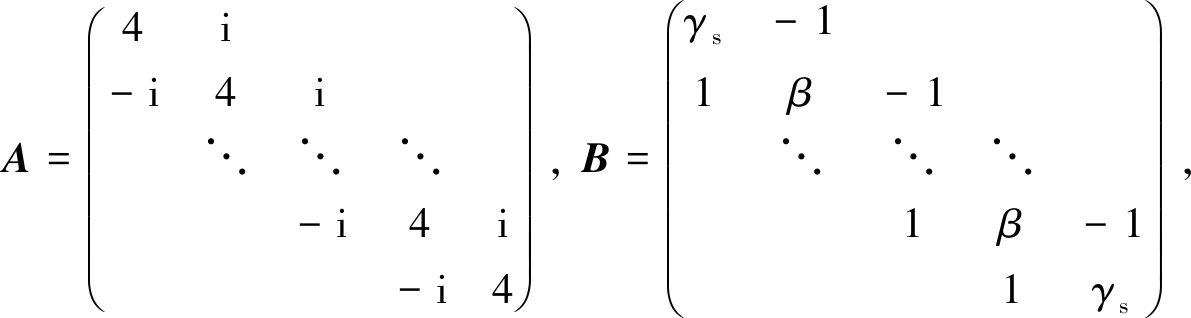
其中β=2-k2h2,γs=2-k2h2-(1+ikh)/(1+k2h2),h=1/(n+1),k=1.右端项F=AX*+X*B,其中X*=I+iE,I为单位矩阵,E=(eij)m×n,且eij=1.CGS算法、TS_COCR算法、TS_COCG算法及TS_CCC_SCBiCR算法的计算结果对比详见表3.
表3 CGS、TS_COCR、TS_COCG及TS_CCC_SCBiCR求解例2的数值结果
Table 3 Numerical results of example 2 obtained with the CGS,TS_COCR,TS_COCG
and TS_CCC_SCBiCR methods

nCGSkt/sTS_COCRkt/sTS_COCGkt/sTS_CCC_SCBiCRkt/s2880.344 7200.057 2200.049 3200.084 321082.459 2191.037 8190.681 8191.651 62128129.220 21864.383 81846.332 31870.753 6
例3 考虑连续Sylvester矩阵方程(1),且m=n,方程(1)中系数矩阵为
A=triu(rand(n),1)×i+diag(qIn+diag(rand(n))),
B=tril(rand(n),1)+diag(qIn+diag(rand(n)))×5i,
其中![]() 表示 n阶随机矩阵,triu(rand(n),1)表示提取n阶随机矩阵rand(n)的上三角矩阵,对角线及对角线以下元素均为0,tril(rand(n),1)表示提取n阶随机矩阵rand(n)的下三角矩阵,对角线及对角线以上元素均为0.右端项矩阵F=AX*+X*B,其中X*=I+iE,I为单位矩阵,E=(eij)m×n,且eij=1.CGS算法、TS_COCR算法、TS_COCG算法及TS_CCC_SCBiCR算法的计算结果对比详见表4.
表示 n阶随机矩阵,triu(rand(n),1)表示提取n阶随机矩阵rand(n)的上三角矩阵,对角线及对角线以下元素均为0,tril(rand(n),1)表示提取n阶随机矩阵rand(n)的下三角矩阵,对角线及对角线以上元素均为0.右端项矩阵F=AX*+X*B,其中X*=I+iE,I为单位矩阵,E=(eij)m×n,且eij=1.CGS算法、TS_COCR算法、TS_COCG算法及TS_CCC_SCBiCR算法的计算结果对比详见表4.
基于表1~4的数值结果,采用INPHSS、CGS、TS_COCR、TS_COCG及TS_CCC_SCBiCR求解连续的Sylvester矩阵方程(1)可得到如下相关结论:
1) 表1表明随着参数q的增加,系数矩阵A和B次对角线元素增大,进而INPHSS算法所涉及的理论拟最优参数值增加,且在同一矩阵维数下,INPHSS算法的迭代次数和迭代时间也随着参数q的增加而增加;相较于CGS算法和TS_CCC_SCBiCR算法,INPHSS算法具有良好的收敛性,然而TS_COCG算法和TS_COCR算法的收敛速度明显优于INPHSS算法,并且避免了最优迭代参数的选取.
2) 表2~4的数值结果表明,相较于直接求解矩阵方程(1)的CGS算法,分裂迭代法(TS_COCR、TS_COCG、TS_CCC_SCBiCR)明显提高了方程(1)的求解速度;此外通过观察文中所提出的分裂迭代法,可以发现随着阶数n的增加,TS_COCG算法具有良好的收敛性,特别是例2,当矩阵阶数达到212时,TS_COCG算法相较于TS_COCR和TS_CCC_SCBiCR算法,迭代速度加快了至少0.25倍,这也进一步说明了TS_COCG算法的有效性和优越性.
表4 CGS、TS_COCR、TS_COCG及TS_CCC_SCBiCR求解例3的数值结果
Table 4 Numerical results of example 3 obtained with the CGS,TS_COCR,TS_COCG
and TS_CCC_SCBiCR methods

nCGSkt/sTS_COCRkt/sTS_COCGkt/sTS_CCC_SCBiCRkt/s10070.014 5180.007 6180.006 6180.012 120080.056 3240.046 9240.039 9240.063 740090.337 0390.335 5390.308 7390.438 2
基于上述结论,可知分裂迭代法中内迭代格式所采用的算法直接影响到整体算法的收敛速度,但对于外迭代次数却毫无影响,这进一步说明内迭代过程针对上述3个算例均进行了精确求解;同时算例结果也说明了文中所提出的分裂迭代法的可行性和有效性.
4 结 束 语
本文主要通过将系数矩阵分裂为对称矩阵和反对称矩阵,而后利用复对称矩阵求解高效的特点,提出了针对连续Sylvester矩阵方程(1)求解的分裂迭代算法,有效提高了算法的计算效率,大大降低了计算时间.以下是针对分裂迭代算法的总结:
1) 相较于传统的CGS算法,分裂迭代算法(TS_COCR、TS_COCG、TS_CCC_SCBiCR)因其利用了系数矩阵分裂后复对称的特点,具有良好的收敛性;此外,所提出的算法与传统的分裂思想不同(分裂为Hermite矩阵和反Hermite矩阵),巧妙避免了最优迭代参数的选取,提高了算法的易实现性、易操作性.
2) 分裂迭代算法由内外迭代格式组成,并且整体算法的收敛性很大程度依赖于内迭代格式的选取,而COCG法和COCR法相较于CCC_SCBiCR法具有较好的收敛性和鲁棒性,因此,从理论层面来看TS_COCR和TS_COCG算法的收敛速度优于TS_CCC_SCBiCR算法的收敛速度,同时数值算例也验证了这一点.
[1] LANCASTER P, RODMAN L. Algebraic Riccati Equations[M]. Oxford: The Clarendon Press, 1995.
[2] CHIANG C Y. On the Sylvester-like matrix equation AX+f(X)B=C[J]. Journal of the Franklin Institute, 2016, 353: 1061-1074.
[3] CALVETTI D, REICHEL L. Application of ADI iterative methods to the restoration of noisy images[J]. SIAM Journal on Matrix Analysis and Applications, 1996, 17(1): 165-186.
[4] ANDERSON B, AGATHOKLIS P, JURY E, et al. Stability and the matrix Lyapunov equation for discrete 2-dimensional systems[J]. IEEE Transactions on Circuits and Systems, 1986, 33(3): 261-267.
[5] BARTELS R H, STEWART G W. Solution of the matrix equation AX+XB=C[F4][J]. Communications of the ACM, 1972, 15(9): 820-826.
[6] GOLUB G, NASH S, VAN LOAN C. A Hessenberg-Schur method for the problem AX+XB=C[J]. IEEE Transactions on Automatic Control, 1979, 24(6): 909-913.
[7] BAI Z Z. On Hermitian and skew-Hermitian splitting iteration methods for continuous Sylvester equations[J]. Journal of Computational Mathematics, 2011, 29(2): 185-198.
[8] ZHOU D M, CHEN G L, CAI Q Y. On modified HSS iteration methods for continuous Sylvester equations[J]. Applied Mathematics and Computation, 2015, 263: 84-93.
[9] XU L, HUO H F, YANG A L. Preconditioned HSS iteration method and its non-alternating variant for continuous Sylvester equations[J]. Computers and Mathematics With Applications, 2018, 75(4): 1095-1106.
[10] DEHGHAN M, SHIRILORD A. A generalized modified Hermitian and skew-Hermitian splitting (GMHSS) method for solving complex Sylvester matrix equation[J]. Applied Mathematics and Computation, 2019, 348: 632-651.
[11] ZHOU R, WANG X, TANG X B. A generalization of the Hermitian and skew-Hermitian splitting iteration method for solving Sylvester equations[J]. Applied Mathematics and Computation, 2015, 271: 609-617.
[12] ZHOU R, WANG X, TANG X B. Preconditioned positive-definite and skew-Hermitian splitting iteration methods for continuous Sylvester equations AX+XB=C[J]. East Asian Journal on Applied Mathematics, 2017, 7(1): 55-69.
[13] ZHENG Q Q, MA C F. On normal and skew-Hermitian splitting iteration methods for large sparse continuous Sylvester equations[J]. Journal of Computational and Applied Mathematics, 2014, 268: 145-154.
[14] XIAO X Y, WANG X, YIN H W. Efficient single-step preconditioned HSS iteration methods for complex symmetric linear systems[J]. Computers and Mathematics With Applications, 2017, 74(10): 2269-2280.
[15] XIAO X Y, WANG X, YIN H W. Efficient preconditioned NHSS iteration methods for solving complex symmetric linear systems[J]. Computers and Mathematics With Applications, 2018, 75(1): 235-247.
[16] 杨丽, 李军. Hilbert空间中分裂可行性问题的改进Halpern迭代和黏性逼近算法[J]. 应用数学和力学, 2017, 38(9): 1072-1080.(YANG Li, LI Jun. Modified Halpern iteration and viscosity approximation methods for split feasibility problems in Hilbert spaces[J]. Applied Mathematics and Mechanics, 2017, 38(9): 1072-1080.(in Chinese))
[17] LI C L, MA C F. On semi-convergence of parameterized SHSS method for a class of singular complex symmetric linear systems[J]. Computers and Mathematics With Applications, 2019, 77: 466-475.
[18] HUANG Z G, WANG L G, XU Z, et al. The generalized double steps scale-SOR iteration method for solving complex symmetric linear systems[J]. Journal of Computational and Applied Mathematics, 2019, 346: 284-306.
[19] HUANG Z G, WANG L G, XU Z, et al. Preconditioned accelerated generalized successive overrelaxation method for solving complex symmetric linear systems[J]. Computers and Mathematics With Applications, 2019, 77(7): 1902-1916.
[20] VAN DER VORST H A, MELISSEN J B M. A Petrov-Galerkin type method for solving Ax=b, where A is symmetric complex[J]. IEEE Transactions on Magnetics, 1990, 26(2): 706-708.
[21] GU X M, CLEMENS M, HUANG T Z, et al. The SCBiCG class of algorithms for complex symmetric linear systems with applications in several electromagnetic model problems[J]. Computer Physics Communications, 2015, 191: 52-64.
[22] SOGABE T, ZHANG S L. A COCR method for solving complex symmetric linear systems[J]. Journal of Computational and Applied Mathematics, 2007, 199(2): 297-303.
[23] CLEMENS M, WEILAND T, VAN RIENEN U. Comparison of Krylov-type methods for complex linear systems applied to high-voltage problems[J]. IEEE Transactions on Magnetics, 1998, 34(5): 3335-3338.
[24] ABE K, FUJINO S. Converting BiCR method for linear equations with complex symmetric matrices[J]. Applied Mathematics and Computation, 2018, 321: 564-576.
[25] HAJARIAN M. Matrix form of the CGS method for solving general coupled matrix equations[J]. Applied Mathematics Letters, 2014, 34: 37-42.