引 言
近年来，我国大气污染问题越来越严重，而交通污染已成为其重要来源[1].2016年，全国机动车排放污染物4 472.5万吨，其中，一氧化碳(CO)3 419.3万吨，碳氢化合物(HC)422万吨，氮氧化合物(NOx)577.8万吨，颗粒物(PM)43.4万吨.根据我国第一批城市大气细颗粒物(PM2.5)来源解析结果，部分城市如北京、上海、杭州、广州和深圳等，机动车排放已成为PM2.5的首要来源[2].一方面，国家制定了诸多政策减轻交通污染，如公交优先、低能耗新能源汽车、限号出行等.另一方面，基于交通运行状态，可以对交通污染物排放进行估计，进而通过合理的交通规划和诱导，改善交通运行状态，有效降低交通污染.
城市交通污染物排放估计包括两部分：动态交通分配模型和污染物排放模型.动态交通分配模型用于模拟城市交通演化和运行状态，污染物排放模型基于交通状态估计排放水平.根据交通路网不同的抽象形式，动态交通分配建模方法可分为离散型和连续型的建模方法[3].离散型建模方法认为路网由离散的路段和交叉口构成，是用于研究交通系统的传统方法[4].连续型建模方法则假设路网足够稠密，可被视为二维连续空间，出行者可选任意方向行驶，研究交通路网的宏观特征[5].
根据出行行为准则，动态交通分配模型可以分为动态系统最优(dynamic system-optimal, DSO)模型和动态用户最优(dynamic user-optimal, DUO)模型.DSO模型从交通系统的角度出发，出行者动态选择路径使得整个系统的总费用最小.DUO模型从用户个体的角度出发，出行者选择使得自身到达目的地总费用最小的路径.DUO模型可以分为：基于当前交通状态瞬时旅行总费用的反应型动态用户最优(reactive dynamic user-optimal, RDUO)模型和基于预测实际旅行总费用的预测型动态用户最优(predictive dynamic user-optimal, PDUO)模型.动态交通分配模型大多采用离散建模方法，一般可以描述为非线性互补问题、数学规划问题、不动点问题和变分不等式问题等[3,6].采用连续型建模方法研究动态交通分配问题的工作相对较少.Tao等[7]提出了DSO路径选择模型；Jiang等[8]提出了多中心城市的RDUO路径选择模型；Du等[9]提出了单一中心城市的PDUO路径选择模型；Lin等将PDUO路径选择模型推广到多中心城市[10]，并在PDUO模型的基础上考虑出行者出发时间，提出了同时考虑出发时间和路径选择的PDUO模型[11].而考虑住房分布的二维连续型动态交通分配问题还未被研究.
交通污染物排放模型可分为宏观模型和微观模型两类[12].宏观模型通常依据交通流平均速度来评估排放总量和平均排放因子，如被广泛应用的MOBILE模型[13]、EMFAC模型[14]和MOVES模型[15]等.此类模型适用于大规模城市区域，宏观上定量估计交通污染物排放水平.微观模型基于车辆个体，研究不同行驶模式下的车辆排放水平，如CMEM模型[16]、VT-micro模型[17]和VERSIT+模型[18]等.微观模型考虑了车辆个体的行驶状态，适用于微观上详细估计交通污染物排放水平.采用连续型动态交通分配模型研究交通污染物排放问题的研究工作相对较少.Jiang等[19]将连续型RDUO模型与Panis等[20]提出的微观污染物排放模型相结合，用于城市交通污染物排放水平估计.Yang等[21]将连续型RDUO模型与VT-micro模型相结合，估计交通污染物排放率，并建立对流扩散方程描述污染物扩散和分布.
本文首先提出一个同时考虑出发时间和路径选择的二维连续型动态交通分配模型，然后将住房分布考虑到该模型中，采用VT-micro模型估计CO2排放水平.
1 模 型 方 程
如图1所示，考虑具有单个中心商业区(CBD)的城市.城市区域Ω的边界为Γ=Γo∪Γi∪ΓCBD，其中Γo为外边界，Γi为内边界(表示湖泊、公园等障碍物)，ΓCBD表示 CBD的边界.假设城市Ω内的路网足够稠密可视为二维连续体，出行用户分布在城市区域内.在研究时段[0,tend]内，用户基于DUO准则选择到达目的地(CBD)费用最小的出行时间和路径.模型中用到的主要变量如下：
1) ρ(x,y,t)(veh/km2)表示交通流在(x,y)处t时刻的密度.
2) v=(u(x,y,t),v(x,y,t))表示交通流在(x,y)处t时刻的速度向量.|v|(km/h)为速度的大小，是由(x,y)处t时刻的密度决定的，即|v|=Uf(x,y)e-βρ2(x,y,t)，Uf(x,y)(km/h)为交通流在(x,y)处的自由流速度，β是反映道路状况的参数.
3) F=(f1(x,y,t), f2(x,y,t))为交通流在(x,y)处t时刻的流量，大小为|F|=ρ|v|.
4) c(x,y,t)(＄/km)表示交通流的费用分布函数，定义为
(1)
其中，κ(＄/h)表示时间费用，κ/|v|表示与出行时间相关的费用，κπ(ρ(x,y,t))表示其他费用，如出行者倾向避免高密度区域等.
5) φ(x,y,t)(＄)表示交通流在(x,y)处t时刻前往CBD所需要的旅行费用.
6) T(x,y,t)(h)表示交通流在(x,y)处t时刻前往CBD所需要的总时间.
7) p(x,y,t)(＄)为交通流在(x,y)处t时刻前往CBD的惩罚函数，表示对迟到或者早到目的地所产生的惩罚费用，依赖于到达时间t+T(x,y,t).
8) C(x,y,t)(＄)为交通流在(x,y)处t时刻前往CBD的总费用：
C(x,y,t)=φ(x,y,t)+p(x,y,t).
(2)
9) q(x,y,t)(veh/(km2·h))为交通流在(x,y)处t时刻的交通需求，q(x,y)(veh/km2)为交通流在(x,y)处的交通需求，Q(veh)为交通总需求，满足
q(x,y,t)≥0, ∀(x,y)∈Ω, t∈[0,tend],
q(x,y,t)dt=q(x,y), ∀(x,y)∈Ω,
本文中“veh”为交通量的单位，表示车辆数；“＄”为费用的单位，表示元.
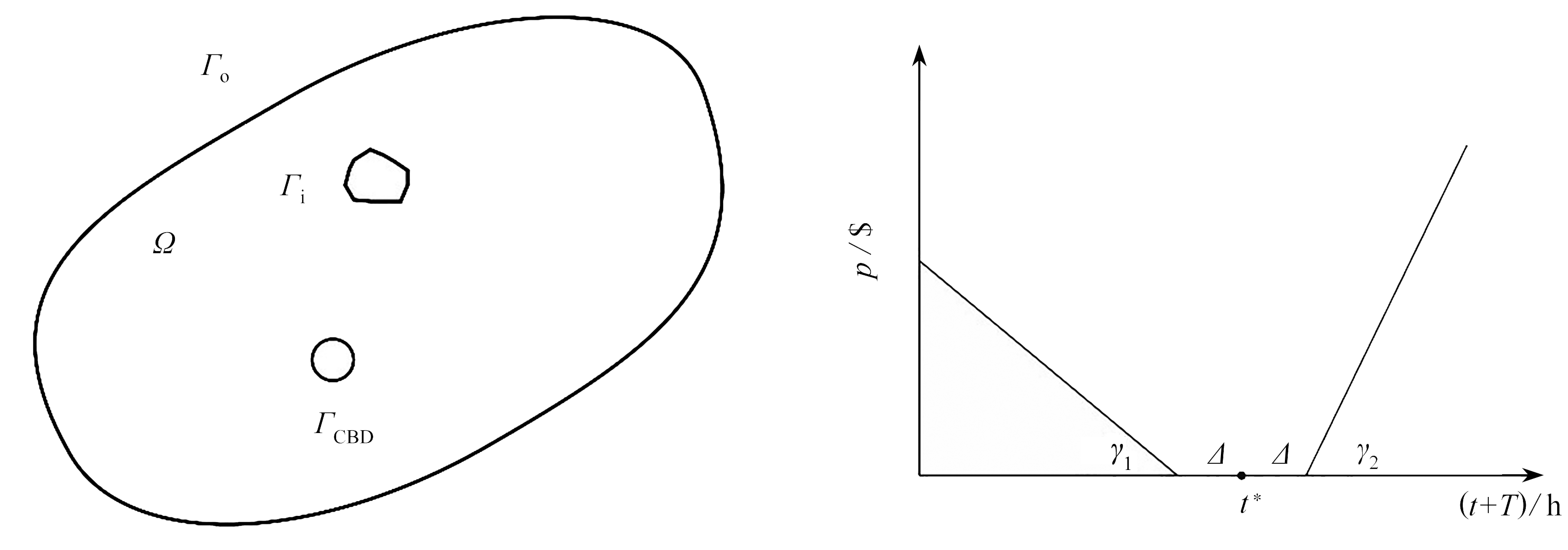
图1 任意形状的单中心城市图2 惩罚函数
Fig. 1 A city with arbitrary configuration Fig. 2 The penalty function
1.1 RDUO路径选择模型
若已知交通需求q(x,y,t),即已知出行者出发时间分布，采用如下RDUO路径选择模型描述交通均衡问题：
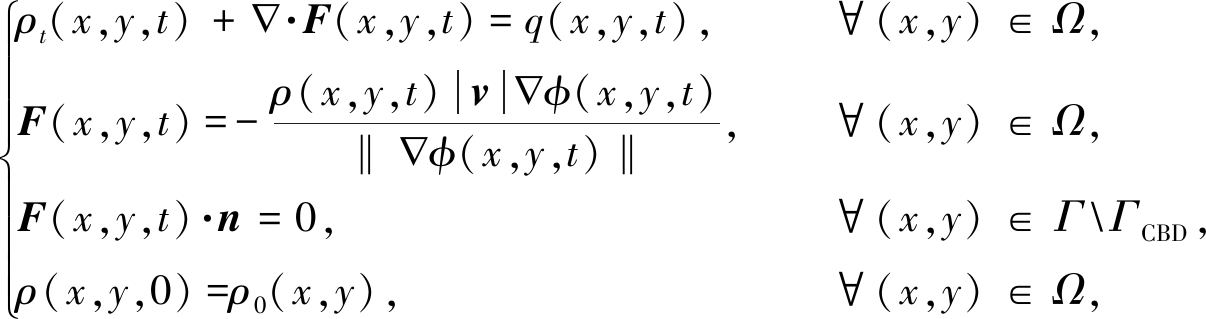
(3)
(4)
模型主要包括描述车流密度的质量守恒方程(3)和描述旅行费用势函数的Eikonal方程(4).出行者选择费用势函数下降最快的方向行驶，即F//-
φ.此时，可证明交通系统满足RDUO准则[8].假定没有车辆可通过城市障碍物或离开城市区域，因此有边界条件：F(x,y,t)·n=0,∀(x,y)∈Γ\ΓCBD,其中，n表示边界外法向量.用ρ0(x,y)表示已知的交通流的初始密度，则有初始条件：ρ(x,y,0)=ρ0(x,y).假设进入CBD所需要的费用为φCBD,则有边界条件：φ(x,y,t)=φCBD,∀(x,y)∈ΓCBD.
通过求解上述RDUO模型，可以得到车流密度、速度和旅行费用等.同时，旅行时间T(x,y,t)可以由以下Eikonal方程描述：
(5)
进一步地，惩罚函数定义为
p(x,y,t)=
(6)
其中，t*表示交通流期望到达时间，Δ为早到或迟到的容忍时间，γ1和γ2为早到和迟到的惩罚参数(如图2).
1.2 同时考虑出发时间和路径选择模型
一般情况下，出行者出行会同时考虑出发时间和路径的选择.如果仅已知交通需求空间分布q(x,y)，则需要在路径选择模型的基础上进一步考虑出发时间，建立同时考虑出发时间和路径选择(SDTRC)模型.Lin等[11]将出发时间选择和PDUO路径选择模型相结合，建立了同时考虑出发时间和路径选择预测型动态用户最优(SDTRC-PDUO)模型.该模型满足出发时间动态用户最优准则，采用等价的连续变分不等式进行描述.实际上，将出发时间与1.1小节中的RDUO路径选择模型结合，可以建立同时考虑出发时间和路径选择反应型动态用户最优(SDTRC-RDUO)模型.与SDTRC-PDUO模型相比，此模型同样可以很好地描述动态交通演化过程，且可以大大减少计算量.
在已知交通需求时空分布q(x,y,t)的情况下，通过求解RDUO模型(1.1小节)可以得到总费用C(x,y,t).因此可记C(x,y,t)=C(x,y,t,q).定义C(x,y,q)=min0≤t≤tendC(x,y,t,q).出行者根据用户最优准则选择出发时间，即出行者任意时刻出发所产生的费用相等且最小，出行者无法通过改变出发时间降低其费用.出行时间用户最优准则定义如下.
定义1 若对所有(x,y)∈Ω,满足以下条件：
其中，q∈V,
则满足出行时间用户最优准则.
与文献[10]中建立的SDTRC-PDUO模型类似，存在如下定理.
定理1 出行时间用户最优准则等价于如下变分不等式问题：寻找q*∈V，使得对所有q∈V，满足
(7)
定理1的证明与文献[10]中定理1的证明本质上相同，此处省略证明步骤.
Gap函数常可用于衡量交通均衡问题数值解的精度，定义为
不难证明：1) Fgap≥0； 2) Fgap=0等价于满足出行时间用户最优条件，等价于q是变分不等式问题的一个解.
1.3 考虑住房分布的SDTRC-RDUO模型
在SDTRC-RDUO模型中，交通需求q(x,y)是给定的.实际上，出行者一般会根据住房费用和交通费用选择居住地.假设住房分布与交通需求q(x,y)之间满足以下关系[22]：
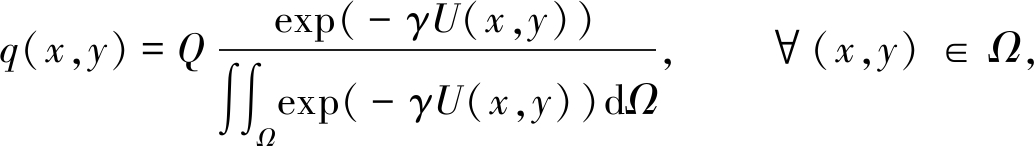
(8)
其中，U(x,y)为负效用函数，包括住房费用r(x,y)和交通费用C(x,y,q)，γ为正值的敏感性参数.住房费用与交通需求分布q(x,y)和住房分布函数H(x,y)有关，定义为
(9)
其中，α(x,y)和β(x,y)为参函数.
由方程(8)可知，用户根据负效用U(x,y)选择居住地，负效用越大，交通需求越小.根据方程(9)，住房供给越多，居住者越少，住房费用越小.方程(8)、(9)和SDTRC-RDUO模型(方程(3)和(4))构成完整的考虑住房分布的SDTRC-RDUO模型.
1.4 交通污染物排放模型
SDTRC-RUDO描述了交通需求空间分布q(x,y)已知的条件下，同时考虑出发时间和路径选择的动态交通分配问题，通过求解该模型可以得到交通状态动态演化过程.而交通污染物排放模型则可以根据交通状态估计交通污染物排放水平，这里采用如下基于车辆速度-加速度的微观VT-micro污染物排放模型：
(10)
其中，
为速度
(km/h)和加速度aj(km/h2)对应的回归系数，Ek表示油耗和污染物的排放率，具体参数见表1.车辆速度v=(u,v)可由SDTRC-RDUO模型直接求得，车辆加速度a=(ax(x,y,t),ay(x,y,t))则可以基于速度通过以下公式得到
移动方向上加速度大小为
(11)
该模型可以用于估计污染物HC(mg/s)，CO(mg/s)和能耗F(gal/s)，而CO2(mg/s)排放率则可以根据碳守恒通过以下公式得到：
ECO2=2 464F-3.175EHC-1.57ECO,
(12)
其中，F=E1,EHC=E2,ECO=E3.在时刻t，城市交通单位面积单位时间CO2排放量为
z(x,y,t)=ECO2(x,y,t)ρ(x,y,t),
时刻t，CO2的总排放量为
时刻t，CO2的累计排放量为
MCE(t)=
QTE(ξ)dξ.
表1 VT-micro 污染物排放模型参数
Table 1 Parameters for the VT-micro model
(i, j)k=1k=2k=3(0,0)-6.79E-18.87E-1-7.28E-1(0,1)3.42E-53.77E-50.00(0,2)1.02E-91.96E-91.50E-9(0,3)-1.93E-14-2.19E-14-1.51E-15(1,0)2.70E-26.47E-22.27E-2(2,0)-2.33E-4-6.56E-4-1.74E-4(3,0)1.13E-63.50E-61.48E-6(1,1)1.11E-68.93E-72.34E-6(2,1)-4.42E-91.96E-8-2.10E-8(3,1)1.06E-11-1.36E-101.18E-10(1,2)4.87E-12-5.43E-11-3.21E-11(2,2)4.99E-142.62E-122.00E-12(3,2)-1.21E-15-1.50E-14-1.02E-14(1,3)-9.02E-160.00-1.63E-15(2,3)4.10E-18-1.89E-174.46E-17(3,3)-5.53E-200.00-2.09E-19
2 求 解 算 法
对计算区域Ω进行三角网格剖分.令Xi(i=1,2,…,NP)和Ti(i=1,2,…,NT)分别为网格节点和三角单元，NP和NT为节点和三角单元的数量.如图3所示，Ai，Nik和lik分别表示三角单元Ti的面积、第k个节点和第k条边. nik表示穿过边lik的单位外法向量，三角单元Ti的第k个邻居单元为Tik.将时间区间[0,tend]划分为N个时间步，时间步长为Δt=tend/N.
2.1 求解RDUO模型的一阶有限体积法
采用一阶有限体积法求解RDUO模型中的质量守恒方程(方程(3)).根据第n个时间步的数值解
可以得到第n+1个时间步的数值解
其中，
和
分别表示交通流第n个时间步三角单元Ti上的密度和交通需求的数值
为Lax-Friedrich数值流通量[8,10]：
其中，
和
表示边lik逆时针方向左右两侧单元的密度值，
对于描述费用势函数φ(x,y,t)和旅行时间T(x,y,t)的Eikonal方程(4)和(5)，采用快速步进法(fast marching method)求解交通流第n个时间步节点Xi处费用势函数和旅行时间的数值解
和
详细过程可参考文献[23-24].
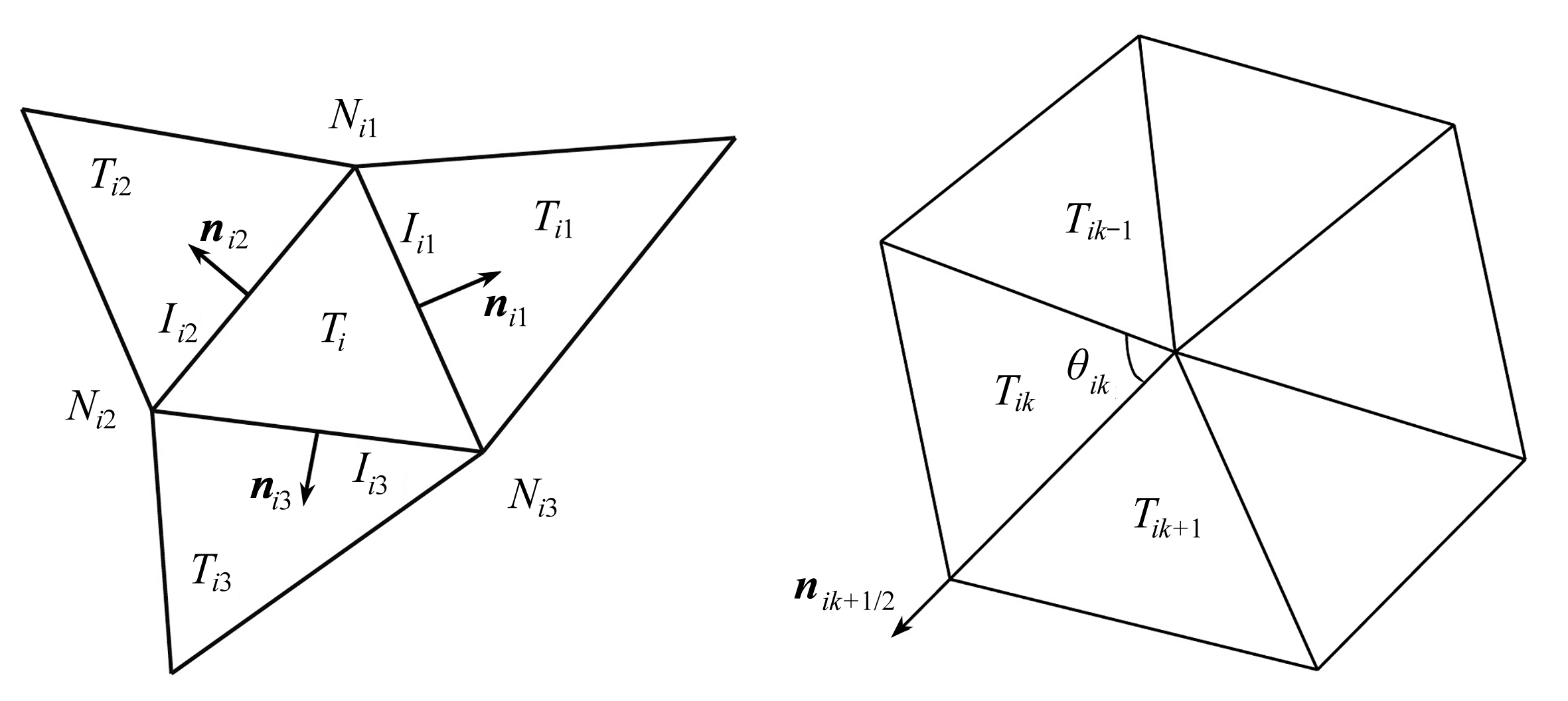
(a) 单元 (b) 节点 (a) The element (b) The node
图3 三角网格
Fig. 3 Triangular meshes
2.2 求解SDTRC-RDUO模型的GLP方法
对连续变分不等式方程(7)进行时空离散后，可以得到有限维离散型变分不等式，从而可以采用传统的投影算法进行求解.
记qi为交通流在节点Xi处的交通需求，定义
则离散型变分不等式为，寻找q*∈Λ，使得对所有的q∈Λ，满足
其中，
为与节点Xi相邻的三角单元数量，ik为节点Xi第k个单元的下标，ikj为单元Tik的第j个节点的下标，
离散型变分不等式问题等价于投影问题，如下定理成立.
定理2 令λ>0,q*∈Λ是离散变分不等式问题的一个解,当且仅当
其中，PΛ(x)表示向量q∈RNP×N在Λ上的投影，定义为
PΛ(x)=arg min{‖y-x‖: y∈Λ}.
Goldstein[25]、Levitin和Polyak[26]提出了GLP迭代算法，即给定初值q0，根据如下方程生成序列{qk}:
(13)
其中,PΛ是正的更新步长.
以下给出求解离散型变分不等式问题的完整算法.
算法1
步骤1 给定初始值q0∈Λ，令k=0.
步骤2 对于k≥0，计算
① 通过求解RDUO模型计算旅行费用φ(x,y,t)；
② 通过求解方程(4)计算旅行时间T(x,y,t)；
③ 根据方程(5)计算惩罚费用p(x,y,t)，并根据方程(2)计算总费用
步骤3 采用Frank-Wolfe方法[27]，根据方程(13)计算qk+1.
步骤4 计算相对gap值：
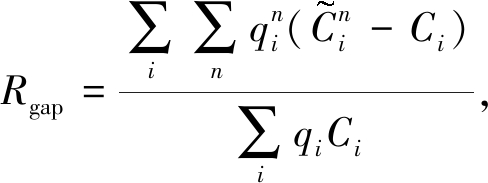
若Rgap<ε1，停止迭代，根据方程(11)计算运动方向上的加速度并根据VT-micro模型(方程(12))计算CO2排放率；否则令k=k+1，转至步骤2.
2.3 求解考虑住房分布的SDTRC-RDUO模型的相继平均法
注意到方程(8)、(9)与SDTRC-RDUO模型相互耦合，可视为一个不动点问题，采用相继平均法(MSA)进行求解.具体地，已知交通需求qold(x,y)，通过求解SDTRC-RDUO模型可以得到交通费用C(x,y,qold)，由方程(9)可以求得住房费用r(x,y).因此，通过方程(8)，可以得到qnew(x,y)=f(qold(x,y)).问题变为求解如下不动点问题：
q(x,y)=f(q(x,y)).
求解不动点问题的相继平均算法如下.
算法2
步骤1 给定如下初始可行解
其中，AΩ为城市区域总面积.
步骤2 对于k≥0，根据算法1求解SDTRC-RDUO模型，并根据方程(8)得到
步骤3 计算k+1个迭代步的数值解：
其中
步骤4 如果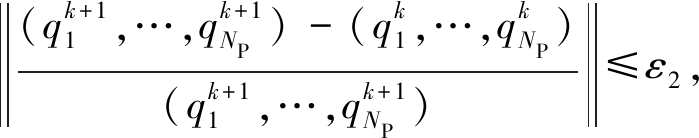
停止迭代；否则，返回步骤2.
3 数 值 算 例
考虑如图4所示的城市区域， 东西长约37 km(4～41 km)， 南北宽约24 km(10～34 km)， 正方形CBD的中心位置为(15 km, 20 km)， 边长为2 km.模拟时间为早上6:00到9:00，t∈[0 h,5 h].出行者的期望到达时间为t*=2.8 h，惩罚函数(方程(6))中的参数取：γ1=48 ＄/h,γ2=108 ＄/h,Δ=0.1 h.城市内的总交通需求Q=467 417 veh(如均匀分布，则q(x,y)=400 veh/km2,∀(x,y)∈Ω).在速度-密度假设关系中，令β=2×10-6，自由流速度为
Uf(x,y)=Umax(1+γ3d(x,y)),
其中，γ3=0.004 km-1,Umax=65 km/h，d(x,y)为(x,y)到CBD的距离.方程(1)中，令κ=72 ＄/h,π=10-8 km2·h/veh.
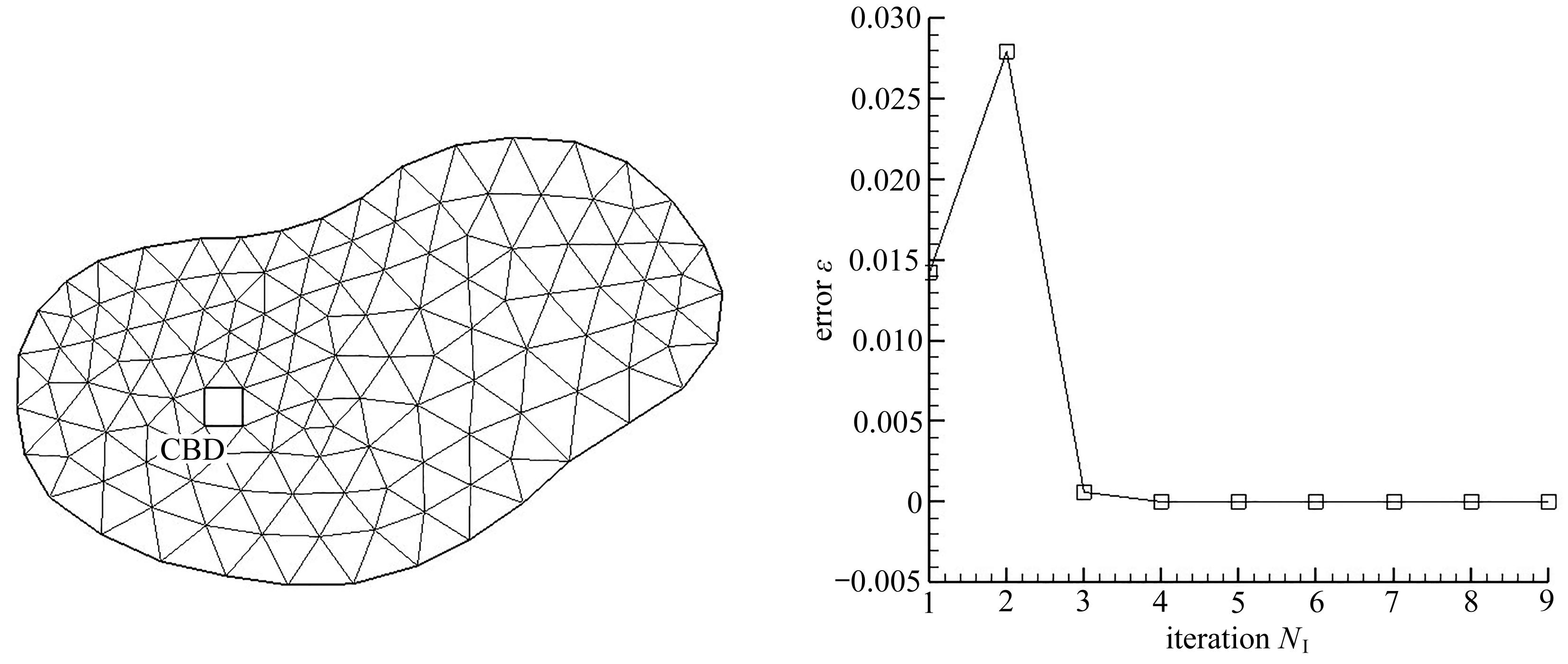
图4 单中心城市区域图5 MSA算法收敛图
Fig. 4 A hypothetical city with one CBD Fig. 5 The convergence of the MSA
假设t=0 h时城市中没有出行者且进入CBD不需要费用，因此有ρ0(x,y)=0,∀(x,y)∈Ω和φCBD=0.对计算区域进行三角网格剖分，其有298个节点、454个单元和844条边，时间划分取Δt=1/180 h.在GLP算法中，令更新步长λk=30,收敛阈值ε1=0.05.
在MSA算法中，收敛阈值ε2=10-7，如图5所示算法具有很好的收敛性，迭代步数大于3时认为结果已收敛.
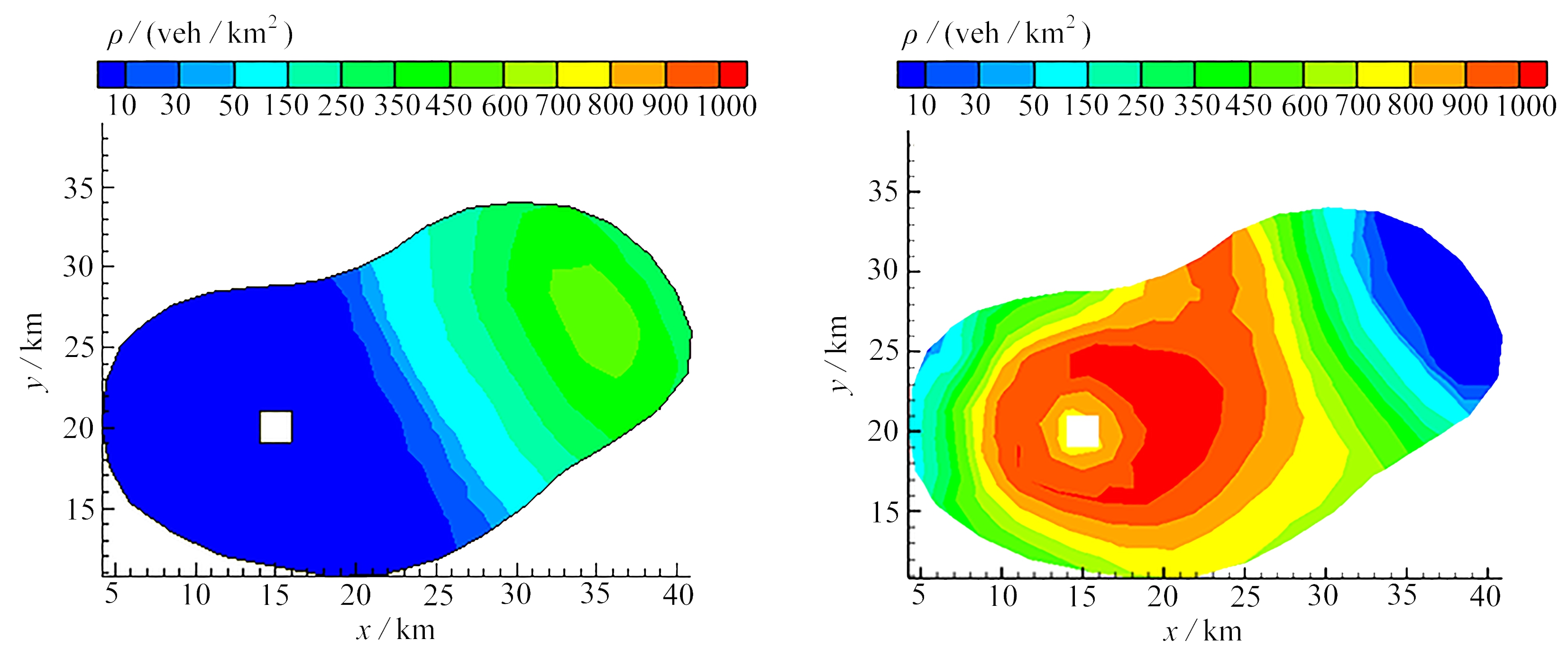
图6为交通密度时空演化图.t=1.95 h时，郊区产生交通需求，出行者从郊区前往CBD(图6(a))；t=2.3 h时，城市出现大面积的拥堵状态，在CBD东侧更为明显(图6(b))；t=2.8 h时，交通出现拥堵高峰，大量出行者集中于CBD附近，而郊区的交通处于畅通状态(图6(c))；当t=3.8 h时，交通拥堵高峰已过，恢复畅通(图6(d)).
(a) t=1.95 h(b) t=2.3 h
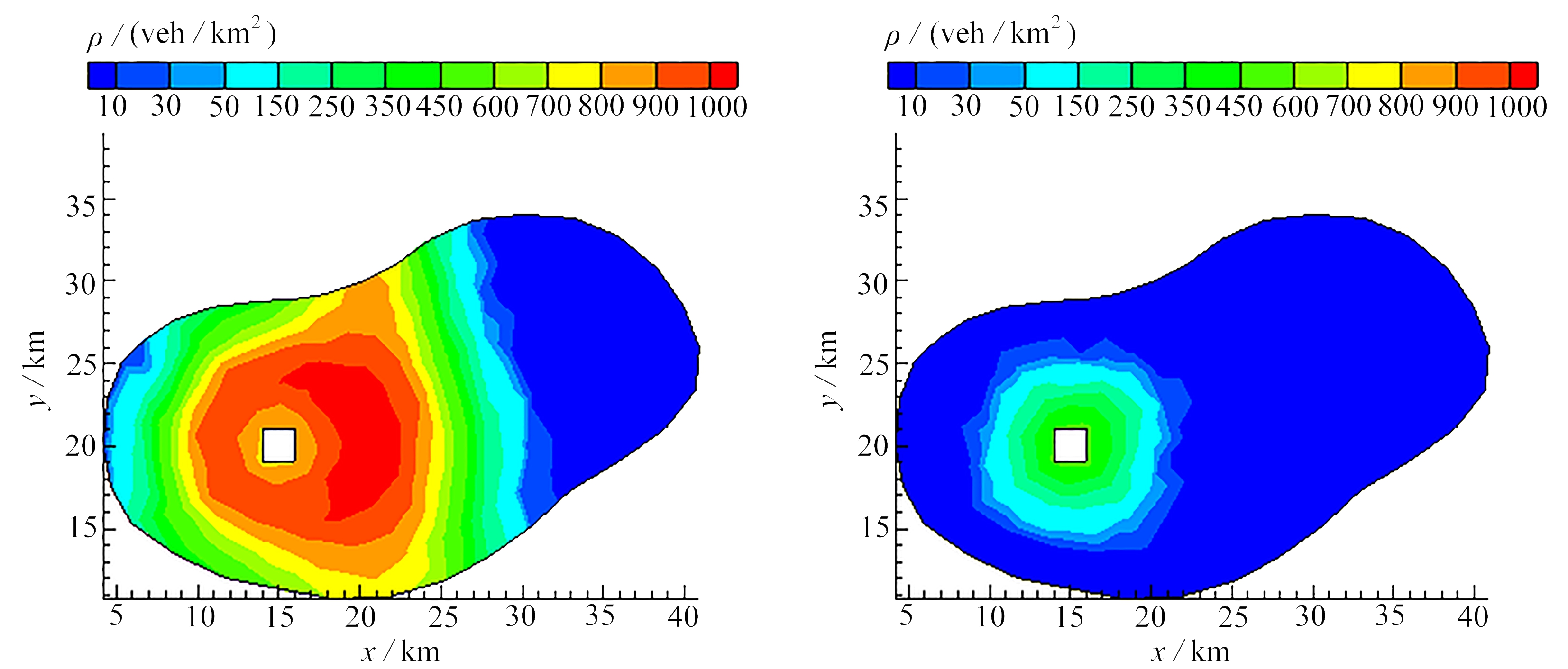
(c) t=2.8 h(d) t=3.8 h
图6 密度分布图
Fig. 6 Density plots
注 为了解释图中的颜色，读者可以参考本文的电子网页版本，后同.
图7(a)为交通需求空间分布图，可以看到距CBD距离越远，交通需求越小.从总体看，在郊区居住比在CBD附近居住的整体成本要高(图7(b)).CBD西侧的交通需求更多，这是由于西侧的拥堵情况较轻，交通费用更小.图7(c)所示为最佳出发时间分布，表示出行人数最多的出发时间，由图可知距CBD距离越远，最佳出发时间越早，因为郊区的出行者需要更多的时间到达目的地.由于西侧的交通拥堵状况相对较轻，所以同样距离下CBD西侧的最佳出发时间要晚于东侧.
图8为CO2排放时空分布图.t=1.95 h时，只有郊区产生出行者从而产生车辆CO2排放，其他区域无CO2排放(图8(a))；t=2.3,2.8 h时，城市发生交通拥堵的地方CO2排放量大(图8(b)、(c))；当t=3.8 h时，只有CBD附近产生CO2排放，对应图8(d)，该区域仍有未到达目的地的用户，而其他区域排放量为零.图9为不同时刻城市内CO2的瞬时排放总量和累计排放总量.在约t=1.9 h时，用户从居住地出发，城市交通CO2的排放量随之增加；t=2.1 h后，部分用户已到达目的地(CBD)，CO2排放量逐渐减少；t=4 h后，用户全部到达终点，不再产生CO2排放.
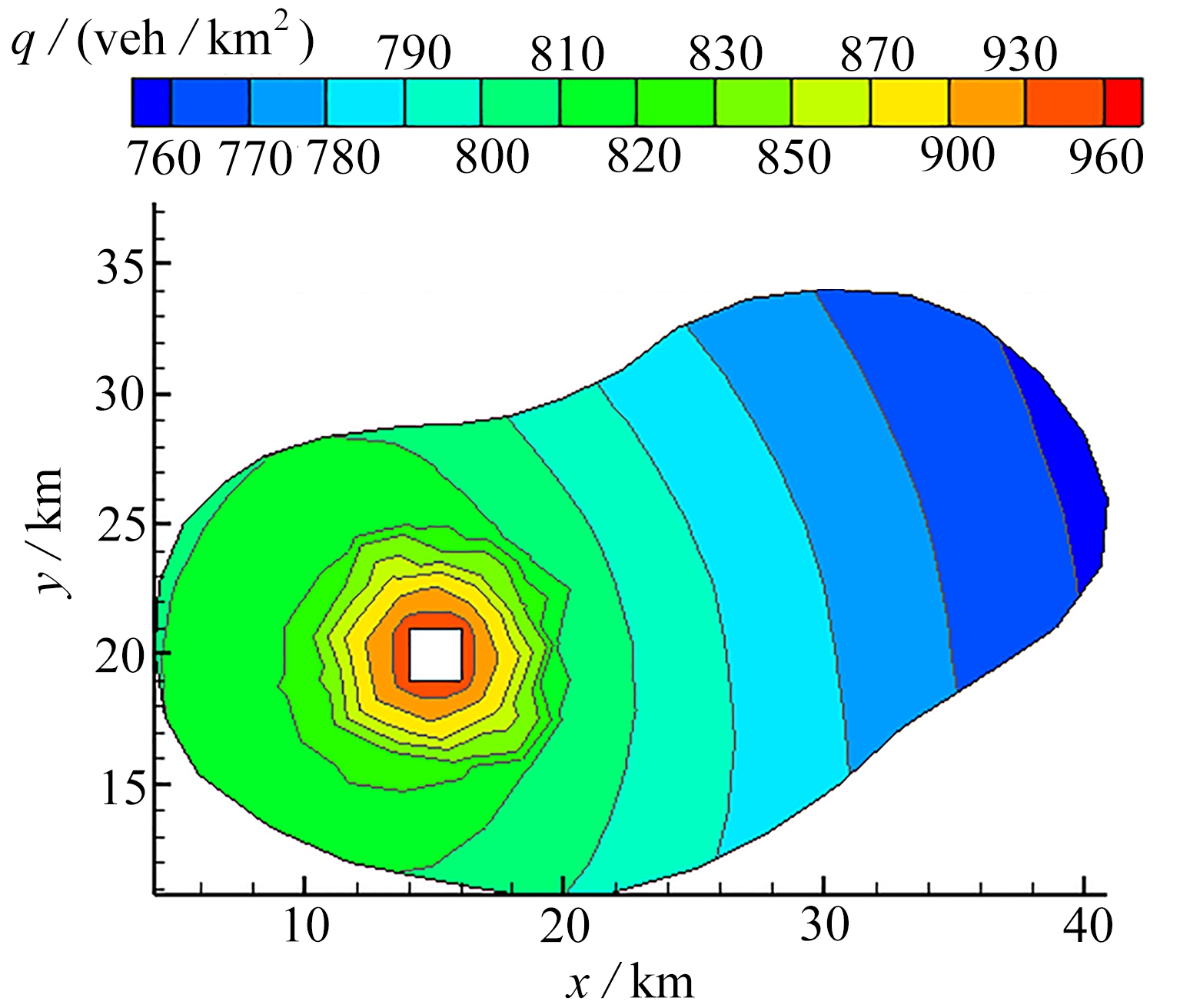
(a) 交通需求分布图 (a) The traffic demand distribution
(b) 负效用分布图 (c) 最佳出行时间分布图 (b) The disutility distribution (c) The optimal travel time distribution
图7 城市区域内的交通需求、用户负效用与用户最佳出行时间分布
Fig. 7 The traffic demand distribution, disutility distribution and optimal travel time distribution of the city
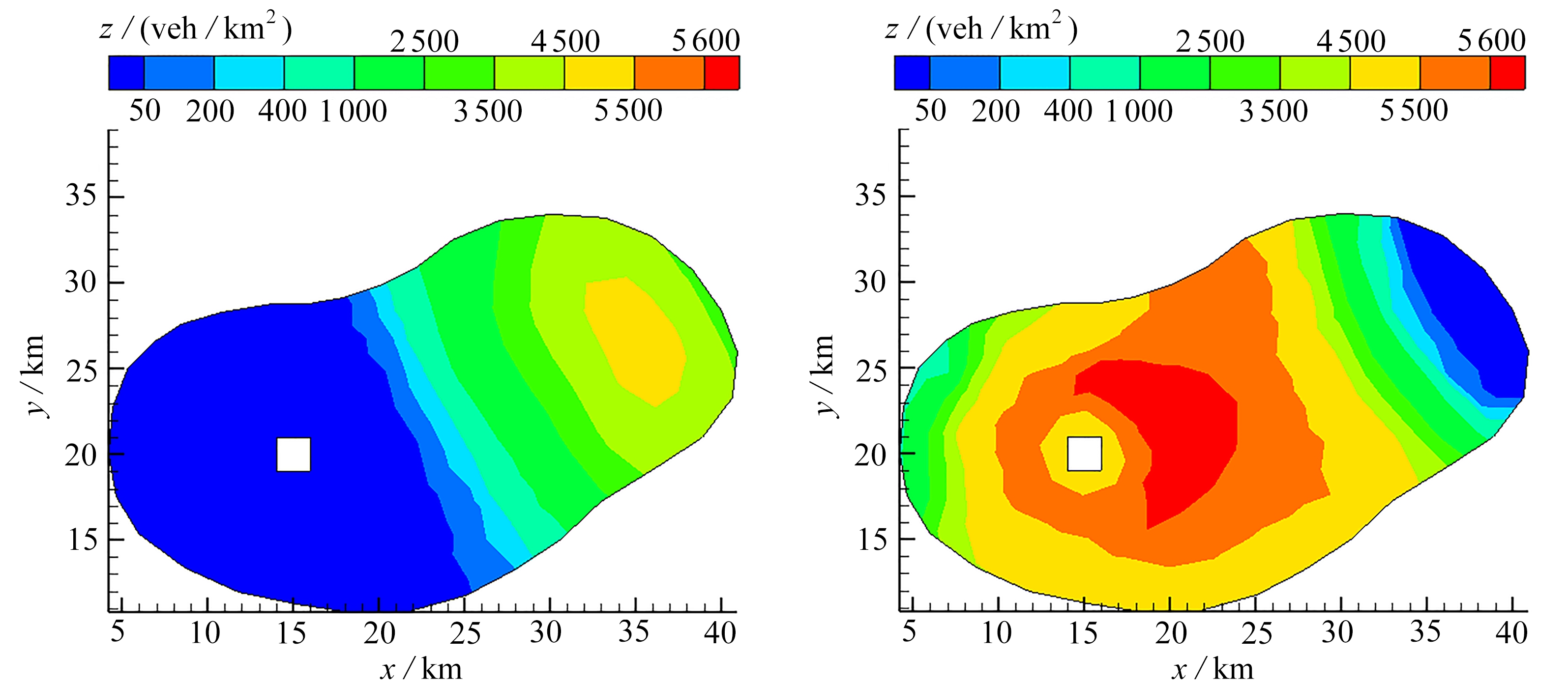
(a) t=1.95 h(b) t=2.3 h
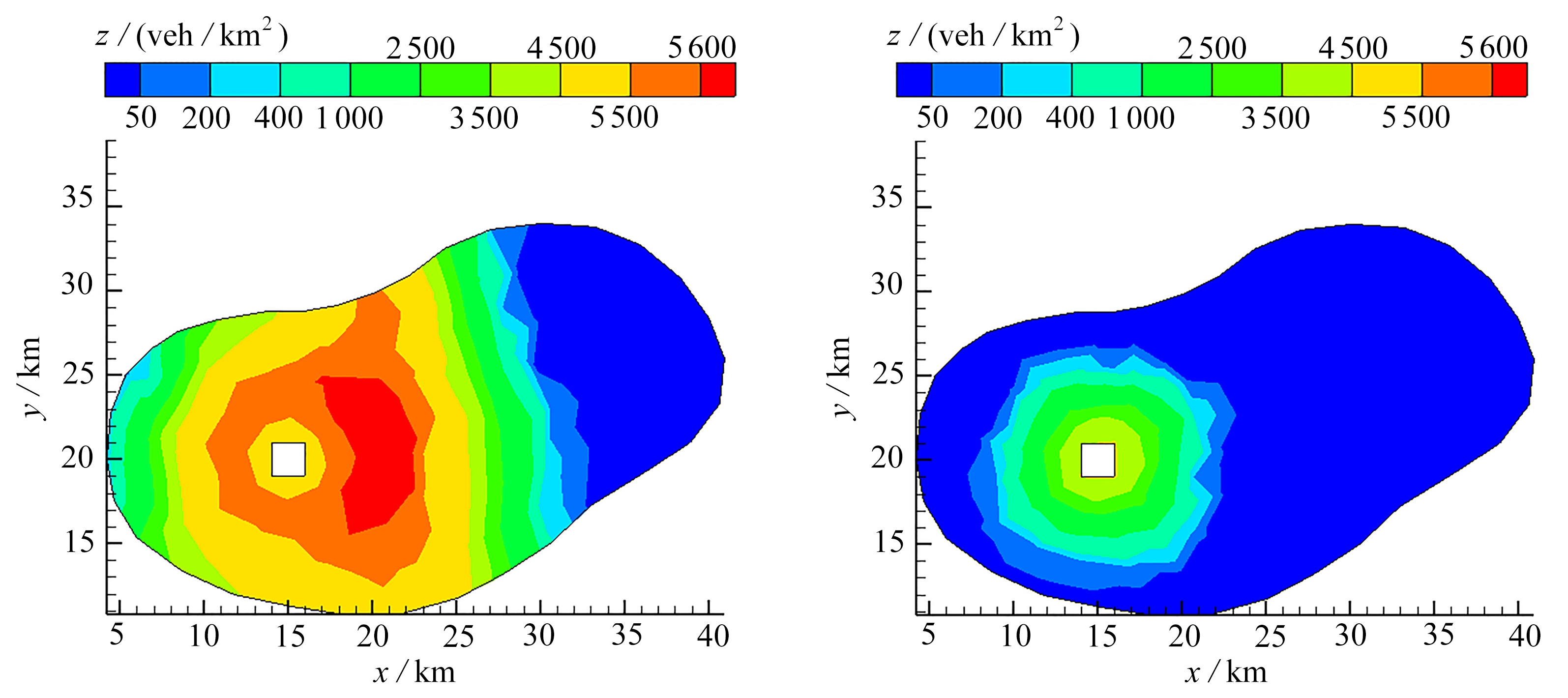
(c) t=2.8 h(d) t=3.8 h
图8 CO2排放时空分布图
Fig. 8 Distributions of the CO2 concentration at various moments
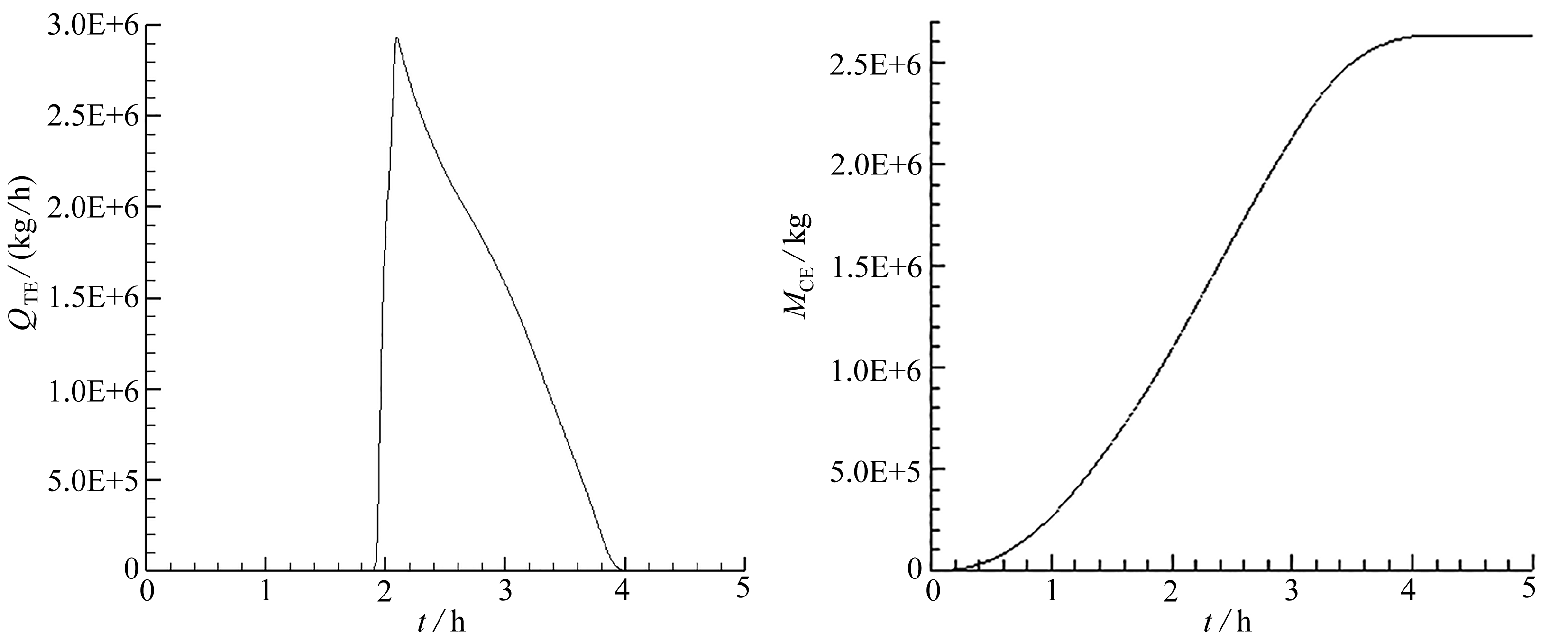
(a) CO2瞬时排放总量 (b) CO2累计排放总量 (a) The total emission rate of CO2 (b) The total cumulative emission of CO2
图9 城市区域内的CO2排放水平
Fig. 9 The emission level of CO2 in the city
4 结论和展望
将城市路网视为二维连续的平面，提出SDTRC-RDUO交通分配模型，并在此基础上进一步建立了考虑住房分配的二维连续型动态交通分配模型.进而，采用考虑速度和加速度的微观交通污染物排放模型VT-micro对CO2动态排放量进行估计.基于三角网格，采用有限体积法、GLP投影算法和相继平均法进行数值求解，由数值算例验证了模型和数值方法的有效性.
将模型推广到多个CBD，并通过优化住房分布，降低交通污染物排放量是未来有意义的工作.
致谢 本文作者衷心感谢陆地交通气象灾害防治技术国家工程实验室开放研究基金(NEL-2019-03)对本文的资助.
[1] International Energy Agency. CO2 emissions from fuel combustion 1971—2004[R]. 2004.
[2] 中华人民共和国环境保护部. 中国机动车环境管理年报(2017)[R]. 2017.(Ministry of Environmental Protection of the People’s Republic of China. China vehicle environmental management annual report(2017)[R]. 2017.(in Chinese))
[3] 林志阳. 二维连续型动态交通分配与土地利用模型及其数值模拟[D]. 博士学位论文. 上海: 上海大学, 2018.(LIN Zhiyang. Two dimensional continuum dynamic traffic assignment with land use models and their numerical simulations[D]. PhD Thesis. Shanghai: Shanghai University, 2018.(in Chinese))
[4] SHEFFI Y. Urban Transportation Networks: Equilibrium Analysis With Mathematical Programming Techniques[M]. New York: Prentice Hall, 1984.
[5] VAUGHAN R. Urban Spatial Traffic Patterns[M]. London: Pion, 1987.
[6] SZETO W Y, WONG S C. Dynamic traffic assignment: model classifications and recent advances in travel choice principles[J]. Central European Journal of Engineering, 2012, 2(1): 1-18.
[7] TAO Y Z, JIANG Y Q, DU J, et al. Dynamic system-optimal traffic assignment for a city using the continuum modeling approach[J]. Journal of Advanced Transportation, 2014, 48(7): 782-797.
[8] JIANG Y Q, WONG S C, ZHANG P, et al. Dynamic continuum model with elastic demand for a polycentric urban city[J]. Transportation Science, 2017, 51(3): 931-945.
[9] DU J, WONG S C, SHU C W, et al. Revisiting Jiang’s dynamic continuum model for urban cities[J]. Transportation Research Part B: Methodological, 2013, 56: 96-119.
[10] LIN Z Y, WONG S C, ZHANG P, et al. A predictive continuum dynamic user-optimal model for a polycentric urban city[J]. Transportmetrica B: Transport Dynamics, 2017, 5(3): 233-252.
[11] LIN Z Y, WONG S C, ZHANG P, et al. A predictive continuum dynamic user-optimal model for the simultaneous departure time and route choice problem in a polycentric city[J]. Transportation Science, 2018, 52(6): 1496-1508.
[12] 周小霞. 城市道路施工区交通流建模与排放研究[D]. 硕士学位论文. 四川: 西南交通大学, 2018.(ZHOU Xiaoxia. Research on traffic flow modeling and emission of urban work zone[D]. Master Thesis. Sichuan: Southwest Jiaotong University, 2018.(in Chinese))
[13] US Environmental Protection Agency (USEPA). User’s guide to mobile 5[Z]. 1994.
[14] California Air Resources Board(CARB). EMFAC 2007: User’s guide[Z]. 2006.
[15] VALLAMSUNDAR S, LIN J. Moves versus mobile: a comparison of GHG and criteria pollutant emissions[J]. Transportation Research Record Journal of the Transportation Research Board, 2011, 2233: 27-35.
[16] BARTH M, AN F, YOUNGLOVE T, et al. Comprehensive modal emission model (CMEM)[Z]. California: University of California, 2002.
[17] AHN K, RAKHA H, TRANI A, et al. Estimating vehicle fuel consumption and emissions based on instantaneous speed and acceleration levels[J]. ASCE Journal of Transportation Engineering, 2002, 128(2): 182-190.
[18] SMIT R, SMOKERS R, RABE E. A new modeling approach for road traffic emissions: VERSIT+[J]. Transportation Research Part D: Transport and Environment, 2007, 12(6): 414-422.
[19] JIANG Y Q, MA P J, ZHOU S G. Macroscopic modeling approach to estimate traffic-related emissions in urban areas[J]. Transportation Research Part D: Transport and Environment, 2018, 60: 41-55.
[20] PANIS L I, BROEKX S, LIU R. Modelling instantaneous traffic emission and the influence of traffic speed limits[J]. Science of the total environment, 2006, 371(1/3): 270-285.
[21] YANG L Z, LI T T, WONG S C, et al. Modeling and simulation of urban air pollution from the dispersion of vehicle exhaust: a continuum modeling approach[J]. International Journal of Sustainable Transportation, 2019, 13(10): 1-19.
[22] YIN J, WONG S C, SZE N N, et al. A continuum model for housing allocation and transportation emission problems in a polycentric city[J]. International Journal of Sustainable Transportation, 2013, 7(4): 275-298.
[23] HUANG L, XIA Y H, WONG S C, et al. Dynamic continuum model for bi-directional pedestrian flows[J]. Proceedings of the Institution of Civil Engineers: Engineering and Computational Mechanics, 2009, 162(2): 67-75.
[24] XIA Y H, WONG S C, ZHANG M P, et al. An efficient discontinuous Galerkin method on triangular meshes for a pedestrian flow model[J]. International Journal for Numerical Methods in Engineering, 2008, 76(3): 337-350.
[25] GOLDSTEIN A A. Convex programming in Hilbert space[J]. Bulletin of the American Mathematical Society, 1964, 70(5): 709-710.
[26] LEVITIN E S, POLYAK B T. Constrained minimization methods[J]. Ussr Computational Mathematics and Mathematical Physics, 1966, 6(5): 1-50.
[27] FRANK M, WOLFE P. An algorithm for quadratic programming[J]. Naval Research Logistics Quarterly, 1956, 3(1/2): 95-110.