引 言
浅水波方程属拟线性双曲型方程,该类方程即使在初始条件光滑的情况下,其解在某一时刻也可能会出现间断,经典解理论不再适用,弱解理论由此产生,而弱解可能并不唯一,因而在数值计算领域,如何构建求解该类方程的具有物理意义的唯一弱解一直是一个研究热点. 2003年,Tadmor[1]研究了求解非线性双曲守恒律的有限差分法的熵稳定性.2009年,Ismail和Roe[2]将二阶、三阶项添加到熵守恒通量函数实现熵相容.2012年,Fjordholm等[3]构造了高精度TeCNO格式,该格式是基于高精度熵守恒通量函数耦合耗散项的ENO重构得到的.2013年,郑素佩等[4]在熵稳定格式的基础上,结合高阶重构方法,得到了一些行之有效的高分辨率熵稳定格式.2015年,Cheng等[5]通过引入限制器、开关函数来识别间断区域,使得数值黏性项在间断区域自动添加,有效地提高了格式的精度.2016年,Ray、Chandrashekar和Fjordholm[6]提出了一种熵稳定的高分辨率有限体积格式来逼近非结构网格上二维双曲守恒律方程.2018年,张海军等[7]利用通量限制函数将一阶熵稳定格式和高阶熵守恒格式结合,提出了一种新的求解带源项浅水波方程的熵稳定格式.
对双曲守恒律方程的求解,数值结果不仅与格式本身有关,还与网格的分布相关.移动网格法(moving mesh method)保持网格节点数目不变,网格节点的位置随解的性质而变化,在解的性质较奇异的区域网格分布密集,解的性质非奇异区域网格分布稀疏,使得数值结果整体误差减少.该方法最先由Harten和Hyman[8]提出,并被广泛研究[9-10].1999年,Cao等[11]使用变分法研究二维自适应网格生成技术,给出了一些如何选取监控函数的方法.2001年,Li、Tang和Zhang [12]提出了一种新的移动网格法,该方法保留了r方法(保持节点的数目不变)和h方法的优点(算法中的两个部分是独立的).2003年,Tang等[13]提出了一种求解一维和二维双曲守恒律方程的移动网格算法,能有效解决激波间断问题.2004年,杨继明和陈艳萍[14] 基于移动网格法将一般迎风格式与中心迎风格式结合求解了对流扩散边值问题.2010年,陈冬冬等[15]基于自适应移动网格技术,利用三角形网格求解了双曲型守恒律方程.2012年,He和Tang[16]将Tang等[13]的自适应移动网格法推广到二维(2D)相对论流体动力学(relativistic fluid dynamics)方程中.2017年,程晓晗等[17]采用熵稳定格式,基于移动网格求解一维Euler方程.
目前,基于移动网格的熵稳定法多用于Euler方程的数值求解中,而用于浅水波方程的文章还很少.本文采用旋转不变性得到混合数值通量,结合熵稳定格式,基于Tang等[13]提出的移动网格法,给出了一种新的求解二维浅水波方程的高分辨率数值方法.最后通过一些数值算例验证了该算法的间断捕捉能力和分辨率.
1 控 制 方 程
考虑二维浅水波方程[18-20]:
Ut+F(U)x+G(U)y=-S,
(1)
其中
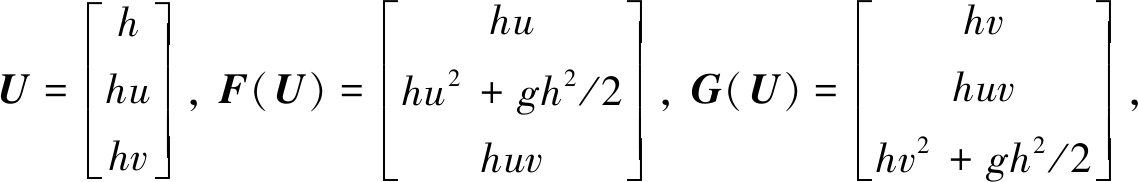
h为水深,g为重力加速度,u,v分别为x方向和y方向上的水流速度,S为源项.源项分为摩擦项和倾斜项:
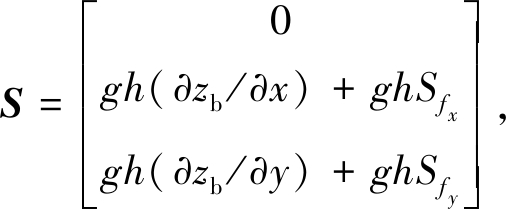
(2)
其中zb为底部地势函数,gh(∂zb/∂x)和gh(∂zb/∂y)为水下底部作用力沿x方向和y方向上的分力,ghSfx和ghSfy为水下底壁摩擦力沿x方向和y方向的分力,Sfx和Sfy为x方向和y方向上的摩阻比率.其值为
(3)
其中K为摩擦因数,通常取K=50.
2 方 程 离 散
对二维浅水波方程(1)的数值求解,首先将方程变形为Ut=-(F(U)x+G(U)y)-S,通过推导得其半离散格式,即![]() (详见2.1小节).在该半离散格式中,混合数值通量Hs通过旋转不变性结合高分辨率熵稳定格式获得.时间方向采用强稳定Runge-Kutta法[21]进行推进,详见下文所述.
(详见2.1小节).在该半离散格式中,混合数值通量Hs通过旋转不变性结合高分辨率熵稳定格式获得.时间方向采用强稳定Runge-Kutta法[21]进行推进,详见下文所述.
2.1 旋转不变性
本文采用有限体积法[22-25],控制体选取任意四边形单元,对浅水波方程(1)左右两侧同时积分,则有
(4)
其中n为界面A的单位外法向量,V为控制体,H=(F,G).
考虑四边形单元,将其作为方程积分的控制体V,V的边界A是N个直线段AsAs+1的并集,其中An+1=A1且N=4.假设已生成网格并且顶点As的坐标(xs,ys)已知,采用旋转不变性[26]求解混合数值通量,通过边界的总通量(4)可以写为
(5)
其中s为单元AsAs+1间的边界.
选择x方向作为参考方向并且定义θs为由x方向和法向量ns形成的角度,ns的分量可以根据θs来得到:ns=(cos θs,sin θs).
方程(5)可化为
(6)
将方程(4)的第一个积分项解释为控制体V内U平均值的时间变化率,写为
(7)
然后将式(6)和(7)代入式(4)中得到
(8)
将式(8)右端项可表示为
(9)
其中Ts为旋转矩阵,![]() 为其逆矩阵:
为其逆矩阵:
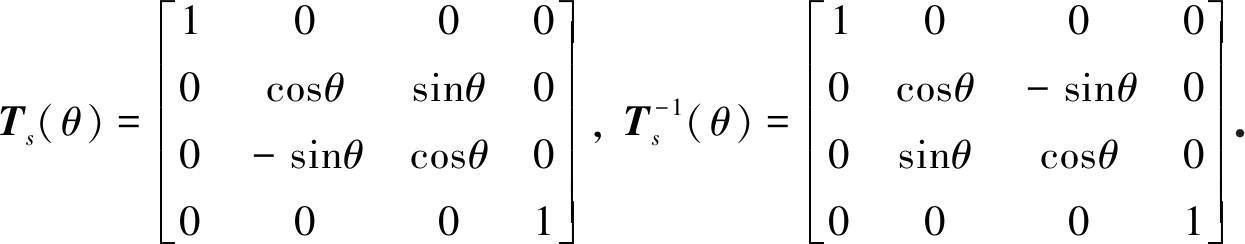
(10)
U是旋转守恒通量并且![]() 将方程(8)变为
将方程(8)变为
(11)
为了定义交界面s上的数值通量函数,使用旋转结构![]() 使其成为一个一维体系:
使其成为一个一维体系:
(12)
其中![]() 其与分裂多维体系一致.
其与分裂多维体系一致.
式(11)右端的近似形式为
(13)
其中ls为AsAs+1的长度,![]() 为与一维体系(12)相应的界面通量.
为与一维体系(12)相应的界面通量.
方程(1)的半离散格式为
(14)
通过对方程(4)右端项积分,则有

(15)
2.2 熵稳定格式
方程(14)的熵稳定格式可表示为
(16)
其中HEC为熵守恒通量,R为右特征向量矩阵,Λ为以特征值为对角线元素的对角阵.
采用算术平均计算熵守恒通量[27]:
HEC=F·nx+G·ny,
(17)
其中
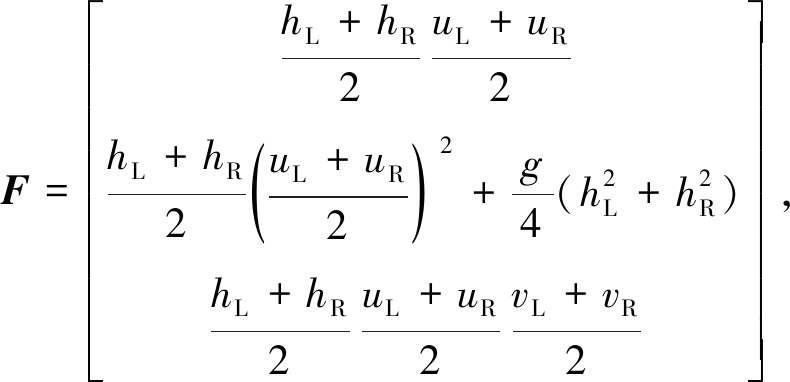
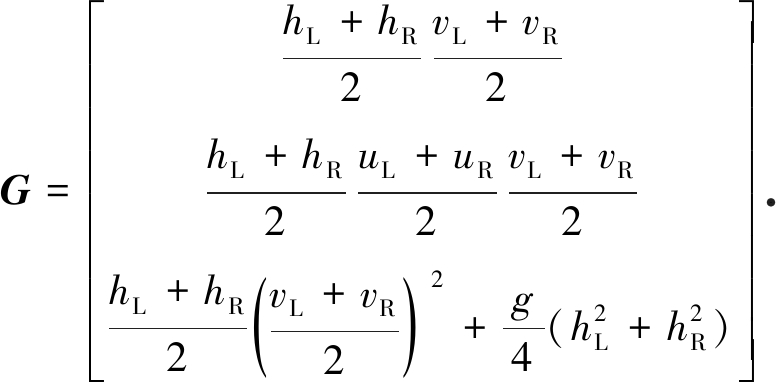
接下来采用Roe均值[23]求式(16)中的耗散项.引入参向量:
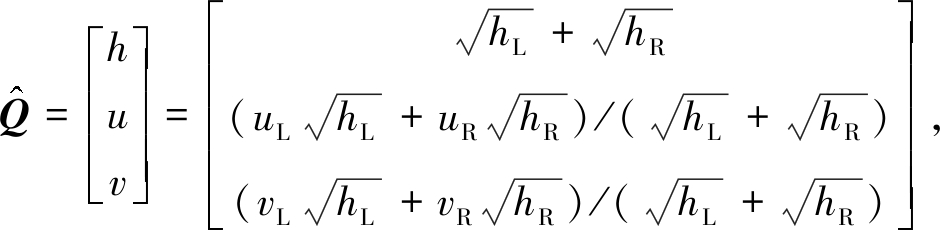
(18)
相应的对角阵和特征值矩阵为

(19)
其中![]() 为声速,一般情况下声速
为声速,一般情况下声速![]()
控制体V是Ii, j的通用计算单元.采用强稳定Runge-Kutta法得到方程(1)的全离散格式,如2.3小节所述.
2.3 时间离散
时间方向上的推进采用三阶强稳定Runge-Kutta法:
![]()
其中Ii, j为控制体V的面积.
3 移动网格法
在二(或更高)维空间中,移动网格法实现网格自适应疏密分布是使用变分法来实现的[28],特别是通过最小化坐标映射函数ξ=ξ(x,y),η=η(x,y)来完成.网格的生成依赖于函数类如何被形成和最小化问题如何被解决.文献[11-12,29]讨论了自适应中使用的最小函数类:
![]()
 ξTG-1
ξTG-1 ξ+
ξ+ ηTG-1
ηTG-1 η)dxdy.
η)dxdy.
(20)
式(20)对应的Euler-Lagrange方程为
(21)
其中G=ωI为控制函数.
对式(21),采用Gauss-Seidel迭代法进行求解:
(22)
其中
ν为迭代步数,一般取3~5步即可.
采用如下公式得到新网格上守恒变量的值:
[(cnu)j+1/2,k+1+(cnu)j+1/2,k].
(23)
控制函数检测函数性质的变化,是确定网格自适应疏密分布的关键因素.大多数情况下,控制函数仅识别激波位置,对接触间断不能起到很好的检测作用,本文选取的控制函数不仅可以检测激波而且可以检测接触间断.具体表达式如下:
(24)
为了避免在解具有较大梯度区域网格出现非常奇异的变化,减少误差的产生,选用如下形式的低通滤波器来平滑控制函数:
(25)
通过数值算例计算知参数α在[0.1,1]变化时,结果良好.
移动网络算法步骤如下:
1) 使用等分布原理给定物理域Ωp的初始分区![]() 使用初始数据u(x,0)计算控制体
使用初始数据u(x,0)计算控制体![]() 上的网格单元均值
上的网格单元均值![]()
2) (a) 网格移动,计算式(21),将网格点由![]() 移动到
移动到![]() 守恒变量的更新,用守恒插值式(23)在新控制体
守恒变量的更新,用守恒插值式(23)在新控制体![]() 上计算
上计算![]()
重复(a)和(b)到指定的迭代步数(3~5步).
3) 在新网格![]() 上使用高分辨率有限体积法求解浅水波方程,以获得tn+1时刻的近似解
上使用高分辨率有限体积法求解浅水波方程,以获得tn+1时刻的近似解![]() 空间方向采用熵稳定通量,时间方向采用三阶强稳定的Runge-Kutta方法.
空间方向采用熵稳定通量,时间方向采用三阶强稳定的Runge-Kutta方法.
4) 如果tn+1<T,令![]() 返回第2)步直至计算结束.
返回第2)步直至计算结束.
4 数 值 算 例
例1 二维潮汐模拟问题
在计算区域[-2,2]×[-2,2]上考虑方程(1),底部地势函数和初始条件为
zb(x,y)=1+0.01cos(πx/2)cos(πy/2),
h(x,y,0)=zb(x,y,0)+ζ(x,y,0), u(x,y,0)=v(x,y,0)=0,
其中初始的水面高度为![]()
空间网格数为50×50,取NCFL=0.45,计算时间t=0.3,g=0.98,采用周期性边界条件.取式(24)中控制函数参数α=0.935.图1为移动网格潮汐问题水面高度变化图;图2为潮汐问题水深等值线图.此问题中存在多个性质出现大变化的情况,网格演化效果不明显,不能很好地凸显移动网格旋转通量法的优势,但所得结果具有高分辨率,没有出现数值振荡或过渡抹平的现象.
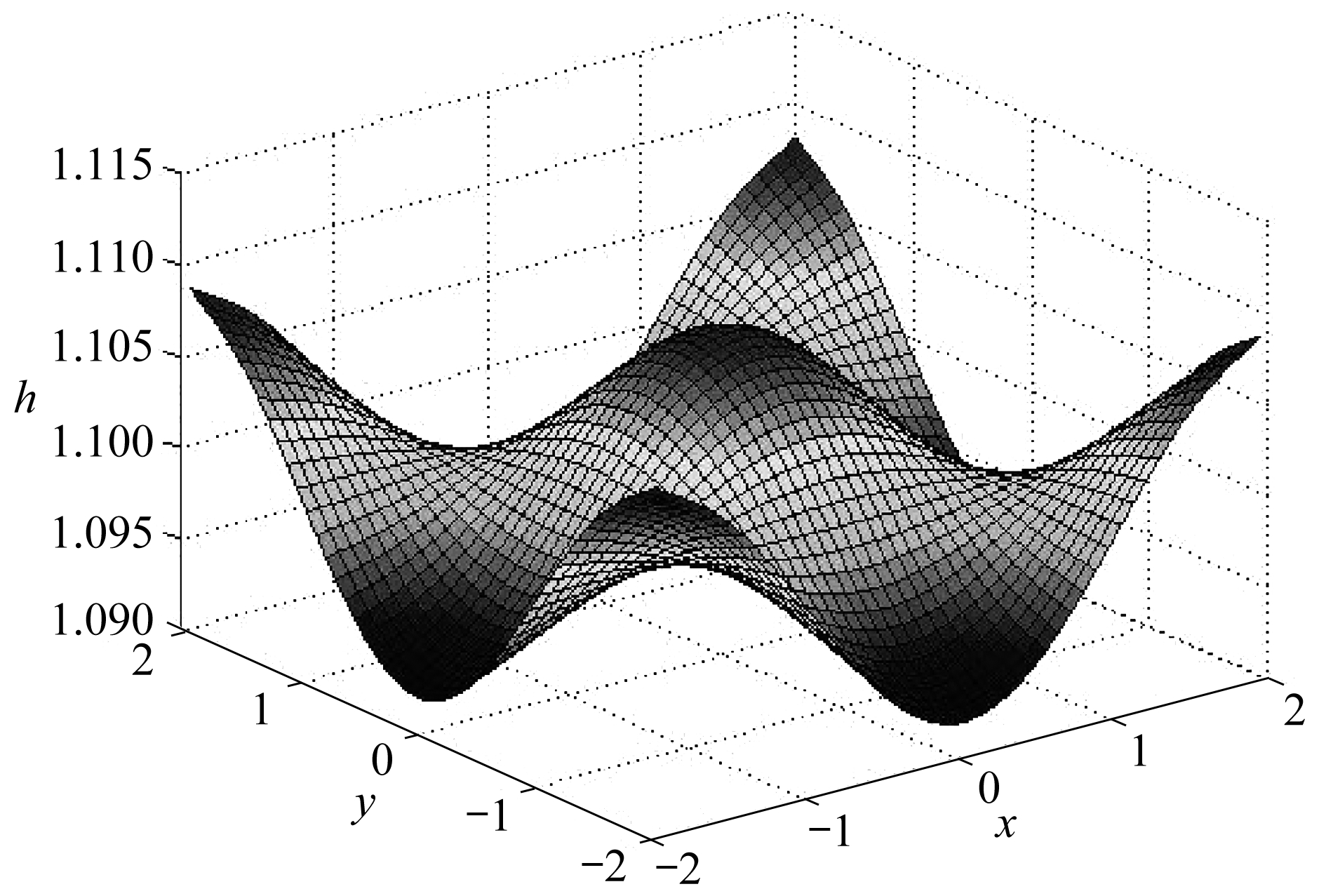
图1 潮汐问题模拟图
Fig. 1 The tide problem simulation
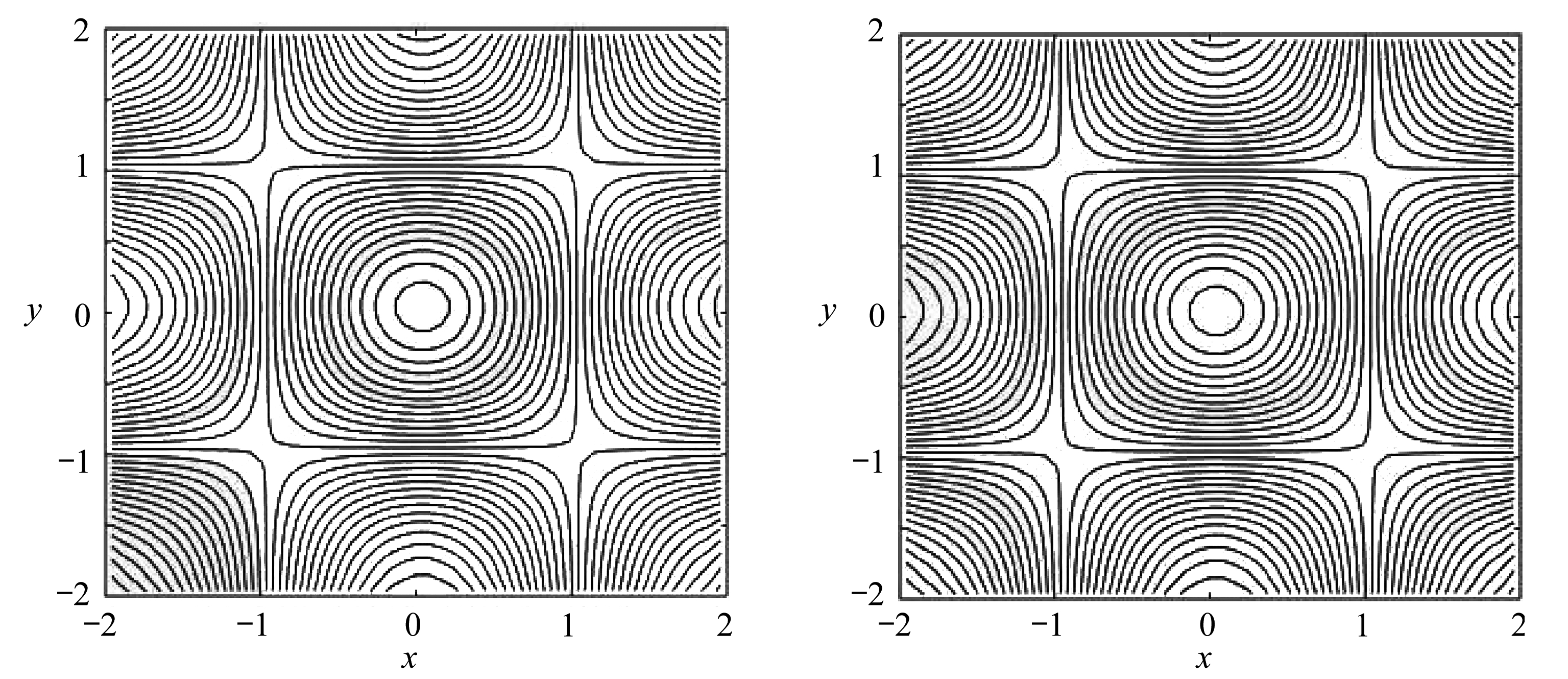
(a) 固定网格结果 (b) 移动网格结果 (a) Fixed grid results (b) Moving grid results
图2 二维潮汐问题水深等值线图
Fig. 2 The 2D tide problem water depth contours
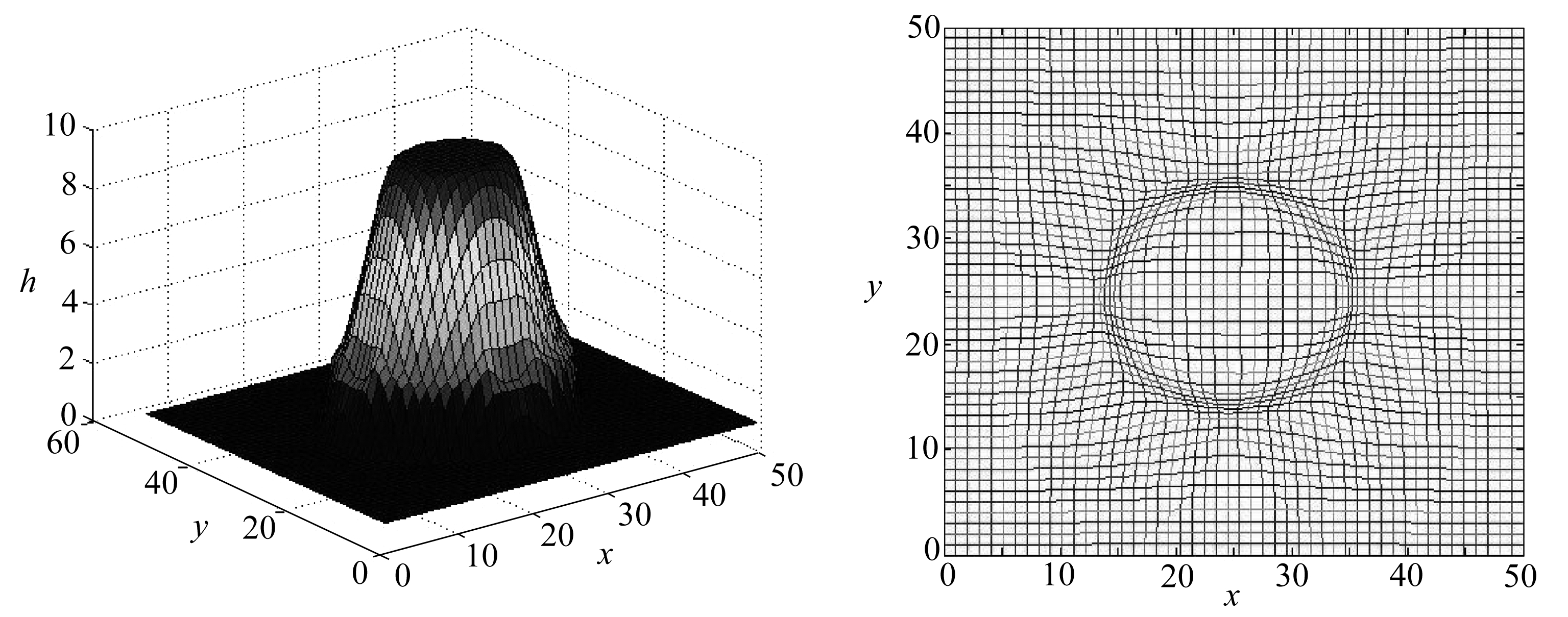
图3 圆柱溃坝模拟图
图4 网格演化图 Fig. 3 The cylindrical dam simulation diagram Fig. 4 The grid evolution map
例2 二维圆柱溃坝问题
在区域[0,50]×[0,50]上求解初值问题:
u(x,y,0)=v(x,y,0)=0, zb(x,y)=0.
空间网格数为50×50,取NCFL=0.45,计算时间t=1,g=0.98,采用周期性边界条件.取式(24)中控制函数参数为α=0.835.图3为移动网格圆柱溃坝问题水面高度变化图;图4为网格随时间演化图;图5为圆柱溃坝问题水深等值线图.由图可以看出移动网格的计算结果良好,分辨率高.
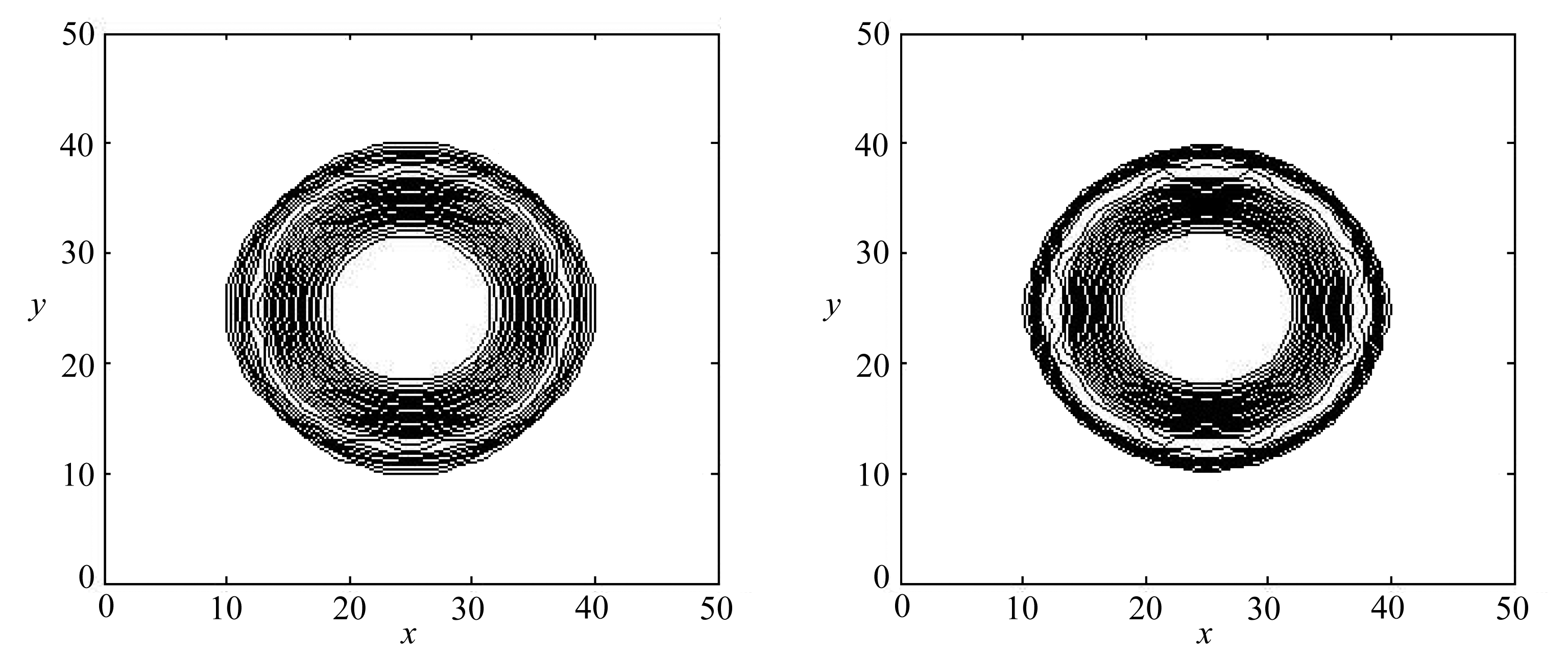
(a) 固定网格结果 (b) 移动网格结果 (a) Fixed grid results (b) Moving grid results
图5 二维圆柱溃坝问题水深等值线图
Fig. 5 The water depth contours of the 2D cylindrical dam failure problem
例3 二维区域上的激波聚焦问题
考虑在二维区域[-1,1]×[-1,1]激波聚焦问题,初始条件满足

u(x,y,0)=v(x,y,0)=0, zb(x,y)=0.
空间网格数为50×50,取NCFL=0.6,计算时间t=0.2,g=0.98,采用周期边界条件,取式(24)中控制函数参数α=0.635.图6为移动网格激波聚焦水面高度变化图;图7为网格随时间演化图;图8为二维激波聚焦问题水深等值线图.从图中可以看出,网格在解变化较大区域自动加密,计算结果具有高分辨率,没有出现过渡抹平现象.
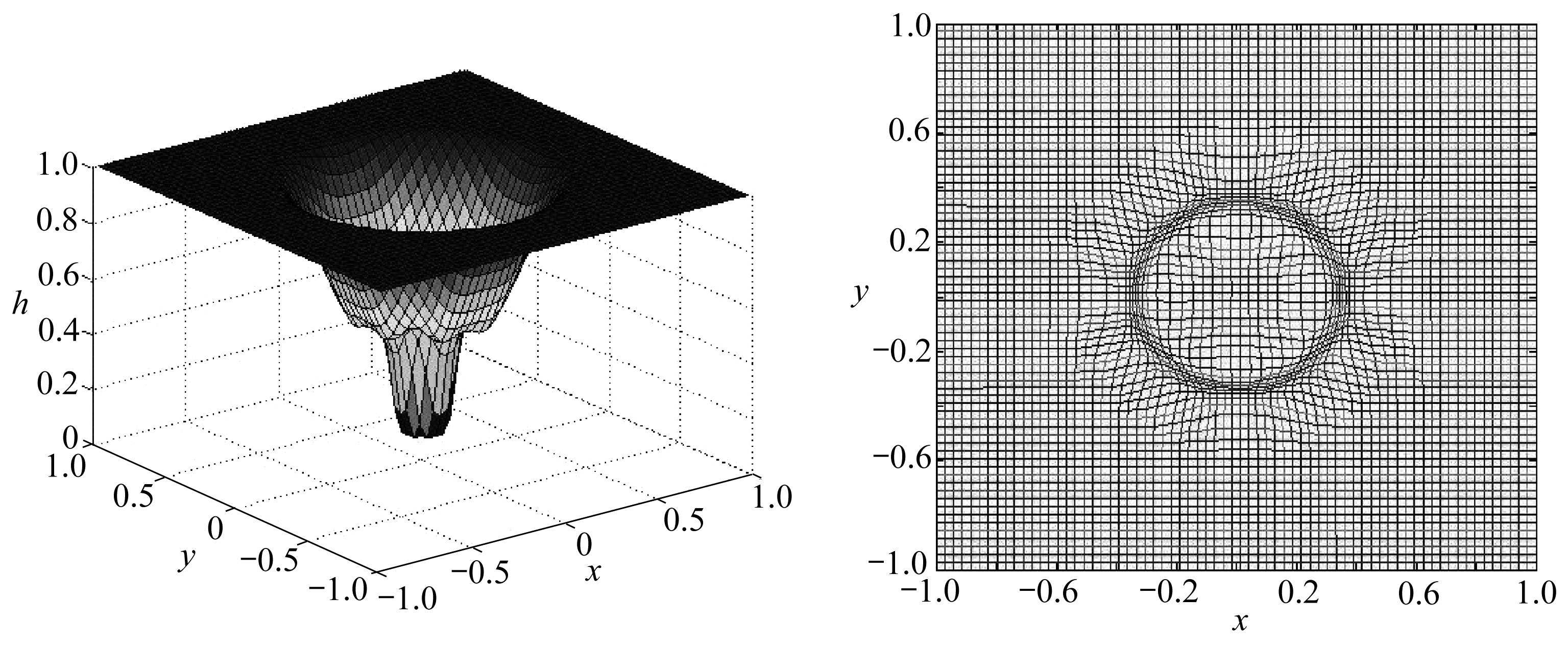
图6 激波聚焦模拟图
图7 网格演化图
Fig. 6 The shock focus simulation Fig. 7 The grid evolution diagram
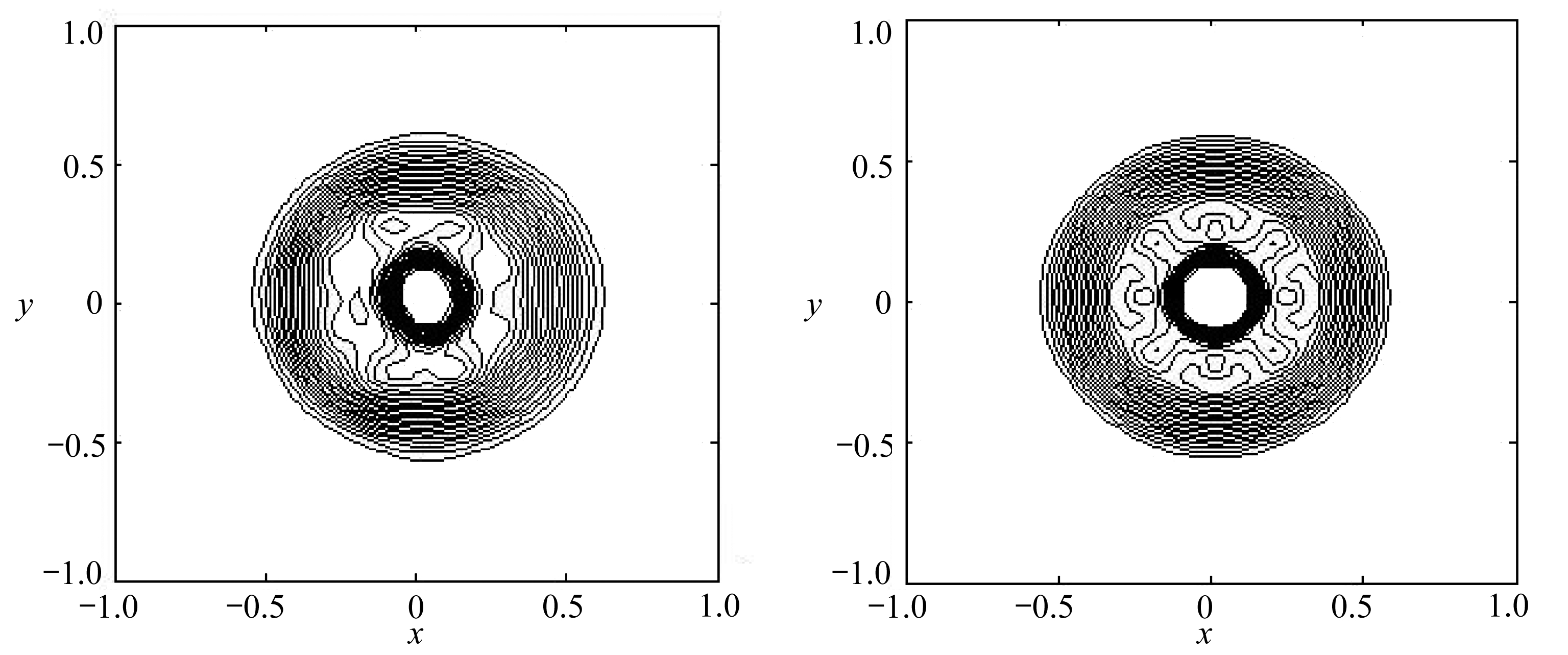
(a) 固定网格结果 (b) 移动网格结果 (a) Fixed grid results (b) Moving grid results
图8 二维激波聚焦问题水深等值线图
Fig. 8 The 2D shock focus problem water depth contours
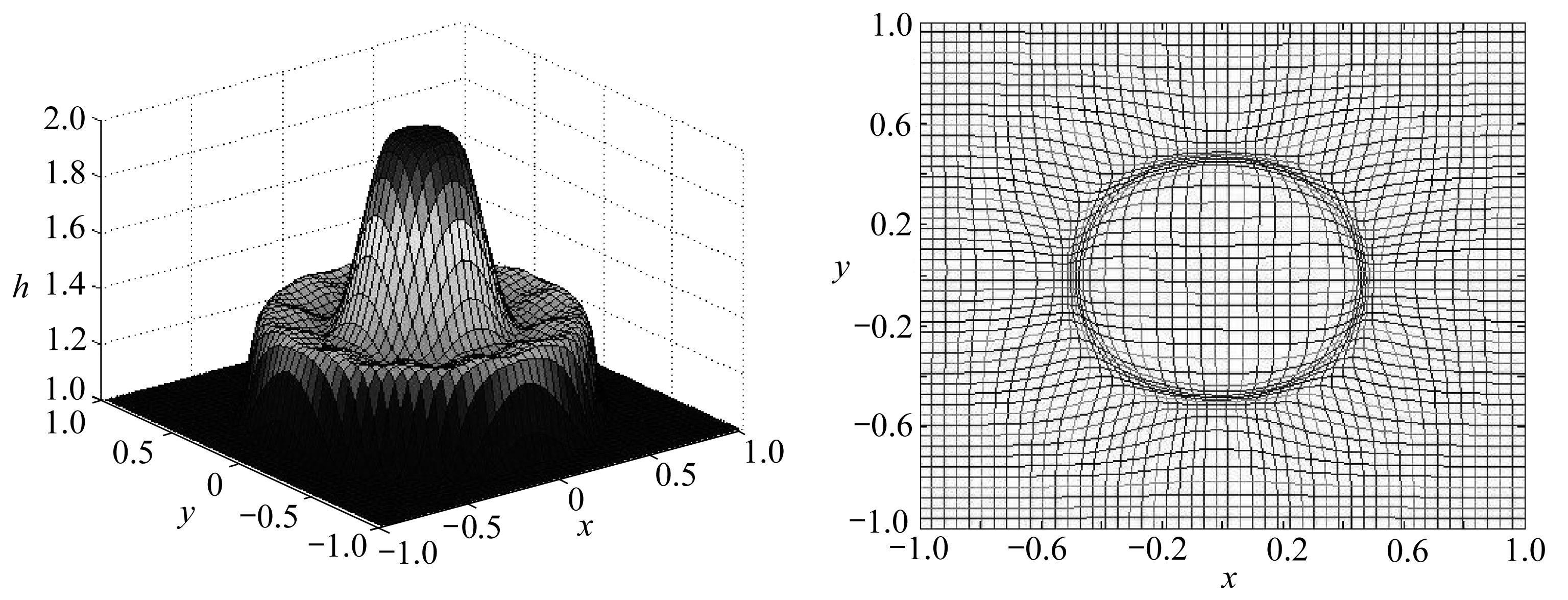
图9 移动网格圆形溃坝模拟图
图10 网格演化图
Fig. 9 The moving grid circular dam simulation diagramFig. 10 The grid evolution map
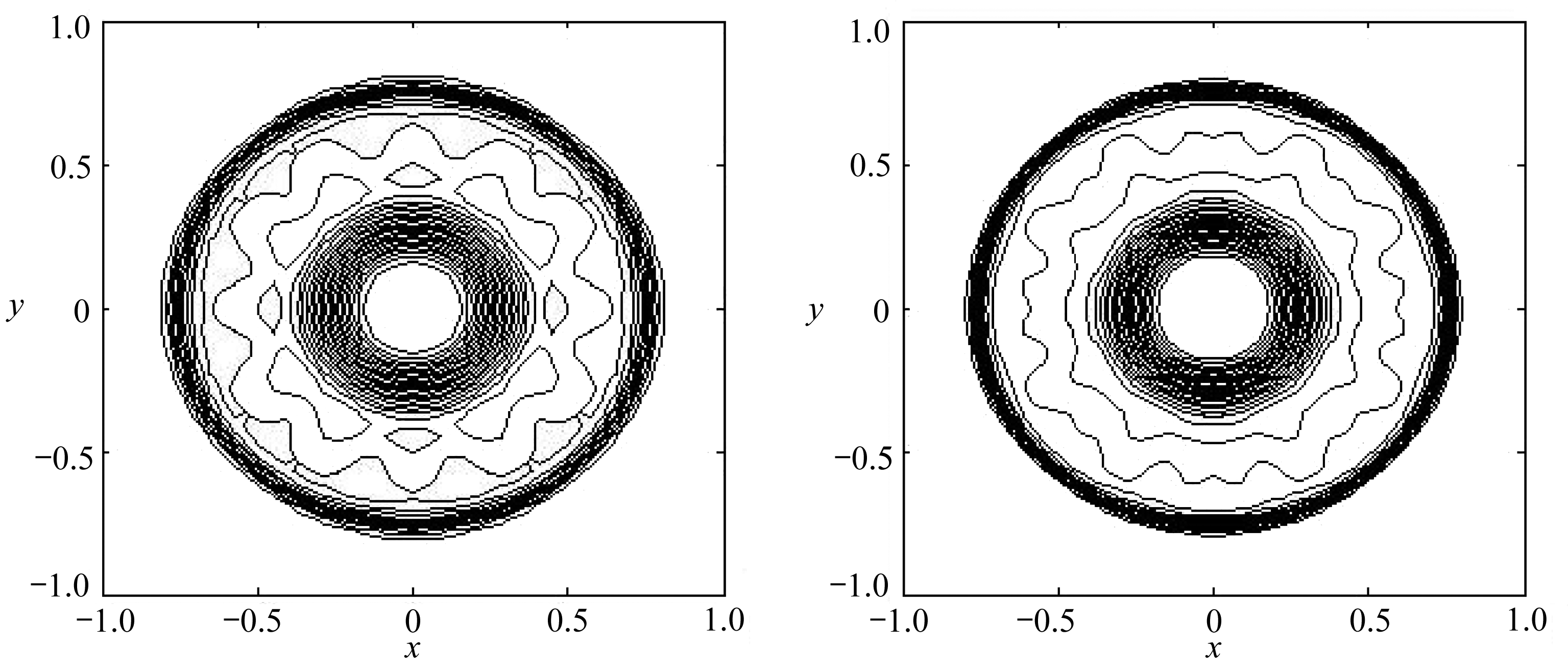
(a) 固定网格结果 (b) 移动网格结果 (a) Fixed grid results (b) Moving grid results
图11 二维圆形溃坝问题水深等值线图
Fig. 11 The water depth contours of the 2D circular dam breach problem
例4 二维区域上的圆形溃坝问题
考虑在二维区域[-1,1]×[-1,1]上方程(1)的溃坝问题,初始条件为
u(x,y,0)=v(x,y,0)=0, zb(x,y)=0.
空间网格数为50×50,取NCFL=0.25,计算时间t=0.2,g=0.98,采用周期边界条件.取式(24)中控制函数参数α=1.图9为移动网格圆形溃坝水面高度变化图;图10为网格随时间演化图;图11为二维圆形溃坝问题水深等值线图.从图中可以看出,基于移动网格的熵稳定格式的数值结果没有出现振荡或过渡抹平现象;从网格图可以看出,在解变化较大的区域网格进行了加密;从水深等值线图可以看出,相比于固定网格,移动网格分辨率更高.
5 总 结
本文提出了一种新的方法:移动网格旋转通量法.利用旋转不变性结合熵稳定格式得到混合数值通量,耦合移动网格法求解二维浅水波方程.采用新方法进行数值模拟时,对于带源项的浅水波方程出现多个激波或多个性质发生大的变化时,移动网格旋转通量法不能凸显其优势,网格演化效果不明显;对于源项为零的浅水波方程,解的性质发生较大奇异变化时,网格演化效果明显.但两种情况的数值模拟结果良好,没有出现振荡或大的抹平现象.通过算例分析,采用本文提出的移动网格旋转通量法求解二维浅水波方程所得到的结果具有良好的间断捕捉能力,分辨率高.
[1] TADMOR E. Entropy stability theory for difference approximations of nonlinear conservation laws and related time-dependent problems[J]. Acta Numerica, 2003, 12(12): 451-512.
[2] ISMAIL F, ROE P L. Affordable, entropy-consistent Euler flux functions Ⅱ: entropy production at shocks[J]. Journal of Computational Physics, 2009, 228(15): 5410-5436.
[3] FJORDHOLM U, MISHRAS, TADMOR E. Arbitrarily high-order accurate entropy stable essentially nonoscillatory schemes for systems of conservation laws[J]. SIAM Journal on Numerical Analysis, 2012, 50(2): 544-573.
[4] 郑素佩, 封建湖, 刘彩侠. 高分辨率熵相容算法在二维溃坝问题中的应用[J]. 水动力学研究与进展(A辑), 2013, 28(5): 545-551.(ZHENG Supei, FENG Jianhu, LIU Caixia. Application of high resolution entropy compatible algorithm in two-dimensional dam failure problem[J]. Journal of Hydrodynamics, 2013, 28(5): 545-551.(in Chinese))
[5] CHENG X H, NIE Y F, FENG J H. Self-adjusting entropy-stable scheme for compressible Euler equations[J]. Chinese Physics B, 2015, 24(2): 020202. DOI: 10.1088/1674-1056/24/2/020202.
[6] RAY D, CHANDRASHEKAR P, FJORDHOLM U S. Entropy stable scheme on two-dimensional unstructured grids for Euler equations[J]. Communications in Computational Physics, 2016, 19(5): 1111-1140.
[7] 张海军, 封建湖, 程晓晗. 带源项浅水波方程的高分辨率熵稳定格式[J]. 应用数学和力学, 2018, 39(8): 935-945.(ZHANG Haijun, FENG Jianhu, CHENG Xiaohan. An entropy stable scheme for shallow water equations with source terms[J]. Applied Mathematics and Mechanics, 2018, 39(8): 935-945.(in Chinese))
[8] HARTEN A, HYMAN J M. Self-adjusting grid methods for one-dimensional hyperbolic conservation laws[J]. Journal of Computational Physics, 1983, 50(2): 235-269.
[9] XU X H, NI G X. A high-order moving mesh kinetic scheme based on WENO reconstruction for compressible flows[J]. Journal of Scientific Computing, 2013, 27(2): 278-299.
[10] HAN E, LI J, TANG H. An adaptive GRP scheme for compressible fluid flows[J]. Journal of Computational Physics, 2010, 229(5): 1448-1466.
[11] CAO W, HUANG W, RUSSELL D. A study of monitor functions for two-dimensional adaptive mesh generation[J]. SIAM Journal on Scientific Computing, 1999, 20: 1978-1994.
[12] LI R, TANG T, ZHANG P. Moving mesh methods in multiple dimensions based on harmonic maps[J]. Journal of Computational Physics, 2001, 170(2): 562-588.
[13] TANG Z H, TANG T. Adaptive mesh method one- and two-dimensional hyperbolic conservation laws[J]. SIAM Journal on Numerical Analysis, 2003, 41(2): 487-515.
[14] 杨继明, 陈艳萍. 一类奇异摄动对流扩散边值问题的移动网格方法[J]. 湘潭大学自然科学学报, 2004, 26(3): 24-29.(YANG Jiming, CHEN Yanping. A moving mesh method for a class of singularly perturbed convection-diffusion boundary value problems[J]. Journal of Natural Science of Xiangtan University, 2004, 26(3): 24-29.(in Chinese))
[15] 陈冬冬, 宋松和. 变形法移动网格求解双曲型守恒律方程研究[J]. 计算机技术与发展, 2010, 20(2): 1-4.(CHEN Dongdong, SONG Songhe. Research of moving mesh method based on deformation in solving hyperbolic conservation laws[J]. Computer Technology and Development, 2010, 20(2): 1-4.(in Chinese))
[16] HE P, TANG H. An adaptive moving mesh method for two-dimensional relativistic hydrodynamics[J]. Communications in Computational Physics, 2012, 11(1): 114-146.
[17] 程晓晗, 聂玉峰, 蔡力. 基于移动网格的熵稳定格式[J]. 计算物理, 2017, 34(2): 175-182.(CHENG Xiaohan, NIE Yufeng, CAI Li. Entropy stable scheme based on moving meshes for hyperbolic conservation laws[J]. Chinese Journal of Computational Physics, 2017, 34(2): 175-182.(in Chinese))
[18] BRADFORD S F, SANDERS B F. Finite-volume model for shallow-water flooding of arbitrary topography[J]. Journal of Hydraulic Engineering, 2002, 128(3): 289-298.
[19] BRUFAU P, GARC A-NAVARRO M E. Zero mass error using unsteady wetting-drying conditions in shallow flows over dry irregular topography[J]. International Journal for Numerical Methods in Fluids, 2004, 45(10): 1047-1082.
A-NAVARRO M E. Zero mass error using unsteady wetting-drying conditions in shallow flows over dry irregular topography[J]. International Journal for Numerical Methods in Fluids, 2004, 45(10): 1047-1082.
[20] THANH M D, KARIM M F, ISMAIL A I M. Well-balanced scheme for shallow water equations with arbitrary topography[J]. International Journal of Dynamical Systems & Differential Equations, 2008, 1(3): 196-204.
[21] GOTTLIEB S, KETCHESON D I, SHU C W. High order strong stability preserving time discretizations[J]. Journal of Scientific Computing, 2009, 38(3): 251-289.
[22] 朱华君. 二维浅水波方程的高阶有限体积法[D]. 硕士学位论文. 长沙: 国防科学技术大学, 2006.(ZHU Huajun. High-order finite volume method for two-dimensional shallow water wave equation[D]. Master Thesis. Changsha: National University of Defense Technology, 2006.(in Chinese))
[23] 刘刚, 金生. 基于修正Roe格式的有限体积法求解二维浅水方程[J]. 水利水运工程学报, 2009(3): 29-33.(LIU Gang, JIN Sheng. Finite volume model for the 2D shallow water equations using modified Roe scheme[J]. Hydro-Science and Engineering, 2009(3): 29-33.(in Chinese))
[24] 潘存鸿. 三角形网格下求解二维浅水方程的和谐Godunov格式[J]. 水科学进展, 2007, 18(2): 204-209.(PAN Cunhong. Well-balanced Godunov-type scheme for 2D shallow water flow with triangle mesh[J]. Advances in Water Science, 2007, 18(2): 204-209.(in Chinese))
[25] WINTERS A R, GASSNER G J. An entropy stable finite volume scheme for the equations of shallow water magnetohydrodynamics[J]. Journal of Scientific Computing, 2016, 67(2): 514-539.
[26] TORO E F. Riemann Solvers and Numerical Methods for Fluid Dynamics[M]. Berlin: Springer, 2013.
[27] 王如云. 浅水波数值模拟的Roe平均法[J]. 计算物理, 2000, 17(2): 199-203.(WANG Ruyun. Roe mean method for numerical simulation of shallow water waves[J]. Chinese Journal of Computational Physics, 2000, 17(2): 199-203.(in Chinese))
[28] AZARENOK B N. Variational method for adaptive mesh generation[J]. Computational Mathematics and Mathematical Physics, 2008, 48(5): 786-804.
[29] EELLS J, SAMPSON J H. Harmonic mappings of Riemannian manifolds[J]. American Journal of Mathematics, 1964, 86(1): 109-160.