引 言
有限空间中的大型转臂式离心机包括土工离心机、装备试验离心机和载人离心机等.当离心机运行时，转子转动会带动工作室内空气运动，引起支座与转子、转子与空气、空气内部各微团，以及空气与工作室墙壁(含顶板、底板和侧壁)之间等发生相对运动而产生热量[1].这些热量若不及时排出，就会在工作室内积累，引起温度升高，进而影响工作室内试验模型/训练人员的状态和测量传感器的性能，最终影响试验测试或训练效果.
为了减小温度升高的影响，必须对工作室进行控温设计，而有效控温设计的前提是准确预测工作室的温度，预测工作室的温度可采用解析理论方法或数值模拟方法.总体来说，迄今解析理论方法已经历了两个发展阶段.第一阶段方法由文献[2]建立.其理论模型中仅考虑了工作室外表面温度恒定不变的等温边界条件和工作室墙壁内部为稳态热传导的情况.第一阶段的方法，由于离心机产生热量的主要来源，也就是求解工作室温度的前提——气动功率理论公式的准确性不足，同时由于求解工作室温度的理论模型本身的准确性也不足，因此其结果的误差较大.第二阶段方法由文献[3]建立.与第一阶段方法相比，第二阶段方法有两点进步：其一是就离心机产生热量的主要来源——气动功率而言，采用了文献[4-6]建立的相对来说更加准确的新公式；其二是求解工作室温度的理论模型中，考虑了机室外表面为第三类温度边界条件的情况.但第二阶段方法的理论模型中，机室墙壁内部仍然处理为稳态热传导.文献[7]采用文献[3]中的第二阶段方法，计算了一台土工离心机工作室内空气的温度，结果表明在离心机运行时间不是很长时，理论结果还是比实测值要大些，并指出这一差异源于对墙壁瞬态热传导效应的忽略.除解析理论方法外，文献[8]采用计算流体力学(computational fluid dynamics，CFD)数值方法分析了转臂式离心机转臂表面和机室内空气的压力，以及机室内的温度，基于所得压力换算的风阻功率与实测值吻合，但由于难于准确确定非均匀运动流场中气-固界面的换热参数值[9]，因此所得温度与实测值相比尚有较大差异.作为与转臂式离心机机室内腔-墙壁结构类似的瞬态温度问题，文献[10]研究了火场-结构联合分析的简化数值模型，实现了火场-结构联合的数值分析.该方法经过适当发展，可用于转臂式离心机机室内温度的数值求解.当然，与解析理论方法相比，CFD数值方法及其与固体有限元方法的联合应用存在建模复杂和计算耗时等问题，使离心机设计周期更长.因此，进一步发展解析理论方法和流-固耦合数值模拟方法，使其满足离心机工程设计对精确分析和快速分析的要求，都是具有积极意义的.
本文在文献[3]第二阶段理论方法的基础上，针对有限空间中大型转臂式离心机的加速-稳定运行过程，考虑墙壁的瞬态热传导，建立了离心机驱动系统和工作室-墙壁系统的能量平衡方程，导出了工作室内空气的瞬态温度公式，即第三阶段理论解，从而将解析理论方法发展到第三阶段.然后，以一台土工离心机为例，计算了工作室内空气的温度，与以前只考虑墙壁稳态热传导的理论计算相比，计算结果更加接近实测结果.本文所建立的工作室内空气的瞬态温度解析计算公式——第三阶段解析理论解，比此前只考虑墙壁稳态热传导的前两个阶段的解更加精确，可用于有限空间中大型转臂式离心机工作室温度控制设计的理论计算，提高了分析和设计的精度.
1 考虑墙壁瞬态导热时透过墙壁内表面的总热流量与工作室内空气温度的关系
为不失一般性，本文以图1所示土工离心机为例，研究有限空间中大型转臂式离心机工作室内空气的瞬态温度问题.设离心机工作室为圆柱形，机室中轴线沿竖直方向，内腔半径为R、外半径为r2(侧壁等效厚度δs=r2-R)、高度为H.为了反映工作室的一般尺寸规模，图1中给出了一实际土工离心机工作室的R为5.25 m、H为4.4 m，设顶板等效厚度为δt、底板等效厚度为δb，则在离心机运行过程中，当初始和环境温度都为T0、工作室内空气温度为T(t)时，机室顶板/底板和侧壁的瞬态热传导控制方程分别为式(1)和(2)：
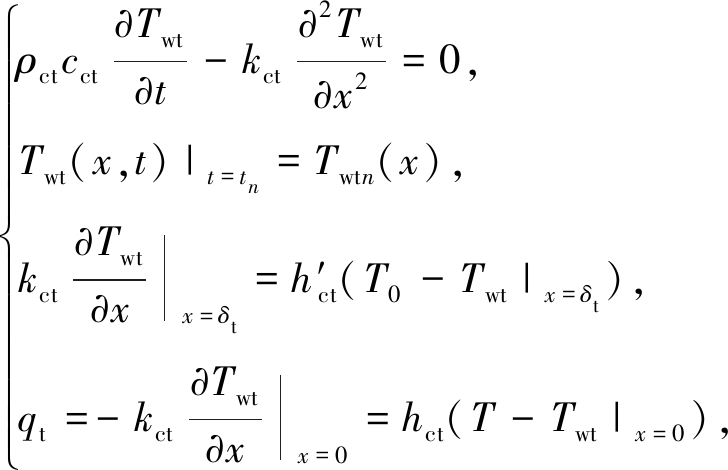
(1)
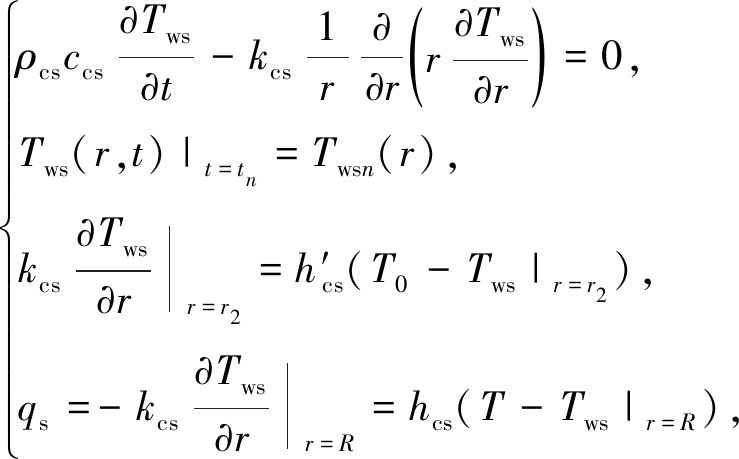
(2)
式中x是直角坐标，对于工作室顶板，其原点位于顶板下表面，正方向向上，对于工作室底板，其原点位于底板上表面，正方向向下；r是径向坐标，其原点位于工作室中心；Twt和Tws分别是工作室顶板/底板和侧壁中的瞬态温度，在t=tn时，它们分别为Twtn和Twsn，在离心机刚开始启动并加速时，tn=0，Twt0=T0和Tws0=T0，在离心机结束加速并开始稳定运行时，tn=t0，Twtn和Twsn由t=0～t0之间工作室温度的初边值问题控制方程求得；ρct和ρcs分别是工作室顶板/底板和侧壁材料的密度；cct和ccs分别是工作室顶板/底板和侧壁材料的比热容；kct和kcs分别是工作室顶板/底板和侧壁材料的导热率；hct和hcs分别是工作室顶板/底板和侧壁内表面的对流换热系数，其值由式(3)确定[2]；h′ct和h′cs分别是工作室顶板/底板和侧壁外表面的对流换热系数，其值由实测或查手册确定；qt和qs分别是工作室顶板/底板和侧壁内表面的热流密度.
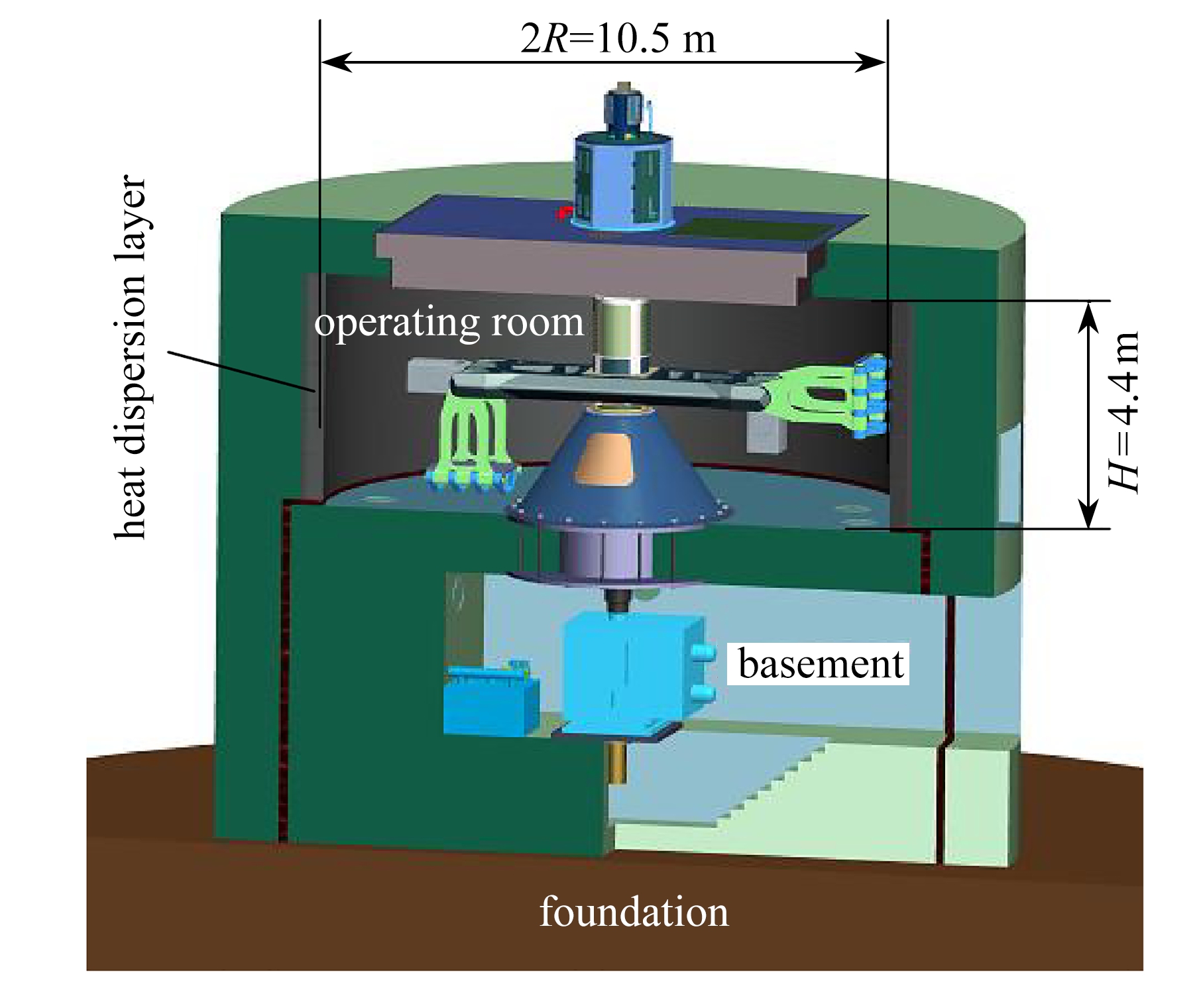
图1 典型土工离心机结构示意图
Fig. 1 Schematic drawing of a typical geotechnical centrifuge
(3a)
(3b)
式中ka是空气的导热率，室温时其值为0.026 7 W/(m·℃)；α是随流比，通过工作室内空气的力矩平衡关系计算，其具体计算方法可参见文献[1，4-6]；ωt是随时间变化的离心机转速；νa是空气的黏性系数，室温时其值为1.5×10-5 m2/s.由于hct与坐标r有关，因此qt也与坐标r有关.但考虑到墙壁内表面的温度升高是以工作室内空气温度T(t)为热源而引起的，而T(t)基本与r无关，因此，可近似认为顶板/底板的温度也与r无关，文献[11]中实测的机室温度结果也表明了这一近似处理的可行性.于是将式(3a)代入式(1)，再将各项同时乘以2πr后在[0，R]上关于r积分，并令
则得
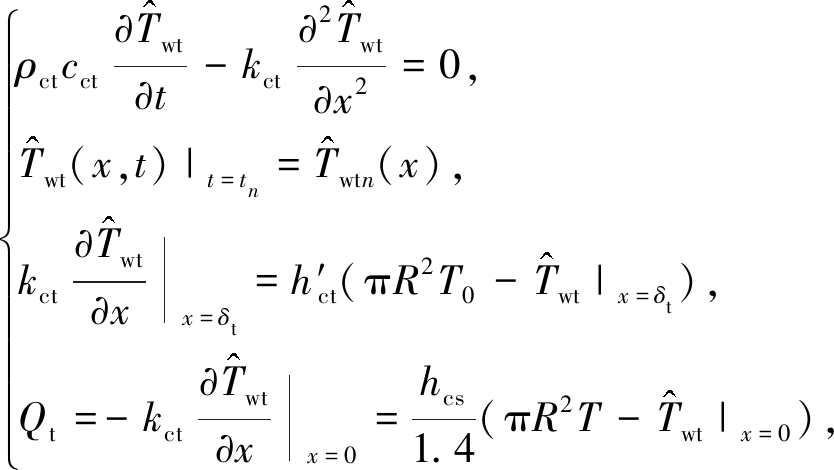
(4)
式中
将式(3b)代入式(2)，再将各项同时乘以2πRH，并令
得到
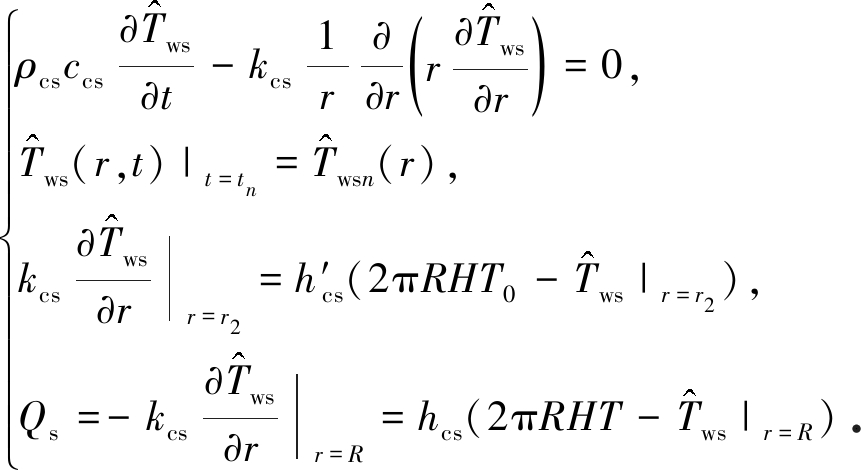
(5)
下面先求解式(4).令
(6)
式中
将式(6)代入式(4)，得到关于
的边界条件为齐次型的控制方程：
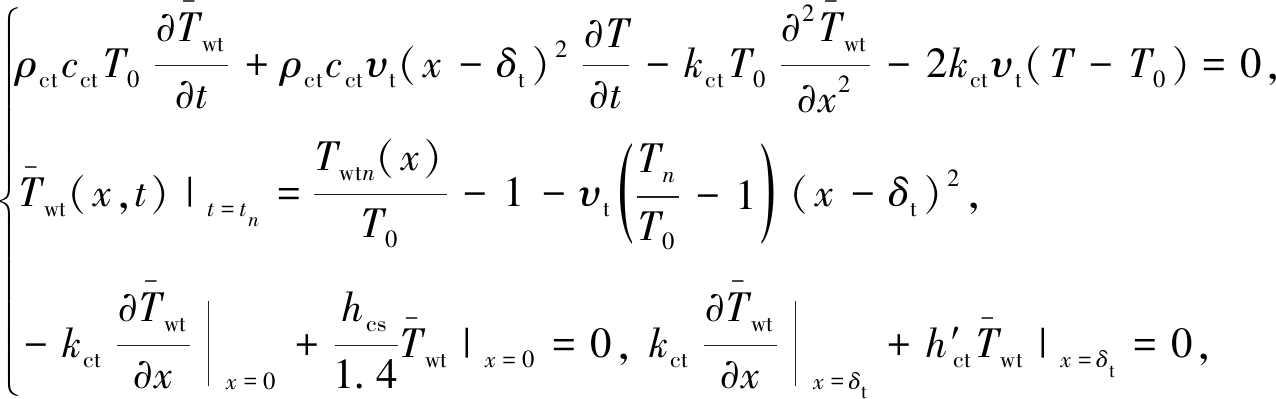
(7)
式中
Tn=T(t)|t=tn.
采用分离变量法求解式(7)对应的齐次方程和齐次边界条件问题，即
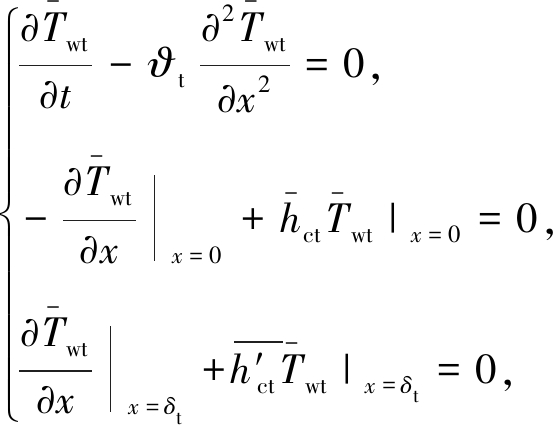
(8)
式中
令
代入控制方程(8)并求解，得到
(9a)
Xt(x)=C1sin(ηtx)+C2cos(ηtx).
(9b)
用Xt(x)表示的边界条件为
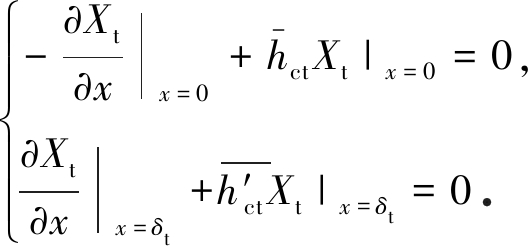
(10)
由式(9b)和(10)得齐次边值问题的特征值方程为
(11)
记特征值方程(11)的解为特征值序列ηti(i=1,2,…)，相应的特征函数为
(12)
容易证明，式(12)确定的函数序列Xti(x)(i=1,2,…)是正交完备的，即满足
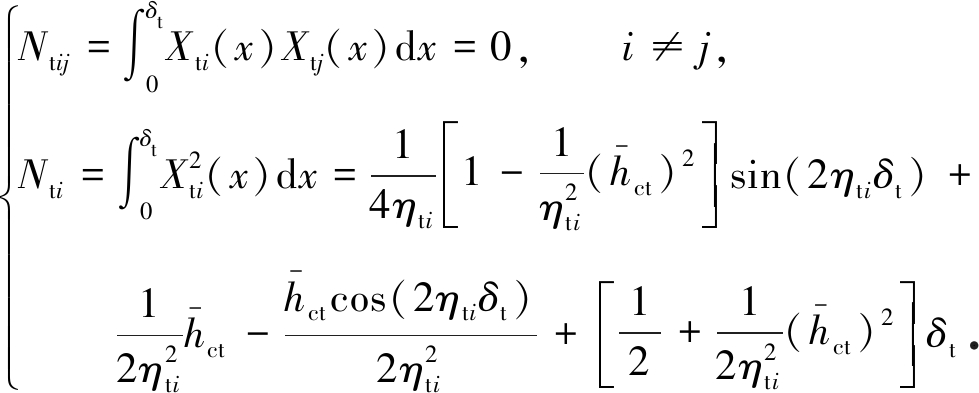
(13)
然后求解式(7)表示的非齐次问题.令
(14)
将其代入式(7)中的第一式，得到
(15)
对该式两边同时乘以
再在[0,δt]上对x积分，利用正交性关系式(13)，得到
(16)
式中
再将式(14)代入式(7)中的初始条件，得到
(17)
式中Utin=Uti(t)|t=tn， 其求解方法是： 对该式两边同时乘以
(j=1,2,…)，再在[0, δt]上对x积分，利用式(13)，即得到
(18)
令
则式(16)成为
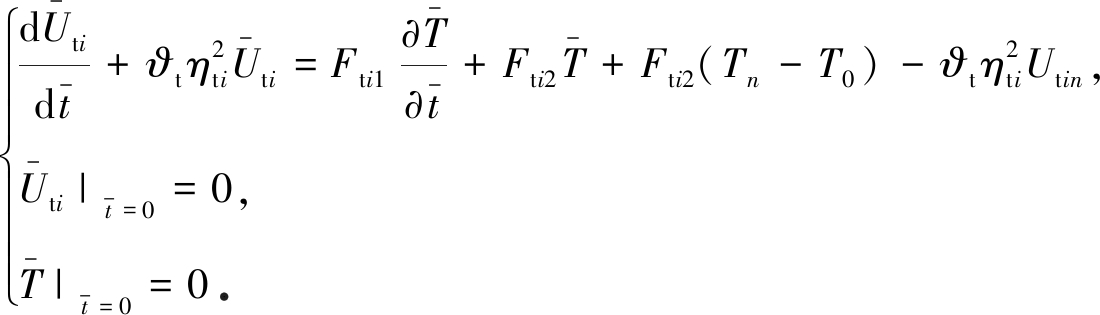
(19)
采用Laplace变换方法求解式(19)表示的初值问题，得到
变换的像函数：
(20)
由式(4)、(6)和(14)，得到透过工作室顶板的总热流量：
(21)
式中Uti由式(20)求得.
与上述求解Qt的方法和过程一样，可求得透过工作室底板的总热流量Qb，但需注意，求解Qb的理论模型和结果中的各变量和参数都应是工作室底板的相应变量和参数.
再求解Qs.由于控制方程式(2)和(5)中的变量是极坐标r的函数，因此求解Qs的方法和过程要相对复杂得多，严格的求解需要用到针对极坐标变量r在R≤r≤r2范围的Hankel变换.但考虑到一般情况下大型转臂式离心机工作室的曲率半径R都很大，因此，为了简化求解，可近似将侧壁作为平板结构处理，即近似将式(2)和(5)中的极坐标变量r作为直角坐标变量处理.这样Qs的求解方法和过程就与Qt的相同，但由于式(2)和(5)中边界条件表达式一些项的系数不同，因此Qs及其过程变量的表达式与Qt的不同.具体如下,首先令
(22)
式中z为沿工作室侧壁厚度的坐标变量，其原点在侧壁内表面，正方向由内指向外；
将式(22)代入式(5)得如下简化形式：
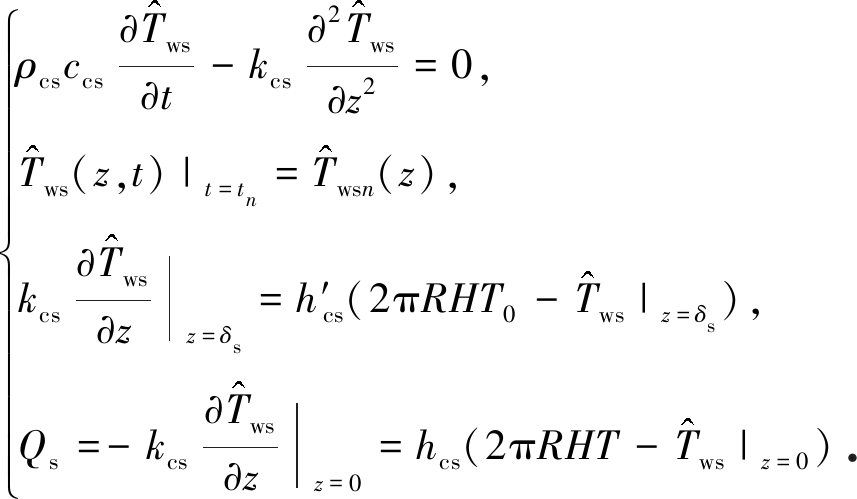
(23)
先得到关于
的边界条件为齐次型的控制方程，然后采用分离变量法求解，得到
(24)
式中
而
由下式求得:
(25)
其中
ϑs=kcs/(ρcsccs).
类似地，由式(5)、(22)和(24)，得到工作室侧壁的总热流量为
(26)
由式(3)、(21)和(26)可见，从t=0的初始时刻到离心机加速段结束的t=t0时刻，离心机的转速ωt由0增大到稳定运行转速ω，导致工作室墙壁内表面的对流换热系数hct和hcs也随时间不断增大，从而使工作室墙壁内表面的总热流量Qt+Qb+Qs也随ωt的增大而增大.尽管如此，一般来说大型转臂式离心机加速段时长t0与稳定运行时长相比都小很多，近似忽略ωt增大过程的影响不会引起明显的计算差异.因此，出于推导和计算的方便性，可从t=0开始就将ωt取为计算关心时刻t(当t<t0时)的转速或者直接取为稳定运行的转速ω.这正是本部分推导过程所采用的.另外，当离心机在顶板/底板或侧壁开有通风口时，通风口会影响墙壁导热，但将这种影响归结到对机室温度的影响上时，与从通风口进入冷气和排出热气对机室温度的影响相比要小很多.因此，对于开有通风口的墙壁，仍可按本部分的方法先求出没有通风口时的Qt/Qb或Qs，然后用通风口面积与无通风口时的相应墙壁面积之比进行简单折算即可.
2 工作室内空气瞬态温度的解析解
2.1 瞬态温度的Laplace变换解
考虑离心机工作室进风口和出风口空气质量流量相同，进风口空气以总质量流量s稳定流入，流入空气的温度为环境温度T0，出风口空气以质量流量s稳定流出，在时刻t和时刻t+dt，流出空气的温度即工作室温度分别为T和T+dT，则在时间t至t+dt内，离心机因支座摩擦和风阻消耗的机械能应等于工作室内空气和结构件吸收的热能，加上出风口排出空气带走的动能和热能与进风口进入空气带入的动能和热能之差，再加上透过工作室墙壁传走的热能.另外， 根据转臂式离心机建设实践经验和设计要求， 工作室温度随时间升高速率一般不大于0.01 ℃/s，而工作室内固体结构材料的导热率大于30.0 W/(m·℃)、横截面平均最小尺寸仅几十厘米，因此，与工作室内固体结构材料的吸热相比，工作室温度的变化率是一个慢得多的物理过程.这样，就可以近似忽略工作室内固体结构材料的导热过程，认为固体结构件很快达到热平衡.类似地，考虑到空气的流动性，可近似忽略工作室内空气的热平衡过程，而认为空气温度在任意时刻t都瞬间达到均匀分布.如此一来，根据能量守恒原理，工作室内空气温度满足方程：
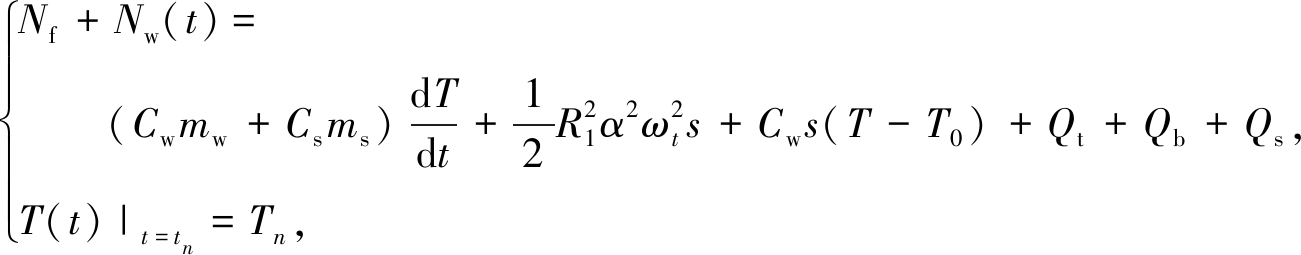
(27)
式中Nf是离心机消耗于支座摩擦的机械功率，即支座摩擦功率，W；Nw是离心机消耗于风阻的机械功率，即风阻功率，在加速段随时间变化，W；Cw是空气定压比热容，J/(kg·℃)；Cs是工作室内结构件的等效比热容，J/(kg·℃)；mw是工作室内空气质量，kg；ms是工作室内结构件的总质量，kg；R1是出风口中心点距工作室中轴线的水平距离，m；s是出风口空气质量流量，kg/s.
将式(21)表达的Qt和相应的Qb以及式(26)表达的Qs代入式(27)，再将
和
代入，得到
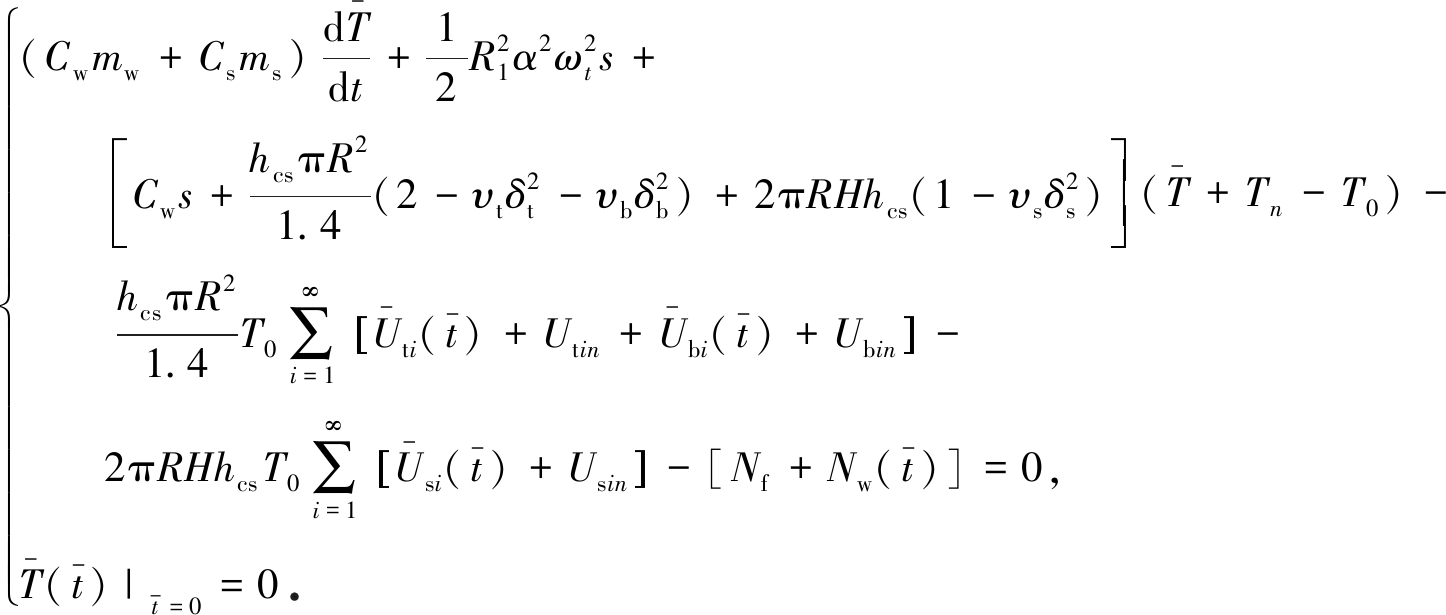
(28)
式(27)和(28)是求解离心机从初始时刻开始经历多个加速-稳定运行过程时工作室内空气温度的通式，只需要从初始时刻开始依次求解，并将每前一特征时间段求得的该段结束的t=tn时刻的T|t=tn=Tn，Uti|t=tn=Utin，Ubi|t=tn=Ubin和Usi|t=tn=Usin等数值作为后一特征时间段的初始值即可.这里的特征时间段指加速阶段或稳定运行阶段.其中，对于每一加速阶段，转速ωt是随时间变化的，且其变化规律可根据离心机运行的控制规则具体确定；当采用自然排风方式时，根据文献[7]，在一般工程应用范围离心机最大转速ω都较小，而在转速ω较小的范围内，自然排风质量流量s随加速阶段转速ωt增大而增大得很缓慢，因此在涉及到时间变量t的运算中可近似将s作为与稳定转速ω对应的常数，忽略ωt由上一特征时间段的转速增大到本特征时间段转速ω过程中s的变化；当采用强制排风方式时，s几乎在整个加速过程都是常数.对于每一稳定运行阶段，转速ω和排风质量流量s都不随时间变化.特别是对于初始加速阶段，如第1节所述，在t=0时刻，工作室内温度初始条件T|t=0=T0，墙壁的温度初始条件Twt0=T0，Twb0=T0和Tws0=T0，环境温度为T0.与之相应，式(28)中，tn=0，Tn=T0，Utin=0，Ubin=0和Usin=0.且当按转速ωt随时间t线性增大控制离心机加速过程时，有ωt=ωt/t0，这里如第1节中所述，t0是离心机加速过程的时间.于是，对于初始加速阶段，式(28)就简化为
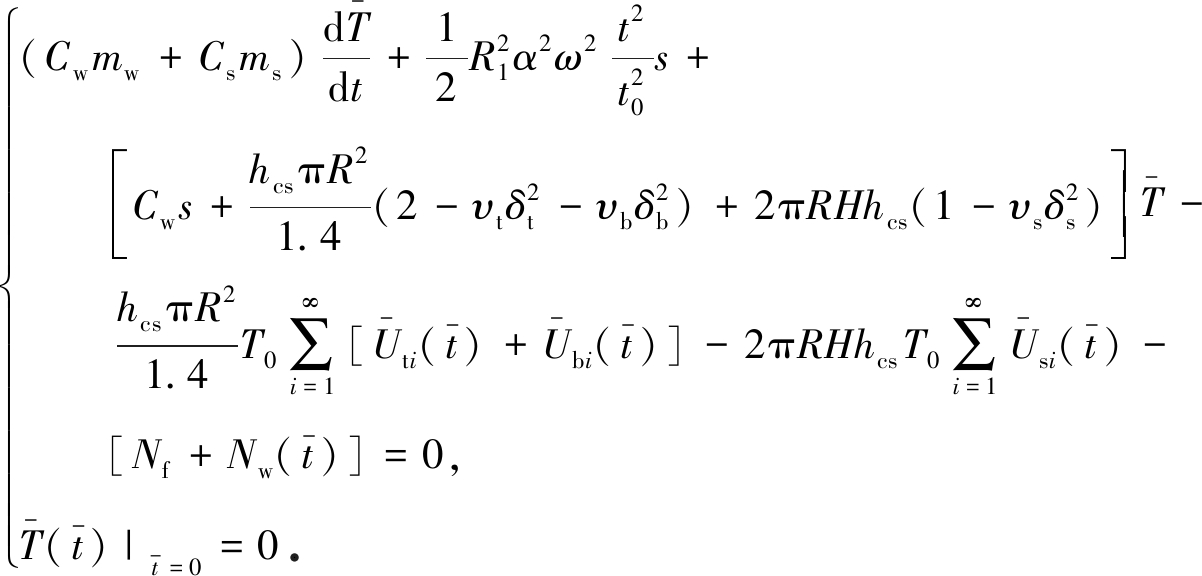
(29)
由式(29)求得初始加速阶段任意时刻
的工作室温度
及T(t)后，就可由第1节相应公式求得墙壁中的温度
和以及Twt，Twb和Tws，并由此得到该加速阶段结束的tn=t0时刻的工作室温度值Tn和墙壁中的温度分布函数Twtn，Twbn和Twsn.
下面针对仅由一个加速阶段和一个稳定运行阶段组成的运行过程，给出基于式(29)和(28)求解工作室内空气瞬态温度的Laplace变换解
的过程，然后再对其求逆变换得到瞬态温度及T(t).
根据文献[4-5]，可近似认为在加速过程中离心机风阻功率Nw(t)与转速ωt的3次方成正比，于是可得加速过程中离心机风阻功率Nw(t)近似与时间t的3次方成正比，即有Nw(t)=ξt3.设离心机加速阶段结束时的风阻功率为Nw0，且加速过程结束后，风阻功率保持恒定，即Nw=Nw0，则在加速和稳定运行的整个过程中，风阻功率随时间t的变化关系为
(30)
又根据文献[12]，可近似认为在离心机从启动到停止的整个运行过程中支座摩擦功率Nf不随时间t变化.
这样，按照式(28)中
的含义及tn的含义，对于t≤t0的初始加速阶段，有
对于t>t0的稳定运行阶段，有
为了区分加速阶段和稳定运行阶段的不同含义，下面分别用
和
表示加速阶段和稳定运行阶段的符号
并将式(29)和(28)进行相应改写.于是式(30)中的两个式子分别变为
(31)
然后将式(31)的第一式和第二式分别代入式(29)和(28)，再分别进行关于变量
和
的Laplace变换，并将由式(20)表达的
和相应的
以及式(25)表达的
代入，再进行整理，分别得到工作室内空气瞬态温度
和
的Laplace变换的像函数，即和的Laplace变换解
和
这里τa和τs都是复数，分别与和对应，和
是复变函数.其中对于加速阶段，为
(32)
式中
对于稳定运行阶段，为
(33)
式中A(τs)与式(32)中的A(τa)表达形式相同，只是自变量一个是τa，另一个是τs，而
2.2 瞬态温度Laplace变换解的奇点特性
由于时变函数的Laplace变换像函数是复变函数，与
对应的τ是复数，因此，理论上说式(32)和(33)分母
和τsA(τs)=0的根τa=τan′和τs=τsn′(n′=1,2,…)都是复数.设τa=xa+iya，A(τa)=fA1(xa,ya)+ifA2(xa,ya)，代入式(32)，得到
fA1-ya fA2-i(xa fA2+ya fA1)]-
(34)
式中
fA1(xa,ya)=(Cwmw+Csms)xa+Cws+
设τs=xs+iys，A(τs)=fA1(xs,ys)+ifA2(xs,ys)，B(τs)=fB1(xs,ys)+ifB2(xs,ys)，将其代入式(33)，得到
(35)
式中fA1(xs,ys)和fA2(xs,ys)分别与fA1(xa,ya)和fA2(xa,ya)的形式相同，而
fB2(xs,ys)=
由式(34)右端各项的分母都含有
可知，在复平面上，除坐标原点(xa,ya)=(0,0)是该式的奇点外，该式的其他奇点为如下方程组的解：
(36)
同样，由式(35)右端各项的分母都含有
可知，在复平面上，除坐标原点(xs,ys)=(0,0)是该式的奇点外，该式的其他奇点为如下方程组的解：
(37)
由方程组(36)中fA2(xa,ya)=0和方程组(37)中fA2(xs,ys)=0分别可得ya≡0和ys≡0，即式(36)和(37)的解都在实轴上，也就是除(xa,ya)=(0,0)和(xs,ys)=(0,0)点外，式(34)和(35)的其他所有奇点都在实轴上.而(xa,ya)=(0,0)和(xs,ys)=(0,0)本身也在实轴上，因此式(34)和(35)的所有奇点都在实轴上，也就是式(32)和(33)的所有奇点都是实数.本文将式(32)和(33)的所有奇点都是实数的特性称为转臂式离心机工作室内空气瞬态温度Laplace变换解的奇点特性.
将基于转臂式离心机工作室内空气瞬态温度Laplace变换解的奇点特性予以一般性推广，从而提出如下物理定律：任何瞬态温度的Laplace变换解的所有奇点都是实数.该定律是否成立，有待于人们在实践中找出反例给以证伪，或者通过一般性实验给以证实.对此，本文不再深入讨论.
2.3 基于Laplace逆变换的瞬态温度解析解
利用瞬态温度Laplace变换解的奇点特性，首先由式(32)和(33)中的A(τa)=A(τs)=0求出其所有实根，记为τa=τs=τn(n=1,2,…).然后注意到τa=0分别是
和
的一阶、三阶和四阶零点，τs=0是τsA(τs)的一阶零点，而τa=τn(n=1,2,…)是和的一阶零点，τs=τn(n=1,2,…)是τsA(τs)的一阶零点，并且有B(0)≠0和B(τn)≠0.因此，根据求Laplace变换的像原函数的展开定理[13]，分别对式(32)和(33)进行Laplace逆变换，得到当
或
时，和分别为
(38)
(39)
式中A(0)，A′(0)，A″(0)和A‴(0)分别是A(τa)或A(τs)及其一阶、二阶和三阶导数在τa=0或τs=0处的值，A′(τn)分别是A(τa)或A(τs)的一阶导数在τ=τn处的值.
值得说明的是，笔者在求解τn(n=1,2,…)时采用了如下技巧：首先根据A(τ)的表达式结构和其中
的特性，判断出A(τ)=0的根都是负根；然后设τ=xτ=-ζ，将其代入A(τ)=0，得到A(ζ)=0；最后求解A(ζ)=0的正根，并在求解过程中再次根据A(ζ)的表达式结构和其中
判断ζn的大致取值范围，并在该范围内通过数值计算搜索各个正根ζn，从而得到τn.如当只求出200个τn时，只需在0<ζ<0.178范围内由小到大寻求ζn即可.实际求解表明，采用这一技巧，可以避免在ζ定义域的大范围内进行数值迭代搜索，从而快速搜索到所需数量的ζn，既可避免漏根，也可减小数值迭代误差.
顺便指出，利用瞬态温度Laplace变换解的奇点特性，可以求解广泛的瞬态温度问题，如文献[13]中的复合圆筒壁非稳态导热问题.显然，与文献[14]中采用Stehfest数值反演技术[15]对瞬态温度Laplace变换解进行近似反演求解相比，采用瞬态温度Laplace变换解的奇点特性进行反演求解，不仅理论上是封闭的，而且也更加容易.
3 算例与分析
以一台已建成的400g t多用途离心机为例，文献[7,13]已实测得到其经历0.5 h加速到转速ω=13.2 rad/s后，再以该转速稳定运行3.5 h过程中的功率和工作室内空气温度数据，并根据转速ω=16.17 rad/s的实测数据将ω=13.2 rad/s稳定运行3.5 h的实测数据外推到9.5 h.在实验开始时，离心机工作室内温度为27.3 ℃，工作室外环境温度为29.8 ℃.在加速0.5 h后离心机开始稳定运行，此时工作室内温度为29.8 ℃，工作室外环境温度也为29.8 ℃.离心机稳定运行过程中，环境温度可近似视为恒定的29.8 ℃；转速ω=13.2 rad/s保持不变；总消耗功率Nout=76 132.41 W保持不变.同时，根据文献[7]的分析，自然排风质量流量s=2.251 kg/s保持不变，根据文献[11]，支座-转子之间的摩擦功率Nf=8 299.39 W保持不变.在这种情况下，文献[7]将离心机以ω=13.2 rad/s稳定运行开始的时刻为等效初始时刻，即时间0点，以此时的工作室内温度为初始温度，且该初始温度与工作室外的环境温度正好相等，给出了稳定运行过程中工作室内空气温度随时间变化的拟合关系式.这里采用前面推导的公式对该离心机在这一稳定运行过程中的工作室内空气温度进行理论计算，以验证理论推导的正确性和考虑墙壁瞬态热传导的必要性.
从离心机加速0.5 h、 工作室内空气温度达到29.8 ℃时开始，计算离心机稳定运行9.5 h过程中的工作室内空气温度.在该情况的计算中，只用到式(33)和(39).根据实际情况， 与文献[7]中一样， 所取计算参数如下： 工作室半径R=5.25 m， 高度H=4.4 m；工作室内空气初始温度T0=29.8 ℃， 环境温度T0=29.8 ℃； 总消耗功率Nout=76 132.41 W，支座摩擦功率Nf=8 299.39 W，转速ω=13.2 rad/s，随流比α=0.444 3；通风口位置R1=5.25 m，自然排风质量流量s=2.251 kg/s；空气密度ρ=1.205 kg/m3，空气定压比热容Cw=1 005 J/(kg·K)，工作室内空气质量mw=460.0 kg，工作室内结构件比热容Cs=460 J/(kg·K)，工作室内结构件质量ms=80 000.0 kg；顶板、底板和侧壁厚度都为0.5 m；顶板和底板外表面对流换热系数都为37 W/(m2·K)，侧壁外表面对流换热系数为74 W/(m2·K)；顶板、底板和侧壁材料导热系数都为1.51 W/(m·K)；顶板、底板和侧壁材料密度都为2 250 kg/m3；顶板、底板和侧壁材料比热容都为470 J/(kg·K).上述参数中，功率和转速通过实测得到，随流比和排风流量通过基于实测功率和温度数据的理论反演得到[7]，材料物性参数通过查询相关机械工程材料手册并结合经验得到.
首先根据式(11)编制求解其根ηt的FORTRAN程序，计算得到特征值序列ηti(i=1,2,…,500).同理得到ηbi和ηsi(i=1,2,…,500).再根据A(τa)=A(τs)=0编制求解其根τn的FORTRAN程序，调用已获得的特征值序列ηti，ηbi，ηsi，计算得到A(τa)=A(τs)的一阶0点值τn(n=1,2,…,300).最后根据式(39)，编制FORTRAN程序，再次调用特征值序列ηti，ηbi，ηsi，并调用一阶0点值τn，计算和T(t).计算中对式(33)中的级数取500项，对式(39)中的级数取300项.为了考查这两个级数的求和项数对计算结果的影响，计算中对这两个级数的项数都减少10项或20项，比较发现，减少10项和20项的计算结果与不减少时的相比相对变化量和绝对变化量都极小，表明两个级数求和所取项数都足够.
计算所得结果如图2所示.图2中同时引用了文献[7, 13]中给出的实测结果和考虑墙壁稳态导热时基于相同前提条件的理论结果.
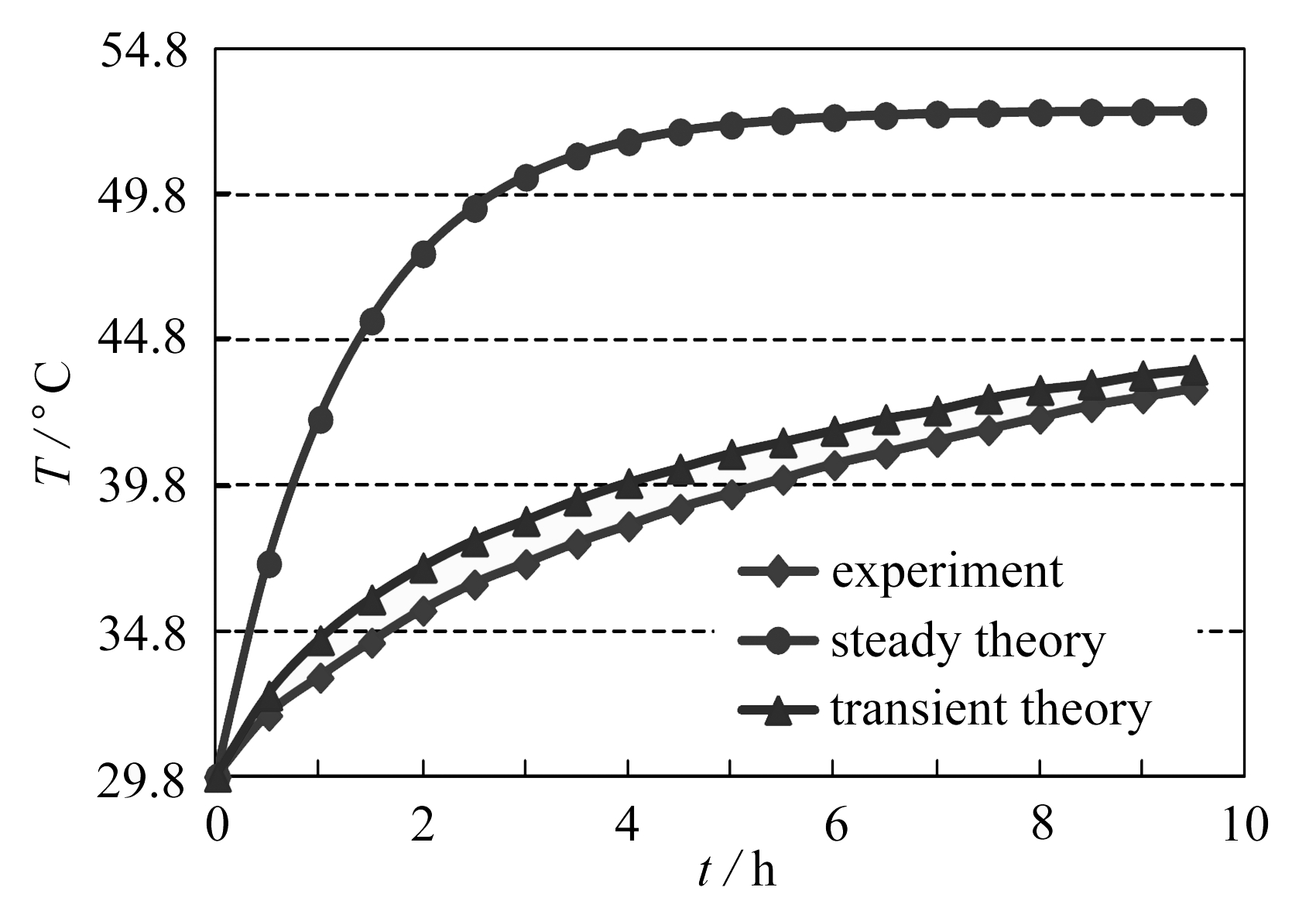
图2 工作室内空气温度随时间的变化曲线
Fig. 2 Curves of air temperature vs. time in the work room
比较不同方法所得温度-时间曲线可见，在整个9.5 h的稳定运行过程中，仅考虑墙壁稳态导热时的理论计算结果偏离实测结果较远，且在运行前几小时比实测结果大1倍以上，说明以前仅考虑墙壁稳态导热的计算方法过于保守，根据应用该方法计算的工作室内空气温度制定工作室温控措施，引起了一定浪费.而考虑墙壁瞬态导热时的理论计算结果，在整个过程中都与实测结果很接近，相对以前的计算方法而言要准确得多.当然，不难理解，由于工作室内空气温度实际上并不严格均匀，不同位置温度的实测值本身也有几摄氏度的差别[11]，而理论计算中假设了工作室内空气温度均匀分布，图2中的实测值又只是特定测点的值；同时由于理论计算中的前提参数也不一定严格准确，理论模型中忽略了工作室内固体结构材料的导热过程等，因此实测值和理论计算值仍然有约2 ℃的绝对偏差.但总而言之，本文考虑墙壁瞬态导热的理论计算模型更加符合物理实际，数学推导、求解过程也是相对封闭的，因此，计算结果自然会相当准确.
另外，当取t=∞进行计算时，可得转臂-工作室-墙壁系统达到热平衡时的工作室内空气温度为52.64 ℃，该数据与文献[7]中基于实测数据的拟合公式计算的结果一致，也与仅考虑墙壁稳态导热时的理论计算结果一致.这说明，考虑墙壁稳态导热和考虑墙壁瞬态导热计算得到的整个系统平衡时的工作室内空气温度是相同的.事实上，将式(39)中的取为
式(39)就直接简化为文献[3]中的相应公式.结合图2中各条曲线的相对情况及其共同的水平渐近线，可见与仅考虑墙壁稳态导热时相比，考虑墙壁瞬态导热时，工作室内空气温度随运行时间延长升高得要缓慢一些，而整个转臂-工作室-墙壁系统达到热平衡的时间要长很多.因此，当关注热平衡时的工作室内空气温度时，可采用以前的仅考虑墙壁稳态导热的理论计算方法，而当关注离心机仅为有限长时间运行时，采用本文的考虑墙壁瞬态导热的理论计算方法更加准确和有效.总之，对于一般来说只运行有限长时间的大型转臂式离心机，应该采用本文的理论计算方法.这也正是本文研究的意义.
4 结 论
本文从大型转臂式离心机气动功率的最新研究结果出发，考虑离心机工作室顶板、底板和侧壁的瞬态导热及墙壁内、外表面满足一般情况的第三类温度边界条件，建立了墙壁的瞬态热传导控制方程与整个离心机驱动系统和转臂-工作室-墙壁系统的能量平衡方程.采用Laplace变换方法和求解Laplace逆变换的展开定理，联立求解所建墙壁瞬态热传导方程和整个系统的能量平衡方程，导出了离心机工作室内空气温度随时间变化的级数型显式表达式.根据导出的理论公式，编制FORTRAN程序，以一台土工离心机为例实施了理论计算.将以前计算方法所得结果、本文方法所得结果与实测值比较，表明考虑墙壁瞬态导热的理论计算结果更加接近实测结果.所建理论公式和编制的程序可用于更准确计算大型转臂式离心机工作室内空气的温度，从而提高工作室温控设计水平.
[1] 贾普照. 稳态加速度模拟试验设备: 离心机概论与设计[M]. 北京: 国防工业出版社, 2013.(JIA Puzhao. Steady-State Acceleration Simulation Test Equipment: Centrifuge Conspectus and Design[M]. Beijing: National Defense Industry Press, 2013.(in Chinese))
[2] CORTE J F. Design of geotechnical centrifuges[C]//Centrifugeuses, Equipements et Instrumentation. Paris, 1988: 9-15.
[3] 尹益辉, 余绍蓉, 冯晓军, 等. 土工离心机的机室温升及其控制方法研究[C]//第18届全国结构工程学术会议论文集 (第Ⅰ册). 北京, 2009.(YIN Yihui, YU Shaorong, FENG Xiaojun, et al. Reseaches into temperature rise and control methods for work room of geotechnical centrifuges[C]//Proceedings of the 18th National Conference on Structural Engineering (Sesion Ⅰ). Beijing, 2009.(in Chinese))
[4] 尹益辉, 刘远东, 王兴伦, 等. 旋臂式离心机负载转矩及其驱动电机额定功率的计算方法[J]. 机电工程, 2011, 28(6): 659-662.(YIN Yihui, LIU Yuandong, WANG Xinlun, et al. Calculations of load rotational moment and rating power of centrifuges with rotation arms[J]. Journal of Mechanical & Electrical Engineering, 2011, 28(6): 659-662.(in Chinese))
[5] 尹益辉, 余绍蓉, 冯晓军, 等. 密闭机室型土工离心机的风阻功率[J]. 绵阳师范学院学报, 2010, 29(2): 1-5.(YIN Yihui, YU Shaorong, FENG Xiaojun, et al. Aerodynamic power of geotechnical centrifuges with closed chamber[J]. Journal of Mianyang Normal University, 2010, 29(2): 1-5.(in Chinese))
[6] 尹益辉, 余绍蓉, 冯晓军, 等. 机室开有通风口的土工离心机的风阻功率[J]. 绵阳师范学院学报, 2010, 29(5): 1-5.(YIN Yihui, YU Shaorong, FENG Xiaojun, et al. Aerodynamic power of geotechnical centrifuges with holed chamber[J]. Journal of Mianyang Normal University, 2010, 29(5): 1-5.(in Chinese))
[7] 尹益辉, 冯晓军, 范志庚, 等. 土工离心机稳定运行时机室的自然排风效应研究[J]. 绵阳师范学院学报, 2017, 36(11): 1-7.(YIN Yihui, FENG Xiaojun, FAN Zhigeng, et al. On natural air exhaust of the chamber of a steady operating geotechnical centrifuge[J]. Journal of Mianyang Normal University, 2017, 36(11): 1-7.(in Chinese))
[8] 郝雨, 尹益辉, 万强, 等. 基于CFD的土工离心机风阻及流场特性分析[J]. 装备环境工程, 2018, 15(2): 52-56.(HAO Yu, YIN Yihui, WAN Qiang, et al. Wind resistance and flow field characteristic analysis of geotechnical centrifuges based on CFD[J]. Equipment Environmental Engineering, 2018, 15(2): 52-56.(in Chinese))
[9] 周焕林, 严俊, 余波, 等. 识别含热源瞬态热传导问题的热扩散系数[J]. 应用数学和力学, 2018, 39(2): 160-169.(ZHOU Huanlin, YAN Jun, YU Bo, et al. Identification of thermal diffusion coefficients for transient heat conduction problems with heat sources[J]. Applied Mathematics and Mechanics, 2018, 39(2): 160-169.(in Chinese))
[10] 陈适才, 徐珊, 张磊, 等. 火场-结构联合分析简化模型及其应用研究[J]. 应用数学和力学, 2017, 38(8): 888-898.(CHEN Shicai, XU Shan, ZHANG Lei, et al. A simplified model for coupled fire-structure analysis and its application[J]. Applied Mathematics and Mechanics, 2017, 38(8): 888-898.(in Chinese))
[11] 黄锦舒, 孔令刚, 韩连兵, 等. ZJU-400离心机工作舱温控效果测试与分析[C]//全国土工离心模拟技术学术交流会会议论文集. 武汉, 2011: 199-202.(HUANG Jinshu, KONG Linggang, HAN Lianbing, et al. Measurement and analysis of the temperature control effect for ZJU-400 centrifuge[C]//Proceedings of the National Conference on Simulation Technology of Geotechnical Centrifuges. Wuhan, 2011: 199-202.(in Chinese))
[12] 四川大学数学系高等数学微分方程教研室. 高等数学[M]. 北京: 人民教育出版社, 1979.(Differential Equation Teaching and Research Section, Departments of Mathematics of Sichuan University. Higher Mathematics[M]. Beijing: People’s Education Press of China, 1979.(in Chinese))
[13] 尹益辉, 黎启胜, 郝雨, 等. 大型旋转机械转子驱动功率的理论与实测融合分析[J]. 工程设计与力学环境, 2018(1): 16-24.(YIN Yihui, LI Qisheng, HAO Yu, et al. Combined theoretical and experimental analysis of drive power of large rotating machines[J]. Engineering Design and Mechanics Environment, 2018(1): 16-24.(in Chinese))
[14] 王照亮, 张克舫, 李华玉, 等. 一种求解复合圆筒非稳态导热问题的新方法[J]. 石油大学学报, 2005, 29(2): 89-92.(WANG Zhaoliang, ZHANG Kefang, LI Huayu, et al. A new approximate solution for multiple-layer cylindrical walls of unsteady-state heat conduction[J]. Journal of the University of Petroleum, 2005, 29(2): 89-92.(in Chinese))
[15] STEHFEST H. Algorithm 368 numerical inversion of Laplace transforms[J]. Communications of ACM, 1970, 13(1): 47-49.