引 言
Rossby波是由地球自转产生的一种行星波,它是一种生命周期较长的大尺度波动,非线性大气和海洋动力学的许多问题都可以归结为Rossby波演变问题,其研究领域涉及天气系统的演变、大气和海洋的相互耦合、大气环流中阻塞形成、海洋涡旋、大气中大尺度包络孤立子理论等内容.因此,Rossby波的理论研究引起了许多国内外学者的关注.在早期,学者们通过各种非线性偏微分方程建立动力学模型去描述Rossby波的演变和发展,去解释大气和海洋运动中观察到的一些自然现象.如Long[1]在β平面近似下得到了Rossby振幅演变满足的KdV方程,对于正压流体做了开创性的工作.Wadati [2]和Redekopp [3]从正压流体和分层流体的模式推导了mKdV 方程,推广了Long的工作.随后,许多学者在正压流体中进一步研究了切变气流中Rossby波的生成和发展[4-7].Boyd[8-9]从基本方程出发,采用多重尺度法得到了正压流体中赤道非线性Rossby波振幅满足的KdV方程和mKdV方程.Meng和Lü[10]从包含地形和外源的正压准地转位涡出发,推导了Rossby波振幅满足的Boussinesq方程.Ono [11]采用多重尺度法,从准地转位涡方程出发,推导出BDO方程刻画Rossby振幅演变的代数孤立波.Luo[12]从大气中的浅水方程出发,通过多重尺度法建立了Benjamin-Ono方程描述代数孤立波.另外,在研究中发现Rossby波影响天气现象和气候变化,如木星红斑、大气阻塞、El Ni
o现象、南方涛动[13-15].因此,对Rossby波的研究不仅能够为天气和海洋预报提供理论依据,而且对大气和海洋非线性动力学具有重要的理论和实际意义.
在真实的大气和海洋运动中,Rossby波的演变和发展会受到诸多物理因素的影响,如推广的β效应、切变基本流、地形、耗散、外源、层结效应以及完整Coriolis力等.蒋后硕等[16]的研究结果表明基本流剪切和地形作用对Rossby波的形成和发展具有重要意义.吕克利等[17]推导了外源和耗散强迫的广义KdV-Burgers方程,分析了外源和孤波的相互作用对局地阻塞的形成.张瑞岗等[18]从大气基本方程组出发,研究了地形效应对近赤道非线性Rossby波的影响.Meng等[19]推导出包含地形和耗散项的非齐次强迫的BDO-Burgers方程,在弱切变基本气流下讨论了地形和耗散对代数孤立波的影响.Yang等[20-21]考虑地形、耗散和外热源等因素对Rossby波的影响,研究了地形效应对大气阻塞等问题.Song等[22-23] 首次在推广的β平面近似(即推广的β效应)下进行了研究,研究结果表明推广的β效应和地形能够诱导非线性Rossby孤立波.李少峰等[24] 在β效应、层结效应和地形效应作用下,推导了Rossby孤立波包演变所满足的非齐次Schrödinger方程.尹晓军等[25]研究了在完整Coriolis作用下外源对Rossby波的影响.Lu等[26]研究了在层结流体中具有耗散作用下的Boussinesq方程.但是,建立带有外源和耗散强迫的Boussinesq方程的数学模型去描述非线性Rossby波振幅的演变和发展还没有出现,这也是本文的主要工作.
许多学者对于获得的动力学模型方程,通过求解结果去解释物理因素对Rossby波动的影响及其波动的运动本质,进而解释大气和海洋中若干物理现象,为海洋物理、大气动力、天气现象及天气预报等提供理论依据和研究价值.但是,大多数非线性偏微分方程都没有解析解,特别是孤立波解.因此,求解非线性偏微分方程也是一个重要的研究课题,不同的方程对应不同的求解方法,许多学者在寻求孤立波解方面做了许多工作[27-32].
本文在推广的β平面近似下,从包含外源和耗散的准地转正压位涡方程出发,利用Gardner-Morikawa变换和摄动法,推导出描述非线性Rossby孤立波的数学模型,即带有外源和耗散强迫的非线性Boussinesq方程.分析了推广的β效应、切变基本流、外源和耗散对非线性Rossby波的影响.利用修正的Jacobi椭圆函数展开法,获得了带有外源和耗散强迫的Boussinesq方程的周期波解和孤立波解,通过分析解的结构,结果表明外源和耗散对非线性Rossby波的影响.
1 方程模型的推导与方法
1.1 控制方程与边界条件
在推广的β平面近似下,带有外源和耗散的无量纲准地转位涡方程为[17,33]
2ψ+β(y)y]=-λ2ψ+Q，
(1)
其中ψ是总的流函数,β(y)y是推广的β平面近似[22],λ>0是耗散系数,Q=Q(x,y,t)为外源,
表示二维的 Laplace算子.
边界条件为
(2)
1.2 带有外源和耗散强迫的非线性Boussinesq方程
假设总的流函数为
(3)
其中c0是线性波的相速度,小参数ε(ε≪1)为考虑弱非线性问题,ψ′是扰动流函数,
是切变基本流,α是量级为1的常数,称为失谐参数[34] .
为了平衡耗散和非线性项,以及消除由切变基本流引起的耗散,假设
(4)
将式(3)和(4)代入到式(1)和(2),得到扰动方程和边界条件：
2ψ′=
-ε3/2μ2ψ′+Q′(x,t),
(5)
(6)
其中
由于大气和海洋运动的时空多尺度性,采用多重尺度法,即Gardner-Morikawa变换：
X=ε1/2x, T=εt.
(7)
将式(7)代入方程(5)和(6),得到
(8)
(9)
这里考虑了外源和非线性项平衡，即Q′(x,t)=ε2Q1(X,T).
将扰动流函数ψ′做如下的小参数展开：
ψ′(X,y,T)=εψ0(X,y,T)+ε3/2ψ1(X,y,T)+ε2ψ2(X,y,T)+….
(10)
将式(10)代入方程(8)和(9),得到各阶摄动问题：
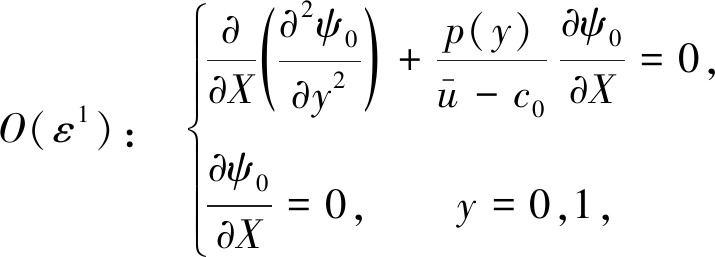
(11)
其中
假设方程(11)有如下形式的分离解：
ψ0(X,y,T)=A(X,T)φ0(y)，
(12)
将式(12)代入方程(11),方程(11)变为
(13)
注意到方程(13)是一个本征值问题，而且本征值问题只能确定Rossby波振幅的径向结构，而不能确定Rossby波振幅随时空的演变.因此,需要考虑高阶问题:
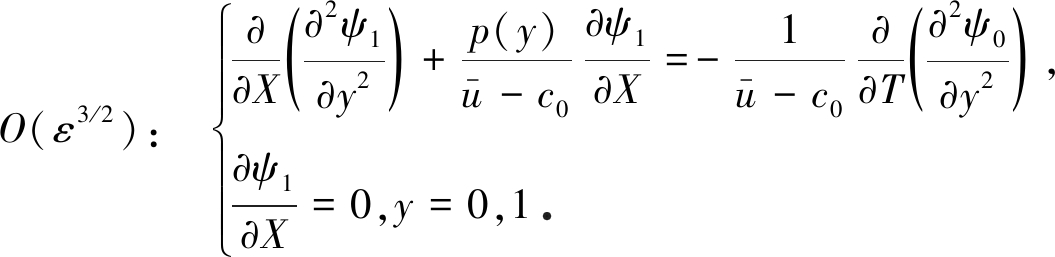
(14)
为了得到Boussinesq方程,在不失一般情况下,假设
(15)
将式(15)代入方程(14) ,方程(14)变为
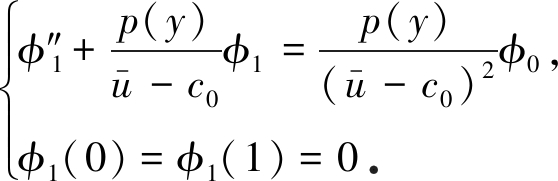
(16)
方程(16)也是一个本征值问题,也不能确定Rossby波振幅A(X,T).继续考虑更高一阶问题:
(17)
其中
(18)
利用本征值函数的正交性,得到方程(17)的可解性条件：
(19)
将方程(18)代入式(19)中,整理后得到
(20)
其中
这里φ0,φ1由本征值方程(13)和(16)来确定.方程(20)是刻画非线性Rossby波振幅演变所满足的数学模型.通过分析方程(20)能够解释非线性Rossby波新的物理机制.系数α2由
以及φ0和φ1表示,这表明推广的β效应和切变基本流都是诱导Rossby波的非线性因素.而且即使没有切变基本流(即
推广的β效应也能诱导非线性Rossby波,这与Song等的结果一样[22].μα4(∂A/∂X)表示由耗散效应引起的强迫项.α5(∂Q1/∂X)表示由外源产生的非齐次强迫项.由此可见,推广的β效应、切变基本流、外源和耗散都是非线性Rossby波的影响因素.当α4=0和α5=0时,方程(20)是标准的Boussinesq方程.因此,方程(20)称为带有外源和耗散强迫的非线性Boussinesq方程.
2 带有外源和耗散强迫的非线性Boussinesq方程的周期波解和孤立波解
当α4=0和α5=0时,方程(20)变为标准的Boussinesq方程,即
(21)
利用Jacobi椭圆函数展开法[28],得到方程(21)的孤立波解为
(22)
其中k为径向线性波数,c为相速度,且
c2=-α1+α3k2.
类似于付遵涛等的方法[31],利用修正Jacobi椭圆函数展开法求解方程(20)的周期波解和孤立波解.为了计算简单,并且能够解释外源对Rossby波的影响,不妨假设
则方程(20)变为
(23)
令
A(X,T)=B(X,T)+τ(T)，
(24)
其中
将式(24)代入方程(23),整理得到
(25)
注意到,方程(25)是关于时间T的变系数Boussinesq方程.
利用修正Jacobi椭圆函数展开法,假设方程(25)具有如下形式解：
(26)
这里ξ=K(T)[X-C(T)]，其中bj(T)，K(T)，C(T)是关于T的待定函数,sn(ξ,m)是Jacobi椭圆函数,m为Jacobi椭圆函数的模数(0≤m≤1).通过平衡方程(25)的最高阶非线性项和最高阶导数项,得到n=2.于是式(26)可写为
B(X,T)=b0(T)+b1(T)sn ξ+b2(T)sn2 ξ.
(27)
将式 (27)代入方程(25),得到
(28)
(29)
为方便计算，不妨设K(T)为线性波数k，而b0(T)满足方程
b″0(T)-24α3m2k4b0(T)=g(T)，
(30)
其中非齐次项
g(T)=24α3m2k4τ(T)-
(31)
注意到方程(30)是二阶常系数非齐次线性常微分方程,并且给定函数τ(T)后,容易求得方程(30)的解.因此,由式(24)、(27)～(31)联立可以得到方程(23)的周期波解为
(32)
由于sn2 ξ+cn2 ξ=1，并且当m→1，cn ξ→sech ξ，于是得到方程(23)的孤立波解为
(33)
孤立波的波速为
Cs=μα4T.
(34)
孤立波解(33)的解释: 由于方程(30)的非齐次项g(T)含有外源τ(T)和耗散系数μ，因此,解b0(T)中必含有τ(T)与μ，从而说明外源和耗散是影响Rossby孤立波的强迫因素.另外,孤立波解(33)中出现非线性项系数α2，说明推广的β效应和切变基本流是诱导非线性Rossby孤立波的重要因素.从式(34)来看,耗散效应影响Rossby孤立波的波速.因此,孤立波解(33)从理论上进一步说明外源和耗散影响Rossby孤立波的演变和发展.
3 结 论
本文推导了带有外源和耗散强迫的非线性Boussinesq方程去描述非线性Rossby波的振幅演变和发展,通过分析得出推广的β效应和切变基本流是诱导Rossby波的非线性因素.最后,利用修正的Jacobi椭圆函数展开法,得到带有外源和耗散强迫的非线性Boussinesq方程的周期波解和孤立波解,从解的结构进一步分析了外源和耗散影响非线性Rossby波的演变和发展.
[1] LONG R R. Solitary waves in the westerlies[J]. Journal of Atmosphere Science, 1964, 21(3): 197-200.
[2] WADATI M. The modified Korteweg-de Vries equation[J]. Journal of the Physical Society of Japan, 1973, 34(5): 1289-1296.
[3] REDEKOPP L G. On the theory of solitary Rossby waves[J]. Journal of Fluid Mechanics, 1977, 82(4): 725-745.
[4] AMBRIZZI T, HOSKINS B J, HSU H H. Rossby wave propagation and teleconnection patterns in the austral winter[J]. Journal of Atmosphere Science, 1995, 52(21): 3661-3672.
[5] GRIMSHAW R. Nonlinear aspects of long shelf waves[J]. Geophysical & Astrophysical Fluid Dynamics, 1977, 8(1): 3-16.
[6] BENNEY D J. Long nonlinear waves in fluid flows[J]. Journal of Mathematics and Physics, 1966, 45(1): 52-63.
[7] REDEKOPP L G. WEIDMAN P D. Solitary Rossby waves in zonal shear flows and their interactions[J]. Journal of Atmosphere Science, 1978, 35(5): 790-804.
[8] BOYD J P. Equatorial solitary waves, part 1: Rossby solitons[J]. Journal of Physical Oceanography, 1980, 10(11): 1699-1718.
[9] BOYD J P. Equatorial solitary waves, part 2: envelope solitons[J]. Journal of Physical Oceanography, 1983, 13(3): 428-449.
[10] MENG L, LÜ K L. Nonlinear long-wave disturbances excited by localized forcing[J]. Chinese Journal of Computational Physics, 2000, 17(3): 259-267.
[11] ONO H. Algebraic Rossby wave soliton[J]. Journal of the Physical Society of Japan, 1981, 50(8): 2757-2761.
[12] LUO D H. On the Benjamin-Ono equation and its generalization in the atmosphere[J]. Science in China(Series B), 1989, 32(10): 1233-1245.
[13] MAXWORTHY T, REDEKOPP L G. New theory of the great red spot from solitary waves in the Jovian atmosphere[J]. Nature, 1976, 260(5551): 509-511.
[14] 罗德海, 季立人, 大气阻塞形成的一个理论[J]. 中国科学(B辑), 1989, 32(3): 323-333.(LUO Dehai, JI Liren. A theory of blocking formation in the atmosphere[J]. Science in China(Series B), 1989, 32(3): 323-333.(in Chinese))
[15] HOREL J D, WALLACE J M. Planetary-scale atmospheric phenomena associated with the southern oscillation[J]. Monthly Weather Review, 1981, 109(4): 813-829.
[16] 蒋后硕, 吕克利. 切变气流中地形强迫激发的非线性长波[J]. 高原气象, 1998, 17(3): 231-244.(JIANG Houshuo, LÜ Keli. The nonlinear long-wave excited by topography in a shear flow[J]. Plateau Meteorology, 1998, 17(3): 231-244.(in Chinese))
[17] 吕克利, 蒋后硕. 外源和孤波的相互作用对阻塞形成的影响[J]. 应用气象学报, 1998, 9(4): 431-440.(LÜ Keli, JIANG Houshuo. Influences of interaction of external source with solitary wave on blocking[J]. Journal of Applied Meteorological Science, 1998, 9(4): 431-440.(in Chinese))
[18] 张瑞岗, 杨联贵, 宋健, 等. 地形作用下的近赤道非线性Rossby波[J]. 地球物理学进展, 2017, 32(4): 1532-1538.(ZHANG Ruigang, YANG Liangui, SONG Jian, et al. Nonlinear Rossby waves near the equator with topography[J]. Progress in Geophysics, 2017, 32(4): 1532-1538.(in Chinese))
[19] MENG L, LÜ K L. Dissipation and algebraic solitary long-wave excited by localized topography[J]. Chinese Journal of Computational Physics, 2002, 19(2): 259-267.
[20] YANG H W, YIN B S, SHI Y L. Forced dissipative Boussinesq equation for solitary waves excited by unstable topography[J]. Nonlinear Dynamic, 2012, 70(2): 1389-1396.
[21] YANG H W, YANG D Z, SHI Y L, et al. Interaction of algebraic Rossby solitary waves with topography and atmospheric blocking[J]. Dynamics of Atmospheres and Oceans, 2015, 71(5): 21-34.
[22] SONG J, YANG L G. Modified KdV equation for solitary Rossby waves with β effect in barotropic fluids[J]. Chinese Physics B, 2009, 18(7): 2873-2877.
[23] 宋健, 刘全胜, 杨联贵. 切变纬向流中β效应与缓变地形Rossby波[J]. 物理学报, 2012, 61(21): 210510.(SONG Jian, LIU Quansheng, YANG Liangui. Beta effect and slowly changing topography Rossby waves in a shear flow[J]. Acta Physica Sinica, 2012, 61(21): 210510.(in Chinese))
[24] 李少峰, 杨联贵, 宋健. 层结流体中在热外源和β效应地形效应作用下的非线性Rossby孤立波和非齐次Schrödinger方程[J]. 物理学报, 2015, 64(19): 199-201.(LI Shaofeng, YANG Liangui, SONG Jian. Nonlinear solitary Rossby waves with external heating source and β effect topographic effect in stratified flows described by the inhomogeneous Schrödinger equation[J]. Acta Physica Sinica, 2015, 64(19): 199-201.(in Chinese))
[25] 尹晓军, 杨联贵, 宋健, 等. 完整Coriolis力作用下带有外源强迫的非线性KdV方程[J]. 应用数学和力学, 2017, 38(9): 1053-1060.(YIN Xiaojun, YANG Liangui, SONG Jian, et al. The nonlinear KdV equation under external forcing with the complete Coriolis force[J]. Applied Mathematics and Mechanics, 2017, 38(9): 1053-1060.(in Chinese))
[26] LU C N, FU C, YANG H W. Time-fractional generalized Boussinesq equation for Rossby solitary waves with dissipation effect in stratified fluid and conservation laws as well as exact solutions[J]. Applied Mathematics and Computation, 2018, 327(1): 104-116.
[27] HEREMAN W, NUSEIR A. Symbolic methods to construct exact solutions of nonlinear partial differential equations[J]. Mathematics and Computers in Simulation, 1997, 43(1): 13-27.
[28] LIU S K, FU Z T, LIU S D, et al. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations[J]. Physics Letters A, 2001, 289(1): 69-74.
[29] FU Z T, LIU S K, LIU S D, et al. New Jacobi elliptic function expansion and new periodic solutions of nonlinear wave equations[J]. Physics Letters A, 2001, 290(2): 72-76.
[30] TRIKI H, TAHA T R, WAZWAZ A M. Solitary wave solutions for a generalized KdV-mKdV equation with variable coefficients[J]. Mathematics and Computers in Simulation, 2010, 80(9): 1867-1873.
[31] 付遵涛, 刘式达, 刘式适, 等. 含变系数或强迫项的KdV方程的新解[J]. 应用数学和力学, 2004, 25(1): 67-73.(FU Zuntao, LIU Shida, LIU Shikuo, et al. New exact solutions to KdV equations with variable coefficients or forcing[J]. Applied Mathematics and Mechanics, 2004, 25(1): 67-73.(in Chinese))
[32] HONG B D, LU C. New exact solutions for the generalized variable-coefficient Gardner equation with forcing term[J]. Applied Mathematics and Computation, 2012, 219(5): 2732-2738.
[33] PEDLOSKY J. Geophysical Fluid Dynamics[M]. New York: Springer, 1979.
[34] WARN T, BRASNETT B. The amplification and capture of atmospheric solitons by topography: a theory of the onset of regional blocking[J]. Journal of the Atmospheric Sciences, 1983, 40(1): 28-38.