引 言
航天器上使用了火工、弹簧等装置来完成解锁分离功能,这些装置的动作会产生强烈的冲击环境[1-2],对电子产品、轻薄结构、脆性材料的破坏作用比较明显,可能会导致灾难性的后果.航天电子设备中常用的带管脚二极管在冲击环境的作用下,其功能很容易失效,由于长细比较大,可以近似看成一根梁,研究梁在冲击激励下的失效准则,对于航天电子设备抗冲击环境适应性设计具有重要的意义.
关于梁的冲击问题,已有很多研究.Yu等分析了两端固支铝合金梁在质量块撞击作用下的冲击响应[3].Yamamoto等用解析和数值的方法分析了考虑接触变形的小球与Timoshenko梁的撞击问题[4].Maiti等使用高阶剪切变形理论和一阶剪切变形理论分析了复合材料叠层梁的冲击响应[5].陈镕等将运动刚体与受其横向冲击的无约束Timoshenko梁看成一个接触冲击系统,用广义Fourier级数方法推导了系统的特征方程和特征函数,得到了系统冲击响应的解析解[6].邢誉峰等给出了四种边界条件的Timoshenko梁在质点撞击下的冲击响应解析解[7],用间接模态法研究了质点与弹性力学梁的冲击问题[8],给出了质点与有限长Timoshenko梁横向弹性碰撞接触问题的半解析解[9].田金梅等用平面应力模型来模拟复合材料叠层梁,得到了正交各向异性叠层梁的频率和模态函数,并用间接模态叠加法求得了叠层梁遭受刚性圆球冲击的瞬态响应[10].陈万祥等求解了具有黏弹性边界梁在质点横向冲击作用下的响应,说明了黏弹性支承对结构动力响应的影响[11].张嫄等建立了横向冲击荷载作用下悬浮隧道的动力学模型,数值模拟了悬浮隧道跨中的响应,分析了张力腿竖向刚度、冲击物质量、冲击速度对悬浮隧道跨中位移的影响[12].余同希以飞射物撞击构件引起破坏为工程背景,研究了端头带有质量块的悬臂梁受到冲击载荷作用后发生剪切失效的可能性[13].康婷等用数值模拟方法,研究了拱结构在爆炸冲击荷载作用下的弹塑性动力响应[14].
以上的研究都集中于梁的冲击响应研究,对冲击失效准则的研究还很少.本文给出了基础激励下Timoshenko梁冲击失效准则设计方法,建立了基于Timoshenko梁的冲击动力学模型.通过求解系统运动方程并结合边界条件,给出了系统固有频率方程,以及固有振型的计算方法.为了克服基础激励下冲击响应求解的困难,对Timoshenko梁的位移响应进行了假设,求解了系统的线位移和角位移冲击响应,进而得到了任意截面的内力,以及截面的最大von Mises等效应力,基于von Mises屈服准则,给出了分别采用位移、速度和加速度确定失效准则的方法.本文揭示了基础激励下Timoshenko梁在冲击环境作用下的失效机理和失效模式,对于每种失效模式给出了相应的失效准则,可以应用于带管脚的元器件抗冲击环境的适应性设计.
1 研究对象及模型简化
对于带管脚的元器件,其管脚一般焊接在电路板上,管脚的顶端是质量块.将带管脚的元器件简化为一端固支、一端自由的梁,在自由端有集中质量,简化模型及坐标系如图1所示.
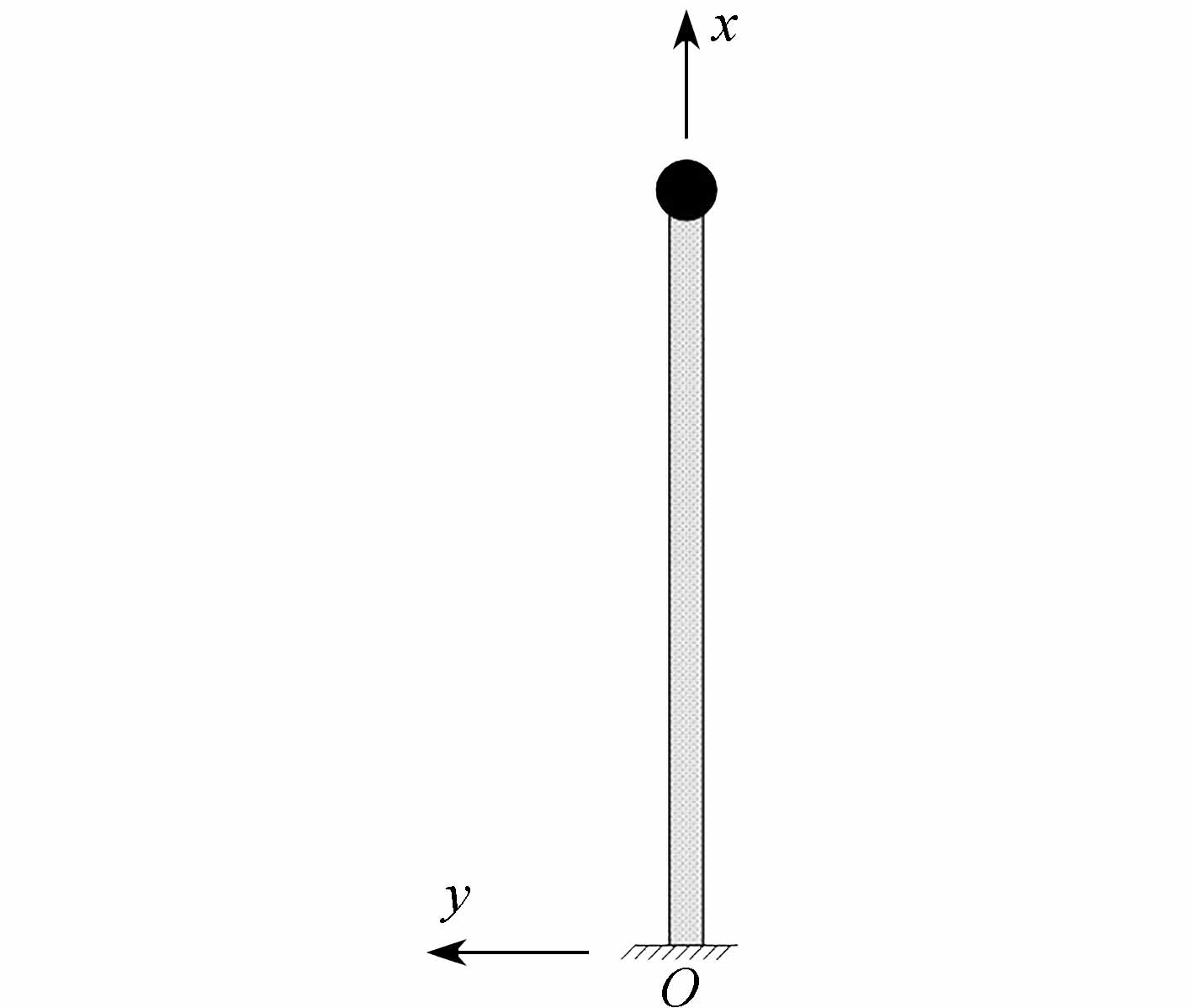
图1 简化后的模型及坐标系
Fig.1 The simplified model and the coordinate system
2 运动方程及边界条件
设梁为等截面梁,其长度为l,截面积为A,密度为ρ,截面绕惯性主轴的惯性矩为I,其横向位移为y(x,t),自由端集中质量为M,转动惯量为J.
采用Timoshenko梁建模,运动方程为
(1)
(2)
式中,y为梁截面的横向线位移,φ为截面角位移,E为弹性模量,G为剪切弹性模量,I为截面惯性矩,A为截面面积,ρ为密度,k为截面剪切系数.
由式(1)、(2)可得
(3)
(4)
梁的边界条件为
y(0,t)=y0(t),φ(0,t)=0,
(5)
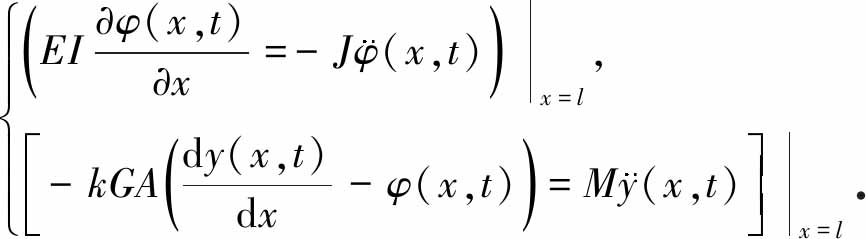
(6)
3 模 态 求 解
梁有约束端的边界条件为
y(0,t)=0,φ(0,t)=0,
(7)
另一端边界条件同式(6).令
y(x,t)=W(x)ejωt.
(8)
将上式代入式(3),可得
(9)
令W(x)=Deλx,代入上式可得
(10)
令
则式(10)的4个根分别为
(11)
其中

(12)
则振型可写为
W(x)=F1cos(a2x)+F2sin(a2x)+F3cosh(a1x)+F4sinh(a1x).
(13)
由式(2)可得
(14)
由式(6)~(8)可得
W=0,at x=0,
(15a)
(15b)
(15c)
(15d)
由式(13)和式(15)可得
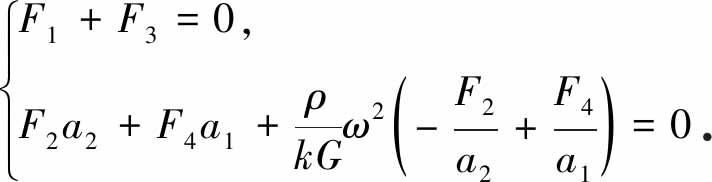
(16)
令
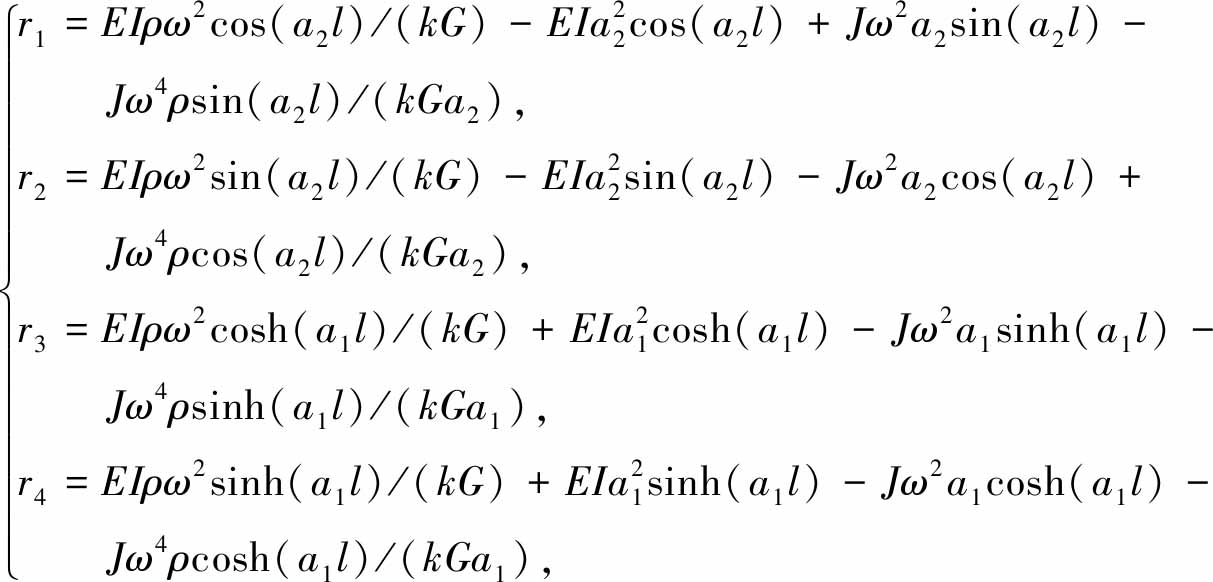
(17)
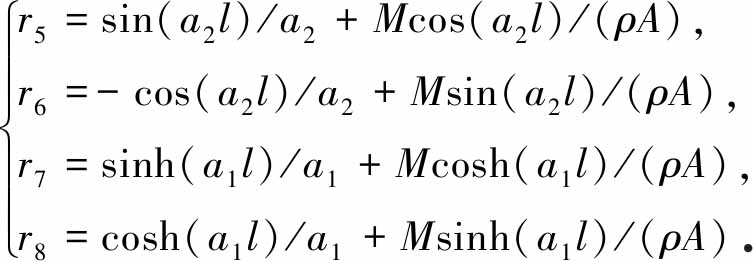
(18)
将式(13)代入式(15),并由式(17)和式(18)可得
(19)
令![]() 由式(16)和式(19)可得系统的频率方程为
由式(16)和式(19)可得系统的频率方程为
(r1-r3)(r6+r8λ)-(r5-r7)(r2+r4λ)=0.
(20)
该方程为超越方程,求解该方程,可得系统的无限阶固有频率,对每阶频率,由式(13)、(16)、(19)、(20)可得对应的振型.
4 冲击响应求解及失效准则设计
设支座的横向位移为
y0(t)=y0sin(ωt),
(21)
式中,y0是支座位移的幅值,ω是支座运动的频率.直接求解支座激励下连续系统的冲击响应较为困难,因此对管脚的线位移和角位移进行假设,令
(22)
式中,f(x)和g(x)为待定的函数.
将式(22)代入式(5)和式(6),可得
f(0)=1,g(0)=0,
(23)
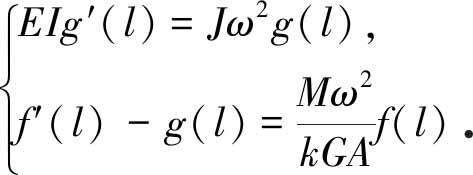
(24)
将式(22)代入式(3)和式(4)中,可得
(25)
(26)
令
则式(25)和式(26)分别可写为
(27)
(28)
令

(29)
则式(27)和式(28)的解可写为
(30)
将式(22)和式(30)代入式(2),可得
-ω2ρA(C1cos(bαx)+C2sin(bαx)+C3cosh(bβx)+C4sinh(bβx))+
kGA[C1b2α2cos(bαx)+C2b2α2sin(bαx)-C3b2β2cosh(bβx)-
C4b2β2sinh(bβx)+(-D1bαsin(bαx)+D2bαcos(bαx)+
D3bβsinh(bβx)+D4bβcosh(bβx))]=0.
(31)
为使得上式成立,需满足
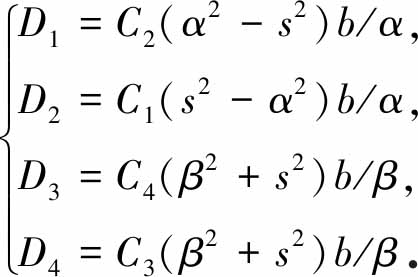
(32)
将式(30)代入边界条件式(5)和式(6),可得
C1+C3=1,D1+D3=0,
(33)
-D1bαsin(bαl)+D2bαcos(bαl)+D3bβsinh(bβl)+D4bβcosh(bβl)=
(34)
-C1bαsin(bαl)+C2bαcos(bαl)+C3bβsinh(bβl)+C4bβcosh(bβl)-
(D1cos(bαl)+D2sin(bαl)+D3cosh(bβl)+D4sinh(bβl))=
(35)
联立式(32)~(35),并令
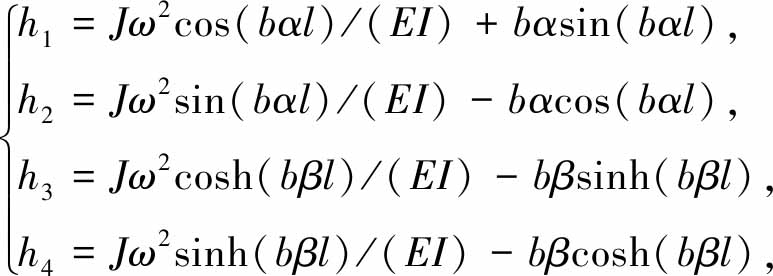
(36)

(37)

(38)
可得
(39)
(40)
由式(32)和式(33),可求得C3,C4和D1~D4,于是f(x)和g(x)可求得.由式(22)可求得线位移y(x,t)和角位移φ(x,t).
求出位移后,可得梁的内力为
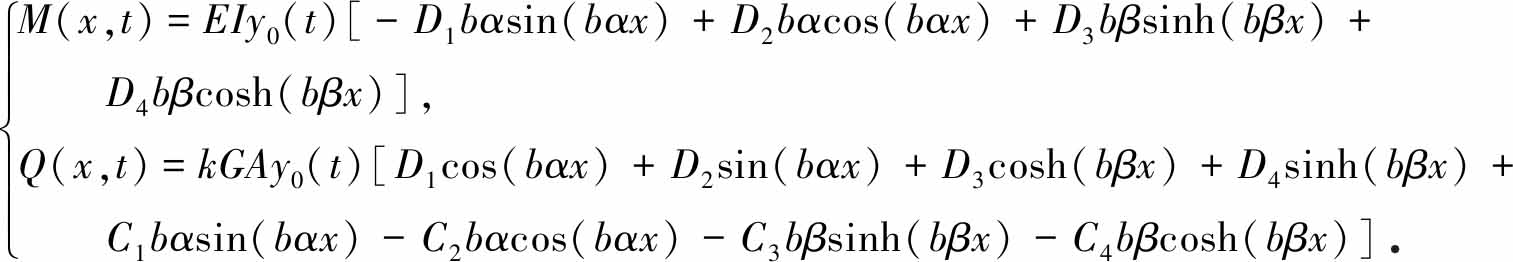
(41)
由式(41)可得梁截面的应力,由von Mises屈服准则可知,当von Mises等效应力σe超过材料的屈服强度时,材料将发生塑性变形,von Mises等效应力σe为
(42)
式中σ1,σ2和σ3为3个主应力,采用式(42)计算截面各位置的von Mises等效应力σe.设材料的屈服强度为σy,由支座的单位位移产生的最大von Mises等效应力为![]() 则为使材料不发生屈服破坏,最大可用的支座位移幅值Ye为
则为使材料不发生屈服破坏,最大可用的支座位移幅值Ye为
(43)
对应的速度幅值Ve和加速度幅值Ae分别为
(44)
(45)
由式(42)~(45)可确定系统的冲击失效准则.
5 算 例
设管脚材料为铝,密度ρ=2 700 kg/m3,弹性模量E=7×1010 Pa,Poisson比ν=0.3,屈服强度σy=300 MPa,管脚长度l=0.01 m,截面形状为圆环,外半径R=2 mm,内半径r=1 mm,M=0.06 kg,J=6×10-6 kg·m2.为了使Timoshenko梁模型计算结果更准确,采用基于应力精确解的梁截面剪切系数计算方法[15],见式(46):
(46)
式中 m=r/R.
用二分法求解式(20)所示的频率方程,令ξ=x/l,设置搜索步长dω=0.01 rad/s,误差为1E-6,计算得到的系统前三阶频率为521.2,1 761.1,100 411.8 Hz,振型见图2.在梁的支座施加冲击激励,激励的形式见式(21),设为半正弦冲击,令y0=1,如图3所示.
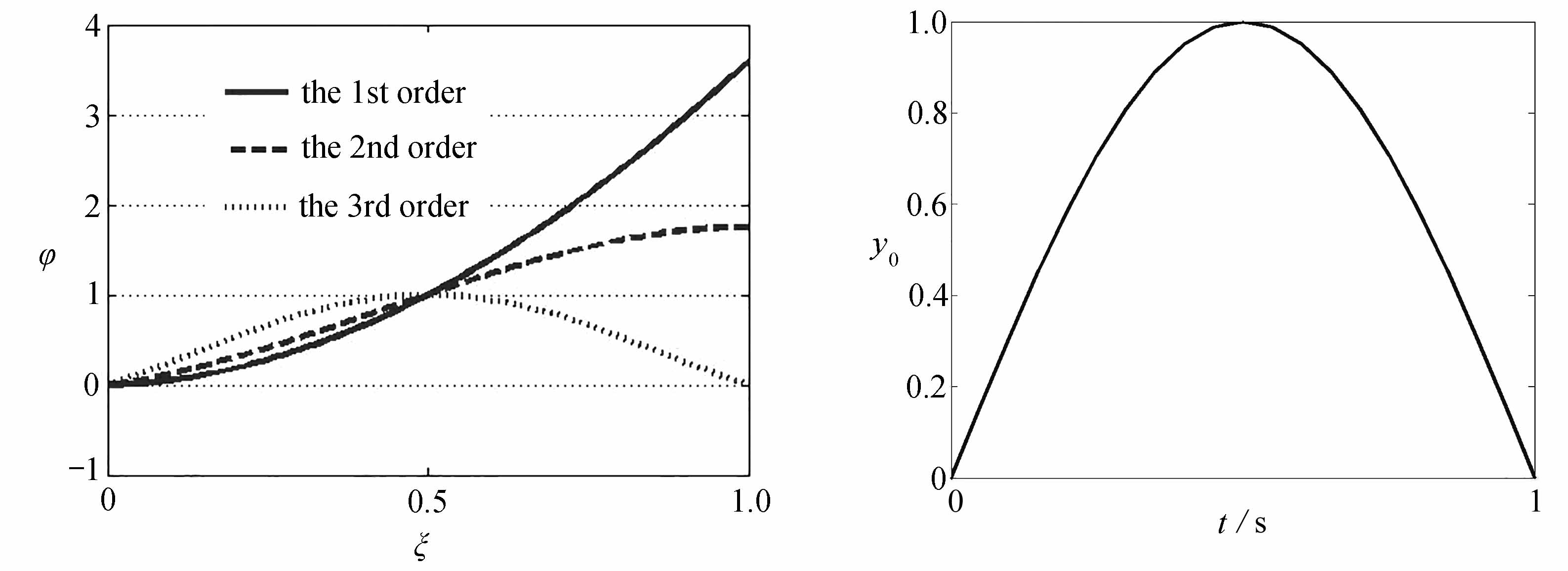
图2 各阶振型 图3 支座冲击激励
Fig.2 Mode shapes Fig.3 The impact excitation at the support
设置不同的激励频率,频率范围为20~5 000 Hz,分别计算管脚各截面的位移响应、内力和von Mises等效应力,记录每个频点管脚的位移、内力和von Mises等效应力.590 Hz下的计算结果见图4~7.
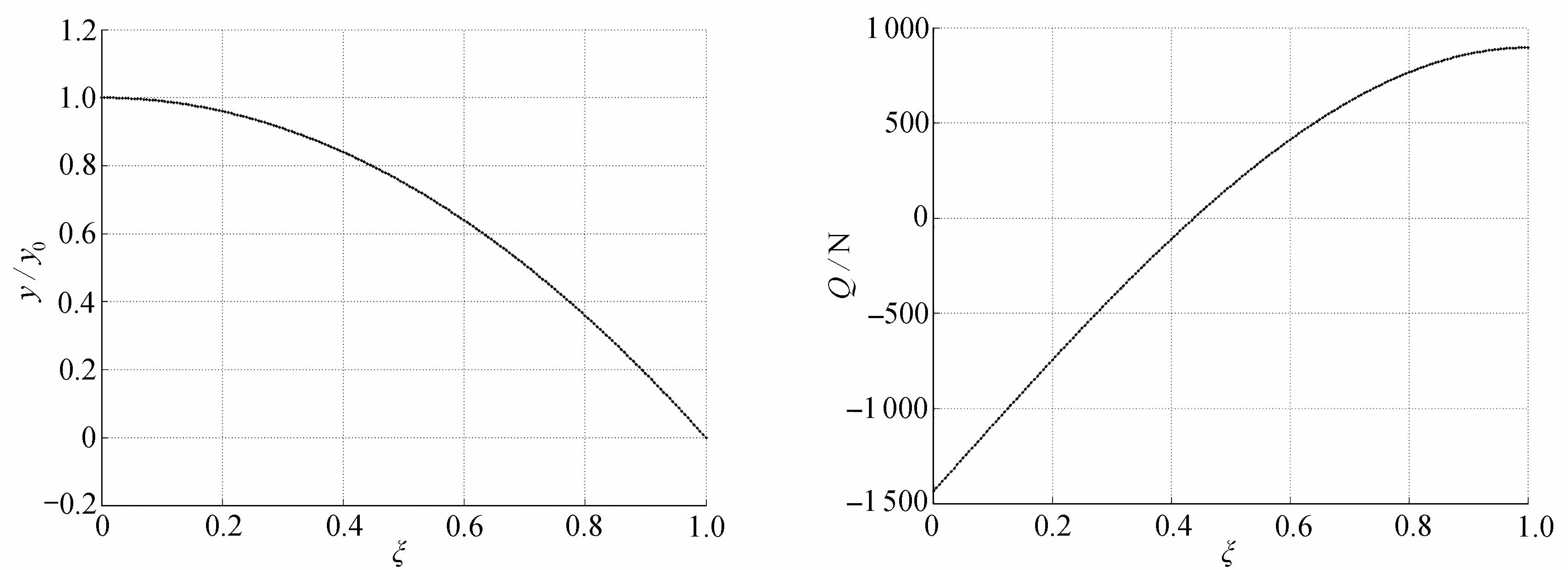
图4 位移计算结果 图5 剪力计算结果
Fig.4 Results of displacements Fig.5 Results of shear forces
计算得到的各频点最大von Mises等效应力见图8,每个频点对应的最大von Mises等效应力出现的相对位置见图9.
图8中的双峰对应于系统的前两阶固有频率.由图9可见,当激励频率低于590 Hz时,最大von Mises等效应力出现于ξ=0处,即管脚根部;当激励频率等于590 Hz时,最大von Mises等效应力出现于管脚中部附近,此时管脚各处的von Mises等效应力相差不大,如图7所示;当激励频率大于590 Hz时,最大von Mises等效应力出现于管脚末端.
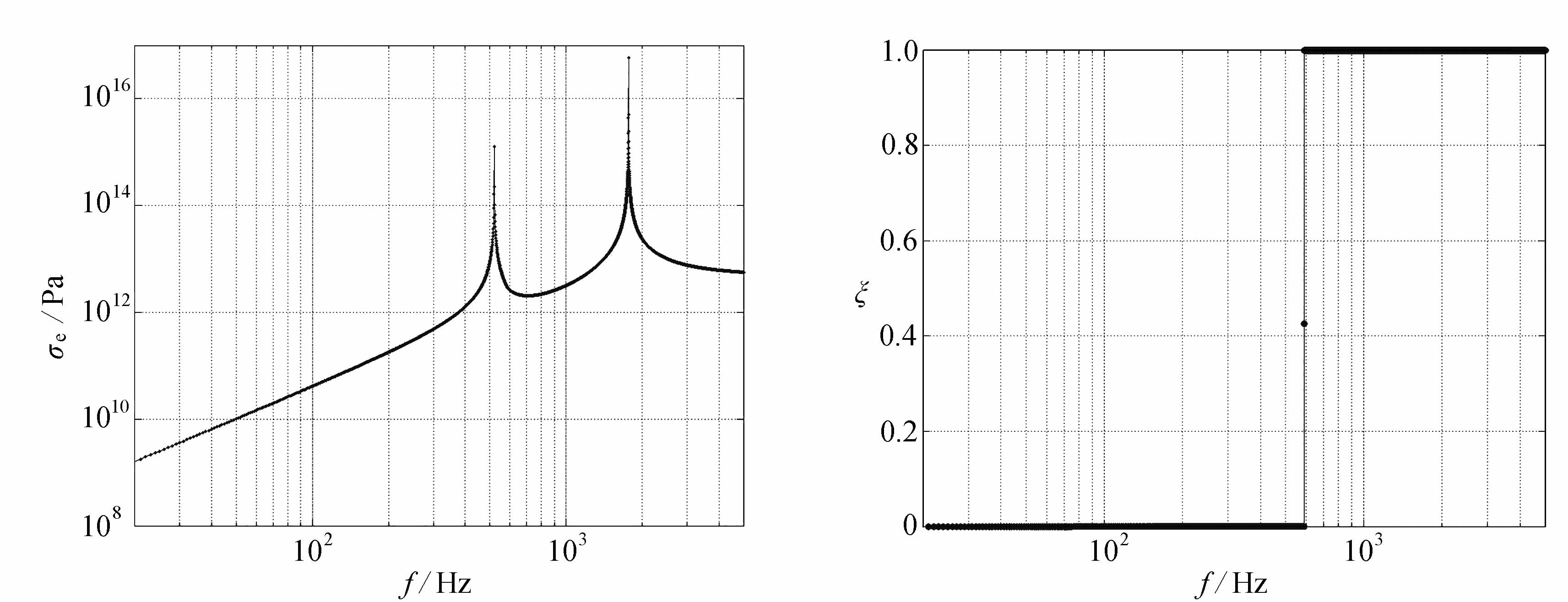
图8 各频点最大von Mises等效应力 图9 最大von Mises等效应力出现的相对位置
Fig.8 Maximum equivalent von Mises stresses at each frequency point Fig.9 Relative positions of maximum equivalent von Mises stresses
为使材料不发生屈服破坏,由屈服强度σy和最大von Mises等效应力,可求出最大可用的支座位移幅值Ye,及对应的速度幅值Ve和加速度幅值Ae,见图10~12.
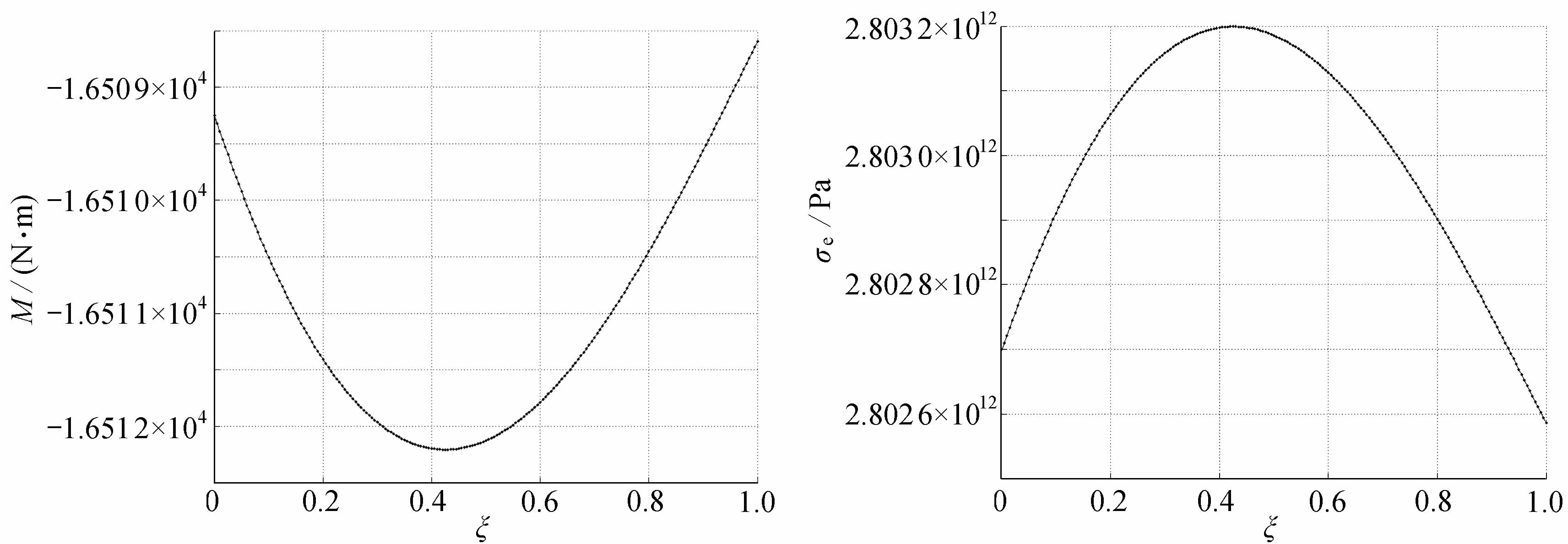
图6 弯矩计算结果 图7 von Mises等效应力计算结果
Fig.6 Results of bending moments Fig.7 Results of equivalent von Mises stresses
由图10~12可知:
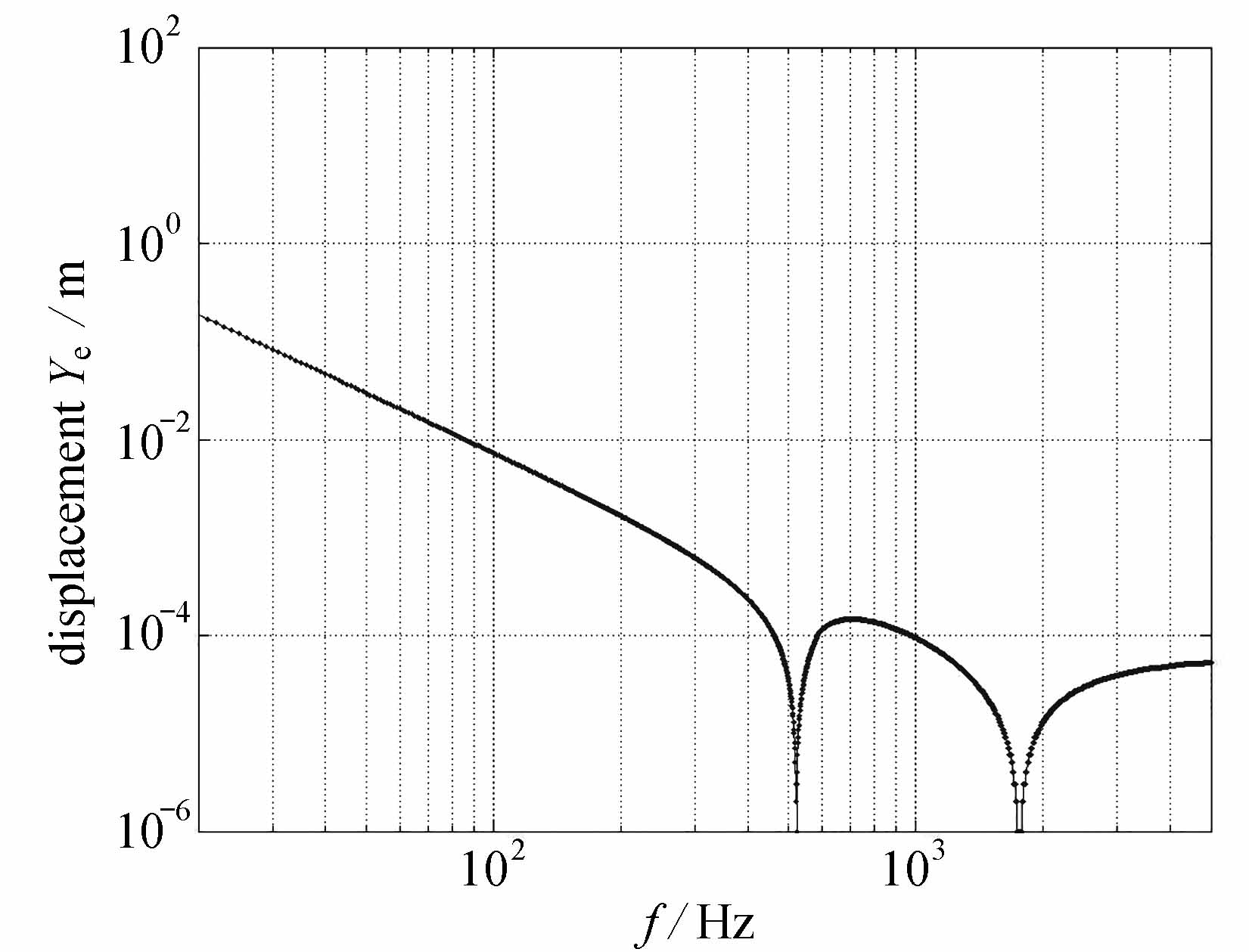
图10 各频点最大可用位移幅值
Fig.10 Maximum available displacement amplitudesat each frequency point
(a) 从20 Hz开始,到系统的一阶固有频率,最大可用位移幅值逐渐减小,最大可用位移幅值在系统前两阶固有频率处达到极小值,当激励频率高于系统第二阶频率,最大可用位移幅值逐渐增加,并逐渐收敛,高频段最大可用位移幅值为0.053 mm;
(b) 从20 Hz开始,到系统的一阶固有频率,最大可用速度幅值逐渐减小,最大可用速度幅值在系统前两阶固有频率处达到极小值,当激励频率高于系统第二阶频率,至5 000 Hz,最大可用速度幅值逐渐增加,高频段最大可用速度幅值为1.671 m/s;
(c) 从20 Hz开始,到200 Hz,最大可用加速度幅值变化平缓,最大可用加速度幅值在系统前两阶固有频率处达到极小值,当激励频率高于系统第二阶频率,最大可用加速度幅值快速增加.
由图9可得,在支座的冲击激励下管脚的失效模式可分为:
(a) 模式Ⅰ,管脚根部发生屈服破坏;
(b) 模式Ⅱ,管脚中部附近发生屈服破坏;
(c) 模式Ⅲ,管脚末端发生屈服破坏.
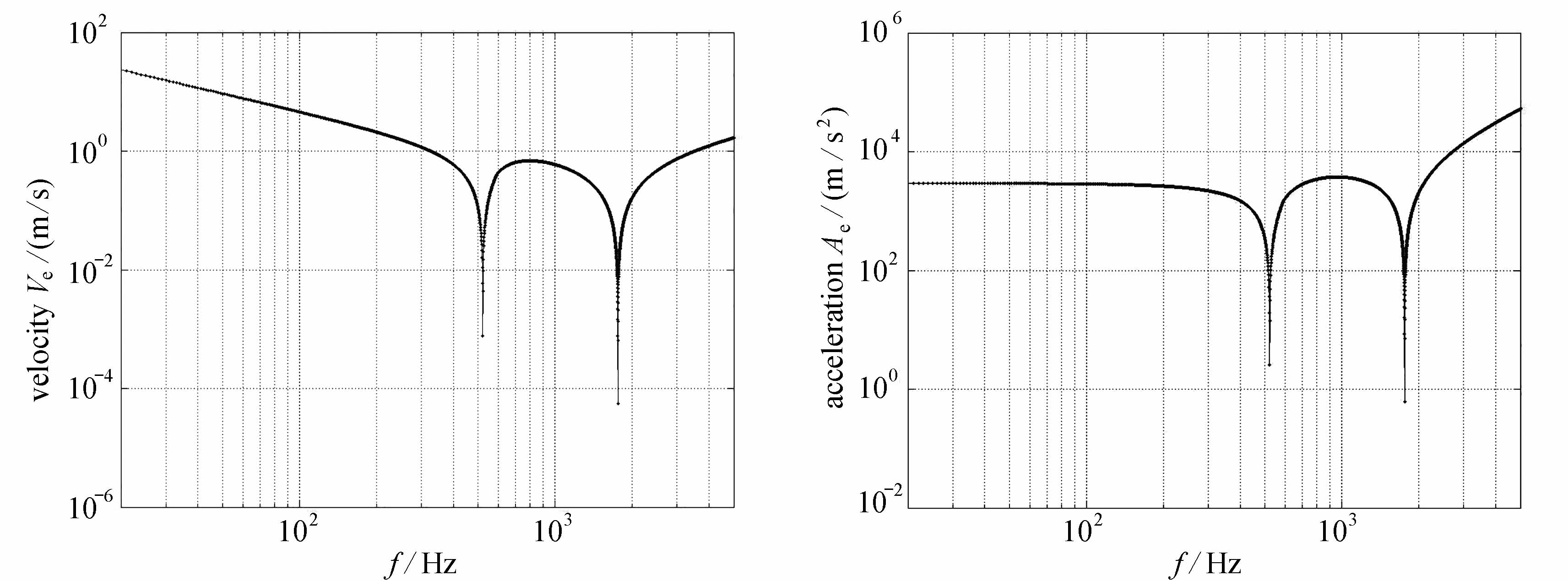
图11 各频点最大可用速度幅值 图12 各频点最大可用加速度幅值
Fig.11 Maximum available velocity amplitudes at each frequency point Fig.12 Maximum available acceleration amplitudes at each frequency point
由图9~12可得,三种失效模式的失效准则分别为:
(a) 当激励频率f<590 Hz,基座位移幅值y0、基座速度幅值v0或基座加速度幅值a0分别达到图10~12中的支座最大可用位移幅值Ye、速度幅值Ve和加速度幅值Ae时,按照模式Ⅰ失效,管脚根部发生屈服破坏;
(b) 当激励频率f达到590 Hz,基座位移幅值y0、基座速度幅值v0或基座加速度幅值a0分别达到图10~12中的支座最大可用位移幅值Ye、速度幅值Ve和加速度幅值Ae时,按照模式Ⅱ失效,管脚中部附近发生屈服破坏;
(c) 当激励频率f>590 Hz,基座位移幅值y0、基座速度幅值v0或基座加速度幅值a0分别达到图10~12中的支座最大可用位移幅值Ye、速度幅值Ve和加速度幅值Ae时,按照模式Ⅲ失效,管脚末端发生屈服破坏.
6 结 论
1) 本文建立了基础激励下Timoshenko梁的冲击动力学模型,可模拟实际工程中相应边界条件梁的冲击响应问题.根据系统的运动方程和边界条件,给出了系统固有频率方程,该方程为超越方程,给出了Timoshenko梁振型的计算方法.
2) 通过对Timoshenko梁截面的线、角位移进行假设,并结合边界条件,求解了其在基础激励下的冲击响应,进一步得到了Timoshenko梁截面的剪力和弯矩.基于von Mises屈服准则,给出了以最大可用基础激励的位移幅值、速度幅值和加速度幅值表示的冲击失效条件.
3) 典型算例的冲击响应计算结果表明,在20~5 000 Hz频率范围内,基础激励下算例中的Timoshenko梁存在3种失效模式,分别是根部、中部附近和末端发生屈服破坏.针对每种失效模式,本文分别给出了以最大可用位移幅值、速度幅值和加速度幅值表示的冲击失效准则.
[1] 高庆,商霖,苏大亮,等.某弹簧分离装置冲击环境统计分析及天地差异性研究[J].振动与冲击,2017,36(17):206-210.(GAO Qing,SHANG Lin,SU Daliang,et al.Shock environment statistical analysis for a spring separate device and shock data difference between flight test and ground one[J].Journal of Vibration and Shock,2017,36(17):206-210.(in Chinese))
[2] 王朋朋,高博,艾永强,等.基于冲击响应分析的星载可展天线解锁策略优化[J].振动与冲击,2017,36(10):57-62.(WANG Pengpeng,GAO Bo,AI Yongqiang,et al.Release strategy optimization for deployable satellite antennas based on shock response analysis[J].Journal of Vibration and Shock,2017,36(10):57-62.(in Chinese))
[3] YU J,JONES N.Numerical simulation of a clamped beam under impact loading[J].Computers &Structures,1989,32(2):281-293.
[4] YAMAMOTO S,SATO K,KOSEKI H.A study on lateral impact of Timoshenko beam[J].Computational Mechanics,1990,6(2):101-108.
[5] KR MAITI D,SINHA P K.Impact behavior of thick laminated composite beams[J].Journal of Reinforced Plastics and Composites,1995,14(3):255-279.
[6] 陈镕,郑海涛,薛松涛,等.无约束Timoshenko梁横向冲击响应分析[J].应用数学和力学,2004,25(11):1195-1202.(CHEN Rong,ZHENG Haitao,XUE Songtao,et al.Analysis on transverse impact response of an unrestrained Timoshenko beam[J].Applied Mathematics and Mechanics,2004,25(11):1195-1202.(in Chinese))
[7] XING Y F,QIAO Y S,ZHU D C,et al.Elastic impact on finite Timoshenko beam[J].Acta Mechanica Sinica(English Series),2002,18(3):252-263.
[8] 邢誉峰,谢文剑,诸德超.厚度效应对梁冲击响应的影响[J].力学学报,2004,36(2):184-190.(XING Yufeng,XIE Wenjian,ZHU Dechao.Influence of thickness effects on impact responses of beam[J].Acta Mechanica Sinica,2004,36(2):184-190.(in Chinese))
[9] 邢誉峰.有限长Timoshenko梁弹性碰撞接触瞬间的动态特性[J].力学学报,1999,31(1):68-74.(XING Yufeng.The characteristics of Timoshenko beam during the process of elastic impact and contact[J].Acta Mechanica Sinica,1999,31(1):68-74.(in Chinese))
[10] 田金梅,邢誉峰,谢文剑.复合材料叠层梁的冲击响应特性[J].振动与冲击,2006,25(4):1-4.(TIAN Jinmei,XING Yufeng,XIE Wenjian.Impact responses of composite laminated beam[J].Journal of Vibration and Shock,2006,25(4):1-4.(in Chinese))
[11] 陈万祥,郭志昆.粘弹性边界梁在低速冲击下的动力响应分析[J].振动与冲击,2008,27(12):69-72.(CHEN Wanxiang,GUO Zhikun.Dynamic responses of beams with flexible supports subjected to low velocity impact[J].Journal of Vibration and Shock,2008,27(12):69-72.(in Chinese))
[12] 张嫄,董满生,唐飞.冲击荷载作用下水中悬浮隧道的位移响应[J].应用数学和力学,2016,37(5):483-491.(ZHANG Yuan,DONG Mansheng,TANG Fei.Displacement responses of submerged floating tunnels under impact loads[J].Applied Mathematics and Mechanics,2016,37(5):483-491.(in Chinese))
[13] 余同希.端头带有质量块的悬臂梁在冲击载荷下的剪切失效[J].爆炸与冲击,1993,13(2):97-104.(YU Tongxi.Shear failure of a cantilever with an attached mass block at the tip under impulsive loading[J].Explosion and Shock Waves,1993,13(2):97-104.(in Chinese))
[14] 康婷,许金余,白应生,等.爆炸冲击荷载作用下拱结构的弹塑性动力响应研究[J].兵工学报,2013,34(9):1097-1102.(KANG Ting,XU Jinyu,BAI Yingsheng,et al.Elastic-plastic analysis on dynamic response of arch subjected to explosive impact[J].Acta Armamentarii,2013,34(9):1097-1102.(in Chinese))
[15] 王乐,王亮.一种新的计算Timoshenko梁截面剪切系数的方法[J].应用数学和力学,2013,34(7):756-763.(WANG Le,WANG Liang.A new method of obtaining Timoshenko’s shear coefficients[J].Applied Mathematics and Mechanics,2013,34(7):756-763.(in Chinese))