引 言
近年来,许多学者对偏微分方程解的连续依赖性进行了广泛的研究,这种对由模型本身系数变化而引起解的变化的研究称之为结构稳定性研究,有关结构稳定性的本质可见文献[1].通过这种结构稳定性的研究,可以帮助我们了解模型在物理中的适用性.由于在实际的建模过程中,数据的测量和计算都会不可避免地产生误差,所以我们需要知道一个微小的误差能否引起解的急剧变化,因而结构稳定性研究是非常有必要的.
多孔介质在我们生活中是广泛存在的,多孔介质中流体方程组的解的性态研究已经成为数学与力学领域的热点问题.目前已有的研究主要是集中在Brinkman和Darcy、Forchheimer方程组的模型上.在Nield和Bejan[2]、Straughan[3]的书中广泛地讨论了多孔介质中的这些模型.文献[4-7]讨论了Brinkman、Darcy、Forchheimer和其他多孔介质方程的Saint-Venant原则,但主要是研究多孔介质中的流体方程组的空间衰减估计结果.关于多孔介质中的流体方程组,Franchi和Straughan[5]、Payne和Straughan[6]、Lin和Payne[7]进行了一些研究.近年来,文献[8-21]取得了一些新的结果.下面我们给出含有速度、压力、温度以及浓度扰动的方程组(见文献[22-23]):
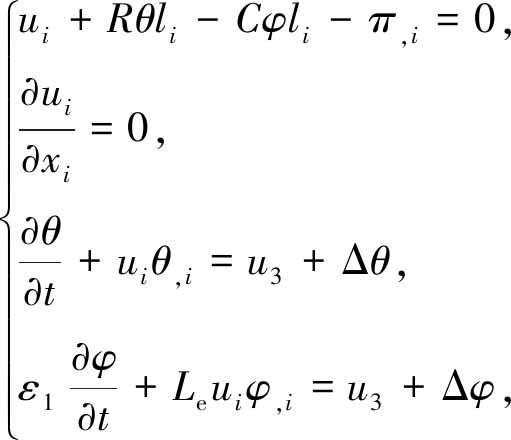
(1)
其中ui,θ,φ,π分别表示速度、温度、浓度扰动和压强,Δ为Laplace算子.在方程组(1)中,R是Rayleigh数,C是盐度Rayleigh数,ε1代表孔隙度,Le是Lewis数,l=(0,0,1)=(l1,l2,l3).方程组(1)在Ω×[0,τ]区域内成立,其中Ω是R3中一个有界单连通的星形区域,τ是给定的常数且0≤τ<∞.
边界条件为
(2)
此外,初始条件为
φ(x,0)=φ0(x),θ(x,0)=θ0(x),x∈Ω.
(3)
本文结构如下:首先在第一节我们得到一些有用的先验估计;其次在第二节借助先验估计的结果,构建了解的差所满足的微分不等式,通过积分该不等式得到了我们需要的结构稳定性结果.对于双扩散扰动模型的结构稳定性研究,目前还没有任何文献涉及.由于式(1)中的温度方程与Brinkman方程组不同,导致无法得到温度的最大值,同时由于速度方程组不含Laplace项,导致速度梯度的估计难度加大,文中通过其他一些估计较好地克服了这些困难.
本文采取以下符号约定,用逗号表示求偏导,用“,i”表示对xi求偏导,如u,i表示∂u/∂xi,重复指标表示求和,
1 先 验 估 计
引理1 对于速度ui,温度θ,浓度扰动φ,有以下估计:
(4)
(5)
其中n2(t),n3(t)是稍后定义的大于零的函数.
证明 在方程(1)1两边同时乘以2ui,并在Ω上积分,由散度定理和式(2),可得
(6)
在方程(1)3两边同时乘以2θ,并在Ω上积分,由散度定理,可得
(7)
由式(2)和Hölder不等式,可得
(8)
联合式(7)和(8),可得
(9)
在方程(1)4两边同时乘以2φ,并在Ω上积分,由散度定理和式(2),可得
(10)
联合式(6)、(9)和(10),可得
(11)
令
对式(11)从0到t积分,可得
F1(t)≤m1![]() F1(η)dη+D1(t).
F1(η)dη+D1(t).
(12)
对于式(12),由Gronwall不等式,可得
F1(t)≤m1em1t![]() D1(η)e-m1ηdη=n1(t).
D1(η)e-m1ηdη=n1(t).
(13)
将式(13)代入式(6),可得
(14)
将式(13)代入式(11),可得
(15)
引理2 对于任意函数ω=ω(x,t),(x,t)∈Ω×[0,τ],有以下估计:
(16)
其中ε0是任意大于零的常数.
证明 对于任意函数ω=ω(x,t),(x,t)∈Ω×[0,τ],由散度定理,可得
![]()
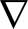 ω)dx.
ω)dx.
(17)
设m=min∂Ω xini>0,d2=maxΩ xixi,由于Ω是有界单连通的星形区域,所以有
![]()
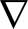 ω)dx.
ω)dx.
(18)
对式(18)利用Schwarz不等式,可得
(19)
由式(19)即可得到式(16)的结果.
引理3 对于速度ui,温度θ,浓度扰动φ,有以下估计:
(20)
(21)
(22)
其中n5(t),n6(t),n7(t)是稍后定义的大于零的函数.
证明 显然,有
(23)
对于具有有界边界的区域Ω,有
(24)
其中k0是取决于∂Ω的Gauss曲率大于零的常数(见文献[24]).
当ω=ui,ε0=2k0时,联合式(16)、(23)和(24),可得
(25)
由方程(1)1,有
由上式,可知
(26)
联合式(14)、(15)、(25)和(26),可得
(27)
利用文献[25]的结果,有
(28)
其中M是大于零的常数.
在式(28)中,令ω=u,可得
(29)
在式(28)中,令ω=θ,可得
(30)
在式(28)中,令ω=φ,可得
(31)
2 Le的连续依赖性
设(ui,θ,φ,π)为Le=Le1时方程(1)~(3)的解,![]() 为Le=Le2时方程(1)~(3)的解.假设
为Le=Le2时方程(1)~(3)的解.假设![]() 则
则![]() 满足下列方程组:
满足下列方程组:

(32)
边界条件为
(33)
此外,初始条件为
(34)
引理4 对于速度差ωi,有以下估计:
(35)
证明 由方程(32)1,有
由上式,可知
定理1 设(ui,θ,φ,π)为Le=Le1时初边值问题(1)~(3)的经典解,![]() 为Le=Le2时初边值问题(1)~(3)的经典解,
为Le=Le2时初边值问题(1)~(3)的经典解,![]() 是这两个解的差,当Lewis数差
是这两个解的差,当Lewis数差![]() 趋于0时,解(ui,θ,φ,π)收敛于解
趋于0时,解(ui,θ,φ,π)收敛于解![]() 且它们解的差
且它们解的差![]() 满足
满足
(36)
其中m3,m4是大于零的常数.
证明 在方程(32)1两边同时乘以2ωi,并在Ω上积分,由散度定理和式(33),可得
由上式,可知
(37)
在方程(32)3两边同时乘以![]() 并在Ω上积分,由散度定理,可得
并在Ω上积分,由散度定理,可得
(38)
对于式(38)右边第二项,由散度定理和式(33),可得
(39)
对于式(38)右边第三项,由散度定理和式(33),可得
(40)
对于式(38)右边第四项,由散度定理和式(33),可得
由上式可知
(41)
联合式(38)~(41),可得
(42)
联合式(16)、(24)和(28),可得
(43)
其中![]()
对式(42)从0到t积分,可得
(44)
其中![]()
在方程(32)4两边同时乘以![]() 并在Ω上积分,由散度定理和式(33),可得
并在Ω上积分,由散度定理和式(33),可得
(45)
对于式(45)右边第二项,由散度定理和式(33),可得
(46)
联合式(45)和(46),并由Hölder不等式,可得
(47)
对式(47)从0到t积分,可得
(48)
其中![]()
联合式(37)、(44)和(48),可得
(49)
其中γ1,γ2,γ3是任意大于零的常数.
令
当![]() 时,有
时,有
由Gronwall不等式,可得
(50)
将式(50)代入式(37),可得
(51)
其中![]()
联合式(50)和(51),可得
(52)
3 结 论
本文研究了多孔介质中一类双扩散扰动模型解对Lewis数Le的连续依赖性结果.采用文中的方法,同样可以研究多孔介质中其他类流体方程组的结构稳定性.对于多孔介质中的流体力学方程组来说,结构稳定性的研究显得至关重要.如果方程组中系数的一个微小变化将导致方程组解的急剧变化,那就说明该模型用来描述多孔介质流体的流动情况是不够精确的.而本文的结果表明,方程组(1)~(3)中的构建系数Lewis数Le的微小变化不会引起解的巨大变化,反映了多孔介质中的一类双扩散扰动模型的解对Lewis数Le的敏感程度,也说明了用方程组(1)~(3)来描述多孔介质中流体的流动情况是精确的.
致谢 本文作者衷心感谢广东财经大学华商学院校内导师制项目(2019HSDS28)对本文的资助.
[1] AMES K A,STRAUGHAN B.Non-Standard and Improperly Pose Problems[M].San Diego:Academic Press,1997.
[2] NIELD D A,BEJAN A.Convection in Porous Media[M].New York:Springer,1992.
[3] STRAUGHAN B.Stability and Wave Motion in Porous Media[M].New York:Springer,2008.
[4] PAYNE L E,SONG J C.Spatial decay in a double diffusive convection problem in Darcy flow[J].Journal of Mathematical Analysis and Applications,2007,330:864-875.
[5] FRANCHI F,STRAUGHAN B.Continuous dependence and decay for the Forchheimer equations[J].Proceedings of the Royal Society A:Mathematical,Physical and Engineering Sciences,2003,459:3195-3202.
[6] PAYNE L E,STRAUGHAN B.Structural stability for the Darcy equations of flow in porous media[J].Proceedings of the Royal Society A:Mathematical,Physical and Engineering Sciences,1998,454:1691-1698.
[7] LIN C,PAYNE L E.Structural stability for a Brinkman fluid[J].Mathematical Methods in the Applied Sciences,2007,30:567-578.
[8] CHEN W H,LIU Y.Structural stability for a Brinkman-Forchheimer type model with temperature dependent solubility[J].Boundary Value Problems,2016,2016.DOI:10.1186/s13661-016-0558-y.
[9] CICHON M,STRAUGHAN B,YANTIR A.On continuous dependence of solutions of dynamic equations[J].Applied Mathematics and Computation,2015,252:473-483.
[10] MA H P,LIU B.Exact controllability and continuous dependence of fractional neutral integro-differential equations with state-dependent delay[J].Acta Mathematica Scientia(English Series),2017,37(1):235-258.
[11] WU H L,REN Y,HU F.Continuous dependence property of BSDE with constraints[J].Applied Mathematics Letters,2015,45:41-46.
[12] HARFASH A J.Structural stability for two convection models in a reacting fluid with magnetic field effect[J].Annales Henri Poincaré,2014,15:2441-2465.
[13] LI Y,LIN C.Continuous dependence for the nonhomogeneous Brinkman-Forchheimer equations in a semi-infinite pipe[J].Applied Mathematics and Computation,2014,244:201-208.
[14] LIU Y,XIAO S Z.Structural stability for the Brinkman fluid interfacing with a Darcy fluid in an unbounded domain[J].Nonlinear Analysis:Real World Applications,2018,42:308-333.
[15] LIU Y,XIAO S Z,LIN Y W.Continuous dependence for the Brinkman-Forchheimer fluid interfacing with a Darcy fluid in a bounded domain[J].Mathematics and Computers in Simulation,2018,150:66-82.
[16] LIU Y.Continuous dependence for a thermal convection model with temperature dependent solubility[J].Applied Mathematics and Computation,2017,308:18-30.
[17] 李远飞.大尺度海洋大气动力学三维黏性原始方程对边界参数的连续依赖性[J].吉林大学学报(理学版),2019,57(5):1053-1059.(LI Yuanfei.Continuous dependence on boundary parameters for three-dimensional viscous primitive equation of large scale ocean atmospheric dynamics[J].Journal of Jilin University(Science Edition),2019,57(5):1053-1059.(in Chinese))
[18] 李远飞.原始方程组对粘性系数的连续依赖性[J].山东大学学报(理学版),2019,54(12):12-23.(LI Yuanfei.Continuous dependence on the viscosity coefficient for the primitive equations[J].Journal of Shandong University(Science Edition),2019,54(12):12-23.(in Chinese))
[19] 李远飞,郭连红.具有边界反应Brinkman-Forchheimer型多孔介质的结构稳定性[J].高校应用数学学报,2019,34(3):315-324.(LI Yuanfei,GUO Lianhong.Structural stability on boundary reaction terms in a porous medium of Brinkman-Forchheimer type[J].Applied Mathematics:a Journal of Chinese Universities,2019,34(3):315-324.(in Chinese))
[20] 李远飞.海洋动力学中二维黏性原始方程组解对热源的收敛性[J].应用数学和力学,2020,41(3):339-352.(LI Yuanfei.Convergence results on heat source for 2D viscous primitive equations of ocean dynamics[J].Applied Mathematics and Mechanics,2020,41(3):339-352.(in Chinese))
[21] CIARLETTA M,STRAUGHAN B,TIBULLO V.Structural stability for a thermal convection model with temperature dependent solubility[J].Nonlinear Analysis:Real World Applications,2015,22:34-43.
[22] STRAUGHAN B.Anisotropic inertia effect in microfluidic porous thermosolutal convection[J].Microfluidics and Nanofluidics,2014,16:361-368.
[23] STRAUGHAN B.Heated and salted below porous convection with generalized temperature and solute boundary conditions[J].Transport in Porous Media,2020,131:617-631.
[24] WEATHERBURN C E.Differential Geometry of Three Dimensions[M].London:Cambridge University Press,1980.
[25] LIN C,PAYNE L E.Continuous dependence on the Soret coefficient for double diffusive convection in Darcy flow[J].Journal of Mathematical Analysis and Applications,2008,342(1):311-325.